Sensitivity and specificity of normality tests and consequences on reference interval accuracy at small sample size: a computer-simulation study
Abstract
Background
According to international guidelines, parametric methods must be chosen for RI construction when the sample size is small and the distribution is Gaussian. However, normality tests may not be accurate at small sample size.
Objectives
The purpose of the study was to evaluate normality test performance to properly identify samples extracted from a Gaussian population at small sample sizes, and assess the consequences on RI accuracy of applying parametric methods to samples that falsely identified the parent population as Gaussian.
Methods
Samples of n = 60 and n = 30 values were randomly selected 100 times from simulated Gaussian, lognormal, and asymmetric populations of 10,000 values. The sensitivity and specificity of 4 normality tests were compared. Reference intervals were calculated using 6 different statistical methods from samples that falsely identified the parent population as Gaussian, and their accuracy was compared.
Results
Shapiro–Wilk and D'Agostino–Pearson tests were the best performing normality tests. However, their specificity was poor at sample size n = 30 (specificity for P < .05: .51 and .50, respectively). The best significance levels identified when n = 30 were 0.19 for Shapiro–Wilk test and 0.18 for D'Agostino–Pearson test. Using parametric methods on samples extracted from a lognormal population but falsely identified as Gaussian led to clinically relevant inaccuracies.
Conclusions
At small sample size, normality tests may lead to erroneous use of parametric methods to build RI. Using nonparametric methods (or alternatively Box–Cox transformation) on all samples regardless of their distribution or adjusting, the significance level of normality tests depending on sample size would limit the risk of constructing inaccurate RI.
Introduction
Per definition, an RI is an estimation of percentile limits of a reference population.1 The 2.5% and 97.5% quantile values of the reference population are usually the limits that are estimated by the RI.2 Unfortunately, the true value of these percentiles cannot be known, as reference limits are determined from only a sample of the population.3 Various statistical methods have been described to estimate the population quantiles and subsequently determine RI limits.3 There are usually 2 possible ways to conduct this statistical analysis: the parametric and the nonparametric approach. In theory, the parametric approach might be better, because it does not require a large sample of animals.4 However, it can be applied only if the analyte level has a Gaussian distribution, and this widely limits its use. Transformation may be attempted when the analyte level does not have a Gaussian distribution.5 If data Gaussianity cannot be achieved despite transformation attempts, alternative methods, such as a nonparametric approach, which does not assume the distribution of analyte level in the reference population6, 7, or the robust method, which is based on iterative processes that estimate the median and spread of the distribution, may be used.6, 8
Guidelines, which clearly indicate which statistical technique should be used based on the size of the sample, have been developed by the American Society of Veterinary Clinical Pathologists (ASVCP).6 When at least 120 reference subjects are included in the sample, the nonparametric method should be used.6 When the sample size is between 20 and 120 animals, the data distribution should be considered before selecting a statistical technique.6 If the data distribution appears Gaussian, the guidelines recommend the parametric method.6 Otherwise, the robust method is the statistical technique of choice.6 Alternatively, the nonparametric method may still be used as long as more than 40 subjects are included.6
The ASVCP guidelines recommend the use of goodness-of-fit tests (also called normality tests) to assess data Gaussianity.6 As data distribution is critical for decision-making, these goodness-of-fit tests should be reliable, in order to ascertain optimal RI accuracy. However, several studies have reported a poor power of these tests, especially at small sample size (ie, below 30–60 subjects).9-11 Clinicians may be unfamiliar with the concept of power, as they are likely more used to dealing with sensitivities and specificities. To the author's knowledge, sensitivity and specificity have not been reported for these normality tests.
The primary objective of this study was, therefore, to determine the sensitivity and specificity for the 4 goodness-of-fit tests recommended in the ASVCP guidelines. In the event of low specificity, some samples will be identified as Gaussian when the original population is actually not Gaussian. A secondary objective of this study was to evaluate the consequences on RI accuracy of using the parametric method improperly on those samples derived from a population incorrectly identified as Gaussian.
Material and Methods
Creation of study populations and samples
A reference population is defined as a hypothetical group consisting of all possible healthy individuals selected for testing.3 Three different analyte population distributions (Gaussian, lognormal, and asymmetric skewed to the left) were simulated using the statistical software of the public domain R version 3.1.1 (Vienna, Austria). Each population was composed of 10,000 values. In order to be clinically relevant, statistical parameters of the distribution of canine glucose values described in a textbook were used to build the Gaussian population distribution (mean: 96.429; SD: 14.619; minimum: 57; maximum: 136).12 The 2 other distributions were constructed based on parameters of the distribution of canine ALT activity values described in a textbook (mean: 4.0801; SD: 0.4759; minimum: 2.8904; maximum: 5.2149), and adjusted to form a lognormal distribution and an asymmetric distribution skewed to the left.12 Noise was added to each value using the jitter function of the software.
A reference sample is a number of individuals extracted from the reference population and that are supposed to be representative of that population.3 For each of the 3 populations of values, samples of 2 different sizes (n = 60 and n = 30) were constructed 100 times by randomly selecting values from the population. Replacement was not authorized inside the same sample, so that the same value could not be chosen twice in the same sample.
Determination of the 2.5% and 97.5% quantiles of the populations, and construction of the RI of the samples
For each population of values, the 2.5% and 97.5% quantiles were determined using the quantile function of the software. These quantiles represented the ‘true’ values that RI were estimating. For each sample, 95% RI were determined using 6 different methods: bootstrap method, nonparametric method, and parametric and robust methods on untransformed and Box–Cox-transformed data.
The bootstrap method was adapted from the methods described earlier.13, 14 One hundred thousand bootstrap samples were built by sampling values with replacement from the original data sample. Each bootstrap sample had the same number of values as the original data sample. The 2.5% and 97.5% quantiles were determined for each bootstrap sample, resulting in 2 vectors of 100,000 2.5% quantile values and 97.5% quantile values, respectively. The median value of these 2 vectors represented the bootstrap estimate of the lower and upper limits of the RI of the original data sample.
The refLimit function of the statistical software was used to build RI by the nonparametric, parametric, and robust methods. When nonparametric reference limits are determined from fewer than 40 values, the limits must be interpolated from the existing values. When RI were built using the parametric and robust methods, the data were either used untransformed from the samples, or were preliminarily Box–Cox-transformed using the bxcx function of the software. The Box–Cox transformation is a parametric power transformation used to move a variable toward normality. The best power transformation is statistically determined in order to optimize the efficacy of normalizing data, regardless of whether they are right- or left-skewed.15 The power transformation parameter was determined via the powerTransform function of the software.
Measures of the accuracy of reference intervals
The accuracy of the RI was determined for each sample and for each statistical method by calculating the absolute distance between the limits of the RI and the 2.5% or 97.5% quantile value of the original population.
Statistical analysis
Gaussianity of the samples was determined by 4 goodness-of-fit tests: the Shapiro–Wilk test, the Kolmogorov–Smirnov test, the D'Agostino–Pearson test, and the Anderson–Darling test. If the P-value associated with these tests was >.05, the sample was considered Gaussian. The sensitivity of each test was calculated from the proportion of samples that correctly identified the parent population as Gaussian among all the samples that came from the Gaussian population. The specificity of each test was calculated from the proportion of samples that correctly identified the parent population as non-Gaussian among all the samples that came from the non-Gaussian populations. The sensitivities and specificities of the goodness-of-fit tests were compared using the McNemar test and were considered significantly different from each other when P < .05.
As the hypothesis was that the performance of the goodness-of-fit tests would not allow the proper distinction between Gaussian and non-Gaussian parent population from the samples using the method described herein, a receiver operating characteristic (ROC) curve analysis was planned to identify the best significance threshold for each test to accept or reject the null hypothesis (ie, the distribution of the parent population of the sample is Gaussian).
Finally, for each of the 3 populations and for each of the 2 sample sizes, the distance between the quantile values of the original population and the limits of the RI when obtained by the different statistical methods were compared using paired Wilcoxon tests. When the original populations were not Gaussian, only the RI limits of the samples identified as Gaussian by the Shapiro–Wilk test (significance level P < .05) were used to compare the different statistical techniques. The Shapiro–Wilk test was preferred over the other goodness-of-fit tests for this purpose because it was previously identified as the one with the best performance at small sample size.9-11 When the original population was Gaussian, all the samples were included in the analysis. In order to limit type-I error exhaustion, only the comparisons between the parametric method on raw data and the 5 other methods and between the robust method on raw data and the 5 other methods were performed. Indeed, the parametric and robust methods on raw data would be the recommended statistical techniques in this situation according to the ASVCP guidelines (small samples identified as Gaussian).6 Bonferroni adjustment of the P-value was applied, leading to a P-value of .01 (.05 divided by 5) considered as significant.
Results
Study populations
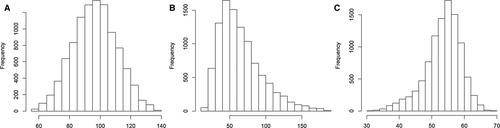
The histograms showing the 3 analyte population distributions are shown in Figure 1. The 2.5% and 97.5% quantile values were 68.6 and 124.5, respectively, for the Gaussian-distributed population, 24.6 and 141.9, respectively, for the lognormal-distributed population, and 39.9 and 62.6, respectively, for the asymmetrically distributed population.
Sensitivity and specificity of the normality tests
The sensitivities and specificities of the goodness-of-fit tests at sample size n = 60 and n = 30 are presented in Table 1A and B, respectively.
| Number of Samples Properly Classified | Sensitivity | Specificity | |||
|---|---|---|---|---|---|
| Gaussian Population | Lognormal Population | Asymmetric Population | |||
| (a) n = 60 | |||||
| Shapiro–Wilk test | 100/100 | 90/100 | 51/100 | 1 | 0.70a |
| Kolmogorov–Smirnov test | 99/100 | 65/100 | 38/100 | 0.99 | 0.51a,b,c |
| D'Agostino–Pearson test | 99/100 | 87/100 | 61/100 | 0.99 | 0.74b |
| Anderson–Darling test | 99/100 | 83/100 | 46/100 | 0.99 | 0.64a,b,c |
| (b) n = 30 | |||||
| Shapiro–Wilk test | 98/100 | 59/100 | 44/100 | 0.98 | 0.51a |
| Kolmogorov–Smirnov test | 97/100 | 32/100 | 30/100 | 0.97 | 0.31a,b,c |
| D'Agostino–Pearson test | 98/100 | 56/100 | 45/100 | 0.98 | 0.50b |
| Anderson–Darling test | 97/100 | 54/100 | 35/100 | 0.97 | 0.44a,c |
- Statistical significance is indicated by different letters (a,b,c); significance level at P < .05; McNemar test. a = significantly different from Shapiro–Wilk test; b = significantly different from D'Agostino–Pearson test; c = significantly different between Kolmogorov–Smirnov test and Anderson–Darling test.
For a sample size of 60 subjects, there was no statistically significant difference in terms of sensitivity among the goodness-of-fit tests. The Shapiro–Wilk test was significantly more specific to properly reject Gaussianity than the Kolmogorov–Smirnov and Anderson–Darling tests (specificity = 0.70, 0.51, and 0.64 respectively; P < .001 and .002, respectively). The D'Agostino–Pearson test was significantly more specific than the Kolmogorov–Smirnov and Anderson–Darling tests (specificity = 0.74, 0.51, and 0.64 respectively; P < .001 for both comparisons). There was no statistically significant difference in terms of sensitivity and specificity between the Shapiro–Wilk and D'Agostino–Pearson tests.
For a sample size of 30 subjects, there was no statistically significant difference in terms of sensitivity among the goodness-of-fit tests. The Shapiro–Wilk test was significantly more specific to properly reject Gaussianity than the Kolmogorov–Smirnov and Anderson–Darling tests (specificity = 0.51, 0.31, and 0.44 and P-value < .001 and .004, respectively). The D'Agostino–Pearson test was significantly more specific than the Kolmogorov–Smirnov (specificity = 0.50 and 0.31, respectively and P < .001). There was no statistically significant difference in terms of sensitivity and specificity between the Shapiro–Wilk and D'Agostino–Pearson tests.
Determination of the best significance level for goodness-of-fit tests
The best significance level associated with Gaussianity identification for each test was different depending on the sample size. The ROC curves of the 4 goodness-of-fit tests for identifying Gaussianity of the population from the samples when n = 60 and n = 30 are shown in Figures 2A and 2B, respectively.

 Shapiro–Wilk test (red);
Shapiro–Wilk test (red);  Kolmogorov–Smirnov test (green);
Kolmogorov–Smirnov test (green);  D'Agostino–Pearson test (purple);
D'Agostino–Pearson test (purple);  Anderson–Darling test (blue).
Anderson–Darling test (blue).For a sample size of 60 subjects, the best significance threshold for population Gaussianity identification determined via ROC analysis for the Shapiro–Wilk test, the Kolmogorov–Smirnov test, the D'Agostino–Pearson test, and the Anderson–Darling test was 0.18, 0.26, 0.19, and 0.27, respectively. These significance levels were associated with a sensitivity of 0.90, 0.84, 0.91, and 0.85, and a specificity of 0.88, 0.83, 0.94, and 0.90 for the Shapiro–Wilk test, the Kolmogorov–Smirnov test, the D'Agostino–Pearson test, and the Anderson–Darling test, respectively. A significant difference in the area under the curve (AUC), which represents the overall performance of each test, was detected between the Shapiro–Wilk test and the Kolmogorov–Smirnov and the D'Agostino–Pearson tests (AUC = 0.95, 0.89, and 0.97 and P-value < .001 and .005, respectively). A significant difference in the AUC was detected between the D'Agostino–Pearson test and the Kolmogorov–Smirnov and the Anderson–Darling tests (area under the curve = 0.97, 0.89, and 0.94 and P < .001 for both comparisons).
For a sample size of 30 subjects, the best significance level identified for the Shapiro–Wilk test, the Kolmogorov–Smirnov test, the D'Agostino–Pearson test, and the Anderson–Darling test was 0.19, 0.24, 0.18, and 0.29, respectively. These significance levels were associated with a sensitivity of 0.84, 0.72, 0.90, and 0.68, and a specificity of 0.72, 0.61, 0.74, and 0.74 for the Shapiro–Wilk test, the Kolmogorov–Smirnov test, the D'Agostino–Pearson test, and the Anderson–Darling test, respectively. A significant difference in the AUC was detected between the Shapiro–Wilk test and the Kolmogorov–Smirnov, the D'Agostino–Pearson, and the Anderson–Darling tests (AUC = 0.82, 0.71, 0.87, and 0.78. respectively; P < .001 for comparisons between the Shapiro–Wilk and the Kolmogorov–Smirnov and Anderson–Darling tests, and P = .01 for the comparison between the Shapiro–Wilk and the D'Agostino–Pearson tests). A significant difference in the AUC was detected between the D'Agostino–Pearson test and the Kolmogorov–Smirnov and the Anderson–Darling tests (AUC = 0.87, 0.71, and 0.78, respectively; P < .001 for all comparisons).
Consequences of misclassification on reference interval accuracy
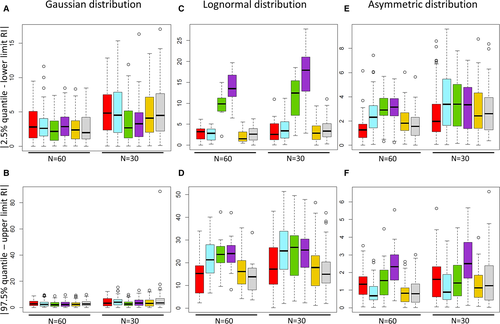
The median RI of the 100 samples for each of the 3 analyte populations and for each of the 2 sample sizes are shown in Table S1. The differences between the lower/upper limit of these RI determined by the 6 statistical methods and the 2.5%/97.5% quantile value of the original population are shown in Figure 3 and are presented in Table 2.
 Nonparametric method (red);
Nonparametric method (red);  bootstrap method (blue);
bootstrap method (blue);  parametric method on untransformed data (green);
parametric method on untransformed data (green);  robust method on untransformed data (purple);
robust method on untransformed data (purple);  parametric method on Box–Cox-transformed data (yellow);
parametric method on Box–Cox-transformed data (yellow);  robust method on Box–Cox-transformed data (gray).
robust method on Box–Cox-transformed data (gray).| Sample Size N = 60 | Sample Size N = 30 | |||||
|---|---|---|---|---|---|---|
| Number of Samples Included in the Analysis | Absolute Difference Between the Lower RI and the 2.5% Percentile Value of the Population; Median (Min–Max) | Absolute Difference Between the Upper RI and the 97.5% Percentile Value of the Population; Median (Min–Max) | Number of Samples Included in the Analysis | Absolute Difference Between the Lower RI and the 2.5% Percentile Value of the Population; Median (Min–Max) | Absolute Difference Between the Upper RI and the 97.5% Percentile Value of the Population; Median (Min–Max) | |
| Gaussian population | ||||||
| Nonparametric | 100 | 2.8 (0.01–9.5)a | 2.8 (0.02–8.9) | 100 | 4.8 (0.03–12.8)a,b | 3.3 (0.03–12.3)a |
| Bootstrap | 100 | 2.6 (0.01–11.6) | 2.4 (0.2–9.6) | 100 | 4.5 (< 0.01–15.3)a,b | 4.0 (< 0.01–15.4)a |
| Parametric | 100 | 2.1 (0.03–7.4)a,b | 2.1 (0.01–8.9)a | 100 | 2.7 (0.03–11.9)a | 2.7 (0.07–9.9)a,b |
| Robust | 100 | 2.8 (0.03–8.5)a,b | 2.3 (0.07–9.7) | 100 | 3.2 (0.01–16.3)b | 3.4 (0.2–13.1)a,b |
| Box–Cox parametric | 100 | 2.4 (0.03–8.3) | 2.4 (< 0.01–9.3) | 100 | 4.1 (0.06–13.5)a,b | 3.1 (0.03–13.1) |
| Box–Cox robust | 100 | 2.0 (0.01–8.5) | 2.7 (0.04–9.8)a | 100 | 4.5 (0.1–17.0)a,b | 3.5 (0.01–88.6)a |
| Lognormal population | ||||||
| Nonparametric | 10 | 3.2 (< 0.01–6.2)a,b | 15.2 (2.4–33.9)a,b | 41 | 2.5 (0.06–11.0)a,b | 17.2 (0.2–42.6)a,b |
| Bootstrap | 10 | 2.8 (0.2–5.1)a,b | 21.2 (6.6–40.0) | 41 | 3.4 (0.1–11.2)a,b | 25.2 (2.1–51.4) |
| Parametric | 10 | 9.8 (2.1–15.0)a,b | 23.6 (9.5–42.3)a | 41 | 12.4 (2.3–18.5)a,b | 26.7 (3.1–49.5)a,b |
| Robust | 10 | 13.5 (6.4–19.7)a,b | 24.0 (8.1–42.0)b | 41 | 17.9 (2.9–27.8)a,b | 25.5 (2.3–47.8)a,b |
| Box–Cox parametric | 10 | 1.5 (0.4–5.5)a,b | 16.1 (4.1–35.3)a,b | 41 | 2.9 (0.03–9.4)a,b | 17.8 (1.1–46.4)a,b |
| Box–Cox robust | 10 | 2.6 (0.02–6.2)a,b | 13.8 (3.6–33.2)a,b | 41 | 3.3 (0.3–11.0)a,b | 14.9 (2.1–41.9)a,b |
| Asymmetric population | ||||||
| Nonparametric | 49 | 1.2 (0.01–6.1)a,b | 1.3 (0.05–3.5)b | 56 | 1.9 (0.05–8.6)a | 1.6 (0.06–5.6)b |
| Bootstrap | 49 | 2.3 (0.06–7.4)a,b | 0.7 (0.03–2.7)a,b | 56 | 3.4 (0.04–9.6) | 0.9 (0.03–3.8)b |
| Parametric | 49 | 2.9 (0.3–5.7)a | 1.5 (0.05–4.4)a,b | 56 | 3.4 (0.1–7.8)a | 1.4 (0.03–4.5)a,b |
| Robust | 49 | 3.1 (0.2–5.5)b | 2.3 (0.4–5.5)a,b | 56 | 3.3 (0.1–7.0)a | 2.5 (0.1–5.6)a,b |
| Box–Cox parametric | 49 | 1.8 (0.08–6.0)a,b | 0.8 (0.01–2.6)a,b | 56 | 2.4 (0.01–8.7)a | 1.1 (0.08–4.0)b |
| Box–Cox robust | 49 | 1.5 (< 0.01–5.6)a,b | 0.8 (0.01–3.0)a,b | 56 | 2.6 (0.3–8.3) | 1.2 (0.03–6.6)b |
- a,b: statistically significant at P < .01, paired Wilcoxon test (only comparisons between parametric method and the other methodsa, and robust method and the other methodsb were performed).
For both sample sizes, the parametric methods applied to raw data tended to result in significantly more accurate RI when the original population distribution was Gaussian. However, despite these statistically significant differences in accuracy between parametric or robust methods applied to raw data and the other methods, the median of these differences were usually less than 4 units regardless of the method used (Figure 3A,B). However, the robust method provided very inaccurate RI limits from one n = 30 sample after Box–Cox transformation (absolute difference between the upper RI and the 97.5% percentile value of the population of 88.6 units; Figure 3B). When the population distribution was originally lognormal, the RI obtained by the parametric and robust methods applied to untransformed data were significantly less accurate than the ones obtained by nonparametric methods and Box–Cox transformation, and the magnitude of the difference in accuracy was high (usually around 15–20 units; Figure 3C,D). When the original population distribution was skewed to the left, the robust methods applied to raw data tended to provide less accurate RI compared to the other methods (Figure 3E,F). However, the magnitude of the difference in accuracy was globally small (less than 2 units).
Discussion
According to the ASVCP guidelines, distribution of reference data must be assessed by one of the 4 goodness-of-fit tests used in this study, and if sample size is between 120 and 20 subjects and the distribution identified as Gaussian, parametric or robust methods on raw data should be used to construct the RI.6 The present study suggests that these recommendations may lead to improper use of parametric or robust methods on raw data and inaccurate RI owing to the low specificity of the normality tests, especially when sample size is very small (n = 30).
The poor performance of the goodness-of-fit tests at a small sample size has been previously reported in statistics articles, but to the knowledge of the author, has never been examined in the context of RI construction.9-11 As a consequence, these tests have been associated with poor power and improper type-I error rate, which are concepts that may be unfamiliar to clinicians.9 In this study, these concepts were replaced by sensitivity and specificity assessments, which allowed a better understanding of the limits of these tests.
The 4 goodness-of-fit tests listed in the ASVCP guidelines are not equivalent in terms of accuracy.6 The Kolmogorov–Smirnov and the Anderson–Darling tests have significantly lower specificity than the Shapiro–Wilk and the D'Agostino–Pearson tests according to the present results and should not be used to assess the distribution of the data at small sample size. This is in accordance with previous studies.9-11 On the other hand, no statistically significant differences in terms of sensitivity and specificity were found between the Shapiro–Wilk and the D'Agostino–Pearson tests, and both tests may be used indistinctly. This is in contrast with other studies that revealed the superiority of the Shapiro–Wilk test for small sized samples, especially when Gaussianity must be rejected in the face of a non-Gaussian distribution.9, 10 This disagreement might be explained by differences in terms of distributions tested, and sample sizes between previous statistics studies and the present study.9, 10 In the present study, sample sizes were chosen based on the ASVCP guidelines and the distributions were extrapolated from real biochemical analyte distributions, in order for the results to be as inferable as possible to clinical settings. The size of the reference population in the present study can be considered representative of a true population of healthy animals. Unlike in a previous computer simulation study, noise was added to the simulated values in order to disconnect them from a pure mathematical model and be as realistic as possible.16 Samples were randomly extracted from the population in the same way as healthy animals would be randomly included to construct a RI in real life.
Even when Shapiro–Wilk and D'Agostino–Pearson tests were used, their specificity was around 0.5 at sample size n = 30. This means that a sample extracted from a non-Gaussian population may erroneously identify the parent population as Gaussian in about half of the cases at very low sample size. In accordance to the ASVCP guidelines, the parametric method would be applied to these data, and the resulting RI might be inaccurate.6 Clinically relevant inaccuracies may however be restricted to improper use of the parametric or robust methods on samples extracted from a lognormal population. The magnitude of the inaccuracies was indeed very small when parametric or robust methods were applied to samples extracted from an asymmetric distribution skewed to the left. Even though analyte distributions skewed to the left have been sporadically reported, most analyte distributions in clinical biochemistry are theoretically considered either Gaussian or lognormal, which makes the risk of inaccurate RI high at a small sample size.12, 17-19
Two potential solutions were explored in this study. Receiver operating characteristic curve analyses were performed in order to determine whether changing the significance levels of the normality tests may improve their performance. Based on the present results, a significance threshold of 0.2 instead of 0.05 may be better suited for the Shapiro–Wilk and D'Agostino–Pearson tests for sample sizes of n = 60 and n = 30. With such significance levels, the specificity of both tests was around 0.91 when n = 60, and 0.73 when n = 30. This means that 27% of all samples extracted from a non-Gaussian population may still falsely identify the parent population as Gaussian with a significance level of 0.2 when n = 30.
The present study also looked at the consequences of applying statistical methods other than the parametric method on raw data to samples extracted from a Gaussian population. Although nonparametric methods and Box–Cox transformation of the data led to RI that were often significantly different from those obtained via the parametric method, the magnitude of the difference was usually small and likely clinically irrelevant. These results would support the use of nonparametric methods or perhaps Box–Cox transformation at all times for sample size as low as 30 subjects and regardless of data distributions. It is noteworthy to mention that the use of nonparametric methods may be preferred, as the Box–Cox transformation may lead, in rare instances, to very inaccurate RI.20 It is also important to keep in mind that the RI become less accurate with smaller samples, regardless of the statistical method used, and that the goal should always be to include as many animals as possible in the sample in order to increase the accuracy of the RI.
Although the ASVCP guidelines acknowledge the fact that robust methods perform better when data are distributed symmetrically, they recommend the robust method when the data distribution does not appear Gaussian and the sample size is small.6 The current study did not reveal that the robust method provided more accurate RI than the parametric or nonparametric methods, and could even result, in rare instances, in very inaccurate RI at sample size n = 30. The International Federation of Clinical Chemistry and Laboratory Medicine (IFCC) and Clinical Laboratory Standards Institute (CLSI) guidelines also mention the overall lack of superiority of the robust method over the nonparametric method for calculation of RI.7
Finally, Gaussianity of the population was assessed using the techniques recommended in the ASVCP guidelines.6 Assessment of Gaussianity by several methods, including kurtosis, goodness-of-fit tests, and histograms, may provide a more accurate determination of the distribution of the reference values before and after Box–Cox or other transformation. This approach was not evaluated in this study.
In summary, although the ASVCP guidelines have represented an indubitable step forward in the area of RI construction, the present results suggest that the current recommendations of assessing data distribution via a goodness-of-fit test when sample size is between 120 and 20 animals in order to guide the choice of the statistical method to construct RI may lead to inaccurate RI up to half of the studies. These inaccuracies are not only frequent (more than 40% of the time at n = 30) but also of high magnitude when a goodness-of-fit test is run on a sample extracted from a lognormal population that falsely identify the parent population as Gaussian and a parametric method is used to build the reference limits. Adjusting the significance levels of the normality tests depending on the sample size may help reduce the risk of erroneously identifying the parent population as Gaussian when the samples are actually extracted from non-Gaussian populations. Another solution would be to avoid the use of parametric and robust methods on untransformed data, and always recommend the nonparametric methods (or alternatively Box–Cox transformation) to build RI from samples as low as 30 animals and regardless of data distribution. Above all, the goal should always be to include as many animals as possible in the sample in order to increase the accuracy of the RI.
Acknowledgments
The author thanks Dr. Julie Danner for technical assistance and Dr. Stephane Lezmi for assisting with the revision of the manuscript.
Disclosure
The author has indicated that he has no affiliations or financial involvement with any organization or entity with a financial interest in, or in financial competition with, the subject matter or materials discussed in this article.




