Compensation schemes for learning a Lingua Franca in the European Union
Abstract
We discuss compensation schemes that should give incentives to EU countries and citizens to acquire a lingua franca. We consider three possible candidate languages: English, French and German, which are already the most widely spoken languages. In our model, countries can claim compensations linked to the number of (young) citizens who do not speak a given candidate language, and the distance between the official language in the country and the suggested lingua franca. We study two sharing schemes that are rooted in ancient sources: the Aristotelian proportional rule and the Talmud rule. The former prevents coalitional manipulations among countries, whereas the latter guarantees meaningful lower bounds in the sharing process for all countries.
1 INTRODUCTION
L'homme qui parle deux langues vaut deux hommes.1
The European Union is faced with 24 official languages, including English whose status is going to be difficult to define after Brexit. Though it was the most widely common language before Brexit, with 37% of Europeans knowing it well or very well, it will be less so after Brexit, as some 60 million native speakers will be gone. Then, German (with 28%), English (28%) and French (21%) will be the leading languages, including some 90 and 65 million German and French native speakers, while English will have only 5 million native speakers in Ireland and Malta.
These negative aspects are exacerbated by the substantial costs needed to maintain 24 official languages, which entails over a billion euros per year in translation and interpretation. The burden is, however, not limited to these direct costs: communication constitutes an even more serious challenge in societies with a large number of official languages. Errors as well as delays caused by translations may end up impairing multilateral discussions and negotiations.
Several solutions can be envisaged. One is to limit the number of official languages. This is impossible since Regulation no. 1 (adopted by the Council in 1958), which states that the official language of a country joining the EU becomes an official language at the EU level, and decisions on languages have to be unanimous. Though the EU authorities are thus fundamentally and adamantly opposed to such a drastic solution, in some countries, it has happened in a smooth way: Swahili was adopted in Tanzania, Bahasa in Indonesia, English in both the United States and England (Laitin, 2000) and Hebrew in Israel (though this is a special case). In others, such as Ceylon after independence, it ended with a civil war that lasted many years and took many lives (Castañeda Dower, Ginsburgh, & Weber, 2017).
Still, many countries with a large number of languages have resorted to such solutions by imposing a unique language in a violent way: Russia in the 1860s (Kadochnikov, 2016), French in France (Wright, 2016). Such standardisation does, however, not necessarily impose a unique language, but rather restricts the number of languages used for official, legal or educational purposes. This was envisaged in India (Laitin, 1989), Nigeria (Fakuade, 1989) and Ghana (Laitin, 1994) by trying to educate citizens to speak one (or several) unifying language(s) in addition to their native languages.
After India's independence in 1948, its Constitution recognised 11 official native languages, including Hindi chosen among the 387 living languages, plus English. Some 60 years ago, the country tried to implement a so-called three-language formula according to which every citizen should learn and speak her native language, Hindi and English. This failed for several reasons, the main being that those whose native language was Hindi were favoured since the only additional language they had to learn was English, while all others had to become fluent in two other languages, Hindi and English. The construction also failed because financing was insufficient, which of course led to a shortage of teachers.
A variant of the three-language formula was introduced in Nigeria in 1977, a country of some 140 million inhabitants who speak 522 languages and are divided into 250 ethnic groups. The three-language formula based on the use of Hausa, Yoruba and Igbo was considered a unifying device for this incredibly diversified country. However, it failed like in India and for the very same reasons.
For Ghana (and possibly for other African countries that had been colonised), Laitin (1994) proposed a language outcome “in which an indigenous national language would get promoted and institutionalised, along with district vernaculars all in the context of continued reliance in many domains on the language of former colonial rule.” His analysis showed that this would be better than the status quo for most Ghanaians, but as Ansah (2014) reports, the many governments that followed each other were not able to implement any changes.
The situation in the EU may be sufficiently different to suggest a similar proposal and see it accepted by most citizens. Indeed, a survey commissioned by the European Commission2 shows that the reactions of Europeans are quite positive. Here are the statements and questions that they had to answer followed by their reactions:
- The European institutions should adopt one single language to communicate with European citizens. Answer: In 16 out of 27 countries, 50% or more voted in favour of a unique language, with an aggregate EU result of 54%.
- Everyone in the EU should be able to speak a common language. Answer: In all countries, with the exception of Bulgaria, 50% or more voted yes, with an aggregate EU result of 69%.
- Everyone in the EU should be able to speak one language in addition to their mother tongue. Answer: In all cases, the idea was adopted by more than 70%. Aggregate result: 83%.
- Everyone in the EU should be able to speak two languages in addition to their mother tongue. Answer: Thirteen countries agreed and cast a vote of 50% or more. Aggregate result: 49%.
- All languages spoken within the EU should be treated equally. Answer: In each country, over 60% agree, with an aggregate result of 72%.
- Which two languages, apart from your mother tongue do you think are the most useful to know for your personal development and career? (any 2 of the 24 official languages could be selected). Answer: English (67%), French (25%), German (22%), Spanish (15%). These are followed by Russian (3.4%), Italian (3.2%) and Chinese (1.5%). Beyond that, usefulness drops to less than 1%.
These answers show that a majority of EU citizens accept the idea of one common language (83%), and some 50% would even be ready to learn or speak two common languages (49%). The languages that are most cited are English (67%, note that the survey predates the Brexit decision), French (25%) and German (22%). This, however, would by no means imply that countries lose their identity and home language and the current translation and interpretation system would remain as is.
This prompted us to look at the possibility for the EU to devote an additional budget that could be included into, or associated with, the Erasmus programme budget and would cover at least part of what it costs to teach language(s) to young generations. The idea could be implemented in various ways, such as paying part of the education of future teachers of the chosen lingua(e) franca(e), helping parents to finance the extra hours needed to take language courses that are not taught at school, or financing schools in their hiring of teachers. The main issue of this paper is to study how this new EU budget, if accepted, could or should be shared across countries which differ in the size of their population of young generations, as well as in the distance between their official language and the possible lingua(e) franca(e).
The EU is crossing difficult waters (Brexit, the Euro, immigration, rumours of secession within some countries such as Catalonia in Spain or Scotland in the UK, rumours of secession by France and Italy from the EU, the bankruptcy of Greece) and having one or two common languages would obviously strengthen the links within the mosaic of populations who speak tongues of very different branches of the linguistic tree (Germanic languages—Danish, Dutch, English, German and Swedish; Romance languages—French, Italian, Portuguese, Romanian and Spanish; Slavic languages—Bulgarian, Croatian, Czech, Latvian, Lithuanian, Polish, Slovak and Slovene; Uralic languages—Estonian, Finnish, Hungarian; other languages—Irish, Greek and Maltese). This may perhaps somewhat soften the curse (is it a “curse”?) expressed by Fernando Pessoa, “Minha pátria é minha lingua” (my homeland is my language), and gently shift EU's citizens closer to “Europe is my homeland.”
For simplicity, we make the following reasonable assumptions in our analysis:
- Each country has its own official (unique) language,3 which is also an official language of the EU;
- The smaller the distance between the official language of the country and the lingua franca, the smaller the cost of learning the latter;4
- Only the younger generations will be learning one (or several) of the linguae francae or, alternatively, the EU should not pay for those who are more than 26 years old;
- The claim of each country on the common learning budget will be based on the number of young individuals (ages 12–26) who do not speak the lingua franca, adjusted by the distance between both languages, and a fixed cost of 500 euros per such individual.
We thus face a problem of adjudicating claims. Such problems refer to a situation in which one has to distribute a common good (land, for instance), or a budget whose available amount is not sufficient to cover all agents’ demands (claims). Reimbursing the debts of a bankrupt firm, collecting a given amount of taxes, or dividing among heirs the insufficient estate of a heritage, are examples of such situations. The reader is referred to Thomson (2003, 2015, 2017) for extensive reviews and surveys of the sizeable literature dealing with the problem that started with O'Neill's (1982) paper. There are two focal rules that can be traced back to ancient economic thought.
A just act necessarily involves at least four terms: two persons for whom it is in fact just, and two shares in which its justice is exhibited. And there will be the same equality between the shares as between the persons, because the shares will be in the same ratio to one another as the persons… What is just in this sense is what is proportional and what is unjust is what violates the proportion.
Another focal (and seemingly unrelated) rule is inspired by suggestions made in the Talmud.6 A canonical one is the so-called contested garment problem, in which two men disagree on the ownership of a garment. The first man claims half of it, and the other claims it all. Assuming both claims are made in good faith, the Talmud recommends that the first agent gets one fourth of the garment, whereas the second agent gets three fourths.7 For instance, if we give the garment a worth of 200, the recommendation made by the Talmud is the division (50, 150).8 Another well-known case is the so-called marriage contract. It involves the three wives of a man who signed contracts with each of them specifying, as is the tradition, how much she should receive in case of dissolution of their marriage (divorce or his death). The man dies and his estate is found to be insufficient to honour the three contracts. Suppose the wives are claiming 100, 200 and 300. If the estate is 100, it should be divided equally. If it is 300, it should be divided proportionally. Finally, if its value is 200, the recommendation is to allocate 50 to the first creditor and 75 to each of the other two.9 The Talmud rule, formalised by Aumann and Maschler (1985), rationalises all these examples. The rule focusses on equal awards or equal losses depending on whether the endowment falls short or exceeds one half of the aggregate claim, using half-claims (instead of claims) as individual bounds.
Though there are other possible rules (e.g., the constrained equal awards rule, which makes awards as equal as possible, subject to the condition that no agent gets more than his claim; the constrained equal losses rule, which makes losses as equal as possible, subject to the condition that no agent gets a negative amount),10 we concentrate on the proportional and the Talmud rules only, for reasons that will become clear later.
The paper is organised as follows. In Section 2, we formally introduce our model and the two rules that can be used to “share the pie.” In Section 3, we provide the results of applying the rules to our problem in the EU. We consider three possible linguae francae: English (as long as it remains an EU official language after Brexit), German and French. Other languages, such as Italian, Spanish, Polish or Dutch, are spoken by relatively large populations (though the number of people who speak them is much smaller than for English, German and French), and mainly in their country of origin. They are not (yet) enough spread to the rest of Europe, but the calculations can be made. Section 4 is devoted to some concluding remarks. The axiomatic analysis leading to the normative foundations of the sharing rules we use is deferred to an Appendix.
2 THE MODEL
Let L denote the set of adopted official languages in the 26 EU countries. We exclude the United Kingdom as it will no longer be part of the EU, and Luxembourg, because its language, Luxembourgish, is not an EU official language, and most of its inhabitants speak either German or French, and in many cases both. This will not change the numbers as the country also has a small population of 500,000 inhabitants only.11
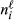 be the number of citizens in the 12 to 26-year-old cohort who do not speak ℓ. Then, country i's claim is:
be the number of citizens in the 12 to 26-year-old cohort who do not speak ℓ. Then, country i's claim is:
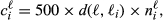 (1)
(1)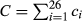 is the aggregate claim.14 It is natural to assume that E < C, for otherwise each country could receive what it claims.
is the aggregate claim.14 It is natural to assume that E < C, for otherwise each country could receive what it claims.Formally, the problem is defined by a 3-tuple 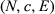 where N is the set of countries, c is the vector of claims containing elements
where N is the set of countries, c is the vector of claims containing elements 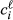 , i = 1, 2, …, 26, described above, and E is the endowment to be allocated among countries. The family of all the problems so described is denoted by
, i = 1, 2, …, 26, described above, and E is the endowment to be allocated among countries. The family of all the problems so described is denoted by 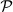 .
.
A rule is a mapping that associates with each problem the allocation each country receives. We impose the efficiency condition that the whole endowment E is allocated, and a boundedness requirement that no country receives a negative amount or an amount larger than its claim. Formally, for each 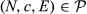 ,
, 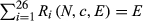 , and for each i = 1, …, 26, 0 ≤ Ri (N, c, E) ≤ ci.
, and for each i = 1, …, 26, 0 ≤ Ri (N, c, E) ≤ ci.
This problem is mathematically equivalent to the so-called problem of adjudicating conflicting claims formalised by O'Neill (1982). We now consider the two focal rules briefly introduced in Section 1:
- The Proportional rule, which awards agents in proportion of their claim. Formally, for each
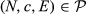 and each i ∈ N:
and each i ∈ N:
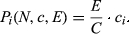
- The Talmud rule, which makes awards (resp. losses) as equal as possible provided the amount to divide falls short (resp. exceeds) one half of the aggregate claim, while using half-claims (instead of claims) as individual bounds. Formally, for each
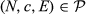 , and each i ∈ N,
where λ and μ are chosen so that
, and each i ∈ N,
where λ and μ are chosen so that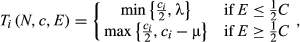
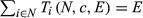 .15
.15
More precisely, the Talmud rule applies equal division until the claimant with the smallest claim has obtained one half of her claim. Then, that agent stops receiving additional units and the remaining amount is divided equally among the other agents until the claimant with the second smallest claim gets one half of her claim. The process continues until every agent has received one half of her claim, or the available amount is distributed. If there is still something left after this process, agents are invited back to receive additional shares. Now agents receive additional amounts sequentially starting with those with larger claims and applying equal division of their losses.
Normative foundations for both rules are provided in the Appendix. As will be shown, there are several properties (axioms) reflecting ethical or operational concerns that both rules satisfy. It should be acknowledged that there are other properties that they violate and that there exist other rules that satisfy and violate different sets of properties. Nevertheless, the two rules are salient in being the only ones satisfying some key properties. We highlight, for instance, that the proportional rule prevents coalitional manipulations among countries: countries would not benefit from the proportional rule by merging with others (think of the case in which countries have official languages equidistant to the lingua franca), or by breaking up in different regions. No other rule shares this feature. On the other hand, the Talmud rule is unique in guaranteeing meaningful lower and upper bounds (in the allocation process) for all countries. These are probably the most distinguishing features of the two rules.
3 SHARING THE BUDGET BETWEEN EU COUNTRIES
To illustrate the idea, we make the assumption that the European Commission would be ready to spend one billion euros to increase the feeling of unity among Europeans, in the same way as it does with its educational Erasmus programme, which has been set 2.3 billion euros per year between 2014 and 2020.16 We try to figure out what the individual countries’ claims would be if the learning of one of the languages (English, German or French) were accepted by all countries (or by the Commission) to become a lingua franca. Obviously, the three languages do not have the same number of speakers in the various countries, and it could well happen that no agreement is reached to propose a unique language. Therefore, in the discussion section, we also briefly consider what could happen if more than one language had to be selected, since, as mentioned earlier, the distances between languages and the number of speakers are not the same.
This action should only be directed to the younger generations. We thus considered the generation of those aged 0–14 years in 2005, who will be 12–26 years old in 2017, and assumed that their proficiency (native, very well and well spoken) of the three languages will be the same17 as what it was for the same generation in 2005, according to the findings of the Special Eurobarometer 243 (2006) survey.
Table 1 collects the linguistic knowledge of the three languages in 2005 by the generations that we are concerned with, as well as the distances of each official language to these three languages.18
| Population (million) | Age group 0–14 in % | Do not speak (%) | Linguistic distances to (×1,000) | |||||
|---|---|---|---|---|---|---|---|---|
| E | G | F | E | G | F | |||
| 2005 | 2005 | 2005 | 2005 | 2005 | ||||
| Austria | 8.2 | 16.1 | 41 | 0 | 85 | 422 | 0 | 756 |
| Belgiuma | 10.4 | 17.2 | 39 | 90 | 25 | 540 | 400 | 454 |
| Bulgaria | 7.8 | 13.7 | 57 | 87 | 95 | 772 | 769 | 791 |
| Croatia | 4.4 | 15.9 | 34 | 76 | 99 | 766 | 764 | 772 |
| Cyprus | 0.7 | 19.9 | 18 | 98 | 91 | 838 | 812 | 843 |
| Czech Rep. | 10.2 | 14.9 | 64 | 80 | 98 | 759 | 741 | 769 |
| Denmark | 5.4 | 18.8 | 9 | 68 | 98 | 407 | 293 | 759 |
| Estonia | 1.3 | 15.4 | 33 | 85 | 100 | 1,000 | 1,000 | 1,000 |
| Finland | 5.2 | 17.5 | 29 | 95 | 97 | 1,000 | 1,000 | 1,000 |
| France | 60.6 | 18.7 | 67 | 95 | 0 | 764 | 756 | 0 |
| Germany | 82.5 | 14.5 | 38 | 0 | 88 | 422 | 0 | 756 |
| Greece | 11.1 | 15.1 | 40 | 93 | 94 | 838 | 812 | 843 |
| Hungary | 10.1 | 15.6 | 76 | 82 | 99 | 1,000 | 1,000 | 1,000 |
| Ireland | 4.1 | 20.7 | 2 | 94 | 85 | 0 | 422 | 764 |
| Italy | 58.5 | 14.1 | 54 | 94 | 85 | 753 | 735 | 197 |
| Latvia | 2.3 | 15.0 | 55 | 96 | 99 | 803 | 800 | 793 |
| Lithuania | 3.4 | 17.1 | 49 | 93 | 99 | 784 | 776 | 779 |
| Luxemburg | 0.5 | 18.6 | 50 | 8 | 3 | 0 | 0 | 0 |
| Malta | 0.4 | 17.6 | 10 | 99 | 92 | 1,000 | 1,000 | 1,000 |
| The Netherlands | 16.3 | 18.5 | 11 | 59 | 88 | 392 | 162 | 756 |
| Poland | 38.2 | 16.7 | 57 | 83 | 97 | 761 | 754 | 781 |
| Portugal | 10.5 | 16.0 | 62 | 99 | 87 | 760 | 753 | 291 |
| Romania | 21.7 | 17.5 | 69 | 97 | 82 | 773 | 751 | 421 |
| Slovakia | 5.4 | 17.1 | 57 | 66 | 98 | 750 | 742 | 765 |
| Slovenia | 2.0 | 14.4 | 22 | 72 | 97 | 751 | 733 | 782 |
| Spain | 43.0 | 14.5 | 65 | 98 | 92 | 760 | 747 | 266 |
| Sweden | 9.0 | 17.6 | 5 | 89 | 96 | 411 | 305 | 756 |
| United Kingdom | 60.0 | 18.1 | 2 | 95 | 90 | 0 | 422 | 764 |
Note
- a Distances lie between 0 and 1. The distances for Belgium result from a weighted average of distances to the Flemish (0.6) and the French-speaking (0.4) populations.
Tables 2 and 3 show the claims (calculated according to equation (1) above) as well as the shares of each country for each of the three linguae francae. We do the calculations for two possible budgets: one and two billion euros.19 Luxembourg and the UK are shown in both tables, but they will receive nothing, for the reasons discussed in Section 1.
| Language | Claims | Sharing a one billion budget | Sharing a two billion budget | ||||||
|---|---|---|---|---|---|---|---|---|---|
| English | German | French | English | German | French | English | German | French | |
| Austria | 112.8 | 0 | 421.7 | 9.1 | 0 | 27 | 18.2 | 0 | 54 |
| Belgium | 191.6 | 320.6 | 99.5 | 15.4 | 18.1 | 6.4 | 30.8 | 36.2 | 12.8 |
| Bulgaria | 233.1 | 357.5 | 401.1 | 18.7 | 20.2 | 25.7 | 37.4 | 40.4 | 51.4 |
| Croatia | 90.6 | 204.2 | 267.9 | 7.3 | 11.5 | 17.2 | 14.6 | 23 | 34.4 |
| Cyprus | 10.4 | 55.5 | 53.5 | 0.8 | 3.1 | 3.4 | 1.6 | 6.2 | 6.8 |
| Czech Rep. | 368 | 452.2 | 570.9 | 29.6 | 25.6 | 36.6 | 59.2 | 51.2 | 73.2 |
| Denmark | 17.8 | 100.8 | 378.7 | 1.4 | 5.7 | 24.2 | 2.8 | 11.4 | 48.4 |
| Estonia | 32.8 | 85.4 | 99.6 | 2.6 | 4.8 | 6.4 | 5.2 | 9.6 | 12.8 |
| Finland | 132.9 | 434.1 | 440.9 | 10.7 | 24.5 | 28.2 | 21.4 | 49 | 56.4 |
| France | 2,913.3 | 4,069.4 | 0 | 234.1 | 230.1 | 0 | 468.2 | 460.2 | 0 |
| Germany | 956.6 | 0 | 3,988.2 | 76.9 | 0 | 255.4 | 153.8 | 0 | 510.8 |
| Greece | 279.5 | 629.5 | 662.7 | 22.5 | 35.6 | 42.4 | 45 | 71.2 | 84.8 |
| Hungary | 596.4 | 647.6 | 783.1 | 47.9 | 36.6 | 50.1 | 95.8 | 73.2 | 100.2 |
| Ireland | 0 | 169 | 276.9 | 0 | 9.6 | 17.7 | 0 | 19.2 | 35.4 |
| Italy | 1,686.3 | 2,846.4 | 690.6 | 135.6 | 161 | 44.2 | 271.2 | 322 | 88.4 |
| Latvia | 75.6 | 131.9 | 135.7 | 6.1 | 7.5 | 8.7 | 12.2 | 15 | 17.4 |
| Lithuania | 112.1 | 208.7 | 224.2 | 9 | 11.8 | 14.4 | 18 | 23.6 | 28.8 |
| Luxemburg | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Malta | 3.6 | 34.7 | 32.5 | 0.3 | 2 | 2.1 | 0.6 | 4 | 4.2 |
| The Netherlands | 64.4 | 143.9 | 1,007.6 | 5.2 | 8.1 | 64.5 | 10.4 | 16.2 | 129 |
| Poland | 1,378.7 | 1,984.2 | 2,423.9 | 110.8 | 112.2 | 155.2 | 221.6 | 224.4 | 310.4 |
| Portugal | 393.9 | 624.3 | 211.7 | 31.7 | 35.3 | 13.6 | 63.4 | 70.6 | 27.2 |
| Romania | 1,005.4 | 1,379 | 653.1 | 80.8 | 78 | 41.8 | 161.6 | 156 | 83.6 |
| Slovakia | 198.8 | 227.5 | 345.4 | 16 | 12.9 | 22.1 | 32 | 25.8 | 44.2 |
| Slovenia | 23.7 | 75.6 | 109.7 | 1.9 | 4.3 | 7 | 3.8 | 8.6 | 14 |
| Spain | 1,549.5 | 2,284.5 | 761.3 | 124.5 | 129.2 | 48.7 | 249 | 258.4 | 97.4 |
| Sweden | 15.6 | 215.5 | 577.2 | 1.3 | 12.2 | 37 | 2.6 | 24.4 | 74 |
| United Kingdom | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Language | Claims | Sharing a one billion budget | Sharing a two billion budget | ||||||
|---|---|---|---|---|---|---|---|---|---|
| English | German | French | English | German | French | English | German | French | |
| Austria | 112.8 | 0 | 421.7 | 52 | 0 | 41.6 | 56.4 | 0 | 91.3 |
| Belgium | 191.6 | 320.6 | 99.5 | 52 | 43.7 | 41.6 | 95.8 | 100.1 | 49.7 |
| Bulgaria | 233.1 | 357.5 | 401.1 | 52 | 43.7 | 41.6 | 116.5 | 100.1 | 91.3 |
| Croatia | 90.6 | 204.2 | 267.9 | 45.3 | 43.7 | 41.6 | 45.3 | 100.1 | 91.3 |
| Cyprus | 10.4 | 55.5 | 53.5 | 5.2 | 27.8 | 26.7 | 5.2 | 27.8 | 26.7 |
| Czech Rep. | 368 | 452.2 | 570.9 | 52 | 43.7 | 41.6 | 134.2 | 100.1 | 91.3 |
| Denmark | 17.8 | 100.8 | 378.7 | 8.9 | 43.7 | 41.6 | 8.9 | 50.4 | 91.3 |
| Estonia | 32.8 | 85.4 | 99.6 | 16.4 | 43.7 | 41.6 | 16.4 | 42.7 | 49.8 |
| Finland | 132.9 | 434.1 | 440.9 | 52 | 43.7 | 41.6 | 66.4 | 100.1 | 91.3 |
| France | 2,913.3 | 4,069.4 | 0 | 52 | 43.7 | 0 | 134.2 | 100.1 | 0 |
| Germany | 956.6 | 0 | 3,988.2 | 52 | 0 | 41.6 | 134.2 | 0 | 91.3 |
| Greece | 279.5 | 629.5 | 662.7 | 52 | 43.7 | 41.6 | 134.2 | 100.1 | 91.3 |
| Hungary | 596.4 | 647.6 | 783.1 | 52 | 43.7 | 41.6 | 134.2 | 100.1 | 91.3 |
| Ireland | 0 | 169 | 276.9 | 0 | 43.7 | 41.6 | 0 | 84.5 | 91.3 |
| Italy | 1,686.3 | 2,846.4 | 690.6 | 52 | 43.7 | 41.6 | 134.2 | 100.1 | 91.3 |
| Latvia | 75.6 | 131.9 | 135.7 | 37.8 | 43.7 | 41.6 | 37.8 | 66 | 67.8 |
| Lithuania | 112.1 | 208.7 | 224.2 | 52 | 43.7 | 41.6 | 56.1 | 100.1 | 91.3 |
| Luxemburg | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Malta | 3.6 | 34.7 | 32.5 | 1.8 | 17.4 | 16.3 | 1.8 | 17.4 | 16.3 |
| The Netherlands | 64.4 | 143.9 | 1,007.6 | 32.2 | 43.7 | 41.6 | 32.2 | 71.9 | 91.3 |
| Poland | 1,378.7 | 1,984.2 | 2,423.9 | 52 | 43.7 | 41.6 | 134.2 | 100.1 | 91.3 |
| Portugal | 393.9 | 624.3 | 211.7 | 52 | 43.7 | 41.6 | 134.2 | 100.1 | 91.3 |
| Romania | 1,005.4 | 1,379 | 653.1 | 52 | 43.7 | 41.6 | 134.2 | 100.1 | 91.3 |
| Slovakia | 198.8 | 227.5 | 345.4 | 52 | 43.7 | 41.6 | 99.4 | 100.1 | 91.3 |
| Slovenia | 23.7 | 75.6 | 109.7 | 11.8 | 37.8 | 41.6 | 11.8 | 37.8 | 54.8 |
| Spain | 1,549.5 | 2,284.5 | 761.3 | 52 | 43.7 | 41.6 | 134.2 | 100.1 | 91.3 |
| Sweden | 15.6 | 215.5 | 577.2 | 7.8 | 43.7 | 41.6 | 7.8 | 100.1 | 91.3 |
| United Kingdom | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Table 2 provides the proportional shares. Note that, for each lingua franca, the different columns of the table are related in an obvious way, as multiplying the budget by any positive number, the proportional solution will simply multiply the shares for each country by the same number.
The proportional rule gives large amounts to countries with a larger population and/or a larger linguistic distance from the chosen lingua franca: France, Italy and Spain would get a large share for English and German, but much less so if French were chosen, since the distances of Italian and Spanish to French are smaller. The opposite occurs for Poland. Germany's share would be reasonably small for English, but much larger for French (again, because of the distances). All other countries would get less than 50 millions (for the one billion budget), with the exception of Romania (for English and German) and Hungary and the Netherlands (for French).
Table 3 provides the shares using the Talmud rule for the same budgets described above. Moving from a budget to a larger one generates larger changes than the proportional rule: a larger number of countries will be awarded half of their claim, whereas less countries get an equal share (at most equal to half of their claim) of the endowment. In the benchmark case of a one billion budget, the number of countries which get equal shares is increasing when going from English (16 countries get 52 million each, the largest share) to German (21 countries get 43.7 million each) and French (23 get 41.6 million each). The remaining countries get half of their claims (except, obviously, Germany and Austria in the case of German, and France in the case of French). Cyprus and Malta are always in that group (something expected as they are the smallest countries). Slovenia too (except for French, which is a more distant language). Two Scandinavian countries (Denmark and Sweden), two Baltic countries (Estonia and Latvia), the Netherlands and Croatia compete in that group in the case of English as lingua franca. These are all reasonably small countries in terms of population; in some cases, their languages are close to English.
With the two billion budget, more countries become part of the group that gets half of their claims for each of the three languages. This is especially so for English, with Austria, Belgium, Bulgaria, Finland, Lithuania and Slovakia. Not surprisingly, with French, Belgium (to which we associated as official language a hybrid between French and Flemish) becomes part of that group, since 40% of its population speaks French.
Finally, there are obviously theoretical differences between the two rules, as exemplified in the axiomatic analysis described in the Appendix, which translate into the numbers shown in the two tables. For instance, the proportional rule obviously imposes the same ratio between award and claim to each country, the Talmud rule does not.
There are also differences in the choices that countries would make between the two rules as long as the endowment is sufficiently small with respect to the aggregate claim. Smaller claimants prefer the Talmud outcome to the proportional one. Obviously, this Talmud-preferring (TP) group will vary across cases (as claims are not always the same, and depend, among others, on the chosen lingua franca). But in all the cases that we consider, the TP group is predominant and fairly stable (mostly made up of larger countries).20 For instance, in the case of English as lingua franca, only six countries (namely France, Germany, Italy, Poland, Romania and Spain) would vote for the proportional outcome.
4 CONCLUSIONS
We assume that the European Commission would be able and willing to provide a new budget to countries of the EU to acquire a common language as lingua franca, and examine how such a budget could be shared fairly. The proposal is meant to ease integration at a difficult moment that the EU is going through.21 We consider three possible candidates as linguae francae: English, German and French. We formalise this as a problem of adjudicating conflicting claims, in which countries claim compensations linked to the number of citizens who do not speak the lingua franca, and the distance between the official language in the country and the lingua franca. We consider two focal rules to solve the resulting problem, which can be traced back to ancient sources.
There are still several open questions. The first is relative to the language that would be chosen as becoming common. There is little doubt that, without Brexit, it would have been English. Today, this is getting more complex, since French or German became more competitive in the EU, though English remains a good candidate since it is also more widespread in the rest of the world than the two other languages.
A second issue is concerned with the fact of selecting more than one such language, in the event that countries disagree on a unique choice, and let them or their citizens choose which one they want to learn. This could be made with or without a budget increase, since the budget could be shared among languages according to a specific rule, and the sharing rules could be applied for each language separately. Doing this is technically possible, but it would be weaker and it would not enhance the same level of unity throughout the EU.
A third question is how countries would use their new budget. There are several possibilities briefly discussed in Section 1: paying part of the education of future teachers of the chosen linguae francae, helping parents to finance the extra hours needed to take language courses that are not taught at school or financing schools in their hiring of teachers by forcing schools to teach the lingua franca.
Finally, the EU would also have to cast a vote on the sharing rule which should be unique.
ACKNOWLEDGEMENTS
We thank an anonymous referee for helpful comments and suggestions. Moreno-Ternero acknowledges financial support from the Spanish Ministry of Economics, Industry and Competitiveness through the research project ECO2017-83069-P.
Notes
APPENDIX A
AN AXIOMATIC APPROACH TO SHARING RULES
We provide normative foundations to the Proportional and Talmud rules. To do so, we first list some axioms that we believe to be reasonable (either from an ethical or from an operational viewpoint).22
Axiom 1 says that if a group S ⊆ N of, say, countries decides to create a union, then the share given to the union should be the same as the total share for its members, before the union. Formally,
Axiom 1.Union Invariance.23 For each 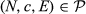 and each S ⊆ N, if
and each S ⊆ N, if 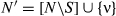 , cν = ∑i∈Sci, and
, cν = ∑i∈Sci, and 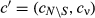
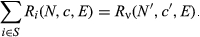
Axiom 2, which has played a fundamental role in axiomatic work on sharing (e.g., Thomson, 2012), suggests that if some claimants leave with their awards and one considers the problem of dividing what is left among the remaining claimants, these claimants should receive the same awards as initially. Formally,
Axiom 2.Consistency. For each 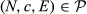 , each M ⊂ N, and each i ∈ M, we have
, each M ⊂ N, and each i ∈ M, we have 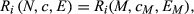 where EM = ∑i∈MRi(N, c, E).
where EM = ∑i∈MRi(N, c, E).
Axiom 3 depends on the possibility that after having divided the allocation of the endowment, say E1, it turns out that the actual value of the endowment is larger than was initially assumed or that an additional endowment E2 is also available. Then, two options are open: either the tentative division is cancelled altogether and the problem is solved using the new endowment E1 + E2, or we add to the initial distribution the result obtained by applying the rule to the additional endowment E2. The requirement formulated next is that both options should result in the same results. Formally,
Axiom 3.Composition up (Young, 1988). For each 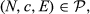 and each pair
and each pair 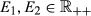 such that E1 + E2 = E,
such that E1 + E2 = E,  .
.
Axiom 4 makes for awards and losses to be allocated in the same way.
Axiom 4.Self-duality. For each 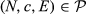 ,
,  .
.
We now move to an axiom modelling the concept of lower bounds, which have a long tradition in the theory of fair allocations. A focal lower bound is the so-called Average Truncated Lower Bound on Awards. It ensures each agent a minimal share of her individual claim, no matter what the other claims are. In particular, for a problem involving n agents, it establishes that any agent holding a feasible claim (a claim not larger than the endowment) will get at least one nth of her claim. And also that those agents whose individual claims are unfeasible will get at least one nth of the endowment.24 Formally,
Axiom 5.Average Truncated Lower Bound on Awards. For each 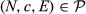 ,
, 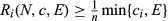 .
.
We have the following characterizations of the two rules we use, based on the above axioms:
Proposition 1.(Ju et al., 2007). A rule satisfies union invariance if and only if it is the proportional rule.
Proposition 2.(Young, 1988). A rule satisfies composition and self-duality if and only if it is the proportional rule.
Proposition 3.(Moreno-Ternero & Villar, 2004) A rule satisfies consistency, self-duality and average truncated lower bound on awards if and only if it is the Talmud rule.
It follows from the above statements that the Talmud rule neither satisfies union invariance nor composition. The proportional rule does satisfy consistency, but it does not satisfy average truncated lower bound on awards. It is also a consequence of the above statements that the Talmud rule satisfies a dual axiom to average truncated lower bound on awards, formalising meaningful upper bounds (or lower bounds on losses), whereas the proportional rule does not.25
At the risk of stressing the obvious, we acknowledge that there exist other axioms that the two rules considered here violate and that there exist other rules that satisfy (and violate) different sets of properties. Nevertheless, these two rules are salient in being the only ones satisfying the key properties mentioned above.
Finally, the other two rules with a strong tradition (and normative support) in this literature are the so-called constrained equal awards and constrained equal losses rules, mentioned in the introduction. One could indeed find properties satisfied by these two rules, whereas the two rules used in this paper do not. In the end, it would just be a value judgement to endorse some properties or others as more important. We did not take that route as it was beyond the scope of this paper. Nevertheless, it should be stressed that the Talmud rule is a hybrid between these two rules, which is not only exemplified in its definition, but also in the fact that it guarantees the lower and upper bounds mentioned above. It turns out that the constrained equal awards rule does the former but not the latter, whereas the constrained equal losses rule does the latter but not the former.




