1 INTRODUCTION

In a multitude of sciences, surfaces constitute a major tool with respect to the visualization and evaluation of spatial phenomena. One only needs to think of geoscientific applications related to air pressure (https://www.dwd.de/EN/ourservices/global_air_pressure/luftdruckglobal.html [accessed 7 March 2024]), precipitation (https://climate.copernicus.eu/esotc/2020/precipitations [accessed 7 March 2024]) or temperature (https://climate.copernicus.eu/surface-air-temperature-maps [accessed 7 March 2024]), social and economic applications concerning accessibilities (Wu & Hine, 2003), risk assessment (Bai et al., 2011) or traffic noise (Debnath & Singh, 2018), or technical applications related to nanotechnology or precision engineering, with the occurring surfaces in these instances being at the micrometer or nanometer scale (Dedkova & Florinsky, 2023; Jiang et al., 2021; Newton et al., 2019).

With respect to the remainder of this article and in order to avoid misunderstandings, some comments concerning (a) the difference between surfaces being studied within the geosciences and other sciences, such as the technical ones, and (b) the difference between the geometrical and topological characterization of surfaces are indispensable.

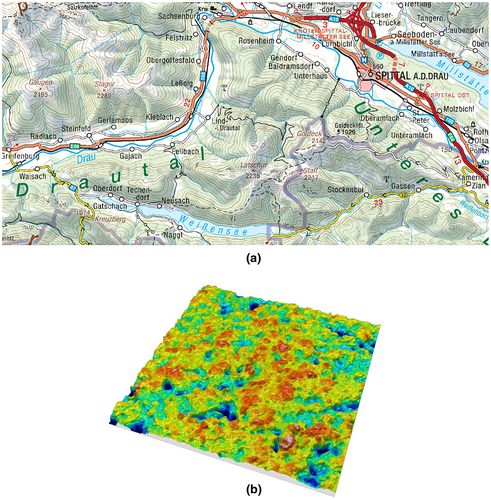
Concerning the first difference, it can be said that the landforms most frequently investigated by geoscientists are fluvially eroded terrains, which are characterized by an intimate interrelationship between their ridge and channel patterns. The main features of terrains like these are, on the one hand, the strong segmentation of the landscape by dendritic river systems and, on the other hand, the absence of depressions, which, except in the case of lakes, are even viewed as artifacts that have to be removed on maps and within geographic information systems by appropriate algorithms. An example of a surface portraying a fluvially eroded terrain is shown in Figure 1a and visualizes the Latschur mountains, located in Carinthia, Austria (https://maps.bev.gv.at/#/center/13.3513,46.7675/zoom/11.6 [accessed 7 March 2024]). Quite different from this type of surfaces are, for example, those that are examined in nanotechnology or precision engineering, with these surfaces being characterized by small-scale features, which are due to the production process, abrasion, wear, etc. In terms of physiognomy, two common features of these surfaces are, on the one hand, the complete absence of river-like structures and, on the other hand, the existence of numerous depressions, with the effect that these surfaces appear as the arrangement of crisscross distributed pits, passes, and peaks. An example of a technical surface is shown in Figure 1b; it visualizes brushed stainless steel, with the data obtained by an optical profiler.

Concerning the second difference, it can be said that each geometrical characterization of a surface relies exclusively on the $x$-, $y$-, and $z$-coordinates of arbitrary data points, which are arranged either in form of a regular grid or a triangular irregular network; in any case, the topological relationships between the respective data points are not taken into account. In contrast, each topological characterization is based merely on the interrelationships between the critical points of the function representing terrain, thereby disregarding their specific locations in space. A study of the literature reveals that the majority of research conducted to date focuses on techniques related to the geometrical description of surfaces, whereas only a minority addresses methods concerning their topological characterization.

In order to avoid misunderstandings, the difference between drainage basins and basins, with the latter being referred to in the heading of this article, will be explained next. As already outlined, drainage basins are related to rivers and are characterized by dendritic structures, with their basic entities being the channels and ridges that shape the respective surfaces. However, the critical points of the surfaces are taken into account not in the least, with this non-consideration being responsible for the fact that drainage basins cannot be described in a Morse theoretic way. In contrast to drainage basins are basins, which represent the images of two-dimensional ascending manifolds of local minima and can be defined by means of calculus, with their interrelationships being the subject of topology and Morse theory (confer Section 2). In colloquial terms, a basin represents the area that starts from a pit, extends upwards around it, and is bordered by a closed series of ridge lines, which in turn alternately connect passes and peaks.¹ Obviously, the pits and basins, which are analyzed within Morse theory, are exactly those that are regarded as artifacts within the geosciences and related disciplines. To summarize, from a formal point of view, the two concepts drainage basin and basin describe two completely different entities that have nothing to do with each other.

While the importance of drainage basins is obvious and requires no further explanation, the question arises as to the relevance of basins. As briefly sketched below, their importance is related to the simplification of surfaces, which denotes the process of deriving from a given topographic surface another of less complexity, but with the structural properties being left unchanged. In the geosciences, this simplification process, which describes the transition from large-scale to medium-scale or small-scale maps, is termed map generalization, while in the technical sciences, it refers to the reduction of measurement noise. Technically speaking, in both cases, basins and/or hills of minor importance are removed, whereby different criteria, such as differences in altitudes, the area of a basin (hill), the circumference of a basin (hill), or the volume of a basin (hill) may be applied. Whereas the simplification process is relatively simple when only differences in altitudes have to be taken into account, in all other instances it is rather complicated, as in these cases two adjacent basins (hills) have to be merged according to some pre-specified criteria.

The standard ISO 25178-2 (ISO, 2021),² which refers, among others, to the feature-based simplification of (technical) surfaces, lists all aforementioned criteria but considers in detail only the generalization based on height differences, with this being due to the topological data structure used for the storage of the respective surfaces. The only data structure specified for this purpose in ISO 25178-2 is the change tree, which, however, suffers from the serious drawback that it does not contain any geometrical information related to the gradient flow (Wolf, 2017, 2021).

Obviously, a generalization process based on the area, circumference, or volume of a basin (hill) may be of interest also for the geosciences and related disciplines. Conceptually, any simplification that is grounded on these criteria may be regarded as a two-step process, with the first step being responsible for the correct identification of the basins (hills) and the second step accounting for the correct fusion of two adjacent basins (hills) according to some pre-specified criteria. Anyway, first of all, an appropriate data structure for the topological characterization of the respective surfaces must be defined.

The topic of the present article is related to the first aforementioned step, viz., the identification of basins (hills) on the basis of critical nets, with this data structure having the great advantage to contain relevant information concerning the gradient flow. The article is structured in such a way that in Section 2 a brief sketch of the required mathematical concepts from multivariable calculus and Morse theory is given. Hereafter, in Section 3, it is demonstrated how graphs can be used to describe the topological structure of topographic surfaces and how the boundaries of two-dimensional ascending and descending manifolds can be characterized in a graph theoretic way. After the presentation of a data structure that may be used for the storage of graphs within computers in Section 4, in Section 5 an algorithm for the delineation of two-dimensional ascending and descending manifolds is described. In this context, not only a particularized description of the algorithm is given, but its modus operandi is also illustrated by means of two practical examples.

2 MATHEMATICAL BACKGROUND

The widespread use of surfaces necessitated an appropriate theoretical framework with respect to their formal characterization, especially as Kweon and Kanade (1991, 1994) realized as early as in the 1990s that the definitions of topographic features in terms of natural languages are ambiguous in many ways. Their criticism initiated a lot of theoretical research in the following years, above all, by mathematicians and computer scientists engaged in computer graphics as well as computational geometry, who tried to rectify the exposed deficiencies by applying $n$-dimensional calculus and topology.

Before focussing on the mathematical essentials, another point must be accentuated, too, viz., that surfaces do not exist per se, but they represent models, thus exhibiting the following three features being first addressed by Stachowiak (1973): (a) models are always representations of natural or artificial originals (mapping feature), (b) models merely capture those characteristics of the originals that seem essential to their creators (reduction feature), and (c) models are always designed for specific subjects, for specific periods of time, and for specific mental or actual operations (pragmatic feature).

Surfaces of any kind are usually described by functions of two variables, whereby the modeling aspect is expressed by the properties that a specific surface must exhibit. In view of the subject of this article, the focus is laid exclusively (a) on functions $f\left(x,y\right)$ of two variables and (b) on functions that are defined on the $\left(x,y\right)$-plane or a subset of it. However, it should be pointed out that the theory also applies to mappings of $n$ variables being defined on $n$-dimensional smooth manifolds; examples of two-dimensional smooth manifolds are, aside from the $\left(x,y\right)$-plane, the Earth's surface (in this case $x$ and $y$ denote the geographical latitude and longitude), the sphere, or the torus. In this context, it must be emphasized that in the theory concerning manifolds, the term surface denotes, in general, the two-dimensional manifold representing the domain on which a function $f\left(x,y\right)$ is defined.

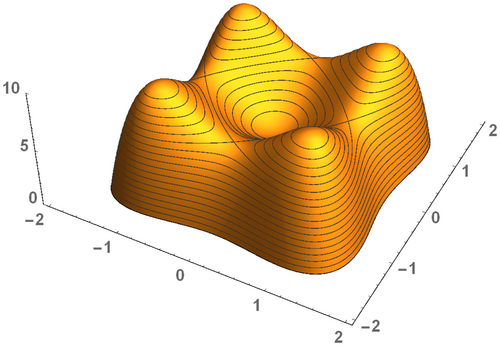
With respect to a better understanding, the underlying theoretical concepts are explained in the following in a rather descriptive way using the function $f\left(x,y\right)=-3x^4+6x^2-3y^4+6y^2+3$ for $x,y\in \left[-2,2\right]$, whose graph is visualized in Figure 2.³ The formal specifications of all definitions and theorems used within the present article can be found in Wolf (2021), whereas exhaustive introductions into $n$-dimensional calculus and Morse theory are provided by any standard textbook on these subjects, such as, for example, by Ghorpade and Limaye (2010) or Moskowitz and Paliogiannis (2011) for the first topic, and, for instance, by Knudson (2015), Matsumoto (2002), or Zomorodian (2005) for the second one.

First of all, the focus is laid on the zero-dimensional elements of interest, whereby it must be strictly distinguished whether the respective points are located in the domain of $f\left(x,y\right)$ or on its graph. To be precise, according to their definitions, the critical points of a function $f$, viz., the local maxima, saddles, and local minima are elements of the domain of $f$ and thus they are situated in the $\left(x,y\right)$-plane. Although this is a mathematical standard, many authors ignore it and use the terms local maximum, saddle, or local minimum for both the argument $\left(x_0,y_0\right)$ and its image $f\left(x_0,y_0\right)$. In the present article, however, a clear distinction between argument and image is made, with the images of local maxima being denoted as peaks or summits, the images of saddles being denoted as passes or cols, and the images of local minima being denoted as pits or depressions (confer Table 2).

Applied to the function $f\left(x,y\right)=-3x^4+6x^2-3y^4+6y^2+3$, it can be said that $f\left(x,y\right)$ has four local maxima at $\left(-1,-1\right),\left(-1,1\right),\left(1,1\right)$, and $\left(1,-1\right)$, four saddles at $\left(-1,0\right),\left(0,1\right),\left(1,0\right)$, and $\left(0,-1\right)$, as well as a local minimum at $\left(0,0\right)$; in addition, it has four peaks at $\left(-1,-1,9\right),\left(-1,1,9\right),\left(1,1,9\right)$, and $\left(1,-1,9\right)$, four passes at $\left(-1,0,6\right),\left(0,1,6\right),\left(1,0,6\right)$, and $\left(0,-1,6\right)$, as well as a pit at $\left(\mathrm{0,\; 0,\; 3}\right)$.

With respect to the explanations given later on, a distinction between the well-known nondegenerate critical points, i.e. the local maxima, saddle points, and local minima, and the less-known degenerate ones must be made.⁴ As can be shown, there exists a multitude of the latter, such as, for instance, crossed pig troughs, monkey saddles, or starfish saddles (confer Figure 3).

In the present article, we will focus exclusively on smooth functions without degenerate critical points, with these functions being termed Morse functions. As can be proved, the local maxima, saddle points, and local minima visualized in Figure 3, are the only types of critical points that Morse functions can have (obviously, the function $f\left(x,y\right)=-3x^4+6x^2-3y^4+6y^2+3$ is a Morse function). Worth mentioning is also another property of Morse functions, viz., that any smooth function can be converted to a Morse function by an arbitrary small perturbation that splits each degenerate critical point into some nondegenerate ones. Presumably, this property is responsible for the great popularity of Morse functions when analyzing real-world data.

The next property of Morse functions to be mentioned in this article concerns the numerical relationship between the different types of critical points. Precisely speaking, it can be proved that for any Morse function $f$, which is defined on a sphere, the number of local maxima minus the number of saddles plus the number of local minima is always two.⁵

Of special importance for geoscientific implementations is the fact that, under an additional criterion, the previous equality also holds for Morse functions that are defined on simply connected domains whose boundaries are closed contour lines on which no critical points are located (Grujić, 2011). A domain like this can be thought of as an island in the ocean, whereas the respective Morse function can be imagined as a mapping that assigns to each point $\left(x,y\right)$ of the island its height $z=f\left(x,y\right)$. Obviously, the domain of the Morse function $f\left(x,y\right)=-3x^4+6x^2-3y^4+6y^2+3$ is simply connected, i.e. it has no holes, and its boundary is a closed contour, viz., the contour line of height zero, on which there are no critical points.

Using the metaphor of the island in the ocean, the additional assumption affects the handling of the points lying beyond the island. To guarantee that the domain is, in a mathematical sense, compact, all these points must be identified as a single local minimum with an assigned height of $-\infty$; the outlined identification process is denoted as one-point compactification (Gyulassy, 2008; Zomorodian, 2005), the pit attained is referred to as surrounding pit (Pfaltz, 1976; Wolf, 2014, 2017, 2020, 2021) or virtual pit (Scott, 2004a; Takahashi, 2004; Takahashi et al., 1995), subject to the particular author. Considering the graph of the function $f\left(x,y\right)=-3x^4+6x^2-3y^4+6y^2+3$ for $x,y\in \left[-2,2\right]$, one realizes that there are four local maxima at $\left(-1,-1\right),\left(-1,1\right),\left(1,1\right)$, and $\left(1,-1\right)$, four saddle points at $\left(-1,0\right),\left(0,1\right),\left(1,0\right)$, and $\left(0,-1\right)$, as well as one local minimum at $\left(0,0\right)$. Taking into account also the local minimum, whose image is the surrounding pit, one obtains for the number of local maxima minus the number of saddles plus the number of local minima $4-4+2=2$, just as it should be according to the equation previously described.

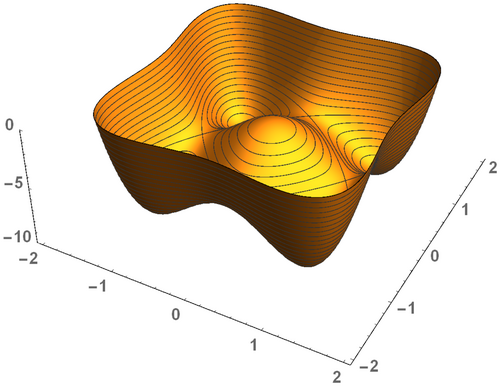
It should be noted that there exists an analogous concept, termed surrounding peak or virtual peak, having an altitude of $+\infty$. Using again the metaphor of the ocean, this concept is required for the analysis of areas lying below the ocean's surface. Such an area is visualized in Figure 4, which illustrates the graph of the function $g\left(x,y\right)=3x^4-6x^2+3y^4-6y^2-3$ for $x,y\in \left[-2,2\right]$. Obviously, $g\left(x,y\right)$ has one local maximum at $\left(0,0\right)$, four saddle points at $\left(-1,0\right),\left(0,1\right),\left(1,0\right)$, and $\left(0,-1\right)$, as well as four local minima at $\left(-1,-1\right),\left(-1,1\right),\left(1,1\right)$, and $\left(1,-1\right)$.

After the discussion of the zero-dimensional elements, namely, the critical points, the focus will next be turned onto the one-dimensional ones, viz., the integral lines, which are also termed integral curves⁶ (for their formal definition confer, for example, Biasotti et al. (2008), Čomić and de Floriani (2011), Edelsbrunner et al. (2003), Knudson (2015), Rote and Vegter (2006), or Zomorodian (2005)). Less formally, an integral line of a function $f\left(x,y\right)$ represents a maximal path $p$, whose tangent vectors agree with the gradient vector field $\left(\genfrac{}{}{0px}{}{f_x}{f_y}\right)$; the two endpoints of an integral line are referred to as origin and destination. An important property of integral lines is that they are, according to their formal definition, open sets, with their two endpoints always being critical points.

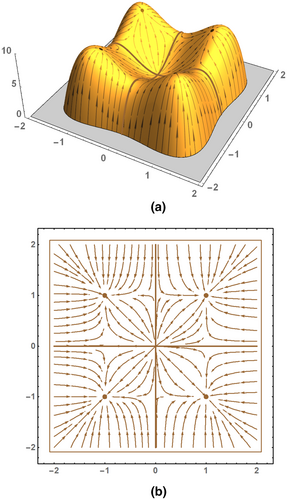
Figure 5a visualizes the graph of the function $f\left(x,y\right)=-3x^4+6x^2-3y^4+6y^2+3$ for $x,y\in \left[-2,2\right]$ as well as some paths of steepest ascent, Figure 5b illustrates those integral lines that correspond to the paths of steepest ascent depicted in Figure 5a.

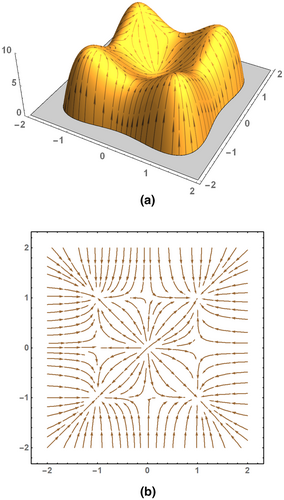
It must be emphasized that the terminology concerning integral lines, like the one relating to critical points, is ambiguous. Despite the fact that integral lines are, due to their formal definition, located in the domain of a Morse function $f$, some authors denote as integral line both the path $p$ and its image $f\left(p\right)$; for these authors, the lines plotted in Figure 5a are thus also integral lines.

Geographically speaking, the difference between the lines of steepest ascent and the integral lines can be characterized as follows: If a mountaineer wants to reach a summit, although he can hardly see anything because of thick fog, his optimal strategy is to follow the line of steepest ascent, i.e. he will follow one of the lines shown in Figure 5a, subject to his actual location. When being home again and describing the route he has taken to his friends, the mountaineer will, however, take a topographic map and show them the projection of the path of steepest ascent on the $\left(x,y\right)$-plane, i.e. he will show them the respective integral line depicted in Figure 5b.

There is one further topic to be addressed in this context, as it will prove to be of utmost importance in the sections to follow. Obviously, Figure 5 seems to disagree with the previously mentioned property of integral lines saying that their endpoints are always critical points; as can be seen, some integral lines originate from the boundary of the domain and not from a critical point (in case of the function $g\left(x,y\right)=3x^4-6x^2+3y^4-6y^2-3$ for $x,y\in \left[-2,2\right]$, some integral lines end at the boundary and not in a critical point). This disagreement, however, is no actual one because, as a result of the one-point compactification, all points lying outside the domain of the function are identified as a single local minimum with an assigned height of $-\infty$. Thus, with respect to topology, those integral lines, which apparently originate from the boundary, originate actually from the local minimum associated with the surrounding pit (the same applies for integral lines, which apparently end at the boundary, but end actually in the local maximum associated with the surrounding peak).

Of particular interest with regard to the remainder of this article are those integral lines whose origin is a local minimum and whose destination is a saddle point, as well as those integral lines that have their origin in a saddle point and their destination in a local maximum. Within this article, integral lines of the first type are denoted as course-separatrices, while integral lines of the second type are termed ridge-separatrices, with integral lines of both types being subsumed under the generic term separatrices (Čomić et al., 2005; Danovaro et al., 2003; Günther, 2012).

Figure 6b illustrates the separatrices of the function $f\left(x,y\right)=-3x^4+6x^2-3y^4+6y^2+3$ for $x,y\in \left[-2,2\right]$, while the respective paths of steepest ascent are visualized in Figure 6a. In everyday language, the paths of steepest ascent associated with course-separatrices are termed course lines or courses, whereas the paths of steepest ascent associated with ridge-separatrices are termed ridge lines or ridges (confer Table 2).

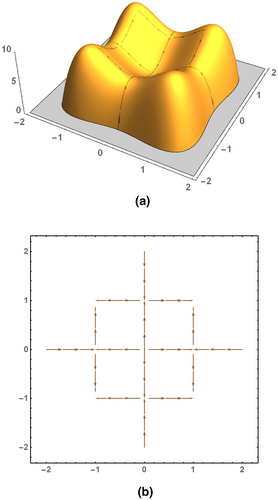
After having provided a brief survey of the zero-dimensional as well as one-dimensional elements of a manifold, i.e. the critical points and integral lines, the focus will next be turned onto the two-dimensional structures, i.e. the ascending manifolds, also referred to as unstable manifolds, and the descending manifolds, also denoted as stable manifolds (for their formal definition confer, for example, Biasotti et al. (2008), Čomić and de Floriani (2011), Günther (2012), Knudson (2015), Rote and Vegter (2006), or Tierny (2017)). Less formally, an ascending manifold $A\left(p\right)$ of a critical point $p$ is the set of all points that belong to integral lines with origin $p$, whereas a descending manifold $D\left(p\right)$ of a critical point $p$ is the set of all points that belong to integral lines with destination $p$.

Figure 7b illustrates some integral lines associated with the ascending manifold of the local minimum $\left(0,0\right)$ of $f\left(x,y\right)=-3x^4+6x^2-3y^4+6y^2+3$ for $x,y\in \left[-2,2\right]$. It should be emphasized that the separatrices forming the boundary do not belong to the ascending manifold, which is, according to its formal definition, an open subset (Biasotti et al., 2008; Tierny, 2017). Figure 7a visualizes the corresponding paths of steepest ascent as well as the ridges that form the boundary of the associated region on the graph of the function. In everyday language, regions like this are termed basins or hollows (confer Table 2). Evidently, in Figure 7b the white area outside the square, which corresponds to the ascending manifold $A\left(\left(0,0\right)\right)$, represents the ascending manifold of the local minimum that is associated with the virtual pit.

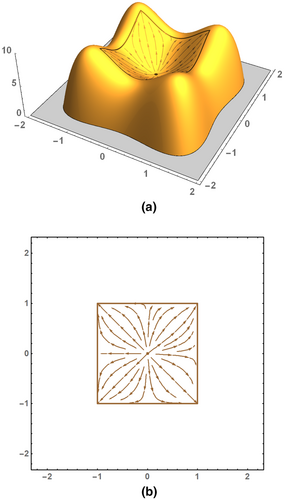
Figure 8b illustrates some integral lines associated with the descending manifolds of the local maxima $\left(-1,-1\right),\left(-1,1\right),\left(1,1\right)$, and $\left(1,-1\right)$ of $f\left(x,y\right)=-3x^4+6x^2-3y^4+6y^2+3$ for $x,y\in \left[-2,2\right]$. Completely analogous to ascending manifolds, the separatrices forming the boundaries do not belong to the descending manifolds, which are, according to their definition, also open subsets of $M$ (Biasotti et al., 2008; Tierny, 2017). Figure 8a visualizes the corresponding paths of steepest ascent as well as the courses that form the boundaries of the associated regions on the graph of the function. In everyday language, regions like these are termed mountains or hills (confer Table 2).

In textbooks, the terms ascending manifold and descending manifold are usually discussed when introducing two-dimensional structures. However, both concepts are not only applicable to two dimensions, but, in the case of a two-dimensional manifold, to all dimensions less than or equal to two. Depending on whether they are defined for a local maximum, saddle, or local minimum, and in dependence of whether they are defined for the ascending or descending case, different forms of appearance are possible. Table 1, whose theoretical foundation can be found in Biasotti et al. (2008), Čomić and de Floriani (2011), or Zomorodian (2005), summarizes the interrelationship between the type of a critical point and the type of manifold associated with it.

As the present article addresses in particular two-dimensional ascending and descending manifolds, some of their most relevant features are itemized next (confer Čomić and de Floriani (2008), Edelsbrunner et al. (2003), or Zomorodian (2005)).

The first property to be mentioned is that the ascending (descending) manifold of a Morse function $f$ is the descending (ascending) manifold of $-f$, with this feature being referred to as duality.

The second property worth mentioning is that the ascending (descending) manifolds are pairwise disjoint, with this being due to the fact that both types of manifolds are open sets.

The third noteworthy property says that the ascending (descending) manifolds cover the manifold $M$, with this being evident when beholding Figures 7b and 8b; the two illustrations demonstrate how the manifold $M$ can be covered either by ascending manifolds or by descending manifolds, with each point of the surface belonging both to a specific ascending manifold and a specific descending one. Obviously, this corresponds to the everyday experience that each point of a topographic surface can be regarded as an element of both a basin and a mountain (confer Maxwell (1870)).

The last property to be mentioned, finally, refers to the boundary of an ascending (descending) manifold stating that it is the union of lower-dimensional cells; to put it differently, it says that a one-dimensional manifold (separatrix) is bounded by zero-dimensional manifolds (critical points), and a two-dimensional manifold (region) is bounded by one-dimensional manifolds (separatrices) in combination with zero-dimensional manifolds (critical points).

Table 2 summarizes the designations for the corresponding elements being located in the domain and on the image of a function $f\left(x,y\right)$. Evidently, there exists a one-to-one correspondence between the individual elements, with this relationship being recoursed in Sections 3 and 5.

After the rather descriptive survey of some important concepts related to Morse theory, in Section 3 the focus is laid on the topic of how to represent the topological structures described in this section by graphs, with this approach offering new perspectives and results.

3 CRITICAL NETS

For more than 100 years, graphs have been used to characterize topographic surfaces in a topological way (to avoid misunderstandings, within the remainder of this article the term topographic surface denotes the image of a Morse function $f\left(x,y\right)$, whereas the term surface refers to the domain of $f\left(x,y\right)$, with the latter being usual in the theory related to manifolds (confer Section 2)). Typical examples of graphs used for the characterization of topographic surfaces with respect to their topology are Reeb graphs, change trees (contour trees), or surface networks (for comprehensive surveys of these topological structures confer, for instance, Biasotti et al. (2008), Heine et al. (2016), Wolf (2017), or Yan et al. (2021)).

Contour trees, being introduced by Boyell and Rushton (1963), were used in the geosciences as early as in the 1970s by Mark (1977, 1979) for the analysis of geomorphic surfaces. Since then, the contour tree was used occasionally for different purposes, such as for the description and storage of landscapes at various levels of detail (Guilbert, 2013), for the identification and investigation of depressions (Wu et al., 2015), or for the exploration of geographic hotspots (Zhang et al., 2021).

(Weighted) surface networks, which were introduced by Pfaltz (1976, 1979) and Wolf (1988a, 1988b, 1989, 1991), are another data structure to characterize topographic surfaces in a topological way. The vertex sets of these graphs are composed of the pits, passes, and peaks, whereas the edge sets consist of the course lines and ridge lines, associated with a Morse function being defined over a domain that is simply connected and whose boundary is a closed contour line on which no critical points are located. In addition, real numbers greater than zero are assigned to the edges and vertices, with these weights indicating their importance for both the macro-structure and the micro-structure of the respective topographic surface. Practical applications of this data structure are primarily related to both a topologically based characterization and generalization of topographic surfaces (Jeong, 2014; Schneider, 2005; Wolf, 1988a, 1988b, 1989) as well as technical surfaces (Scott, 2003, 2004a, 2004b; Wolf, 1991, 2017, 2020, 2021).

In the following, however, the focus is not on the elements situated on the topographic surfaces, i.e. the pits, passes, peaks, courses, and ridges, as in the case of weighted surface networks, but rather on the corresponding elements located in the respective domains, i.e. the local minima, saddles, local maxima, course-separatrices, and ridge-separatrices, with this approach being much more intuitive with regard to the explanations given in Section 2.

Throughout the remainder of this article, it is assumed that the critical points as well as the separatrices are known. For their determination as well as the determination of other surface features numerous algorithms were designed over the past decades, whereby the most powerful of them do not only extract the critical points and separatrices, but entire topological structures like contour trees (Carr, 2004; Pascucci & Cole-McLaughlin, 2004; Takahashi, 2004; Takahashi et al., 1995; Weber et al., 2007) or surface networks (Schneider, 2005; Takahashi, 2004; Takahashi et al., 1995).

For illustration, let us consider the critical points as well as the separatrices depicted in Figure 6, this time, however, arranged in a quite different way, viz., in the one that is shown in Figure 9a. Evidently, the set of all critical points can be subdivided into three disjoint subsets LMIN, SADD, and LMAX, with the first one comprising the local minima, the second one the saddles, and the third one the local maxima. In this context, the local minima are ${\mathit{\text{lmin}}}_1=\left(0,0\right)$ and ${\mathit{\text{lmin}}}_2$, which represents the pre-image of the surrounding pit; the saddles are ${\mathit{\text{sadd}}}_1=\left(-1,0\right)$, ${\mathit{\text{sadd}}}_2=\left(0,1\right)$, ${\mathit{\text{sadd}}}_3=\left(1,0\right)$, and ${\mathit{\text{sadd}}}_4=\left(0,-1\right)$, whereas the local maxima are ${\mathit{\text{lmax}}}_1=\left(-1,-1\right)$, ${\mathit{\text{lmax}}}_2=\left(-1,1\right)$, ${\mathit{\text{lmax}}}_3=\left(1,1\right)$, and ${\mathit{\text{lmax}}}_4=\left(1,-1\right)$ (in Figure 9 the points are denoted by lmin_1, lmin_2, etc.). The lines leading from the local minima to the saddles represent the course-separatrices, whereas the lines leading from the saddles to the local maxima represent the ridge-separatrices.

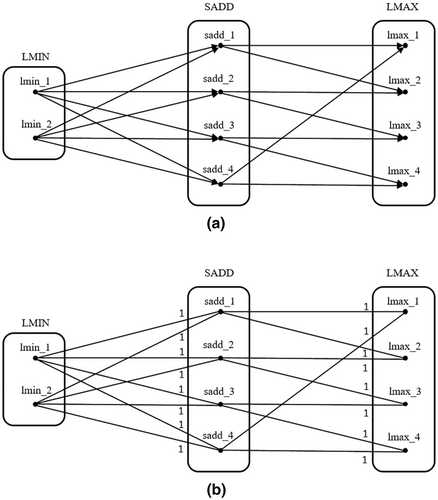
In mathematics, a structure that looks like the one depicted in Figure 9a is termed directed graph and defined formally as follows (for an introduction into graph theory, confer, for instance, Bondy and Murty (1976)).

Obviously, the graph depicted in Figure 9a is moreover a directed tripartite graph because its vertex set $V$ can be subdivided into three disjoint subsets $V_1$, $V_2$, and $V_3$ in such a way that each edge joins either one vertex of $V_1$ with one vertex of $V_2$, or one vertex of $V_2$ with one vertex of $V_3$. In the present case, the three disjoint subsets are LMIN, SADD, and LMAX, with each arc being incident either with one vertex of LMIN and one vertex of SADD, or with one vertex of SADD and one vertex of LMAX; as a consequence, the two subgraphs [LMIN, SADD] and [SADD, LMAX] are bipartite.

As required by P0, each critical net must be planar because an intersection of the arcs, which would be equivalent to an intersection of the corresponding separatrices, would imply the non-realisability of the associated topographic surface. P1 ensures, on the one hand, that all local minima and saddles are connected by course-separatrices and, on the other hand, that all saddles and local maxima are connected by ridge-separatrices. While P2 is a consequence of the Morse inequality, P3 is due to the definition of a Morse function (confer Section 2). P4 ensures that if there exists a path from the local minimum ${\mathit{\text{lmin}}}_i$ via the saddle ${\mathit{\text{sadd}}}_j$ to the local maximum ${\mathit{\text{lmax}}}_k$ that consists only of arcs with valency one, then there exists another path from the local minimum ${\mathit{\text{lmin}}}_i$ to the local maximum ${\mathit{\text{lmax}}}_k$ via a distinct saddle ${\mathit{\text{sadd}}}_l$. P5a and P5b exclude arc configurations that would result in nonrealisable critical nets (Pfaltz, 1976). To illustrate, let us consider Figure 11b: Obviously, the saddle point $\mathit{sad}11$ is connected via two course-separatrices with the local minimum $\mathit{min}1$, representing the pre-image of the surrounding pit. These arcs represent a circuit in the bipartite graph [LMIN, SADD]. P5a ensures that $\mathit{sad}11$ must be connected via ridge-separatrices with two different local maxima, in the present case with $\mathit{max}1$ and $\mathit{max}9$. If $\mathit{sad}11$ would be adjacent to the same local maximum, this would be equivalent to a circuit in [SADD, LMAX], thus implying intersecting courses and ridges (the same holds for the saddle point $\mathit{sad}13$ and the two local maxima $\mathit{max}1$ and $\mathit{max}10$).

Next, a new type of graph is derived from the critical net by the following two modifications: (a) the arc directions are ignored (consequently, the arcs are referred to as edges in these instances, as this is the standard term in graph theory) and (b) a weight of one is assigned to each edge. In this way, the associated undirected weighted critical net, which is depicted in Figure 9b, is obtained. Formally, a structure like this, whose importance will become apparent in Section 5, can be specified as follows.

In weighted graphs, the length of a path, which is defined as the sum of the individual edge weights, constitutes an important theoretical concept. A special case occurs when all edge weights are one as, in this instance, the length of the path indicates the number of edges it consists of.

In many optimization problems, but also in the context of the delineation of two-dimensional ascending and descending manifolds, the problem of finding the shortest path, i.e. the path of minimal length, between two or more specified vertices has to be solved. Suffice it to say here that this can be achieved by using the algorithm of Dijkstra, which is discussed in Section 5.1.

After having introduced the previous theoretical concepts, it is possible to characterize the boundaries of two-dimensional ascending and descending manifolds in terms of graph theory as follows.

After having shown how the boundaries of two-dimensional ascending and descending manifolds can be characterized in a graph theoretic way, the next issue is to present a data structure that is eligible for the storage of graphs within computers.

4 STORAGE OF GRAPHS WITHIN COMPUTERS

Different methods for the storage of both weighted and unweighted graphs within computers were developed over the past decades. The best-known approaches for the storage of unweighed graphs are adjacency matrices and ordered pairs, whereas the most frequently used techniques for weighted graphs are weighted adjacency matrices and arrays of triples. With respect to the algorithm presented in Section 5, however, the pointer structure, which is discussed next, seems to be much more promising. In addition, it is demonstrated how the computer representation of the graph depicted in Figure 9b looks like. For the sake of simplicity, the critical points are enumerated as ${\mathit{\text{lmin}}}_1=1$, ${\mathit{\text{lmin}}}_2=2$, ${\mathit{\text{sadd}}}_1=3$, ${\mathit{\text{sadd}}}_2=4$, ${\mathit{\text{sadd}}}_3=5$, ${\mathit{\text{sadd}}}_4=6$, ${\mathit{\text{lmax}}}_1=7$, ${\mathit{\text{lmax}}}_2=8$, ${\mathit{\text{lmax}}}_3=9$, and ${\mathit{\text{lmax}}}_4=10$ in this context.

Furthermore, the array node contains the adjacent nodes of the first, the second, $\dots$, the nth vertex consecutively, while the array weight does the same with the corresponding arc weights (in case of an unweighted graph this array is not required). Due to its definition, the array pointer ensures that in the section between $\mathit{\text{node}}\left(\mathit{\text{pointer}}\left(v\right)\right)$ and $\mathit{\text{node}}\left(\mathit{\text{pointer}}\left(v+1\right)-1\right)$ of the array node all adjacent vertices of the vertex $v$ are located, with the analogy holding for the arc weights and the section between $\mathit{\text{weight}}\left(\mathit{\text{pointer}}\left(v\right)\right)$ and $\mathit{\text{weight}}\left(\mathit{\text{pointer}}\left(v+1\right)-1\right)$ of the array weight.

To illustrate, let us consider the graph visualized in Figure 9b and its representation shown in Table 3. As the graph has 10 vertices and 16 edges, i.e. $2\cdot 16=32$ arcs, the length of the array pointer is $10+1=11$, whereas the lengths of the two arrays node and weight are 32. As can be seen, in the array node the adjacent nodes of the vertices $1,2,\dots ,10$, i.e. the nodes $\mathrm{3,\; 4,\; 5,\; 6,\; 3,\; 4,\; 5,\; 6},\dots \mathrm{,\; 5,\; 6}$, are recorded in succession, with the arc weights being recorded in an analogue way in the array weight. The vertical bars depicted in Table 3 delimit the sections of the arrays node and weight in which the adjacent nodes as well as the corresponding arc weights of the first, the second, $\dots$, the tenth vertex can be found. The equivalent of the vertical bars is the array pointer whose elements refer to the indices immediately after the vertical bars. The adjacent vertices of the vertex $v=1$ can thus be found between the positions pointer$\left(1\right)=1$ and pointer$\left(1+1\right)-1=$ pointer$\left(2\right)-1=5-1=4$, the adjacent vertices of the vertex $v=2$ between the positions pointer$\left(2\right)=5$ and pointer$\left(2+1\right)-1=$ pointer$\left(3\right)-1=9-1=8$, etc.

When comparing the pros and cons of the pointer structure with those of other data structures for the storage of graphs, it can be said that the pointer structure is very complex, which makes it almost impossible to add and/or remove arcs manually, but it provides rapid access to adjacent vertices and corresponding arcs weights via indices. With respect to practical applications, the most efficient approach is thus to capture a graph by an easily manageable structure and to convert it hereafter into the pointer structure, with this strategy resulting in significantly shorter execution times. This approach has been chosen for identifying the boundaries of two-dimensional ascending and descending manifolds in Section 5.

5 DELINEATION OF TWO-DIMENSIONAL ASCENDING AND DESCENDING MANIFOLDS

Although delineation of two-dimensional ascending and descending manifolds sounds to be a bulky issue, it represents the theoretical basis for a large number of applications in which functions $f\left(x,y\right)$ are used to describe phenomena related to climate, economy, or engineering, to mention only a few. All of these applications, however, do not refer to the domains of the respective functions, where the two-dimensional ascending and descending manifolds are located, but rather to their images.

In the present section, an algorithm is presented, with the help of which the boundaries of two-dimensional ascending and descending manifolds can easily be identified, with this being the mathematical equivalent to the identification of basins or hills. As mentioned in Section 2, each of these boundaries is the union of lower-dimensional cells, i.e. in the present case, of zero-dimensional cells (critical points) and of one-dimensional cells (separatrices). Due to Theorem 3.1, which establishes the connection between two-dimensional ascending manifolds and graphs, the boundary of such a manifold $A\left(\mathit{\text{lmin}}\right)$ of a local minimum lmin corresponds in the associated UWCN to the unique circuit of that subgraph of [SADD, LMAX] that is induced by all saddle points being adjacent to lmin in combination with the local maxima being adjacent to these saddle points. In addition, a second theorem was presented with the help of which the boundary of the descending manifold $D\left(\mathit{\text{lmax}}\right)$ of a local maximum lmax can be determined.

With respect to an efficient data management, the pointer structure described in Section 4 is used for the storage of the UWCN. For the determination of the circuits in the bipartite graphs, a modified version of the algorithm of Dijkstra, which is described separately in Section 5.1, is applied. The algorithm for the identification of the boundary of a two-dimensional ascending or descending manifold itself is presented in Section 5.2, with two examples given in Sections 5.3 and 5.4.

5.2 An algorithm for the identification of the boundaries of two-dimensional ascending and descending manifolds

For the sake of comprehensibility, the algorithm for the identification of the boundary of a two-dimensional ascending and descending manifold is implemented as a program package that consists of the master routine Main together with four auxiliary procedures Bin_Search, Insert, Manifold_Ascending, and Manifold_Descending. The tasks performed by these five procedures are described next, the interrelationships between them are illustrated in Figure 10. The whole package, which is implemented in C# (Microsoft^® Visual Studio^® 2022, version 17.5.1), is available as supplementary material on https://github.com/GWWGWWGWW/TGIS in the file _TGIS_ascending_and_descending_manifolds.zip.

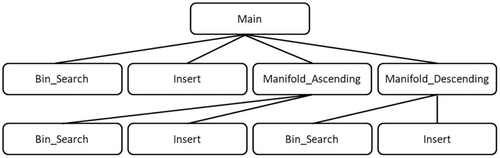
Procedure Main represents the driver routine of the package. It is responsible for the specification of the virtual pit or virtual peak, respectively, the input of the data, the execution of the one-point compactification, the specification of the critical point whose associated two-dimensional manifold has to be delineated, the call of the correct procedure for the determination of the boundary and, finally, for the output of the results. Algorithm 2 describes the method Main in pseudocode. Depending on whether the boundary of a two-dimensional ascending manifold (lines (8)–(10)) or descending manifold (lines (11)–(13)) has to be determined, Algorithm 3 or a procedure that represents its dual version is applied.

Algorithm 2. (Procedure Main)

1: procedure Main

2: Specification of the local minimum associated with the virtual pit or the local maximum associated with the virtual peak

3: Input of the critical net

4: Execution of the one-point compactification

5: Creation of the arrays containing the local minima, saddles, and local maxima

6: Creation of the array containing the slms-edges, which provide information related to circuits of length two, on condition that such edges exist

7: Specification of the critical point whose associated two-dimensional manifold has to be delineated

8: if critical point is a local minimum then

9: Determination of the boundary of the associated two-dimensional ascending manifold by calling Algorithm 3

10: end if

11: if critical point is a local maximum then

12: Determination of the boundary of the associated two-dimensional descending manifold by calling a procedure that represents the dual version of Algorithm 3

13: end if

14: Output of the results

15: end procedure

Procedure Bin_Search determines the position of an element in an array whose elements must be different from each other and have to be sorted in ascending order.

Procedure Insert inserts an element into an array, whose elements must be different from each other and have to be sorted in ascending order, provided the element does not already occur in the array.

Procedure Manifold_Ascending determines the boundary of a two-dimensional ascending manifold, with Algorithm 3 describing the procedure in pseudocode. After a check for possible input errors (line (2)), the subgraph $S$, which consists of the saddle points being adjacent to lmin in combination with the local maxima being adjacent to these saddles, is extracted and transformed into its undirected form (line (3)). Technically, this is achieved by creating, first of all, the array subgraph, containing the saddles and local maxima, and building, in the second step, the two arrays subgraph_pointer and subgraph_index, containing the pointer structure (confer Sections 4, 5.3, and 5.4); in addition, each edge is implicitly assigned a weight of one. According to Theorem 3.1, the vertices of $S$ are identical with the boundary nodes of $A\left(\mathit{\text{lmin}}\right)$. To obtain their correct order within the circuit, the following steps are essential.

First, it is checked whether slms-edges exist or not, whereby slms-edges represent a tool for the identification of the correct order of the vertices in the case of circuits of length two (confer Sections 5.3 and 5.4). Provided there exist any, the array slms_edge_index is created and they are stored by a pointer structure. In addition, all vertices with incident slms-edges are identified (lines (4)–(7)). Second, the boundary $B$ of the two-dimensional ascending manifold, which is stored in the array boundary, is determined, whereby it must be distinguished whether the subgraph $S$ contains slms-edges or not (lines (8)–(18)).

In the absence of slms-edges, the first vertex of the array subgraph is chosen as the starting point for the boundary $B$ and the shortest paths to all other nodes are determined. They are added successively to the array boundary, with the first vertex of the array being added once again as the last one (lines (9)–(12)).

In the presence of slms-edges, the first vertex of the array subgraph with no incident slms-edge is chosen as starting point for the boundary $B$ and the shortest paths to all other nodes are determined. The key for obtaining the correct order is the proper handling of the vertices with incident slms-edges, whereby the point of interest are the saddles. As will be shown in Section 5.4, a saddle point can be incident with zero, one, or two slms-edges, whereas a local maximum can be incident with zero, two, four, etc. slms-edges, with all these vertices having been tagged before (line (6)). If a saddle point is incident with no slms-edge, it is added to the array boundary and the next adjacent local maximum is processed. If a saddle point is incident with one slms-edge, this edge is processed first and the adjacent local maximum as well as the second saddle point specified by the slms-edge are added to the array boundary. If a saddle point is incident with two slms-edges, one of them is chosen arbitrarily and processed as in the case of only one edge. By this approach, it is ensured that all circuits of length two are processed and all involved vertices are added in the correct order to the array boundary (lines (14)–(17)).

Algorithm 3. (Procedure Manifold_Ascending)

1: procedure Manifold_Ascending

2: Check for possible input errors

3: Extraction of the subgraph $S$ that consists of the saddle points being adjacent to lmin in combination with the local maxima being adjacent to these saddle points from the bipartite graph [SADD, LMAX], with the adjacency relationships being stored by a pointer structure

4: if slms-edges exist then

5: Storage of the slms-edges by a pointer structure

6: Identification of the vertices with incident slms-edges

7: end if

8: if no slms-edges exist then

9: Determination of the boundary $B$ in the following way:

10: (a) Starting point is the first vertex of $S$, which is stored as first element in $B$ that, finally, contains the elements of $S$ in that order as they form the boundary

11: (b) The shortest paths from the first vertex of $S$ to all other nodes of $S$ are determined by a simplified version of Dijkstra‘s algorithm, with the nodes obtained being added successively to $B$

12: (c) The first vertex of $B$ is added once again as the last because the boundary of $A\left(\mathit{\text{lmin}}\right)$ is a closed curve

13: else

14: Determination of the boundary $B$ in the following way:

15: (a) Starting point is the first vertex of $S$ with no incident slms-edge

16: (b) The shortest paths from the first vertex of $S$ to all other nodes of $S$ are determined by a modified version of Dijkstra‘s algorithm, with the nodes obtained being added successively to $B$. The modification refers to the handling of vertices with incident slms-edges in that way that at first all incident slms-edges of a vertex are processed

17: (c) The first vertex of $B$ is added once again as the last because the boundary of $A\left(\mathit{\text{lmin}}\right)$ is a closed curve

18: end if

19: end procedure

Procedure Manifold_Descending determines the boundary of a two-dimensional descending manifold of a local maximum. It is the dual version of the procedure Manifold_Ascending, starting from a local maximum and performing all subsequent operations in the subgraph [LMIN, SADD].

5.3 Example 1: Delineation of the ascending manifold $A\left(\mathit{min}4\right)$

The topographic surface shown in Figure 11a¹⁰ may help to illustrate the modus operandi of the algorithm presented in Section 5.2. For this purpose, the relevant data are stored in two different files (both data files are available as supplementary material on https://github.com/GWWGWWGWW/TGIS in the file _TGIS_ascending_and_descending_manifolds.zip), with the first one containing the geometrical information, i.e. the x-, y-, and z-coordinates of the pits, passes, and peaks, and the second one containing the topological information, i.e. the critical net in combination with a list of the slms-edges, which provide information related to circuits of length two. The importance of the latter will become obvious from the example presented in Section 5.4, whereas in the present example they are meaningless. While the geometrical information is needed for drawing, the topological information is required for identifying the boundaries of the two-dimensional ascending and descending manifolds.

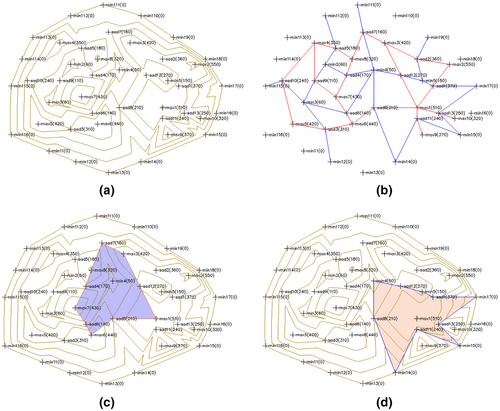
A portion of the first data file Example_coordinates_of_data_points is listed in Table 4. It should be noted that the points $\mathit{min}11$, $\mathit{min}12,\dots$, $\mathit{min}116$, which specify the boundary of the domain of the topographic surface, are, from a geometrical point of view, different from each other, whereas, from a topological point of view, they are identical and represent the pre-image of the surrounding pit $\mathit{min}1$, which is referred to in the second data file (confer Tables 5 and 6). It should also be emphasized that the z-coordinates of the aforementioned data points correspond to their real altitudes in nature and are not set to $-\infty$, as they should according to topology.

TABLE 4. Portion of the data file Example_coordinates_of_data_points containing the type and number as well as the x-, y-, and z-coordinates of the pits, passes, and peaks of the topographic surface depicted in Figure 11.

pit	1	35	20	0	min11
pit	2	60	10	0	min12
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
pit	16	0	35	0	min116
pit	17	55	100	60	min2
pit	18	35	65	60	min3
pit	19	100	95	50	min4
pit	20	145	85	150	min5
pass	21	155	80	370	sad1
pass	22	140	105	360	sad2
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
pass	33	160	55	250	sad13
peak	34	140	60	510	max1
peak	35	170	100	550	max2
$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
peak	43	175	50	320	max10

TABLE 5. Data file Example_critical_net containing the critical net as well as the slms-edges associated with the topographic surface depicted in Figure 11a (comment lines at the beginning of the file are omitted); the critical net is visualized in Figure 11b. ${\mathit{\text{lmin}}}_1$ and ${\mathit{\text{lmin}}}_2$ specify the first and second local minimum adjacent to sadd, whereas ${\mathit{\text{lmax}}}_1$ and ${\mathit{\text{lmax}}}_2$ do the same for the first and second local maximum.

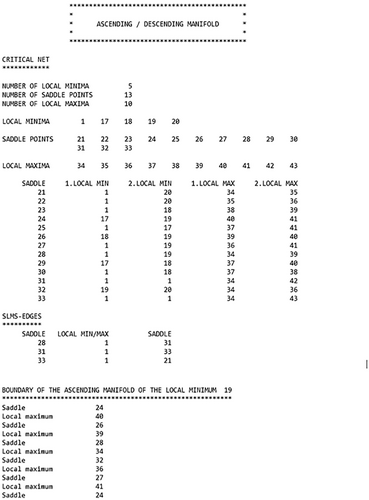
CRITICAL NET
sadd	${\mathit{\text{lmin}}}_1$	${\mathit{\text{lmin}}}_2$	${\mathit{\text{lmax}}}_1$	${\mathit{\text{lmax}}}_2$
21	7	20	34	35
22	9	20	35	36
23	2	18	38	39
24	17	19	40	41
25	12	17	37	41
26	18	19	39	40
27	11	19	36	41
28	4	19	34	39
29	17	18	37	40
30	15	18	37	38
31	4	5	34	42
32	19	20	34	36
33	5	7	34	43
SLMS-EDGES
sadd	lmin/lmax	sadd
28	4	31
31	5	33
33	7	21

TABLE 6. Critical net and slms-edges from Table 5 after the one-point compactification.

CRITICAL NET
sadd	${\mathit{\text{lmin}}}_1$	${\mathit{\text{lmin}}}_2$	${\mathit{\text{lmax}}}_1$	${\mathit{\text{lmax}}}_2$
21	1	20	34	35
22	1	20	35	36
23	1	18	38	39
24	17	19	40	41
25	1	17	37	41
26	18	19	39	40
27	1	19	36	41
28	1	19	34	39
29	17	18	37	40
30	1	18	37	38
31	1	1	34	42
32	19	20	34	36
33	1	1	34	43
SLMS-EDGES
sadd	lmin/lmax	sadd
28	1	31
31	1	33
33	1	21

The second data file Example_critical_net is listed in Table 5. As can be seen, the adjacency relationships are specified with respect to the numbers and not the names of the respective data points (confer Table 4). The boundaries of the two-dimensional ascending and descending manifolds are identified by using only the information contained within this file. The critical net, which is displayed in Table 5 and visualized in Figure 11b, is, however, from a topological point of view, not correct because the required one-point compactification (confer Section 2) has not yet been accomplished and the boundary of the domain of the topographic surface is represented by 16 different local minima. After performing the required compactification by identifying these 16 data points as one local minimum lmin and assigning it the point number one, one obtains the topologically correct critical net shown in Table 6. Technically speaking, the compactification is accomplished by Algorithm 2 (line 4), with the correct critical net being passed over to Algorithm 3 or the analogous procedure for two-dimensional descending manifolds.

With respect to the determination of the boundary of $A\left(\mathit{min}4\right)$, Algorithm 3 extracts, first of all, the array subgraph, which consists of all saddle points being adjacent to $\mathit{min}4$ in combination with the local maxima being adjacent to these saddle points from the bipartite graph [SADD, LMAX], and stores it by a pointer structure.¹¹ Apart from the array subgraph, whose elements are arranged in ascending order and refer to the numbers and not to the names of the data points as specified by the file Example_coordinates_of_data_points, two further arrays, viz., subgraph_pointer and subgraph_index, are required for the characterization of the adjacency relationships, with all three arrays being displayed in Table 7.

TABLE 7. Arrays used by Algorithm 3 for the determination of the boundary of the ascending manifold $A\left(\mathit{min}4\right)$.

$j$	0	1	2	3	4	5	6	7	8	9
$\mathit{\text{subgraph}}\left(j\right)$	24	26	27	28	32	34	36	39	40	41

$j$	0	1	2	3	4	5	6	7	8	9	10
$\mathit{\text{subgraph}}\_\mathit{\text{pointer}}\left(j\right)$	0	2	4	6	8	10	12	14	16	18	20

$k$	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
$\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(k\right)$	8	9	7	8	6	9	5	7	5	6	4	3	4	2	3	1	1	0	2	0

Analogous to the explanations given in Section 4, in the array subgraph_index the adjacent nodes of the vertices $\mathit{\text{subgraph}}\left(0\right)$,¹² $\mathit{\text{subgraph}}\left(1\right)$, $\mathit{\text{subgraph}}\left(2\right),\dots$, i.e. the nodes $\mathrm{8,\; 9,\; 7,\; 8,\; 6,\; 9},\dots$, are recorded in succession, with the vertical bars specifying the sections associated with the individual vertices. To put it differently, the vertical bars represent the equivalents of the elements of the array subgraph_pointer, which refer to the indices immediately after the bars.

To illustrate, let us consider the first three elements of the array subgraph_pointer, starting with $\mathit{\text{subgraph}}\_\mathit{\text{pointer}}\left(0\right)$, i.e. $\mathrm{0,\; 2,\; 4},\dots$ , in combination with the first six elements of the array subgraph_index, starting with $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(0\right)$. From the combined information of these two arrays it follows that $\mathit{\text{subgraph}}\left(0\right)$, i.e. vertex 24 $\left(\mathit{sad}4\right)$, is adjacent to $\mathit{\text{subgraph}}\left(8\right)$, i.e. vertex 40 $\left(\mathit{max}7\right)$, and $\mathit{\text{subgraph}}\left(9\right)$, i.e. vertex 41 $\left(\mathit{max}8\right)$. In an analogous way it can be concluded that $\mathit{\text{subgraph}}\left(1\right)$, i.e. vertex 26 $\left(\mathit{sad}6\right)$, is adjacent to $\mathit{\text{subgraph}}\left(7\right)$, i.e. vertex 39 $\left(\mathit{max}6\right)$, and $\mathit{\text{subgraph}}\left(8\right)$, i.e. vertex 40 $\left(\mathit{max}7\right)$. For the adjacency relationships of $\mathit{\text{subgraph}}\left(2\right)$, i.e. vertex 27 $\left(\mathit{sad}7\right)$, finally, holds that it is adjacent to $\mathit{\text{subgraph}}\left(6\right)$, i.e. vertex 36 $\left(\mathit{max}3\right)$, and $\mathit{\text{subgraph}}\left(9\right)$, i.e. vertex 41 $\left(\mathit{max}8\right)$ (confer Figure 11).

The undirectedness of the graph is taken into account by the duplication of all arcs and the assignment of the opposite directions to the duplicates. To give an example, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(0\right)$ specifies the arc pointing from $\mathit{\text{subgraph}}\left(0\right)$ to $\mathit{\text{subgraph}}\left(8\right)$, whereas the arc specifying the opposite direction, i.e. from $\mathit{\text{subgraph}}\left(8\right)$ to $\mathit{\text{subgraph}}\left(0\right)$, is recorded as $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(17\right)$.

As already mentioned, the slms-edges specified in the section SLMS-EDGES of the file Example_critical_net are of no importance for the present example, as the boundary does not contain an edge belonging to a circuit of length two (an example, in which slms-edges are essential, is given in Section 5.4). For this reason, Algorithm 3 starts with $\mathit{\text{subgraph}}\left(0\right)$, i.e. vertex 24 $\left(\mathit{sad}4\right)$, and adds it as first element to the array boundary (line (10)).¹³ In the following, the first incident edge of $\mathit{\text{subgraph}}\left(0\right)$, i.e. $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(0\right)$, is taken, thus implying that the algorithm continues with $\mathit{\text{subgraph}}\left(8\right)$, i.e. vertex 40 $\left(\mathit{max}7\right)$, and adds it to the array boundary (line (11)). The next vertex to be added is $\mathit{\text{subgraph}}\left(1\right)$, with this being obvious from $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(16\right)$ and $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(17\right)$. While $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(17\right)$ indicates that $\mathit{\text{subgraph}}\left(8\right)$ is entered by the edge coming from $\mathit{\text{subgraph}}\left(0\right)$, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(16\right)$ implies that the next vertex to be processed is $\mathit{\text{subgraph}}\left(1\right)$, i.e. vertex 26 $\left(\mathit{sad}6\right)$. In an analogous way, it can be said that in the following step $\mathit{\text{subgraph}}\left(7\right)$ has to be added to the boundary, with this being apparent from $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(2\right)$ and $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(3\right)$. While $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(3\right)$ indicates that $\mathit{\text{subgraph}}\left(1\right)$ is entered by the edge coming from $\mathit{\text{subgraph}}\left(8\right)$, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(2\right)$ implies that $\mathit{\text{subgraph}}\left(7\right)$, i.e. vertex 39 $\left(\mathit{max}6\right)$, has to be processed next. The following steps are completely analogous, with the vertices $\mathit{\text{subgraph}}\left(3\right)$, $\mathit{\text{subgraph}}\left(5\right)$, $\mathit{\text{subgraph}}\left(4\right)$, $\mathit{\text{subgraph}}\left(6\right)$, $\mathit{\text{subgraph}}\left(2\right)$, and $\mathit{\text{subgraph}}\left(9\right)$, i.e. $\mathrm{28,\; 34,\; 32,\; 36,\; 27,\; 41}$, being processed and added to the boundary in this sequence. When processing $\mathit{\text{subgraph}}\left(9\right)$, i.e. vertex 41 $\left(\mathit{max}8\right)$, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(18\right)$ indicates that this vertex is entered by the edge coming from $\mathit{\text{subgraph}}\left(2\right)$, while $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(19\right)$ implies that the next vertex to be processed is $\mathit{\text{subgraph}}\left(0\right)$, i.e. vertex 24 $\left(\mathit{sad}4\right)$. As this vertex is identical with the first element of the array boundary, the algorithm terminates (line (12)).

The result produced by Algorithm 2 for the ascending manifold $A\left(\mathit{min}4\right)$ is displayed in Figure 12 and visualized in Figure 11c, with the two-dimensional ascending manifold being highlighted in blue. As can be seen in Figure 12, the output produced by Algorithm 2 refers to the numbers and not to the names of the respective data points. With reference to Table 4 and the supplementary material, however, it is easy to derive from the sequence $24-40-26-39-28-34-32-36-27-41-24$ of the numbers, the sequence $\mathit{sad}4-$ $\mathit{max}7-$ $\mathit{sad}6-$ $\mathit{max}6-$ $\mathit{sad}8-$ $\mathit{max}1-$ $\mathit{sad}12-$ $\mathit{max}3-$ $\mathit{sad}7-$ $\mathit{max}8-$ $\mathit{sad}4$ of the names of the respective data points, with the latter being displayed in Figure 11c.

5.4 Example 2: Delineation of the descending manifold $D\left(\mathit{max}1\right)$

For the determination of the boundary of the descending manifold $D\left(\mathit{max}1\right)$ and its visualization as shown in Figure 11d, the two data files Example_coordinates_of_data_points and Example_critical_net are likewise necessary (confer Section 5.3). The determination of the boundary, however, is more complicated as compared to that of the ascending manifold $A\left(\mathit{min}4\right)$, because the critical net contains two circuits of length two, viz., $<\mathit{min}1$, $\mathit{sad}11$, $\mathit{min}1>$ and $<\mathit{min}1$, $\mathit{sad}13$, $\mathit{min}1>$, whose edges are elements of the boundary. Due to the information provided by the critical net alone, it cannot be excluded that instead of the correct sequence $<\dots ,$ $\mathit{sad}8$, $\mathit{min}1$, $\mathit{sad}11$, $\mathit{min}1$, $\mathit{sad}13$, $\mathit{min}1$, $\mathit{sad}1,\dots >$ one of the wrong ones $<\dots ,$ $\mathit{sad}8$, $\mathit{min}1$, $\mathit{sad}13$, $\mathit{min}1$, $\mathit{sad}11$, $\mathit{min}1$, $\mathit{sad}1,\dots >$ or even $<\dots ,$ $\mathit{sad}8$, $\mathit{min}1$, $\mathit{sad}1,\dots >$ would be determined. To overcome this deficiency, the so-called slms-edges are used, with each slms-edge consisting of two edges of the boundary, leading either from a saddle via a local minimum to another saddle, or from a saddle via a local maximum to another saddle. As can be seen from Tables 5, 6 and Figure 11d, in the present example three slms-edges exist, with the first one leading from saddle 28 $\left(\mathit{sad}8\right)$ via the local minimum 1 $\left(\mathit{min}1\right)$ to saddle 31 $\left(\mathit{sad}11\right)$, the second one leading from saddle 31 $\left(\mathit{sad}11\right)$ via the local minimum 1 $\left(\mathit{min}1\right)$ to saddle 33 $\left(\mathit{sad}13\right)$, and the third one leading from saddle 33 $\left(\mathit{sad}13\right)$ via the local minimum 1 $\left(\mathit{min}1\right)$ to saddle 21 $\left(\mathit{sad}1\right)$ (for the relationships between the names and the numbers of the critical points, confer Table 4 and the supplementary material). The so-defined slms-edges provide the required information to add the critical points to the array boundary in the correct order.

As can be seen from Table 8 and Figure 11d, the array subgraph contains all saddle points of the bipartite graph [LMIN, SADD] that are adjacent to $\mathit{max}1$ in combination with the local minima being adjacent to these saddles, with its elements being arranged in ascending order. The two arrays subgraph_pointer and subgraph_index are used to characterize the adjacency relationships by a pointer structure (confer Section 4), whereby the elements of subgraph_index do not refer to the numbers of the data points as specified by the file Example_coordinates_of_data_points, but to the respective positions within the array subgraph (confer Section 5.3). To give an example, the first six elements of the array subgraph_index, starting with $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(0\right)$, are $\mathrm{7,\; 7,\; 5,\; 5,\; 4,\; 3},\dots$, thus implying the following adjacency relationships: $\mathit{\text{subgraph}}\left(0\right)$, i.e. vertex 1 $\left(\mathit{min}1\right)$, is adjacent to $\mathit{\text{subgraph}}\left(7\right)$, i.e. vertex 33 $\left(\mathit{sad}13\right)$, two times; further, it is adjacent to $\mathit{\text{subgraph}}\left(5\right)$, i.e. vertex 31 $\left(\mathit{sad}11\right)$, two times; in addition, vertex 1 $\left(\mathit{min}1\right)$ is adjacent to $\mathit{\text{subgraph}}\left(4\right)$, i.e. vertex 28 $\left(\mathit{sad}8\right)$, and $\mathit{\text{subgraph}}\left(3\right)$, i.e. vertex 21 $\left(\mathit{sad}1\right)$.

TABLE 8. Arrays used by the dual version of Algorithm 3 for the determination of the boundary of the descending manifold $D\left(\mathit{max}1\right)$.

$j$	0	1	2	3	4	5	6	7
$\mathit{\text{subgraph}}\left(j\right)$	1	19	20	21	28	31	32	33

$j$	0	1	2	3	4	5	6	7	8
$\mathit{\text{subgraph}}\_\mathit{\text{pointer}}\left(j\right)$	0	6	8	10	12	14	16	18	20

$k$	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
$\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(k\right)$	7	7	5	5	4	3	6	4	6	3	0	2	0	1	0	0	1	2	0	0
$\mathit{\text{slms}}\_\mathit{\text{edge}}\_\mathit{\text{index}}\left(k\right)$	2	3	1	2	1	3	0	0	0	0	3	0	1	0	1	2	0	0	2	3

The array slms_edge_index provides information related to the slms-edges, whereby its elements must be considered in combination with the elements of the array subgraph_index. In this context, the elements of slms_edge_index are defined as follows: If $\mathit{\text{slms}}\_\mathit{\text{edge}}\_\mathit{\text{index}}\left(k\right)=0$, this implies that the corresponding edge $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(k\right)$ is no slms-edge. If $\mathit{\text{slms}}\_\mathit{\text{edge}}\_\mathit{\text{index}}\left(k\right)$ is a non-negative integer $i$, this implies that the corresponding edge $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(k\right)$ is an element of the ith slms-edge as specified in the section SLMS-EDGES of the file Example_critical_net.

The following two examples may illustrate the previous explanations. The first example refers to $k=6$: as $\mathit{\text{slms}}\_\mathit{\text{edge}}\_\mathit{\text{index}}\left(6\right)=0$, it follows that the arc specified by $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(6\right)$ is no slms-edge; evidently, this is the arc leading from subgraph $\left(1\right)$, i.e. vertex 19 $\left(\mathit{min}4\right)$, to $\mathit{\text{subgraph}}\left(6\right)$, i.e. vertex 32 $\left(\mathit{sad}12\right)$. The second example refers to $k=15$: as $\mathit{\text{slms}}\_\mathit{\text{edge}}\_\mathit{\text{index}}\left(15\right)=2$, it follows that the arc specified by $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(15\right)$ is both an element of a circuit of length two in the subgraph [LMIN, SADD] and an element of the second slms-edge specified in the section SLMS-EDGES of the file Example_critical_net (confer Tables 5 and 6). Evidently, it is the arc leading from $\mathit{\text{subgraph}}\left(5\right)$, i.e. vertex 31 $\left(\mathit{sad}11\right)$, to $\mathit{\text{subgraph}}\left(0\right)$, i.e. vertex 1 $\left(\mathit{min}1\right)$, with the arc pointing into the opposite direction being specified by $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(3\right)$. The second part of the slms-edge, leading from the local minimum to the second saddle point, is stored as $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(0\right)$, leading from $\mathit{\text{subgraph}}\left(0\right)$, i.e. vertex 1 $\left(\mathit{min}1\right)$, to $\mathit{\text{subgraph}}\left(7\right)$, i.e. vertex 33 $\left(\mathit{sad}13\right)$, with the information related to the opposite direction being stored by $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(18\right)$ and $\mathit{\text{slms}}\_\mathit{\text{edge}}\_\mathit{\text{index}}\left(18\right)$.

Due to the existence of slms-edges, the dual version of Algorithm 3 scans the vertices of the array subgraph until a vertex with no incident slms-edge is detected. In the present case, it is $\mathit{\text{subgraph}}\left(1\right)$, i.e. vertex 19 $\left(\mathit{min}4\right)$, which is added as first element to the array boundary (line (15)).¹⁴ As both incident edges of $\mathit{\text{subgraph}}\left(1\right)$ are not slms-edges, the first one, i.e. $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(6\right)$, is taken, thus implying that the algorithm continues with $\mathit{\text{subgraph}}\left(6\right)$, i.e. vertex 32 $\left(\mathit{sad}12\right)$, and adds it to the array boundary (line (16)).¹⁵ The next vertex to be added is $\mathit{\text{subgraph}}\left(2\right)$, with this being obvious from $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(16\right)$ and $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(17\right)$. While $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(16\right)$ indicates that $\mathit{\text{subgraph}}\left(6\right)$ is entered by the edge coming from $\mathit{\text{subgraph}}\left(1\right)$, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(17\right)$ implies that the next vertex to be processed is $\mathit{\text{subgraph}}\left(2\right),$ i.e. vertex 20 $\left(\mathit{min}5\right)$. In an analogous way, it can be said that in the following step $\mathit{\text{subgraph}}\left(3\right)$ has to be added to the boundary, with this being apparent from $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(8\right)$ and $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(9\right)$. While $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(8\right)$ indicates that $\mathit{\text{subgraph}}\left(2\right)$ is entered by the edge coming from $\mathit{\text{subgraph}}\left(6\right)$, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(9\right)$ implies that $\mathit{\text{subgraph}}\left(3\right)$, i.e. vertex 21 $\left(\mathit{sad}1\right)$, has to be processed next. In an analogous manner, it can be argued that in the next step $\mathit{\text{subgraph}}\left(0\right)$, i.e. vertex 1 $\left(\mathit{min}1\right)$, will be added to the boundary, with this being evident from $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(10\right)$ and $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(11\right)$. While $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(11\right)$ indicates that $\mathit{\text{subgraph}}\left(3\right)$ is entered by the edge coming from $\mathit{\text{subgraph}}\left(2\right)$, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(10\right)$ implies that the next vertex to be processed is $\mathit{\text{subgraph}}\left(0\right)$, i.e. vertex 1 $\left(\mathit{min}1\right)$.

While up to now only edges belonging to no circuit of length two were dealt with, $\mathit{\text{slms}}\_\mathit{\text{edge}}\_\mathit{\text{index}}\left(10\right)$ indicates that $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(10\right)$ is part of the third slms-edge specified in the section SLMS-EDGES of the file Example_critical_net. The sequence of the next points to be added to the array boundary is determined by both the arrays subgraph_index and slms_edge_index in that way that the third slms-edge must be completely processed, with the elements of subgraph_index determining the correct sequence of the vertices. In the present example, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(10\right)$, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(5\right)$, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(1\right)$, and $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(19\right)$ must be handled in this order, with the two nodes $\mathit{\text{subgraph}}\left(0\right)$, i.e. vertex 1 $\left(\mathit{min}1\right)$, and $\mathit{\text{subgraph}}\left(7\right)$, i.e. vertex 33 $\left(\mathit{sad}13\right)$, being added to the array boundary.

As indicated by $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(19\right)$ and $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(18\right)$, $\mathit{\text{subgraph}}\left(7\right)$ is entered by an edge coming from $\mathit{\text{subgraph}}\left(0\right)$ and belonging to the third slms-edge, while it is left in direction to $\mathit{\text{subgraph}}\left(0\right)$, with this edge belonging to the second slms-edge specified in the section SLMS-EDGES of the file Example_critical_net. In an analogous way as described before, the second slms-edge must be completely processed, with the elements of subgraph_index determining the correct sequence of the vertices. In the present instance, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(18\right)$, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(0\right)$, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(3\right)$, and $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(15\right)$ must be handled in this succession, with the two nodes $\mathit{\text{subgraph}}\left(0\right)$, i.e. vertex 1 $\left(\mathit{min}1\right)$, and $\mathit{\text{subgraph}}\left(5\right)$, i.e. vertex 31 $\left(\mathit{sad}11\right)$, being added to the array boundary.

The following step is completely analogous to the previously described ones. From $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(14\right)$ and $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(15\right)$ it is evident that $\mathit{\text{subgraph}}\left(5\right)$ is entered by an edge coming from $\mathit{\text{subgraph}}\left(0\right)$ and belonging to the second slms-edge, while it is left in direction to $\mathit{\text{subgraph}}\left(0\right)$, with this edge being an element of the first slms-edge specified in the section SLMS-EDGES of the file Example_critical_net. In the following, the first slms-edge must be completely processed, with the elements of subgraph_index determining the correct sequence of the vertices. In the present example, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(14\right)$, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(2\right)$, $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(4\right)$, and $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(12\right)$ must be handled in this order, with the two nodes $\mathit{\text{subgraph}}\left(0\right)$, i.e. vertex 1 $\left(\mathit{min}1\right)$, and $\mathit{\text{subgraph}}\left(4\right)$, i.e. vertex 28 $\left(\mathit{sad}8\right)$, being added to the array boundary.

The final step that remains to be done, is to process $\mathit{\text{subgraph}}\left(4\right)$, which is, according to $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(12\right)$, entered by the edge coming from $\mathit{\text{subgraph}}\left(0\right)$. As indicated by $\mathit{\text{subgraph}}\_\mathit{\text{index}}\left(13\right)$, the vertex is left in direction to $\mathit{\text{subgraph}}\left(1\right)$, i.e. vertex 19 $\left(\mathit{min}4\right)$, with this edge being no slms-edge. As this vertex is identical with the first element of the array boundary, the algorithm terminates (line (17)).

The result produced by Algorithm 2 for the descending manifold $D\left(\mathit{max}1\right)$ is displayed in Figure 13 and visualized in Figure 11d, with the descending two-dimensional manifold being highlighted in red. As can be seen in Figure 13, the output produced by Algorithm 2 refers to the numbers and not to the names of the respective data points. With reference to Table 4 and the supplementary material, however, it is easy to derive from the sequence $19-32-20-21-1-33-1-31-1-28-19$ of the numbers, the sequence $\mathit{min}4-\mathit{sad}12-\mathit{min}5-\mathit{sad}1-\mathit{min}1-\mathit{sad}13-\mathit{min}1-\mathit{sad}11-\mathit{min}1-\mathit{sad}8-\mathit{min}4$ of the names of the critical points.

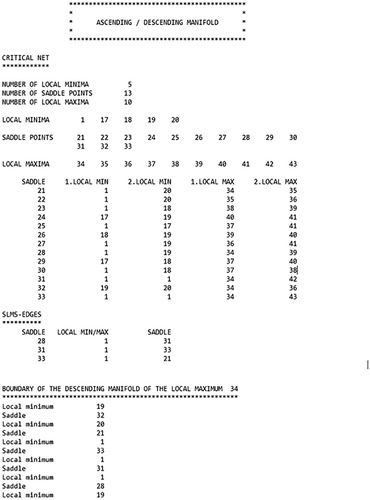
6 CONCLUSIONS

In contrast to the surfaces investigated by geoscientists and hydrologists, which predominantly represent fluvially eroded terrains, the surfaces under investigation in other sciences, such as the technical ones, are characterized by the absence of river-like structures and the presence of a large number of crisscross distributed pits, passes, and peaks instead. As surfaces of this type are by far the most common, theoretical research conducted by mathematicians and computer scientists has focused exclusively on them, with the studies concentrating on geometrical and, more recently, increasingly on topological issues. The present article is devoted to such a topological issue, namely the Morse theory based delineation of basins and hills, whereby the former must be strictly distinguished from the drainage basins as studied within hydrology, the geosciences, and some related fields.

With respect to a better readability of this article, the most important concepts from $n$-dimensional calculus and Morse theory were briefly sketched first, thereby showing how the elements related to Morse theory (local minima, saddles, local maxima, course-separatrices, ridge-separatrices, two-dimensional ascending manifolds of local minima, two-dimensional descending manifolds of local maxima), and the elements of geoscientific interest (pits, passes, peaks, course lines, ridge lines, basins, hills) correspond to each other. Furthermore, it was demonstrated how the gradient flow between the critical points of a Morse function $f\left(x,y\right)$ representing terrain can be characterized by a critical net, with this data structure offering the possibility to analyze topographic surfaces in a graph theoretic way. In the following, an algorithm based on critical nets was presented that can be used to identify the boundaries of two-dimensional ascending manifolds of local minima and two-dimensional descending manifolds of local maxima, with these topological concepts representing the pre-images of basins and hills. In addition, the modus operandi of the algorithm implemented in C# was illustrated by two examples.

While the importance of drainage basins is undisputed, the question arises as to the relevance of basins. As already mentioned, their importance is related to the simplification of surfaces, which corresponds in the geosciences to map generalization and in the technical surfaces to the reduction of measurement noise. Technically speaking, in both cases basins and/or hills of minor importance are removed according to different criteria, such as differences in altitudes, the area of a basin (hill), the circumference of a basin (hill), or the volume of a basin (hill). Whereas the simplification process is relatively simple when only differences in altitudes have to be taken into account, in all other instances it is rather complicated, as in these cases two adjacent basins (hills) have to be merged according to some pre-specified criteria.

Obviously, a generalization process based on the area, circumference, or volume of a basin (hill) may not only be of interest for the technical sciences, for which it is defined in the standard ISO 25178-2, but also for the geosciences. Conceptually, any simplification that is grounded on these criteria constitutes a two-step process, with the first step being responsible for the correct identification of the basins (hills) and the second step accounting for the correct fusion of two adjacent basins (hills) according to some pre-specified criteria.

The topic of the present article refers to the first aforementioned step, viz., the identification of two-dimensional ascending manifolds of local minima and two-dimensional descending manifolds of local maxima, with these topological concepts representing the pre-images of basins and hills. The second step, viz., the fusion of these manifolds according to the area, circumference, or volume of the corresponding basins and hills is beyond the scope of this article and contents of future research. A second focus of future research should be the attempt to integrate Werner's approach of interlocking ridge and channel networks into a Morse theoretic framework to obtain, finally, a topological model for both topographic surfaces with and without pronounced river systems.

CONFLICT OF INTEREST STATEMENT

The author declares no conflict of interest.