Review of Income and Wealth
Volume 71, Issue 1 e12686
ORIGINAL ARTICLE
Open Access

The three I's of downward income mobility: A directional subgroup decomposable measure

Elena Bárcena-Martín, 

Elena Bárcena-Martín

Departamento de Estadística y Econometría, Universidad de Málaga

Search for more papers by this author
Olga Cantó, 

Corresponding Author

Olga Cantó

Departamento de Economía, Universidad de Alcalá

Correspondence to: Olga Cantó, Departamento de Economía, Facultad de CC. Económicas, Empresariales y Turismo, Universidad de Alcalá. Plaza de la Victoria s/n, 28802 Alcalá de Henares (Madrid), Spain ([email protected])

Search for more papers by this author
First published: 14 March 2024
https://doi.org/10.1111/roiw.12686
Citations: 1

Authors acknowledge financial support provided by the RandD Program in Social Sciences and Humanities by the Autonomous Communities of Madrid, OPINBI project (Ref: H2019/HUM-5793). Elena Bárcena-Martín acknowledges the finance from Grant PID2020-115429GB-I00 funded by MCIN/AEI/ 10.13039/501100011033 and Olga Cantó Grant PID2022-137352NB-C42 funded by MCIN/AEI/ 10.13039/501100011033/FEDER, UE for their research activities.

Abstract

The Foster-Greer-Thorbecke class of indices and the TIP curve have become classical tools to measure poverty. In this paper we adapt these indices and curve to the income mobility literature and measure downward income mobility considering its three dimensions of incidence, intensity, and inequality. This strategy allows us to incorporate reference dependence, loss aversion and diminishing sensitivity, features emphasized as welfare determinants in Prospect Theory. We propose the use of a class of measures and a Three I's of Downward Mobility curve as a useful graphical device in the income growth framework. Based on this curve we can evaluate the degree of regressivity (or progressivity) of income losses. We provide an empirical illustration for Spain in two recent recession periods. Results show that even if for most households the pandemic shock was not as severe as the Great Recession, some sociodemographic groups had a more similar downward mobility experience in both crises.

1 Introduction

Mobility is a multifaceted concept (Fields & Ok, 1999), and studies have traditionally concentrated on one of its many aspects, which has made comparing the results quite confusing. According to Fields (2008), income mobility can be understood as measuring six different issues: time independence, positional change, share movement, non-directional income movement (risk and uncertainty), directional income movement, and equalizer of longer-term incomes. A relevant strand of the literature has emphasized the necessity of using pure measures of societal positional change to assess income mobility, as it considers mobility is a societal characteristic more than an individual one (Bossert et al., 2016a, 2016b; D'Agostino & Dardanoni, 2009). Another important strand has made a variety of proposals for an aggregate social measure of income movement, or “individual income growth”, which are based on the idea that a measure of mobility should be the result of an aggregate of changes in income experienced by each individual in a society (Demuyck & Van de gaer, 2012; Jenkins & Van Kerm, 2011, 2016; Palmisano & Peragine, 2015; Palmisano & Van de gaer, 2016; Schluter & Van de gaer, 2011).

Regardless of the concept of mobility, either related to positional change or individual income growth, the actual direction of the movement (upwards or downwards) is a crucial issue that provides important information about the social desirability of mobility. In a social aggregate measure, it is not clear how the individual experience of an income loss should be compensated by the gain of another individual in the same society. Thus, a very discussed issue is how to aggregate gains and losses in the social calculus, as the evaluation of society's well-being requires measuring gains and losses of individuals, which may be controversial and could generally imply that “one would want the former (gains) to represent an improvement in circumstances and the latter (losses) a deterioration” (Jäntti & Jenkins, 2015). In this vein, Cowell and Flachaire (2018) propose a general framework of income mobility measurement distinguishing between upward and downward mobility and allowing researchers to choose the weight of each of them in the social aggregate. Another directional proposal is Bossert et al. (2016b) who suggest a measure of positional (not income) mobility that uses only incidence of rank mobility and is decomposable into two head-count indices: upward and downward rank mobility.

Additionally, new developments of behavioral economic models suggest using measurement tools that consider reference-dependent utility, loss aversion and the principle of diminishing sensitivity, as the main ingredients of Prospect Theory. In this context, it is key to link both static and dynamic well-being measures with a behavioral perspective (Kahneman & Tversky, 1979) as Barberis (2013) and Jäntti et al. (2014) suggest. Prospect Theory underlines that people derive utility from changes in income (gains and losses) measured to some reference point (reference-dependent utility) and have loss aversion, so losses are felt more strongly than gains of equal size, so that, in Barberis' (2013, p. 175) words: “people are much more sensitive to losses—even small losses—than to gains of the same magnitude.” Moreover, this theory suggests a principle of diminishing sensitivity which implies that as losses grow, their marginal disutility should grow, underlying the welfare relevance of large losses. Jäntti et al. (2014) propose a social aggregate measure where gains and losses contribute to utility in a separate way and suggest the use of a loss aversion parameter that weighs losses approximately double than equal gains by different individuals following Kahneman and Tversky (1979) estimations of loss aversion based on experimental data.

In line with this idea of differentiating losses and gains, in this paper we propose a class of downward income mobility measures that analyze downward movements separately from upward ones. We adapt two classical tools for the measurement of poverty—the Foster-Greer-Thorbecke, FGT class of indices (Foster et al., 1984) and the TIP curve (Three I's of Poverty (TIP) by Jenkins & Lambert, 1997, 1998)—to the income mobility literature and measure downward income mobility considering its three dimensions of incidence, intensity, and inequality. This proposal also allows us to incorporate three behavioral economics ingredients in our measurement: reference-dependence, loss aversion and diminishing sensitivity. Given that this class of measures is consistent with an intuitive graphical device similar to the TIP curve, we propose the use of a new TIDM curve in the income growth framework. Based on that we can also evaluate the degree of regressivity (or progressivity) of income losses, i.e. the extent to which losses are larger (or smaller) for the poor.

We contribute to the literature in different ways. First, we quantify downward mobility separately from upward mobility avoiding any compensation between different individual's gains and losses in a framework that is consistent with key ingredients of Prospect Theory. Second, we separately identify the relevance of all three important dimensions of the individual downward mobility experience: incidence, intensity, and inequality. Third, our downward mobility measure is subgroup decomposable so researchers can evaluate mobility across population subgroups in a coherent way. Fourth, our approach is consistent with a simple but complete and informative graphical device that allows for further intuitive and detailed analyses of the distribution of income losses for different population subgroups. Fifth, by using a minimal set of judgements, we can identify situations in which income loss profiles are independent of the index chosen, as all indices yield the same ordering of income loss distributions. This makes our analysis significantly more robust. Sixth, based on the graphical device we propose a progressivity (regressivity) index of downward mobility that measures the extent to which income losses are smaller (larger) for the poor than for the rest of the population. Seventh, our methodology is directly applicable to the measurement of a large list of other relevant topics in economics, such as intergenerational, occupational, educational or wage mobility. Finally, its simple structure facilitates comprehension and eases communication with policymakers without leaving any desirable properties aside.

As an empirical illustration we study downward income mobility in two recent recession periods in Spain using EU-SILC (European Union Statistics on Income and Living Conditions) longitudinal data: the first shock of the Great Recession (2008/2009) and the pandemic shock (2019/2020).

The paper is organized as follows. In Section 2, we review the literature on measuring income mobility by aggregating “individual income growth”, mostly focusing on the most recent contributions to the topic. In the Section 3, we present our subgroup decomposable income mobility measure and discuss its properties. In Section 4, we describe the characteristics of the graphical device linked to this class of downward income mobility measures: the TIDM curve and we link it to a measure of progressivity of income losses. Section 5 includes an empirical illustration for Spain in two recent recession periods and Section 6 concludes.

2 Literature Review

In the analysis of the distributional impact of income growth, the literature usually compares the situation before and after the growth process and provides an evaluation of changes in mean growth, inequality indices, or poverty indicators between two moments in time. To provide more detail, it is common to construct growth incidence curves (GICs) that calculate mean income changes by percentile and show the pro-poorness of income growth (Ravallion & Chen, 2003). However, all these results focus on pure distributional changes and are unsatisfactory if one is interested in evaluating income growth in terms of social welfare (Palmisano & Peragine, 2015).

For a complete social welfare evaluation, income dynamics along the distribution cannot be ignored, so removing the axiom on anonymity is a key issue. Grimm (2007) and Van Kerm (2009) independently developed the concept of non-anonymous GIC (na-GIC), which measures the dimension of “individual income growth” given an individual's initial position and introduces plots, usually called “income mobility profiles”, to depict the na-GICs in a meaningful graph. Clearly, “income mobility profiles” provide researchers with detailed information on individual income growth, but they are unable to consistently provide an unambiguous rank of growth processes amongst different countries or population subgroups. Income mobility indices can do this, and the most well-known proposals of both directional and non-directional income movement indices were proposed by Fields and Ok (1996, 1999). Later, Bourguignon (2011) suggested the use of “inequality-corrected cumulative non-anonymous growth incidence curves” to evaluate the social welfare impact of growth depending on both income change and initial income. Advances in this area, such as Schluter and Van de gaer (2011) and Demuyck and Van de gaer (2012), have used unequal weights when aggregating income movements, unlike Fields and Ok (1999). This different weighting scheme translates into priority for lower growth.

Some of the subsequent literature, such as Palmisano and Peragine (2015), Jenkins and Van Kerm (2016), and Palmisano and Van de gaer (2016), consider that when aggregating individual income growth, weights should depend on the individual position in the base-year distribution, i.e. a social preference for pro-poor income growth. However, it is arguable that mobility should be sensitive to individual identity, as exposed by Cowell and Flachaire (2018). These authors propose a very flexible approach to the measurement of mobility based on a general measure of distance for a wide variety of status concepts, including income, wealth, or rank, and introduce a directional sensitivity parameter that determines the type of mobility measure. In fact, depending on the value of the sensitivity parameter, researchers can apply their own judgement as to whether greater weight should be placed on upward or downward income mobility. Differently from their proposal our class of measures differentiates upward and downward moves from the start while that is only the case in their measures if one decides to focus on one of the two but not when an intermediate sensitivity parameter is chosen. Note that, even if generally flexible, their weights on individual income changes are determined by a logarithmic function of income ratios and researchers cannot modulate this functional form. In contrast, our approach uses an exponential weight, so that the shape of the function can be chosen by the researcher by choosing a value of a parameter depending on value judgements related to the relevance of larger versus smaller losses.

The idea of following the insights of unidimensional poverty measurement in an FGT framework to measure other interesting social phenomena has been previously proposed by Alkire and Foster (2011) in their counting-based multidimensional poverty class of measures, by Jenkins (1994) and Del Río et al. (2011) in their measurement of gender wage discrimination and by Gradín et al. (2012) in their family of intertemporal poverty indices. In the same vein, Creedy and Gemmell (2018, 2019 and 2022) have recently proposed the construction of a graphical device to measure non-directional overall income mobility. These authors construct an overall mobility TIM curve, based on the TIP curve. Their approach is related to ours in the use of a framework that is traditionally used in the measurement of poverty but puts the focus on measuring overall income mobility (i.e. a non-directional approach) which is closer to a concept of income volatility.

Most importantly, Creedy and Gemmell's (2018) proposal to study income mobility pro-poorness puts forward a curve that is drawn ordering individuals by their first-period income level, similarly to growth incidence curves (GICs) proposed by Ravallion and Chen (2003) or income growth profiles (IGPs) proposed by Jenkins and Van Kerm (2016). This is an essential difference with our proposal where individuals are always ordered by the relative dimension of their income loss, whatever their first-period income. Therefore, we consider that the experience of a change in individual income between two moments in time can be advantageously analyzed as a genuine, individual income gap, and downward income mobility incidence, dimension (intensity), and distribution should play a crucial role when quantifying the aggregate level of downward mobility in a society.

3 A Subgroup Decomposable Downward Income Mobility Measure

This section exposes the normative framework for the empirical study of income mobility based on the poverty and deprivation literature, which provides us with aggregate indicators that are explicit in incorporating necessary judgements about how to aggregate individual income gaps. We adapt the family of poverty indices proposed by Foster et al. (1984) and construct a downward mobility index based on the relative income gap. This gap is determined by the ratio of the difference between an individual threshold (equal to income in the base period) and the level of individual income reached at a later moment in time.

Let x ∈ ℝ + + n $$ x\in {\mathbb{R}}_{++}^n $$ be a vector of individual incomes and suppose that some dynamic process transforms it into y ∈ ℝ + + n $$ y\in {\mathbb{R}}_{++}^n $$ . Let Γ i = x i − y i x i $$ {\Gamma}_i=\frac{x_i-{y}_i}{x_i} $$ be the relative income gap of the i $$ i $$ th individual; let Q be the set of downward movers, q = q ( x , y ) $$ q=q\left(x,y\right) $$ the number of individuals with downward mobility (income falls or losses); and n = n ( y ) $$ n=n(y) $$ the total number of individuals in the population. Consider a mobility measure DM α $$ {\mathrm{DM}}_{\alpha } $$ for α ≥ 0 $$ \alpha \ge 0 $$ defined by:
DM α ( x , y ) = 1 n ∑ i ∈ Q x i − y i x i α = 1 n ∑ i ∈ Q Γ i α = 1 n ∑ i ∈ Q x i − y i x i x i − y i x i α − 1 . $$ {\mathrm{DM}}_{\alpha}\left(x,y\right)=\frac{1}{n}\sum \limits_{i\in Q}{\left(\frac{x_i-{y}_i}{x_i}\right)}^{\alpha }=\frac{1}{n}\sum \limits_{i\in Q}{\Gamma_i}^{\alpha }=\frac{1}{n}\sum \limits_{i\in Q}{\left(\frac{x_i-{y}_i}{x_i}\right)\left(\frac{x_i-{y}_i}{x_i}\right)}^{\alpha -1}. $$ (1)

The downward mobility measure is a weighted sum of the individual relative income losses of all individuals experiencing them in society. The weights are the relative income decrease itself. The reference point is past income (even if other references related to society could also be used such as society's mean or median income), the degree of loss aversion is captured by the choice of the parameter α $$ \alpha $$ , the larger the higher loss aversion and finally, diminishing sensitivity is considered if α > 1 $$ \alpha >1 $$ .

Unlike Demuyck and Van de gaer (2012), our weights do not depend on the rank order in the distribution of the individual relative change nor on the individual rank order in the base-year distribution. As in Jenkins and Van kerm (2016), Palmisano and Peragine (2015), and Palmisano and Van de gaer (2016), we opt for a transformation of the individual relative income change before aggregating. For α > 1 $$ \alpha >1 $$ , this measure attaches greater weights to greater downward movements and therefore implies taking value judgements into account. This choice is in line with the idea that large mobility implies that, for individuals for whom other characteristics do not change, income changes may require abrupt lifestyle changes and is in line with the prospect theory ingredient of diminishing sensitivity that considers, as Jäntti et al. (2014) underline, that even if the economy is growing, many citizens will highly value social policy that cushions against large income losses. Consequently, this measure shows sensitivity towards greater relative losses and considers inequality in the distribution of individual mobility within a population for α > 1 $$ \alpha >1 $$ . Alternatively, we can express DM α ( x , y ) $$ {\mathrm{DM}}_{\alpha}\left(x,y\right) $$ as:
DM α ( x , y ) = 1 n ∑ i ∈ Q x i − y i 1 x i α x i − y i α − 1 . $$ {\mathrm{DM}}_{\alpha}\left(x,y\right)=\frac{1}{n}\sum \limits_{i\in Q}\left({x}_i-{y}_i\right){\left(\frac{1}{x_i}\right)}^{\alpha }{\left({x}_i-{y}_i\right)}^{\alpha -1}. $$
Thus, this index attaches more weight the greater the absolute income losses and more the lower the initial income for α > 1 $$ \alpha >1 $$ .

The DM α $$ {\mathrm{DM}}_{\alpha } $$ class of measures resembles the index of relative mobility proposed by Schluter and Van de gaer (2011). Differently from theirs, we impose a more restrictive property of focus on those who experience income losses while disregarding the upward movements. This does not mean that our measures are necessarily independent of the existence of upward movements, but we do require that these upward movements are not considered when measuring aggregate downward movements. Only when focusing on downward movements can we provide a class of measures that incorporates information about the proportion of downward movers (incidence), mean relative income loss of downward movers (intensity), and the inequality of relative income losses of downward movers (inequality).

We provide a graphical comparison of our weighting strategy with that of Demuyck and Van de gaer (2012) in Appendix 1 Figure A.1. Given that it is not clear how the individual experience of an income loss should be compensated by the gain of another individual in the same society, separating the weighting system depending on the direction of the income movement seems more adequate than using a unique weighting system for both losses and gains.

As in the poverty literature (Foster et al., 1984), we can interpret our index for different values of α $$ \alpha $$ , in terms of incidence, intensity and inequality of income losses. For α = 0 $$ \alpha =0 $$ , the measure DM 0 $$ {\mathrm{DM}}_0 $$ is the proportion of individuals who experience income losses, which we may call incidence of losses or incidence of downward mobility, H.
DM 0 ( x , y ) = q n = H , $$ {\mathrm{DM}}_0\left(x,y\right)=\frac{q}{n}=\mathrm{H}, $$ (2)
while DM 1 $$ {\mathrm{DM}}_1 $$ is the renormalization of the mean relative income loss:
DM 1 ( x , y ) = 1 n ∑ i ∈ Q x i − y i x i = H 1 q ∑ i ∈ Q x i − y i x i . $$ {\mathrm{DM}}_1\left(x,y\right)=\frac{1}{n}{\sum}_{i\in Q}\frac{x_i-{y}_i}{x_i}=H\frac{1}{q}{\sum}_{i\in Q}\frac{x_i-{y}_i}{x_i}. $$ (3)
If we denote the mean relative income loss per downward mover as intensity of losses or intensity of downward mobility, L = 1 q ∑ i ∈ Q x i − y i x i $$ L=\frac{1}{q}{\sum}_{i\in Q}\frac{x_i-{y}_i}{x_i} $$ , then,
DM 1 ( x , y ) = HL . $$ {\mathrm{DM}}_1\left(x,y\right)=\mathrm{HL}. $$
For α = 2 , $$ \mathrm{For}\ \alpha =2, $$
DM 2 ( x , y ) = 1 n ∑ i ∈ Q x i − y i x i 2 . $$ {\mathrm{DM}}_2\left(x,y\right)=\frac{1}{n}{\sum}_{i\in Q}{\left(\frac{x_i-{y}_i}{x_i}\right)}^2. $$ (4)
As the variance of the relative income losses, Var D , $$ {Var}_D, $$ is
Var D x i − y i x i = 1 q ∑ i ∈ Q x i − y i x i 2 − 1 q ∑ i ∈ Q x i − y i x i 2 , $$ {Var}_D\left(\frac{x_i-{y}_i}{x_i}\right)=\frac{1}{q}\sum \limits_{i\in Q}{\left(\frac{x_i-{y}_i}{x_i}\right)}^2-{\left(\frac{1}{q}\sum \limits_{i\in Q}\frac{x_i-{y}_i}{x_i}\right)}^2, $$
we can write,
DM 2 ( x , y ) = H Var D x i − y i x i + H 1 q ∑ i ∈ Q x i − y i x i 2 = H Var D x i − y i x i + L 2 = H L 2 1 + CV D 2 , $$ {\displaystyle \begin{array}{cc}{\mathrm{DM}}_2\left(x,y\right)& =H\ {Var}_D\left(\frac{x_i-{y}_i}{x_i}\right)+H{\left(\frac{1}{q}{\sum}_{i\in Q}\frac{x_i-{y}_i}{x_i}\right)}^2\\ {}& =H\left[\left({Var}_D\left(\frac{x_i-{y}_i}{x_i}\right)+{L}^2\right)\right]=\mathrm{H}{\mathrm{L}}^2\left[1+{{\mathrm{CV}}_D}^2\right],\end{array}} $$ (5)
where CV D $$ {\mathrm{CV}}_D $$ is the coefficient of variation of the relative income losses. Therefore, DM 2 $$ {DM}_2 $$ includes a well-known inequality measure—the square coefficient of variation—which is the generalized entropy index when the parameter α = $$ \alpha = $$ 2. Consequently, this parameter α $$ \alpha $$ can be viewed as a measure of loss aversion: a larger α $$ \alpha $$ gives greater emphasis to the largest relative losses. As α $$ \alpha $$ becomes very large, DM α $$ {\mathrm{DM}}_{\alpha } $$ approaches the Rawlsian measure, which only considers the downward income change of the individual with the greatest loss.
The DM α $$ {\mathrm{DM}}_{\alpha } $$ class satisfies the following properties (see Appendix 2 for proofs):
  1. Downward mobility focus. For all, x , y , z ∈ ℝ + + n $$ x,y,z\in {\mathbb{R}}_{++}^n $$ , DM α ( x , y ) = DM α ( x , z ) $$ {\mathrm{DM}}_{\alpha}\left(x,y\right)={\mathrm{DM}}_{\alpha}\left(x,z\right) $$ whenever z $$ z $$ is obtained from y $$ y $$ by an income change of a non-downward mover. That is, DM α ( x , y ) $$ {\mathrm{DM}}_{\alpha}\left(x,y\right) $$ is not concerned about what happens to non-downward movers.
  2. Continuity. DM α ( x , y ) $$ {\mathrm{DM}}_{\alpha}\left(x,y\right) $$ is a continuous function for any vector of relative income changes in its domain.
  3. Anonymity. For all, x , y , x ′ , y ′ ∈ ℝ + + n DM α ( x , y ) $$ x,y,{x}^{\prime },{y}^{\prime}\in {\mathbb{R}}_{++}^n\ {\mathrm{DM}}_{\alpha}\left(x,y\right) $$ is symmetric to DM α ( x , y ) = DM α x ′ , y ′ $$ {\mathrm{DM}}_{\alpha}\left(x,y\right)={\mathrm{DM}}_{\alpha}\left({x}^{\prime },{y}^{\prime}\right) $$ whenever x ′ , y ′ $$ {x}^{\prime },{y}^{\prime } $$ are obtained after applying the same permutation of downward movers on x $$ x $$ and y $$ y $$ .
  4. Replication invariance. For all, x , y , x ′ , y ′ ∈ ℝ + + n $$ x,y,{x}^{\prime },{y}^{\prime}\in {\mathbb{R}}_{++}^n $$ DM α ( x , y ) = DM α x ′ , y ′ $$ {\mathrm{DM}}_{\alpha}\left(x,y\right)={\mathrm{DM}}_{\alpha}\left({x}^{\prime },{y}^{\prime}\right) $$ whenever x ′ , y ′ $$ {x}^{\prime },{y}^{\prime } $$ are obtained after applying the same k $$ k $$ -replication on downward movers on x $$ x $$ and y $$ y $$ .
This is a technical property that allows for comparisons between distributions of different size.
  1. Monotonicity. Given the vector x = x 1 , … , x i , … , x j , … , x q , … , x n ∈ ℝ + + n $$ x=\left\{{x}_1,\dots, {x}_i,\dots, {x}_j,\dots, {x}_q,\dots, {x}_n\right\}\in {\mathbb{R}}_{++}^n $$ and y = y 1 , … , y i , … , y j , … , y q , … , y n ∈ ℝ + + n $$ y=\left\{{y}_1,\dots, {y}_i,\dots, {y}_j,\dots, {y}_q,\dots, {y}_n\right\}\in {\mathbb{R}}_{++}^n $$ , consider any E ∈ ℝ + + $$ \mathcal{E}\in {\mathbb{R}}_{++} $$ such that y E ( i ) = y 1 , … , y i − E , … , y j , … , y q , … , y n $$ {y}^{\mathcal{E}(i)}=\left\{{y}_1,\dots, {y}_i-\mathcal{E},\dots, {y}_j,\dots, {y}_q,\dots, {y}_n\right\} $$ . For all i ∈ Q $$ i\in Q $$ and all x , y ∈ ℝ + + n $$ x,y\in {\mathbb{R}}_{++}^n $$ , DM α x , y E ( i ) > DM α ( x , y ) $$ {\mathrm{DM}}_{\alpha}\left(x,{y}^{\mathcal{E}(i)}\right)>{\mathrm{DM}}_{\alpha}\left(x,y\right) $$ . This property is satisfied for α ≥ 1 $$ \alpha \ge 1 $$ .
  2. Individualistic and additive in relative income changes. For all x , y ∈ ℝ + + n $$ x,y\in {\mathbb{R}}_{++}^n $$ , DM α ( x , y ) $$ {\mathrm{DM}}_{\alpha}\left(x,y\right) $$ is the sum of individual relative income changes for a person with income x i $$ {x}_i $$ in the initial period and y i $$ {y}_i $$ in the final period.
From this property we can propose the decomposition of the index by population subgroups according to any socio-demographic characteristics of interest. Consider that the population is divided in G $$ G $$ subgroups. Let g $$ g $$ be the index for the groups. Let P $$ P $$ be a partition of the set N = { 1 , … , n } $$ N=\left\{1,\dots, n\right\} $$ in G $$ G $$ subsets of individuals and let ℘ $$ \wp $$ denote the set of all such possible partitions of N $$ N $$ . For each group g $$ g $$ of size n g $$ {n}^g $$ , the income vectors are partitioned into x g , y g $$ \left({x}^g,{y}^g\right) $$ . For all P ∈ ℘ $$ P\in \wp $$ ,
DM α x 1 , x 2 , … , x G , y 1 , y 2 , … , y G = ∑ g = 1 G n g n DM α g x g , x g . $$ {\mathrm{DM}}_{\alpha}\left({x}^1,{x}^2,\dots, {x}^G,{y}^1,{y}^2,\dots, {y}^G\ \right)=\sum \limits_{g=1}^G\frac{n^g}{n}{\mathrm{DM}}_{\alpha}^g\left({x}^g,{x}^g\right). $$ (6)
This feature is particularly valuable in identifying if some population subgroups are experiencing more downward mobility than others, which can help policymakers design effective and consistent anti-downward mobility strategies. This property can also be used to account for the contribution of each population subgroup to overall downward mobility.
  1. Invariant to simultaneous scale changes in x and y. For all x , y , ∈ ℝ + + n $$ x,y,\in {\mathbb{R}}_{++}^n $$ and > 0 $$ >0 $$ DM α ( x , y ) = DM α ( λ x , λ y ) $$ {\mathrm{DM}}_{\alpha}\left(x,y\right)={\mathrm{DM}}_{\alpha}\left(\lambda x,\lambda y\right) $$ .
This property allows the downward mobility index to not be sensitive to the unit of measurement of income.
  1. Concern about downward absolute movement of poorer individuals. Given the vector x = x 1 , … , x i , … , x j , … , x q , … , x n ∈ ℝ + + n $$ x=\left\{{x}_1,\dots, {x}_i,\dots, {x}_j,\dots, {x}_q,\dots, {x}_n\right\}\in {\mathbb{R}}_{++}^n $$ arranged in ascending order, x 1 < x 2 < … x i < … x j < x n $$ {x}_1<{x}_2<\dots {x}_i<\dots {x}_j<{x}_n $$ and y = y 1 , … , y i , … , y j , … , y q , … , y n ∈ ℝ + + n $$ y=\left\{{y}_1,\dots, {y}_i,\dots, {y}_j,\dots, {y}_q,\dots, {y}_n\right\}\in {\mathbb{R}}_{++}^n $$ , and Γ i = Γ j $$ {\Gamma}_i={\Gamma}_j $$ , consider any E ∈ ℝ + + $$ \mathcal{E}\in {\mathbb{R}}_{++} $$ such that y E ( i ) = { y 1 , … , y i − E , … , y j , … , y q , … , y n } $$ {y}^{\mathcal{E}(i)}=\left\{{y}_1,\dots, {y}_i-\mathcal{E},\dots, {y}_j,\dots, {y}_q,\dots, {y}_n\right\} $$ and y E ( j ) = y 1 , … , y i , … , y j − E , … , y q , … , y n $$ {y}^{\mathcal{E}(j)}=\left\{{y}_1,\dots, {y}_i,\dots, {y}_j-\mathcal{E},\dots, {y}_q,\dots, {y}_n\right\} $$ . For all i , j ∈ Q $$ i,j\in Q $$ and all x , y ∈ ℝ + + n $$ x,y\in {\mathbb{R}}_{++}^n $$ , DM α x , y E ( i ) > DM α x , y E ( j ) $$ {\mathrm{DM}}_{\alpha}\left(x,{y}^{\mathcal{E}(i)}\right)>{\mathrm{DM}}_{\alpha}\left(x,{y}^{\mathcal{E}(j)}\right) $$ . This property is satisfied for α > 1 . $$ \alpha >1. $$

That is, given two downward movers with the same proportional income change, the same additional absolute reduction in income between the two moments in time increases the index more if it is allocated to an individual who initially had a lower income. Therefore, our index is more sensitive to losses of the poorest individuals (see Appendix 2 for a formal proof). This property implies inequality aversion with respect to the distribution of individual income losses, being equivalent to the Pigou-Dalton principle of transfers in the inequality literature.

In Appendix 3 we undertake some comparisons of our proposal with other well-known mobility indices. Indices that are constructed to measure a linear relationship between two variables are not sensitive to proportional income changes in the distribution, so even in the presence of mobility they do not detect it in those scenarios. This is also the case for Cowell-Flachaire's scale-independent measure ( M 0 $$ {\mathrm{M}}_0 $$ ). In turn, the Cowell-Flachaire translation-independent measure ( M ′ 0 $$ \mathrm{M}{\prime}_0 $$ ), is sensitive to proportional changes in incomes but is translation invariant and does not detect movement when equal absolute income decreases occur. Fields and Ok (1996) measure is scale dependent so it detects mobility where others do not capture it and is larger when downward mobility is larger. Nonetheless, it does not distinguish where in the distribution downward mobility takes place and, given that it aggregates absolute changes in income, it does not allow researchers to discriminate between upward and downward mobility. Our proposed class of measures is sensitive to proportional income changes along the distribution and to translation of incomes and it is larger the larger the proportional reduction of incomes (diminishing sensitivity) and the poorer the individuals that suffer it.

4 A Graphical Device and Progressivity in Downward Mobility Analysis

In this section we discuss the characteristics of an interesting graphical device for the analysis of downward mobility that is analogous to Three I's of Poverty (TIP) curve in poverty analysis (Jenkins & Lambert, 1997, 1998): the TIDM curve. This curve is based on relative income losses and provides a revealing picture of downward mobility and its distribution. We construct downward mobility profiles and develop dominance criteria to rank downward mobility distributions according to their downward mobility level. The name of the curve, Three I's of Downward Mobility (TIDM) curve, is derived from its ability to simultaneously represent and summarize three aspects of downward mobility: incidence, intensity, and inequality.

Let g i = max Γ i , 0 $$ {\mathrm{g}}_i=\max \left\{{\Gamma}_i,0\right\} $$ . Curves are obtained by ranking g i $$ {\mathrm{g}}_i $$ , in descending order (greatest losses first), and by cumulating and plotting the relative income losses per individual.

The TIDM curve is denoted by TIDM ( p , g $$ p,\mathrm{g} $$ ), where 0 ≤ p ≤ 1 $$ 0\le p\le 1 $$ , and p represents the cumulative proportion of individuals in the population ranked in descending order of relative income losses. The curve plots against p the sum of the first p percent g $$ \mathrm{g} $$ -values divided by the total number of individuals in the population, n $$ n $$ , once they have been ranked from larger to smaller relative (downward) income changes. Thus, TIDM ( 0 , g $$ 0,\mathrm{g} $$ ) = 0 and TIDM ( k n , g ) $$ \left(\frac{\mathrm{k}}{\mathrm{n}},\mathrm{g}\right) $$ = 1 n ∑ i = 1 k g i $$ \frac{1}{n}{\sum}_{i=1}^k{\mathrm{g}}_i $$ for integer values k ≤ n $$ k\le n $$ and at intermediate points TIDM ( p , g $$ \mathrm{p},\mathrm{g} $$ ) is determined by linear interpolation. Therefore, TIDM(p, g $$ \mathrm{g} $$ ) is a positive, increasing, and concave function of p, where the slope at each given percentile is equal to the mean relative income loss experienced by individuals in that particular percentile.

The shape of a TIDM curve provides us with very useful information (Figure 1). The incidence of downward mobility, i.e. proportion of downward movers, H, is represented by the value of p, in the horizontal axis, which graphically corresponds to the point in the x-axis where the TIDM curve reaches its maximum height. The mean relative income loss is represented by the maximum height of the TIDM curve and is related to the intensity of downward movements. The inequality of income losses in the downward movers' population is captured by its curvature, i.e. its concavity, in the non-horizontal section of the TIDM curve. If downward movers were to experience the same relative income losses, the TIDM curve in the section of the curve for downwards movers would be a straight line. The more unequal relative income losses are, the more curved the TIDM will be.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The TIDM curve and the three “I”s of downward movement

The extreme cases of the TIDM curve are as follows. The maximum downward mobility in a population is when all individuals lose all their income. This means that, in the final period, all of them have zero income; therefore, the dimension of the relative income loss would take the value 1 for the whole population. In this case, the TIDM curve is the bisector of the first quadrant, a 45° line from the origin with slope one and vertical intercept one at p = 1. Its shape would be analogous to the Lorenz curve in the case of maximum equality. At the other extreme, when there are no downward movers in a population, the curve coincides with the horizontal axis.

Regarding dominance in TIDM curves, we can establish an ordering of relative income loss profiles by non-intersecting TIDM curves. Moreover, these curves allow researchers to identify how income gaps are distributed within a population to evaluate the relevance of large income drops versus medium or small ones. Consequently, these curves provide extremely valuable additional information to the DM α $$ {\mathrm{DM}}_{\alpha } $$ class of measures to help interpret the nature of downward mobility in any population of interest. It is also possible to use them to compare income mobility across time, countries, regions, or any other population subgroup.

Definition of dominance in downward mobility. Given two relative income loss profiles, Γ a $$ {\Gamma}^a $$ and Γ b $$ {\Gamma}^b $$ , we would say that Γ a $$ {\Gamma}^a $$ dominates Γ b $$ {\Gamma}^b $$ in a downward mobility sense, Γ a > DM Γ b $$ {\Gamma}^a{>}_{\mathrm{DM}}{\Gamma}^b $$ , if Γ a ≠ Γ b $$ {\Gamma}^a\ne {\Gamma}^b $$ and TIDM p , g a > TIDM p , g b $$ \mathrm{TIDM}\ \left(p,{g}^a\right)>\mathrm{TIDM}\ \left(p,{\mathrm{g}}^b\right) $$ for any p ∈ [ 0 , 1 ] $$ p\in \left[0,1\right] $$ .

This dominance is linked to the properties previously mentioned. We can establish a relationship between dominance in a downward mobility sense and the set of indices of downward mobility that satisfy the properties. This is done in the inequality and poverty analysis, where valuable theorems establish a relationship between the income distribution ranking obtained by the three “I's” of poverty (TIP) or Lorenz's dominance criteria and those obtained by complete poverty and inequality indices compatible with those criteria (Jenkins & Lambert, 1998). In this sense, by using a minimal set of judgements, we are able to identify particular cases where downward movement distribution ranking is independent of the index chosen, as all indices yield the same result. This makes our analysis of downward movement significantly more robust.

Theorem 1.For any pair of income losses profiles,

Γ a > DM Γ b ⇔ DM x a , y a > DM x b , y b for any DM ( . ) ∈ DM * , $$ {\Gamma}^a{>}_{DM}{\Gamma}^b\iff \mathrm{DM}\left({x}^a,{y}^a\right)>\mathrm{DM}\left({x}^b,{y}^b\right)\ \mathrm{for}\ \mathrm{any}\ \mathrm{DM}(.)\in {\mathrm{DM}}^{\ast }, $$
where DM * $$ {\mathrm{DM}}^{\ast } $$ is the set of indices that satisfy the downward mobility focus, continuity, anonymity, replication invariance, monotonicity, and concern about downward absolute movement of poorer individuals' properties. That is, DM * $$ {\mathrm{DM}}^{\ast } $$ is the class of downward mobility indices in the form:
DM = F 1 n ∑ i ∈ Q ϕ Γ i , $$ \mathrm{DM}=F\left[\frac{1}{n}{\sum}_{i\in Q}\phi \left({\Gamma}_i\right)\right], $$ (7)
with ϕ ( o ) = 0 $$ \phi (o)=0 $$ and ϕ ′ Γ i > 0 $$ {\phi}^{\prime}\left({\Gamma}_i\right)>0 $$ and ϕ ′ ′ Γ i > 0 $$ {\phi}^{\prime \prime}\left({\Gamma}_i\right)>0 $$ for all Γ > 0 $$ \Gamma >0 $$ . Therefore, a higher TIDM curve leads to a higher downward mobility index for an extensive set of downward movement indices.

We also propose an index of downward mobility progressivity based on the TIDM curve that can provide us with a measure of the extent to which income losses are smaller for the poor than for the rest of the population (progressivity) or the contrary (regressivity). This measure allows to link the concept of economic mobility and that of its capability of reducing inequality in the short and medium run. In some sense we could say that this is a measure of shared adversity in difficult times, that is, an indicator of the extent to which income losses are comparatively smaller for those placed at the lower end of the income distribution as opposed to a situation where income losses are larger for the poor. In the latter, adversity during recessions would be suffered proportionally more by those already at the bottom of the income distribution while in the former the contrary would be happening.

In this setting it is natural to consider an index of downward mobility progressivity by proposing the construction of a new curve, the non-anonymous cumulative downward mobility curve (nac-DM). The nac-DM consists of the plot of cumulative relative losses per capita against the cumulative proportion of individuals in the population ranked in descending order of initial income. Thus, nac-DM ( 0 , Γ ) $$ \left(0,\Gamma \right) $$  = 0 and nac-DM k n , Γ $$ \left(\frac{\mathrm{k}}{\mathrm{n}},\Gamma \right) $$ = 1 n ∑ i = 1 k Γ ˜ i $$ \frac{1}{n}{\sum}_{i=1}^k{\tilde{\Gamma}}_i $$ , where Γ ˜ i $$ {\tilde{\Gamma}}_i $$ are the Γ i $$ {\Gamma}_i $$ ranked in descending order of initial income, and at intermediate points nac-DM ( p , Γ $$ \mathrm{p},\Gamma $$ ) is determined by linear interpolation. Therefore, nac-DM (p, Γ $$ \Gamma $$ ) is a positive, non-decreasing function of p, and it is never over the TIDM curve. Note that the nac-DM will be horizontal at some points corresponding to the lack of downward income mobility of some individuals.

Let us now define the line of maximum downward mobility (max-DM). This line corresponds to the case in which everyone loses all his/her income so that it can be represented as a straight line with slope one (see Figure 2). Twice the area between the nac-DM curve and the line of maximum downward mobility (max-DM) is:
A = 1 n 1 n − Γ ˜ 1 + ∑ k = 1 n ∑ i = 1 k 1 n − Γ ˜ i + ∑ i = 2 k + 1 1 n − Γ ˜ i = $$ \mathrm{A}=\frac{1}{n}\left\{\left(\frac{1}{n}-{\tilde{\Gamma}}_1\right)+\sum \limits_{k=1}^n\left(\sum \limits_{i=1}^k\left(\frac{1}{\mathrm{n}}-{\tilde{\Gamma}}_i\right)+\sum \limits_{i=2}^{k+1}\left(\frac{1}{\mathrm{n}}-{\tilde{\Gamma}}_i\right)\ \right)\right\}= $$
= 1 n ∑ i = 1 n ( 2 n − 2 i + 1 ) 1 n − Γ ˜ i = 1 − 1 n ∑ i = 1 n ( 2 n − 2 i + 1 ) Γ ˜ i . $$ =\frac{1}{n}\sum \limits_{i=1}^n\left(2n-2i+1\right)\left(\frac{1}{\mathrm{n}}-{\tilde{\Gamma}}_i\right)=1-\frac{1}{n}\sum \limits_{i=1}^n\left(2n-2i+1\right){\tilde{\Gamma}}_i. $$ (8)
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Max-DM, TIDM and nac-DM curves.

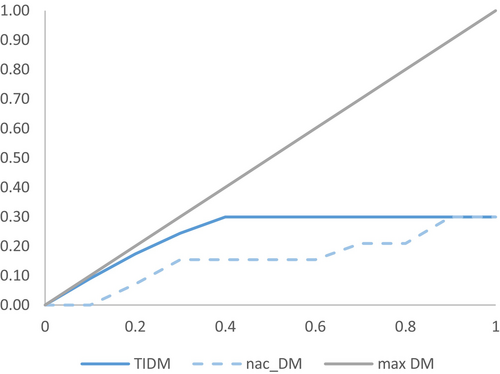
Given an empirically observed downward mobility vector, the difference between the area between nac-DM and max-DM curves and the area between TIDM and max-DM curves in Figure 2 quantifies the cost of not having a more pro-poor distribution. That is, if the same relative losses occurred but were distributed more equally in the population, we could have had a situation where downward mobility was much more progressive, i.e. more inequality reducing.

Interestingly, if the TIDM curve is conceived as the generalized inverse Lorenz curve of g i $$ {\mathrm{g}}_i $$ , we can interpret the distance between the nac-DM curve and the TIDM curve. Therefore, the TIDM curve can also be interpreted as a benchmark case in which the losses observed in the population are distributed in the most progressive way possible, i.e. when greater losses are attached to highest income individuals. At the same time the nac-DM curve can be interpreted as the concentration curve of the vector g $$ \mathrm{g} $$ when the individuals are arranged in descending order of the initial income.

In this setting, we can also quantify how far society is from the benchmark conformed from the observed downward movements arranged in the most progressive order possible, that is, the TIDM curve. A measure for this relative to the benchmark downward mobility progressivity, DMP $$ \mathrm{DMP} $$ , is:
DMP = 1 n Γ ˜ 1 − Γ 1 + ∑ k = 1 n ∑ i = 1 k Γ ˜ i − Γ i + ∑ i = 2 k + 1 Γ ˜ i − Γ i = $$ \mathrm{DMP}=\frac{1}{n}\left\{\left({\tilde{\Gamma}}_1-{\Gamma}_1\right)+\sum \limits_{k=1}^n\left(\sum \limits_{i=1}^k\left({\tilde{\Gamma}}_i-{\Gamma}_i\right)+\sum \limits_{i=2}^{k+1}\left({\tilde{\Gamma}}_i-{\Gamma}_i\right)\ \right)\right\}= $$
= 1 n ∑ i = 1 n ( 2 n − 2 i + 1 ) Γ ˜ i − Γ i . $$ =\frac{1}{n}\sum \limits_{i=1}^n\left(2n-2i+1\right)\left({\tilde{\Gamma}}_i-{\Gamma}_i\right). $$ (9)

The DMP index is always positive and smaller than one because the nac-DM is always weakly dominated by the TIDM curve, and the greater the area (and therefore the index) the further away society is from the most progressive downward mobility benchmark, that is, more regressive are the distribution of losses.

We can further quantify in income terms the amount of money needed to have the most progressive downward mobility by comparing the absolute income loss there would be if the greater income losses were experienced by the richest people with the absolute income loss effectively experienced in our society with the current distribution of income losses. Thus DMP_COST can be defined as:
DM P COST = ∑ i = 1 n Γ ˜ i x i − ∑ i = 1 n Γ i x i . $$ \mathrm{DM}{\mathrm{P}}_{\mathrm{COST}}=\sum \limits_{i=1}^n{\tilde{\Gamma}}_i{x}_i-\sum \limits_{i=1}^n{\Gamma}_i{x}_i. $$ (10)

Recall that Γ ˜ i $$ {\tilde{\Gamma}}_i $$ are income loss rates arranged according to decreasing initial incomes, x i $$ {x}_i $$ are initial incomes arranged in descending order and Γ i $$ {\Gamma}_i $$ are the losses arranged in descending order. This expression allows us to assess, in economic terms, the cost in absolute income losses of a more progressive downward mobility.

5 An Empirical Illustration: the Different Dimensions of Downward Income Mobility in Two Recession Periods in Spain

Evidence for the United States shows that the prevalence of income losses in the last two decades has grown significantly (Dynan et al., 2012; Hacker et al., 2010, 2014). In the European context, Ayala and Sastre (2008), Van Kerm and Pi Alperin (2013), and Cantó and Ruiz (2015) underline that in some EU countries disposable incomes are particularly volatile in time. For instance, in the case of Spain during the Great Recession, a very large part of the population lost more than 25 percent of their income from 1 year to the next, more than in any other EU country in the same period.

In this section we measure the incidence, intensity, and inequality of downward income mobility in two recent recession periods: 2008/2009 and 2019/2020, in Spain, a country where income losses have been large and persistent at both moments in time. We exploit the longitudinal structure of the EU-SILC database for Spain. We will first analyze the levels of downward mobility between two consecutive years and then, given the empirical evidence on the relevant role of the position in the income distribution (social classes) and age groups in determining the opportunities to descend the income ladder, we will compare levels and dimensions of downward income mobility by classes and age groups.

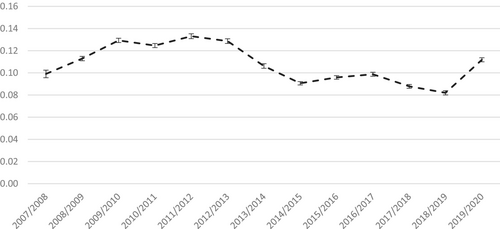
Figure 3 shows that even in regular growth periods around a 40 percent of the Spanish population experiences income losses. In recessions, however, the occurrence of losses increases sharply, approximately 10 pp. per year of economic difficulty. During the worse years of the Great Recession (GR), income losses affected more than 60 percent of the population growing from 40 percent in 2007/2008 to 50 percent first (2008/2009) and then to 61 percent (2009 to 2010). The increase we find in the incidence of losses in the first year of the pandemic was quite similar to that of the first year of the GR. Indeed, from 2019 to 2020, income losses grew from the regular 40 percent to a 50 percent.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Income losses: Incidence (H), Intensity (I) and Inequality (CV, Coefficient of variation).

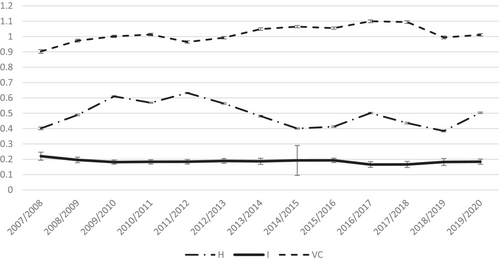
Note: Vertical lines show 95 percent confidence intervals based on the bootstrap procedure with 1,000 bootstrapped estimates for each point estimation.

In turn, inequality of income losses shows a sustained growing tendency up to recent years, it is lowest in 2007 and highest in 2017, which underlines that the downward income mobility tends to be more dissimilar after the GR until a new economic shock comes along, and inequality of income losses registers a very similar level in both recession periods.

Ayala and Sastre (2008) studied income mobility in five EU countries in the second half of the nineties and found that mobility was significantly different by age groups, so that young household heads (together with individuals in single-parent households) experienced the greatest income fluctuations, even if the intensity of this instability varied greatly across countries. Cantó and Ruiz (2015) find that one of the main determinants of the probability of suffering income losses, both in the United States and Spain, was the individual's age cohort. The young and middle-aged groups are more likely to lose incomes compared to older individuals. In addition, Aristei and Perugini (2015) have concluded that the levels and determinants of short-term mobility differ remarkably in the various institutional models across Europe, particularly regarding household composition, demographic attributes, education levels, and job positions. In terms of age, we analyze trends amongst two different groups: individuals living in households where all members are young (below 45 years of age) and individuals living in households where all members are middle-aged or old (over 45 years of age). In terms of the role of other sociodemographic characteristics and income levels, we have found particularly useful to consider four different income-related social class groups: low-income, lower-middle, upper-middle and high-income. These groups are identified following Atkinson and Brandolini (2013) as in Ayala and Cantó (2018), so that thresholds are 75 percent median equivalent income for the low-income class, from 75 percent to 125 percent for the lower-middle, from 125 percent to 200 percent for the upper-middle and over 200 percent for the high-income class.

In Figure 4 we depict the TIDM curve for two recession periods: 2009/2010 and 2019/2020. We conclude that in the pandemic shock fewer individuals were affected by income losses and the intensity of their per capita losses was lower than in the GR. In fact, 33 percent of year-to-year income losses were larger than 10 percent and up to 16 percent were over a 25 percent. During the first year of the pandemic, these numbers were: 27 percent and 14 percent. Thus, the per capita loss during the GR was larger than during the pandemic, due mainly to the larger frequency of smaller losses and not so much to their intensity.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
TIDM curves for 2009/2010 and 2019/2020: general.

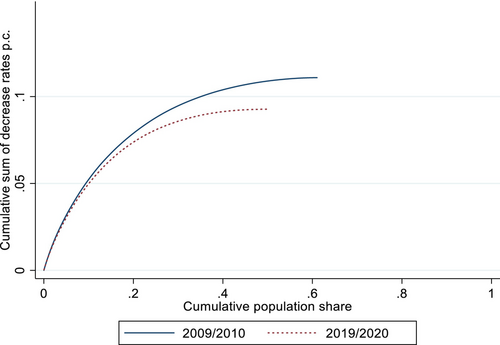
Note: The horizontal part of the TIDM curve has been omitted to ease the identification of the point at which the curve reaches its maximum.

Focusing on age differences, in Figure 5 we present the TIDM curves by age for each pair of years. It becomes most clear that even if the GR affected approximately the same proportion of individuals across household age types, those who are older had lower per capita losses. During the pandemic both the frequency of income losses is lower for young and mixed ages households. Comparing both recessions, the impact of the GR shock was much more similar for young and mixed households than the pandemic has been. In fact, the pandemic was relatively worse for the young than for the mixed ages household group, who appear to have been significantly more protected from losses in this shock.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
TIDM curves by age for 2009/2010 and 2019/2020.

Note: The horizontal part of the TIDM curve has been omitted to ease the identification of the point at which the curve reaches its maximum.

Turning our analysis to income-related classes, we find that the GR compared to the pandemic affected a much larger number of individuals across economic classes (Figure 6): a 50 percent or more of each group experienced an income loss. Incidence was nevertheless significantly higher in the low-income class (67 percent) compared to the high class (50 percent) and per capita losses were higher for the former, quite distinctively form the rest. This shows that the intensity of losses was particularly concentrated in that group and losses in all three other classes were much smaller.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
TIDM curves by income class for 2009/2010 and 2019/2020.

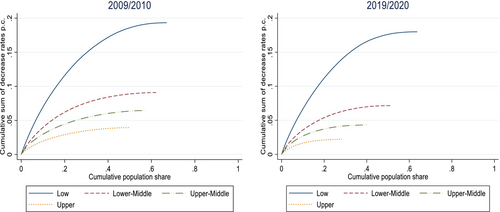
Note: The horizontal part of the TIDM curve has been omitted to ease the identification of the point at which the curve reaches its maximum.

In the pandemic shock, the frequency of losses was even more different across classes (Figure 6). Middle and upper classes were much more protected from the shock: only 28 percent of the upper class experienced a loss, 41 percent of the upper-middle class, 52 percent of the lower-middle class while it reached a 62 percent of the low-income households. Nevertheless, the largest differences between the low-income class and the rest are observed in their per capita losses. This shows a very different experience of the shock for this group due to a much higher vulnerability to downward income mobility in this recession compared to the GR: 49 percent (in the pandemic) to 45.6 percent (in the GR) of losses in the low-income class are over 10 percent. Thus, both recessions have not been so different for the low-income classes, differently from the evidence regarding the whole income distribution. In fact, if we gave more weight to the downward mobility of the low-income class, both recessions would be very similar in terms of downward mobility.

Finally, in Figure 7 we depict the evolution of our index of downward income mobility progressivity. It is easy to see that in periods of recession, downward income mobility is more regressive than in periods of growth because it disproportionally affects individuals in the lowest tail of the income distribution. Downward mobility regressivity is found to be similar in the initial year of both recessions while in the GR we confirm that it continued to be regressive for various years, we still need to see if that is the case or not for the recent pandemic shock.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Evolution of the index of downward mobility progressivity.

Note: Vertical lines show 95 percent confidence intervals based on the bootstrap procedure with 1,000 bootstrapped estimates for each point estimation.

6 Conclusions

We propose a subgroup decomposable class of income mobility measures with good properties by adapting the concept of individual income gap between two moments in time to a framework that is traditionally used in the measurement of poverty and deprivation which allows us to be consistent with various ingredients of behavioral economics.

Our class of measures quantifies downward mobility separately from upward mobility by avoiding compensation between different individual's gains and losses and provides some distribution-sensitive assessment of mobility. It can identify the relevance of all three important dimensions of the individual mobility experience: incidence, intensity, and inequality. Our class of measures is subgroup decomposable, which allows researchers to evaluate mobility across population subgroups in a coherent way. An attractive feature of our measures is that they are consistent with a simple, intuitive, and largely informative graphical device, which allows for further intuitive analyses of incidence and intensity of income changes between two moments in time and for different population subgroups. Moreover, we establish a relationship between dominance in a downward mobility sense and the minimal set of properties the indices of mobility should satisfy to produce the same downward movement distribution ranking independently of the index chosen, which makes any analysis significantly more robust. Most advantageously, its simple structure facilitates comprehension and eases communication with policymakers without leaving any desirable properties aside. Finally, we propose an index of the progressivity of income losses that is, it evaluates if income losses are smaller of larger for the poor than for the rest of the population.

Our proposal is versatile as it allows a potential formulation of a mobility index that can consider the situation of the individual in the starting distribution. Moreover, a similar analysis could easily be developed using a more relative evaluation of individual mobility by expressing each period's income relative to the mean of the contemporaneous period. This would allow for the comparison of an individual's own losses with those of the rest of society but at the cost of not satisfying some of the properties.

We provide an empirical illustration of our proposed measures for the case of Spain in two recessions. Our main results reveal that our class of measures is particularly useful for showing (both cardinally and graphically) how remarkably different components of downward income mobility contribute to its social evaluation, which allows us to identify each of the main drivers of the well-being impact of income losses: incidence, intensity, inequality, and progressivity. We can also analyze how these recession periods differ in their impact on incomes and how individuals in different income classes or age groups had different experiences of income loss.

Results show that even if the pandemic shock was not as large as the GR shock, some sociodemographic groups have had different experiences. The young and the low-income classes experienced a similar shock in both recessions while households with mixed ages and all members over 45 together with those in better income positions were much more protected from losses in the pandemic than in the GR. Interestingly, the large impact of the GR on the lower-middle class did not occur as much in the pandemic shock. These differences are much clearer when considering the intensity and inequality of downward income mobility than when we only measure its incidence. Finally, the index of progressivity shows, as one would expect, that in periods of recession, downward income mobility is more regressive than in periods of growth. However, our index of progressivity can show that not in all recession periods downward mobility is equally regressive, this has relevant implications in the interpretation of the role of downward income mobility in shaping individual well-being and can be very revealing for policy makers.

  • 1 We could introduce larger weights for smaller downward movements if α < 1 $$ \alpha <1 $$ .
  • 2 Jäntti and Jenkins (2015, p. 63) ask a key question related to this: “Why should we be concerned about the inequality of individual growth rates independently of incomes in the initial period?”. We would argue that given that it is most likely that a large income loss will take place at the lowest part of the income distribution, and recalling our definition of income change, x i − y i x i $$ \frac{x_i-{y}_i}{x_i} $$ , our measures consider that an equal absolute income change has a larger impact on downward mobility. This is because the same absolute loss produces a larger relative loss the smaller initial income. Therefore, our approach gives greater importance to income falls of the poor.
  • 3 We assume all individuals in the society have non-negative incomes.
  • 4 Given initial incomes, dominance still holds if all downward movers experience an identical proportional income change.
  • 5 This expression resembles the one of Cowell and Flachaire (2018) in Theorem 1.
  • 6 Consider that TIDM curves are the accumulation of losses arranged in descending order of the loss and in this graph, they should be understood as a sort of anonymous representation not directly related to the initial level of income represented in the x-axis.
  • 7 That is the reflection of the Lorenz curve of the vector g, when the values are non-decreasingly ordered, around the line of equality (see Jenkins & Lambert, 1997).
  • 8 Note that in the nac-DM curve individuals are identified by their ill-fare ranks in the initial distribution of incomes while in the TIDM they are identified by their ranks in the distribution of losses. Consequently, we have the same vector of losses but ordered in two different ways.
  • 9 See Jenkins and Van Kerm (2016) for an alternative measure of the return to progressive growth.
  • 10 The information on incomes for the years 2008, 2009, 2019 and 2020 is collected in EU-SILC survey years 2009, 2010, 2020 and 2021 due to the time lag of the survey.
  • 11 For a review of the advantages and disadvantages of EU-SILC for comparing income dynamics across countries, see Jenkins and Van Kerm (2017).
  • 12 See Figure 3 for 95% confidence intervals based on the bootstrap procedure with 1,000 bootstrapped estimates for each point estimation.
  • 13 For robustness, we have trimmed the tails of the distribution (1% of each tail), as strongly suggested by Cowell and Schluter (1998) due to the sensitivity of income mobility indices to the presence of outliers. Our database includes, for every two consecutive years, around 20,000 observations (Table A.3. Appendix). Our income variable in both moments in time is household equivalized disposable income in euros at constant 2022 prices adjusted for household size using a modified OECD scale. As in Van Kerm and Pi Alperin (2013) and Aristei and Perugini (2015), all estimates are obtained using sampling weights provided by Eurostat that are designed to adjust for attrition and non-response biases.
  • 14 Bootstrapped 95% confidence intervals confirm the difference between the two periods: they are 32–34%, 15–17%, 27–28% and 14–15%, respectively.
  • 15 Interestingly, we also find significant differences in the incidence and magnitude of incomes losses by age. See Table A.4 for confidence intervals. Individuals living in young households suffered a higher incidence of losses in the GR than in the pandemic and per capita loses were also significantly higher. Nevertheless, for one-third of the young income losers the per capita loss was similar in both recessions. In fact, a large fraction of individuals living in older households' experience only small losses in both recession periods. This implies that inequality of income losses is larger within old than within young households.
  • 16 See Table A.5 for confidence intervals.
  • 17 Bootstrapped confidence intervals are 48–51% in the pandemic and 44–47% in the GR, respectively.
  • 18 Note that the GR and the pandemic were not so different in their impact on the low-income class (30% of the total population). Almost one third of the losers in the low-income class experienced similar losses in both moments in time. In contrast, in the case of the lower-middle class (33% of the total population), both recessions were significantly different. They suffered a much lower incidence in the pandemic (52 vs. 62%) and per capita losses were much smaller in comparison to the GR for most of the population of this group.

The full text of this article hosted at iucr.org is unavailable due to technical difficulties.