Optimal Abort Rules for Multiattempt Missions
Abstract
Many real-world systems use mission aborts to enhance their survivability. Specifically, a mission can be aborted when a certain malfunction condition is met and a risk of a system loss in the case of a mission continuation becomes too high. Usually, the rescue or recovery procedure is initiated upon the mission abort. Previous works have discussed a setting when only one attempt to complete a mission is allowed and this attempt can be aborted. However, missions with a possibility of multiple attempts can occur in different real-world settings when accomplishing a mission is really important and the cost-related and the time-wise restrictions for this are not very severe. The probabilistic model for the multiattempt case is suggested and the tradeoff between the overall mission success probability (MSP) and a system loss probability is discussed. The corresponding optimization problems are formulated. For the considered illustrative example, a detailed sensitivity analysis is performed that shows specifically that even when the system's survival is not so important, mission aborting can be used to maximize the multiattempt MSP.
1 INTRODUCTION
When survival of a system has a higher priority than accomplishing a mission, a mission can be aborted if the risk of losing a system becomes too high and a rescue procedure aimed at saving a system can be activated. This is relevant, for example, for aircrafts, submarines, or complex costly technological processes, where the mission abort policy can improve survivability and thus decrease a risk of casualties and/or of substantial economic losses.
In practice, aborting a mission often follows when some degradation parameter describing a system state indicates that system deterioration has reached a critical level. For instance, the number of external impacts (shocks) experienced by a system can be a decision parameter for a possible mission termination, as with each shock, survivability of a system decreases (Levitin & Finkelstein, 2018c). A real-world example of the described scenario is an aircraft that can be required to abort a mission after a certain number of external impacts associated with, for example, malicious activity or nature conditions (e.g., lightning inducing electrical peaks in the electrical circuits). These impacts can cause deterioration of critical systems, which makes risks associated with mission completion unacceptable (Levitin, Finkelstein, & Dai, 2018).
When systems with the mission abort and rescue option are considered, two distinct performance measures should be balanced: the mission success probability (MSP), that is, the probability of successfully completing a mission with or without a specific time frame, and the system loss probability (SLP) indicating the risk that the entire system can be irreparably lost during the mission (Levitin, Xing, & Dai, 2018b; Myers, 2009).
As traditional reliability models are not applicable for addressing effects of mission aborts for evaluating and balancing the MSP–SLP tradeoff, we had to develop a new approach for modeling and evaluating the MSP and the SLP of systems operating in a random environment and subject to mission aborts. This was performed to some extent in our previous work, where relevant optimization problems were also considered (Levitin & Finkelstein, 2018c; Levitin et al., 2018b).
Though the optimal mission aborting rules and relationship between MSP and SLP have become recently a field of intensive study (Cha, Finkelstein, & Levitin, 2018; Levitin & Finkelstein, 2018a, 2018b, 2018c; Levitin et al., 2018; Levitin, Xing, & Dai, 2018a, 2018b; Levitin, Xing, & Luo, 2019; Myers, 2009; Peng, 2018; Qiu & Cui, 2019), all papers in the literature dealing with aborting or termination of a mission consider a single attempt to accomplish a mission, whereas in practice, this can be done several times when the time frame and resources allow for multiple attempts.
Thus, the main objective of this study is to develop a probabilistic model and obtain the optimal aborting rules for situations when the successfully aborted mission can be attempted again. We show that even when mission completion is the only concern (e.g., for the non-safety-critical systems), aborting a mission in the multiattempt policy can substantially improve the MSP, whereas in the single attempt case, a mission abort is never beneficial with respect to the MSP. This interesting and not intuitively evident observation considerably widens the class of systems to which mission aborts can be applied.
Systems in our study operate and perform missions in a random environment modeled by the Poisson process of adverse impacts (shocks). There is an extensive literature on shocks modeling in reliability and risk analysis (see, e.g., the monographs mostly devoted to shocks modeling; Finkelstein, 2008; Finkelstein & Cha, 2013; Nakagawa, 2007). Traditionally, one distinguishes between two major types of shock models: the cumulative shock models, when systems fail due to some cumulative effect, and the extreme shock models when systems can fail with certain probabilities upon any shock (Cha & Mi, 2007; Gut & Husler, 2005; Klefsjo, 1981; Mallor & Omey, 2001). In this article, we develop our approach based on the generalized extreme shock model (Cha & Finkelstein, 2011) when the probability of a failure upon a shock increases with each experienced shock, thus describing the corresponding deterioration in the remaining lifetime of a system. We consider a policy when a mission in the jth attempt is aborted and the rescue procedure is activated immediately after the mjth shock. The mission abort during the jth attempt is allowed only during the time ξj from the start of this attempt.
Missions with a possibility of multiple attempts can occur in different real-world settings when accomplishing a mission is really important and the cost-related and time-wise restrictions for this are not very severe. As far as we know, this type of problem was not considered in the literature so far. The possible motivating examples are discussed below.
Consider an unmanned aerial vehicle (UAV) performing a surveillance mission. During the mission, it should cover the distance W. The adversary uses electronic interference (shocks) to destroy the UAV's control system, which can cause the UAV to crash. Each subsequent interference attack has a larger success probability than the previous one due to overheating and deterioration of the onboard interference filters. Attacks are detected by the UAV's operators and the mission attempt can be aborted upon the occurrence of a predetermined number of attacks. The rescue procedure presumes returning to the base after changing the flight altitude, which causes reduction of the interference attacks rate. After landing, the interference filters are changed and the next attempt to perform the mission starts. If, during any of the attempts, an attack succeeds in destroying the electronic equipment, the UAV is lost and the mission fails. The possible number of attempts, K, is determined by the time window during which the surveillance information remains vital and the time needed to accomplish the surveillance mission (single attempt). The mission succeeds when one of the K attempts to complete the surveillance task succeeds. If all K attempts fail, the entire mission fails.
Another example is a system performing an online “software as a service” task (the mission) consisting of W computational operations. Hackers’ attacks (shocks) can cause data corruption (the mission failure). As each attack, even when it fails, reveals to a hacker some information about the system protection, the probability of the attack success increases with its number. The attacks are detected by the system and the mission attempt can be aborted upon an attack with the predetermined number. When it happens, data check-pointing/backup and software reinstallation is performed (in cloud systems, software migration is usually performed as well), which constitutes the rescue procedure. The protection system is updated to make the information obtained by a hacker in the previous attacks useless. During the rescue procedure, the system is partially disconnected from the communication channels, which causes attack rate reduction compared to the phase of primary mission. After the system rescue, the next attempt to perform the service task starts. If an attack is successful (i.e., it succeeds in corrupting the data) at any attempt, the mission fails. The possible number of attempts, K, is determined by the maximum allowed service time and the time needed to accomplish a single task. The mission succeeds when one of the K attempts to complete the service task succeeds. If all K attempts fail, the entire mission fails.
A number of recent publications (Levitin, Xing, Amari, & Dai, 2013; Lu, Wu, Liu, & Lundteigen, 2015; Ma & Trivedi, 1999; Peng, Zhai, Xing, & Yang, 2014; Wang, Xing, & Levitin, 2015; Wang, Xing, Peng, & Pan, 2017 to name a few) are devoted to analysis of the phased-mission systems that somewhat resemble our setting. However, all referenced papers consider neither abort policies and the MSP-survivability tradeoff, nor the influence of random shocks. The latter is the main goal of our article.
The rest of the article is organized as follows. Sections 2 and 3 present the problem formulation and derivation of the MSP and the SLP. Section 4 presents an illustrative example and the corresponding analysis. Section 5 concludes the article and outlines possible directions for future research. Some supplementary material can be found in the Appendix.
2 PROBLEM FORMULATION
A system performs a mission task that should be completed within a predetermined time θ. The time needed to complete the task without failures is τ < θ. To perform the task, a system should operate in a random environment modeled by the homogeneous Poisson process (HPP) }, with rate , where is the number of shocks in [0, t) and are the random arrival times of shocks. Each shock can result in a failure of a system with probability that increases with the number of experienced shocks, thus describing deterioration of a system due to shocks. This means that the more shocks a system survives, there is less probability that it will survive the next shock (see the more detailed description in Section 3).
We assume that shocks are the only cause of system failures. Generalization to the case of internal failures independent from the shock process can be considered in a straightforward way (Levitin et al., 2018).
When some observed factors indicate that system survival in the case of mission continuation is unlikely, a mission can be aborted and a rescue procedure activated. Note that often the environment for the rescue procedure differs from that for the primary mission. Thus, we assume that the shock rate during the rescue, λR, differs from that during the primary mission (see example in Section 4).
In this work, we consider aborting a mission upon experiencing the predetermined number of shocks. This creates a possibility of considering the corresponding optimization problem when this number acts as a decision parameter for balancing the MSP and the SLP.
The duration of the rescue procedure is usually a function of the time of its beginning. If the mth shock triggers the mission abort, the rescue procedure duration is φ = φ(tm), where is the realization of the random Tm. The larger m corresponds to the larger level of deterioration of a system and, therefore, to the larger risks of failure and system loss. When increases, the remaining mission time decreases. Thus, it may become unreasonable to start the rescue procedure if a mission is close to termination and a system has good chances to complete it. Therefore, we assume that the system continues executing the mission if tm ≥ ξ, where ξ is a time after which the mission should never be aborted. Thus, ξ, along with m, can be considered as a decision variable that can be chosen to achieve a proper balance between the MSP and system survivability.
The above description refers to the case with a single attempt to perform a mission. However, if K attempts are allowed and j < K attempts were aborted with the successful consequent system rescue, the next (j + 1)th attempt can start. In each new attempt, all initial parameters and the attempt duration are the same as before. We will now generalize the single-attempt case to the multiple-attempt one.
It is important to note that although Equations 5, 7, and 8 present a simple multiplicative model, the parameters , k = 1, 2, …, K can be different at each attempt, which eventually requires obtaining their optimal values while considering the corresponding optimization problem.
The cost of performing the mission and the cost of maintenance before each attempt can also be taken into consideration. However, usually, these costs are negligible compared to the costs associated with mission failure and system loss.
When system safety considerations are not relevant or the system's loss cost is negligible compared with the cost of the mission failure, the unconstrained max R(ξ, m) problem can be also considered.
3 MISSION SUCCESS PROBABILITY AND SYSTEM LOSS PROBABILITY
Our approach is based on the generalized extreme shock model developed in Cha and Finkelstein (2011) when the probability of a failure upon a shock increases with each experienced shock. Let the shock survival probability of a system depend on the number of shocks it has survived in the past, which is a meaningful generalization of the simplest extreme shock model. Indeed, often the resistance of elements to shocks decreases with the number of experienced shocks. Thus, if the probability that a system survives the ith shock at each attempt is q(i), then the probability of surviving all n shocks in this attempt is , where q(0) ≡ 1 by definition.
The computational aspects of obtaining the infinite sum in Equation 13 are addressed in the Appendix.
Remark. In the derivations above, we assume perfect repair after each successful rescue. However, due to various reasons, this repair can be imperfect and the system's initial resistance to shocks can deteriorate with each attempt. To model imperfect repairs, we can assume that the first shock survival probability Ωj before the jth attempt is smaller than for the previous attempt.
Having the MSP and the SLP evaluation algorithm described above, one can find the optimal mission attempts abort policy m, ξ using any general optimization procedure. In this work, we apply the genetic algorithm (GA) heuristic, the most widely used method in reliability optimization due to its advantages of having flexibility in solution representation, parallel computation possibility, quick convergence to near optimal solutions, and so on (Goldberg, 1989; Levitin, 2006).
4 ILLUSTRATIVE EXAMPLE
Consider an UAV that should cover a distance of 1,250 km between two locations (landing fields) performing a surveillance mission. The UAV speed during the mission is 212.5 km/h. Thus, the mission time is τ = 1,250/212.5 = 5.88 hours. During the surveillance mission, the UAV should remain on the altitude where it is exposed to external shocks caused by electronic interference that can destroy the UAV's control equipment and cause a crash. The shock rate is λM = 0.5. The interference filters protecting the UAV deteriorate with the number of experienced shocks because of overheating, which causes the decrease of their resistance to shocks. Model 16 with Ω = 0.99, ω = 0.93 is used to take this deterioration into account.
If the flight mission is aborted when the distance covered from the source location is x = 212.5⋅t, the UAV has to return to the closest landing field, covering the distance min(x, 1,250 – x). To perform the rescue procedure, the UAV descends to the altitude where the electronic interference shocks have the smaller rate, λR = 0.1 and reduces its speed to 160 km/h. Thus, the duration of the rescue procedure can be obtained as φ(t) = min(212.5⋅t, 1,250 – 212.5⋅t)/160. After the successful rescue procedure, the interference filters are replaced and the UAV is ready for the next mission attempt. The number of attempts is limited by the time window when the surveillance mission can provide relevant information.
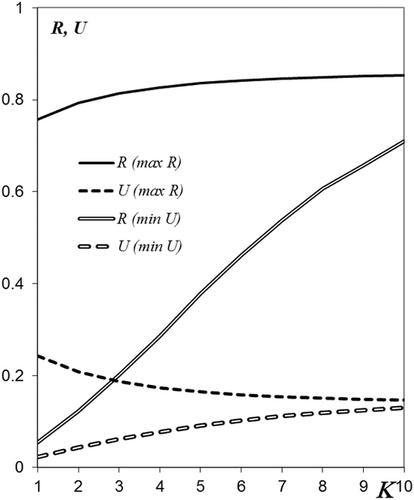
Fig. 1 presents the MSP, R and the SLP, U as functions of the number of attempts K for unconstrained max R and min U solutions (for notational convenience, the arguments of the considered functions are omitted) obtained using the GA. It can be seen that with the increase of the number of attempts, the MSP increases. The SLP for the max R solutions is larger than that obtained for the min U solutions, which means that the compromise max R s.t. U < U* can be found. Table I presents the optimal mission abort policies corresponding to some unconstrained max R and min U solutions. It can be seen that for K = 1, the largest MSP is achieved when no mission abort is allowed and the UAV tries to complete the mission independently from the number of experienced shocks.
| Attempt 1 | Attempt 2 | Attempt 3 | Attempt 4 | Attempt 5 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K | U | R | m | ξ/τ | m | ξ/τ | m | ξ/τ | m | ξ/τ | m | ξ/τ |
| Max R solutions | ||||||||||||
| 1 | 0.2433 | 0.7567 | ∞ | – | ||||||||
| 3 | 0.1865 | 0.8135 | 1 | 0.34 | 1 | 0.25 | ∞ | – | ||||
| 5 | 0.1643 | 0.8357 | 1 | 0.40 | 1 | 0.39 | 1 | 0.34 | 1 | 0.25 | ∞ | – |
| Min U solutions | ||||||||||||
| 1 | 0.0225 | 0.0544 | 1 | 1.0 | ||||||||
| 3 | 0.0615 | 0.2011 | 1 | 0.80 | 1 | 0.89 | 1 | 1.0 | ||||
| 5 | 0.0912 | 0.3782 | 1 | 0.65 | 1 | 0.74 | 1 | 0.8 | 1 | 0.89 | 1 | 1.0 |
On the contrary, the “most cautious” min U mission abort strategy presumes aborting the mission after the first shock independently from the time of the shock's occurrence (m = 1, ξ = τ). With the increase of the number of attempts, the time interval ξ, when the mission can be aborted, increases for the max R solutions and decreases for the min U solutions. For the max R solutions in the last attempt, the mission abort is not allowed (m = ∞) to maximize the UAV's chances to complete the mission. For the min U solutions in the last attempt, the mission is aborted when the first shock happens at any time (to minimize the SLP).
Observe that unlike the single attempt case when the mission abort cannot improve the MSP, in the multiattempt policy aborting the mission can improve the MSP even when the system's survival is not of interest. This happens because the next attempts can still complete the mission and the overall MSP depends not only on the attempt success probabilities, but also on the probabilities of successful system rescue. This expands the set of situations when mission aborting is justified.
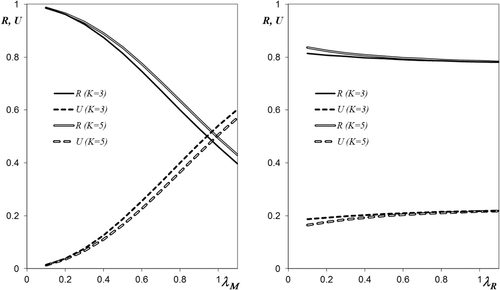
Fig. 2 presents the MSP and the SLP obtained for the max R solutions as functions of the shock rates λM and λR for K = 3 and K = 5, whereas Tables II and III present abort policies for some of these solutions. It can be seen that both the MSP and the SLP are much more sensitive to variation of the shocks rate during the primary mission than to variation of the shocks rate during the rescue procedure. With the increase in the shocks rate, the max R abort policy allows for more shocks to happen and increases the duration of the mission interval when no aborts are allowed. These changes give the UAV more chances to complete the mission.
| Attempt 1 | Attempt 2 | Attempt 3 | Attempt 4 | Attempt 5 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λM | U | R | m | ξ/τ | m | ξ/τ | m | ξ/τ | m | ξ/τ | m | ξ/τ |
| K = 3 | ||||||||||||
| 0.1 | 0.0134 | 0.9866 | 1 | 0.30 | 1 | 0.30 | ∞ | – | ||||
| 0.5 | 0.1865 | 0.8135 | 1 | 0.34 | 1 | 0.25 | ∞ | – | ||||
| 1.0 | 0.5402 | 0.4598 | 1 | 0.23 | 2 | 0.29 | ∞ | – | ||||
| K = 5 | ||||||||||||
| 0.1 | 0.0133 | 0.9867 | 1 | 0.35 | 1 | 0.35 | 1 | 0.30 | 1 | 0.30 | ∞ | – |
| 0.5 | 0.1643 | 0.8357 | 1 | 0.40 | 1 | 0.39 | 1 | 0.34 | 1 | 0.25 | ∞ | – |
| 1.0 | 0.5056 | 0.4944 | 1 | 0.29 | 1 | 0.25 | 1 | 0.23 | 2 | 0.29 | ∞ | – |
| Attempt 1 | Attempt 2 | Attempt 3 | Attempt 4 | Attempt 5 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λR | U | R | m | ξ/τ | m | ξ/τ | m | ξ/τ | m | ξ/τ | m | ξ/τ |
| K = 3 | ||||||||||||
| 0.1 | 0.1865 | 0.8135 | 1 | 0.34 | 1 | 0.25 | 9 | 0.23 | ||||
| 0.5 | 0.2060 | 0.7940 | 1 | 0.2 | 1 | 0.18 | 8 | 0.13 | ||||
| 1.0 | 0.2180 | 0.7820 | 1 | 0.14 | 1 | 0.12 | 9 | 0.19 | ||||
| K = 5 | ||||||||||||
| 0.1 | 0.1643 | 0.8357 | 1 | 0.4 | 1 | 0.39 | 1 | 0.34 | 1 | 0.25 | ∞ | – |
| 0.5 | 0.1990 | 0.8010 | 1 | 0.23 | 1 | 0.22 | 1 | 0.2 | 1 | 0.18 | ∞ | – |
| 1.0 | 0.2156 | 0.7844 | 1 | 0.14 | 1 | 0.14 | 1 | 0.14 | 1 | 0.12 | ∞ | – |
Tables IV and V present the best obtained max R s.t. U < U* mission abort policies for K = 3, K = 5, and different values of U*. It can be seen that for most of the obtained solutions, mission attempts should be aborted after the first shock and the balance between the MSP and the SLP is achieved by changing the intervals [0, ξj] when abort is allowed.
| Attempt 1 | Attempt 2 | Attempt 3 | ||||||
|---|---|---|---|---|---|---|---|---|
| U* | U | R | m | ξ/τ | m | ξ/τ | m | ξ/τ |
| 0.10 | 0.0996 | 0.5864 | 1 | 0.43 | 1 | 0.40 | 1 | 0.38 |
| 0.12 | 0.1196 | 0.6596 | 1 | 0.40 | 1 | 0.34 | 1 | 0.26 |
| 0.14 | 0.1395 | 0.7141 | 1 | 0.35 | 1 | 0.25 | 1 | 0.21 |
| 0.16 | 0.1597 | 0.7653 | 1 | 0.35 | 1 | 0.30 | 2 | 0.31 |
| 0.18 | 0.1798 | 0.8042 | 1 | 0.33 | 1 | 0.25 | 2 | 0.13 |
| 0.20 | 0.1865 | 0.8135 | 1 | 0.34 | 1 | 0.25 | ∞ | – |
| Attempt 1 | Attempt 2 | Attempt 3 | Attempt 4 | Attempt 5 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U* | U | R | m | ξ/τ | m | ξ/τ | m | ξ/τ | m | ξ/τ | m | ξ/τ |
| 0.10 | 0.1000 | 0.5744 | 1 | 0.56 | 1 | 0.58 | 1 | 0.60 | 1 | 0.57 | 1 | 0.59 |
| 0.11 | 0.1099 | 0.6602 | 1 | 0.49 | 1 | 0.47 | 1 | 0.45 | 1 | 0.54 | 1 | 0.50 |
| 0.12 | 0.1198 | 0.7127 | 1 | 0.44 | 1 | 0.46 | 1 | 0.48 | 1 | 0.41 | 1 | 0.36 |
| 0.13 | 0.1299 | 0.7516 | 1 | 0.43 | 1 | 0.38 | 1 | 0.40 | 1 | 0.32 | 1 | 0.35 |
| 0.14 | 0.1400 | 0.7827 | 1 | 0.40 | 1 | 0.43 | 1 | 0.39 | 1 | 0.3 | 1 | 0.19 |
| 0.15 | 0.1500 | 0.8058 | 1 | 0.39 | 1 | 0.39 | 1 | 0.34 | 1 | 0.21 | 1 | 0.15 |
The values of ξj decrease in U*, which corresponds to a “more risky” policy that gives the UAV more chances to complete the mission attempts. If for some reason the value of ξj cannot vary from attempt to attempt (e.g., when environmental conditions do not allow the UAV's descent to the safe altitude during a part of its route), the proper balance between the MSP and the SLP is achieved by changing the number of allowed shocks mj. Tables VI and VII demonstrate the best obtained max R s.t. U < U* mission abort policies for ξj = τ in all attempts and ξj = 0.8τ in all attempts. It can be seen that with the increase of the allowed value of the SLP, the number of allowed shocks increases, which weakens the abort conditions and gives the UAV more chances to complete mission attempts.
| m | |||||||
|---|---|---|---|---|---|---|---|
| U* | U | R | Attempt 1 | Attempt 2 | Attempt 3 | Attempt 4 | Attempt 5 |
| 0.15 | 0.0970 | 0.2273 | 1 | 1 | 1 | 1 | 1 |
| 0.16 | 0.1503 | 0.3398 | 1 | 1 | 1 | 1 | 2 |
| 0.20 | 0.1991 | 0.4942 | 3 | 1 | 1 | 1 | 1 |
| 0.21 | 0.1991 | 0.4942 | 3 | 1 | 1 | 1 | 1 |
| 0.22 | 0.1991 | 0.4942 | 3 | 1 | 1 | 1 | 1 |
| 0.23 | 0.2262 | 0.6275 | 4 | 1 | 1 | 1 | 1 |
| 0.24 | 0.2379 | 0.7064 | 5 | 1 | 1 | 1 | 1 |
| 0.25 | 0.2433 | 0.7567 | 10 | 8 | 3 | 1 | 1 |
| m | |||||||
|---|---|---|---|---|---|---|---|
| U* | U | R | Attempt 1 | Attempt 2 | Attempt 3 | Attempt 4 | Attempt 5 |
| 0.10 | 0.0928 | 0.3704 | 1 | 1 | 1 | 1 | 1 |
| 0.15 | 0.1386 | 0.4977 | 1 | 1 | 1 | 1 | 2 |
| 0.18 | 0.1712 | 0.5825 | 1 | 1 | 1 | 2 | 2 |
| 1.19 | 0.1821 | 0.6306 | 1 | 1 | 1 | 1 | 3 |
| 0.20 | 0.1949 | 0.6382 | 1 | 1 | 2 | 2 | 2 |
| 0.21 | 0.2088 | 0.7168 | 1 | 1 | 1 | 1 | 4 |
| 0.22 | 0.2183 | 0.7314 | 1 | 1 | 1 | 4 | 2 |
| 0.23 | 0.2265 | 0.7735 | 1 | 1 | 1 | 1 | 10 |
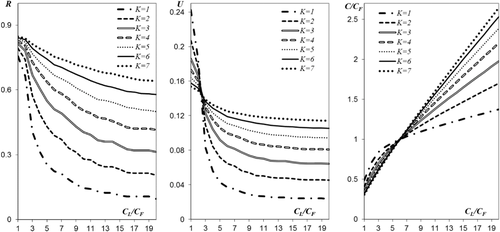
Fig. 3 presents the MSP, the SLP, and the normalized expected losses C(ξ, m)/CF = (1–R(ξ, m)) + U(ξ, m)CL/CF for solutions of the min C(ξ, m) problem as functions of the cost ratio CL/CF for different numbers of attempts, K. Table VIII presents the best abort policies for some of these solutions. It can be seen that when the CL/CF ratio is small (mission completion is much more important than system survival), one should choose the maximum possible number of attempts to minimize the expected losses. On the contrary, when the CL/CF ratio is large (system survival is much more important than mission completion), one should choose the one-attempt policy to minimize the risk of system loss.
| Attempt 1 | Attempt 2 | Attempt 3 | Attempt 4 | Attempt 5 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K | CL/CF | U | R | m | ξ/τ | m | ξ/τ | m | ξ/τ | m | ξ/τ | m | ξ/τ |
| 1 | 0.7561 | 0.2426 | 4 | 0.18 | |||||||||
| 1 | 2 | 0.6633 | 0.1861 | 2 | 0.25 | ||||||||
| 10 | 0.1454 | 0.0271 | 1 | 0.64 | |||||||||
| 1 | 0.7925 | 0.2068 | 1 | 0.25 | 4 | 0.18 | |||||||
| 2 | 2 | 0.7412 | 0.1758 | 1 | 0.28 | 2 | 0.25 | ||||||
| 10 | 0.2797 | 0.0507 | 1 | 0.6 | 1 | 0.64 | |||||||
| 1 | 0.8133 | 0.1862 | 1 | 0.34 | 1 | 0.25 | 4 | 0.18 | |||||
| 3 | 2 | 0.7810 | 0.1667 | 1 | 0.35 | 1 | 0.28 | 2 | 0.25 | ||||
| 10 | 0.4044 | 0.0712 | 1 | 0.55 | 1 | 0.6 | 1 | 0.64 | |||||
| 1 | 0.8356 | 0.1642 | 1 | 0.4 | 1 | 0.39 | 1 | 0.34 | 1 | 0.25 | 4 | 0.18 | |
| 5 | 2 | 0.8209 | 0.1553 | 1 | 0.4 | 1 | 0.39 | 1 | 0.35 | 1 | 0.28 | 2 | 0.25 |
| 10 | 0.5919 | 0.1012 | 1 | 0.5 | 1 | 0.54 | 1 | 0.55 | 1 | 0.6 | 1 | 0.64 | |
5 CONCLUSIONS
Previous works on mission aborting have discussed a situation when only one attempt to complete a mission is allowed and this attempt can be aborted. In this article, we develop the relevant probabilistic model and formulate the corresponding optimization problems for the multiattempt setting. The detailed example illustrates the solution of the optimization problems both for the constrained/nonconstrained maximization of the MSP and for the minimization of the cost of losses.
In the one-attempt setting, obviously, the mission abort cannot increase the MSP and is performed only for increasing the corresponding survivability. However, even when system's survival is not important, mission aborting can be used to maximize the MSP when several attempts to complete a mission are allowed. This is an important observation that considerably widens the class of systems that can employ mission aborting.
The detailed sensitivity analysis is performed for both optimization problems with two decision parameters in each attempt, that is, the number of shocks experienced by the system, and the time after which aborting is not performed. For instance, it can be seen that both the MSP and the SLP are much more sensitive to variation of the shock rate during the primary mission than to that during the rescue procedure. It is shown that when considering minimization of expected losses and the CL/CF ratio is small (mission completion is much more important than system survival), one should choose the maximum possible number of attempts to minimize the expected losses. On the contrary, when the CL/CF ratio is large (system survival is much more important than mission completion), one should choose the one-attempt policy to minimize the risk of system loss.
As a possible direction for future research, one can consider more general imperfect repair models than those discussed in the Remark. Specifically, imperfect repair after system rescue can decrease the damage accumulated by the system after experiencing the observed number of shocks (condition-based imperfect repair). The overall mission cost minimization that includes expected cost of rescue procedures and repairs along with the penalties associated with mission failure and system loss can be considered. The case when a part of the mission task that was accomplished in the earlier attempts can be saved (additively) and not discarded should also be addressed.
ACKNOWLEDGMENTS
This work was supported in part by the National Natural Science Foundation of China (Grant No. 51875089) and by the Government of the Russian Federation (Grant No. 08-08).
NOMENCLATURE
-
- Lj
-
- system's lifetime in the jth attempt
-
- λM, λR
-
- shocks rate during the primary mission, and rescue procedure, respectively
-
- Tm
-
- random time of the mth shock occurrence
-
- τ
-
- duration of a mission attempt
-
- θ
-
- maximum allowed mission time
-
- K
-
- maximum allowed number of attempts to perform the mission
-
- mj
-
- maximum allowed number of shocks in the jth attempt
-
- ξj
-
- time from the start of the jth attempt after which the mission is not aborted
-
- φ(t)
-
- duration of the rescue procedure activated at time t from the attempt beginning
-
- Uj
-
- probability of system loss in attempt j
-
- Rj
-
- unconditional success probability of attempt j
-
- rj
-
- conditional success probability of attempt j given the attempt has started
-
- Zj
-
- unconditional rescue success probability in attempt j
-
- zj
-
- conditional rescue success probability in attempt j given the attempt has started
-
- CF, CL
-
- costs of mission failure and system loss, respectively
-
- C
-
- expected losses (risk) associated with the multiattempt mission
-
- P(t, i, λ)
-
- probability of occurrence of i shocks in [0, t) given the shock rate is λ
-
- q(i)
-
- probability that a system survives the ith shock
-
- Ω
-
- probability of the first shock survival
-
- ω
-
- shock resistance deterioration factor
APPENDIX A
Evaluating the infinite sum .
-
k = 0; S = P = exp(–λt); z = ωi(i–1)/2; Ψq = Ωi z;
-
k = k + 1; P = Pλt/k; z = zω; Ψq = Ψq Ω z; S = S + PΨq;
-
If PΨq > ε, go to step 2 otherwise stop.




