An Empirical Agent-Based Model to Simulate the Adoption of Water Reuse Using the Social Amplification of Risk Framework
Abstract
Water reuse can serve as a sustainable alternative water source for urban areas. However, the successful implementation of large-scale water reuse projects depends on community acceptance. Because of the negative perceptions that are traditionally associated with reclaimed water, water reuse is often not considered in the development of urban water management plans. This study develops a simulation model for understanding community opinion dynamics surrounding the issue of water reuse, and how individual perceptions evolve within that context, which can help in the planning and decision-making process. Based on the social amplification of risk framework, our agent-based model simulates consumer perceptions, discussion patterns, and their adoption or rejection of water reuse. The model is based on the “risk publics” model, an empirical approach that uses the concept of belief clusters to explain the adoption of new technology. Each household is represented as an agent, and parameters that define their behavior and attributes are defined from survey data. Community-level parameters—including social groups, relationships, and communication variables, also from survey data—are encoded to simulate the social processes that influence community opinion. The model demonstrates its capabilities to simulate opinion dynamics and consumer adoption of water reuse. In addition, based on empirical data, the model is applied to investigate water reuse behavior in different regions of the United States. Importantly, our results reveal that public opinion dynamics emerge differently based on membership in opinion clusters, frequency of discussion, and the structure of social networks.
1. INTRODUCTION
Water reuse provides a sustainable alternative water supply source for urban water services by treating wastewater and distributing it for potable or nonpotable uses.1 Wide-scale implementation of water reuse within an existing water infrastructure system is challenged, however, by the need for community-wide public acceptance and adoption.2 Consumers typically perceive recycled water negatively,3 and as a consequence, water reuse has often been omitted in municipal water management plans. Research shows that consumer attitudes toward new technologies are based on an intuitive analysis of risks and benefits,4 and perceptions may change based on discussions with other consumers.5 Knowledge about these opinion dynamics within a community would be useful in the planning and decision-making process for integrating water reuse within existing water supply systems. The goal of this research is to develop such knowledge through an “acceptance-resistance” agent-based model6, 7 to simulate adoption or rejection of water reuse among individual members of a community. As a practical matter, city planners and municipal water managers face a great deal of uncertainty if they choose to introduce water reclamation to a municipality. Will residents accept the technology or resist its implementation? Will public opinion dynamics be favorable to this policy choice or provide an obstacle to it? These questions are not aimed at controlling or manipulating residents, but rather at understanding how public opinion dynamics can influence economically effective and environmentally friendly policy decisions in a democracy.
In an attempt to provide an initial answer to such questions, this study develops a simulation model by drawing on social science research of risk perception and the social amplification of risk framework (SARF) to elaborate upon the idea of “risk publics.”8 The dynamics of these risk publics are implemented and made operational using agent-based modeling, which is a modeling approach for simulating social systems and the interactions among social actors.7, 9, 10 Survey data representative of the U.S. population were analyzed to determine empirical relationships among individuals, social groups, and informational and communicative variables. With this research, we aim to provide a better understanding of how individual attitudes and interpersonal communication behaviors influence community-level opinions in a longitudinal framework not often seen in social scientific approaches to risk perception. The agent-based model simulates water reuse adoption behavior both at the national level and in different regions of the United States, with two goals. First, we aim to provide insight about the influence of community risk and benefit profiles on the receptiveness to water reuse. Second, we investigate emergent regional patterns and variations in water reuse behavior among regions.
2. BACKGROUND
2.1. Water Reuse and Its Benefits and Risks
From a technical perspective, water reuse is the practice of using treated wastewater as a substitute source for freshwater, and water reclamation refers to the process of treating wastewater to prescribed water quality and treatment reliability standards for reuse.11, 12 Water reuse may be used to conserve and extend water supplies by using reclaimed water for uses that do not require high-quality, potable water.13, 14 Research has shown that water agencies face a number of challenges in implementing water reuse projects, such as facilities and infrastructure planning and siting;12 economic challenges of constructing new infrastructure;15 institutional barriers;4 conflicting agency priorities;16 and limited or uncertain public support.2, 17, 18
Public attitudes, acceptance, and support have been particularly recognized as essential for the success of water reuse projects and are often a significant obstacle in implementing water reuse projects.2, 15, 18 In spite of expert assurances on the safety of reclaimed water, perceptions of high risk persist among large segments of the general public. Disgust of reclaimed water, commonly referred to as the “yuck” factor, arises from perceptions of reclaimed water as unclean due to its association with human waste.18 Citizens may perceive health risks19 or suspect that pathogens and chemicals are present in reclaimed water, and evidence suggests that perceptions of health risks increase where use of reclaimed water involves human contact.15
Various explanations for these reactions have been explored by researchers. Trust in technologies and the scientific knowledge about water reclamation may affect risk perceptions. Technologies associated with water reuse are relatively new, and the public may perceive a higher risk when evaluating reclaimed water in comparison with familiar water sources, such as surface and groundwater. Other innovations and new technologies, such as antibiotics, genetically modified seed, and railway networks, have overcome similar initial negative perception to gain acceptance and eventual wide-spread adoption.20, 21
Citizens may also perceive risks associated with aspects of social justice,4, 18 as it remains unclear which segments of a population will pay for and receive reclaimed water. Water reuse programs have been subsidized by governments or industry, and the economic feasibility of these programs without the subsidies is uncertain.15 The public may perceive equity issues in water supply and reuse planning, based on previously established trust in urban institutions.22
Our study takes a different approach. While we acknowledge the roles of trust and social justice, our interests lie in developing a model for understanding the longitudinal dynamics of risk perception and risk communication. In developing this model, we rely on several assumptions. First, perceived risks and benefits affect the acceptance of new technologies such as reclaimed water.15, 18 Perceptions are subjective and are influenced by knowledge, attitudes, values, and beliefs.4 Second, people subjectively assess the risks of technology based on a variety of qualitative and quantitative characteristics that are typically different from the quantitative risk assessments used by experts.23 Interpersonal and mass communication,24 group membership,25 and shared values5, 26 affect the development of risk and benefit perceptions. Finally, perceptions regarding water reuse are not static but, instead, change over time with increased knowledge, interactions, and experience.27, 28 The risk publics concept, described below, provides a framework for studying and simulating dynamics of risk perception that emphasizes communication processes in the development and transmission of beliefs about water reclamation.
2.2. Risk Perception, Social Influence, and Risk Publics
One conceptualization of how perception of risk works at individual, group, and societal levels is described by the SARF.29 According to the SARF, a hazard event produces a signal that is disseminated throughout a group of people. The initial signal may be amplified and attenuated, resulting in a mismatch between a quantitative risk assessment of the hazard and the social definition of the risk.30 The research presented here develops an empirical model of risk publics, which defines social clusters that are bound by similar core beliefs about a technology.8 The simulation model is, essentially, a dynamic model of social influence based on the SARF.
Models of social influence have been developed in a wide range of disciplines,31, 32 and their fundamental elements include: the sources of information; influence of information; and the structure and direction of links between individuals.31 Influence processes, even when they can be identified and studied at the individual level, can result in complex and nonintuitive emergent dynamics at the community level, as communication is exchanged among multiple individuals over time. Examples of relevant social influence models include diffusion of innovation models32, 33 and social contagion models.34, 35
The diffusion of innovations approach20 explains how innovations spread through a social system. The model has been demonstrated in the fields of sociology, economics, and political science20, 36, 37 to explain the spread of ideas, practices, and technologies. Similarly, social contagion theory suggests that attitudes and behaviors of individuals in a community are heavily influenced by those in their social network and by their relationships within social networks.34, 35 The network theory of contagion has been applied to environmental and resource management problems. For example, risk perceptions about the impact of an environmental cleanup project on a community's water supply are explored using network theory,34 and social contagion theory is applied to explain risk perceptions of wildlife management.38
Using the SARF as a starting point was an important decision for us because of how the framework has been described. The SARF has been especially praised for its explanatory value;39 it identifies many elements from past research, including citizens, government entities, the mass media, cultural values, etc., and places them in a single model. Where much of the research has fallen short, however, is in exploring how the dynamics of these elements play out over time. Thus, while we might know from past research that the initial opinion distribution in a community has an effect on outcomes,40 that the frequency of interpersonal discussion has an impact on risk perception,5 or that the nature of discussion produces polarized opinions,41 the literature has not always provided a foundation for understanding the process—the question of “how?”—these dynamics unfold.
The present study develops a social influence model, based on the concept of risk publics, which is a conceptual framework for understanding public opinion dynamics about local issues, such as the development of new facilities that have a high risk profile or the introduction of new and unfamiliar technologies. The risk publics approach was originally developed in an unpublished study analyzing the community dynamics surrounding development of a high-risk bio- and agro-defense research facility.8 The approach divides the population into distinct belief clusters or risk publics, and individuals in each cluster have a similar assessment of the risks and benefits associated with a specific technology. Clusters are empirically derived for the issue of concern and are not based on a priori assumptions.
Similar to social contagion models, the risk publics model is able to overcome some of the limitations of other modeling approaches. Traditional diffusion models20, 33 might be criticized for featuring actors who are fixed in their beliefs and cannot change opinions over time. In the risk publics approach, we expect individuals to change their opinion regarding technology based on interactions with other individuals. A second limitation of diffusion models is the assumption that adoption of technology will succeed globally. The risk publics approach neither presupposes global adoption nor assumes that adoption will succeed. The model allows for social conflict surrounding community issues,5 and the possibility that some groups of people—or even the whole community—may resist the adoption of new technology.
3. METHODS
Agent-based modeling techniques6, 7, 42 have been recognized as effective computational techniques to simulate social influence processes.43, 44 Agent-based modeling provides a computational approach to simulate the group-level dynamics that emerge from interactions within a community of individual agents. Agents follow rules that represent the decision-making and behavioral choices of individuals; they can also interact and influence other agents through predefined communication networks.
Several studies demonstrate the utility of agent-based modeling for the social sciences. Moussaid45 developed an agent-based model of opinion formation that allows for exploration of the collective dynamics of risk perception. The model simulated the emergence of collective patterns of risk perception, such as clustering and polarization. Schwarz and Ernst46 developed an empirical agent-based model to simulate the diffusion of water savings technology in southern Germany. For a model using survey data, the population was clustered into five groups representing distinct attitudes and behaviors toward adoption of water savings technology. Another agent-based model was developed to simulate changes in residential water use based on reactions to water pricing and educational and information campaigns.32
An agent-based modeling6, 7 framework is developed here to simulate opinion dynamics and the acceptance and rejection of water reuse in groups defined as risk publics. Parameters for the risk publics are defined empirically from survey data. Within the agent-based model, households serve as the smallest computational unit, and each household is represented as an agent. Each household agent is assigned to one of the risk publics; risk and benefit perceptions and model parameters are initialized based on this assignment. Each agent's risk and benefit perceptions can change over time, based on communications with other households, and overall community dynamics emerge from the aggregate behavior and interaction of individual households.
3.1. Development of Risk Publics Model Parameters
The risk publics approach was applied to survey data that were collected in early 2013. The survey was conducted by GfK (formerly Knowledge Networks) using its Knowledge Panel®, which provides a nationally representative sample of adults in the United States. The final sample size was 2,800 respondents. The questionnaire included measures of knowledge, attitude, and behavioral intentions about (1) municipal water systems, (2) water reuse, (3) health, safety, and environmental implications of those systems for local communities, and (4) potential risks and benefits of using reclaimed water. The survey also measured social and communicative variables to understand the role of interpersonal channels of communications and mass media.
3.1.1. Cluster Analysis
The set of survey questions used in the cluster analysis is described in detail below. The survey required respondents to evaluate water reuse on the basis of the various risk and benefit statements. Responses were reported on a Likert-type scale of 1 (strongly disagree) to 7 (strongly agree). The following five statements were used to measure risk perception: (1) Even if reclaimed water is treated to certain standards, using it at home could still have harmful effects on people's health; (2) Eating fruits or vegetables that are irrigated with reclaimed water might make people sick; (3) I think that using reclaimed water could decrease property values in my community; (4) Using reclaimed water would be like spreading sewage throughout the environment; and (5) Investment in reclaimed water systems will take resources away from other more important problems in my community. Five statements were also used to measure benefit perception: (1) If we used reclaimed water, there would be more safe drinking water available for people in my community; (2) Using reclaimed water will protect us against water shortages in the next few years; (3) Installing a new municipal system for reclaimed water would be beneficial because it would provide jobs to people in my community; (4) Having reclaimed water in my community would be beneficial because we wouldn't waste drinking water to flush toilets or water lawns; and (5) Using reclaimed water just sounds like a good idea.
Social groups or risk publics were determined using a cluster analysis1 on the survey measures of risk and benefit beliefs in two steps. First, a Ward's hierarchical clustering method used the squared Euclidean distance of measures to create four clusters. Ward's method has known drawbacks, and most importantly for this study, the random start point for the iterative clustering process biases the cluster membership of the first individuals analyzed; in essence, these first individuals become “stuck” in the initial cluster they are sorted in with no chance of joining a different, perhaps more suitable cluster.47 As a result of this drawback, K-means cluster analysis was used subsequently to create a second clustering solution based on the cluster centers (i.e., average values for each measure used in the cluster analysis) from the Ward's method results.
Cluster analysis results were obtained for solutions of two to six clusters, and these were compared for construct validity and ease of interpretation. To assess construct validity, we evaluated the ability of the clusters to explain variance in a criterion variable, which was the overall support or opposition to the use of reclaimed water in one's community. To evaluate ease of interpretation, we looked at the parsimony of the clusters in identifying distinct groups within a two-dimensional risk (x-axis)/benefit (y-axis) space.2 The best solution corresponded to four clusters (see Table I), which were each given a descriptive label.
Members of the “optimistic” cluster perceive that the risks of water reuse are low and benefits high. They represent the segment of the population most likely to adopt water reuse. Members of the “disengaged” cluster have neutral risk and benefit perceptions, and represent individuals who have not formed particularly strong risk or benefit perceptions. Members in the “alarmed” cluster perceive that the risk of water reuse outweigh benefits and are most unfavorable toward water reuse. Members of the “conflicted” cluster have medium-to-neutral risk and benefit perceptions and represent those who are apprehensive of the risks associated with water reuse but at the same time recognize some benefits associated with water reuse.
| Cluster | Risk Perceptiona | Benefit Perceptionb | N | Percent |
|---|---|---|---|---|
| 1 – Optimistic (OP) | 2.43 | 5.77 | 706 | 25.20 |
| (0.71) | (0.65) | |||
| 2 – Disengaged (DE) | 3.61 | 3.91 | 1,110 | 39.60 |
| (0.65) | (0.70) | |||
| 3 – Alarmed (AL) | 5.52 | 2.65 | 330 | 11.80 |
| (0.78) | (0.88) | |||
| 4 – Conflicted (CO) | 4.63 | 4.88 | 654 | 23.40 |
| (0.71) | (0.68) | |||
| Total: | 2,800 | 100.00 | ||
| 1A – Adopter | <2.43 | >5.77 | 5.00 | |
| (subset of OP cluster) | ||||
| 3A – Resistor | >5.52 | <2.65 | 5.00 | |
| (subset of AL cluster) |
- a Risk perception values are defined as continuous variables ranging from 1 (low) to 7 (high).
- b Benefit perception values are defined as continuous variables ranging from 1 (low) to 7 (high).
Because reclaimed water is not in widespread use in the United States, we could not identify individuals who have adopted or resisted reclaimed water technology. Thus, we defined two additional belief clusters for modeling purposes. “Adopters” form a subset of the optimistic cluster and represent those who have adopted water reuse. Adopters have the lowest risk perception and highest benefit perception within the general population. “Resistors” are defined as a subset of the alarmed cluster. They represent individuals who have hard-set opposition toward water reuse and are unlikely to change their opinion. They represent the population having the highest risk and lowest benefit perception. Characteristics of these two additional belief clusters are summarized in the bottom two rows of Table I.
3.1.2. Communication Parameters
We measured heterogeneity of interpersonal communication by using questions about political discussions as a proxy for overall discussion patterns among respondents. First, we measured political ideology by asking: “In terms of [(1) economic issues/(2) social issues], would you say you are … ?” (1 = Very liberal to 7 = Very conservative). Second, we asked respondents: “Regardless of the topic of conversation, how often do you talk to … (1) People with extreme liberal views? (2) People with extreme conservative views?” (1 = Never to 5 = Very often). Our variables representing levels of homogeneous and heterogeneous talk were calculated by matching responses to the political ideology questions (averaged) to responses to each of the frequency of discussion questions. For example, if a respondent scored on the liberal side of ideology (less than the average) and responded “Never (1)” to the question about discussion with people of extreme conservative views, the respondent was given a score of zero for the variable heterogeneous talk. The same procedure was followed for those falling on the conservative side of the ideological spectrum.
The procedure produced two variables: Heterogeneous Talk (M = 1.00, SD = 1.05) and Homogeneous Talk (M = 1.28, SD = 1.26), respectively representing communication with individuals belonging to the same and to different social groups. To get a sense of the total amount of talk, these two variables were averaged to represent a single variable, Total Talk (M = 2.29, SD = 2.16), indicating the total amount of talk for each respondent. The variables Total Talk, Homogeneous Talk, and Heterogeneous Talk determined communication frequency by cluster (Table II).
| Description | Homogenous Talk | Heterogeneous Talk | Total Talk | Homogenous/Total | Heterogeneous/Total | Normalized Total Talk |
|---|---|---|---|---|---|---|
| 1 Optimistic | 1.72 | 1.33 | 3.05 | 0.56 | 0.44 | 1.00 |
| 2 Disengaged | 1.16 | 0.92 | 2.08 | 0.56 | 0.44 | 0.68 |
| 3 Alarmed | 1.30 | 0.87 | 2.17 | 0.60 | 0.40 | 0.71 |
| 4 Conflicted | 1.40 | 1.13 | 2.53 | 0.55 | 0.45 | 0.83 |
| Average | 1.40 | 1.06 | 2.46 | 0.57 | 0.43 |
Relative communication frequencies (Normalized Total Talk) were obtained by normalizing communication frequency values by the largest communication frequency, in this case among the optimistic group (see Table II). For model parameterization, we assumed that the normalized communication frequency could be used to represent both the relative number of message sent (Messages Sent Fraction) and received by individuals (Messages Received Fraction) in each cluster.
3.2. Rules for Communication and Changing Perceptions
In the simulation model, computational agents representing households are assigned to a risk publics cluster, and a set of initial risk and benefit perception values are randomly generated from a distribution of values specific to the cluster and assigned to an agent. Agents are assigned to small-world communication networks for sending messages. A household agent is linked to a predetermined number of household agents from the same cluster and one household agent from each other cluster, representing how individuals have more links internal than external to their social network.31 Bidirectional links may be created in the initialization process, as pairs of household agents can be randomly chosen to serve as both the source and target of messages.
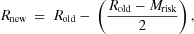 (1)
(1)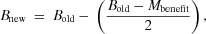 (2)
(2)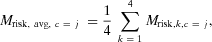 (3)
(3)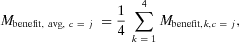 (4)
(4)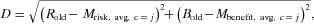 (5)
(5)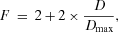 (6)
(6)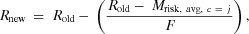 (7)
(7)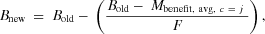 (8)
(8)After having readjusted the risk and benefit perception values, household agents in the optimistic, alarmed, and conflicted clusters evaluate the distance from their revised risk and benefits perception value to mean values of each of these three belief clusters and assume membership in the nearest cluster. Household agents in the disengaged cluster evaluate the distance from their revised risk and benefits value to that of all four clusters and assume membership in the closest cluster. Household agents can originate in the disengaged cluster, but household agents from other clusters cannot gain membership to this cluster. In effect, our model assumed that individuals who are engaged on an issue and hold a set of beliefs can change their beliefs but will remain active participants in social discussion related to the issue.
4. RESULTS
4.1. Theoretical Model—Impact of Varying Starting Population Proportions
Model behavior and sensitivity were explored by conducting a set of simulation runs using a baseline model in which key parameters were modified in a systematic manner. A set of theoretical risk public clusters were defined with risk and benefit parameter values as shown in Fig. 1. A population of 1,000 household agents was initialized with predefined distribution among clusters. A total of 286 distinct initial population proportion combinations were evaluated, in which each cluster's initial population varied from 0% to 100% in increments of 10% while maintaining the sum of all four proportions equal to 100%. For evaluations where the population of the optimistic cluster was greater than or equal to 10% of the total population, 5% of the total population was initialized as adopters. Similarly, for the alarmed population, for simulations in which the number of household agents was greater than or equal to 10% of the total population, 5% of the total population was initialized as resistors. A communication frequency of 12 messages/year was used for all agents. Thirty-year simulations were executed using a one-year time step, and each simulation was replicated 25 times (results are reported as the average of the 25 simulations).

4.1.1. How Initial Population Proportions Influence Final Proportions of Risk Publics
The range of observed population states in each cluster for year 30 is shown as an example in Fig. 2. Both optimistic and alarmed clusters exhibited similar behavior and converged to a range of potential population states for different starting population proportions. As the number of household agents that were initially alarmed or optimistic increased, the minimum number of household agents that would be in either of these respective clusters 30 years in the future also increased (represented by the lower bound of the scatter graphs in Figs. 2(a) and (c)). It is possible for either of the alarmed or optimistic cluster to become the dominant risk public even when their initial proportion of the total population is only 10% (as observed in the upper bound of the scatter graphs in Figs. 2(a) and (c)).

The disengaged and conflicted clusters converged on a more limited number of possible population states. An initial disengaged population of up to 90% results in a population of approximately zero by year 30 (Fig. 2(b)); in contrast, an initial disengaged population of less than 40% results in close to none or very few household agents associated with this cluster by year 10 (not shown). A set of results showed dominant disengaged populations when the initial disengaged population is greater than or equal to 60%; these results corresponded to scenarios where initial population consists solely of disengaged and conflicted members.
For the conflicted cluster, initial proportions of 30% or less result in conflicted populations being close to zero by year 10 (not shown). Initial populations of 40% or more, however, result in a relatively broad range of possible population states in year 10. By year 30 (see Fig. 2(d)), the residual population in the conflicted cluster is significantly reduced; only scenarios that have an initial population of 80% or greater retain a residual population in the conflicted cluster.
In our theoretical model, the alarmed and optimistic risk publics were observed as the dominant belief clusters, and most of the household agents converge to risk and benefit beliefs associated with one of the two clusters. The adopter and resistor populations, which did not update their perceptions, served as anchors. The net impact was a gradual movement in perception values toward the perception values of the adopter and resistors. A positive feedback loop was initiated, and every household that became an adopter or resistor further reinforces the influence of that cluster.
4.1.2. How a Risk-Benefit Ratio Defined from Measures of Interpersonal Communication Represents Public Opinion Climate
Frequency and valence of discussion were identified as two major dimensions of interpersonal discussion that impact risk and benefit perceptions.5 Characterization of the strength of both of these dimensions of communication at the community level provided indications on the opinion climate within the community on the issue of water reuse. For example, if optimists were more vocal of all four communities, it would be expected that the opinion climate would be in favor of water reuse, thus increasing the likelihood of their message influencing others.
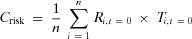 (9)
(9)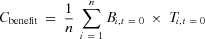 (10)
(10)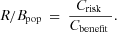 (11)
(11)A risk-to-benefit value of 1 would indicate that the overall strength of communication of risks and benefits within the community were balanced. Risk-to-benefits values greater than 1 indicate a shift toward a dominant risk perception, or a relative increase in the frequency of communication from households that perceive increased levels of risk. Conversely, risk-to-benefit values less than 1 indicate an opinion climate with a dominant benefit perception in the community.
We observed the time required for different community compositions to converge toward one dominated by either the alarmed or optimistic populations. Out of the 286 combinations evaluated, 63 runs (equal to 22%) reach states dominated by the adopters and 67 runs (equal to 23%) reach states dominated by resistors. When looking at the populations in year 30, where risk-to-benefit values were less than 1, the optimistic population is—not surprisingly—always at least greater than that of the alarmed population. This trend reverses for risk-to-benefit values greater than 1, where alarmed populations are dominant. Based on this comparison, it seems the risk-to-benefit value can serve as a possible heuristic indicator on whether the population will converge to one of two dominant belief perceptions.
4.2. Theoretical Model—Impact of Varying Communication Frequencies
A second set of simulations was executed to assess the impact of the communication frequency parameter on the community opinion climate. A discrete set of communication frequency values was evaluated, from no communication to weekly communication (equivalent to 0, 4, 12, 26, and 52 messages/year). A total of 625 combinations, where each cluster could take on any one of the five communication frequency values, were evaluated. A household population of 1,000 was used, and a hypothetical opinion distribution was applied with 25% of households assigned to each of the disengaged and conflicted clusters; 20% to the optimistic and alarmed clusters; and 5% to the adopter and resistor clusters. Hypothetical risk and benefit perception values were assigned from the distribution of values shown in Fig. 1. Simulations were executed for a 30-year period, using one-year time steps. Simulations were replicated 25 times; results reported are the average of the 25 simulations.
4.2.1. How Discussion Frequency Influences Membership in Risk Publics
The range of observed population states by cluster at the end of the simulation runs (year 30) was assessed as a function of cluster communication frequency (Fig. 3). The optimistic and alarmed clusters (Figs. 3(a) and (c)) showed similar behavior with a wide range of potential population states. When these clusters did not communicate, populations in year 30 can range from 50 to 250 household agents. Scenarios in which 250 household agents (the number initialized for that cluster) remained in the optimistic or alarmed cluster in year 30 represents the conditions where no, or very limited, messages are being sent to household agents in this cluster. The lower limit of 50 represented the scenario in which all members of the cluster, except those initialized as adopters or resistors, are influenced by messages and revise their perceptions. Even communication frequencies as low as four messages per year resulted in the optimistic or alarmed perceptions becoming the dominant opinion (as depicted by the upper bound in Figs. 3(a) and (c)). In addition, as the communication frequency increased, the minimum expected population that would still be affiliated with either of these risk beliefs increased (shown as the lower bound in Figs. 3(a) and (c)).

Population states for the disengaged cluster (Fig. 3(b)) showed an upper bound of 250 household agents and a lower bound close to zero. Based on the rules used in the model, the disengaged cluster was limited to the number of household agents initialized within the cluster. Under conditions where messaging from outside clusters was dominant, members of the disengaged cluster changed their viewpoints, resulting in a migration out of the cluster.
The conflicted cluster exhibits a wider range of potential population states in year 30 (Fig. 3(d)). Under the condition when frequency of communication within this cluster is zero, population states can range from 250 household agents to close to zero household agents. If external messaging was strong, then a majority or all household agents will change their risk and benefit perception values and move to other clusters. On the other hand, if there was no or limited external messaging, household agents remained as initialized. For other communication frequencies, a wide range of possible ending population states was observed.
4.2.2. How Discussion Frequency Influences Public Opinion Climate
Community-wide measures of the strength of risk and benefit communications and the associated risk-to-benefits ratio were calculated using Equations 9–11. As observed in the analysis in Section 4.1., lower risk-to-benefit ratios indicate conditions where convergence toward optimistic viewpoints is favored. A risk-to-benefits ratio of 1 serves as the cutoff point, with risk-to-benefit ratios greater than 1 favoring convergence toward alarmed viewpoints.
As an example, Fig. 4 summarizes the alarmed populations in year 30 as a function of risk-to-benefit ratios, based on the alarmed population's communication frequency. No communication resulted in a reduction of the alarmed population. Low communication frequencies (four messages/year) generated a range of outcomes; however, for a majority of simulations, the alarmed population remained less than 50% of the total population in year 30. As the communication frequency increased (12 and 26 messages/year) the number of scenarios where alarmed population was greater than 50% of the final population steadily increased. The highest communication frequency (52 messages/year) resulted in all the scenarios having an alarmed population greater than 50%, and a majority of these scenarios result in an alarmed population in excess of 75% of the total population. The results indicated that increasing the communication frequency of the alarmed population generally results in a larger alarmed population by year 30. The optimistic population exhibited similar behavior.

4.3. Testing the Empirical Model
The risk publics model was modified to incorporate parameters obtained from the water reuse survey. Risk and benefit values obtained from the survey analysis (Table II) were used to define and initialize the clusters, a communication frequency was set to 12 messages/year (equal to one message per month), and variability in frequency of communication among the clusters was incorporated using data reported earlier. Variability was introduced to the communication network size, and household agents were randomly assigned six, seven, or eight network connections (i.e., each agent as a source sent messages to six, seven, or eight targets) to create a small-world network. Each agent was connected to one randomly selected agent in each of the three external clusters, and remaining links were generated internal to the network. The network sizes that are used here are comparable to those reported in a survey about risk communications concerning mad cow disease in Germany.48 Population proportions were reported in Table I.
A second set of simulation runs were executed for the empirical-based model described above. Fractional communication rates of 0.6, 0.7, 0.8, 0.9, and 1.0, were used in the simulation runs to cover the full range of observed communication frequencies, which range from 0.68 to 1.00 (see Section 3.1.2.). Each cluster's fractional communication rate was varied from 0.6 to 1.0, resulting in 625 possible combinations evaluated. Each combination run was replicated 25 times, and the average results obtained from the 25 runs are reported in Fig. 5. Simulations were run for a 30-year period using one-year time steps.
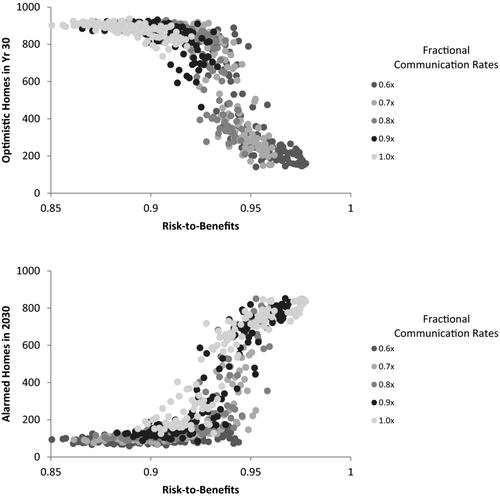
4.3.1. Results of the Empirical Model
Because the optimistic cluster was larger than the alarmed cluster (see Table I), the risk-to-benefit ratios were always lower than 1. When optimistic members communicated at a fractional rate of 0.9 or greater, more than half the population is in the optimistic cluster by the year 30. Even at the lowest measured talk fraction of 0.6, a large number of scenario runs indicate that the population will be predominantly optimistic in 2030.
The communication of the alarmed cluster was weaker than that of the optimistic cluster. Consequently, the symmetry in behavior between the optimistic and alarmed clusters observed in the previous theoretical runs (for example, see Figs. 2 and 3) was absent. For low communication fractions (0.6 and 0.7), the population in the alarmed cluster never exceeded 50% of the total population. For high communication fractions, there were a limited set of scenarios under which the alarmed cluster became the dominant cluster. In most cases, these scenarios required the optimistic population to communicate at a lower frequency than the alarmed population; survey results, however, indicate that this was not the case at a national level (Table II).
4.3.2. Results of Regional Analysis in the United States
Up to this point, our analysis has treated individual responses as equal regardless of their geographic location. Since we knew the state of residence for respondents to the national survey, another question presents itself: How would these opinion dynamics play out in different regions of the United States? We executed a set of simulations with population proportions initialized to represent different regions of the United States based on nine divisions defined by the U.S. Census Bureau.51 Each division includes between three and eight states identified by their abbreviations in Table III.
| Cluster | ||||
|---|---|---|---|---|
| Region | 1 Optimistic | 2 Disengaged | 3 Alarmed | 4 Conflicted |
| 0 National | 25.2% | 39.6% | 11.8% | 23.4% |
| 1 New England (ME, VT, NH, MA, CT, RI) | 23.4% | 43.3% | 7.8% | 25.5% |
| 2 Mid-Atlantic (NY, NJ, PA) | 20.1% | 38.6% | 15.3% | 25.9% |
| 3 East-North Central (WI, IL, IN, MI, OH) | 21.3% | 43.8% | 14.0% | 20.9% |
| 4 West-North Central (ND, MN, SD, IA, NE, MO, KS) | 24.8% | 41.6% | 8.4% | 25.2% |
| 5 South Atlantic (VA, MD, WV, DE, NC, SC, DC, GA, FL) | 25.1% | 37.5% | 12.7% | 24.7% |
| 6 East-South Central (KY, TN, MS, AL) | 21.9% | 41.7% | 17.2% | 19.2% |
| 7 West-South Central (AR, OK, LA, TX) | 22.1% | 42.5% | 11.9% | 23.5% |
| 8 Mountain (ID, MT, NV, WY, UT, CO, AZ, NM) | 38.8% | 32.7% | 8.7% | 19.9% |
| 9 Pacific (AK, WA, OR, CA, HI) | 31.9% | 37.7% | 7.5% | 22.9% |
Thirty-year simulations were conducted with varying population proportions to initialize the model. Other model parameters were set using survey data as before: cluster risk and benefit values used were from Table I; a baseline messaging frequency of 12 messages/year was adjusted by cluster using the relative frequencies shown in Table II; and network connections of either 6, 7, or 8 links were randomly assigned.
Different opinion dynamics were observed across the regions, and these were closely linked to the initial population proportions. As shown in Fig. 6, there was a notable difference in the alarmed population across regions. The Mountain region had the highest initial optimistic population and the fastest growth in an optimistic viewpoint in an S-shaped growth curve (Fig. 7). Convergence to the optimistic viewpoint occurred rapidly and reached near completion after 10 years into the simulation run. The East-South Central region had the highest alarmed population and a relatively smaller optimistic population than other regions. However, even in this most skeptical region the optimistic population was larger than the alarmed population. Optimistic population growth followed an S-shaped growth curve, but growth occurred more gradually than in the Mountain region.


Overall, growth of the optimistic viewpoint occurred in all regions, similar to the national level, following an S-shaped growth. Growth rates and the resulting S-shaped curves were distinct for each region; differences arose primarily due to the different starting population proportions. For the Mountain, Pacific, and South Atlantic regions, disengaged and conflicted populations in year 10 were nearly zero. For all remaining regions, population in these clusters remained larger than zero in year 10, but reached zero by year 20.
Finally, we evaluated the length of time required for optimistic population to reach 50%, 75%, and 90% of the total population. All regions converged on a majority optimistic population. In each case, the initial optimistic population was larger than the alarmed population; in addition, as described in the previous section, the frequency of communication among the optimistic population was greater than in the alarmed population. The differences in population proportions, however, lead to different growth rates and patterns among the regions. Four of the regions reached the state where the optimistic population is 90% or greater by the year 2030.
5. DISCUSSION
We began this study with the idea that municipal water reclamation has been recognized as a sustainable alternative for urban water services,1 and the success of water reuse projects is dependent on community-wide acceptance and adoption.2 In particular, community leaders who choose to introduce water reclamation into their municipality face the risk of residents rejecting that technology. Our goal was to investigate empirically a number of assertions surrounding the potential success or failure of such projects. The results provide several contributions to the risk communication literature, primarily in enumerating several underdeveloped aspects of the SARF. First, the longitudinal aspects of opinion dynamics are difficult to observe and study, and the simulation approach we took offers new opportunities for research and understanding in this area. Second, few studies have addressed questions related to the processes of risk amplification and attenuation, but our model sheds light on how community dynamics play a role in shaping these outcomes. Third, the results can help inform municipal planners who are considering the technology as a water-conserving alternative on whether the technology will be accepted by their community. Of course, our study was not without its limitations, which we summarize prior to examining its contributions in greater detail.
5.1. Limitations of the Current Study
In terms of methodology, we acknowledge several limitations. Model parameters were developed using a national survey and may not be representative of specific individual communities. Surveys conducted among a representative sample of the local population can help develop more location-specific insights. In addition, discussion networks (number of contacts, nodes, and links) and the number of discussions were two model inputs that were not obtained directly from the survey and were based on values from other studies. Because discussion groups and amount of discussion are bound to differ based on the topic of discussion, empirical data specific to water reuse for these two parameters could help further refine the model.
In operationalizing the model, we took observations at the individual level (survey respondent) and used them to represent decisions at the group level (household). This operational choice is, at least in part, inherent to joining the engineering approach to agent-based models (where household data are readily available from water utilities) with the social science approach to measuring attitudes through a survey (where the unit of observation is the individual). To our knowledge, no published research has provided an adequate methodological solution to this mismatch, and so our models were developed with the assumption that one individual's perception would at least be proximate to how the household as a whole might react to water reclamation. Further research, however, is certainly warranted on this question.
5.2. Contributions to Risk Communication Research
We identified three main contributions of our study to the risk communication literature in general and the social amplification of risk research in particular. First, through our agent-based models, we were able to simulate large-scale, longitudinal opinion dynamics that are not easily observed through other methods. The multiple simulations that were described here indicate that a wide variety of population states are possible based on variations in starting population proportions and defined communication characteristics (frequencies) of the risk publics. These findings provide novel insight into the SARF, which was originally introduced as a complex model encompassing many discrete elements of how a group, community, or even an entire country responds to a hazard or threat. In our model, individual households served as amplification stations, having the potential to transform community-level perceptions of the technology to focus more on the perceived risks or the benefits. Beyond the individual level, however, agents’ social networks served as amplification stations as well; one individual's perception of risk was highly dependent upon his or her interactions with other individuals in the community.
For example, our national-level model was formulated so that the optimistic and alarmed populations served as the major attractors, with the population converging to either of these clusters. Both the optimistic and alarmed clusters were anchored by a subset population, which has fixed risk and benefit perceptions and exerts an increased level of influence on dynamics. The model could be revised to make the conflicted or disengaged viewpoint as the dominant perception, if such parameters were empirically justified. Model results demonstrated the importance of both frequency and valence of discussion on opinion. Increases in the frequency of communication either as an innate property of the particular risk publics cluster, or due to a larger relative population, increases the strength of the message broadcast by the risk public. Valence of discussion reflected by the risk and benefits perception values of the message sender also increases the strength of the message.
Second, the simulation model showed the emergence of a number of community-level social groupings surrounding the issue of water reuse that resemble patterns of opinion formation observed in real life, such as consensus formation, polarization, and clustering.45 Under certain conditions explored in this research, the risk and benefit perceptions of individuals within the community converge to a set of beliefs espoused by one particular cluster. A consensus is formed within the community, and acceptance (due to risk attenuation) or rejection (due to risk amplification) becomes the dominant risk belief. Polarization within the community is observed when the population divides into two main risk benefits belief clusters: optimistic and alarmed. Clustering phenomena was also observed, where multiple beliefs, and not just the extreme positions, coexist or emerge over time.
These empirically derived observations from our simulation models inform the social amplification of risk further. For one, as other recent research has demonstrated, both the risk perception and benefit perception matter when it comes to novel and unfamiliar technologies.49, 50 The two perceptions may be correlated with one another, but they also represent distinct attributes of the technology itself and seem to be key factors underlying the two outcomes proposed in SARF: risk amplification and risk attenuation. As a recent review of SARF studies indicated, the phenomenon of risk amplification seems to have received much more attention in the literature than risk attenuation, and both tend to be the subject of cross-section analyses that are unable to address the longitudinal process underlying these outcomes.30
In our study, the model addresses this amplification/attenuation process—or “how?”—question by simulating patterns of emergent community opinion dynamics based on interpersonal communication. The model revealed how risk perception at the micro level translates into interpersonal communication at the dyadic level within a dynamic and relatively large social network, and how these dynamic social interactions translate into shifts in public opinion at the macro-level. Results demonstrated how risk perceptions can be affected when disparities exist in communication characteristics between risk publics. The social amplification/attenuation of risk is observed to occur when a particular risk benefits belief cluster has a larger population or sends messages (communicates) more frequently than others. Application of the model to nine empirically defined regional population profiles indicates the potential of the modeling framework to evaluate alternative water reuse adoption dynamics. In contrast to most studies applying the SARF, we observed risk attenuation both at the national level and in regional analyses. The result was not an artifact of the model; indeed, we took great care to ensure that the model itself would not be biased toward producing amplification or attenuation. Instead, these outcomes were observed due to the empirical data from the national survey, where we observed both the proportion of individuals in the risk publics and their levels of communication. For water reclamation technology, it seems consistent that the individuals in the optimistic cluster were also the most engaged discussion partners in their communities. For other technologies—or, in fact, for water reclamation technology in the future—these dynamics could very well shift, and we might observe a different outcome (risk amplification) through a nearly identical process.
Finally, the framework described can serve as a tool to explore the opinion dynamics surrounding the issue of water reuse. Planners may benefit from the use of this model to assess the likelihood of water reuse projects succeeding in a community. As we suggested above, the economic resources required for investing in water reclamation technology are substantial, and for such municipal projects to be worthwhile it would be ideal to have some promise of widespread adoption by residents. Our study informs a key question for water use planners: Will people embrace this technology in our community? The model results suggested that certain conditions suggest a successful adoption scenario. Other things equal, conditions of widespread adoption were dependent on the initial public opinion of residents and how often they discuss the technology with their neighbors. As these elements varied, so did rates of adoption, suggesting for planners that different implementation scenarios might work better for different communities. Again, our model in no way suggests that residents could or should be manipulated into accepting a technology that they do not want in their community, but the model does represent the process underlying how the community makes such decisions.
Experiments or scenarios can be developed to explore how a set of community beliefs leads to enhanced receptiveness or rejection of water reuse. Model users may also ascertain the presence of certain thresholds that may create difficulties in gaining acceptance of water projects. The model highlights the importance of communications in opinion dynamics, and water agencies and utilities can evaluate the potential impact of communication strategies in encouraging adoption of water reuse. For example, broadcasting public service messages may engage the public, or working with and enabling community leaders may increase discussion and communication among supporters of water reuse, with the potential of influencing larger portions of the community. At the same time, significant water supply incidents, e.g., the cryptosporidium contamination in Milwaukee in 199352 or the more recent concerns about lead in Flint, Michigan, were outside the scope of the current study, but these may well play a substantial role in shifting community discussions toward a risk amplification rather than attenuation result. Only future research can shed further light on these possibilities.
ACKNOWLEDGMENTS
This material is based upon work supported by the National Science Foundation under Grant No. 1233197.




