Bogen's Critique of Linear-No-Threshold Default Assumptions

1. INTRODUCTION

Current guidelines of the U.S. Environmental Protection Agency (EPA) for risk assessment differentiate carcinogenic and noncarcinogenic responses. Quantitative estimates of risk are not developed for assessments of noncarcinogenic effects or for carcinogenic effects thought to be mediated by a nonlinear mode of action (MOA). In its “Silver Book,”2 the National Research Council (NRC) Science and Decisions Committee proposed methods for unifying risk assessment procedures that would involve developing quantitative estimates of risk for all health effects. The paradigm for risk assessment proposed by the Committee is based on three conceptual models that envision three categories of dose responses derived from mechanistic considerations:

Conceptual Model 1 (threshold dose response on individual level, linear1 on population level);

Conceptual Model 2 (threshold response on individual level, nonlinear on population level);

Conceptual Model 3 (linear response on individual level, linear on population level).

Conceptual Model 3 applies to those carcinogenic effects that are thought to have a fundamentally linear MOA. However, it also applies to effects that have been traditionally thought to have a nonlinear MOA, but which are low-dose linear by virtue of the dose response being “additive to background” (AB).3 Conceptual Model 1 applies to health effects that have a threshold on an individual level, but that are linear on the population level by virtue of their being “substantial interindividual heterogeneity” (SIH) in susceptibility in the exposed human population sufficient to smooth out the individual thresholds and result in a population dose response with no threshold, and in fact one that exhibits linearity.4 Thus, the NRC Committee relied on two different arguments (AB and SIH) in proposing that Conceptual Models 1 and 3 were linear. Conceptual Model 2 is therefore the only model in which the population dose response is assumed to be nonlinear. However, Crump et al.5 identified problems with implementing Model 2 and recommended caution in the use of this model for estimating low-dose risks from human exposures to toxic chemicals.

An article published earlier in this journal (Bogen1) was critical of the arguments for linear dose responses underlying Conceptual Models 1 and 3, claiming that the SIH argument for linearity is false and the AB argument is “either false or effectively meaningless.” In this article I evaluate Bogen's critique. In the process I confirm Bogen's claim regarding the SIH argument by outlining a formal proof. I also point out how Bogen mischaracterized the AB argument in Crump et al.3 in some important ways.

2. ADDITIVE TO BACKGROUND

The AB argument for linearity (AB), first proposed in Crump et al.,3 states that if a toxicant operates by augmenting a process that is already producing adverse effects in background, then the additional response caused by the exposure to dose D can be reasonably expected to vary approximately linearly with exposure at low exposures. Although Crump et al. presented this argument for linearity in the context of cancer risk, it clearly is not restricted to carcinogenesis and applies much more generally (e.g., Crawford and Wilson6). The response at dose D can be represented by , where D₀ is the effective dose responsible for background disease and F is the effective dose–response function. Therefore, near , we have . If , then the dose response will be approximately linear at low exposures (i.e., have a positive slope at and be “low-dose linear”; see Crump et al.3 for a more complete description of AB). This is the argument used by the NRC2 for linearity in its Conceptual Model 3 that included some MOA traditionally thought to be nonlinear.

Bogen's stated concerns with AB are twofold. First he states it is “false or effectively meaningless if it refers to additions to an independent background response.” However, Crump et al.3 clearly point out the necessity of the assumption that there are background responses that occur by the same toxic mechanism as the substance of interest. So, rather than “false or effectively meaningless” it would be more accurate to say AB is “not applicable” if the background response occurs by a mechanism that is completely independent of that of the substance of interest. However, it will generally be difficult to determine whether the background rate of disease is completely independent of disease caused by the toxicant of interest. For the protection of human health it may be prudent to assume that a common mechanism is involved.

Second, Bogen1 is concerned that the positive slope of the dose response at may not be well-predicted by the trend of the dose response at higher doses. To illustrate this point he presents an example of a dose response that is a mixture of two dose responses, one of which is essentially saturated at background (. ). The mixture produces a flat-looking dose response (at least in Bogen's Fig. 1), which Bogen labels a “quasi-threshold.” However, our Fig. 1 contains a plot of Bogen's dose response plotted on a different scale, which illustrates that this “quasi-threshold” is actually linear at low dose as predicted by AB (albeit with a slope that is smaller than suggested by the response at higher doses). This illustrates that Bogen is technically correct, in that additivity to background, without additional conditions, does not assure that the low-dose slope guaranteed by AB can be well-predicted by data gathered at higher doses. However, one might expect that conditions similar to those illustrated by Bogen's Fig. 1, where the dose response is a mixture of two dose responses, one of which is completely saturated at background, occur only rarely, if ever, in practice. In fact, it seems plausible that in general there would be some relationship between the low-dose slope and the responses at higher doses. Crump et al.3 investigated this issue for a class of multistage models of cancer.

The bolded part of the quote was omitted by Bogen. The full quote from Crump et al. makes it clear that the first part of the quote provided by Bogen refers generally to AB under practically any model, whereas the second part of the quote refers specifically to application of AB to a class of multistage models of carcinogenesis. In fact, Crump et al. provide a detailed analysis of this issue for this class of models and derive bounds for the errors in the AB linear approximation that support the conclusion regarding the accuracy of the linear approximation with this class of models of carcinogenesis.

Bogen1 noted that dose–response functions can appear linear throughout a range of risks and yet be nonlinear at low dose. In his illustrations of this point (Fig. 2 in Bogen), Bogen fit dose responses, defined as mixtures of two log-normal distributions, by linear regression to 30 points equally spaced in risk (0.01, 0.02, …, 0.30). He showed that the R² on these “linear” fits ranged from 0.9992 to 0.9996. However, based on these R²s, he did not restrict the constant term in the regressions to be zero, and consequently the “linear” fits he obtained were actually from threshold models, and true linear models do not fit nearly as well (Fig. 2). Nevertheless, Bogen's basic point is valid—a dose response may appear to be reasonably linear at higher doses and still be low-dose nonlinear. Mixtures of log-normal distributions are not necessary to illustrate this point. There is no compelling reason why a dose response to a toxicant should follow any particular well-known distribution or mixtures of such distributions (see Crump et al.5 for a discussion of this point in relation to the log-normal distribution.) Therefore, one can easily define ad hoc distributions that have as much theoretical standing as mixtures of two log-normal distributions, and that are low-dose nonlinear but appear approximately linear at higher doses. But such examples, including those of Bogen, tell us nothing about how often such distributions might occur in practice. It should be noted that the NRC Committee did not recommend choosing among the three conceptual models based on shapes of the observed dose responses, but rather on mechanistic considerations.

3. SUBSTANTIAL INTERINDIVIDUAL HETEROGENEITY

The SIH argument for linearity, as formulated by Lutz4 and quoted by Bogen, is as follows: “Human variability with respect to the individual thresholds for a nongenotoxic cancer mechanism can result in linear dose–response relationships in the population (Lutz4).” Bogen refuted this claim by mathematizing it and presenting several examples that did not exhibit linearity. Bogen assumed that the SIH argument could be explained mathematically in terms of a population dose response of the type:

(1)

where is a family of dose–response functions representing dose–response functions in a large population indexed by α (α is vector-valued in some of Bogen's examples), is the distribution function for α in the population, and the integration is over the support of . Bogen considered a number of specific cases for and , all of which satisfy the condition 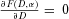at for all α (e.g., all of the individual dose responses are nonlinear at low dose), and showed that in each of these examples the population dose response is also nonlinear at low dose (i.e., ). However, it is easy to show that this result is not true just for the specific examples examined by Bogen but is generally true. By Leibniz's formula for differentiating an integral (e.g., Sokolnikoff and Redheffer8, p. 348), under general conditions, Equation 1 for can be differentiated with respect to D by taking the partial derivative of the integrand with respect to D. But upon doing this and setting , the entire integrand becomes 0 and consequently = 0. Therefore, the SIH argument for linearity is generally false, and not just in the special cases considered by Bogen. At least that is true when SIH is formulated in the manner assumed in Equation 1. However, it is easy to show that if each of the distributions have a true threshold (represented by α), and the distribution of thresholds in SIH includes thresholds arbitrarily close to zero (i.e., for ) then, although will be nonlinear, it will not have a threshold, even if each member of the family of distribution functions, , has a threshold. Also, if the mathematical description of SIH is expanded slightly so that is slightly positive and is low-dose linear then the mixture distribution will also be low-dose linear. Thus, even though SIH, as formulated by Equation 1, does not result in a dose response, , that is low-dose linear, it does result in a nonthreshold distribution. Furthermore, slight variations to assumptions in SIH can result in low-dose linearity.

Just as with the earlier Bogen quote from Crump et al.,3 Bogen omitted the part of the quote that is bolded. However, this part of the quote contains the notation for AB used by Crump et al. and therefore makes it clear that, in contradistinction to Bogen's claim, Crump et al. incorporated AB in their argument for linearity in this case as well. Thus, Bogen's claim that Lutz's SIH argument for linearity, which does not involve the AB argument, originated with Crump et al.3 is incorrect.

4. DISCUSSION

Bogen critiques two arguments for low-dose linearity used by the NRC Science and Decisions Committee2 for incorporating low-dose linearity into its proposed framework for risk assessment (AD and SIH). Bogen shows by examples that the “SIH” argument for low-dose linearity used by the NRC Committee as the basis for a linear dose response at the population level in Conceptual Model 1 can be false. In this article, a proof is outlined that supports Bogen's contention and shows that the SIH argument for linearity is generally false. However, SIH does lead to a nonthreshold distribution at the population level, and a slight weakening of assumptions in SIH will result in this distribution being low-dose linear.

Bogen calls the AB argument “false” because the AB argument would fail to apply whenever the background level of response is due to mechanisms completely independent of the MOA by which the substance of interest causes a response. Here “false” is inappropriate because the AB argument only specified linearity when the external agent acts additively with an already ongoing process (Crump et al.3). Bogen does not discuss conditions under which background disease would occur by a totally independent MOA, or the difficulty in demonstrating an independent mechanism. However, it seems unlikely that background levels and dose-dependent levels of the same disease would normally occur by totally independent mechanisms.

Bogen also calls the (AB) argument “effectively meaningless” because, even if the dose response is low-dose linear, using the trend at higher doses to estimate the low-dose slope may result in overestimation. However it seem that, in the absence of additional information (say, about the MOE of background disease compared to that of disease due to the substance of interest), it is plausible to assume that there is a quantitative relationship between the low-dose slope and the slope suggested by higher doses. There is nothing that Bogen states that effectively contradicts this supposition (the highly artificial example depicted in his Fig. 1 notwithstanding).

This statement was buttressed by several sets of in vitro data that are claimed to show nonlinear dose responses.

But, as pointed out in Crump,7 any set of dose–response data will be consistent with both a threshold and a low-dose linear response. Therefore, distinguishing between a low-dose linear dose response and a threshold dose response on the basis of dose–response data is impossible—it is something that science is incapable of doing. Thus, both of these statements by Bogen, to the extent that they are claiming the existence of data that are incompatible with low-dose linearity, are misleading.

Bogen1 contains numerous references to “quasi-thresholds” but he does not define this term. Apparently, Bogen simply decides subjectively on a case-by-case basis whether or not to call a result a “quasi-threshold.” But none of the “quasi-thresholds” identified by Bogen are actually thresholds. In fact, all of them are low-dose linear, and thus every increased dose, no matter how small, carries some increased risk. For example, Fig. 1 is a graph of the “quasi-threshold” dose response in Bogen's Fig. 1 plotted on a different risk scale. From this perspective there is no suggestion that the term “threshold” should be associated with this dose response. The term “quasi-threshold” seems to suggest a situation in which the increased risk, if any, is so small that it is not a concern. However, to decide whether or not the increased risks at these “quasi-thresholds” are large enough to be of concern in individual situations would require further analysis.

Crump7 compiled a list of terms found in the scientific literature that involve the term “threshold” in combination with other qualifiers, including “practical threshold, “apparent threshold,” and “operational threshold,” which have the following characteristics in common with Bogen's “quasi-threshold.” None of them have a scientific definition and none of them refer to a true threshold, but rather to a situation where there is some increase in risk at every dose. Whether these increases are large enough to be a cause for concern would require a wider analysis. But, as is pointed out in Crump,7 if the definition of “threshold” is relaxed to include the possibility of some nonzero change in response, any dose response can be considered to have a “threshold” at sufficiently small doses, and thus the threshold concept becomes devoid of meaning. Consequently, the use of the term “threshold” to describe responses that are not true thresholds promotes confusion and muddled thinking, and is best avoided.

Bogen1 showed by examples that the SIH assumption will not always result in low-dose linearity. In this article, I showed that, under Bogen's formulation of SIH, the population dose response will generally not be linear at low dose. But I also noted that SIH, under Bogen's formulation, will generally produce a nonthreshold (albeit nonlinear) dose response. Bogen also called attention to the possibility that the low-dose slope under AB may not be well-estimated by the dose response observed at higher doses. However, he provided little guidance on when this occurs, or how often. However, it seems reasonable to assume that generally there is a quantitative relationship between the low-dose slope and the slope suggested by higher doses if the true dose response is actually low-dose linear.