Leaf water 18O and 2H maps show directional enrichment discrepancy in Colocasia esculenta
Abstract
Spatial patterns of leaf water isotopes are challenging to predict because of the intricate link between vein and lamina water. Many models have attempted to predict these patterns, but to date, most have focused on monocots with parallel veins. These provide a simple system to study, but do not represent the majority of plant species. Here, a new protocol is developed using a Picarro induction module coupled to a cavity ringdown spectrometer to obtain maps of the leaf water isotopes (18O and 2H). The technique is applied to Colocasia esculenta leaves. The results are compared with isotope ratio mass spectrometry. In C. esculenta, a large enrichment in the radial direction is observed, but not in the longitudinal direction. The string-of-lakes model fails to predict the observed patterns, while the Farquhar–Gan model is more successful, especially when enrichment is accounted for along the radial direction. Our results show that reticulate-veined leaves experience a larger enrichment along the axis of the secondary veins than along the midrib. We hypothesize that this is due to the lower major/minor vein ratio that leads to longer pathways between major veins and sites of evaporation.
Introduction
Understanding plant water isotope composition is key to many important questions in Earth Sciences, from partitioning evaporation and transpiration (Farquhar & Cernusak, 2005; Welp et al. 2008) to using cellulose (Gray & Thompson, 1976) and fossilized leaves (Sachse et al. 2012) as indicators of past temperatures and relative humidity. The isotope composition of plant tissues is set by the photosynthetic pathways (Sternberg et al. 1984) and the isotope composition of the water used in photosynthesis (Roden et al. 2000; Affek et al. 2005). Leaf water isotope composition depends not only on the isotope composition of precipitation (Flanagan & Ehleringer, 1991) but also on stomatal conductance (Barbour, Fisher, et al. 2000), which is directly linked to the leaf transpiration rate. Because stomatal conductance is tightly connected to environmental parameters, leaf water isotope composition has been found to be correlated to CO2 concentration (Cooper & Norby, 1994), temperature (Kahmen et al. 2008) and relative humidity (Liu et al. 2016).
Transpiration is however not homogeneous within a leaf, and the transpiration patterns can in turn affect intra-leaf isotope differences, as well as bulk leaf water composition (Holloway-Phillips et al. 2016). As new experimental techniques developed and high density mapping became possible, new evidence indicated that the range of variation of leaf water isotope composition within a single leaf was more complex than previously thought (Cernusak et al. 2016). Over the past few decades, multiple mechanisms for leaf water enrichment have been proposed, and every new model presented a higher degree of process-level complexity compared with the previous one. The initial model was the Craig–Gordon (CG) model (Craig & Gordon, 1965), which predicts that the isotopic enrichment taking place at the surface of an evaporating surface of water can be applied to evaporating sites within a leaf. In this model, the fractionation is driven by the difference of vapour pressure between the interior of the leaf and the atmosphere and by the difference of diffusivity of the isotopologues. The CG model was rapidly found to overestimate the enrichment of bulk leaf water above source water, Δl (Allison et al. 1985; Yakir et al. 1990). Two corrections to the CG model were developed in response to this conclusion: (1) the two-pool model, which represents the leaf as a pool of enriched water (the lamina) and a pool of unenriched water (the veins) (Leaney et al. 1985; Yakir et al. 1990; Song et al. 2015) and (2) the Péclet model, which takes into account the balance between the diffusion of enriched water away from the evaporative sites and the advection of unenriched vein water towards them (Farquhar & Lloyd, 1993; Cernusak & Kahmen, 2013). The Péclet model is characterized by a dimensionless Péclet number ℘: when ℘ > 1, advection is the dominant transport process, and when ℘ < 1, diffusion is the dominant transport process (Cuntz et al. 2007).
Although both the two-pool and Péclet models include considerations of water movement within the leaf, neither accounts for spatial variability in water movement across the leaf. Based on evidence of spatial patterns in leaf water isotopes (Gan et al. 2002), modifications to the two-source and Péclet models have been developed that attempt to capture the observed progressive enrichment of leaf water when moving towards the edges of the leaf. The string-of-lakes (SoL) model (Gat & Bowser, 1991) expands upon the two-source approach by describing the leaf as a string of successively enriched pools. This model was successful in reproducing the longitudinal enrichment observed along grass leaves (Helliker & Ehleringer, 2000). Farquhar and Gan (FG, 2003) developed a hybrid model that combines the two-pool model and an advanced version of the Péclet model. In the FG model, different Péclet numbers are attributed to the lamina and the veins in order to produce a two-dimensional model of leaf isotopic enrichment (Farquhar & Gan, 2003). Most recently, the steady-state assumption made in all the previous models that the transpired water has the same composition as the supplying water was pointed out as a potentially large source of error in estimating the isotope composition of transpired water (Dubbert et al. 2014), and efforts were made to incorporate non-steady-state conditions into the FG model (Ogee et al. 2007). A more thorough review of these approaches can be found in Cernusak et al. (2016).
In this study, we will confront the current understanding of leaf water isotopes patterns to high density maps of Colocasia esculenta leaves. This species is a monocot native to South East Asian tropical forests (Nauheimer et al. 2012) but has been cultivated across the world for many centuries under the common name of taro. Its leaves can easily reach a size of up to c. 80 cm in length and c. 60 cm in width (Ivancic & Lebot, 1999), making it a good candidate for high density sampling. C. esculenta venation is characterized by a thick midrib and a pinnated pattern of secondary veins (Fig. 1). Higher order veins all run generally parallel to the secondary veins towards the edge of the leaf, forming a reticulate network. This is very different from the pattern observed in maize and grass leaves used to test leaf water isotope models up to now. In these leaves, most veins run parallel towards the tip of the leaf, with the exception of small and short transverse veins that link intermediate veins together (Gan et al. 2003).

As Holloway-Phillips et al. (2016) pointed out, reticulate-veined leaves have multiple orders of major veins, which feed enriched water into higher order veins. The reticulate venation effectively increases the time spent by water inside minor veins. Indeed, at equal size, reticulate-veined leaves have been shown to have a higher minor vein density than parallel-veined ones (Niinemets et al. 2007). In addition, increase in leaf size is associated with a general decrease of the major/minor vein ratio (Sack et al. 2012). Enrichment at the sites of evaporation diffuses back into minor veins, and from there into secondary veins, which leads to the lamina often showing stronger gradients of enrichment than the major veins (Gan et al. 2002; Farquhar & Gan, 2003; Barbour & Farquhar, 2004). Based on Fig. 1, we found that C. esculenta has a major/minor vein ratio of c. 0.04. In comparison, Scoffoni et al. (2011) provide a list of such ratios for 11 other species and found values ranging from 0.05 to 0.38. In their data, the major/minor vein ratio decreases exponentially with increasing leaf area (R2 = 0.42). Giant elephant ear leaves, C. esculenta, are therefore expected to show a strong radial pattern of enrichment associated with the decreased major/minor vein ratio.
In the following sections, we start by describing a novel sampling method using the induction module (IM) by Picarro Inc. (Sunnyvale, CA, USA) combined to a cavity ringdown spectroscopy (CRDS) analyser. The IM allows us to collect a large number of small-sized samples and analyse them rapidly to create maps of the leaf water isotopes, δ18O and δ2H. The IM has been available commercially since 2011, but the number of published studies making use of it is still very limited (Berkelhammer et al. 2013; Johnson et al. 2017; Cui et al. 2017). Here, we present a protocol for the analysis and the post-processing of leaf samples using the IM. The method is tested against traditional isotope ratio mass spectrometry (IRMS). We then present a short review of the mathematical expressions of some of the models introduced previously and analyse our observed spatial patterns of leaf water isotopic enrichment in the context of leaf water isotope model predictions. Specifically, we compare our results with the SoL and the FG model of enrichment. We find that C. esculenta has a clear and reproducible pattern of isotopic enrichment in the radial, but not in the longitudinal direction. We hypothesize that this is due to the low major/minor vein ratio that leads to longer pathways between major veins and sites of evaporation. These patterns can be better captured by the FG than by the SOL model, taking into account the interaction between veins and lamina.
Materials and Methods
Six bulbs of C. esculenta plants were planted in 15 gallon pots filled with garden soil (Miracle Gro, Marysville, OH, USA) and grown to maturity. The pots were placed in a courtyard with low wind, receiving full sun in the afternoon. The plants were watered daily with tap water (δ18O = −5.96 and δ2H = −37.63) during their growth. A few days before leaf collection started, the pots were moved to a covered shaded area to minimize differences in transpiration rates because of differences in sun exposure. For the water isotope analysis, each leaf was sampled in two different ways. In sampling (1), the lamina of the first half of each leaf was sampled in 20 ± 1.8 (mean ± SE) different locations with variations depending on the size of the leaf. On average, the length of the sampled leaves measured 37 ± 4.5 cm. Across all leaves, sampling density averaged 5.4 ± 1.1 samples/dm2. All of the sampling points were located on the same half of the leaf, and each point consisted of four holes (6 mm diameter) punched next to each other forming a square. A half-leaf sampled in 20 different locations therefore corresponded to 80 individual punch holes to be analysed. Each hole was punched as quickly as possible to avoid evaporation, which would influence the isotope composition of the neighbouring holes. Leaf disks were individually secured in aluminium strips provided by the IM manufacturer and inserted in a 4 mL sealed glass vial provided by the instrument manufacturer. The prepared vials were then stored at 4 °C until further analysis. It took about 15 min to sample a single half-leaf. The analysis started as soon as the sampling was over. For batches to be analysed at a later time, freezing the samples could further prevent any change in the isotope composition of the samples. In this case, we recommend analysing ‘blank’ vials that have been stored in the same conditions as the sample. In sampling (2), the second half of each leaf was kept intact, and the lamina and vein water was extracted using a traditional cryogenic extraction method (Ehleringer & Osmond, 1989). Each of these half-leaves produced between 6 and 8 mL of bulk water, which was stored in 2 mL glass vials equipped with septa caps adapted for use with the integrated autosampler (Picarro Inc.). The vials were wrapped in parafilm and kept at 4 °C until further analysis. Six different leaves were sampled over a period of 20 d (Table 1). The bulk water data for leaf 2 had to be discarded because of an issue with the cryogenic extraction.
| Leaf number | Collection date | Air temperature | Relative humidity | Wind speed | Leaf temperature | Stomatal conductance | Lamina water IM-CRDS | Vein water liq-CRDS | Bulk leaf water liq-CRDS | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (in Fig. 5) | (°C) | (%) | (m s−1) | (°C) | (mol m−2 s−1) | δ18O | δ2H | δ18O | δ2H | δ18O | δ2H | |
| 1 | 11/07/2014 | 19.9 | 81.7 | 1.3 | 26.6 | 0.042 | 16.4 | 19 | −2.6 | −21.4 | 5.4 | −6.6 |
| 2 | 14/07/2014 | 21.24 | 95.0 | 0.53 | 27.3 | 0.041 | 9.8 | 4.6 | N/A | N/A | N/A | N/A |
| 3 | 22/07/2014 | 19.6 | 81.4 | 0.68 | 26.4 | 0.044 | 12.3 | 15.5 | −4.4 | −35.6 | 3.6 | −11.2 |
| 4 | 24/07/2014 | 20.7 | 84.1 | 0.81 | 27.0 | 0.071 | 10.5 | −4.7 | −2.5 | −18.5 | 2.5 | −13.5 |
| 5 | 30/07/2014 | 15.9 | 73.1 | 0.82 | 23.1 | 0.144 | 19.0 | 10.7 | −2.4 | −18.3 | 5.0 | −9.6 |
| 6 | 30/07/2014 | 15.9 | 73.1 | 0.82 | 22.7 | 0.130 | 10.6 | −5.7 | −2.9 | −21.1 | 5.2 | −6.3 |
- Vein and bulk water data are not available for leaf 2 because the cryogenic extraction failed. Lamina water was obtained using sampling (1), vein water was obtained by cryogenically extracting petiole water and bulk leaf water was obtained by cryogenically extracting water as described in sampling (2), which included both lamina and vein water.
Punched leaf samples (from sampling (1), on one half of the leaf) were analysed using the IM coupled to a CRDS L2103-i from Picarro Inc. The IM instrument inductively heats up the aluminium strips within each individual glass vial for several minutes. The close contact between the leaf sample and the heated aluminium strip vaporizes any water contained inside of the leaf sample. The IM offers two different settings: ‘normal leaf’ and ‘thick leaf’. The ‘thick leaf’ setting heats up the leaf samples for a longer cycle (600 versus 300 s for the ‘normal leaf’ setting), in order to extract water from thicker or more sclerophyllous leaves. We found that C. esculenta leaves samples were consistently burned when using the ‘thick leaf’ setting, which led to carbonization of leaf tissues and the potential release of compounds that might interfere with the water analyser (Chang et al. 2016). However, when set on ‘normal leaf’, the leaf disks did not appear carbonized. To verify that all the water had been extracted from the leaf samples, we collected the sample disks after the analysis and oven dried them at 60 °C for 48 h. The leaf sample disks showed no further decline in weight (data not shown), which suggested the leaf samples had been completely desiccated during the analysis without being carbonized. The IM is equipped with a micro-combustion module (MCM), which has been proven to efficiently reduce the interference due to the presence of organics (Dennis et al. 2014) in water samples extracted from plants (A. G. West et al. 2010).
IM-CRDS analysis sequence
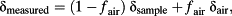 (1)
(1)| Identifiers | |||
|---|---|---|---|
| ID | Type | Standard water | Injections |
| Blank 1 | Empty vial | 1 | |
| ⋮ | |||
| Blank 6 | Empty vial | 1 | |
| DEST | Drift ref. water | ER1 | 10 |
| HIS | High ref. water | ER4 | 10 |
| ANTA | Low ref. water | 3 | 10 |
| DEST | Drift ref. water | ER1 | 10 |
| HERA | QC ref. water | 5A | 4 |
| Sample 1 | Sample | 4 | |
| ⋮ | |||
| Sample 10 | Sample | 4 | |
| DEST | Drift ref. water | ER1 | 6 |
| Sample 11 | Sample | 4 | |
| ⋮ | |||
| Sample 20 | Sample | 4 | |
| DEST | Drift ref. water | ER1 | 6 |
- Following the method by van Geldern & Barth (2012), HIS and ANTA are the names of the reference waters with high and low δ values, respectively. DEST and HERA are intermediate waters. DEST is the drift-monitoring reference water, whereas HERA is treated as a sample for quality control. All reference waters except HERA are used for memory and VSMOW correction. The standard water used have the following isotope composition (ABB – Los Gatos Research Inc.): ER4: δ18O = 81.33 ± 0.3‰, δ2H = 654.1 ± 1.0‰; ER1: δ18O = 12.34 ± 0.3‰, δ2H = 108.7 ± 1.0‰; 5A: δ18O = −2.80 ± 0.15‰, δ2H = −9.5 ± 0.5‰; and 3: δ18O = −11.54 ± 0.1‰, δ2H = −79.0 ± 1.0‰ (all referenced to VSMOW).
Following the protocol developed for liquid water samples in previous work (van Geldern & Barth, 2012), the data were corrected for drift and memory effects and rescaled back to VSMOW (Table 2). The drift of the instrument was determined by rerunning the drift-monitoring standard (DEST, working standard ER1) at the beginning, the end and half-way through the samples. This standard water was chosen to have an isotope composition close to that of the leaf samples analysed. A linear regression was then used to realign all the measurements, according to the sample order. The effect of the drift was found to be small for both isotope ratios, with a slope of −0.004 ± 0.005 per sample in δ18O and −0.05 ± 0.07 per thousand per sample in δ2H. These values are comparable with values found for liquid water samples (van Geldern & Barth, 2012). For the memory effect, three standard waters with large isotopic differences were injected 10 times in a row each. An isotopically high (HIS, working standard ER4) and low (ANTA, working standard 3) standard waters were used along with DEST to determine memory effects from high-to-low and low-to-high transitions. A memory coefficient was associated with each successive injection. The coefficients were determined using the ‘Solver’ function in Excel (Microsoft, Redmond, WA, USA) so as to minimize the standard deviation of all three standard waters simultaneously. The memory coefficients are presented in Supporting Information Figs S1 and S2. The evolution of the memory coefficients has a similar exponential shape for all our runs, and the memory effect has completely disappeared by the fifth injection. The scaling to VSMOW was performed using the DEST, HIS and ANTA standard waters of known isotope composition and using a linear regression to correct for potential deviations from the 1:1 line. A fourth intermediate standard water (HERA, working standard 5A) was used for quality control, and we found a precision of ±0.2 (SE of the difference from true value) in δ18O and ±1.1 in δ2H.
Liq-CRDS and IRMS analysis
Water samples (from sampling (2), bulk water from one whole half of the leaf) were analysed using both IRMS and conventional CRDS (coupling the CRDS analyser with an autosampler and a vaporizer). In this study, we use the mature conventional CRDS technique as a stepping stone to compare the new IM-CRDS technique, and the proved, but expensive IRMS analysis. Indeed, we found that standard waters analysed on IM-CRDS and conventional CRDS showed similar results (data not shown). In addition, users of the IM-CRDS technique are likely to be equipped for conventional CRDS analysis, but many might not have easy access to a mass spectrometer. By comparing all three set-ups, we aim at providing a useful resource for people without access to IRMS.
Ten samples of liquid water extracted from C. esculenta leaf and stem samples were sent to the Center for Stable Isotope Biogeochemistry at the University of California in Berkeley, USA, for IRMS analysis. Deuterium was obtained by chromium combustion using a hot chromium reactor unit (H/Device, similar to the one used in A. G. West et al. (2010), Thermo Finnigan, Bremen, Germany): the water sample was injected in the H/Device and reduced to H2 gas. The ratio of D/H was then measured on a Thermo Delta Plus XL mass spectrometer with a precision of ±0.60. For the 18O analysis, water from standards and samples was pipetted into glass vials and quickly sealed. The vials were then purged with 0.2% CO2 in helium and allowed to equilibrate at room temperature for at least 48 h. The 18O in the CO2 taken from the overhead in the sample vials was then analysed by continuous flow using a Thermo Gas Bench II interfaced to a Thermo Delta Plus XL mass spectrometer with a long-term external precision of ±0.10 (Wenbo Yang, private communication). The values of the standards used for the IRMS calibration were (δ2H/δ18O): SPW3: −251/−31.77‰; CSIB: −88.3/−12.21‰; BWW: −35.5/−4.77‰; and BSMOW: 6.0/4.63‰.
Aliquots of the samples analysed on IRMS were also analysed by conventional CRDS at the Ecohydrology Laboratory at Princeton University, USA. For this analysis, 1.8μL of water was injected into an A0211 high-precision vaporizer by Picarro Inc., and the vapour was pushed with dry air through an MCM similar to that of the IM, before reaching the analyser. Concentrations of
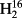 O,
O,
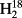 O and HD16O were measured on a CRDS analyser (L2103-i) from Picarro Inc. In the following, this method will be referred to as liq-CRDS.
O and HD16O were measured on a CRDS analyser (L2103-i) from Picarro Inc. In the following, this method will be referred to as liq-CRDS.
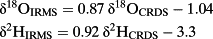 (2)
(2)
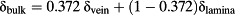 (3)
(3)
Isotope mapping
Once sampling (1) was completed, the leaves were pressed and scanned. The position of the midrib, the secondary veins and the sampling locations was hand digitized on the image of the leaf. The data were checked for normality, and a White's (1980) test was performed, and no heteroskedasticity was detected. We interpolated the isotope composition of the leaf in-between sampling locations using an inverse distance weighting (IDW) method with a fixed weight parameter available in the ‘gIDW’ add-on package developed by Giuliano Langella for matlab (Mathworks Inc., Natick, MA, USA). The IDW method was chosen because it is commonly used to produce isoscapes (J. B. West et al. 2009). The interpolation was used to help visualizing the isotope patterns within the leaf, but only the actual samples and their locations were used for comparison with the models, so our results are not dependent on the interpolation technique. In order to obtain a global estimate of the uncertainty associated with the IDW interpolation, we used an n-1 jackknifing method (Bowen & Revenaugh, 2003): the interpolation was rerun n times, each time removing one of the data points and using the remaining n-1 data points for the interpolation. We then compared the estimated value at the sampling location with the actual value and provided the root mean squared error (RMSE) associated with each map.
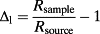 (4)
(4)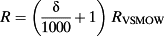 (5)
(5)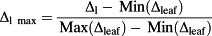 (6)
(6)Environmental and physiological data
Environmental data were collected at the Butler Roof Station located about 500 m away from the location of the plants and maintained by the Hydrometeorology Research Group at Princeton University (http://hydrometeorology.princeton.edu/#stations). The station records air temperature, relative humidity, rainfall, wind speed and upward and downward shortwave radiation. Data are available hourly for the entire duration of the experiment (11 July to 30 July 2014). Stomatal conductance and leaf temperature were recorded prior to leaf sampling using an SC-1 Leaf Porometer (Decagon Devices Inc., Pullman, WA, USA). Six random locations around the edge of the lamina (the porometer could not reach far into the leaf) were measured each time, and the average value of all six locations at each sampling time is used here. Environmental and physiological data for each leaf are listed in Table 1.
Modelling leaf isotopes spatial patterns
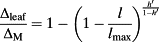 (7)
(7)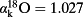 and
and
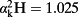 . ΔM is the maximum possible enrichment and is defined as
. ΔM is the maximum possible enrichment and is defined as
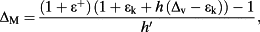 (8)
(8)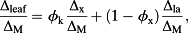 (9)
(9)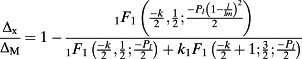 (10)
(10)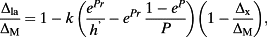 (11)
(11)Results
Testing the induction module
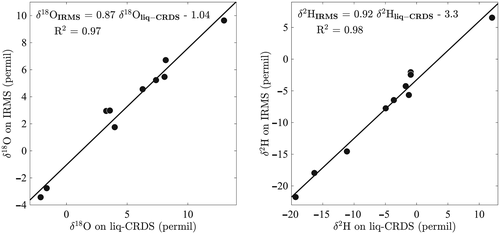
For the five leaves analysed by IM-CRDS for which bulk water was available, we compare the half-leaves analysed by IRMS with the bulk estimates of the other half of the leaves obtained from the IM-CRDS analysis (see Section on Liq-CRDS and IRMS analysis for details). The average difference between IRMS and IM-CRDS was 9.4 ± 1.4‰ in δ18O (mean ± SE) and 16.4 ± 5.0‰ in δ2H (Fig. 3). This difference is larger than, and therefore not attributable to, the difference observed between the two halves of the same leaf (0.3 ± 0.2‰ in δ18O and 1.9 ± 1.2‰ in δ2H) in four C. esculenta leaves cryogenically extracted (vein + lamina water) and analysed on liq-CRDS. When correcting the IM-CRDS analysed samples to take into account the influence of the vein water using a simple mass balance (Eqn 3), we obtained that the difference between the IM-CRDS and IRMS techniques dropped to 2.6 ± 0.83‰ in δ18O and 3.4 ± 2.1‰ in δ2H (Fig. 3).
Spatial patterns
On average, the lamina isotope composition obtained by IM-CRDS varied between 8.6 ± 0.5 and 17.6 ± 0.9‰ in δ18O and −3.9 ± 1.2 and 16.7 ± 2.0‰ in δ2H. The maps of the isotopic enrichment above source water of six different C. esculenta leaves (Fig. 5, RMSE (
 /
/
 ): leaf 1: 3.2/22.3‰; leaf 2: 1.85/13.8‰; leaf 3: 2.2/34.9‰; leaf 4: 3.5/4.2‰; leaf 5: 2.7/9.2‰; and leaf 6: 1.4/2.9‰) show generally similar patterns of increased enrichment when moving away from the midrib towards the edge of the leaf. This pattern is observed for both 18O and 2H. While all leaves cover a similar range of isotopic enrichment from midrib to edge of 5, the leaves show different absolute values, despite being normalized for source water isotope composition, here taken to be equal to petiole water (Table 1). This difference can be explained by the wide range of deuterium excess (d-excess) values observed in the different leaves. D-excess evaluates the deviation from the global meteoric water line and is defined as follows: d-excess = δ2H − 8 δ18O. D-excess measures the influence of kinetic fractionation of water isotopes and can sometimes provide information on the transpiration regime (Voelker et al. 2014), with more negative values of d-excess indicating more transpiration from the leaf. In our case, leaves with higher isotopic enrichments also show a more negative d-excess (Fig. 5, bottom row), indicating that despite being grown in similar conditions, some leaves experienced more transpiration likely because of small differences in sun exposure during growth. These differences obscure the similitude in relative enrichment throughout the leaf.
): leaf 1: 3.2/22.3‰; leaf 2: 1.85/13.8‰; leaf 3: 2.2/34.9‰; leaf 4: 3.5/4.2‰; leaf 5: 2.7/9.2‰; and leaf 6: 1.4/2.9‰) show generally similar patterns of increased enrichment when moving away from the midrib towards the edge of the leaf. This pattern is observed for both 18O and 2H. While all leaves cover a similar range of isotopic enrichment from midrib to edge of 5, the leaves show different absolute values, despite being normalized for source water isotope composition, here taken to be equal to petiole water (Table 1). This difference can be explained by the wide range of deuterium excess (d-excess) values observed in the different leaves. D-excess evaluates the deviation from the global meteoric water line and is defined as follows: d-excess = δ2H − 8 δ18O. D-excess measures the influence of kinetic fractionation of water isotopes and can sometimes provide information on the transpiration regime (Voelker et al. 2014), with more negative values of d-excess indicating more transpiration from the leaf. In our case, leaves with higher isotopic enrichments also show a more negative d-excess (Fig. 5, bottom row), indicating that despite being grown in similar conditions, some leaves experienced more transpiration likely because of small differences in sun exposure during growth. These differences obscure the similitude in relative enrichment throughout the leaf.
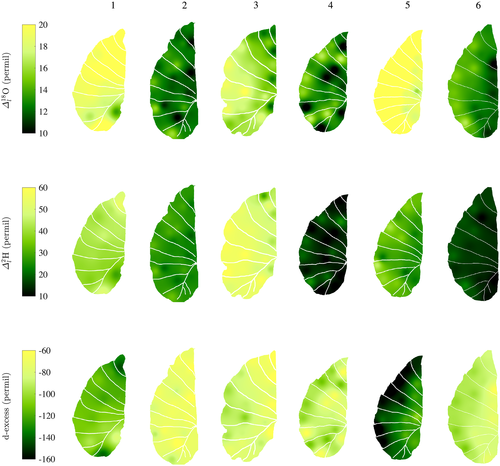
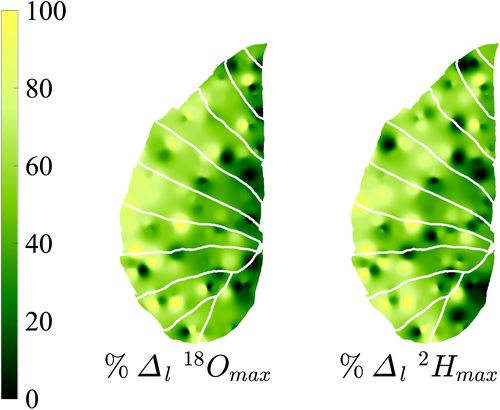
Maps of the same leaves with values normalized by the maximum enrichment within each leaf (Supporting Information Fig. S4, RMSE (
 ): leaf 1: 28.0/27.9%; leaf 2: 29.3/29.4%; leaf 3: 25.3/32.4%; leaf 4: 42.8/44.6%; leaf 5: 22.6/25.6%; leaf 6: 21.5/23.0%; and combined leaves in Fig. 6: 30.8/31.5%) help remove the dependence to transpiration rate prior to the beginning of the experiment and highlight the general lack of enrichment along the entire length of the midrib. In contrast, enrichment increases rapidly when moving radially, that is, perpendicularly from the midrib. Based on the data presented in Fig. 6, Table 3 summarizes the enrichment at three locations along a radial and a longitudinal gradient in the leaf. A significant enrichment is found along the radial direction with an increase of enrichment above source water by c. 30 percentage points from the midrib to the edges (Table 3), but no pattern is found for enrichment in the longitudinal direction along the axis of the midrib.
): leaf 1: 28.0/27.9%; leaf 2: 29.3/29.4%; leaf 3: 25.3/32.4%; leaf 4: 42.8/44.6%; leaf 5: 22.6/25.6%; leaf 6: 21.5/23.0%; and combined leaves in Fig. 6: 30.8/31.5%) help remove the dependence to transpiration rate prior to the beginning of the experiment and highlight the general lack of enrichment along the entire length of the midrib. In contrast, enrichment increases rapidly when moving radially, that is, perpendicularly from the midrib. Based on the data presented in Fig. 6, Table 3 summarizes the enrichment at three locations along a radial and a longitudinal gradient in the leaf. A significant enrichment is found along the radial direction with an increase of enrichment above source water by c. 30 percentage points from the midrib to the edges (Table 3), but no pattern is found for enrichment in the longitudinal direction along the axis of the midrib.
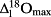 (%) and
(%) and
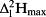 (%) for the lamina water at three position along the radial direction (columns) and the longitudinal direction (rows) using the maps shown in Fig. 6
(%) for the lamina water at three position along the radial direction (columns) and the longitudinal direction (rows) using the maps shown in Fig. 6| Midrib | Middle | Edge | |||||||
|---|---|---|---|---|---|---|---|---|---|
| n | Δl18Omax | Δl2Hmax | n | Δl18Omax | Δl2Hmax | n | Δl18Omax | Δl2Hmax | |
| Bottom | 13 | 33.1 (2.0) | 30.8 (2.3) | 14 | 49.0 (1.9) | 50.3 (2.3) | 14 | 63.4 (2.6) | 64.8 (2.5) |
| Middle | 13 | 26.6 (1.6) | 34.7 (1.9) | 19 | 45.7 (1.1) | 44.9 (1.4) | 14 | 69.8 (1.5) | 68.1 (1.8) |
| Tip | 11 | 29.6 (2.9) | 44.3 (2.2) | 10 | 56.9 (1.7) | 55.0 (2.8) | 13 | 58.2 (2.0) | 51.6 (2.3) |
- Values in parentheses show the standard error. n is the number of data points considered, and the standard error is given in parentheses. In the radial direction, areas represented by each section are c. equal. In the longitudinal direction, areas were split by dividing the total length of the leaf in three, which lead to the ‘tip’ to represent a slightly smaller area because of the tapering of the leaf at its tip. Overall, enrichment in the longitudinal direction is inconsistent, whereas a strong progressive enrichment is found in the radial direction.
Testing leaf water isotope models
Both the SoL and the FG models were tested against our data to determine whether the models could capture the radial enrichment observed in C. esculenta leaves. The SoL model with infinite number of evaporative elements (Farquhar & Gan, 2003) was chosen instead of having a finite number of evaporative elements, as it is most appropriate for leaves in which transpiration occurs in virtually all photosynthetically active tissues. We tested the model against three different l/lmax parameters (example of leaf 5 in Fig. 7): the longitudinal distance llon is taken to be the distance from the petiole along the axis represented by the midrib. The radial distance lrad is the distance from the midrib, measured perpendicularly to it. The total distance is defined as the total distance from the petiole, calculated as
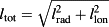 . For the longitudinal distance, the SoL model exhibits no significant correlation with the actual data (R2 = 0.02, P = 0.5 for student t-test for Fig. 7; see Table 4 for the other leaves). In the case of the radial and the total distance models, the SoL shows a stronger correlation with the data (R2 = 0.38, P < 0.001, slope of the best linear regression = 0.27 and R2 = 0.57, P < 0.0001, slope of the best linear fit = 0.78, respectively. See Table 4 for the other leaves), but overestimates the enrichment at the edges. The overestimation of the enrichment at the edges by the desert river version of the SoL model has already been pointed out by Gan et al. (2003) and can be corrected for by including Péclet effects into the model. In addition, the lack of lamina–vein interaction in the SoL model means that it cannot capture the variations observed in large reticulate-veined leaves such as C. esculenta, in which the pattern of enrichment is driven by long dense minor veins.
. For the longitudinal distance, the SoL model exhibits no significant correlation with the actual data (R2 = 0.02, P = 0.5 for student t-test for Fig. 7; see Table 4 for the other leaves). In the case of the radial and the total distance models, the SoL shows a stronger correlation with the data (R2 = 0.38, P < 0.001, slope of the best linear regression = 0.27 and R2 = 0.57, P < 0.0001, slope of the best linear fit = 0.78, respectively. See Table 4 for the other leaves), but overestimates the enrichment at the edges. The overestimation of the enrichment at the edges by the desert river version of the SoL model has already been pointed out by Gan et al. (2003) and can be corrected for by including Péclet effects into the model. In addition, the lack of lamina–vein interaction in the SoL model means that it cannot capture the variations observed in large reticulate-veined leaves such as C. esculenta, in which the pattern of enrichment is driven by long dense minor veins.
| Farquhar–Gan | String-of-lakes | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Leaf number | Model direction | P | Pl | Pr | R2 | P value | Slope | R2 | P value | Slope |
| Longitudinal | 2.1 × 10−5 | 1.0 | 0.7 | 0.32 | * | 1.02 | 0.18 | ns | ||
| 1 | Total | 0.55 | 79 | 1.1 × 10−4 | 0.46 | ** | 0.98 | 0.46 | ** | 0.79 |
| Radial | 0.04 | ns | 0.04 | ns | ||||||
| Longitudinal | 0.024 | ns | 0.098 | ns | ||||||
| 2 | Total | 0.04 | ns | 0.012 | ns | |||||
| Radial | 3.3 × 10−6 | 9.8 | 0.58 | 0.16 | * | 0.40 | 0.15 | * | 0.27 | |
| Longitudinal | 0.16 | ns | 0.04 | ns | ||||||
| 3 | Total | 0.015 | ns | 0.043 | ns | |||||
| Radial | 1.3 × 10−2 | 1.2 | 0.02 | 0.52 | *** | 1.0 | 0.49 | *** | 0.30 | |
| Longitudinal | 0.005 | ns | 0.007 | ns | ||||||
| 4 | Total | 0.025 | ns | 0.014 | ns | |||||
| Radial | 0.08 | ns | 0.09 | ns | ||||||
| Longitudinal | 0.09 | ns | 0.02 | ns | ||||||
| 5 | Total | 0.43 | 1.5 | 8.7 × 10−6 | 0.60 | *** | 0.99 | 0.57 | *** | 0.78 |
| Radial | 1.4 × 10−5 | 1.7 | 0.16 | 0.47 | *** | 1.00 | 0.38 | ** | 0.27 | |
| Longitudinal | 0.001 | ns | 0.0009 | ns | ||||||
| 6 | Total | 2.0 × 10−5 | 9.8 | 0.26 | 0.22 | * | 0.5 | 0.23 | * | 0.44 |
| Radial | 3.7 × 10−6 | 2.0 | 0.10 | 0.67 | *** | 1.00 | 0.56 | *** | 0.34 | |
- R2 is the coefficient of determination for the linear correlation between the model output and the data, and stars denote a significant correlation (ns, not significant, *P < 0.05, **P < 0.01, ***P < 0.001). When a significant correlation is found, the slope of the best linear fit is included. In addition, for the FG model, we give the fitted values of P, Pl and Pr, the lamina radial, the longitudinal and the total radial Péclet numbers, respectively, obtained from Mathematica.
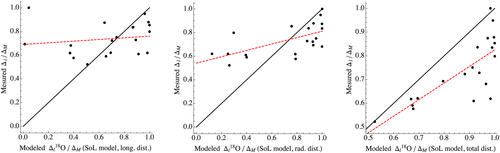
The FG model, by incorporating a much more complex system of leaf water enrichment, is expected to better capture the observed data (example of leaf 5 in Fig. 8). P, Pr and Pl are fitted to the data using Mathematica, and the values obtained for the different Péclet numbers are presented in Table 4. Similarly to the SoL model, there is no significant relation between the longitudinally ordered data and the longitudinal FG model (for the example shown in Fig. 8: R2 = 0.09, P = 0.2, slope of the best linear fit = 0.27), with most of the data being largely underestimated by the model. There is however a significant relationship between the data and the model for both the radial and the total distance case, and unlike the SoL model, the slope of the regression for the FG model is always very close to 1 (radial case: R2 = 0.46, P = 0.001, slope of the best linear fit = 1.00; total distance case: R2 = 0.60, P < 0.0001, slope of the best linear fit = 0.99). The radial model is consistently performing better than the longitudinal model (Table 4), except for leaf 4, which shows no significant pattern in either direction (also visually appreciated in Fig. 5). In leaf 1, the model appears to be strongly influenced by a very depleted sample close to the petiole and a very enriched sample towards the tip. The values of Pl, P and Pr are in agreement with previous values found in maize (Gan et al. 2003). Their relative differences agree with the anticipated patterns, with Pl expected to be the largest of all three Péclet numbers because of the large advection mechanism entraining water in the major veins, while P is expected to be the smallest because it is associated with dominantly diffusive processes in the leaf lamina (Cernusak et al. 2016).
Discussion
Applications of the IM-CRDS technique
The discrepancy observed between IM-CRDS and IRMS analysis suggests that further testing is still necessary before using the IM-CRDS technique as an absolute method (Fig. 3). In particular, it would be interesting to inject extracted leaf water samples onto filter paper for IM-CRDS analysis and compare these results with IRMS. However, the method is appropriate when using isotopically enriched water as tracers, as well as in situations such as this case study, in which the range of variation observed is about one order of magnitude bigger than the range of variation of the difference between IM-CRDS and IRMS. Some of the observed differences between the two techniques might be due to some evaporation in the sampled punch holes used for the IM-CRDS, which did not occur for the whole-leaf extraction used for the IRMS analysis. Freezing the leaves before sampling might help reducing evaporation, although freezing leaves as large as for C. esculenta might present other logistic challenges. Freeze-clamping the leaf using liquid nitrogen cooled instruments might be another alternative.
Understanding the radial isotopic enrichment in C. esculenta
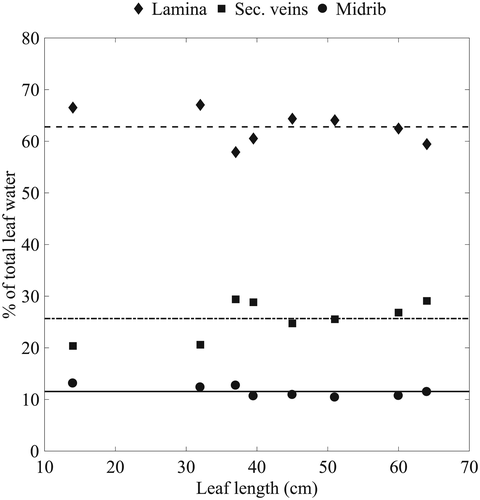
The lack of longitudinal enrichment and the strong radial enrichment gradient observed in Fig. 5 differs from previous results of leaf water isotopic enrichment in monocots (Helliker & Ehleringer, 2000; Gan et al. 2003; Ogee et al. 2007) that showed that the midrib was the main axis of enrichment. For C. esculenta, the observed pattern is likely due to the large proportion of water contained in the veins, in particular, the midrib (Fig. 4). The enrichment from transpiration does not affect the vein water composition, because of the relatively small losses of water compared with the large water content of the vein, as well as the low hydraulic resistance, and therefore large flux in the midrib (Cochard et al. 2004). Using Eqn 10, we calculated that the expected enrichment along the midrib for the order of magnitude of the Péclet numbers obtained (Table 4) should be less than 1 (Supporting Information Fig. S5). This is in agreement with the results from Table 3 that show that no significant enrichment occurs along the longitudinal direction. Indeed, the isotopic enrichment happens along the axes of the secondary veins, where we see an increase in enrichment above of source water between the midrib and the edge of the leaf (Table 3). Radial isotope enrichment has been observed before in banana leaves (Cernusak et al. 2016) and cotton leaves (Gan et al. 2002). In addition, giant leaves similar to C. esculenta have been shown to have a lower major/minor vein ratio, which in turn leads to a decrease in hydraulic supply when moving from the midrib towards the edges (Li et al. 2013). Leaves with a higher minor vein density have an increased effective path length from vein to evaporative site (Holloway-Phillips et al. 2016), therefore increasing enrichment when moving away from the midrib and towards the edges, as also seen in Cernusak et al. (2016).
The lack of longitudinal enrichment can also be linked to (1) the large amount of water inside the midrib, which likely increases advection and decreases the relative effect of back diffusion of enriched water from the secondary veins into the midrib, and (2) the large pressure drop between major and minor veins (Zwieniecki et al. 2002), which inhibits back diffusion from the minor veins into the secondary veins. The longitudinal enrichment observed in maize and grass leaves is related to the very different vein structure of these leaves compared with C. esculenta. In these leaves, the connection between parallel major veins is minimal. Instead, each parallel vein is directly influenced by the back diffusion of enriched water from the lamina adjacent to it. Moreover, unlike C. esculenta where the midrib holds a large portion of the leaf water, the major veins are frequent and numerous in maize (distance between lateral veins: 1.7 mm) and wheat (distance between lateral veins: 0.8 mm (Gan et al. 2003), compared with several centimetres for C. esculenta), therefore decreasing the relative water held in each vein. This might in turn further increase back diffusion effects, therefore intensifying longitudinal enrichment.
Finally, for giant leaves such as C. esculenta, the differences in boundary layer effects cannot be ignored. In low wind conditions such as the courtyard in which the plants were grown for this study, or the understory they belong to in the wild, the leaf boundary layer is expected to be thicker at the centre of the leaf than at the edges (Schuepp, 1993), leading to an increase in transpiration at the edges, causing increased enrichment.
Testing the ability of the SoL and the FG models to capture the observed radial enrichment, we find that the FG model was adapted to reproduce the pattern, but that this was not true of the SoL model. The SoL model has been successful in capturing spatial patterns in grass (Helliker & Ehleringer, 2000), but its limitations were quickly pointed out (Gan et al. 2002; Farquhar & Gan, 2003). The addition of a two-dimensional Péclet effect in the FG model took into account the progressive enrichment of the xylem (Farquhar & Gan, 2003) and was successfully tested on maize leaves (Gan et al. 2003). With the exception of the SoL tested on cotton leaf (Gan et al. 2002), both models have so far only been tested on monocots with longitudinal veins and high major/minor vein ratios like maize (Gan et al. 2003; Affek et al. 2005; Ogee et al. 2007) and grass (Helliker & Ehleringer, 2000; Ogee et al. 2007). Here, we showed that the models can be applied to more complexly veined leaves, such as C. esculenta. Most importantly, the values of the Péclet numbers found give us an insight into water transport mechanisms through the leaf, with advection dominating transport along the midrib, and slow, diffusion processes happening at the interface between secondary veins and the lamina, as well as within the lamina. The slow diffusion of water through the lamina makes the water more prone to enrichment because of the longer residence time of water close to evaporative sites.
Implications
Transpiration patchiness could also in part explain the patterns in isotope composition observed in the results. Indeed, the leaf edges of such large leaves are subjected to very different temperature and wind speed than the rest of the leaf, leading to changes in stomatal conductance. Under high leaf temperature, stomatal conductance in giant leaves has been found to decrease towards the edges of the leaf (Li et al. 2013), likely due to increased vapour pressure deficit at the edges that would drive water losses. This effect would likely be dependent on leaf size, as leaf temperature and boundary layer vary strongly with leaf size. On the other hand, leaf hydraulic resistance does not correlate with leaf size (Sack & Frole, 2006). We anticipate that under moderate leaf temperature, smaller leaves with similar venation patterns will exhibit comparable leaf water isotope distribution.
The isotope composition of the leaf organic matter is directly linked to leaf water isotopes, because of the exchange of oxygen between water and carbonyl groups (Lehmann et al. 2017). However, comparisons of leaf water and dry matter within one leaf have showed that the isotopic enrichment of organic matter is usually less pronounced than that of leaf water (Barbour, Schurr, et al. 2000; Gan et al. 2003; Kimak et al. 2015), possibly because of the influence of sucrose coming from other leaves and used during the early stages of leaf development. Consequently, the pattern of leaf water enrichment observed here is likely to be attenuated in leaf organic matter.
The photosynthetic capacity of leaves has been found to consistently correlate with vein patterns across many different species (Brodribb et al. 2007; Ocheltree et al. 2012). The photosynthetic capacity is also known to correlate with stomatal conductance (Brodribb et al. 2005), and we would therefore expect stomatal conductance to increase radially when moving away from the midrib. Patchiness in stomatal conductance has been widely observed in a number of different species (Terashima, 1992), but the exact mechanism by which the patchiness develops is yet to be fully understood (Mott & Peak, 2006). Some evidence has been found that even if stomata density does not appear to vary within the leaf, guard cell length significantly decreases when moving from the midrib towards the edge of the leaf (Li et al. 2013), which would lead to a decrease in leaf conductance to water vapour (Nardini et al. 2008) and an increase in leaf temperature at the edges. The heterogeneity of produced sugars due to the differences in stomatal conductance would in turn have consequences for sugar loading strategies (Reidel et al. 2009; Fu et al. 2011), an area of research still at its infancy and where new evidence now points at the possibility of multiple loading strategies coexisting within a single leaf (Slewinski et al. 2013).
Conclusion
In this study, we proposed an adapted protocol for the rapid analysis of the spatial patterns of water isotopes in large leaves using the Picarro IM. We applied the protocol to C. esculenta leaves to produce high-quality maps of the leaf isotopes. We found a strong gradient of enrichment in the radial distance, perpendicularly to the midrib, but almost no enrichment along the midrib itself. A study of the spatial patterns obtained showed that the SoL model of enrichment failed to capture the patterns of enrichment, while the more complex Farquhar–Gan predicted the enrichment accurately when looking at the enrichment along the total distance from the petiole, instead of the original longitudinal distance. Our results bring new evidence that isotopic enrichment is occurring along the axis of the secondary veins, but not along the midrib, likely because of the large unenriched pool of water contained in the midrib itself, which dilutes back diffusion of enriched water, as well as the low hydraulic resistance and high water flow in the midrib. We have demonstrated that the Farquhar–Gan could be successful in predicting the enrichment in the complexly shaped leaves of a monocot. Increasing the collection of isotopic maps of complexly shaped monocots and eudicots thanks to the fast rate of technological progress should provide new and exciting information that will improve our understanding of water transport in leaves.
Acknowledgments
The authors thank Todd Dawson and Wenbo Yang from the Center for Stable Isotope Biogeochemistry at the University of California in Berkeley for the IRMS analysis. C.G.S. and K.K.C. acknowledge the financial support of NASA Headquarters under the NASA Earth and Space Science Fellowship Program – grant 14-EARTH14F-241 – and of the Science, Technology, and Environmental Policy Fellowship from the Princeton Environmental Institute. C.G.S. thanks Missy Holbrook and the department of Organismic and Evolutionary Biology at Harvard University for hosting her during part of this work.



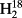 O between veins and the sites of evaporation within leaves?
O between veins and the sites of evaporation within leaves?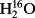 ,
, 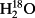 in gases
in gases
