Demographic model selection using random forests and the site frequency spectrum
Abstract
Phylogeographic data sets have grown from tens to thousands of loci in recent years, but extant statistical methods do not take full advantage of these large data sets. For example, approximate Bayesian computation (ABC) is a commonly used method for the explicit comparison of alternate demographic histories, but it is limited by the “curse of dimensionality” and issues related to the simulation and summarization of data when applied to next-generation sequencing (NGS) data sets. We implement here several improvements to overcome these difficulties. We use a Random Forest (RF) classifier for model selection to circumvent the curse of dimensionality and apply a binned representation of the multidimensional site frequency spectrum (mSFS) to address issues related to the simulation and summarization of large SNP data sets. We evaluate the performance of these improvements using simulation and find low overall error rates (~7%). We then apply the approach to data from Haplotrema vancouverense, a land snail endemic to the Pacific Northwest of North America. Fifteen demographic models were compared, and our results support a model of recent dispersal from coastal to inland rainforests. Our results demonstrate that binning is an effective strategy for the construction of a mSFS and imply that the statistical power of RF when applied to demographic model selection is at least comparable to traditional ABC algorithms. Importantly, by combining these strategies, large sets of models with differing numbers of populations can be evaluated.
1 INTRODUCTION
Since before the term “phylogeography” was coined (Avise et al., 1987), the discipline has developed in response to advances in data-acquisition technology (reviewed in Garrick, Bonatelli, & Hyseni, 2015). Recently, phylogeographic investigations have transformed from traditional studies using data from a handful of genetic loci to contemporary studies where hundreds or thousands of loci are collected (Garrick et al., 2015). With the proliferation of next-generation sequencing (NGS) data sets, researchers can now access genetic data to investigate complex patterns of divergence and diversification in nonmodel species. In recent years, the field has increasingly relied upon model-based methods (Nielsen & Beaumont, 2009). These methods are primarily of two classes: those that estimate parameters under a predefined model and those that compare a number of user-defined models. The former type of approach has expanded recently to methods that are applicable to NGS data sets. For example, sequential Markovian coalescent (SMC) approaches can estimate population size histories and divergence times using whole genomes (Terhorst, Kamm, & Song, 2016). However, such methods require that researchers identify a model a priori, and are generally limited to relatively simple models that omit many potentially important parameters, due to computational constraints. For example, while Terhorst et al.'s SMC approach can estimate divergence times and population size changes, it does not incorporate gene flow between lineages. Instead, researchers may wish to compare models that include different parameters and determine which model best fits their data, and this has led to an increase in the use of approximate methods, due to the computational challenges of comparing such complex models. A particularly flexible method in this regard is approximate Bayesian computation (ABC; e.g., Beaumont, 2010), which has been used in a wide range of applications outside of population genomics and phylogeography, including ecology, epidemiology and systems biology (Beaumont, 2010).
ABC methods enable researchers to customize demographic models to their empirical system, and allows formalized model selection (Table 1). Under each prespecified model, parameters of interest, θi, are drawn from a prior distribution, π(θ), specified by the researcher (step 1). Data, xi, are then simulated from the distribution of the data given the parameters, p(x | θi) (step 2), and a vector of summary statistics, S, is calculated from the simulated and empirical data (step 3). The efficiency of ABC is a result of the optimization. Simulations that exceed a user-defined threshold, ε, as measured by the distance function, ρ(S(xi), S(y)), are rejected (step 4) such that the remaining θi constitute the posterior distribution. If data are simulated under multiple models, the proportions of simulations that each model contributes to the posterior distribution correspond to the posterior probabilities of the models under consideration (step 5). ABC was developed in the context of a handful of microsatellite loci (Pritchard, Seielstad, Perez-Lezaun, & Feldman, 1999), but in theory can be extended to any amount of data. In practice, however, extending it to large NGS data sets is difficult due to the “curse of dimensionality” (Blum, 2010). This term describes the situation that occurs as the vector of summary statistics grows large, as would be the case if data were summarized on a locus-by-locus basis for hundreds to thousands of loci, and simulation of data near the vector requires an increasingly large number of simulations, which leads to high error rates. Although ABC has been applied to large NGS data sets (e.g., Roux et al., 2010; Veeramah et al., 2015), these applications have typically required that researchers summarize thousands of loci using a small vector of summary statistics (e.g., in Roux et al., 2010; the average and standard deviation over loci for 11 summary statistics). Summarizing data from 1,000s of loci with dozens of summary statistics results in a substantial loss of the information content of the data and limits the number of models that researchers have statistical power to distinguish. While methods have been suggested to guide researchers in their choice of summary statistics (e.g., partial least-squares transformation; Wegmann, Leuenberger, & Excoffier, 2009), they still result in a large decrease in the information content of the data. Some recent studies have used the bins of the site frequency spectrum (SFS) as a summary statistic for ABC inference (e.g., Boitard, Rodriguez, Jay, Mona, & Austerlitz, 2016; Prates, Rivera, Rodrigues, & Carnaval, 2016; Stocks, Siol, Lascoux, & De Mita, 2014; Xue & Hickerson, 2015), but these approaches have not taken advantages of joint or multidimensional SFS (mSFS). Consideration of the mSFS is necessary to make inferences about multiple populations, but the dimensionality of the mSFS increases as the number of individuals and populations sampled increases such that the number of bins in the joint or multidimensional SFS becomes very large, and the “curse of dimensionality” becomes a limiting factor. One possible solution to the limitations of ABC that would allow researchers to avoid reducing their data to a small number of summary statistics is to follow Pudlo et al. (2015) in replacing the traditional rejection step (steps 4-5; Table 1) with a machine-learning approach such as Random Forests (RF) for model selection.
| Comparison of ABC and RF algorithms for model selection | |
|---|---|
| Both ABC and RF | |
| 1. Draw parameters θi from the prior distribution π(θ). | |
| 2. Simulate data xi from the distribution of the data given the parameters p(x | θi). | |
| 3. Summarize the data using some statistic S(xi). | |
| ABC | RF |
| 4. Reject θi when some function ρ(S(xi),S(y)) measuring the distance between the simulated and observed data exceeds a user-defined threshold. | 4. Train a RF classifier using S(xi) as predictor variables and the model under which the S(xi) were simulated as the response variable. |
| 5. The retained θi approximate the posterior distribution and are used to approximate model posterior probabilities. | 5. Apply classifier to the observed data set to choose the best model. |
| 6. Estimate the probability of misclassification for the observed data using oob error rates. | |
In the RF approach to phylogeographic model selection, the data simulation and summarization steps (Table 1, steps 1-3) remain unchanged from the traditional ABC algorithm. However, instead of using a rejection step that relies on a specified distance function between the observed and simulated data, model selection proceeds using a classification forest. This forest consists of hundreds of decision trees and is trained on the simulated data, with the summary statistics serving as the predictor variables and the generating model serving as the response variable. Once built, this classifier can be applied to the observed data. Decision trees will favour (i.e., vote for) a particular model, and the model receiving the most votes will be selected as the best model. Although this approach does not include the approximation of the posterior probability, in contrast to ABC approaches that utilize a rejection step, uncertainty in model selection can be estimated using the error rates of the constructed classifier. Both experimental (Hastie, Tibshirani, & Friedman, 2009) and theoretical (Biau, 2012; Scornet, Biau, & Vert, 2015) justifications of RF have been offered, with RF shown to be robust both to correlations between predictor variables (here, the summary statistics) and to the inclusion of a large number of noisy predictors. An additional advantage of the RF approach is the reduction in computational effort required for model selection, as >50-fold gains in computational efficiency have been reported (Pudlo et al., 2015).
Although the data simulation and summary statistic calculation steps (steps 2-3 in Table 1) of the ABC algorithm may be extended to NGS data sets from a first-principles argument, issues arise in the implementation. First, the simulation of data scales linearly with the number of loci and thus becomes computationally intensive when the data sets in question are large (Sousa & Hey, 2013). Additionally, calculating a set of traditional summary statistics for each locus for use as summary statistics is impractical given the large number of loci. Although it is possible to calculate certain traditional summary statistics directly from the SFS, rather than on a locus-by-locus basis, such a calculation results in the loss of much of the information content of the data (Sainudiin et al., 2011).
In response to these issues, we explore the use of the multidimensional site frequency spectrum (mSFS; the joint distribution of allele frequencies across three or more populations) for data simulation and summarization in the RF model selection algorithm. The mSFS is a useful summary of the SNP data sets that are frequently collected using NGS methods, and can be considered a complete summary of the data when all polymorphic sites are independent (i.e., unlinked) and biallelic (e.g., Gutenkunst, Hernandez, Williamson, & Bustamante, 2009). Furthermore, the mSFS is expected to reflect demographic events including expansion, divergence and migration (Gutenkunst et al., 2009), although inferences based on the SFS may be inaccurate when too few segregating sites are sampled (Terhorst & Song, 2015). To address this issue, we apply a binning approach to coarsen the mSFS. The use of the mSFS for data summary can also facilitate data simulation; for example, the coalescent simulation program fastsimcoal2 (FSC2) uses a continuous time approximation to calculate the mSFS from simulated SNP data (Excoffier, Dupanloup, Huerta-SÃnchez, Sousa, & Foll, 2013). Here, we propose an approach to phylogeographic model selection that combines the use of a RF classifier with the use of the mSFS to summarize NGS data. We apply this approach to evaluate demographic models in Haplotrema vancouverense, a land snail endemic to temperate rainforests of the Pacific Northwest of North America (PNW).
2 MATERIALS AND METHODS
2.1 Study system and models
2.1.1 Study system
The PNW of North America can be divided into three distinct regions: the Cascades and Coastal Ranges in the west, the Northern Rocky Mountains in the east and the intervening Columbia Plateau (e.g., Figure 1; Brunsfeld, Sullivan, Soltis, & Soltis, 2000). The coastal and inland mountain ranges are characterized by mesic, temperate coniferous forests, but the intervening basin is characterized by a shrub–steppe ecosystem generated by the rain shadow of the Cascade Range that has developed since its orogeny in the early Pliocene. The Okanogan Highlands to the north and the Central Oregonian highlands to the south partially mitigate the ecological isolation of the inland and coastal forests, but the Columbia Plateau has nevertheless been a substantial barrier to dispersal for many of the taxa endemic to these temperate forests (e.g., Carstens, Brunsfeld, Demboski, Good, & Sullivan, 2005). In addition to being influenced by mountain formation, the distributions of taxa in the rainforests of the PNW have likely been impacted by climatic fluctuations throughout the Pleistocene (Pielou, 2008). Glaciers formed and retreated several times during these fluctuations, covering large portions of the northern parts of species’ current ranges. Thus, species may have been entirely eliminated in the northern parts of their ranges or may have survived in small isolated glacial refugia.
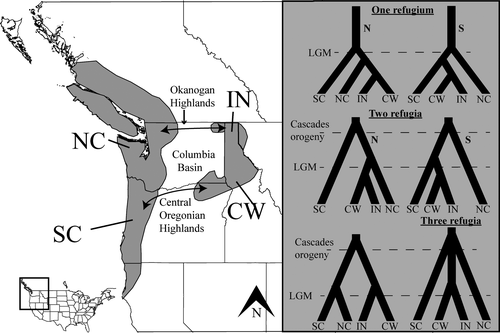
Several biogeographic hypotheses have been proposed to explain the disjunct distribution of the PNW mesic forest endemics (reviewed in Brunsfeld et al., 2000). Here, we explore models that include from one to three glacial refugia (South Cascades, North Cascades and Clearwater River drainages). In one class of models, no refugia persisted in the inland region, and these models posit dispersal to the inland via either a southern or a northern route. In addition, to test whether or not there was population structure present, we evaluated models that included from one to four distinct populations (South Cascades, North Cascades, Clearwater River drainages and northern Idaho drainages). In total, we include 15 demographic models that differed in the number of populations, the number and location of refugia and the dispersal route (Figure 1; Fig. S1). We applied the approach proposed here to Haplotrema vancouverense, a land snail endemic to the PNW. No previous work has used genomic data to investigate the demographic history of this species. However, one study used environmental data to predict that H. vancouverense did not harbour cryptic diversity across the Columbia Basin (Espíndola et al., 2016).
2.2 Specimen collection and data generation
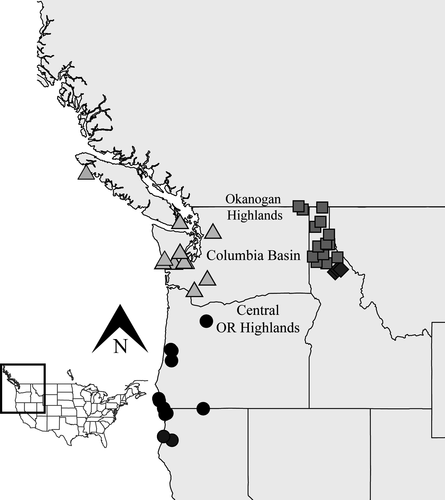
Samples were collected for this study during the spring of 2015 and 2016, in addition to loans provided by the Idaho Fish and Game and museum collections (the Royal British Columbia Museum and the Florida Museum of Natural History). In total, we acquired 77 snails from throughout the range of H. vancouverense (Figure 2; Table S1). This included 31 snails from 24 localities in the northern and southern Cascades and 46 snails from 18 localities in the Clearwater River and northern Idaho drainages. After collection, snails were preserved in 95% ethanol and DNA was extracted using Qiagen DNeasy Blood and Tissue Kits (Qiagen, Hilden, Germany) following the manufacturer's protocol. Prior to library preparation, DNA was quantified on a Qubit fluorometer (Life Technologies), and 200–300 nanograms of DNA was used for library preparation.
Library preparation followed the double-digest restriction-associated DNA (ddRAD) sequencing protocol developed in Peterson, Weber, Kay, Fisher, & Hoekstra, 2012, with modifications. DNA was digested using the restriction enzymes SbfII and MspI (New England Biolabs, USA), and adapters were ligated using T4 ligase (New England Biolabs). Ligated products were cleaned using magnetic beads in a PEG/NaCl buffer (Rohland & Reich, 2012). A subset of the ligation products was amplified and analysed by qPCR using the library quantification kit for Illumina libraries (KAPA Biosystems, USA) to ensure that no adapter had failed to ligate during the ligation step. All ligation products were quantified on the Qubit fluorometer (Life Technologies) and pooled across index groups in equimolar concentrations. 10–20 nanograms of this pool was used in each subsequent PCR. PCRs used the Phusion Master Mix (Thermo Fisher Scientific, USA) and were run for an initial step of 30 s at 98°C, followed by 16 cycles of 5 s at 98°C, 25 s at 60°C and 10 s at 72°C and a final extension for 5 min at 72°C. To minimize PCR bias, reactions were replicated seven times for each index group, and products were pooled within index groups. We analysed 4 μl of this pooled PCR product on a 1% agarose gel. A second clean-up using magnetic beads in a PEG/NaCl buffer (Rohland & Reich, 2012) was performed. Finally, PCR products were quantified on the Qubit fluorometer (Life Technologies) prior to selection for 300- to 600-bp fragments using the Blue Pippin (Sage Science, USA) following manufacturer's standard protocols. The remaining products were quantified using the Qubit fluorometer (Life Technologies) and the Bioanalyzer (Agilent Technologies, USA) before being pooled and sent for sequencing on an Illumina Hi-Seq at the Genomics Shared Resource Center at Ohio State University.
2.3 Bioinformatics
Raw sequence reads were demultiplexed and processed using pyrad (Eaton, 2014). Sites with a Phred quality score <20 were masked with Ns, and reads with more than four Ns were discarded. A minimum of ten reads was required for a locus to be called within an individual. Filtered reads were clustered using the program vsearch v.2.0.2 (https://github.com/torognes/vsearch) and aligned using muscle v.3.8.31 (Edgar, 2004) under a clustering threshold of 85%. Consensus sequences with more than three heterozygous sites or more than two haplotypes for an individual were discarded, and loci represented in fewer than 60 per cent of individuals were discarded. Cut-sites and adapters were removed from sequences using the strict filtering in pyrad.
To deal with missing data when constructing the mSFS, we applied a downsampling approach to maximize the number of SNPs included in the mSFS. A threshold of 50% was set in each population, meaning that only SNPs scored in at least half of the individuals in each population would be used in downstream analyses. For SNPs that exceeded this threshold, we randomly subsampled alleles. We repeated this downsampling approach ten times to create ten different mSFS to be used in downstream analyses in an attempt to account for rare alleles potentially missed during the downsampling procedure. Downsampling followed Thomé and Carstens (2016) and was performed using custom python scripts modified from scripts developed by J. Satler (https://github.com/jordansatler; modified version at https://github.com/meganlsmith). This approach was chosen over including only loci sampled across all individuals because such an approach would have limited the number of SNPs included in the study and has been shown to bias parameter estimates due to the nonrandom sampling of genealogies (Huang & Knowles, 2014).
2.4 Random forest model selection using the mSFS as a summary statistic
2.4.1 Data simulation and summarization
The RF approach to model selection (Figure 3) follows the algorithm for RF model selection presented in Table 1. Parameters were drawn from prior distributions (Table S2) under each of the fifteen models considered (Figure 3; Step 1). mSFS were simulated in FSC2 (Excoffier et al., 2013) under each model, using a folded mSFS with a number of SNPs equivalent to the observed mSFS (Figure 3; Step 2). Monomorphic sites were not considered, and 10,000 replicate mSFS were simulated under each model in FSC2, leading to a total prior of 150,000 mSFS.
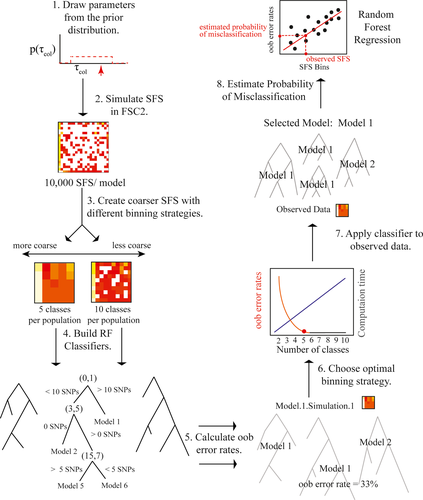
Given the number of populations included as well as the number of SNPs obtained by our sequencing protocol (see Results), use of all bins from the mSFS could result in limited coverage across the mSFS and thus to poor estimates of the mSFS; therefore, we used a custom Python script (https://github.com/meganlsmith) to coarsen the mSFS (Figure 3, Step 3). For example, for the “quartets” data set, SNPs were categorized based on which quartile they belonged to in each population, and all combinations of quartiles across populations were used as bins for a final data set consisting of 256 bins. In this example, the first bin would consist of SNPs occurring at a frequency <¼ in all four populations. We tested other binning strategies with the number of classes ranging from three to ten, enabling a joint exploration of the coarseness of the mSFS, the accuracy of model selection and the computational requirements of the classification procedure.
2.4.2 Choosing the optimal binning strategy
To determine the optimal binning strategy, eight RF classifiers were constructed using the simulated data (i.e., Figure 3, Step 4), one at each level of mSFS coarseness considered here (i.e., 3–10 classes per population). Each classifier was constructed with 500 trees using the r package “ABCRF” (Pudlo et al., 2015), with the bins of the mSFS treated as the predictor variables and the generating model for each simulated data set treated as the response variable. At each node in each decision tree, the RF classifier considers a bin of the mSFS and constructs a binary decision rule based on the number of SNPs in the bin. When this classifier is applied to other data sets, it makes decisions at each node until it reaches a leaf of the decision tree, which in this instance is a model index. When a leaf is reached, the decision tree is said to “vote” for the model index assigned to that leaf. Each decision tree is constructed in reference to only a portion of the training data set, minimizing the correlation between decision trees. Prior to construction of the random forest, columns in which there was no variance in the entire prior (e.g., bins that contained no SNPs for any of the simulated data sets) were removed from the prior. These same columns were removed from the observed data set.
Because only a portion of the prior is used in the construction of each decision tree in RF classification, the error rate of the classifier can be assessed using the “out-of-the-bag” (oob) error rates (Figure 3; Step 5). Oob error rates are calculated by considering only decision trees constructed without reference to a particular element of the prior. For each simulated mSFS, we used a smaller classifier that consisted only of trees constructed without reference to the mSFS in question. We applied this classifier to the simulated mSFS and calculated the proportion of trees that voted for an incorrect model; this is the oob error rate for the simulated mSFS. To choose the optimal binning strategy (Figure 3, Step 6), we plotted the average misclassification rate and the computation effort required as a function of the binning strategy.
2.4.3 Model selection and the misclassification rate
After the optimal binning strategy was determined, we applied the corresponding classifier to the observed data (Figure 3, Step 7). The “predict” function in the “abcrf” package was used to select the best model for the observed data, which was the model receiving the most votes (i.e., the model selected by the largest number of decision trees). One limitation of the RF approach is that the number of votes allocated to different models has no direct relationship to the posterior probabilities of the models and may be a poor measure of the probability of misclassification for the observed data. Following Pudlo et al. (2015), we estimated the probability of misclassification in a second step by regressing over the selection error in the prior to build a regression RF, in which the oob error rate is the response variable and the mSFS bins are the predictor variables. We then applied this RF to the observed data to estimate the probability of misclassification for the observed model (Figure 3; Step 8), again using the “predict” function in the r package “abcrf” (Pudlo et al., 2015). A Python script that simulates data, constructs a reference table, builds a classifier, selects the best model for the empirical data and calculates error rates and the probability of misclassification using FSC2 and the r package “abcrf” is available on github (https://github.com/meganlsmith).
To assess the power of the RF approach, we simulated 100 mSFS under each of the 15 models (Fig. S1), drawing priors from the same distributions used in model selection (Information on Prior Distributions; Table S2). We used custom python scripts (https://github.com/meganlsmith) to coarsen the simulated mSFS using five classes. We then applied the RF classifier built from the quintets prior to each of the simulated data sets using the “predict” function in the r package “abcrf” (Pudlo et al., 2015) and recorded which model was selected for each replicate.
2.5 AIC-based model selection
To validate the results of our model selection using RF, we compared the above results to a commonly used information theoretic approach to phylogeographic model selection with NGS data sets (e.g., Carstens et al., 2013), where model selection in FSC2 followed the procedure suggested in Excoffier et al. (2013). FSC2 maximizes the composite likelihood of the observed data under an arbitrary number of models, and Akaike information theory can then be used to select among several tested models. The Brent algorithm implemented in FSC2 was used for parameter optimization, with parameter optimization replicated 100 times. For each replicate, 100,000 simulations were used for the calculation of the composite likelihood and 40 cycles of the Brent algorithm were used for parameter optimization. The maximum-likelihood estimates for the parameters were then fixed, and the likelihood was approximated for each model across 100 different replicates. The maximum likelihood across these 100 replicates for each model was used in model comparison. AIC scores were then calculated and converted to model weights as in Excoffier et al. (2013).
To assess the power of FSC2 to distinguish among the tested models, we used the same 100 simulated mSFS as in the RF power analysis. We used 100,000 simulations for the calculation of the composite likelihood, and 40 cycles of the Brent algorithm were used for parameter optimization. The likelihood was approximated for each model and used in model comparisons. AIC scores were calculated and converted to model weights as in Excoffier et al. (2013), and we recorded which model was selected for each replicate. Due to computational constraints, we did not perform the replication recommended for model selection in FSC2, as was done for the observed data. We also conducted a conventional ABC analysis (see Supporting Information).
3 RESULTS
3.1 Bioinformatics
After the filtering thresholds were applied, 1,943 loci were called in 77 individuals. This resulted in 1,716 unlinked biallelic SNPs and 5,996 total variable sites. When only unlinked SNPs were used, the downsampling approach resulted in data sets including SNPs from 12 alleles per locus from the Clearwater drainages, 14 alleles per locus from the North Cascades, 34 alleles per locus from the northern inland drainages and 17 alleles per locus from the South Cascades. These data sets included between 879 and 908 SNPs.
3.2 RF model selection with the mSFS as a summary statistic
3.2.1 Oob error rates and optimal binning strategy
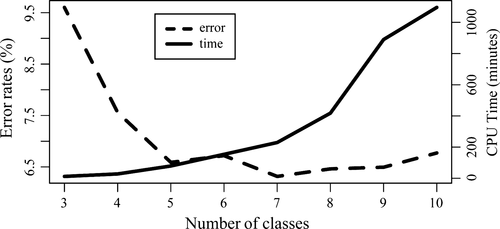
Oob error rates decreased as the number of classes used to build the coarse mSFS increased, until the number of classes reached five (Figure 4). The error rate is no worse for five as opposed to a greater number of classes, and the computation effort increases considerably with larger numbers of classes (Figure 4). We therefore determined that five classes represented the optimal binning strategy for our data, and as such present results only from the “quintets” data set below. Using the “quintets” data set, the overall prior error rate, calculated using oob error rates, was 6.59 per cent. Error rates varied across models (Fig. S2) and were highest between those models for which the only difference was whether dispersal occurred via a northern or a southern route (Table 2). Misclassification across models with different numbers of populations was less common, and data sets were never classified as belonging to a model having a different number or identity of refugia than the generating model (Table 2). Error rates appeared to plateau in relation to the number of trees used to construct the model, suggesting that more trees did not improve the predictive ability of the RF classifier (Fig. S3).
| Misclassification probabilities | |
|---|---|
| Description of Misclassification | Probability |
| Misclassified as model with a different number of populations | 1.44% |
| Misclassified as model with different number of refugia | 0.00% |
| Misclassified as model with different dispersal route | 4.95% |
3.2.2 Model selection with random forests and AIC-based model selection
In analyses of the “quintets” data set, RF selected the four-population model that included recent southern dispersal to the inland region (Figure 5: Model 1; Table 3). The next best model was similar, but with colonization of the inland region via a northern instead of a southern route (Figure 5: Model 2; Table 3). The probability of misclassification of the best model was estimated to be 0.3514 (corresponding to an approximated posterior probability of 0.6846). The best model did not change between data sets built with different binning strategies, but the probability of misclassification varied across data sets (Table 3). To account for variation in the downsampling procedure, ten downsampling replicates were analysed using five categories per population to bin the data; the best model did not change between data sets, but the misclassification probability of the best model varied across data sets (Table S3). This analysis (constructing the RF from the prior, calculating oob error rates and applying the RF classifier to the observed data) was run on six processors with 24GB RAM and used 78.9 min of CPU time. Under the likelihood-based approach, the best model was a four-population model of recent dispersal to the inland with colonization via a northern route (Figure 5: Model 2; Table 4). The next best model was the same, except that colonization of the inland occurred via a southern route (Figure 5: Model 1; Table 4). This analysis required more than 1,500 CPU hr, largely due to the replication required in calculating the composite likelihood.
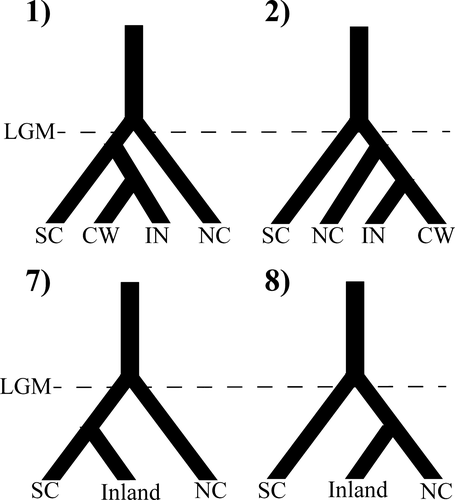
| Results of ABC RF Model Selection | |||||
|---|---|---|---|---|---|
| # Categories | Model 1 | Model 2 | Model 7 | Model 8 | 1-Pr(Misclassification) |
| 3 | 234 | 121 | 80 | 45 | 0.6241 |
| 4 | 252 | 132 | 44 | 28 | 0.7292 |
| 5 | 212 | 109 | 72 | 52 | 0.6846 |
| 6 | 168 | 124 | 74 | 55 | 0.6933 |
| 7 | 170 | 100 | 56 | 43 | 0.6565 |
| 8 | 194 | 131 | 48 | 31 | 0.6546 |
| 9 | 134 | 129 | 61 | 59 | 0.6927 |
| 10 | 164 | 131 | 65 | 40 | 0.6364 |
| Model probabilities for the four best models | |||||||
|---|---|---|---|---|---|---|---|
| Populations | Refugia | Dispersal Route | K | LnLhood | AIC | Δi | wAIC |
| 4 (NC, SC, NID, CW) | SC | South | 8 | −7,351 | 14,718 | 3 | 0.173 |
| 4 (NC, SC, NID, CW) | SC | North | 8 | −7,349 | 14,715 | 0 | 0.827 |
| 3 (NC, SC, NID+CW) | SC | South | 7 | −7,705 | 15,423 | 708 | 0.000 |
| 3 (NC, SC, NID+CW) | SC | North | 7 | −7,712 | 15,438 | 723 | 0.000 |
- NC, North Cascades; SC, South Cascades; NID, Northern Inland Drainages, CW, Clearwater.
3.2.3 Power analyses in random forests and AIC-based model selection
In the power analysis for the RF approach, the overall error rate was 7.67 per cent (Table S4). The highest error rates were for models 1 and 2 (Fig. S1) at 22 and 42 per cent, respectively. The power analysis in RF used approximately ~285 CPU hr.
In the power analysis for the FSC2 approach, the overall error rate was 3.33 per cent (Table S4). The highest error rates were for models 1 and 2 at 10 and 15 percent, respectively. Although we were not able to perform a full power analysis (with fixed MLE parameter estimates and replicates to approximate the composite likelihood of each model) due to computational constraints, the partial power analysis used approximately 2,205 resource units (~22,205 CPU hr). Model selection results of the conventional ABC analysis were similar, but our simulations suggested that the power to detect the best model was lower overall (Supporting Information).
4 DISCUSSION
4.1 Model selection using random forests
The combination of RF classification and the binning strategy for mSFS data appear to perform well in the context of phylogeographic model selection, and the use of the RF algorithm for model selection in place of a traditional ABC approach allowed us to circumvent many of the issues associated with using a traditional ABC approach on NGS data sets, with error rates much lower than those obtained when a classical ABC approach was applied to this data (ABC error rate = 30%, Supporting Information). The low error rate obtained in the RF approach to model selection (6.59%) can likely be attributed both to the more efficient approach to model selection and to the more complete summary of the data provided by the mSFS. Computational requirements (Figure 4) were much less than those of FSC2. In comparison with AIC-based methods, RF model selection is favourable in certain situations. Although AIC-based methods, such as FSC2, have proven powerful in certain contexts (Excoffier et al., 2013), the power of such analyses when applied to the smaller NGS data sets frequently collected using protocols such as ddRAD sequencing (Peterson et al., 2012) on nonmodel organisms has not been thoroughly evaluated in most studies using FSC2. Particularly when the number of bins in the mSFS greatly exceeds the number of SNPs, as is likely to occur as the number of populations increases, it may be inappropriate to use the full mSFS due to the reduction in the accuracy of parameter estimations (and thus of the likelihood calculation) that such data sets are expected to provide, as inferences based on SFS with small-to-moderate numbers of SNPs have been shown to be inaccurate (Terhorst & Song, 2015). Although FSC2 and the RF approach had similar power to distinguish among the models we tested, due to the computational requirements, it was difficult to assess the power of FSC2 given the data collected. The approach proposed here has the advantage of oob error rates, which enable an efficient evaluation of the power of the method given the collected data. Then, researchers can generate coarser mSFS according to the characteristics of their data and system.
While the RF approach has several advantages for model selection, joint estimation of parameters is not straightforward (but see Raynal et al., 2017). Additionally, as the monomorphic cell (the cell with counts of sites without variation) of the mSFS is not used in our approach, the timing of demographic events is relative rather than absolute. For cases when researchers prefer to test explicit a priori hypotheses based on geological data (e.g., Carstens et al., 2013), other approaches (including FSC2) should be preferred. In general, we suggest that parameter estimation using methods such as FSC2 using the model(s) selected following this approach as well as all available SNPs is likely the most effective strategy for nonmodel systems.
4.2 Future directions
Model selection using RF has many potential advantages that future investigations should explore. Here, we highlight two such possibilities: (i) testing a large number of models and (ii) species delimitation. Using RF, we were able to test a moderate number (N = 15) of demographic models without sacrificing our ability to distinguish between models. The error rate associated with model selection using traditional ABC algorithms appears to increase as the number of models increases, particularly when more than four models are included (Pelletier & Carstens, 2014). Our results suggest that it may be possible to compare a larger number of models using the RF model selection approach, allowing researchers to make fewer assumptions about the historical processes that may have influenced their focal organisms. The out-of-the-bag error rates generated in this approach allow researchers to assess whether they can distinguish among the models tested, given their data, and should thus prevent researchers from testing more models than they have the power to differentiate among. As with other approaches to demographic model selection, we were still limited in the number of models that we could compare, and our results can only highlight the best model among those tested. Although assessing model fit can help researchers understand how well their data fit a model, such an approach is not straightforward with the RF approach.
Additionally, we were able to compare models that included different numbers of populations with a low misclassification rate (1.44%). It has been challenging to use ABC in such cases because some of the most useful summary statistics are based on comparisons within and between populations (e.g., Hickerson, Dolman, & Moritz, 2006), and the summary statistic vectors used in such a comparison would necessarily have different dimensionalities. Here, we were able to circumvent this issue by calculating the mSFS as if there were four populations, regardless of the number of populations used to generate the SNP data. Our results suggest that the model selection approach implemented here could be used for population and potentially species delimitation. Additionally, although we focused on Random Forests here, other machine-learning algorithms have been used to infer demographic histories (e.g., Deep Learning; Sheehan & Song, 2016), and future work should investigate the use of these algorithms in conjunction with the binned mSFS.
4.3 Empirical results
Results from both ABC (Table 3) and FSC2 (Table 4) suggest that H. vancouverense survived in one or more refugia in the south Cascades throughout the Pleistocene glacial cycles. A previous investigation using environmental and taxonomic data to make predictions concerning the evolutionary histories of organisms predicted that H. vancouverense colonized the inland after the Pleistocene (Espíndola et al., 2016), and the results presented here support this prediction. Following glaciation, H. vancouverense expanded its range north to the North Cascades and east to the Northern Rocky Mountains. Our results were incongruent across the ABC and FSC2 analyses in regard to whether H. vancouverense colonized the Northern Rockies via a northern route across the Okanogan highlands or via a southern route across the Central Oregonian highlands. In our RF analysis, these two models are misclassified at proportions of 0.19 (southern route classified as northern route) and 0.18 (northern route classified as southern route), based on out-of-the-bag error rates. In the power analysis for FSC2, these models were misclassified 10 and 15 percent of the time (Power Analysis in FSC2; Table S5), and in the power analysis for the RF approach, these two models were misclassified 22 and 42 per cent of the time. In combination with the ambiguity across methods, this suggests that we have limited power to distinguish between these two models, given the data collected here.
5 CONCLUSION
Our results indicate that binning can be an effective strategy for the summarization of the mSFS. This comes at an important time, when SNP data sets from hundreds to thousands of SNPs are being collected from a variety of nonmodel species. Our work demonstrates that, using the binning strategy together with the RF strategy for model selection, researchers can make accurate phylogeographic inferences from NGS data sets that may be too small for accurate estimation of the true mSFS. Finally, we show that by allowing researchers to evaluate a larger number of models and to compare models with different numbers of populations, RF model selection could have important implications for the future of model-based approaches.
ACKNOWLEDGEMENTS
Funding was provided by the US National Science Foundation (DEB 1457726/14575199). MLS was supported by a NSF GRFP (DG-1343012) and a University Fellowship from The Ohio State University. We thank the Royal British Columbia Museum and the Florida Museum of Natural History for providing samples. We thank Michael Lucid of Idaho Fish and Game for donations of samples and the Ohio Supercomputer Center for computing resources (allocation grant PAS1181-1). We thank the Carstens laboratory for comments that improved this manuscript prior to publication. We would also like to thank Graham Stone and three anonymous reviewers for helpful comments during the review process.
DATA ACCESSIBILITY
Raw reads, the parameters used for data processing and a full SNP data set are available on Dryad (https://doi.org/10.5061/dryad.2j27b). Scripts developed as a part of the work presented here are available on github (https://github.com/meganlsmith).
AUTHOR CONTRIBUTIONS
M.L.S and B.C.C designed the study. Funding and support were obtained by B.C.C, D.C.T and J.S. M.L.S and M.R collected samples. M.L.S collected genomic data, performed genetic analyses and wrote the article. All authors edited the article and approved the final version of the article.




