Urban land use limits regional bumble bee gene flow
Abstract
Potential declines in native pollinator communities and increased reliance on pollinator-dependent crops have raised concerns about native pollinator conservation and dispersal across human-altered landscapes. Bumble bees are one of the most effective native pollinators and are often the first to be extirpated in human-altered habitats, yet little is known about how bumble bees move across fine spatial scales and what landscapes promote or limit their gene flow. In this study, we examine regional genetic differentiation and fine-scale relatedness patterns of the yellow-faced bumble bee, Bombus vosnesenskii, to investigate how current and historic habitat composition impact gene flow. We conducted our study across a landscape mosaic of natural, agricultural and urban/suburban habitats, and we show that B. vosnesenskii exhibits low but significant levels of differentiation across the study system (FST = 0.019, Dest = 0.049). Most importantly, we reveal significant relationships between pairwise FST and resistance models created from contemporary land use maps. Specifically, B. vosnesenskii gene flow is most limited by commercial, industrial and transportation-related impervious cover. Finally, our fine-scale analysis reveals significant but declining relatedness between individuals at the 1–9 km spatial scale, most likely due to local queen dispersal. Overall, our results indicate that B. vosnesenskii exhibits considerable local dispersal and that regional gene flow is significantly limited by impervious cover associated with urbanization.
Introduction
Pollinators facilitate reproduction for an estimated 87% of all flowering plant species (Ollerton et al. 2011) and protect global food security by increasing the quantity, quality and stability of over 60% of world crops (Klein et al. 2007; Garibaldi et al. 2011). Although humans depend on pollination services for many food, fibre and forage plants, wild pollinators face a number of threats in human-altered landscapes, including the degradation of essential nesting habitat (Winfree et al. 2011). Nesting and dispersal across landscapes is essential for gene flow, which can prevent inbreeding and maintain adaptive genetic variation (Wright 1931). Despite this fact, little is known about native pollinator gene flow processes, especially for bees, one of the most important and effective pollinators (Roubik 1995). Furthermore, with the recent worldwide growth in urban and suburban agriculture (Hodgson et al. 2011), it is increasingly important to understand the gene flow processes of native bees in urban and suburban landscapes. Despite this fact, bee gene flow processes remain poorly understood (reviewed in Packer & Owen 2001), especially in human-altered landscapes. Given that declines in native pollinator communities within human-altered landscapes may have occurred since 1980 (Biesmeijer et al. 2006; Potts et al. 2010), and possibly earlier (Kevan 1975), it is essential to build an understanding of human land use impacts on native bee gene flow processes across temporal and spatial scales.
In particular, bumble bees (Bombus sps.) are one of the most important and effective native pollinators on a per visit basis, facilitating reproduction for a large number of both wild and cultivated plants (e.g. Stubbs & Drummond 2001; Kremen et al. 2004). Bumble bees are often considered ‘keystone’ species within plant—pollinator communities because of their generalist behaviour, whereby they pollinate both rare and abundant plant species (Goulson 2003; reviewed in Goulson et al. 2008). Because of this high level of interaction with the plant community, studies have suggested that the loss of bumble bees within plant—pollinator networks could lead to marked declines in native plant reproduction and long-term losses in community-level plant diversity (Memmott et al. 2004). Unfortunately, bumble bees are often the first bee species to be extirpated with human land use intensification (Larsen et al. 2005) and have exhibited population declines across a wide range of geographic regions (reviewed in Goulson et al. 2008). Studies have found that at least four North American species have exhibited sharp declines in relative abundance and substantial range contractions in the past 20–30 years (Cameron et al. 2011); however, interestingly, these species also exhibit patterns of extensive gene flow across continental scales (>1000 km) (e.g. FST = 0.007 and Dest = 0.044 for B. pensylvanicus, Cameron et al. 2011; Lozier et al. 2011). Given this discordance, these past findings suggest that population genetics examined at continental scales may not capture recent changes in bumble bee gene flow expected to accompany abundance declines.
In contrast, we posit that genetic differentiation patterns measured at regional (≈200 km) scales may be more indicative of local dispersal patterns and could provide insight into local barriers to bumble bee dispersal, such as topographic features and human-altered habitat. Unlike bumble bees in the United Kingdom, where regional-scale differentiation across and within islands is largely attributed to the presence of large water bodies (Darvill et al. 2010; Goulson et al. 2011), North American bumble bee populations are relatively land-locked, though they may be similarly influenced by topographic variation (as in B. bifarius in Lozier et al. 2011). One unexplored potential dispersal barrier to bumble bee gene flow is human land use, which has changed dramatically in the United States over the last century (Sisk 1998), with greater human-development and suburbanization across both eastern and western coasts, and greater agricultural abandonment and forest regeneration in many north-eastern states (Brown et al. 2005). Prior to 1950, land use change in the United States was largely comprised of wildland conversion to agriculture, urban and suburban uses. Since 1950, suburban fringe areas have grown rapidly (Ullman 1954), as have exurban areas, which include the development of housing and transportation infrastructure in rural areas (Brown et al. 2005). Given that impervious land cover limits bumble bee nesting densities (Jha & Kremen 2013), it is possible that the recent expansion of urban, suburban and exurban areas may also pose barriers to the North American bumble bee gene flow. We conjecture that regional gene flow for North American bumble bees may be limited by historic (1900s), recent-past (1980s) and/or contemporary (2000s) land use. Though a large number of pollinator species have exhibited declines within human-altered landscapes in the past century (reviewed in Winfree et al. 2011), virtually nothing is known about the role of historic, recent-past or contemporary land use in mediating pollinator gene flow and dispersal.
Finally, despite the relevance of local dispersal to ecology and conservation (reviewed in Koenig et al. 1996; Broquet & Petit 2009), little is known about patterns of genetic structure amongst pollinator populations across fine spatial scales (1–20 km). Evidence of local dispersal can be gathered by investigating the ‘relatedness’, or the degree of shared genotypes, between individuals over small spatial scales (e.g. Loiselle et al. 1995). Bumble bee relatedness patterns are particularly interesting because they provide insight into queen and male dispersal; this is because bumble bees are social, where workers do not usually reproduce, thus only the dispersal patterns of new queens and males contribute to annual gene flow. Furthermore, because new spring queens carry the male gametes in their spermatheca when they are dispersing to nest sites, fine-scale relatedness patterns in bumble bees are strongly influenced by queen dispersal patterns. In other words, if male bumble bee dispersal movements were limited, but queen dispersal movements extensive, spatial genetic structure would be low; in contrast, if male dispersal movements were extensive but queen dispersal movements largely local, then spatial genetic structure would be strong across local scales. This follows the same logic that seed-dispersal, not pollen-dispersal, is most important for explaining plant spatial genetic structure given that seeds (2N) carry the full genetic information of an individual compared with the gamete pollen grain (1N) (Dick et al. 2008). Given these biological attributes, the genetic signature of relatedness at fine scales could provide unique insight into bumble bee queen dispersal patterns.
In this study, we examine the genetic structure of the yellow-faced bumble bee, Bombus vosnesenskii, to determine if human land use influences regional (200 km) genetic differentiation patterns and to investigate whether bees exhibit fine-scale (1–20 km) relatedness indicative of local dispersal. While continental-scale studies suggest that B. vosnesenskii is not exhibiting declines in relative abundance (Cameron et al. 2011), at regional scales, this species is often the first to be extirpated with increasing human land use intensity (Larsen et al. 2005). Furthermore, B. vosnesenskii is one of the most effective native pollinators for agricultural crops (Kremen et al. 2002) and exhibits some of the same life history traits shared by many Bombus species, such as univoltine reproductive cycles, high foraging demands, and subterranean nesting (Thorp et al. 1983). We develop our hypotheses based on recent research that has highlighted (i) a decline in the relative abundance of North American bumble bee species since 1980 (Cameron et al. 2011); (ii) lower bumble bee nesting densities in habitats with higher impervious cover (Jha & Kremen 2013); and (iii) evidence of local queen dispersal (<8 km), in addition to likely long-distance events (Lepais et al. 2010). Specifically, we hypothesize that (i) recent land use (since 1980) will best explain regional genetic differentiation compared with historic (1900s) and contemporary (2000s) land use; (ii) genetic differentiation will be greatest between bumble bees separated by large areas of impervious land cover; and (iii) bumble bees will exhibit high levels of relatedness at the 1–5 km spatial scale, indicative of local queen dispersal. We test these hypotheses using field surveys, land use maps and regional and fine-scale population genetic analyses.
Methods
Study species and region
This study was conducted across the Delta bioregion of California, an area that has experienced recent expansions in agriculture, suburbanization and exurbanization (39.2918–123.7509 NW corner, 37.8445–119.6805 SE corner) (Fig. 1A). Bees were sampled in eight study regions that ranged 0–690 m elevation, were separated by 3.89–118.25 km (mean 49.76 ± 28.09 km) and varied in current and past land uses (Fig. 1A-D, Fig. S1, Supporting information). Specifically, between the study regions, the landscape is currently comprised of approximately 16% agricultural land, 24% urban/suburban/exurban land, 20% grassland and pasture and 40% wooded habitat. We examined the influence of contemporary (2000s), recent-past (1980s) and historic (1900s) land use patterns on genetic structure by utilizing land cover data for the bioregion from the National Land Cover Database (NLCD, http://www.mrlc.gov/) for 2006, 1987 and an estimated map of 1900 (described below) (Fig. 1B–D). The NLCD provides land classification data at 30 m resolution, and 11 different land use types were classified for the study region (1. open water, 2. high intensity commercial/industrial/transportation land with >50% impervious cover, 3. moderate intensity commercial/industrial/transportation with 20–49% impervious cover, 4. crops, 5. Low-intensity developed space with <20% impervious cover, 6. bare ground, 7. disturbed grassland, 8. pasture, 9. forest, 10. woodland and 11. scrubland). We assessed the influence of elevation using a digital elevation map of the study region, available through the National Elevation Dataset (NED, http://ned.uspatial genetic structure.gov/).
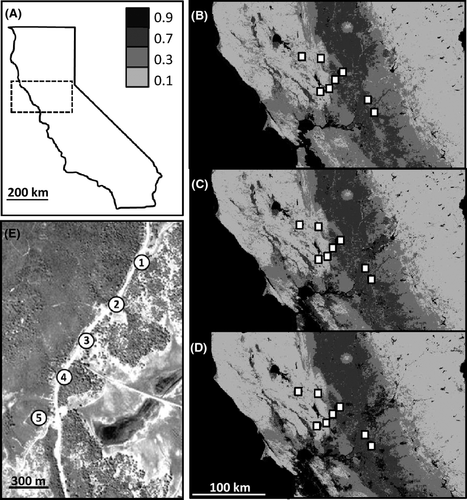
We estimated land use for 1900 by re-classifying the 1987 map to convert high-intensity urban, suburban and exurban land to low-intensity developed land, given that paving of major roads and highways was less extensive pre-1950 (Norstrand 1992) and the size of exurban areas was much smaller or non-existent pre-1950 (Brown et al. 2005). Specifically, we converted ‘high-intensity commercial/industrial/transportation land with >50% impervious cover’ to ‘low-intensity developed land with <20% impervious cover’ (Fig. 1C). Given the long history of crop cultivation and human settlement in California (Vaught 1999), all remaining human-altered land use types (e.g. pasture and cultivated crop) and natural land use types (e.g. forest and grassland) from the 1987 map were unaltered for the 1900 map estimate. This map is supported by two independent data sets. First, based on surveys conducted between 1900 and 2000, it is evident that suburban and exurban populations in the San Francisco Bay area increased by more than 10 times in this period (Barbour 2002). Second, comparing land use maps of the study region from 1973 and 2000, it is apparent that the extent of agricultural area remained relatively constant, while the extent of exurbanization in the study region increased by more than 30% (Sleeter et al. 2011).
Sampling and genotyping
Within each of the eight study regions, an average of 20.8 (±2.18 SE) bees were collected at each of five equidistant sites located along a 1.2 km linear transect (approximately 300 m apart), for a total of 40 sampling sites (Fig. 1E). These sampling points were utilized for examining fine-scale genetic structure (1–20 km) and allowed for regional pooling required for comparison with other studies (e.g. Cameron et al. 2011). DNA was extracted from the tarsal segment of each bee sample using the HotShot protocol (Truett et al. 2000) and was screened at 13 microsatellite loci, B96, B100 and B119 (Estoup et al. 1995), and BT33, BT43, BT65, BT72, BT124, BT125, BT128, BT131, BT132 and BT136 (Stolle et al. 2009), which are located on 10 different chromosomes, based on the B. terrestris genome v1.1 (Stolle et al. 2011). Multiplex polymerase chain reactions (PCRs) were performed in a final volume of 20 μL, containing approximately 2 ng of DNA, 2 μL of 10 × PCR buffer, 1.5 mm MgCl2, 300 μm of each dNTP, 1 U of Taq Polymerase and 0.25 μm of each primer. The thermal cycle began with a 5-min denaturation step at 95 °C, and was followed by 37 cycles: 30 s at 94 °C, 60 s at the locus-specific annealing temperature and 30 s at 72 °C, followed by a final extension at 72 °C for 20 min. One primer from each pair was labelled with FAM, HEX or ROX, and genotyped on an ABI 3730 Sequencer. Alleles were scored manually using GENEMARKER® (Softgenetics) and only samples with >8 genotypes scored per individual were included in the analyses.
Colony identity, Hardy–Weinberg equilibrium (HWE), allelic richness & STRUCTURE analyses
First, full siblings collected from each study region were assigned to colonies using COLONY 2.0 (Wang 2004) where the genotyping error rate was set to 0.001, based on replicate genotyping of a random subset of individuals and error rates documented in previous studies (Knight et al. 2005). Since the majority of bumble bee species are assumed to be monandrous (Estoup et al. 1995), and because we are interested in the genetic structure unrelated to full sib-ship, we randomly removed colony-mates (or full siblings) so that only one representative per colony remained in the data set. This resulted in six sites with <10 representatives (colonies). Second, we did not want our analyses of differentiation to be biased by sample size, therefore we removed the six sites that had fewer than 10 representatives/colonies and also capped the number of representatives/colonies per site to 20. Thus, in cases where more than 20 unique colonies were collected per site (13 sites), we randomly selected individuals to exclude from the analyses, for a total of 542 individuals representing 542 unique colonies across 34 sites (561 site pairs). Data regarding colony densities and intra-colony movement patterns are discussed elsewhere (Jha & Kremen 2013).
The probability of null alleles was calculated using the software Micro-Checker (van Oosterhout et al. 2006). Deviations from HWE and linkage disequilibrium (LD) were tested in GENEPOP v 4.0.10 (Raymond & Rousset 1995) with 1000 dememorizations, 100 batches and 1000 iterations per batch using the Markov chain approximation for the exact tests and likelihood-ratio tests respectively. We estimated the allelic richness (AR) per region using rarefaction, standardized to 10 gene copies per site, in HP-RARE (Kalinowski 2005). We estimated heterozygosity using Nei's gene diversity (HE; Nei & Kumar 2000) (Table S1, Supporting information). Regions were examined for evidence of population bottlenecks using the program BOTTLENECK (Piry et al. 1999) with 1000 replications and under the assumption of the Stepwise Mutation Model and the Two-Phase Mutation Model, instead of the Infinite Alleles Model, which can be less conservative in estimates of heterozygote excess (Luikart & Cornuet 1998). Significance was assessed using Wilcoxon's test. We also examined population structure using the clustering method STRUCTURE 2.3.3 (Falush et al. 2003) which assumes that individuals comprise K unknown populations to which individual or fractional genotypes can be assigned. We allowed for correlated allele frequencies and admixture with 20 000 burn-in steps and 100 000 samples, with 10 iterations for each K.
Regional scale differentiation
We calculated pairwise and overall genetic differentiation, FST, using weighted analysis of variance (weighted for sample size) in the software FSTAT (Goudet 1995). We also calcuated Jost's Dest (Jost 2008), another estimate of differentiation especially appropriate when heterozygosity levels are high, with the software DEMEtics (Gerlach et al. 2010) within the R platform. For both calculations, we estimated the 95% confidence intervals using 10 000 bootstrap repetitions. We chose to examine pairwise FST and Dest across sites (561 site pairs) and across the eight regions (28 region pairs), the latter conducted to facilitate comparison between our study and others’.
We hypothesize that bee gene flow is dependent on nesting habitat because bumble bee queen dispersal involves at least two nesting steps, dispersal from the natal colony to a winter hibernaculum and then dispersal again from the hibernaculum to a final nest site (Thorp et al. 1983; Thorp 1983). Thus, three sets of resistance distances (RD, McRae 2006) based on nest-site suitability in 1900, 1987 and 2006, respectively, were calculated for each pair of sites based on maps from the National Land Cover Database (described in the previous section). Specifically, the RD was calculated utilizing the software CIRCUITSCAPE v 3 (McRae 2006) and 30 m resolution resistance maps created in ArcGIS v 9.3.1. Resistance maps were created by coding each pixel of the original NCLD land use map as a ‘resistance’ to dispersal based on the landscape type. Resistance surfaces for landscape genetics can be generated in a variety of ways (Spear et al. 2010), but one of the primary approaches is to test hypotheses regarding landscape features and gene flow (Storfer et al. 2007; Holderegger & Wagner 2008). There is substantial research examining bumble bee nest-site suitability across land use types; therefore, we used past studies, which demonstrate lower nesting densities in paved and human-altered landscapes than in grassland or forested areas (Svensson et al. 2000; Goulson et al. 2010; Jha & Kremen 2013) to classify ‘resistance’ from a scale of 0–1, where 0 represents no resistance and 1 represents the highest resistance. The generation of the resistance land use maps allows us to compare pairwise effective resistance values between all sites, where the higher resulting resistance value corresponds with higher expected costs to traverse between sites (McRae 2006). These pairwise resistance values can then be compared with pairwise genetic distance between sites.
Specifically, based on previous bumble bee nesting density studies (Svensson et al. 2000; Goulson et al. 2010; Jha & Kremen 2013), we classify the 11 NLCD habitats into four nesting types: those with strong nest limitation (1. open water and 2. high intensity commercial/industrial/transportation land with >50% impervious cover), moderate nest limitation (3. moderate intensity commercial/industrial/transportation with 20–49% impervious cover and 4. crops), weak nest limitation (5. low intensity developed space with <20% impervious cover, 6. bare ground, 7. disturbed grassland and 8. pasture), and no nest limitation (9. forest, 10. woodland and 11. scrubland). To explore the sensitivity of our analysis to the assigned resistance values, we created four distinct resistance models for each time period by gradually increasing the resistance for land with moderate nest limitation and decreasing the resistance of land with weak nest limitation (Tables 1, 2). Because all landscape variables were combined to make a single resistance map for each time period, there is no expected inflation of explained variance with additional landscape variables (ESRI 2006). Geographic distance between each pair of sites was calculated using the Euclidean (straight-line) distance. Also, because the generation of resistance distances uses a grid-based system, where distances are calculated across each 30 m pixel, unlike the continuous coordinate system used to calculate the straight-line Euclidean distance, we calculated a second measure of ‘straight-line’ distance within the grid-based system, which we call ‘Equal-resistance’ geographic distance. We did this by assigning all categories a 0.5 resistance and then calculating resistance distances, which represent the shortest geographic path for this landscape. Finally, because we are interested in examining the independent effects of elevation, given that it has been shown to correlate with genetic differentiation (Lozier et al. 2011), we created a resistance landscape to independently test for the effects of elevation, which ranged from −30 to 638 m in the study region. Thus, we divided this elevation range equally into five categories and coded the categories of −30 to 136, 137–304, 305–471, 472–638 and 639–806 m as resistances of 0.1, 0.3, 0.5, 0.7 and 0.9 respectively.
| Land use examined | Land use cost | ||||
|---|---|---|---|---|---|
| Strong nest limit | Mod. nest limit | Weak nest limit | No nest limit | ||
| 1900 model 1 | 0.5 | 0.5 | 0.3 | 0.3 | r = 0.220 (0.185–0.260) P < 0.001 |
| 1900 model 2 | 0.7 | 0.7 | 0.1 | 0.1 | r = 0.287 (0.240–0.329) P < 0.001 |
| 1900 model 3 | 0.9 | 0.9 | 0.1 | 0.1 | r = 0.271 (0.230–0.306) P < 0.001 |
| 1900 model 4 | 0.9 | 0.7 | 0.3 | 0.1 | r = 0.289 (0.242–0.331) P < 0.001 |
| 1987 model 1 | 0.5 | 0.5 | 0.3 | 0.3 | r = 0.221 (0.182–0.265) P < 0.001 |
| 1987 model 2 | 0.7 | 0.7 | 0.1 | 0.1 | r = 0.289 (0.247–0.335) P < 0.001 |
| 1987 model 3 | 0.9 | 0.9 | 0.1 | 0.1 | r = 0.271 (0.229–0.309) P < 0.001 |
| 1987 model 4 | 0.9 | 0.7 | 0.3 | 0.1 | r = 0.289 (0.244–0.337) P < 0.001 |
| 2006 model 1 | 0.5 | 0.5 | 0.3 | 0.3 | r = 0.253 (0.222–0.284) P < 0.001 |
| 2006 model 2 | 0.7 | 0.7 | 0.1 | 0.1 | r = 0.362 (0.303–0.399) P < 0.001 |
| 2006 model 3 | 0.9 | 0.9 | 0.1 | 0.1 | r = 0.316 (0.264–0.355) P < 0.001 |
| 2006 model 4 | 0.9 | 0.7 | 0.3 | 0.1 | r = 0.368 (0.311–0.408) P < 0.001 |
- The Pearson correlation coefficient (r, and its 95% CI) and P-value (P) is listed for each model.
| Land use examined | Land use cost | Controlling | |||||
|---|---|---|---|---|---|---|---|
| Strong nest limit | Mod. nest limit | Weak nest limit | No nest limit | Geographic distance (95% CI) | 1900 Land use (95% CI) | 1987 Land use (95% CI) | |
| 1900 model 1 | 0.5 | 0.5 | 0.3 | 0.3 | r = 0.225 (0.174–0.279) P < 0.001*** | — | — |
| 1900 model 2 | 0.7 | 0.7 | 0.1 | 0.1 | r = 0.253 (0.191–0.300) P < 0.001*** | — | — |
| 1900 model 3 | 0.9 | 0.9 | 0.1 | 0.1 | r = 0.235 (0.172–0.280) P < 0.001*** | — | — |
| 1900 model 4 | 0.9 | 0.7 | 0.3 | 0.1 | r = 0.254 (0.177–0.304) P < 0.001*** | — | — |
| 1987 model 1 | 0.5 | 0.5 | 0.3 | 0.3 | r = 0.227 (0.170–0.275) P < 0.001*** | r = 0.203 (0.137–0.247) P < 0.001*** | — |
| 1987 model 2 | 0.7 | 0.7 | 0.1 | 0.1 | r = 0.255 (0.196–0.312) P < 0.001*** | r = 0.201 (0.148–0.242) P < 0.001*** | — |
| 1987 model 3 | 0.9 | 0.9 | 0.1 | 0.1 | r = 0.234 (0.161–0.278) P < 0.001*** | r=−0.098 (−0.141–0.051) P = 0.981 | — |
| 1987 model 4 | 0.9 | 0.7 | 0.3 | 0.1 | r = 0.255 (0.183–0.308) P < 0.001*** | r=−0.012 (−0.044 to 0.068) P = 0.122 | — |
| 2006 model 1 | 0.5 | 0.5 | 0.3 | 0.3 | r = 0.319 (0.245–0.367) P < 0.001*** | r = 0.187 (0.104–0.234) P < 0.001*** | r = 0.184 (0.100–0.229) P < 0.001*** |
| 2006 model 2 | 0.7 | 0.7 | 0.1 | 0.1 | r = 0.343 (0.267–0.389) P < 0.001*** | r = 0.254 (0.192–0.302) P < 0.001*** | r = 0.252 (0.187–0.295) P < 0.001*** |
| 2006 model 3 | 0.9 | 0.9 | 0.1 | 0.1 | r = 0.289 (0.211–0.335) P < 0.001*** | r = 0.218 (0.138–0.276) P < 0.001*** | r = 0.219 (0.138–0.275) P < 0.001*** |
| 2006 model 4 | 0.9 | 0.7 | 0.3 | 0.1 | r = 0.347 (0.269–0.389) P < 0.001*** | r = 0.259 (0.199–0.301) P < 0.001*** | r = 0.262 (0.201–0.313) P < 0.001*** |
- The Pearson correlation coefficient (r, and its 95% CI) and P-value (P) is listed for each model.
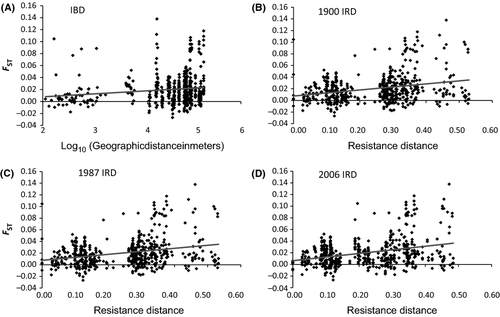
At the regional geographic scale (200 km), we tested for isolation by geographic distance (IBD) and isolation by resistance distance (IBR) for each set of resistance maps (1950, 1987 and 2006) and the elevation map using Mantel and partial Mantel tests implemented with the R package ECODIST (Goslee & Urban 2007). We used Mantel tests (Mantel 1967) and partial Mantel tests to compare the relationship between genetic distance (FST), log10 of geographic distance (IBD), hereafter geographic distance and resistance distance (IBR) for the three time periods. While the Mantel is less powerful in detecting significant linear relationships compared with other tests, it is especially appropriate for examining hypotheses related to distances, such as genetic and geographic distance (Legendre & Fortin 2010). Specifically, we used partial Mantel tests to control for the effects of geographic distance (as in Cushman et al. 2006; Zellmer & Knowles 2009) and elevation while assessing the effect of resistance distance on genetic distance. We examined Pearson correlation coefficients (r) to determine the relative support for each map, and we estimated the 95% confidence limits (CL) using 10 000 bootstrap repetitions and setting the level of re-sampling for bootstrapping to 0.90 as per the default settings (Goslee & Urban 2007).
Fine-scale relatedness
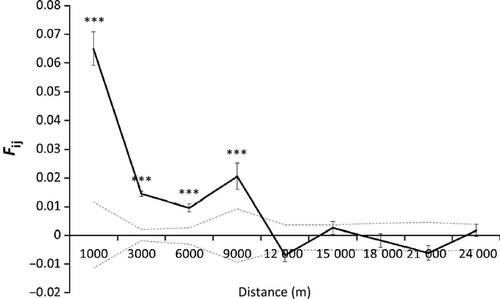
At a fine geographic scale (1–20 km), we examined spatial genetic structure using spatial autocorrelation analysis in the software SPAGeDi (Hardy & Vekemans 2002). In this program, we computed the pairwise relatedness metric Fij which is based on the regression slope of relatedness, bF, to distance, and which is robust to our sampling method and sample size (Loiselle et al. 1995). We computed relatedness for distance intervals binned approximately every 3 km up to 24 km (0–1, 1–3, 3–6, 6–9, 9–12, 12–15, 15–18, 18–21, 21–24 km). Standard errors (SE) were estimated by jackknifing over loci. We obtained the 95% confidence limits (CL) around the null expectation of no genetic structure (Fij = 0.00) by permuting multi-locus genotypes and spatial coordinates (1000 iterations).
Results
Colony identity, HWE, allelic richness & STRUCTURE analyses
MICRO-CHECKER results indicate that none of the loci exhibit signs of having null alleles. One locus (BT136) was significantly out of HWE across all regions, therefore we chose to exclude it from the analysis. The remaining loci exhibited either no significant deviations from HWE across all regions (B119, BT33, BT43, BT65, BT72, BT131 and BT132) or exhibited a significant deviation from HWE in only one region (B96, B100, BT124, BT125 and BT128). Significant LD was detected for multiple loci, but only within single regions, therefore we elected to retain all markers, except for BT136 (excluded for HWE disequilibrium), for the analyses. Average allelic richness per site based on rarefaction was 4.39 (±0.43) and average private allelic richness per site was 0.082 (± 0.119). Average heterozygosity across sites was 0.687 (± 0.182) (Table S1, Supporting information). None of the regions showed significant evidence of a bottleneck (excess heterozygosity) for either of the models tested (Wilcoxon test, P > 0.088 for all regions and all models). Analysis using STRUCTURE indicated that log likelihood (LnP(D)) did not increase monotonically from K = 1 as is theoretically expected of individuals structured into genetic groups (Pritchard et al. 2007). While the Evanno method suggests a K = 2 for our study, we document high levels of co-ancestry between two groups and suggest that, as per Falush et al. (2003) and Pritchard et al. (2007), the simplest explanation is that there is no strong genetic structuring of distinct genetic groups in our study region.
Regional scale differentiation
Sites were significantly differentiated from one another using both FST (FST = 0.019, 95% CI = 0.010–0.032) and Dest (Dest = 0.054, 95% CI = 0.049–0.058) and exhibited low but significant levels of inbreeding (FIS = 0.047, 95% CI = 0.005–0.121). The eight study regions were also significantly differentiated from one another using FST (FST = 0.012, 95% CI = 0.005–0.021) and Dest (Dest = 0.049, 95% CI = 0.012–0.085), while inbreeding levels were no longer significantly different from zero (FIS = 0.054, 95% CI = −0.006 to 0.168).
We found no support for isolation by elevation gradient (Mantel test: r = −0.114 (−0.172 to 0.025) and P = 0.979), but we found significant support for isolation by Euclidean geographic distance (Mantel test: r = 0.142 (0.100–0.192) and P < 0.001) (Fig. 2A) and Equal-resistance geographic distances (Mantel test: r = 0.137 (0.085–0.188) and P = 0.001, Table S2, Supporting information). We found strong support for isolation by resistance distance for all three land use periods (1900, 1987, and 2006 maps), and across all four resistance models, which vary in the strength of nest-limitation due largely to impervious cover (Table 1) (Resistance Model 4 depicted, Fig. 2B–D). When controlling for geographic distance, there was significant support for isolation by resistance distance for all three land use periods, with the strongest support for the 2006 land use period, though the correlation coefficient was not significantly different between the three land use periods. Furthermore, even when controlling for previous land use resistance, there was significant support for isolation by resistance distance across all four resistance models for the 2006 land use map (Table 2).
Fine-scale relatedness
We found significant spatial genetic structure within a 9 km scale, with highest spatial genetic structure within 1 km (Fij=0.065, P < 0.0001) and declining at 3 km (Fij=0.017, P < 0.0001), 6 km (Fij = 0.009, P < 0.0001) and 9 km scales (Fij = 0.015, P = 0.0009) (Fig. 3).
Discussion
From our data, we can infer that regional gene flow is high for B. vosnesenskii, with no significant evidence of population substructure. However, this gene flow is significantly limited by contemporary land use patterns. Specifically, we show that B. vosnesenskii genetic differentiation is best explained by dispersal limitation due to urbanization, not only by geographic distance. Furthermore, at fine spatial scales, our analyses indicate that genetic structure is significantly greater than zero at the 1–9 km scale, indicative of local dispersal, most likely via limited dispersal ability or high natal nest-site loyalty of queens.
Regional scale differentiation mediated by contemporary land-alteration
We show that levels of genetic differentiation in our study system (FST = 0.019, Dest = 0.054) are higher than those measured for the same species at continental scales (1000 km) (e.g. FST = 0.005, Cameron et al. 2011; e.g. Dest = 0.018, Lozier et al. 2011) and more similar to those of United Kingdom bumble bees studied at regional scales (200 km) (FST = 0.13 for B. muscorum and FST = 0.034 for B. jonellus in Darvill et al. 2010; e.g. FST = 0.16 for B. hortorum in Goulson et al. 2011). While the past North American studies examined different and fewer (eight) loci, we found that random selection of just eight loci in the current study did not change the overall differentiation patterns (FST = 0.020, 95% CI = 0.010–0.041); thus, sampling scale and locus selection, not locus number, most likely explain the distinctions in the studies. Our study system does not have the same oceanic dispersal barriers as the UK studies, yet we confirm that significant levels of bumble bee differentiation exist even when examined at the regional scale (eight study regions, FST = 0.012, Dest = 0.049), analyses less prone to error associated with the site sample size. In addition, in this study we present the first evidence that human-altered landscapes limit B. vosnesenskii gene flow.
Specifically, our results demonstrate that human land use best explains the variation in genetic differentiation across our study sites. This finding is significant across four distinct models that varied in the resistances assigned for land uses with strong, moderate, weak and no nest-site limitation, even when controlling for geographic distance. Furthermore, the model with the strongest correlation (highest r) between resistance distance and genetic distance was Model 4, which assigned the highest resistance for high-intensity human land use (>50% of impervious structure), moderate resistance for moderate intensity human land use (20–49% of impervious structure), lower resistance for low-intensity human land use (<20% impervious structure) and lowest for forested habitats (Table 2). Our results additionally show that resistance to contemporary land use (2006) significantly explains genetic differentiation across all four resistance models, even when controlling for past land use. Overall, given that the resistance models that most penalized for high-intensity human land use had the greatest support across time periods, our analyses uphold the hypothesis that B. vosnesenskii gene flow is limited by urban development.
Though this study is the first to document that urbanization can limit bumble bee gene flow, closer examination of this bumble bee's life cycle and ground cavity-nesting behaviour highlights the potential relevance of contemporary urban land use to population genetics. Specifically, there are a number of biological explanations for the negative impact of recent urbanization on bumble bee dispersal. First, the shortest time period between our land use maps is 19 years, or 19 generations given the annual life cycle of B. vosnesenskii, which may be sufficient time for population differentiation due to land alteration. Second, urban, suburban and exurban development has been increasing rapidly in North America since the 1950s, especially in the study region (Sleeter et al. 2011), and urban and suburban landscapes often have large amounts of impervious cover, which can limit the density of ground-nesting bees (e.g. Jha & Kremen 2013). Finally, urban development may limit bumble bee dispersal movement, preventing gene flow across human-altered habitats. Interestingly, one past study has provided evidence that impervious cover may limit bumble bee foraging (Bhattacharya et al. 2003); our results additionally suggest that urbanized landscapes may also limit bumble bee dispersal movement. While the negative effects of urbanization on native bees may seem intuitive, most past population –genetics studies have ignored the role of land use in bee genetic structure, instead examining the influence of geographic distance, not resistance distance, on genetic differentiation patterns, often finding little or no evidence of isolation by distance (IBD) (e.g. Beveridge & Simmons 2006; Exeler et al. 2010; Suni & Brosi 2012). Only one previous study, conducted on Colletes floralis, has indirectly examined human land use impacts on bee population genetics and likewise provides evidence that urban areas can act as barriers to gene flow, also for smaller-bodied bees (Davis et al. 2010).
A number of taxa have been documented to exhibit gene flow limitations in contemporary human-altered landscapes, including small mammals (e.g. Munshi-South 2012), amphibians (e.g. Zellmer & Knowles 2009), and non-pollinating insects (e.g. Watts et al. 2004) and many of these past studies propose that population differentiation across human-altered habitat could occur via population bottlenecks, inbreeding and/or demographic processes such as recurrent extinction or colonization (e.g. Zellmer & Knowles 2009). In this study, we do not find evidence of bottlenecks and find only low levels of inbreeding. Thus, we posit that increased differentiation across human-altered landscapes is due to limited dispersal of reproductive individuals and reduced colony establishment in the least hospitable human land use types.
Fine-scale relatedness indicates local queen dispersal
Specifically, we provide evidence that B. vosnesenskii exhibits limited dispersal and/or natal site fidelity, indicated by significant relatedness within our study system at the 1–9 km spatial scale. This pattern declines with increasing distance, a signature of local dispersal, as seen in plants (reviewed in Dick et al. 2008), animals (e.g. Zeyl et al. 2009), and other insects (e.g. Davis et al. 2010). Colony-mates have been removed from this analysis, thus the pattern of significant fine-scale spatial genetic structure is not a result of sibship, but rather a signal of shared ancestry at other generational levels. Furthermore, we propose that this pattern of spatial genetic structure may be due to local queen dispersal. As described earlier, new queens carry male gametes in their spermatheca; thus if they exhibit largely local dispersal, then local spatial genetic structure would be strong, even if male dispersal were extensive. While our analyses suggest that a portion of B. vosnesenskii queens exhibit dispersal at the 1–9 km scale, it is most likely that the tail end of the dispersal kernel extends beyond 9 km, as evidenced by the rapid rate that other Bombus spp. have spread across uninhabited landscapes (e.g. 15–30 km/year in Macfarlane & Gurrb 1995). Overall, the 1–9 km scale of high relatedness documented in this study is comparable with mark–recapture distances for B. pascuorum and B. lapidarius queens of 5–8 km (Lepais et al. 2010) and additionally indicates that a non-trivial portion of emerging queens exhibit this local dispersal pattern.
Conclusions
In this study, we provide evidence that regional genetic differentiation for B. vosnesenskii is significantly explained by urbanized landscapes. Specifically, we find that the resistance models that most strongly penalize urban land use (commercial, industrial, and transportation-areas with >50% impervious cover) are most predictive of current B. vosnesenskii genetic structure. A number of previous studies have shown that bumble bees may be less abundant in highly altered habitats (reviewed in Goulson et al. 2008) and, in the same study system, we have found that bumble bees exhibit lower nesting densities in areas with greater impervious cover (Jha & Kremen 2013). However, the current study is the first to demonstrate that bumble bee gene flow patterns can be limited by impervious land use and appear to be particularly sensitive to recent land use patterns. In addition, we provide evidence for strong fine-scale spatial genetic structure and propose that this pattern is explained by differential male and queen bumble bee dispersal. Because male bumble bees can exhibit longer flight ranges than females (Kraus et al. 2009), we hypothesize that long-distance male dispersal, in combination with occasional long-distance queen dispersal, could be maintaining low levels of differentiation seen at continental scales in multiple North American species (Cameron et al. 2011; Lozier et al. 2011). Overall, our results indicate that species with high gene flow and no apparent declines in relative abundance at continental scales, like B. vosnesenskii, may still be experiencing barriers to gene flow at regional and fine spatial scales.
The ecological and conservation implications of our findings are trifold. First, our results indicate that high-intensity urbanization (with more than 50% impervious cover) creates the greatest barrier to B. vosnesenskii gene flow. Thus, while it is difficult to control the process of urbanization, ecologically oriented urban growth which restricts 20–50% or more of the land cover to permeable materials, such as woodland, bare ground, or open green space, could benefit bumble bee dispersal. The increased exposure of soil, vegetation, and other permeable surfaces in urban areas has long been promoted as a solution for improved water storage and water quality (e.g. Hall & Ellis 1985) but only recently acknowledged as an important resource for soil-nesting bees (Frankie et al. 2009). Specifically, studies have shown that bumble bees can be found in relatively high densities in urban parks and green spaces (McFrederick & LeBuhn 2006). Our study provides evidence that the act of limiting impervious surface cover in urban habitats could also make substantial contributions to conserving bumble bee dispersal across rapidly urbanizing areas.
Second, our fine-scale analyses suggest that queens may be limited in their dispersal abilities or may prefer to nest within 1–9 km of their natal colonies. Thus, in urban or intensified agricultural landscapes, the placement of conservation areas within this 1–9 km radius and the overall improvement of matrix quality within this radius may be most effective at promoting new queen establishment and survival. The improved matrix quality approach can reduce isolation for pollinators (e.g. Ricketts 2001); likewise a ‘stepping stone’ or ‘corridor’ of suitable habitat can increase dispersal potential across otherwise unsuitable habitat (e.g. Wehling & Diekmann 2009). In the case of bumble bees, the act of local matrix improvement or the creation of spatially linked refugia may not only improve bumble bee queen dispersal and survivorship, but may also increase the spatial extent of pollination services, as predicted by theoretical and spatially explicit models (Brosi et al. 2008; Keitt 2009; Lonsdorf et al. 2009; Ricketts & Lonsdorf ).
Finally, our results indicate that contemporary anthropogenic land use has the strongest impact on current patterns of population genetic structure for B. vosnesenskii. In other words, B. vosnesenskii dispersal and gene flow processes may be responding to habitat availability and composition on relatively short time scales. Ironically, this finding presents us with a hopeful opportunity for pollinator conservation because it suggests that effective conservation practices may, likewise, have positive impacts within short time scales. While it is unknown how quickly bumble bee populations and gene flow processes recover after habitat restoration, bumble bee abundance has been shown to increase substantially within multiple years of wild flower restoration plantings (Pywell et al. 2005, 2006). If these increased abundance levels represent true local population growth and not simply a concentration effect, then it is possible that gene flow patterns may also recover quickly. Further research is needed to address the ability of restoration practices to promote dispersal across unsuitable habitat and to support long-term population persistence. Overall, in the face of potential pollinator declines and increased reliance on pollinator-dependent crops, our results highlight the importance of regional and fine-scale pollinator gene flow processes for advancing understanding of basic pollinator biology and for developing informed conservation practices.
References
Data accessibility
Microsatellite and geographic collection data: DRYAD digital repository entry - doi:10.5061/dryad.n1922.
S.J. and C.K. designed study, S.J. conducted field, molecular and statistical analyses, and S.J. and C.K. wrote the manuscript. Both authors have a general interest in native bee ecology, evolution and conservation.




