Self-recruitment in a Caribbean reef fish: a method for approximating dispersal kernels accounting for seascape
Abstract
Characterizing patterns of larval dispersal is essential to understanding the ecological and evolutionary dynamics of marine metapopulations. Recent research has measured local dispersal within populations, but the development of marine dispersal kernels from empirical data remains a challenge. We propose a framework to move beyond point estimates of dispersal towards the approximation of a simple dispersal kernel, based on the hypothesis that the structure of the seascape is a primary predictor of realized dispersal patterns. Using the coral reef fish Elacatinus lori as a study organism, we use genetic parentage analysis to estimate self-recruitment at a small spatial scale (<1 km). Next, we determine which simple kernel explains the observed self-recruitment, given the influx of larvae from reef habitat patches in the seascape at a large spatial scale (up to 35 km). Finally, we complete parentage analyses at six additional sites to test for export from the focal site and compare these observed dispersal data within the metapopulation to the predicted dispersal kernel. We find 4.6% self-recruitment (CI95%: ±3.0%) in the focal population, which is explained by the exponential kernel y = 0.915x (CI95%: y = 0.865x, y = 0.965x), given the seascape. Additional parentage analyses showed low levels of export to nearby sites, and the best-fit line through the observed dispersal proportions also revealed a declining function y = 0.77x. This study lends direct support to the hypothesis that the probability of larval dispersal declines rapidly with distance in Atlantic gobies in continuously distributed habitat, just as it does in the Indo-Pacific damselfishes in patchily distributed habitat.
Introduction
Connectivity influences virtually all ecological and evolutionary processes in metapopulations, including population growth rates, resilience to perturbations, gene flow, local adaptation and divergence (Hanski 1999; Hanski & Gaggiotti 2004; Cowen et al. 2007; Cowen & Sponaugle 2009). For many organisms with bipartite life cycles, population connectivity is primarily driven by propagule dispersal. Therefore, quantifying spatial patterns of propagule dispersal is essential to predicting metapopulation dynamics and to designing effective management plans (Fahrig & Merriam 1994; Botsford et al. 2001, 2009; Roberts et al. 2003; Sale et al. 2005; Blowes & Connolly 2012).
While much research has focused on the predictors, patterns and consequences of dispersal in terrestrial species (Nathan & Muller-Landau 2000; Clobert et al. 2001), marine dispersal research has lagged behind. This lag is attributable to the fact that most marine species disperse via larvae, and sampling marine larvae – extremely small propagules that travel in the pelagic environment for weeks to months – is logistically challenging. Recently, the application of genetic parentage analysis to marine systems has led to great progress in quantifying local patterns of dispersal for marine fishes (Jones et al. 2005; Planes et al. 2009; Christie et al. 2010; Saenz-Agudelo et al. 2011; Buston et al. 2012; Harrison et al. 2012). The advantage of genetic parentage analysis over other methods lies in the ability to directly uncover demographic connectivity, or the movement of individuals, which is essential for understanding metapopulation dynamics (Hanski 1999; Hanski & Gaggiotti 2004; Hedgecock et al. 2007; Broquet & Petit 2009; Leis et al. 2011).
A simple comparison of published marine dispersal estimates suggests that there is large variation in local dispersal patterns, measured by self-recruitment. Self-recruitment is defined as the percentage of locally settling individuals that were spawned by local parents and is a relatively easy dispersal metric to measure. Empirical data have revealed self-recruitment estimates ranging from 0% (Amphiprion polymnus, Saenz-Agudelo et al. 2011) to upwards of 60% (Amphiprion percula and Chaetodon vagabundus, Almany et al. 2007), and spanning the range in between (Jones et al. 2005; Planes et al. 2009; Saenz-Agudelo et al. 2011; Harrison et al. 2012). It has been suggested that major determinants of variation in self-recruitment may be species' traits (e.g., pelagic larval duration) and seascape. Understanding the causes of the observed variation is, however, challenging because most of the studies have been conducted in one seascape (Kimbe Bay) using one genus (Amphiprion), although new studies are emerging (Christie et al. 2010; Harrison et al. 2012). An important next step in dispersal research is to collect empirical data from different systems, e.g., different taxa and seascapes, and test how potential predictors of dispersal affect variation in local dispersal estimates.
The idea that habitat patchiness, or fragmentation, can have profound impacts on patterns of demographic and genetic connectivity has strong foundations in the terrestrial literature (Hanski 1999; Manel et al. 2003; Hanski & Gaggiotti 2004; Storfer et al. 2007), but has only recently come to the fore in marine ecology (Jones et al. 2009; Saenz-Agudelo et al. 2011; Pinsky et al. 2012). A recent model with a marine focus explicitly illustrates that isolated populations in patchy seascapes are predicted to have high self-recruitment, whereas populations situated in continuous seascapes are predicted to have low self-recruitment (Pinsky et al. 2012). This follows from the fact that the denominator of the self-recruitment fraction increases with the influx of larvae from additional patches on the seascape, creating a dilution effect [Fig. 1(a1) vs. (b1)]. Further, if the probability of dispersal declines with distance, the presence or absence of nearby reef patches will have a disproportionate effect on self-recruitment estimates, relative to the presence or absence of distant reef patches. The same applies to measures of larval export [Fig. 1(a2) vs. (b2)]. Importantly, this dilution phenomenon will hold even if the underlying dispersal kernel is the same in these two scenarios. Following this logic, it may be possible to estimate marine dispersal kernels from empirical self-recruitment estimates and the seascape structure.

We propose a framework for incorporating seascape analyses into quantitative marine dispersal estimates using the sponge-dwelling neon goby Elacatinus lori as a study organism. Elacatinus lori has several characteristics that make it a tractable study organism for direct dispersal studies. First, E. lori is an endemic to the Mesoamerican Barrier Reef (MBR) system, where it is a specialist on tube sponges (Colin 1975, 2002, 2010), particularly the yellow tube sponge Aplysina fistularis (D'Aloia et al. 2011). This microhabitat association enables efficient location and collection of individuals within a study area. Second, a life history transition that is correlated with body size facilitates genetic parentage analysis – in this system, we define ‘settlers’ as individuals that have recently settled on the outer surface of the sponges upon completing the larval phase (SL < 18 mm), and ‘residents’ as individuals that have recruited inside the sponge (SL ≥ 18 mm) (D'Aloia et al. 2011). Parentage analyses can therefore focus on assigning settlers to resident parents. Third, its location on the MBR, a reef system that is relatively continuous over 1000 km, offers an important spatial contrast to dispersal studies that have focused on patchy seascapes in the Pacific (Jones et al. 2005; Almany et al. 2007; Planes et al. 2009; Harrison et al. 2012). Capitalizing on these characteristics of E. lori, we develop a method for combining estimates of self-recruitment with knowledge of the seascape structure to approximate a simple dispersal kernel.
We characterize E. lori dispersal in three steps: (i) we apply genetic parentage analysis to a focal study population on the MBR to describe the pattern of local dispersal (i.e. self-recruitment) along a 0.5-km stretch of reef; (ii) we assess which simple negative exponential function can explain the observed self-recruitment percentage, accounting for influx from all other sites; (iii) we complete additional parentage analyses to test for export to six nearby sites and compare the best-fit line through the observed dispersal data with the approximated dispersal function. This study provides further direct empirical support for the hypothesis that there is a rapid decline in the probability of marine larval dispersal with respect to distance.
Materials and methods
Study metapopulation
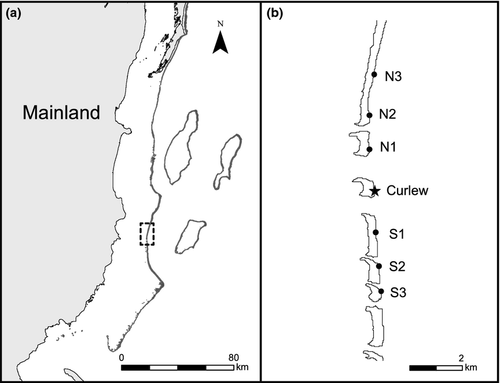
This study was focused on a population of E. lori inhabiting A. fistularis within a 500-m long by 125-m wide area, between depths of 10 m and 25 m, on the barrier reef at Curlew Caye, Belize (16° 47′ 23″ N 88° 04′ 33″ W) (Fig. 2). This depth range represents the depths at which the fish and their host sponge are most abundant (D'Aloia et al. 2011); the width of the study area simply represents the width of the barrier reef between these depths. The area between 10 and 25 m was sampled completely, that is, all E. lori individuals in A. fistularis >10 cm in length were sampled. We excluded sponges <10 cm in length from our study because they are rarely occupied by E. lori (D'Aloia et al. 2011).
To characterize self-recruiting dispersal trajectories in three dimensions (distance, direction and depth change), we measured depth at the base of each sponge (m) and marked the location of every sponge in the study area using a GPSMAP® 76Cx (Garmin, USA) in an underwater housing (Sound Ocean Systems, Inc., Redmond, WA, USA). From here, we calculated the net distance, depth displacement and directional change (N-S and E-W) between the origin and destination sponges of the self-recruiting trajectories.
To uncover self-recruiting dispersal trajectories, we collected tissue from all residents and settlers in the study area. All residents (n = 425) were collected using slurp guns and fin-clipped using scissors. Then, they were placed in a plastic bag and their standard length (SL) was measured to the nearest mm before they were returned to their sponge. Settlers (n = 194) were collected using slurp guns and transported to the surface in plastic bags. There, they were euthanized using MS-222 because they were too small for nonlethal fin clipping. All tissue samples were stored in 95% EtOH.
Additional tissue samples were collected from nearby sites along the barrier reef to test whether export from the Curlew population could be detected. We sampled three sites to the north and three sites to the south of Curlew (Fig. 2b). These additional sites were chosen based on their proximity to the focal site and were spaced 1–1.5 km apart. Approximately 30 settlers were collected at each site.
Isolation and characterization of microsatellites
Elacatinus lori genomic DNA was digested with the restriction enzyme Hinc II and ligated to a double-stranded linker (Andrés & Bogdanowicz 2011). Digested, ligated DNA fragments were enriched for microsatellites by hybridization to 3′-biotinylated oligonucleotide repeat probes representing two dimers, five trimers, five tetramers and two pentamers. Enriched fragments were captured by streptavidin-coated magnetic beads, amplified by PCR and ligated to a Roche/454 rapid library adapter. The sample was submitted to the Sequencing and Genotyping Facility at the Cornell Life Sciences Core Laboratory Center (CLC) for Titanium 454 sequencing.
Raw data were imported to SeqMan Pro (Lasergene v 8.1.1, DNASTAR, Inc.) and assembled (average Q score = 16 for quality trimming, mer size = 120, minimum match percentage = 94, repeat handling on). Postassembly, sequences smaller than 150 base-pairs were discarded; both multi-read and single-read contigs above this size were kept. We used the program msatcommander (version 1.0.3, for Mac OSX) to scan the data for all dimeric, trimeric, tetrameric, pentameric and hexameric microsatellites and design primers. Minimum perfect repeat lengths were six for dimers, and five for all other repeat types selected. Minimum, optimum and maximum primer lengths were set to 22, 23 and 24 bases, respectively. All other settings in msatcommander were kept at defaults.
We used the three-primer PCR method (Schuelke 2000) to assay loci for PCR quality and levels of polymorphism, on 3100 and 3730xl DNA Analyzers (Life Technologies). Loci that appeared ‘clean’ and polymorphic had one primer resynthesized with a 5′ fluorescent dye compatible with the G5 dye set (Life Technologies). All reverse primers were ‘pig-tailed’ (Brownstein et al. 1996) to promote adenylation of the fluorescently labelled strand. Allele sizing data at the three-primer PCR stage were used to inform PCR multiplexing of loci for high throughput genotyping.
Genotyping
Genomic DNA was extracted with the Agencourt DNAdvance kit (Beckman Coulter, Inc., USA), and individuals were genotyped at 14 microsatellite loci (Table 1) using two sets of multiplex PCR with the Type-It Microsatellite PCR kit (Qiagen, USA). Each 10 μL PCR contained 1 μL DNA, 3 μL H2O, 5 μL 2× Type-it Multiplex PCR Master Mix and 1 μL 10× primer mix. Thermal cycling followed a touchdown protocol: 95 °C for 5 min; six cycles of 94 °C for 50 s, 59–54 °C for 90 s (annealing temperature reduced 1 °C each cycle), 72 °C for 30 s; 23 cycles of 94 °C for 50 s, 53 °C for 90 s, 72 °C for 30 s; 60 °C for 30 min. Diluted amplicons (1 PCR product: 35 H2O) were combined with formamide and GeneScan LIZ-500 size standard (Life Technologies) and screened on an ABI 3730 automated sequencer. Allele sizes were determined with genemapper v. 4.0 (Life Technologies).
| Locus | Repeat motif | Primer sequence (5′-3′) | k | H O | H E | HWE |
|---|---|---|---|---|---|---|
| 1419tri | AAC |
CGAGTTTTCCCAGTCACGACGCGACGGGGAGCCTCAAAT GTTTCTTCGAGTTTTCCATGATTCGGCCGATACGATGGA |
17 | 0.323 | 0.688 | <0.001* |
| 14528tet | AAAC |
CGAGTTTTCCCAGTCACGACGCGCATGAGCCCGTTTTT GTTTCTTCGAGTTTTCCGTGCCACCGGTTGCTCTTG |
19 | 0.856 | 0.874 | 0.518 |
| 18144tri | AAC |
CGAGTTTTCCCAGTCACGACGACCCGGATTAGTCCTGGTTTG GTTTCTTCGAGTTTTCCGACCGGAGTAAATGTTGGCTCAC |
13 | 0.567 | 0.572 | 0.282 |
| 21378tri | AAC |
CGAGTTTTCCCAGTCACGACCCTCCCTCCCCAGCACA GTTTCTTTTTGTCCAAGTCTAGCAGGTATTC |
35 | 0.811 | 0.935 | <0.001* |
| 23415tet | AACT |
CACCGTTATTGACTAAAGTGTTCT GTTTCTTTACAGATCCAGATCATCATCCA |
25 | 0.889 | 0.893 | 0.364 |
| 23889tri | AAAC |
GGTGACTCCCGTGTGAAGAGC GTTTCTTAACATGCTATGGCTAACACTGACG |
21 | 0.901 | 0.885 | 0.643 |
| 25362tri | AAC |
GCTAAAGGCGGTCCATCAAAA GTTTCTTCAGCGTCCAACAGTGTCTTCAGT |
29 | 0.890 | 0.923 | 0.382 |
| 25632tet | AAAC |
TCCAGTGCTATTTGTGGCATTGTT GTTTCTTCTTATTCCCGGTTCCTCCACTGAT |
33 | 0.947 | 0.945 | 0.053 |
| 25745tet | AAAC |
CAGTCACGACGGGGGAGGCATGTGATGT GTTTCTTAAACTTCCTCTCGCCATAGTGA |
10 | 0.629 | 0.772 | <0.001* |
| 29109tet | AAAC |
CGAGTTTTCCCAGTCACGACAGCCGGGGATTTAGGCAGGAATAA GTTTCTTCGAGTTTTCCGAGAGGCTAAATTGATTAAATGCTC |
43 | 0.961 | 0.959 | 0.300 |
| 6231tet | AAAC |
CCAGGGATAGTTTCACGATGTT GTTTCTTATGGATTTCCCCTTCAGTGTTT |
29 | 0.942 | 0.941 | 0.720 |
| 6266tri | AAC |
CGAGTTTTCCCAGTCACGACGTAGACGGACGTGTGAGGTTGTT GTTTCTTTCGAGTTTTCCCCCCCAGACTTGTGAATAATGTGA |
22 | 0.816 | 0.842 | 0.787 |
| 6326tet | AAAC |
GGTCCATGGTCCCAAAGAAAC GTTTCTTCAATGTTAGCGCCCAATGTTCG |
10 | 0.711 | 0.700 | 0.799 |
| 985tet | AGAT |
CGAGTTTTCCCAGTCACGACTTTCCCTGCAGCTGTCAGACT GTTTCTTCGAGTTTTCCAAAGCTCCACATCCGATTTCA |
76 | 0.917 | 0.982 | <0.001* |
Summary statistics (allele frequencies, observed and expected heterozygosity) were generated in cervus v. 3.0 (Kalinowski et al. 2007). Deviations from Hardy–Weinberg equilibrium (HWE) were tested with genepop v. 4.1.4 (Raymond & Rousset 1995) using Markov chain methods (dememorization number = 10 000; number of batches = 10 000; iterations per batch = 1000). The presence of null alleles, large allele dropout and stuttering was checked on micro-checker (van Oosterhout et al. 2004).
Parentage analysis and self-recruitment
To assign self-recruiting offspring from Curlew to their parents, a categorical likelihood-based parentage analysis was conducted in cervus v 3.0. Prior to running the parentage analysis, a simulation was run to determine the critical LOD value (natural log of the likelihood ratio) for assigning offspring to parents at a 95% confidence level. The simulation generated both true parents and unrelated candidate parents for 10,000 hypothetical offspring created from the observed allele frequencies in the population. The critical LOD value was determined by comparing the LOD distribution when the true parents were assigned with the LOD distribution when unrelated candidates were assigned. Because CERVUS requires an estimate of the proportion of candidate parents sampled, we tested a range of proportions (0.01–0.70) but found that the input value did not ultimately affect the results of the subsequent parentage analysis. However, parameter inputs do affect the number of expected assignments through the parentage simulation, so we use a conservative sampling proportion of 0.01 to report the simulation results.
Once the simulation was complete, a parentage analysis was run to test the pool of offspring (n = 194) against potential parents (n = 425) with a mistyping percentage of 1% to account for potential genotyping errors. This level of mistyping is conservative, but consistent with percentages used in previous studies of this type (Jones et al. 2005; García et al. 2007; Christie et al. 2010; Saenz-Agudelo et al. 2011). Putative parent–offspring assignments were only accepted if they had a LOD score exceeding the critical value. Once assignments were made, the observed self-recruitment (SRO) was calculated as SRO = nC/nT, where nC is the number of settlers assigned to Curlew parents and nT is the total number of settlers collected from Curlew.
Approximating a dispersal kernel
To generate a first approximation of a dispersal kernel for E. lori, we created a map of Curlew and all nearby reef patches, so that larval exchange between the focal population and these nearby populations could be simulated. A map of the MBR was obtained from the IMaRS Millennium Coral Reef Mapping Project (Andréfouët et al. 2005), and subsequent GIS analyses were performed in ArcMap 10 (ESRI). We focused on the Belizean portion of the MBR and only used areas of the reef designated as ‘forereef’ by the IMaRS. We then divided the reef into 500 m by 500 m square grids to break the reef into patches approximating the size of our study area. Some areas of the ‘forereef’ on the IMaRS maps are wider than 500 m; however, we know that E. lori are only abundant on the outer reef slope, which is never >500 m wide (D'Aloia et al. 2011). Therefore, to ensure that this gridded reef represented the true width of the MBR where E. lori are present (i.e. <500 m wide), we manually removed excess reef patches whenever the gridded forereef was >500 m wide. Next, a distance matrix was generated that included the distance between Curlew and every other reef patch, restricted to within 35 km (inclusion of longer distances will not significantly alter the outcome of our analyses because the expected influx of larvae from such distant sites has a negligible effect on self-recruitment estimates).

where y0 = 1, xj = distance to Curlew and b = the decay rate, ranging from 0.00 to 1.00 by intervals of 0.005. In this way, we iteratively simulated dispersal to Curlew from all reef patches for each potential value of the decay rate. This approach assumes that all reef patches are occupied, population density and reproductive output are equal among patches, and larval dispersal is represented by the same function from each patch. Elacatinus lori is well-suited to such a simple approach, as personal surveys throughout the MBR revealed that E. lori is densely distributed all along the barrier reef and atolls. Further, previous studies on simulated dispersal data suggest that spatial variation in reproductive output does not significantly alter dispersal kernel estimates, provided that the variation is randomly distributed (Robledo-Arnuncio & García 2007; Robledo-Arnuncio 2008).
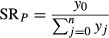
Export from focal site
To test for export from the focal site, we used the same genotyping and assignment methods described above to assign settlers from six additional sites on the MBR to the resident population at Curlew (Fig. 2b). For each export site, we calculated the proportion of settlers originating from Curlew (# settlers assigned to Curlew parents/total # settlers collected). Finally, we added an exponential best-fit line through the observed self-recruitment and export proportions, using nonlinear least-squares regression, to determine whether a function similar to the approximated dispersal kernel captured the observed data.
Results
Summary statistics and tests of HWE
The 14 microsatellite markers were highly polymorphic: there was an average of 27 alleles per locus, ranging from 10 to 76 (Table 1). Exact tests for deviations from HWE revealed that four loci were potentially out of HWE, but MICRO-CHECKER analyses suggested that all four deviations were due to the presence of null alleles. This set of highly polymorphic markers provided a combined nonexclusion probability of P = 1.8 × 10−7 for the first parent, and P = 1.17 × 10−17 for a parent pair. Because the probability of incorrectly assigning an offspring to a parent is so low, the potential deviations from HWE due to null alleles should not significantly bias parentage assignments.
Self-recruitment
The local parentage analysis assigned nine settlers collected at Curlew to parents, revealing a self-recruitment percentage of 4.6% (9 assigned settlers/194 total settlers) (95% CI: 1.7%, 7.6%). All assigned parent–offspring pairs mismatched at 1 or 0 loci and had LOD scores exceeding the critical value for 95% confidence (LODcritical = 4.00). Further, the simulation revealed that offspring were assigned to true parents 96% of the time, and that there was a 0% chance of false exclusion (Type II error) when the true parent was sampled, and only a 4% chance of false assignment (Type I error) when the true parent was unsampled. As mentioned in the Methods section, however, these error estimates are dependent on parameter input values.
A local connectivity network of these nine self-recruiting trajectories reveals the pattern of dispersal in terms of distance, direction and depth (Table 2; Fig. 3). While there are too few data points to statistically test for the association between these variables and the probability of dispersal, the network shows that seven of the nine trajectories have a northward directional change. Interestingly, one parent produced two of the self-recruiting offspring. There were also two self-recruiting offspring that settled on the same sponge. These data provide a preliminary description of the pattern of local dispersal and provide a foundation for future tests of the predictors of local dispersal.
| Offspring size (mm) | Parent (s) size (mm) | Origin sponge length (cm) | Destination sponge length (cm) | Distance (m) | Depth change (m) | N-S change | E-W change | |
|---|---|---|---|---|---|---|---|---|
| 1 | 9 | 40 | 34 | 56 | 256.5 | −2.5 | N | W |
| 2 | 9 | 48 | 46 | 47 | 19.5 | 1.8 | N | E |
| 3 | 10 | 51 | 46 | 18 | 174.3 | −2.6 | N | W |
| 4 | 10 | 52 | 38 | 26 | 112.2 | 3.3 | S | E |
| 5 | 10 | 54; 42 | 42 | 22 | 127.2 | 9.1 | N | W |
| 6 | 10 | 29 | 17 | 46 | 303.1 | −7.5 | S | E |
| 7 | 12 | 36 | 25 | 46 | 189.7 | 7.6 | N | W |
| 8 | 14 | 35 | 37 | 16 | 44.7 | −1.1 | N | W |
| 9 | 17 | 35 | 37 | 40 | 63.8 | 6.8 | N | W |
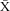 |
11.2 | 42.2 | 35.2 | 38.3 | – | – | – | – |
Predicted dispersal kernel
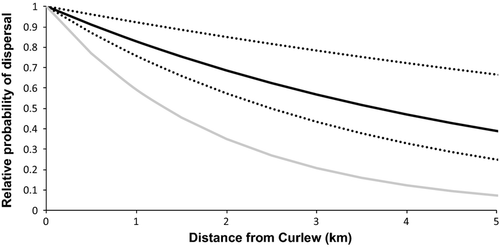
Of the simple exponential functions tested, y = 0.915x was the best predictor of observed self-recruitment (Fig. 4). This dispersal kernel explains the observed self-recruitment percentage of 4.6% at Curlew, accounting for the influx of offspring from nearby reef patches. The 95% CI around this approximation of the dispersal kernel was generated by determining which exponential functions explained the 95% CI around the observed self-recruitment percentage (Fig. 4; Lower 95% CI: SR = 1.7%; y = 0.965x; Upper 95% CI: SR = 7.6%; y = 0.865x).
Export analyses
Additional parentage analyses revealed an overall export percentage of 1.1% to six nearby sites within the metapopulation (two settlers assigned to Curlew parents/184 total settlers collected; 95% CI: 0%, 2.6%). Of the two settlers assigned to Curlew parents, one was collected from the north (site N2) and one was collected from the south (site S1) (Fig. 2b). The exponential best-fit curve through the observed self-recruitment and export proportions was y = 0.77x (Fig. 4; NLS regression: t = 679; d.f. = 5; P = 0.001). While the low sample size limits our ability to estimate a kernel directly from the observed data points, this best-fit line also reveals a rapid decline in the probability of dispersal, suggesting that the dispersal kernel approximated in this study may coarsely capture dispersal patterns within the metapopulation.
Discussion
Quantifying patterns of larval dispersal remains a major goal of marine ecology because it is essential for a complete understanding of marine population dynamics, and because of the potential benefits of incorporating connectivity data into marine reserve design. To date, the logistical difficulties of collecting marine dispersal data have limited most empirical studies to point estimates of self-recruitment or export. To advance our understanding of marine population connectivity, the focus must progress from making point estimates to fitting dispersal kernels to empirical data and testing the predictions derived from such kernels. In this study, we take a first step towards approximating a dispersal kernel for the coral reef fish E. lori along an 8-km stretch of reef on the barrier reef in Belize. Through genetic parentage analyses, we uncovered a 4.6% self-recruitment percentage. Working under the hypothesis that seascape patchiness is a primary determinant of observed measures of self-recruitment, we used habitat maps to estimate a simple exponential function, y = 0.915x, that would explain the observed self-recruitment and took that function to be a first approximation of the dispersal kernel. An analysis of export from the focal site suggests that an even more rapidly declining kernel may explain observed levels of dispersal within the metapopulation, although this analysis lacks statistical power due to the limited data. Taken together, the results of this study indicate a rapid decline in the probability of dispersal with respect to distance for E. lori.
These results add to the growing body of research that suggests the scale of marine larval dispersal is much shorter than previously assumed, as evidenced by other direct genetic estimates of dispersal (Jones et al. 2005; Planes et al. 2009; Buston et al. 2012), patterns of genetic differentiation (Taylor & Hellberg 2003, 2006) and bio-physical oceanographic models (Cowen et al. 2006). Our data are consistent with the only other empirically derived marine dispersal kernel, which was constructed for another microhabitat specialist – the anemonefish A. percula. As in E. lori, the probability of dispersal with respect to distance declined rapidly – fivefold over the first kilometre from source (Buston et al. 2012). Moreover, indirect dispersal data specific to the genus Elacatinus spp. suggest that neon gobies may have particularly short dispersal distances, as evidenced by their limited distributions (Colin 1975, 2010) and remarkably high levels of genetic differentiation between populations separated by as little as 23 km (Taylor & Hellberg 2003, 2006). With few obvious geographic barriers, short larval dispersal distances were initially proposed as the mechanism behind the unusually high genetic differentiation in Elacatinus spp. (Taylor & Hellberg 2003, 2006), but direct dispersal data have been lacking until now. A rapidly declining dispersal kernel such as the one proposed in this study could help explain observed genetic structure patterns found in this genus.
We found that the rapidly declining exponential function y = 0.915x was the best approximation of an E. lori dispersal kernel. This approximation was based on the observed self-recruitment percentage and accounted for the influx of larvae from all nearby reef patches on the MBR. We do not, however, claim that this simple function represents the true, underlying dispersal kernel. Instead, we believe that it serves two valuable purposes. First, it provides an initial approximation of the E. lori dispersal kernel. This approximation will guide the sampling design of future large-scale studies that will rigorously fit dispersal distributions to larger empirical data sets. Second, it lays out a quantitative framework for incorporating measurable empirical data and the seascape into kernel approximations. Shifting dispersal research towards more quantitative analyses will enable researchers to make predictions about dispersal. A predictive approach is essential to making progress in the field because it is the key to forecasting dispersal patterns under different scenarios and generalizing across systems (Nathan & Muller-Landau 2000; Botsford et al. 2009; Jones et al. 2009).
Eventually, a rigorous approximation of a marine dispersal kernel must be based on empirical dispersal events at many distance classes and should evaluate alternative functional forms of the kernel. A framework for these analyses can already be found in the terrestrial seed dispersal literature (Nathan & Muller-Landau 2000; Austerlitz et al. 2004; Greene et al. 2004). We chose to evaluate solely the negative exponential distribution in this study because it is a potential dispersal kernel form that is a 1-parameter probability distribution. Other distributions that are frequently used in seed dispersal studies, including the lognormal (Greene & Johnson 1989), Weibull (Ribbens et al. 1994) and 2Dt (Clark et al. 1999), require multiple parameter estimates. As marine ecologists continue to make progress in collecting empirical dispersal data, we will eventually be able to use a maximum-likelihood framework to evaluate alternative functional forms of the dispersal kernel. This study sets a foundation for this future quantitative work by testing whether the simplest functional form of the potential dispersal kernels can explain an observed empirical pattern.
The simple exponential kernel proposed in this study, and the probability distributions described above, represents phenomenological models of dispersal, which differ importantly from mechanistic models of dispersal (Nathan & Muller-Landau 2000). Phenomenological models characterize the function that best describes the observed relationship between dispersal and distance. These models are an important first step in quantifying dispersal patterns, especially because the spatial pattern of dispersal is what ultimately influences ecological and evolutionary processes such as recruitment dynamics, competition, mating, gene flow and local adaptation (Hanski 1999; Nathan & Muller-Landau 2000; Clobert et al. 2001; Hanski & Gaggiotti 2004). To begin generalizing across species and seascapes, the next step will be to assess how potential predictors shape these observed patterns (Nathan & Muller-Landau 2000). Because marine larval dispersal is a bio-physical process, realized dispersal patterns are certainly influenced by oceanographic processes and species-specific larval behaviours, in addition to seascape structure (Cowen & Sponaugle 2009; Jones et al. 2009).
In conjunction with other recent work (Buston et al. 2012), this study begins to build a framework for approximating marine dispersal kernels from empirical data. We show that simple kernels can be approximated from point estimates of self-recruitment and the structure of the seascape. Such simple kernels may serve an important role in conservation planning if a coarse approximation of larval exchange within an area is the goal, or if there are limited resources to quantify dispersal for many target species. Simple rules of thumb could also help identify key areas for stepping stone reserves that are well connected in a reef network. Quantitative estimates of dispersal kernels will also be useful in cases when the aim is to explicitly maximize connectivity in a reserve network because they can be used to assign connectivity values between potential reserve sites. Ultimately, understanding the patterns and predictors of dispersal across species and seascapes will enable us to build better predictive models of metapopulation dynamics and will strengthen our ability to predict the impacts of marine reserve design on connectivity and metapopulation persistence.
Acknowledgements
We thank the staff at Wee Wee Cay Marine Lab for use of their facilities, Marian Wong, Udell Foreman and Alissa Rickborn for assistance in the field, and Phil Lobel for logistical diving support. We are also grateful to Sean Mullen's laboratory for assistance with laboratory work, and two anonymous reviewers for helpful comments. Funding for this project was provided by a Boston University start-up award to PMB. CCD was supported by a NSF Graduate Research Fellowship and a Boston University Dean's Fellowship. JEM was supported by a Warren McLeod summer research fellowship. All work was approved by Belize Fisheries and the Boston University IACUC.
References
C.C.D. and P.M.B. planned the study. C.C.D., J.E.M. and P.M.B. conducted the field research. C.C.D., S.M.B. and R.G.H. contributed to genetic work. S.M.B. developed the microsatellite markers. C.C.D. wrote the paper and all authors contributed to revisions.
Data accessibility
Microsatellite data, dispersal simulations, sampling GIS waypoints, raw field data and all relevant GIS shape files are available via Dryad (doi:10.5061/dryad.76dc8).




