Sampling variables and their thresholds for the precise estimation of wild felid population density with camera traps and spatial capture–recapture methods
Editor: DR
ABSTRACT
- Robust monitoring, providing information on population status, is fundamental for successful conservation planning. However, this can be hard to achieve for species that are elusive and occur at low densities, such as felids. These are often keystones of functioning ecosystems and are threatened by habitat loss and human persecution.
- When elusive species can be individually identified by visible characteristics, for example via camera-trapping, observations of individuals can be used in combination with capture–recapture methods to calculate demographic parameters such as population density. In this context, spatial capture–recapture (SCR) outperforms conventional non-spatial methods, but the precision of results is inherently related to the sampling design, which should therefore be optimised.
- We focussed on territorial felids in different habitats and investigated how the sampling designs implemented in the field affected the precision of population density estimates. We examined 137 studies that combined camera-trapping and SCR methods for density estimation. From these, we collected spatiotemporal parameters of their sampling designs, monitoring results, such as the number of individuals captured and the number of recaptures, as well as SCR detection parameters. We applied generalised linear mixed-effects models and tree-based regression methods to investigate the influence of variables on the precision of population density estimates and provide numerical thresholds.
- Our analysis shows that the number of individuals, recapture frequency, and capture probability play the most crucial roles. Surveys yielding over 20 captured individuals that were recaptured on average at least once obtain the most precise population density estimates.
- Based on our findings, we provide practical guidelines for future SCR studies that apply to all territorial felids. Furthermore, we present a standardised reporting protocol for study transparency and comparability. Our results will improve reporting and reproducibility of SCR studies and aid in setting up optimised sampling designs.
INTRODUCTION
When occurring at their natural population densities, carnivores play important roles in ecosystem functioning, as they influence lower trophic levels by affecting the abundance of their prey and mesopredators (Estes et al. 2011). Their populations are increasingly threatened by human activities and direct persecution (Wolf & Ripple 2018), and concerted efforts are required for their conservation. Successful conservation actions need robust information on demographic parameters (or vital rates sensu Mills 2013), such as survival and population growth rate (O'Connell et al. 2011), preferably estimated over long periods. However, obtaining such parameters for species such as territorial carnivores with solitary lifestyles can be challenging, since they are elusive, tend to occur at low densities, and have large spatial requirements (Wolf & Ripple 2018).
Capture–recapture methods have emerged as powerful tools for monitoring elusive species such as territorial felids (O'Connell et al. 2011). These statistical methods use repeated camera-trap captures (recaptures) of individuals that are distinguished by uniquely identifying coat patterns to create capture histories over sampling occasions and derive demographic parameters. Spatial capture–recapture (SCR) models evolved from non-spatial capture–recapture models and, by incorporating the spatial information, that is the location of individuals and detectors, eliminate the need to calculate an effective trapping area (Efford 2004, Royle et al. 2009). The distribution of individual activity centres (density) in the state space S can then be estimated as a random spatial point process based on a detection function with two parameters: the capture probability g0 and the detection function scale σ as the distance over which the capture probability decreases (Efford 2004).
Spatial capture–recapture methods statistically outperform their non-spatial predecessor (Sollmann et al. 2011). Therefore, combined with camera traps as detectors, they have become the method of choice for surveying territorial solitary felids in demographic studies (Tourani 2022). The main weakness of SCR methods is that they require large sample sizes and a high number of recaptures to deliver precise results (Sollmann et al. 2012), which are often hard to achieve for felids (Howe et al. 2013).
In the last decades, literature reviews and simulation studies have provided protocols and sampling design guidelines for SCR methods, which are currently used by researchers. These protocols can be general (Foster & Harmsen 2012), species-specific (Tobler & Powell 2013) or even species- and area-specific (Weingarth et al. 2015). The key advice is that sampling designs should prioritise available resources to maximise capture probability and hence improve estimate precision (Tobler & Powell 2013). Therefore, the camera-trapping array size and intercamera spacing should be coupled to the target species' spatial ecology (e.g. mean male home range size) to maximise sample sizes and spatial recaptures (Tobler & Powell 2013). Further guidelines concern the survey length, which can be extended to capture more individuals (Harmsen et al. 2020) provided the demographic closure assumption remains unviolated (Dupont et al. 2019). Alongside the sampling design guidelines, researchers sought minimum thresholds for the most important parameters, that is sample size and recaptures, to secure precise results. Existing guidelines suggest that a minimum of 10–20 individuals should be captured during a survey (Otis et al. 1978), with a minimum of 20 total recaptures (Efford et al. 2009). Finally, the guidelines concerning the detection parameters and the model design suggest that the capture probability should be at least 0.20 (Boulanger et al. 2004) and the buffer width used to create the state space should be at least 2.5σ (Royle et al. 2014).
Fulfilling these recommendations can be challenging, especially when species have large spatial requirements, for example felids. Consequently, studies often used suboptimal sampling designs because of resource constraints and their adequacy is rarely evaluated beforehand through simulations (Green et al. 2020). Indeed, a recent review on camera-trapping and SCR methods found generally low-precision density estimates in a sample of studies on felids, due to small sample sizes (Green et al. 2020). Still, the existing guidelines have weaknesses that should be resolved. Protocols with general guidelines for SCR methods may not be broadly applicable as they are based on a limited number of species, local studies, and habitats. Even the use of species-specific protocols can be misleading when they are applied to different contexts, for example for the Eurasian lynx Lynx lynx, many SCR studies in Europe (e.g. Kubala et al. 2019) transferred the sampling design (e.g. survey length and season) and the model design (e.g. occasion length) from Zimmermann et al. (2013), who surveyed the species in areas of Switzerland with high capture probabilities due to particular habitat characteristics. In contrast, Weingarth et al. (2015) derived a different optimised survey length and season for lynx monitoring in the Bohemian Forest, Central Europe. Recommended parameter thresholds (e.g. the minimum number of individuals and capture probability) have been provided from simulations on non-spatial capture–recapture models (Otis et al. 1978, Boulanger et al. 2004) or from specific datasets and contexts (Efford et al. 2009), assuming their applicability to other contexts, including different data collection methods and species.
To date, no study has provided practical guidelines that can be applied to a wide range of species across different habitats. Furthermore, updated baselines for SCR parameters are needed. We fill these gaps with a systematic literature study and by reporting minimum standards that should provide precise estimates across diverse felid species and habitats. We focussed on territorial solitary felids (henceforth: felids), whose demography was surveyed with camera-trapping and SCR methods (ctSCR studies). We evaluated how the precision of population density estimates was influenced by sampling design and monitoring results and demonstrated the consequences of inadequate surveying effort. In particular, we investigated the effect of 1) the camera-trapping array size (hereafter array size) in relation to the home range sizes, 2) the total number of camera-trapping sites (hereafter the number of sites), 3) the total number of sampling occasions (hereafter the number of occasions), 4) the sample size or the number of individuals), 5) the total number of recaptures, 6) the capture probability, 7) the detection function scale and 8) the buffer width of the state space in relation to the detection function scale. Furthermore, we provide updated thresholds for numerical variables, particularly for the number of individuals, as references for future ctSCR studies. Finally, we summarise our findings to create a standardised reporting protocol that can serve as a basis for future ctSCR studies and contribute to the development of SCR applications of felid demography.
METHODS
Literature review
We used Google Scholar to search systematically for ctSCR studies (papers) on felids and kept only those indexed in the ISI Web of Science, as peer-reviewed studies are more likely to report complete information and their quality is assured by the review process. The following topic terms were used, for example, for tigers: ‘Tiger OR Panthera tigris spatial capture-recapture’ AND ‘Tiger OR Panthera tigris spatially explicit capture-recapture’, and studies using camera traps were collected (see Appendix S1 for a complete list of search strings). In total, we collected 161 studies targeting 20 felid species. Of these studies, 24 were discarded because of various reasons. For example: 1) sampling designs that were not tailored to the target species, leading to bycatches (n = 7), which are discouraged (Sollmann et al. 2012); 2) baited sites (n = 6), leading to potentially biased capture probabilities (Foster & Harmsen 2012); 3) unspecified density estimates or uncertainties (n = 4); or 5) SCR models with partial identity (Augustine et al. 2018) (n = 4), so that the sample size could not be correctly reported (see details in Appendix S2).
When a study comprised multiple surveys, each survey was considered to be independent. This was the case for all multisurvey studies because both fixed and varying sampling designs could result in different sample sizes and different density estimates. However, individuals from one study area can be recaptured over different surveys, and capture probability can change over time if individuals have seasonal behaviours or exhibit different site-response behaviours, for example if they become trap-happy or trap-shy (Rovero & Zimmermann 2016). Therefore, we accounted for this by using a random effect for the studies (intercept) and the number of recaptures (slope) in a generalised linear mixed-effects model (GLMM), as described below. The full dataset consisted of 522 surveys from 137 unique studies (Appendix S3), but only those with complete information regarding all variables were included in the analysis. We also included 11 studies with a sampling design that was tailored to multiple felid species (Appendix S3). Variables were extracted from the ‘Material and methods’, ‘Results’ or ‘Appendices’. In total, we included seven numerical variables and one categorical (Table 1).
| Variable | Description | Range | |||||
|---|---|---|---|---|---|---|---|
| Type | Name | Min | Max | ||||
| Numerical | Dependent | Coefficient of variation (CV) | Uncertainty measures divided by density estimates as an indicator of their precision | 0.01 (jaguar Panthera onca) | 2.56 (ocelot Leopardus pardalis) | ||
| Independent | HRA index | Index of array size adequacy in relation to mean male home range size | 0.47 (common leopard Panthera pardus) | 501.75 (leopard cat Prionailurus bengalensis) | |||
| Number of sites | Total number of paired or unpaired camera-trapping sites | 9 (European wildcat Felis silvestris silvestris; Iberian lynx Lynx pardinus) | 1129 (tiger Panthera tigris) | ||||
| Number of occasions | Length of surveys according to occasion length | 4 (jaguar Panthera onca) | 481 (tiger Panthera tigris) | ||||
| Number of individuals | Total number of individuals captured during one survey | 1 (Ocelot Leopardus pardalis) | 118 (tiger Panthera tigris) | ||||
| Number of recaptures | Total number of recaptures | 0 (Ocelot Leopardus pardalis) | 370 (ocelot Leopardus pardalis) | ||||
| Capture probability | SCR parameter for capture probability | 0.001 (jaguar Panthera onca; Sunda clouded leopard Neofelis diardi; tiger Panthera tigris) | 1.58 (common leopard Panthera pardus) | ||||
| Detection function scale (km) | SCR parameter for the distance from the activity centre over which an individual is not captured | 0.03 (common leopard Panthera pardus) | 55.58 (common leopard Panthera pardus) | ||||
| Levels with observations (percentage) for the full dataset | |||||||
| Categorical | State space adequacy | Adequacy of the buffer width used for the state space according to the rule of thumb of 2.5σ (Royle et al. 2014) | Adequate 241 (46) | Inadequate 52 (10) | Unknown 229 (44) | – | |
We used the maximum likelihood estimation (MLE) standard error (SE) or Bayesian posterior standard deviation (SD) – in a few cases, SE was reported for Bayesian methods – as a measure of uncertainty for density estimates. The ratio between uncertainty and density estimates indicated the coefficient of variation (CV), which was used as a reference for the precision of density estimates (Green et al. 2020). A CV <0.20 indicated high precision, while a CV between 0.20 and 0.30 indicated moderate precision and acceptable results (Dormann 2017). When studies only reported a confidence interval or posterior confidence interval, we calculated SE or SD following Altman and Bland (2005). In only one case, an 85% confidence interval was reported; thus the confidence interval range was divided by 2.88. For 20 studies that used both MLE and Bayesian methods on the same dataset (51 surveys per framework), we investigated their performance by comparing the precision of density estimates with a paired t-test.
Although the use of unpaired sites could hinder individual identification and thus reduce sample sizes, we considered paired and unpaired sites together in the number of sites because most studies reporting this information (n = 111; 83%) used paired sites.
The survey length was mostly reported in days. Alternatively, when the number of months was indicated, we calculated days by multiplying the months by 30 days. In a few studies (n = 28; 5%), the survey length was reported with ranges and we calculated the mean. We then divided the survey length by the occasion length to obtain the total number of occasions. Most studies reporting this information (n = 78; 72%) used a one-day occasion length while a few studies used other approaches (from 2 days to 2 weeks). Testing the effect of different occasion lengths was beyond the scope of this study and also impossible because studies did not test multiple occasion lengths.
Concerning sample sizes, we did not include information on individual identification (i.e. how complete and partial identities were treated) in the analysis, because that information was provided in only 18 studies. However, we reported on studies that mentioned such details in the descriptive results.
The information on spatial recaptures, that is recaptures at different sites, was poorly reported. Therefore, we accounted for the overall number of recaptures from all sites. This information was taken as reported or calculated by subtracting the number of individuals from the number of independent captures to discard each individual's first capture (Avgan et al. 2014). The number of recaptures is correlated to the number of individuals (Appendix S4): if all individuals were recaptured once, the number of individuals and recaptures would be equal. We considered the two variables separately but took into account their relationship for further discussion.
If covariates were used on the capture probability and detection function scale, we calculated the mean for the parameters. When the Akaike Information Criterion was used for model selection (73 studies), we extracted the results of the best model as reported by each study. The information regarding parameter covariates was included in the descriptive results.
As we did for the model frameworks, we inspected what model approaches were used, and, for studies applying both closed and open population models (10 surveys per approach), we compared their performance with a Wilcoxon signed-rank test on the CVs because of the non-independence of the few observations. Furthermore, we collected additional information on the model designs for the descriptive results. Concerning the state space adequacy, when different buffer widths were tested on the same dataset, we created a row for each value and duplicated information on the sampling design and monitoring results.
Statistical analysis
The collinearity of numerical variables was checked via Spearman cross-correlation, and the variables with a correlation coefficient | ρ | > 0.70 were discarded (Dormann et al. 2013). First, we checked for the linearity of all variables with CV using a generalised additive mixed-effects model (GAMM) in the R package ‘mgcv’ (Wood 2011). Hence, numerical variables were scaled to z-scores. Information from the GAMM was then used to model appropriate functions for each variable in a GLMM with gamma error distribution (log-link function) in the R package ‘lme4’ (Bates et al. 2015). We accounted for the potential effect of multisurvey studies (intercept) and the number of recaptures (slope) through random effects in the model. Hence, we compared the GLMM with the random effect to a basic generalised linear model (GLM) through a likelihood ratio test. Finally, we extracted the conditional modes of the random effects from the model.
This step allowed us to make inferences about the behaviour of each study in relation to the observed overall mean response of densities to the model variables. Hence, a study differing significantly from the mean was considered an exception and the reasons for this were investigated by referring back to the study, for example, if a study had high precision for density estimates despite a low number of recaptures and vice versa.
All variables that were significant in the GLMM were used to fit a conditional inference tree (CTree) in the R package ‘partykit’ (Hothorn & Zeileis 2006), again to test their influence on the precision of density estimates. Statistical significances between the CV boxplots in the CTree results were evaluated based on the overlap of boxplot whiskers, which indicate variability outside the lower and upper quartiles of a boxplot and precede outliers. All variables were ranked using random forest models that were fitted using the R package ‘randomForest’ (Liaw & Wiener 2002). For the latter, we fitted a number of trees equal to five times the number of observations, ensuring each variable could be predicted multiple times (Breiman 2001). Uncertainty was estimated by bootstrapped random forest fittings 500 times. The response to significant variables from the GLMM used in the random forest was then checked through accumulated local effects plots using the R package ‘ALEPlot’ (Apley 2018). All statistical analyses were conducted in the R software version 4.2.0 (R Core Team 2022). The R code used for the analysis can be found in Appendix S5.
RESULTS
Literature review
Concerning the 161 studies we found in the literature, the total number of ctSCR studies per species varied between 1 and 48, with the majority (66%) focussing on three large felids: the common leopard Panthera pardus (n = 48), tiger Panthera tigris (n = 36) and jaguar Panthera onca (n = 22; Fig. 1). The number of papers published increased from one in 2009 to 17 in 2021.
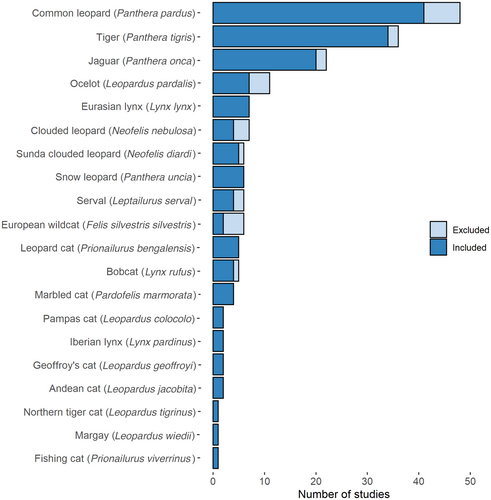
Overall, we observed wide ranges for all numerical variables (Table 1). The CV ranged from 0.01 to 2.56 with a mean of 0.30 and high precision (<0.20) for 50 studies out of 137 (36%). The HRA index ranged from 0.47 to 501.75; an index of <1 means that the array size was smaller than the HRS. State space adequacy could not be verified in 44% of the cases (‘unknown’ level) because of missing information on the detection function scale or the buffer widths. MLE was the most frequent model framework (87 studies). Based on 20 studies that applied both frameworks, the performance of Bayesian methods was significantly better than MLE (P < 0.001). Analyses mainly used a closed population model (124 studies), while open population models were rarely adopted (n = 5). Eight studies used multisession models enabling a data-pooled model fitting with shared parameter values across surveys. Open population models significantly (P < 0.001) outperformed (lower CV) closed population models. A null model with no covariates on the detection parameters was the most common approach (91 studies), and in 39 studies, this was selected by the Akaike Information Criterion as the best model. Sex was the most frequently tested covariate on the detection parameters (n = 41), followed by site-response covariates (n = 7), on/off-road sites (n = 4), and age (n = 1). Environmental predictors about topography, for example elevation, slope or forest cover, were included in the models for the density or detection parameters in 14 studies, and a habitat suitability mask was used in 52 studies. Finally, 11 studies simulated the adequacy of the sampling design before field implementation.
Only 47 studies gave details on the individual identification process or how complete (both flanks) and partial (single flank) identities were treated to avoid overcounting. In most studies, two or three independent observers identified pictures, which were cross-checked by one additional observer. Alternatively, the Extract-Compare Software (Hiby et al. 2009) was used for matching individual patterns (n = 6 studies). For capture histories, six studies used both flanks plus the single flank with the highest number of captured individuals, 10 studies used only the single flank with the highest number of captured individuals and two studies discarded single flanks.
Statistical analysis
A total of 151 surveys (29%) referring to 44 unique studies reported complete information regarding all variables of interest and could be used for the analysis. Variables were affected by missing data in the following order: the number of recaptures (48%), HRA index (24%), capture probability (24%), number of occasions (23%), detection function scale (23%) and the number of sites (3%).
None of the variables was strongly correlated, and therefore, all were included in the subsequent modelling (Appendix S6). Results of the GAMM showed linearity for all variables except for the number of individuals (Appendix S7), which was subsequently modelled as a linear variable because of the wide confidence interval at higher values. The best GLMM had an adjusted R-squared of 0.71 indicating a high explanation of variance by the model. Results of the likelihood ratio test indicated that the GLMM performed significantly better than the GLM (P < 0.001). In order of importance, the number of individuals and the number of recaptures were the only variables having a significant influence on the CV (Table 2), indicating a threshold after ≈ 20 individuals and ≈ 100 recaptures, respectively (Appendix S4).
| Fixed effect | Estimate (SE) | P-value |
|---|---|---|
| Intercept | −1.23 (0.08) | <0.001*** |
| HRA index | 0.003 (0.04) | 0.93 |
| Number of sites | 0.03 (0.09) | 0.76 |
| Number of occasions | −0.05 (0.04) | 0.23 |
| Number of individuals | −0.30 (0.06) | <0.001*** |
| Number of recaptures | −0.10 (0.05) | 0.04* |
| Capture probability | −0.06 (0.03) | 0.04* |
| Detection function scale | −0.05 (0.03) | 0.07 |
| State space adequacy | ||
| (Adequate) | −0.004 (0.07) | 0.95 |
| (Unknown) | –0.01 (0.16) | 0.95 |
| Random effect | Variance (SD) | |
| Study (Intercept) | 0.03 (0.18) | |
| Number of recaptures | 0.004 (0.07) | |
| R-squared (adjusted) | ||
| Total | Fixed effect | Random effect |
| 0.73 (0.71) | 0.44 (0.40) | 0.29 (0.30) |
- * p < 0.05.
- *** p < 0.001.
Inspection of the conditional modes in the random effect revealed studies that differed significantly from the overall mean response (Appendix S8). Four studies (Ramesh et al. 2017, Lamichhane et al. 2019, Mena et al. 2020, Searle et al. 2021) had surveys with a high number of recaptures and low CVs. Surveys from these studies were found in the CTree node with the highest density precision. Two studies (Brodie & Giordano 2012, Ramesh et al. 2012) had a very low number of individuals and, despite relatively high recaptures, very low density precision. Surveys from these studies were found in the CTree node with the lowest density precision. Finally, one study (Duľa et al. 2021) had a very low number of individuals and low CVs.
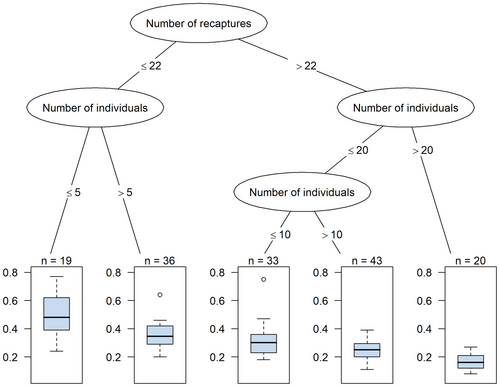
The number of individuals, the number of recaptures, and the capture probability were significant in the GLMM approach and subsequently included in the CTree analysis. The main tree node divided data into two major groups with terminal nodes including clusters of surveys: number of recaptures ≤22 and >22, with higher precision for density estimates in the latter (Fig. 2). Here, the terminal node with 20 surveys from nine studies (Hearn et al. 2016, Ramesh et al. 2017, Wang et al. 2017, Balme et al. 2019, Lamichhane et al. 2019, Tempa et al. 2019, Kittle et al. 2021, Palmero et al. 2021, Searle et al. 2021) with the number of individuals >20 had the highest precision (mean CV = 0.16; SD = 0.06). The lowest precision results (mean CV = 0.49; SD = 0.17) were obtained in the first group and a terminal node with 19 surveys from 10 studies (Ramesh et al. 2012, Sunarto et al. 2013, Singh et al. 2014, Thornton & Pekins 2015, Ramesh et al. 2017, Hearn et al. 2019, Mohamed et al. 2021, Naing et al. 2019, Noor et al. 2020, Duľa et al. 2021) with low numbers of individuals (≤5) and recaptures (≤22). When the number of individuals was between 11 and 20, more than 22 recaptures, that is more than one recapture per each individual, helped obtain moderate precision (mean CV = 0.25). Finally, a number of individuals ≤10 led to imprecise results, independently of the number of recaptures.
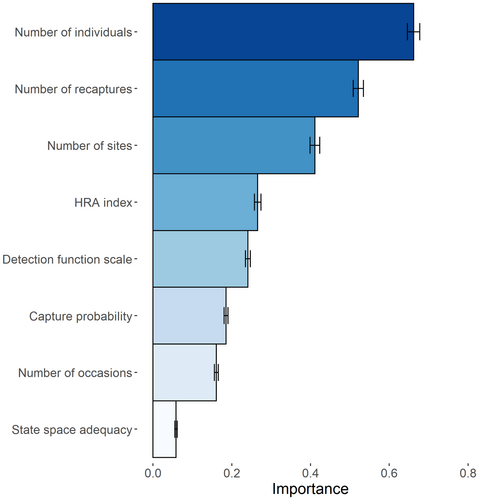
We fitted 755 trees for the random forest, which ranked the number of individuals and the number of recaptures highest, that is importance equal to 0.66 (SD = 0.01) and 0.52 (SD = 0.01), while the state space adequacy was ranked lowest with an importance of 0.06 (SD = 0.003; Fig. 3). Although capture probability was significant in the GLMM, its importance was 0.18 (SD = 0.005). The results of the accumulated local effect plots were coherent with the previous approaches and indicated a decrease in the CV (decreasing accumulated local effects main effect) with increasing numbers of individuals, numbers of recaptures and capture probability (Appendix S9).
DISCUSSION
Our analyses revealed that the precision of population density estimates is mainly influenced by the number of individual felids captured, the number of recaptures, and the capture probability. In particular, we found studies with a sample size of >20 individuals that were recaptured at least once provided the most precise density estimates. More than one recapture per individual helped obtain moderate precision when the sample size was >10. According to our methods, all other variables were not statistically significant, which might indicate that all other study design factors, such as the number of occasions, were already well set up.
Overall, the most important variable was the number of individuals. This finding is corroborated by previous simulation studies and reviews (Sollmann et al. 2012, Green et al. 2020). Collectively, our results indicated that a sample size greater than 10 and 20 individuals is needed for moderate and high precision, respectively. These thresholds are in line with the recommended minimum of 10–20 individuals for conventional non-spatial models (Otis et al. 1978). Hence, we can state such a value is robust for capture–recapture methods in general, both non-spatial and spatial. This finding directly relates to the array size, as array size influences the sample size of individuals (Sollmann et al. 2012, Green et al. 2020), although the number of individuals was not correlated to the HRA index (Appendix S6). According to guidelines from the literature, the array size should be at least as large as the mean male home range size of the target species (Efford & Boulanger 2019). However, a minimum sample size of 20 requires surveying an area that is as large as several male home range sizes. On the contrary, non-resident (transient) individuals are inevitably captured during surveys for which demographic closure is assumed, and they increase the sample size independently of the array size, which could explain the low correlation between the number of individuals and the HRA index. However, these individuals do not provide valuable information on animal movement, because they have no territory; they decrease the overall capture probability and inflate density estimates (Larrucea et al. 2007). To conclude, researchers should mainly devote resources to enlarging the array size, as also recommended by Green et al. (2020), to include a higher number of resident individuals that are meaningful for density estimations.
The second most important variable resulting from our analyses was the number of recaptures. The positive relationship between this variable and the precision of density estimates is supported by previous simulation studies (Efford 2004, Sollmann et al. 2012). Our optimum of 22 is in line with Efford et al. (2009) from simulations on stoats Mustela erminea identified by genotyping. This indicates that the minimum value of 22 recaptures is robust and can be considered generally valid for SCR methods across different species and data collection methods. However, we have to consider that we found the same optimum value for the number of recaptures and the number of individuals due to an artefact deriving from their relationship: if all individuals are recaptured at least once, the number of recaptures equals that of individuals. Therefore, instead of considering an optimum value for the number of recaptures, our findings indicate that each individual should be recaptured at least once for precise results. We observed that an increasing number of recaptures compensated for decreasing numbers of individuals, ensuring acceptable results for density estimates. This finding is important, as it represents a potential solution when the array size is limited by resource constraints, as is often the case. Enlarging the array sizes can increase the number of recaptures (Sollmann et al. 2012). Other parameters can also be manipulated for this purpose: the intercamera spacing controlling the number of sites and the survey length. Multiple sites should be set within the smallest home range area of the target species to increase the number of recaptures. In territorial carnivores, females commonly have smaller home ranges than males (Sollmann et al. 2011). Therefore, intercamera spacing should be shorter than the radius of the mean female home range with a maximised number of sites within the array (Tobler & Powell 2013). Furthermore, survey length can be extended to increase both sample size and recaptures. Although care is required as an overlap with the breeding season can cause bias (Dupont et al. 2019), the benefits of an elongated survey length are shown to outweigh the risk of violating the assumption of demographic closure (Harmsen et al. 2020).
The last significant variable in the GLMM was capture probability, which again is in line with existing literature (Tobler & Powell 2013). Although this variable was included in the CTree, the model output did not provide a threshold, showing that the number of individuals and recaptures was dominant. This was reflected in the random forest output that ranked capture probability among the lowest. The rule of thumb for the non-spatial capture–recapture method from Boulanger et al. (2004), derived from a simulation study on the grizzly bear Ursus arctos, states that capture probability should be at least 0.20. However, such a value is unrealistic for elusive carnivores occurring at low densities, and most studies in our dataset obtained values below this threshold (mean capture probability was 0.06). A high capture probability provides precise density estimates and allows researchers to reduce the array size or the survey length, thus saving resources. It is therefore crucial that camera traps are placed in a way that maximises capture probability. When dealing with felids, the best choice is to place camera traps on trails or forestry roads, as felids use them to move over larger distances with low effort (Sollmann et al. 2011). Considering species with specific marking spots, these could be targeted as sites to increase detection probability (Fabiano et al. 2020). In addition, information from telemetry or kill sites can be used to select suitable places for camera traps. As mentioned, transient individuals can decrease overall capture probabilities. Therefore, researchers should time data collection outside the mating season, when transients are less likely to be observed (Weingarth et al. 2015).
Our results indicated that Bayesian methods performed better than MLE. This finding is consistent with Royle et al. (2009), who demonstrated that Bayesian methods cope better with small sample sizes. Considering that large sample sizes are often hard to achieve, Bayesian methods are generally preferable, and many R packages are available to support the methods, for example Royle et al. (2014), which provides several coding examples.
We found that open population models provided more precise density estimates than their closed counterparts. Although the number of observations was low (1 study, 20 surveys), this finding is in line with the literature. The single study adopted open population models in a Bayesian framework, which shares information across multiple surveys to produce unbiased posterior distributions of the demographic parameters (Chandler & Clark 2014). Though such models are less popular than conventional closed population models because of their high complexity and computational requirements (Tourani 2022), we recommend their use in future multiyear studies.
We detected outliers in the studies we investigated. Inspection of a study with a low number of individuals but a high number of recaptures (Brodie & Giordano 2012) revealed that most recaptures were of only one individual, which is likely to have caused low precision. Spread-out recaptures of individuals inform the model of animal movements in space, providing robust density estimates (Sollmann et al. 2012). When this information is only available for a small subset of the individuals, movement may not be representative of a larger sample size. Therefore, the model struggles to produce reliable results. One other study (Duľa et al. 2021) had a comparable number of individuals and recaptures to Brodie and Giordano (2012), but with high precision. The study did not report the details, but we assume that the recaptures were well distributed among individuals, providing realistic movement estimates.
Literature- and study-based guidelines
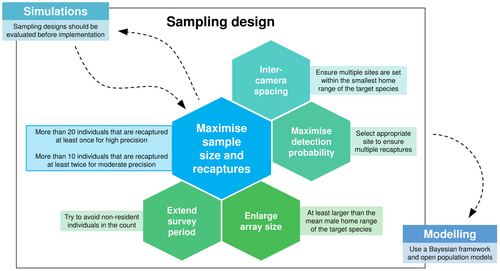
Our results were in line with the guidelines provided by previous protocols and rules of thumb, highlighting their robustness. We propose the following guidelines based on our findings, which can serve in future ctSCR studies on felids to foster high precision. Researchers should prioritise maximising the sample size for high precision, ensuring >20 individuals are captured per survey with recaptures that are approximately evenly distributed across individuals; that is, each individual should be recaptured on average at least once. For moderate precision, > 10 individuals should be recaptured at least twice. High values for the sample size can be accomplished by enlarging the array size, extending the survey length or increasing detection probability by focussing camera deployments at highly used sites (Sollmann et al. 2012, Green et al. 2020, Harmsen et al. 2020). If possible, the array size should be larger than the mean male home range of the target species (Efford & Boulanger 2019). Where available, information on home range sizes for the calculation of array size and intercamera spacing ensuring multiple spatial recaptures should be retrieved from telemetry studies previously conducted in the area (Sollmann et al. 2012, Tobler & Powell 2013). To conclude, for a given number of sites, researchers should seek a trade-off between increasing the array size and ensuring multiple spatial recaptures controlled by adequate intercamera spacing. Alternatively, researchers can rely on studies from other areas to make sure ecological characteristics, such as prey availability and habitat features, are comparable. Moreover, capture probability should be maximised by selecting appropriate sites to ensure that individuals are (re)captured, for example forestry roads or marking sites (Sollmann et al. 2011, Fabiano et al. 2020). Like Green et al. (2020), we found that few researchers evaluated the adequacy of sampling designs before field implementation. This procedure can reveal sampling design weaknesses, and we encourage future researchers to perform simulations for this purpose. Finally, we suggest fitting models under a Bayesian framework, especially when the sample size is small, and using open population models. All these guidelines are summarised in Fig. 4.
Study limitations
Not all the variables were significant in our analysis, which could also be due to how they were tested. For the HRA index, we used the allometric home range scaling with body mass (Tamburello et al. 2015). However, this might be unreliable because felid home ranges can vary considerably across habitats, for example by a factor of 10 for the Eurasian lynx in its European range (Kvam et al. 2001). Ideally, home range sizes would be area-specific and inform the chosen array size, but local information is rarely available. Our verification of the adequacy of intercamera spacing was impeded because the smallest observed female home range size in the area is required for verification, and this information was missing (only 24 studies reported mean female home range sizes in the study areas). To overcome the artefact given by the relationship between the number of individuals and recaptures, one solution would be to calculate a ratio between the two variables, including how the recaptures are distributed across individuals, that is skewness. The skewness of recaptures could then be investigated using indices such as Shannon's Hill number. To do this, full capture histories indicating the distribution of recaptures across individuals are necessary, but, unfortunately, full capture histories were rarely found in the studies we investigated.
Our approach was limited by data gaps. Many ctSCR studies did not report important parameters, causing their exclusion from the analysis because of missing data. This primarily concerned the number of recaptures and their distribution across individuals, followed by the HRA index because of unspecified array sizes, then both the detection parameters, and lastly, the number of occasions because of unreported occasion lengths. While including it caused a considerable reduction in the dataset, we decided to keep the variable ‘number of recaptures’ in our analysis because of its importance, as reported in the literature (Sollmann et al. 2012), which was also repeatedly observed in our findings.
Standardised reporting protocol
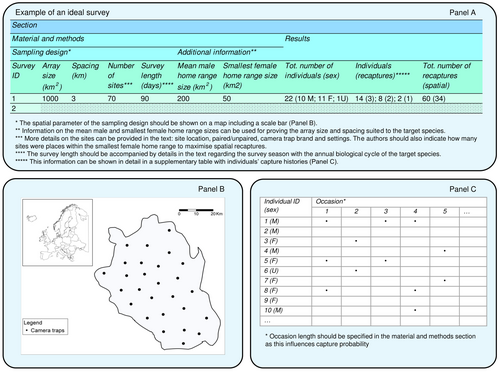
To overcome the issue of unreported parameters in future studies of felid populations, we propose a standardised protocol for reporting the results in SCR studies (Fig. 5). Following this protocol will help improve the transparency and reliability of studies, allowing careful interpretation of results and facilitating meta-analyses. Since details on individual identification methods were rarely reported, we recommend that future SCR studies also follow the Individual Identification Reporting Checklist (Choo et al. 2020), indicating minimum standards for this purpose. Finally, authors should delineate the model design, that is the model framework, approach, and covariates, and indicate estimates and uncertainties for the density, the capture probability and the detection function scale.
CONCLUSIONS
Spatial capture–recapture methods have been increasingly used for estimating demographic parameters of rare and elusive mammalian species, but generally provide low precision because of inadequate sampling efforts. Based on an analysis of studies on territorial felid species, we were able to identify the sample size of individuals, the number of recaptures and the capture probability as the most important parameters affecting the precision of SCR density estimates, and we provide updated thresholds for achieving acceptable values.
Our findings can be used as guidelines for supporting future ctSCR studies to survey various species of interest. In particular, researchers and other professionals can use recommendations from this work to achieve precise density estimates, which are at the core of effective conservation plans. Moreover, we highlight incomplete and/or incoherent reporting of key sampling and output parameters across many ctSCR studies and therefore suggest that future researchers should strive towards more complete and transparent reporting of all parameters, thus allowing proper evaluation of sampling design adequacy for the target species. To this end, we provide an example protocol for improving the reporting of SCR methods.
ACKNOWLEDGEMENTS
Open Access funding enabled and organized by Projekt DEAL.
FUNDING
The study was funded by the German Academic Exchange Service (DAAD), and open access was facilitated by the University of Freiburg.




