The evolution of species abundances in terrestrial vertebrates
Abstract
Interspecific differences in species abundances are one of the oldest and most universal patterns in ecology, yet little is known about how these differences are generated over evolutionary time. In this study, we test whether there is evidence for phylogenetic signal in population densities of four large groups of terrestrial vertebrates, namely birds, mammals, amphibians, and squamates. In addition, we test the hypothesis that the relative number of species in a clade might be a predictor of the abundance of its constituent species. However, given that the number of species in a clade is the outcome of both its age and diversification rate, and each of these factors was tested separately. Our results provide strong support for phylogenetic signal in species densities for all clades, regardless of differences in how species density was computed, or phylogenetic uncertainty. On the other hand, there was no evidence for a relationship between species abundance and the diversity of its encompassing clade. The implications of phylogenetic signal are discussed in the context of models of species abundance distributions, including Hubbell's neutral theory of biodiversity and biogeography.
1 INTRODUCTION
Nearly all biological communities share a similar phenomenon: their species abundance distributions (SADs) tend to follow a "hollow curve" in which most species are rare, whereas some species are disproportionately abundant (Rosenzweig, 1995). This pattern is one of ecology's oldest and most universal laws (Preston, 1948; Raunkiaer, 1909), and a variety of models have been proposed to properly describe SADs, including log series (Fisher et al., 1943), modified lognormal (Preston, 1948), broken-stick (MacArthur, 1957), and zero-sum multinomial (Hubbell, 2001) distributions. However, surprisingly few models are effectively rejected, probably because most theories do not make any predictions beyond the hollow-curve SAD itself, and it is unlikely that small variations in the nature of the hollow curve will ever lead to strong inference and decisive tests of SAD theories (McGill et al., 2007). One tacit assumption of this approach is that there would not be anything peculiar about common or rare species. Rather, they would merely represent the tails of SADs, such that interspecific variation in species abundances is simply the result of different independent manifestations of common underlying probability distributions. Instead of a phenomenological perspective focused on the SADs themselves, one might envision an alternative approach that would rather explore more mechanistic models of the macroevolutionary processes that actually generate and change species and their relative abundances.
Despite considerable advances in phylogenetic comparative methods over the past few decades, surprisingly little is known about how species abundances evolve at macroevolutionary timescales. On the other hand, many models of species abundance distributions implicitly make assumptions regarding their evolution. For instance, according to Hubbell's neutral theory (Hubbell, 2001), species abundances vary randomly over time in a manner analogous to genetic drift of alleles on a gene pool (i.e., ecological drift). As a consequence, there would be no expectation for closely related species to show abundances that are more similar than one would expect by chance. This is especially the case for the assumption of "point-mutation" speciation, as each speciation event would effectively erase all history with respect to the abundance of its parent species. To the best of our knowledge, only four studies to date have explicitly tested this assumption. First, Purvis et al. (2005) estimated the phylogenetic signal in species abundances in primates and carnivores and found estimates comparable to other traits that are typically recognized as being phylogenetically autocorrelated, such as body size. In addition, Kelly et al. (2008) compared the abundances of pairs of bird species in a highly diverse Mexican forest and found that congeneric species shared similar abundances, yet this pattern became non-significant at higher taxonomic levels. Finally, Dexter and Chave (2016) and Loza et al. (2017) found significant levels of phylogenetic signal in Amazonian and Andean plant species, respectively. These studies contradict the assumption of no phylogenetic signal in species abundances, yet the extent to which those results are general is still unclear.
An intriguing pattern has been recently uncovered in studies on species abundance patterns: the relative number of species in a clade might be a predictor of the abundance of its constituent species (Dexter & Chave, 2016; Schwartz & Simberloff, 2001; Ulrich, 2005). If true, this pattern could suggest a causal link between species abundance and the actual process of lineage diversification. However, these studies have been inconsistent with respect to the direction of this association. For instance, Schwartz and Simberloff (2001, see also Pitman et al., 2001; and Lozano & Schwartz, 2005) found that species-rich plant families tended to show higher proportions of rare species. Also, Dexter and Chave (2016) found a negative relationship between species richness of genera and mean abundances across species in Amazonian plants. On the other hand, the opposite was found by Webb and Pitman (2002), which showed that plant species from species-rich families also tended to be locally abundant, a pattern that was also previously found in a study of carnivores and primates, in which rare species were associated with species-poor taxa (Gittleman & Purvis, 1998). Similarly, Ulrich (2005) found a positive relationship between mean species density and family richness for European Hymenoptera. Finally, Edwards and Westoby (2000) compared the abundance of species of the same plant families in different continents and found no consistency across continents as to which families have high or low proportions of rare species and argued that the unique biogeographic history of the location in which studies are conducted is equally (if not more) important in explaining patterns of rarity within lineage than their biological traits. The causes for this incongruence between studies are still poorly understood, but it is likely to involve differences in geographical scale (local/regional) and taxa. However, and perhaps more importantly, the species richness of a clade can more strongly reflect differences in clade age than in their underlying diversification rates (Scholl & Wiens, 2016), yet variation in family/genus age was consistently not accounted for in previous studies. Finally, most of these studies failed to use phylogenetic comparative methods, which could possibly lead to increased chances of false positives.
In this study, we provide a comprehensive assessment of the evolution of species abundances in terrestrial vertebrates. In particular, our goals were (1) to assess the level of phylogenetic signal in species abundances in four large vertebrate clades (i.e., mammals, birds, squamates, and anurans) and (2) to test, using phylogenetic comparative methods, the relationship between clade richness and species abundance.
2 MATERIALS AND METHODS
2.1 Data sources
Our analyses included data on abundance, body size, and geographical range of species from four terrestrial vertebrate taxa, namely mammals, birds, amphibians, and squamates. Given that population abundances depend on the size of the area being assessed, all analyses were based on population densities (i.e., number of individuals/km²). We obtained population density information for terrestrial vertebrate species using the TetraDensity database (Santini, Isaac, & Ficetola, 2018). We only considered estimates in terms of the numbers of individuals and omitted estimates based on pairs or males alone. If estimates were provided with respect to hectares, they were transformed to km prior to the analyses. We also obtained estimates of body mass for the same species compiled above using four different databases: PHYLACINE (version 1.2.1; Faurby et al., 2020), Elton Traits (version 1.0; Wilman et al., 2014), AmphiBIO (Oliveira et al., 2017), and Slavenko et al. (2019). We tried to use as much data as possible for each taxon from the same dataset, such that most body mass data were obtained from PHYLACINE for mammals, EltonTraits for bird species, AmphiBIO for amphibians, and Slavenko et al. (2019) for squamates. Because body mass is rarely recorded in amphibians, we also used a measure of snout to vent length (SVL) for all the amphibian species in our dataset. The SVL measure is highly correlated with body mass (Santini, Benítez-López, Ficetola, & Huijbregts, 2018). If a species had density data available, but its body mass/SVL was not available from the abovementioned sources, we completed the final datasets by searching the primary literature, and references corresponding to the data for each species are available in Table S1. The average number of density estimates per species was 7.21 (SD = 17.27, range = 1–408).
Geographical range sizes were obtained from polygons of geographical distribution in the IUCN Red List of Threatened Species database version 2018–2 and complemented with new data available in version 2020–3. Our range size estimate for each species excluded areas of the ranges classified as invasive or uncertain by IUCN. The species taxonomy followed the IUCN classification since among the databases used the platform presents more accuracy in recent taxonomic changes. Finally, phylogenetic data for amphibians, squamates, birds, and mammals were obtained from Jetz and Pyron (2018), Tonini et al. (2016), Jetz et al. (2012), and Upham et al. (2019), respectively. If a species with density data was missing from the phylogeny, its name simply replaced one randomly chosen species of the same genus in the corresponding tree, given that all species in a monophyletic genus share the same divergence time with respect to its sister clade. In total, we replaced 30, 80, 4, and 7 species of mammals, birds, amphibians, and squamates in the trees with only genetic data, and 4, 3, and 2 species of mammals, birds, and squamates, respectively, in the complete trees. The final datasets included 529, 821, 66, and 237 species of mammals, birds, amphibians, and squamates in the trees with only genetic data, and 546, 838, 66, and 237 species of mammals, birds, amphibians, and squamates, respectively, in the complete trees.
2.2 Analyses
As sensitivity analyses, we used three measures of species density, namely the median, the mean, and the maximum density across all estimates. Phylogenetic signals of the measures of density, range size, body mass, and SVL were estimated using both Pagel's λ (1999) and Blomberg et al. (2003), with significance tests obtained either using likelihood ratio tests or using randomizations, respectively. These tests were performed using the phylosig function in “phytools” 0.7–70 (Revell, 2012). We made one important addition—because body size and geographical range usually have strong phylogenetic signal (e.g., Blomberg et al., 2003; Pie & Meyer, 2017) and that both are commonly shown to correlate with abundance (e.g., White et al., 2007), one could envision a scenario in which significant phylogenetic signal in abundance could be a by-product of strong phylogenetic signal in body size or geographical range. To test this scenario, we used phylogenetic generalized least squares (PGLS; Grafen, 1989; Symonds & Blomberg, 2014) to estimate residuals of densities after controlling for body size and geographical range using the phyl.resid function in “phytools” 0.7–70 (Revell, 2012), and estimated the phylogenetic signal of the residuals using Pagel's λ (1999) and Blomberg et al. (2003), and using the phylosig function. All traits were log-transformed prior to the analyses.
We tested the relationship between species abundance and clade richness using PGLS, with species median abundance as the dependent variable, and diversification rate and clade age as independent variables, using the pgls function in “caper” 1.0.1 (Orme et al., 2018). Diversification rate was approximated as ln(S)/t, where S is the number of species in a given clade and t is the divergence time between the clade and its sister group (stem age). Also, t was used as the estimate for the clade age. These analyses were repeated both at the level of genera and of families. We also used PGLS to test the relationship between species abundance and body mass, and species abundance and SVL for amphibians. For the phylogenetic signal analyses, we exclusively used phylogenies including species with only genetic data, given that the phylogenetic imputation used to produce the complete topologies can bias the inferred phylogenetic signal, but we used the complete topologies for the other analyses. To account for phylogenetic uncertainty, we carried out phylogenetic signal analyses across 1000 alternative topologies in the case of mammals and birds, and, for the PGLS analyses, across 1000 alternative topologies for all clades, using “sensiPhy” 0.8.5 (Paterno et al., 2018). We modified the tree_physig in “sensiPhy” to return the estimates as mean and confidence intervals calculated as the 2.5% and 97.5% quantiles. All analyses were performed using R 4.0.3 (R Core Team, 2020).
3 RESULTS
Variation in median population density across the studied taxa is shown in Figure 1a. Despite some overlaps, there were clear differences between taxa in their distributions, with ectotherms (amphibians and squamates) showing considerably higher densities than endotherms (mammals and birds), as expected. Moreover, there was a clear relationship between density and both range size and body mass (Figure 1b,c, respectively, see below). Analyses using mean and maximum densities instead of medians showed nearly identical results (Figures S1 and S2) and will not be explored further.
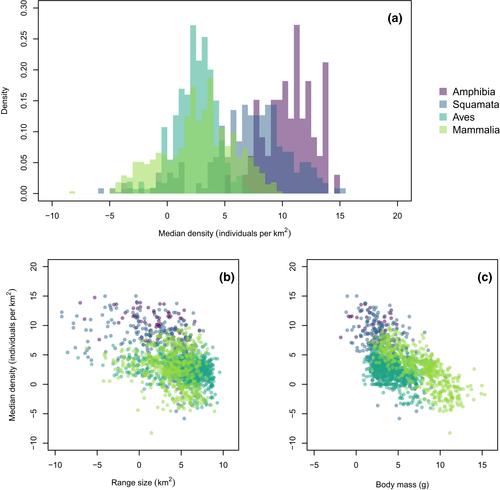
There was a strong support for significant phylogenetic signal in population density across all studied taxa using both Pagel's λ (1999) and Blomberg et al. (2003) (Table 1). This conclusion is robust not only to phylogenetic uncertainty in the case of birds and mammals, but also across different measures of population density (Table S2). There was also strong phylogenetic signal for body mass and range size (Table 1), so that the signal found for density could potentially be an indirect consequence of the strong phylogenetic signal in these two correlates. However, when we repeated analyses using the residuals of PGLS of population density, there was still strong evidence for phylogenetic signal (Table 1), although the results using Blomberg et al. (2003) for birds and mammals were marginally significant in some of the alternative topologies.
| Trait | Taxon | N | λ | logL | logL0 | p | K | p |
|---|---|---|---|---|---|---|---|---|
| Median density | Amphibia | 66 | 0.966 | −131.194 | −143.222 | 0 | 0.315 | 0.001 |
| Squamata | 237 | 0.851 | −547.788 | −627.378 | 0 | 0.490 | 0.001 | |
| Aves | 821 | 0.502 (0.468–0.544) | −1527.125 (−1529.940–−1525.004) | −1637.479 (−1637.479–−1637.479) | 0 (0–0) | 0.087 (0.046–0.155) | 0.038 (0.001–0.111) | |
| Mammalia | 529 | 0.916 (0.906–0.925) | −1044.162 (−1046.874–−1042.086) | −1359.424 (−1359.424–−1359.424) | 0 (0–0) | 0.109 (0.080–0.134) | 0.001 (0.001–0.001) | |
| Body mass | Amphibia | 35 | 0.242 | −67.103 | −68.093 | 0.159 | 0.200 | 0.017 |
| Squamata | 231 | 0.923 | −411.833 | −497.621 | 0 | 0.491 | 0.001 | |
| Aves | 820 | 0.993 (0.986–0.997) | −739.554 (−755.361–−726.248) | −1547.871 (−1547.871–−1547.871) | 0 (0–0) | 1.638 (1.049–2.620) | 0.001 (0.001–0.001) | |
| Mammalia | 529 | 0.999 (0.998–1) | −601.269 (−610.060–−593.639) | −1298.754 (−1298.754–−1298.754) | 0 (0–0) | 0.908 (0.801–0.977) | 0.001 (0.001–0.001) | |
| Range size | Amphibia | 66 | 0.000 | −171.005 | −171.004 | 1 | 0.125 | 0.218 |
| Squamata | 237 | 0.878 | −618.979 | −655.380 | 0 | 0.255 | 0.001 | |
| Aves | 821 | 0.656 (0.624–0.694) | −1761.073 (−1765.715–−1756.857) | −1890.055 (−1890.055–−1890.055) | 0 (0–0) | 0.094 (0.06–0.141) | 0.021 (0.001–0.078) | |
| Mammalia | 529 | 0.658 (0.639–0.687) | −1105.778 (−1106.555–−1105.022) | −1212.705 (−1212.705–−1212.705) | 0 (0–0) | 0.023 (0.010–0.035) | 0.242 (0.001–0.941) | |
| SVL | Amphibia | 66 | 0.835 | −51.009 | −53.608 | 0.023 | 0.257 | 0.002 |
| Median density ~ Body mass | Amphibia | 35 | 1.000 | −58.733 | −70.666 | 0 | 0.53 | 0.001 |
| Squamata | 231 | 0.815 | −529.010 | −591.553 | 0 | 0.426 | 0.001 | |
| Aves | 820 | 0.424 (0.391–0.466) | −1514.425 (−1516.481–−1512.756) | −1572.120 (−1573.205–−1570.897) | 0 (0–0) | 0.063 (0.039–0.107) | 0.094 (0.001–0.171) | |
| Mammalia | 529 | 0.835 (0.821–0.853) | −1016.318 (−1017.941–−1014.670) | −1159.549 (−1163.361–−1155.084) | 0 (0–0) | 0.05 (0.037–0.062) | 0.001 (0.001–0.001) | |
| Median density ~ SVL | Amphibia | 66 | 0.966 | −131.193 | −143.210 | 0 | 0.314 | 0.001 |
| Median density ~ range size | Amphibia | 66 | 0.936 | −127.563 | −137.402 | 0 | 0.29 | 0.001 |
| Squamata | 237 | 0.816 | −541.830 | −615.906 | 0 | 0.451 | 0.001 | |
| Aves | 821 | 0.467 (0.432–0.509) | −1519.013 (−1521.477–−1516.987) | −1616.849 (−1617.184–−1616.433) | 0 (0–0) | 0.088 (0.055–0.148) | 0.03 (0.001–0.095) | |
| Mammalia | 529 | 0.915 (0.906–0.924) | −1039.48 (−1042.117–−1037.317) | −1352.967 (−1353.090–−1352.850) | 0 (0–0) | 0.113 l^l (0.088–0.135) | 0.001 (0.001–0.001) |
Note
- Estimates are provided as means and ranges (in brackets) across all alternative topologies to reflect the influence of phylogenetic uncertainty on parameter estimation.
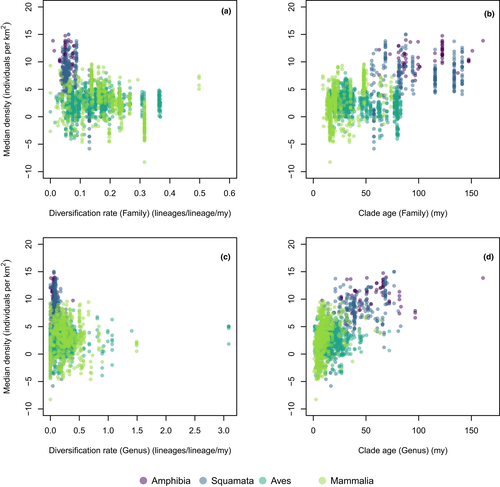
Phylogenetic generalized least squares analyses of the relationship between population density and either clade age or diversification rate failed to show any significant relationship across the studied taxa, neither at genus nor at family levels (Table 2). Indeed, while some apparent relationships can be observed in the raw data (Figure 2), further inspection shows that this is due to differences among taxa in their average densities, but no discernible pattern is found within them. Again, the results using alternative measures of species density provided nearly identical results (Figures S3 and S4, and Table S3). Interestingly, the strong negative relationship across all species in body size and local density (Figure 1c) is driven by large differences among the major clades, and there is no significant relationship once these grade differences are accounted for using PGLS (Table S4). None of the tests using median density (Table 3) or SVL for amphibians were significant (Table S5).
| Taxon | N | Diversification rate | Clade age | R² | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Slope | SE | t | p | Slope | SE | t | p | ||||
| Genus | Amphibia | 66 | 0.741 (−2.874–6.803) | 5.934 (3.187–8.575) | 0.070 (−0.658–0.990) | 0.749 (0.311–0.991) | 0.019 (0.007–0.034) | 0.020 (0.017–0.024) | 0.988 (0.379–1.672) | 0.353 (0.100–0.706) | 0.023 (0.006–0.049) |
| Squamata | 237 | 4.337 (1.449–7.427) | 2.280 (1.128–3.101) | 1.888 (0.872–3.118) | 0.091 (0.002–0.384) | 0.040 (0.024–0.056) | 0.027 (0.024–0.029) | 1.504 (0.898–2.132) | 0.153 (0.034–0.370) | 0.022 (0.011–0.042) | |
| Aves | 838 | 0.023 (−0.183–0.227) | 0.308 (0.043–0.625) | 0.097 (−0.653–0.896) | 0.775 (0.320–0.994) | −0.006 (−0.015–0.002) | 0.024 (0.019–0.043) | −0.280 (−0.685–0.105) | 0.773 (0.493–0.993) | 0.000 (0.000–0.001) | |
| Mammalia | 546 | −0.175 (−1.514–1.081) | 0.459 (0.088–0.672) | −0.336 (−3.432–2.270) | 0.499 (0.000–0.965) | 0.001 (−0.023–0.026) | 0.045 (0.038–0.056) | 0.022 (−0.494–0.567) | 0.841 (0.500–0.994) | 0.004 (0.000–0.029) | |
| Family | Amphibia | 66 | 22.522 (11.702–34.105) | 38.446 (31.232–46.328) | 0.589 (0.303–0.870) | 0.562 (0.388–0.763) | 0.026 (0.012–0.038) | 0.032 (0.027–0.036) | 0.834 (0.383–1.232) | 0.418 (0.222–0.703) | 0.013 (0.004–0.024) |
| Squamata | 237 | 33.616 (23.456–44.655) | 34.938 (31.783–39.374) | 0.962 (0.677–1.251) | 0.342 (0.212–0.499) | 0.022 (0.010–0.039) | 0.045 (0.040–0.052) | 0.483 (0.235–0.796) | 0.633 (0.427–0.814) | 0.004 (0.002–0.007) | |
| Aves | 838 | 1.859 (−0.571–4.15) | 4.872 (2.837–8.884) | 0.394 (−0.139–0.879) | 0.689 (0.380–0.978) | −0.002 (−0.011–0.008) | 0.038 (0.030–0.069) | −0.061 (−0.331–0.227) | 0.902 (0.739–0.996) | 0.000 (0.000–0.001) | |
| Mammalia | 546 | 1.357 (0.150–2.747) | 6.179 (0.761–10.143) | 0.226 (0.084–0.339) | 0.822 (0.735–0.928) | 0.027 (0.018–0.036) | 0.059 (0.049–0.075) | 0.455 (0.297–0.617) | 0.650 (0.537–0.766) | 0.000 (0.000–0.001) | |
Note
- Estimates are provided as means and ranges (in brackets) across all alternative topologies to reflect the influence of phylogenetic uncertainty on parameter estimation.
| Trait | Taxon | N | Slope | SE | t | p | R² |
|---|---|---|---|---|---|---|---|
| Median density | Amphibia | 35 | −0.188 (−0.223–−0.138) | 0.121 (0.108–0.131) | −1.555 (−1.798–−1.262) | 0.133 (0.081–0.216) | 0.069 (0.046–0.089) |
| Squamata | 231 | −0.182 (−0.251–−0.093) | 0.111 (0.105–0.116) | −1.641 (−2.394–−0.819) | 0.125 (0.017–0.414) | 0.012 (0.003–0.024) | |
| Aves | 837 | −0.488 (−2.213–0.297) | 0.138 (0.113–0.211) | −3.377 (−13.61–2.485) | 0.066 (0–0.643) | 0.028 (0–0.244) | |
| Mammalia | 546 | −0.254 (−0.628–0.32) | 0.142 (0.122–0.173) | −1.776 (−4.237–2.205) | 0.148 (0–0.854) | 0.011 (0–0.037) |
Note
- Estimates are provided as means and ranges (in brackets) across all alternative topologies to reflect the influence of phylogenetic uncertainty on parameter estimation.
4 DISCUSSION
Our results strongly indicate the existence of phylogenetic signal in species densities across all four terrestrial vertebrate groups (Table 1). Such congruent results, despite the substantial ecological, biogeographical, and life-history differences between the studied taxa, suggest that phylogenetic signal in species densities is the norm, at least for terrestrial vertebrates. These results are particularly relevant to the development of models of species abundance distributions. For instance, the combination of a "point-mutation" speciation and the per-capita (functional) equivalence of each species in Hubbell's neutral model (Hubbell, 2001, 2005) postulates that species abundances would be largely independent, even for closely related species. It is important to note that the existence of phylogenetic signal is not itself evidence for particular evolutionary processes. However, it suggests that whatever mechanisms that determine the abundance of species, such as diet (e.g., Robinson & Redford, 1986) and territoriality (e.g., Maher & Lott, 2000), tend to evolve gradually and slowly enough, so that closely related species tend to display similar population densities. It is interesting to note that one of the main motivations for the actual development of Hubbell's theory was the realization that one of its main components, the temporal fluctuations in population size known as ecological drift, took place at a time scale in which macroevolutionary mechanisms such as speciation could not be overlooked (Hubbell, 2001). Indeed, our results suggest that his theory actually did not go far enough in time, such that explicitly modeling the mechanisms driving variation in species abundances seems like an indispensable element of more realistic models of community dynamics.
The consistency of phylogenetic signal of population density across the many terrestrial vertebrate clades is intriguing, given the well-known average differences in population density between them (e.g., Santini, Isaac, Maiorano, et al., 2018). For instance, ectotherms tend to show considerably higher densities than endotherms, and mammals tend to be even higher densities in relation to birds (Currie & Fritz, 1993; Silva et al., 1997; Figure 1). Much of this discrepancy is likely due to differences between taxa in body weight (Currie & Fritz, 1993), given the commonly observed negative relationship between body size and population density (e.g., Damuth, 1981; Elton, 1927). On the other hand, important advances have also been obtained in relating population density of terrestrial vertebrates and environmental conditions, such as temperature and productivity (e.g., Santini, Isaac, Maiorano, et al., 2018). New methodological advances, such as phylogenetic path analysis (von Hardenberg & Gonzalez-Voyer, 2013), might provide important new insight into the relative importance of these internal and external potential drivers of species abundance evolution.
The lack of association between clade-level average population density and either clade age or diversification rate is intriguing, given the results of previous studies. For instance, plants with anti-herbivory adaptations tend to show higher diversification rates and higher population abundance (Farrell et al., 1991). On the other hand, the results shown in Figure 1 might provide important insight to explain the positive and negative associations found in previous studies. Different clades showed considerable variation in their density distributions, possibly due to their own biological characteristics and habitat preferences (see above). Under these conditions, tests that do not explicitly account for phylogenetic non-independence among species are likely to lead to a higher probability of false positives, which could explain why studies that showed an association between clade richness and abundance disagreed on whether that relationship was positive or negative, although future studies should reanalyze previous datasets using phylogenetic comparative methods to confirm this conjecture.
Our understanding of the evolution of species abundances has lagged behind its main counterparts—body size and geographic range—in macroevolutionary studies. By showing that the temporal dynamics of species abundances include macroevolutionary timescales, we hope that future studies will use advances in phylogenetic comparative methods to understand the causes and consequences of interspecific diversity in species abundances and their role in community dynamics.
ACKNOWLEDGMENTS
We thank Mauricio O. Moura for valuable comments on the manuscript. This paper is developed in the context of the National Institutes for Science and Technology (INCT) in Ecology, Evolution, and Biodiversity Conservation, supported by MCTIC/CNPq (proc. 465610/2014-5) and FAPEG (proc. 201810267000023). MRP was partially funded by a grant from CNPq/MCT (302904/2020-4). RD was funded through a graduate scholarship from CAPES (Grant 88887.351866/2019-00).




