Competing for Attention: Lobbying Time-Constrained Politicians
This project benefited greatly from conversations with Steve Callander, Steve Coate, Ralph Boleslavsky, David Kelly, Arnaud Dellis, and seminar participants at Queen's University, Cornell University, Stanford GSB, University of Alberta, University of Miami, University of Pittsburgh, and University of Padua, as well as the First Caribbean Game Theory Conference and the 2011 Tournaments, Contests and Relative Performance Evaluation conference. The author is grateful for financial support provided through his position as the Jarislowsky-Deutsch Chair in Economic and Financial Policy at Queen's University.
Abstract
We develop a model of lobbying in which a time and resource constrained policymaker first chooses which policy proposals to learn about, before choosing which to implement. The policymaker reviews the proposals of the interest groups who provide the highest contributions. We study how policy outcomes and contributions depend on policymaker constraints and the design of the “Contest for Attention.” Among other results, awarding attention to the highest contributors generally guarantees the first best policy outcome. It can also lead to the highest possible contributions, suggesting that a policymaker may not need to sacrifice policy in order to maximize contributions. Our results also give insight into other settings where agents compete for a decision maker's attention.
“About all you get [in exchange for a contribution] is a chance to talk to them.… If you have a good case you can win them over. But you have to be able to talk to them.”
—Interest group representative interviewed in Herndon (1982, p. 1000)
“Access to the president should never be for sale.”
—Bob Edgar, president of Common Cause, February 26, 20131
1. Introduction
Popular opinion is that political contributions corrupt policymaking. The majority of Americans believe that “money buys results in Congress,” and that money biases legislation away from the needs of average constituents and in favor of deep-pocketed special interests (Lessig 2011, p. 88). Theoretical models of politics largely support these popular views, with classic models depicting lobbying as little more than a quid pro quo exchange of political contributions for policy (e.g., Tullock 1980; Grossman and Helpman 1994). Insider accounts of policymaking, however, describe overtly corrupt behavior as the rare exception, with most policymakers trying to do the right thing, while facing severe constraints on their time and limits to their expertise (e.g., Bauer, Dexter, and de Sola Pool 1963; Hansen 1991; Schram 1995; Baumgartner et al. 2009; Baumgartner and Jones 2015). We present a model of the political process consistent with the insider accounts of policymaking. Ours is a model of informational lobbying, where political contributions help special interest groups (IGs) capture the attention of a time constrained policymaker, and are not provided in the direct exchange for policy favors. We show how political contributions lead the policymaker to focus his efforts on the most beneficial policies. By allocating his limited attention based on political contributions, the policymaker can guarantee better policy outcomes than in the absence of contributions.
We develop a model of lobbying that approximates the political process described in a number of insider accounts, which emphasize how severely constrained policymakers are in their ability to learn about and implement policy proposals (e.g., Bauer et al. 1963; Hansen 1991; Baumgartner and Jones 2015). In our model, a policymaker faces a number of policy proposals and must choose which to implement. The proposals may involve earmark funding for projects within the policymaker's home district. Due to budget constraints, the policymaker may not be able to fund all of the projects he believes are beneficial.2 Alternatively, the proposals may involve introducing legislation reforming policy on alternative issues. Drafting, introducing, and promoting legislation is time-consuming, preventing the policymaker from introducing legislation in all areas that may benefit his constituents. Although the proposals may not by nature be mutually exclusive alternatives,3 resource and time constraints necessitate that the policymaker prioritize proposals and choose only some on which to focus his efforts.
Before choosing which proposals to implement, the policymaker can assess the costs and benefits of alternative options by meeting with IGs and experts, reading government reports or independent research, holding legislative hearings, or asking staff or government agencies to research the political feasibility and constituent benefits of different options.4 If the policymaker carefully assesses all alternatives, then he can be certain to implement the most beneficial options. But, this is generally not feasible. Time and resource constraints prevent the policymaker from carefully assessing all proposals, just as they limit the number of proposals he can implement. Faced with binding time and resource constraints, the policymaker must prioritize proposals, first choosing which to review and then choosing which to implement.
The main contribution of this paper is to analyze in detail one method the policymaker may use to choose which proposals to review: a Contest for Attention. In a contest for attention, IGs representing each policy proposal pay political contributions in competition for the policymaker's limited attention, with the policymaker reviewing the proposals whose IGs paid the highest contributions. The policymaker sells political access to the highest bidders. This is the type of exchange between policymakers and IGs that the general public and campaign finance reform advocates view as corrupt and detrimental for the average citizen.
Our main result stands in contrast to the popular idea that selling access is necessarily detrimental for policy outcomes. We show that a policymaker who sells his limited attention to the highest bidder will become fully informed about the quality of all proposals even though he can directly review only some of them. Allocating attention to the highest contributors is not detrimental for policy, but rather leads to a fully informed policymaker and the first best policy.5
The reason for this is as follows. Each IG's equilibrium contribution is strictly increasing in the quality of its proposal. IGs involved with high-quality proposals are willing to pay more to capture the policymaker's attention (leading him to review their proposals) than IGs with lower quality proposals. This means the policymaker directly observes the proposal quality of those who win attention (the highest contributors), and indirectly infers the proposal quality of others from their contributions. As a result, the policymaker is fully informed about the quality of all proposals, and implements policy as if he directly observed each proposal's quality. Although in equilibrium the IGs who submit the highest payments see their proposals implemented, this is not because they submitted the highest payments. Rather, it is because the groups with the highest quality proposals submit the highest payments, and in equilibrium the policymaker implements the highest quality proposals. We show that this insight is robust to a number of alternative assumptions and generalizations, which we discuss in the paper and explore in detail in an online appendix in the Supporting Information.
The analysis also considers equilibrium contributions, an important consideration as the policymaker may benefit from both collecting contributions and implementing good policy. We show that giving attention to the highest contributors not only leads to the first best policy, it can also result in the first best level of contributions.6 This means that a policymaker may not need to sacrifice policy in order to maximize contributions. The result stands in contrast to other models of lobbying in which the trade-off between implementing good policy and collecting campaign contributions plays a central role (e.g., Prat 2002; Coate 2004; Cotton 2009). This is the case in our model when IGs share the same valuation for having their proposals implemented, when the policymaker reviews no more proposals than he is able to implement, and when attention is allocated through an all-pay contest for attention. Here, a policymaker who cares about both policy and contributions can be no better off than when he allocates attention through a contest for attention before implementing the proposals he believes are best. There exists no other mechanism by which the policymaker can choose which proposals to implement that will result in higher payoffs. In other settings, the contest for attention still leads to the first best policy, but does not necessarily maximize contributions compared to the selling policy directly. There, using a contest for attention is preferable to any other method of implementing policy when the policymaker cares enough about policy relative to payments.
The environment with asymmetric IGs gives insight into the effects of special interest wealth on policy outcomes. In that setting, contributions are maximized when the policymaker allocates attention through a handicapped contest for attention. Such a contest is biased against wealthy IGs, requiring them to pay higher contributions for the same contest “score” as a lower paying, less wealthy group. In the payment-maximizing full-information equilibrium, rich IGs tend to contribute more than poor IGs, but they are no more likely to have their proposals implemented. Despite higher payments from rich interest groups, the contest for attention still leads to a fully informed policymaker who implements the first best policy.
Although the analysis is motivated by lobbying and policymaking, the underlying framework and the implications of competing for attention are applicable to a number of settings beyond politics. Consider the following examples. An employer wants to hire the highest ability applicants and grants interviews to the most persistent applicants, those who have undertaken the greatest costs to gain the employer's attention.7 Similarly, a venture capitalist may listen to pitches from the entrepreneurs who have done the most to gain his attention. A bachelorette may accept a date from the suitor who is most persistent or makes the biggest fool out of himself in order to capture her attention, or she may accept a date from the suitor who offers to take her out to the most expensive restaurant. In each of these situations, a decision maker must allocate a limited number of “prizes” among agents, and prefers to award the prizes to the highest quality agents (where quality is orthogonal to an agent's willingness to pay for a prize). The decision maker may review some (but not all) agents to learn their quality before choosing how to allocate prizes.8 Agents make payments or undertake costly actions (or submit bids) observable to the decision maker, who reviews the agents who submit the highest payments. The model suggests that by awarding attention to the highest bidder, the decision maker may be better able to identify and award the prizes to the most qualified agents.
2. Relationship with the Literature
The only other paper to consider a contest for attention is Cotton (2009), which brings a highly stylized version of the contest for attention into a more traditional model of lobbying, and uses the model to study campaign finance reform policies. A policymaker chooses whether to sell policy or sell political access (which allowed disclosure of private evidence) through an all-pay auction. When the policymaker sells policy, the game is similar to a traditional all-pay auction for policy (e.g., Hillman and Riley 1989). When the policymaker sells access, the game becomes a highly stylized version of the divisible resource framework that we consider in Section 4. and the online appendix. Both Cotton (2009) and the current paper make the point that a policymaker who sells attention (i.e., political access) can become informed about a policy by observing payments made by IGs as they vie for attention. Cotton (2009) makes this point with a very simple version of the contest for attention in the process of deriving results about contribution limits and taxes. The focus there is on campaign finance reform, not the contest for attention itself. The current paper, on the other hand, considers contests for attention in detail. We generalize the contest for attention, show that the main insight extends to a variety of environments, and derive a number of important new results that were not possible in the stylized version of the contest for attention considered previously.9
A handful of other papers have also modeled the connection between political contributions and access to policymakers (i.e., attention). In Austen-Smith (1998) and Cotton (2012), IGs must pay a price set by a policymaker in order to engage in informational lobbying. Both consider how a policymaker may offer more access to wealthy IGs, who are willing to pay more.10 These papers focus on how a policymaker restricts access in order to extract rent from the political process. In contrast, we focus on whether a time-constrained policymaker can sell attention in such a way that he is able to learn about and implement the best policy, despite not having the capacity to review all policy options.11 Groll and Ellis (2014) model a market for political access where commercial lobbying firms connect citizens to politicians. In the political access models of Austen-Smith (1995) and Lohmann (1995), contributions lend credibility to unverifiable information presented by IGs. This is in contrast to our framework, as well as the other political access papers discussed above, where information is verifiable and may be observed by a policymaker who devotes attention to an issue. In Levy and Razin (2013), IGs compete in an all-pay auction, and the winner has its proposal considered by policymakers. What is meant by consideration differs greatly between their framework and ours. In their framework, there is no uncertainty about proposals, and consideration means being put up for a vote in the legislature, facing off against the status quo policy. In our framework, consideration means a policymaker learns about the costs and benefits of a proposal before deciding whether to move forward with it. Their work focuses on how a status quo policy evolves over time. Ours focuses on how competing for attention improves the policymaker's ability to learn about the best policy.
The majority of the literature models lobbying as a system of quasi-bribery, where contributions are given in exchange for policy outcomes (e.g., Tullock 1980; Grossman and Helpman 1994), or as a system of information provision in the absence of political contributions (e.g., Austen-Smith and Wright 1992; Cotton and Dellis Forthcoming). Bennedsen and Feldmann (2006) and Dahm and Porteiro (2008) consider both information provision and the exchange of money for policy.12 Although the theoretical literature focuses on the use of political contributions to buy policy, this role of contributions is supported by neither insider accounts of the lobbying process nor empirical evidence.13 Rather, empirical accounts of lobbying suggest that contributions help IGs capture the attention of policymakers, assuring that their policies receive full consideration. For example, Langbein (1986), Ansolabehere, Snyder, and Tripathi (2002), and Hall and Wayman (1990) present evidence that IGs provide political contributions in order to secure access to policymakers. See also the excellent descriptions of the policymaking process in Bauer et al. (1963); Hansen (1991), and Baumgartner et al. (2009), and the surveys by Herndon (1982); Schram (1995), and Makinson (2003).
There is a substantial literature on the efficient allocation of resources. Esteban and Ray (2006) show that both high wealth and economic desirability increase lobbying by special interests, and show that this can lead to greater misallocation when these factors are not observable. Cotton (2013) and Fullerton and McAfee (1999) consider environments in which a decision maker wants to allocate a limited resource based on some characteristic orthogonal to applicant value. Most related to our current paper is Fullerton and McAfee (1999), where a contest designer must select a subset of agents to participate in a research tournament. They show that using a contest to allocate entry into the research tournament ensures that only the most promising researchers enter the tournament. In our setting and in Fullerton and McAfee, higher quality agents (e.g., those advocating on behalf of higher quality policies) are willing to pay more to “participate” in the next stage of the game, whether the next stage is our paper's review process or Fullerton and McAfee's research tournament.
All-pay auctions are typically used to directly allocate prizes (e.g., Hillman and Riley 1989; Baye, Kovenock, and de Vries 1993). In our framework the all-pay auction is used to allocate the policymaker's attention. When we allow for observable agent asymmetries, the policymaker's preferred method for choosing which proposals to review involves a handicapped all-pay auction. Such an auction fully adjusts IG payments to account for known heterogeneity. There exists a growing literature on handicapping contests. Siegel (2014) develops a general all-pay contest framework with handicaps in an environment with complete information. Kirkegaard (2012) considers the use of handicaps in a model with private information about valuations. Eso and Szentes (2007) show that a version of a handicap auction can maximize revenue in a game in which the auctioneer chooses how much information to reveal to the bidders about the value of the good. The present paper assumes that bidders reveal information to the auctioneer (not the other way around), and the auctioneer's goal is to collect as much information as possible (rather than revenue maximization). We show how a handicapped auction can be used to maximize the revelation of information, not only to maximize revenue. None of these other models use a contest to elicit information about bidder types.
3. Model with Symmetric IGs
We begin with a relatively simple version of the model. There are n symmetric policy proposals that differ only in quality. The policymaker reviews one of the proposals before choosing one proposal to implement. This symmetric game with one review slot and one implementation slot provides a simple setting in which to develop intuition for our main results. After presenting the results for the game with one review slot and one implementation slot, we show that the results continue to hold when the policymaker reviews and implements multiple proposals. In later sections, we allow for observable asymmetries between the proposals (specifically, preference intensity of the IGs advocating in favor of the proposals).
3.1. Setting
A policymaker is faced with a set of policy proposals 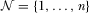 , and must choose which of these n proposals to implement. The proposals may represent different earmark funding requests for projects within the policymaker's district, or reform proposals on different issues. Let
, and must choose which of these n proposals to implement. The proposals may represent different earmark funding requests for projects within the policymaker's district, or reform proposals on different issues. Let 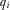 denote the quality of proposal
denote the quality of proposal 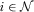 and
and 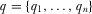 the underlying state of the world. Each
the underlying state of the world. Each 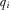 is the independent realization of a random variable distributed on
is the independent realization of a random variable distributed on 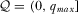 according to continuously differentiable distribution F with density f.14 Distribution F is common knowledge. The policymaker is ex ante uncertain about the realized quality of each proposal.
according to continuously differentiable distribution F with density f.14 Distribution F is common knowledge. The policymaker is ex ante uncertain about the realized quality of each proposal.
The policymaker has the resources to implement one of the proposals. Let 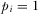 (
(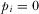 ) indicate that the policymaker implements (does not implement) proposal i, where
) indicate that the policymaker implements (does not implement) proposal i, where 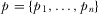 denotes the full policy outcome.
denotes the full policy outcome.
Before implementing a proposal, the policymaker may review one of the proposals to directly observe its quality. Let 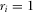 (
(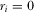 ) indicate that the policymaker reviews (does not review) proposal i, where
) indicate that the policymaker reviews (does not review) proposal i, where 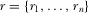 . A review may involve meeting with IGs or lobbyists to gain a better understanding of the proposal, asking staff or government agencies to conduct research, or holding legislative hearings. When the policymaker reviews proposal i, he perfectly observes
. A review may involve meeting with IGs or lobbyists to gain a better understanding of the proposal, asking staff or government agencies to conduct research, or holding legislative hearings. When the policymaker reviews proposal i, he perfectly observes 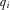 . Let
. Let 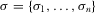 represent the information directly observed by the policymaker by reviewing a proposal, where
represent the information directly observed by the policymaker by reviewing a proposal, where 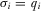 when he reviews i and
when he reviews i and  when he does not review i.
when he does not review i.
Each proposal 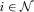 is supported by an independent IG, an advocate on behalf of its proposal.
is supported by an independent IG, an advocate on behalf of its proposal. 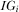 refers to the IG associated with issue i. Each IG, an expert on its respective project or policy area, privately observes
refers to the IG associated with issue i. Each IG, an expert on its respective project or policy area, privately observes 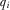 at the beginning of the game. Before the policymaker decides which proposal to review, the IGs may independently provide payments to the policymaker in an effort to capture his attention. Such payments may be monetary political contributions or in-kind transfers. Let
at the beginning of the game. Before the policymaker decides which proposal to review, the IGs may independently provide payments to the policymaker in an effort to capture his attention. Such payments may be monetary political contributions or in-kind transfers. Let 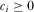 denote any “contribution” made by IGi, where
denote any “contribution” made by IGi, where 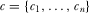 .
.
We adopt an all-pay auction to model the allocation of the “review slot” based on payments. The IGs provide payments, and the policymaker reviews the proposal associated with the IG that provided the highest payment. In the “contest for attention” for a single review slot, 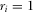 if
if 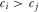 for all
for all 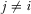 , and ties are broken randomly.
, and ties are broken randomly.
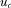 and policy utility
and policy utility 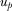 :
:
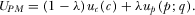 (1)
(1)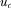 is strictly increasing in individual contributions
is strictly increasing in individual contributions  (and total payments
(and total payments 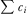 ). Policy utility is strictly increasing in the quality of the implemented proposal,
). Policy utility is strictly increasing in the quality of the implemented proposal, 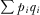 . All else equal, the policymaker prefers to implement the highest quality proposal. Therefore, quality may represent net benefit to the policymaker's constituents or effects on the policymaker's chances of reelection. Parameter
. All else equal, the policymaker prefers to implement the highest quality proposal. Therefore, quality may represent net benefit to the policymaker's constituents or effects on the policymaker's chances of reelection. Parameter 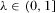 represents how much the policymaker cares about policy relative to contributions.
represents how much the policymaker cares about policy relative to contributions.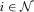 ,
,
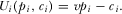 (2)
(2)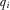 , and then chooses contribution
, and then chooses contribution  . Second, the policymaker reviews the proposal associated with the highest payment, directly learning that proposal's quality. He updates his beliefs about the quality of the other proposals accounting for the payments made by the IGs. Third, the policymaker chooses one proposal to implement.
. Second, the policymaker reviews the proposal associated with the highest payment, directly learning that proposal's quality. He updates his beliefs about the quality of the other proposals accounting for the payments made by the IGs. Third, the policymaker chooses one proposal to implement.3.2. Preliminaries
- (1) Equilibrium contribution strategy
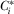 for each IG, where
for each IG, where 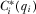 describes the equilibrium value of
describes the equilibrium value of  when IGi observes that its proposal is quality
when IGi observes that its proposal is quality 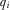 .
. - (2) Equilibrium implementation strategy,
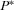 , used by the policymaker to determine which proposal to implement given c and σ.
, used by the policymaker to determine which proposal to implement given c and σ. - (3) The policymaker's posterior beliefs, given c and σ. We denote these beliefs by μ.
These components constitute an equilibrium if (1) no IG has an incentive to deviate from 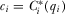 given the payment strategies of the other IGs and the implementation strategy of the policymaker, (2) the policymaker's implementation strategy
given the payment strategies of the other IGs and the implementation strategy of the policymaker, (2) the policymaker's implementation strategy 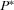 is sequentially rational given his beliefs μ, and (3) the policymaker's posterior beliefs μ are consistent with
is sequentially rational given his beliefs μ, and (3) the policymaker's posterior beliefs μ are consistent with  and σ. Function μ denotes the policymaker's updated beliefs about q, where
and σ. Function μ denotes the policymaker's updated beliefs about q, where 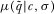 is the probability the policymaker puts on state
is the probability the policymaker puts on state 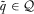 given contribution profile c and review outcome σ. Similarly,
given contribution profile c and review outcome σ. Similarly, 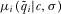 is the posterior probability proposal i is quality
is the posterior probability proposal i is quality 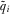 .
.
We impose an assumption on the behavior of IGs when indifferent between multiple contributions.
ASSUMPTION 1.An IG that is indifferent between multiple contributions chooses the contribution that maximizes the expected probability that its proposal is implemented, given the equilibrium strategies of the other IGs and the policymaker.
This assumption plays a role in the analysis only in cases where IGs are indifferent between contributing according to equilibrium function 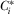 and contributing other amounts. Any equilibrium found under Assumption 1 will also be a perfect Bayesian equilibrium in the absence of the assumption. In the online appendix, we consider implications of both this assumption and the alternative assumption that an indifferent IG minimizes payments.
and contributing other amounts. Any equilibrium found under Assumption 1 will also be a perfect Bayesian equilibrium in the absence of the assumption. In the online appendix, we consider implications of both this assumption and the alternative assumption that an indifferent IG minimizes payments.
3.2.1. Full-information equilibria
The primary insight of our paper shows how the policymaker becomes fully informed about the quality of all proposals when he sells attention (i.e., the review slot) to the highest bidder. We say that the contest for attention leads to the policymaker being “fully informed” if there exists an equilibrium of the contest for attention in which his equilibrium beliefs, μ, put probability 1 on the true state of the world: 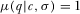 . We begin by providing a sufficient condition on the IGs' equilibrium payment strategies to guarantee that the policymaker is fully informed.
. We begin by providing a sufficient condition on the IGs' equilibrium payment strategies to guarantee that the policymaker is fully informed.
LEMMA 1.If 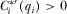 for each
for each 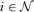 and all possible
and all possible 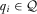 , then the policymaker is fully informed in equilibrium. All Proofs are relegated to the Appendix.
, then the policymaker is fully informed in equilibrium. All Proofs are relegated to the Appendix.
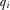 , and therefore has correct beliefs about its quality. Lemma 1 shows that in equilibrium the policymaker will also have correct beliefs about the quality of the
, and therefore has correct beliefs about its quality. Lemma 1 shows that in equilibrium the policymaker will also have correct beliefs about the quality of the  proposals he does not review. Strictly monotonic payment functions mean there is a one-to-one mapping between the quality of each proposal and the payment made by its IG. In equilibrium, when the policymaker observes payment
proposals he does not review. Strictly monotonic payment functions mean there is a one-to-one mapping between the quality of each proposal and the payment made by its IG. In equilibrium, when the policymaker observes payment  , he expects the payment was generated by the IG's equilibrium contribution function
, he expects the payment was generated by the IG's equilibrium contribution function  . Because
. Because 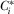 is strictly increasing, it is invertible; we define
is strictly increasing, it is invertible; we define 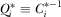 . The policymaker therefore updates his beliefs about
. The policymaker therefore updates his beliefs about 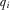 upon observing
upon observing  , expecting that
, expecting that 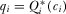 . In equilibrium, these beliefs are correct.
. In equilibrium, these beliefs are correct.
We refer to any perfect Bayesian equilibrium for which the condition in Lemma 1 is satisfied as a full-information equilibrium. The analysis limits attention to such equilibria.
Before proceeding with the analysis, it is helpful to determine the policymaker's sequentially rational policy choice in any full-information equilibrium. In the final stage of the game, the policymaker implements the proposal with the highest expected quality given his beliefs μ.16 Denote the policymaker's posterior beliefs about 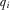 by
by 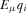 .
.
LEMMA 2.If the policymaker is fully informed, then in equilibrium he implements the highest quality proposal with probability 1.
3.2.2. Payment-maximizing full-information equilibrium
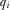 expects equilibrium benefit
expects equilibrium benefit 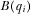 , where
, where
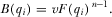 (3)
(3)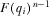 is the probability that proposal i is the highest quality proposal. Expression 3 gives the expected benefit to an IG when the policymaker certainly implements the highest quality proposal. It implies an individual rationality constraint for each IGi:
is the probability that proposal i is the highest quality proposal. Expression 3 gives the expected benefit to an IG when the policymaker certainly implements the highest quality proposal. It implies an individual rationality constraint for each IGi:
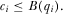 (4)
(4)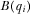 .
.
LEMMA 3.There does not exist a full-information equilibrium in which 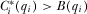 for any
for any 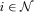 and
and 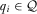 .
.
The maximum feasible payment from IGi equals 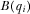 . We define a payment-maximizing full-information equilibrium as a full-information equilibrium in which all IGs pay their maximum feasible amounts:
. We define a payment-maximizing full-information equilibrium as a full-information equilibrium in which all IGs pay their maximum feasible amounts: 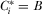 for each
for each 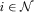 and
and 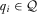 .
.
3.3. Solving the Contest for Attention
The preliminary analysis determined that in any full-information equilibrium, the policymaker's posterior beliefs are always correct, and he implements the first best policy. Here, we begin with a full characterization of the set of symmetric full-information equilibria of the contest for attention game. In a symmetric full-information equilibrium, all IGs play the same strategy 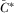 , where
, where 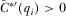 for all possible
for all possible 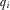 .
.
To derive the equilibrium payment function, we consider IGi's best response when all other IGs contribute according to 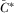 . Because the other
. Because the other  IGs contribute according to the equilibrium payment function, the policymaker has correct beliefs about their proposal qualities, regardless of whether they win attention. If they do win attention, the policymaker observes
IGs contribute according to the equilibrium payment function, the policymaker has correct beliefs about their proposal qualities, regardless of whether they win attention. If they do win attention, the policymaker observes 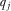 directly. If they do not win attention, the policymaker (correctly) believes
directly. If they do not win attention, the policymaker (correctly) believes 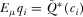 , where
, where 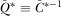 . We derive equilibrium payment functions
. We derive equilibrium payment functions 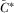 such that IGi has no incentive to deviate from contributing according to the strategy when it expects other IGs to do the same.
such that IGi has no incentive to deviate from contributing according to the strategy when it expects other IGs to do the same.
No incentive to over-contribute—We first explain why IGi prefers 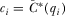 to any higher contribution. If IGi provides the equilibrium contribution, it submits the highest contribution, wins attention, and has its proposal implemented if and only if it has the highest quality proposal.17 Contributing
to any higher contribution. If IGi provides the equilibrium contribution, it submits the highest contribution, wins attention, and has its proposal implemented if and only if it has the highest quality proposal.17 Contributing 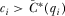 introduces the possibility that IGi wins attention even when it does not have the highest quality proposal. This does not increase the probability that proposal i is implemented, however, because winning attention guarantees that the policymaker reviews and directly learns
introduces the possibility that IGi wins attention even when it does not have the highest quality proposal. This does not increase the probability that proposal i is implemented, however, because winning attention guarantees that the policymaker reviews and directly learns 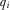 . Since the policymaker's beliefs about the quality of the other
. Since the policymaker's beliefs about the quality of the other 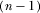 proposals are accurate, the policymaker continues to implement proposal i if and only if it is the highest quality proposal. Therefore, overbidding requires a larger payment without providing an expected benefit to the IG.
proposals are accurate, the policymaker continues to implement proposal i if and only if it is the highest quality proposal. Therefore, overbidding requires a larger payment without providing an expected benefit to the IG.
No incentive to under-contribute—The equilibrium contribution function must also be such that no IG wants to under-contribute compared to the equilibrium payment. If IGi deviates downward, its costs decrease (a benefit). But, it also decreases the probability that IGi submits the highest payment and has its policy implemented (a cost). To rule out such deviations, a decrease in contribution must lead to a sufficiently large decrease in the probability of winning attention. This will be the case when the slope of the equilibrium contribution function is sufficiently low.18
We will derive a condition on the equilibrium contribution function 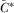 such that each IGi prefers
such that each IGi prefers 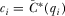 to any lower amount when the other IGs contribute according to the equilibrium function. Notice that for any contribution
to any lower amount when the other IGs contribute according to the equilibrium function. Notice that for any contribution 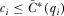 , IGi wins attention and has its proposal implemented if and only if it provides the highest contribution. If another IG provides a higher contribution, then IGi will not win attention. The policymaker will have expectations that
, IGi wins attention and has its proposal implemented if and only if it provides the highest contribution. If another IG provides a higher contribution, then IGi will not win attention. The policymaker will have expectations that  , which will be less than the observed quality of the IG that contributes according to the equilibrium function and wins attention. The policymaker does not observe the true quality of
, which will be less than the observed quality of the IG that contributes according to the equilibrium function and wins attention. The policymaker does not observe the true quality of 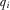 , and will therefore implement the other proposal regardless of whether that proposal was actually higher quality than i. If, on the other hand, IGi provides the highest contribution, then IGi wins attention. Even before the policymaker reviews proposal i, he expects that it is highest quality proposal based on the contributions. After he reviews the proposal, he learns that i is even higher quality than he expected, and will implement it over the other options.
, and will therefore implement the other proposal regardless of whether that proposal was actually higher quality than i. If, on the other hand, IGi provides the highest contribution, then IGi wins attention. Even before the policymaker reviews proposal i, he expects that it is highest quality proposal based on the contributions. After he reviews the proposal, he learns that i is even higher quality than he expected, and will implement it over the other options.
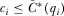 is
is
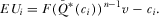 (5)
(5)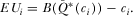 (6)
(6)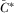 to constitute an equilibrium, IGi must prefer contributing
to constitute an equilibrium, IGi must prefer contributing 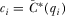 to any lower value. Contributing the equilibrium amount results in expected payoff
to any lower value. Contributing the equilibrium amount results in expected payoff 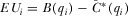 , which must be larger than 6 for all
, which must be larger than 6 for all 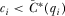 . This will be true for all possible
. This will be true for all possible 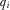 when
when
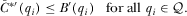 (7)
(7)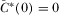 .
.Summary of equilibrium requirements—These conditions and the requirement that a full-information equilibrium requires 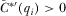 for all
for all 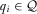 are the foundation of the first proposition.
are the foundation of the first proposition.
PROPOSITION 1.For any function 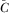 such that
such that 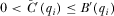 for all
for all 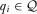 and
and 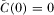 , there exists a full-information equilibrium in which
, there exists a full-information equilibrium in which 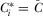 for each
for each 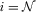 . No other symmetric full-information equilibria exist.
. No other symmetric full-information equilibria exist.
Notice the implications of this result. First, it establishes that the policymaker may become fully informed about the quality of all proposals, even if he only reviews one of them. In equilibrium, the fully informed policymaker is guaranteed to implement the highest quality proposal. Selling attention to the highest contributor improves policy outcomes. Second, it shows that there are in fact many full-information equilibria.
Payment-maximizing equilibrium—Next, we describe the full-information equilibrium that maximizes contributions from all IGs, and the payments received by the policymaker. Such an equilibrium corresponds with the highest level of competition between the IGs, an equilibrium characteristic that may serve as a focal point and lead to coordination on such an equilibrium.
COROLLARY 1.There exists an equilibrium in which 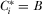 for each
for each  . This is the payment-maximizing full-information equilibrium.
. This is the payment-maximizing full-information equilibrium.
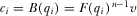 . The policymaker extracts all rent from the policymaking process. From an ex ante perspective, the expected individual contribution is
. The policymaker extracts all rent from the policymaking process. From an ex ante perspective, the expected individual contribution is  , and the sum of total expected contributions equals
, and the sum of total expected contributions equals
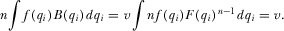
PROPOSITION 2.The payment-maximizing full-information equilibrium results in the first best policy and the first best level of contributions for the policymaker. There exists no other method for implementing policy that leads to higher expected payoffs for the policymaker.
This results implies that a policymaker who cares about both the quality of the implemented proposal and collecting payments can do no better than first allocating attention through a contest and then implementing the proposal he believes best. Such an allocation method guarantees both the first best policy outcome and the maximum expected payments.
This means there does not necessarily exist a trade-off between implementing the best policy and maximizing political contributions. This result is in contrast to other papers on lobbying, where there is a trade-off between implementing policy that is good for constituents, and implementing policy that encourages contributions from special interests (e.g., Prat 2002; Coate 2004; Bennedsen and Feldmann 2006; Cotton 2009).
This result, however, is not as strong in Section 3.5., where we consider IG asymmetries. There, we show that the contest for attention continues to guarantee the first best proposal implementation even if IGs differ in their valuations. However, the contest for attention will no longer guarantee the highest possible total payments from IGs, although it will maximize payments compared to any other method that guarantees the first best policy.
3.4. Implementing Multiple Proposals
The above results extend to a setting where the policymaker reviews the k proposals associated with the highest IG payments, and then implements the m proposals he believes are highest quality, where 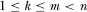 . Here, we focus on the case where the number of review slots is no greater than the number of proposals the policymaker can emphasize, including the extreme case where the policymaker reviews only a single proposal before implementing multiple proposals.19 By allocating as few as one review slot through a contest for attention, the policymaker becomes fully informed about the quality of all proposals and is able to implement the m highest quality alternatives.
. Here, we focus on the case where the number of review slots is no greater than the number of proposals the policymaker can emphasize, including the extreme case where the policymaker reviews only a single proposal before implementing multiple proposals.19 By allocating as few as one review slot through a contest for attention, the policymaker becomes fully informed about the quality of all proposals and is able to implement the m highest quality alternatives.
 that we consider above, and the analysis in this section. First, the ex ante expected benefit to IGi when the policymaker certainly implements the m highest quality proposals is now
that we consider above, and the analysis in this section. First, the ex ante expected benefit to IGi when the policymaker certainly implements the m highest quality proposals is now
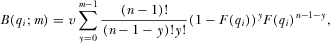 (8)
(8)Second, when 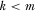 there is the possibility that in equilibrium the policymaker implements a proposal without first reviewing it. This is consistent with the idea that a legislator may vote on issues he has not had time to study in detail.20 This means the policymaker will implement some proposals without first reviewing them, thereby altering the incentives IGs have to over-contribute and signal higher quality proposals than they actually have. If it is sufficiently low-cost to inflate the policymaker's beliefs about
there is the possibility that in equilibrium the policymaker implements a proposal without first reviewing it. This is consistent with the idea that a legislator may vote on issues he has not had time to study in detail.20 This means the policymaker will implement some proposals without first reviewing them, thereby altering the incentives IGs have to over-contribute and signal higher quality proposals than they actually have. If it is sufficiently low-cost to inflate the policymaker's beliefs about 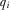 , then the IG will prefer to over-contribute compared to equilibrium. This means that
, then the IG will prefer to over-contribute compared to equilibrium. This means that 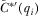 must not be too low; it must be sufficiently costly to signal a marginally higher quality. Otherwise, IGs would have the incentive to at least marginally inflate their payments in an effort to provide the impression (when they are not reviewed) that their proposals are higher quality than they truly are.
must not be too low; it must be sufficiently costly to signal a marginally higher quality. Otherwise, IGs would have the incentive to at least marginally inflate their payments in an effort to provide the impression (when they are not reviewed) that their proposals are higher quality than they truly are.
The incentives IGs have to under-contribute compared to equilibrium are similar to the previous section. The equilibrium requires that 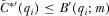 for all
for all 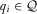 , which is the multiple-proposal equivalent to 7 from the previous section. Proposition 3 establishes that the constraint that
, which is the multiple-proposal equivalent to 7 from the previous section. Proposition 3 establishes that the constraint that 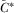 be increasing at a sufficiently hight rate never contradicts the constraint that it must be increasing at no greater rate than B.
be increasing at a sufficiently hight rate never contradicts the constraint that it must be increasing at no greater rate than B.
PROPOSITION 3.In the contest for attention game where 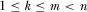 , there exists a function
, there exists a function 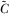 such that
such that
- (1)
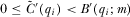 for all
for all 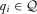 , and
, and - (2) for all functions
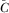 such that
such that 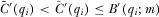 for all
for all 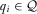 and
and 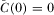 , there exists a full information equilibrium in which
, there exists a full information equilibrium in which 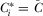 for each
for each 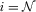 .
.
The equilibrium in which 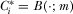 is the unique payment-maximizing full-information equilibrium.
is the unique payment-maximizing full-information equilibrium.
In the payment-maximizing equilibrium, total expected payments equal 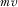 , implying that once again the policymaker is able to fully extract all of the rent from the policymaking process. Again, a policymaker who cares about both the quality of the implemented proposal and collecting IG payments will never expect higher utility than when he allocates attention to the highest bidder before implementing the proposals he believes best.
, implying that once again the policymaker is able to fully extract all of the rent from the policymaking process. Again, a policymaker who cares about both the quality of the implemented proposal and collecting IG payments will never expect higher utility than when he allocates attention to the highest bidder before implementing the proposals he believes best.
PROPOSITION 4.Consider the contest for attention game with k review slots and m implemented proposals, where 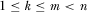 . The payment-maximizing full-information equilibrium results in the first best policy and the first best level contributions for the policymaker. There exists no other method for implementing policy that leads to higher expected payoffs for the policymaker.
. The payment-maximizing full-information equilibrium results in the first best policy and the first best level contributions for the policymaker. There exists no other method for implementing policy that leads to higher expected payoffs for the policymaker.
3.5. Importance of Reviewing at Least One Proposal
In equilibrium, each IG contributes according to a payment function that is strictly increasing in its proposal's quality, and the policymaker correctly infers the quality of each proposal from the IG payments. This means that ex post, after the IGs provide their contributions, reviewing a proposal never improves the accuracy of the policymaker's (already fully accurate) beliefs. Despite the ex post redundancy of the review process, it remains an essential part of the policymaker's allocation method, essential for the policymaker to become fully informed.
PROPOSITION 5.If the policymaker reviews no proposals, then there does not exist a full-information equilibrium.
The intuition behind this result is straightforward. Some probability of being reviewed is needed to maintain the separating equilibrium in which an IG's payment is strictly increasing in the quality of its proposal. If the policymaker reviews no proposal but continues to expect that IGs contribute according to strictly increasing payment functions, then the IGs each have an incentive to increase their payments, effectively inflating the policymaker's beliefs about the quality of their proposals. In this case, each IG deviates to pay 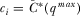 , resulting in the maximum policymaker beliefs about the quality of its proposal. Without any review, the policymaker is unable to infer anything about a proposal from its IG's payment, and in equilibrium
, resulting in the maximum policymaker beliefs about the quality of its proposal. Without any review, the policymaker is unable to infer anything about a proposal from its IG's payment, and in equilibrium 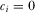 for all i.21
for all i.21
Under the assumptions of the model, the policymaker never has an incentive to review more than one proposal, as he becomes fully informed about the quality of all proposals in equilibrium, even when 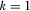 . In Section 4., we discuss cases of noisy IG quality signals, and unobservable IG asymmetries— cases where reviewing additional proposals may be beneficial.
. In Section 4., we discuss cases of noisy IG quality signals, and unobservable IG asymmetries— cases where reviewing additional proposals may be beneficial.
4. Model with Asymmetric IGs
In reality, IGs differ in their benefit from having their proposal implemented, or opportunity costs of providing political contributions. In this section, we allow for such observable asymmetries between the IGs. Except for the following changes, the underlying setting remains identical to the previous sections.
The IGs' payoffs depend on whether their proposal is implemented and their payment: 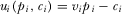 . Parameter
. Parameter 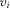 represents the relative value IGi puts on policy outcomes relative to payments. A higher
represents the relative value IGi puts on policy outcomes relative to payments. A higher 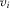 may be interpreted as either IGi having more at stake from their proposal being implemented, or as i being more wealthy or having lower costs of funds.22 Without loss of generality, we rank-order IGs according to their value, such that
may be interpreted as either IGi having more at stake from their proposal being implemented, or as i being more wealthy or having lower costs of funds.22 Without loss of generality, we rank-order IGs according to their value, such that 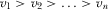 .23
.23
The policymaker reviews k and then implements m proposals, where 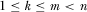 . The expected benefit to IGi if the policymaker always implements the m highest quality proposals can be defined as
. The expected benefit to IGi if the policymaker always implements the m highest quality proposals can be defined as 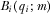 , which differs from
, which differs from 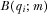 as defined in 8 only in that v is replaced by
as defined in 8 only in that v is replaced by 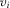 in its argument. Where clear, we refer to
in its argument. Where clear, we refer to 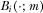 by
by 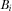 . Given that
. Given that  , it follows that
, it follows that 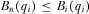 for all i and
for all i and 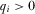 ; the benefit to
; the benefit to 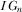 from participating in a full-information equilibrium is lower than the benefit to any other IG.
from participating in a full-information equilibrium is lower than the benefit to any other IG.
In the previous section, the contest for attention was symmetric, giving the same weight to all IGs' payments, and awarding attention to the k IGs that provided the highest payments. If the policymaker uses such a symmetric contest to allocate attention when IGs are asymmetric, he will still become fully informed and implement the first best policy in equilibrium, as long as the differences between the IGs are not too large. While a symmetric contest for attention results in the first best policy, it is not optimal for a policymaker who also cares about contributions.24 For the remainder of this section, we allow for a more general asymmetric (i.e., “handicapped”) contest for attention, which requires greater payments from some IGs than from others for the same equilibrium probability of winning attention. We show how such a contest is optimal for the policymaker compared to any other method that guarantees the first best policy.
We generalize the contest for attention, modeling it as an asymmetric all-pay contest defined as a set of score functions 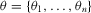 , one for each IG. When IGi provides payment
, one for each IG. When IGi provides payment  , its “score” is given by
, its “score” is given by 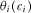 , where
, where 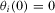 and
and 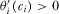 for all
for all 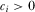 . The proposals associated with the highest scores in the contests receive attention. That is, the policymaker reviews proposal i if fewer than k other proposals have
. The proposals associated with the highest scores in the contests receive attention. That is, the policymaker reviews proposal i if fewer than k other proposals have 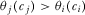 .
.
A policymaker may require higher payments from IGs with higher 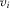 than from IGs with lower
than from IGs with lower 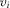 , in exchange for the same equilibrium probability of winning attention. The revenue-maximizing contest for attention involves score functions that fully adjust for observable IG asymmetries. Such a contest involves
, in exchange for the same equilibrium probability of winning attention. The revenue-maximizing contest for attention involves score functions that fully adjust for observable IG asymmetries. Such a contest involves 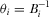 for all
for all 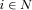 . In equilibrium, each IG provides a payment
. In equilibrium, each IG provides a payment 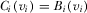 , and an IG wins attention and has its policy implemented if and only if it has one of the k highest
, and an IG wins attention and has its policy implemented if and only if it has one of the k highest 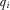 . In equilibrium, the policymaker implements the first best policy, and collects the maximum possible revenue compared to any other mechanism that guarantees the first best policy. We provide a detailed analysis in the online appendix. Proposition 6 summarizes this result.
. In equilibrium, the policymaker implements the first best policy, and collects the maximum possible revenue compared to any other mechanism that guarantees the first best policy. We provide a detailed analysis in the online appendix. Proposition 6 summarizes this result.
PROPOSITION 6.Consider the game with asymmetric IGs and a handicapped contest for attention in which 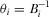 for all i, and where
for all i, and where 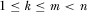 . There exists a full-information equilibrium in which
. There exists a full-information equilibrium in which 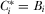 for all
for all 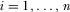 . This is the unique payment-maximizing full-information equilibrium.
. This is the unique payment-maximizing full-information equilibrium.
In equilibrium, IGs with higher 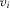 tend to pay more than IGs with lower
tend to pay more than IGs with lower 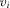 , implying higher contributions from more wealthy groups or groups with more to gain from having their proposal implemented. This does not, however, translate into either the attention or implementation decisions being biased in favor of more wealthy IGs. In equilibrium, more wealthy groups pay more, but the contest accounts for observable differences between IGs, and in equilibrium only the highest quality IGs (regardless of wealth) gain attention and have their proposals implemented.
, implying higher contributions from more wealthy groups or groups with more to gain from having their proposal implemented. This does not, however, translate into either the attention or implementation decisions being biased in favor of more wealthy IGs. In equilibrium, more wealthy groups pay more, but the contest accounts for observable differences between IGs, and in equilibrium only the highest quality IGs (regardless of wealth) gain attention and have their proposals implemented.
COROLLARY 2.Consider the game with asymmetric IGs and a handicapped contest for attention in which 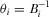 for all i, and where
for all i, and where 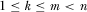 . In equilibrium, wealthy IGs tend to contribute more than less wealthy IGs, but they are no more likely to have their proposals implemented and are no better off than less wealthy IGs.
. In equilibrium, wealthy IGs tend to contribute more than less wealthy IGs, but they are no more likely to have their proposals implemented and are no better off than less wealthy IGs.
When IGs differ only in proposal quality, a policymaker who cares about both collecting payments and proposal quality can be no better off than when he sells attention to the highest bidders before implementing the proposals he believes best. This procedure for implementing policy results in the first best total payment (equal to 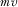 in expectation) and the first best policy outcome. It no longer guarantees the first best total payment in the environment with asymmetric IGs. In this section, the payment-maximizing full-information equilibrium guarantees the first best policy outcome, and guarantees the highest possible payments compared to any other full-information equilibrium. But it no longer guarantees the highest payments compared to certain methods of selling policy.25 The payment-maximizing full-information equilibrium describes the most profitable outcome associated with any mechanism that guarantees the first best policy outcome. A contest for attention that results in this outcome is preferred to any other method of awarding policy, as long as the policymaker cares enough about policy relative to payments (i.e., as long as λ in his payoff function is not too small).
in expectation) and the first best policy outcome. It no longer guarantees the first best total payment in the environment with asymmetric IGs. In this section, the payment-maximizing full-information equilibrium guarantees the first best policy outcome, and guarantees the highest possible payments compared to any other full-information equilibrium. But it no longer guarantees the highest payments compared to certain methods of selling policy.25 The payment-maximizing full-information equilibrium describes the most profitable outcome associated with any mechanism that guarantees the first best policy outcome. A contest for attention that results in this outcome is preferred to any other method of awarding policy, as long as the policymaker cares enough about policy relative to payments (i.e., as long as λ in his payoff function is not too small).
5. Other Considerations
We summarize a number of extensions, which illustrate the generality of our results. Detailed consideration of these extensions is provided in the online appendix.
Awarding attention through a winner-pay auction— We have thus far modeled the contest for attention as an all-pay auction. The policymaker may still be fully informed and guaranteed to implement the first best policy if he uses a winner-pay auction to award attention. However, with a winner pay contest, no payment-maximizing full-information equilibrium exists. This means that potential revenue is higher when the contest for attention takes the form of an all-pay contest rather than a winner-pay contest.
Other methods for allocating attention— The online appendix discusses alternative ways that the policymaker may sell access or choose policy. We also consider an alternative version of the game in which IGs can send cheap talk messages instead of payments prior to the allocation of attention.
Noisy quality signals— The model assumes that IGs perfectly observe the quality of their own proposals. It is possible, however, that IGs only observe an imperfect signal of their proposal's quality and are not perfectly aware of how the policymaker will perceive their proposal's quality following a review. In this case, the policymaker learns about the private signal of all IGs from their contributions, but he only becomes fully informed about the true quality of the proposals he actually reviews.
Allocating a divisible resource— We consider an alternative setting in which the policymaker chooses how to allocate a divisible resource when a project's optimal allocation is increasing in its own quality and decreasing in the quality of the other proposals. It is a generalized version of the competition for attention that appeared in Cotton (2009). We show in this alternative setting that a contest for attention leads the policymaker to become fully informed about the optimal allocation.
We reserve the detailed consideration of other extensions for future research. These include the following:
IG budget constraints—Assuming that IGs face binding budget constraints changes the equilibrium outcomes. When all IGs face the same budget constraint, the constraint may represent the implementation of campaign contribution limits as in Cotton (2009). An asymmetric constraint may represent cash or borrowing constraints which may differ across IGs. With budget constraints, an IG's equilibrium payment strategy is no longer strictly increasing in proposal quality, but rather strictly increasing in quality up to a point, before jumping to the maximum budget. This implies that the policymaker will fail to become fully informed about the quality of all proposals when more than k IGs have high enough realizations of quality that they contribute their entire budget.
Unobservable IG asymmetries—When IG differences in v are unobservable, a policymaker will be uncertain whether high contributions are due to IGs having high v or high proposal quality. He will only learn the true quality of proposals he reviews, and will remain less informed about the quality of the other proposals. This adds noise to the policymaking process, which we anticipate is similar to the extension with noisy IG quality signals.
IG have opposing positions on the same policy space—The model requires IGs to have some uncertainty about the proposal quality of the other IGs. The model would apply in a situation where the policymaker is deciding whether to eliminate steel tariffs, where the steel industry knows how many jobs the tariffs save in the steel industry, and manufacturers know how many manufacturing jobs the tariffs costs, but the opposing interests have uncertainty about the effect of the tariffs on jobs in the other industry. Such a situation is consistent with our framework. However, our framework is not consistent with a situation where the opposing interests are fully informed about the policymaker's optimal policy on their issue. That is a different model that may be explored in future research.
6. Conclusion
The paper shows how a policymaker who sells political access to IGs based on contributions may become fully informed about the quality of all policy proposals, and be guaranteed to implement the best policy. This is the case when the policymaker allocates his limited attention through a “contest for attention” before implementing the proposals he believes are best. This result stands in contrast to popular intuition that assumes the exchange of political contributions for access must be detrimental for policy. We find exactly the opposite. Selling political access to the highest bidders can guarantee the first best policy.
We establish that this main insight holds across a variety of assumptions and extensions to the model. The result holds regardless of how constrained the policymaker is, whether IGs are symmetric or asymmetric, whether the contest for attention involves an all-pay or winner-pay contest, and whether the policy proposals involve the allocation of a nondivisible or divisible resource. Our analysis suggests that a contest for attention can result in a fully informed policymaker and the first best policy in a wide variety of settings.
The paper goes on to establish that in some settings a contest for attention may result in both the first best policy and the first best level of total contributions. When this is the case, a policymaker does not need to sacrifice political contributions in order to implement the best policy. This result is in contrast to numerous models of lobbying in which a policymaker can bias policy in favor of IGs in order to increase political contributions. With a contest for attention, it is possible for a policymaker to maximize both contribution and policy utility. When this is the case, it is impossible for a policymaker to be better off in terms of either contributions or policy than when he allocates attention to the highest bidder before implementing the proposals he believes best.
Additional insights are gained when the analysis allows IGs to differ in terms of wealth or policy valuation, as well as proposal quality. In this setting, the payment-maximizing contest for attention is handicapped to fully account for interest group asymmetries. A rich interest group must pay more than an otherwise similar poor group for the same equilibrium probability of access (e.g., big oil must pay more than a local community nonprofit). The result gives insight into the popular intuition that the rich have better access to politicians, and that policy must therefore be biased in favor of the rich. This is not true in our analysis. Although we find that rich interest groups tend to contribute more than poor interest groups, this does not imply that the rich have a higher probability of winning attention or having their proposals implemented. In equilibrium, the policymaker devotes attention to and implements the highest quality proposals. Under our assumptions about policymaker behavior, policy is independent of interest group wealth.
Finally, the competition for attention framework may provide insight into other settings beyond political lobbying. A contest for attention may improve allocation decisions in other environments in which the primary goal is to choose the highest-quality or most qualified options, including the selection of candidates for jobs, scholarships, admissions, or marriage, and the selection of investment opportunities. We leave further consideration of these and other applications to future research.
Appendix A
Throughout the proofs, we use “PM” in place of “policymaker.”
Proof of Lemma 1.The strict monotonicity of 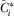 means there exists a one-to-one mapping between proposal i's quality,
means there exists a one-to-one mapping between proposal i's quality, 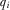 , and the payment made by IGi,
, and the payment made by IGi,  . If the PM reviews proposal i, then he observes
. If the PM reviews proposal i, then he observes 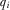 directly. If the PM does not review proposal i, then he infers
directly. If the PM does not review proposal i, then he infers 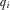 from his observation of
from his observation of  anticipating the IGs' equilibrium contribution strategy. That is, he believes that
anticipating the IGs' equilibrium contribution strategy. That is, he believes that 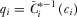 , and given the one-to-one relationship between
, and given the one-to-one relationship between  and
and 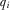 these beliefs are accurate in equilibrium.
these beliefs are accurate in equilibrium.
Proof of Lemma 2.The PM's policy choice must be sequentially rational given his beliefs about q, which means he must choose the policy with the highest posterior expected quality. When the PM is fully informed, his beliefs are correct, and he implements the highest quality proposal with probability 1.
Proof of Lemma 3.Follows from the analysis in the body of the paper.
Proof of Proposition 1.The analysis here complements the analysis in the body of the paper. In the body, we show that 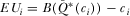 for any
for any 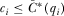 . In equilibrium, IGi must (weakly) prefer
. In equilibrium, IGi must (weakly) prefer 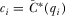 to any lower contribution, including a marginal decrease in
to any lower contribution, including a marginal decrease in  . The IG has no incentive to marginally decrease
. The IG has no incentive to marginally decrease  from its equilibrium payment if
from its equilibrium payment if 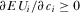 when evaluated at
when evaluated at 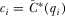 , meaning that IGi prefers to increase his contribution to
, meaning that IGi prefers to increase his contribution to 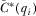 from any value lower than but close enough to this amount. This is the case when
from any value lower than but close enough to this amount. This is the case when
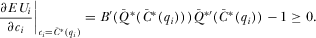 (A1)
(A1)Note that 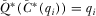 and that
and that 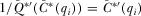 is implied by
is implied by 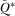 being the inverse function of
being the inverse function of 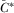 . Therefore, A1 may be rewritten
. Therefore, A1 may be rewritten
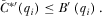 (A2)
(A2)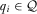 . The requirement that A2 holds for all
. The requirement that A2 holds for all 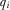 implies that
implies that 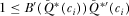 for all
for all 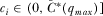 , which guarantees that
, which guarantees that 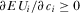 for all relevant
for all relevant  . Therefore, A2 for all
. Therefore, A2 for all 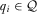 is both a necessary and sufficient condition for an IG not to have an incentive to deviate downward from its equilibrium contribution.
is both a necessary and sufficient condition for an IG not to have an incentive to deviate downward from its equilibrium contribution.The rest of the existence argument follows from the analysis in the body of the paper. The claim that no other symmetric full-information equilibria exist follows because the analysis fully characterizes the set of strictly increasing contribution functions that correspond to symmetric perfect Bayesian equilibria of the game. Because a full-information equilibrium is defined as one in which all contribution functions are strictly increasing, our characterization includes all symmetric full-information equilibria.
Proof of Proposition 2.Follows from Proposition 1 and the definition of a payment-maximizing full-information equilibrium as one in which all IGs contribute according to 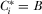 .
.
Proof of Corollary 1.Suppose 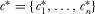 constitutes the equilibrium contribution profile under any arbitrary mechanism for the PM choosing which policy to implement. Each IG's equilibrium contribution
constitutes the equilibrium contribution profile under any arbitrary mechanism for the PM choosing which policy to implement. Each IG's equilibrium contribution 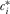 must satisfy an individual rationality constraint,
must satisfy an individual rationality constraint, 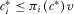 , where
, where 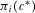 is the probability the PM chooses policy i conditional on equilibrium contribution profile
is the probability the PM chooses policy i conditional on equilibrium contribution profile 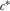 . The set of individual rationality constraints implies that
. The set of individual rationality constraints implies that
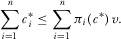 (A3)
(A3)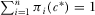 . Therefore, A3 simplifies to
. Therefore, A3 simplifies to
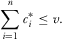 (A4)
(A4)In a full-information equilibrium, the PM also implements the proposal that maximizes his policy payoff. Therefore, the equilibrium involves both the highest possible payments and the best possible policy outcome, and the PM expects the maximum theoretically feasible payoff.
Proof of Proposition 3.The analysis in the body of the paper establishes that no IG has an incentive to under-contribute (i.e., pay 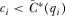 ) when
) when 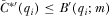 for all
for all 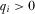 . It also argues that no IG has an incentive to over-contribute (i.e., pay
. It also argues that no IG has an incentive to over-contribute (i.e., pay 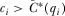 ) when
) when 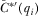 is sufficiently large, and that
is sufficiently large, and that 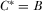 is always consistent with this requirement. Here, we formally establish these components of the result. The body of the paper establishes that no IG has an incentive to over-contribute when
is always consistent with this requirement. Here, we formally establish these components of the result. The body of the paper establishes that no IG has an incentive to over-contribute when  ; we therefore focus on the case where
; we therefore focus on the case where 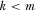 .
.
Consider the decision of IGi when all other IGs contribute according to strictly increasing function 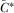 , and where
, and where 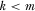 . IGi's expected payoff from contribution
. IGi's expected payoff from contribution 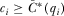 is
is
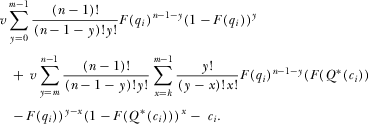 (A5)
(A5)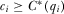 , the PM will implement proposal i regardless of whether IGi wins attention. If IGi wins attention, the PM observes
, the PM will implement proposal i regardless of whether IGi wins attention. If IGi wins attention, the PM observes 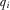 and expects it to be one of the m highest values. If i has one of the m highest quality proposals but does not win attention, the group will still have submitted one of the m highest payments and will still have its policy implemented. The second line of A5 is v times the probability that IGi does not have one of the m highest quality proposals, but still has its policy implemented (i.e., submits one of the m highest payments but does not receive attention).
and expects it to be one of the m highest values. If i has one of the m highest quality proposals but does not win attention, the group will still have submitted one of the m highest payments and will still have its policy implemented. The second line of A5 is v times the probability that IGi does not have one of the m highest quality proposals, but still has its policy implemented (i.e., submits one of the m highest payments but does not receive attention).Notice that the first line of A5 equals 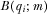 as given by 8.
as given by 8.
We can approach the analysis from the perspective of mechanism design. Under a contest mechanism, IGs choose contributions conditional on the quality of their proposals. The Revelation Principle implies that we can model this choice as IGs announcing their quality (possibly dishonestly), and being assigned a contribution amount given their announcement according to their equilibrium payment function 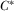 . We denote agent i's announcement of its type by
. We denote agent i's announcement of its type by 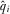 , which is equivalent to i choosing a contribution
, which is equivalent to i choosing a contribution  and
and 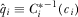 . Equilibrium payment functions must be such that each IG prefers to truthfully announce their quality, with
. Equilibrium payment functions must be such that each IG prefers to truthfully announce their quality, with 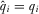 . This means that we can rewrite A5 in terms of
. This means that we can rewrite A5 in terms of 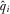 rather than
rather than  .
.
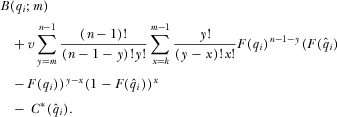 (A6)
(A6)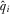 (i.e., does not over contribute), the second line of A6 equals zero, and its expected payoff is
(i.e., does not over contribute), the second line of A6 equals zero, and its expected payoff is
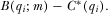 (A7)
(A7)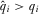 . And this must hold generally for all
. And this must hold generally for all 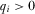 in order for i never to have an incentive to deviate. A7 is at least as great as A6 if
in order for i never to have an incentive to deviate. A7 is at least as great as A6 if
 (A8)
(A8) and every
and every  when
when  is sufficiently large. Given that we focus on full-information equilibria where by definition
is sufficiently large. Given that we focus on full-information equilibria where by definition 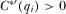 , this condition requires that
, this condition requires that 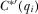 is sufficiently large for all
is sufficiently large for all  . If A8 does not hold, then IGi prefers to deviate to announce a value
. If A8 does not hold, then IGi prefers to deviate to announce a value 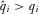 (i.e., to contribute more than
(i.e., to contribute more than 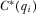 ), violating the equilibrium strategy.
), violating the equilibrium strategy.The above analysis verifies the claim that 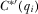 must be sufficiently large. Next, we show that
must be sufficiently large. Next, we show that 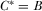 always satisfies this required equilibrium condition;
always satisfies this required equilibrium condition; 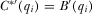 is always sufficiently large. Expression A7, the expected utility to IGi of playing the equilibrium strategy
is always sufficiently large. Expression A7, the expected utility to IGi of playing the equilibrium strategy 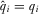 , simplifies to
, simplifies to 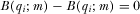 . To establish that IGi prefers
. To establish that IGi prefers 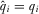 to any higher value, we must show that A8 always holds when
to any higher value, we must show that A8 always holds when 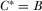 . First, we rewrite an expression for
. First, we rewrite an expression for 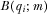 in terms of both i's true quality
in terms of both i's true quality 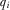 and some arbitrary alternative
and some arbitrary alternative 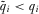 .
.
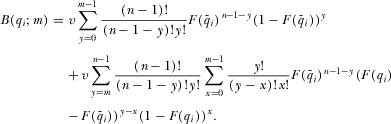
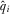 greater than
greater than 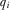 . We may therefore write
. We may therefore write
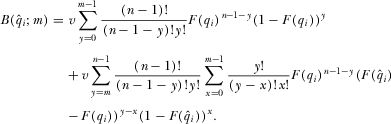 (A9)
(A9)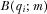 from 8. Next, we plug A9 and 8 into A8 for
from 8. Next, we plug A9 and 8 into A8 for 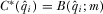 and
and 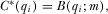 respectively. Simplifying the resulting expression allows us to rewrite A8:
respectively. Simplifying the resulting expression allows us to rewrite A8:
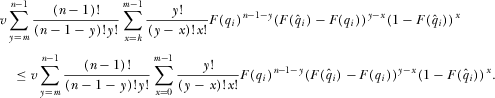 (A10)
(A10)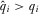 , establishing that IGi prefers to announce
, establishing that IGi prefers to announce 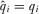 any higher value. This equivalently means that IGi prefers
any higher value. This equivalently means that IGi prefers 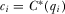 to any higher contribution.
to any higher contribution.
Proof of Proposition 4.It is straightforward to adapt the proof of Corollary 2 for the multiple policy environment.
Proof of Proposition 5.By definition, a full information equilibrium is one in which 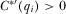 for all
for all 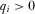 . As we previously determined, in equilibrium the PM will implement the proposals he believes are highest quality. His beliefs when he does not review proposal i put probability 1 on
. As we previously determined, in equilibrium the PM will implement the proposals he believes are highest quality. His beliefs when he does not review proposal i put probability 1 on 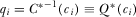 for any
for any  on the domain of
on the domain of 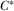 .
.
Consider IGi's optimization problem when the other  IGs contribute according to equilibrium function
IGs contribute according to equilibrium function 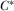 , and the PM reviews no proposals (relying only on observed contributions when updating his beliefs). IGi's expected payoff from contributing
, and the PM reviews no proposals (relying only on observed contributions when updating his beliefs). IGi's expected payoff from contributing  is
is
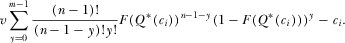
 signals one of the m highest qualities. Given that the other
signals one of the m highest qualities. Given that the other  IGs contribute according to the equilibrium function, proposal i is implemented when fewer than m other
IGs contribute according to the equilibrium function, proposal i is implemented when fewer than m other 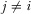 give
give 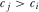 , which happens whenever fewer than m others have
, which happens whenever fewer than m others have 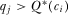 . Given the continuous distribution of qualities, ties happen with zero probability. Equation 8 means that this payoff is equivalent to
. Given the continuous distribution of qualities, ties happen with zero probability. Equation 8 means that this payoff is equivalent to
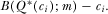 (A11)
(A11) is positive if
is positive if
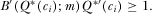
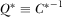 , we know
, we know 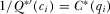 . Therefore, we may rewrite the previous inequality as
. Therefore, we may rewrite the previous inequality as
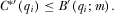 (A12)
(A12)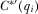 can be no greater than
can be no greater than 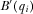 for
for  to be an equilibrium, guaranteeing that A12 is satisfied. Therefore, no full information equilibrium exists in which
to be an equilibrium, guaranteeing that A12 is satisfied. Therefore, no full information equilibrium exists in which 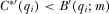 for any
for any 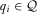 .
.We must also show that there does not exist an equilibrium in which 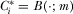 . When this is the case, IGi is indifferent between all
. When this is the case, IGi is indifferent between all 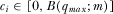 ; any contribution gives IGi an expected payoff of zero. A1 requires that an indifferent IG maximize the probability of having its policy implemented. This probability is maximized at a value of 1 when IGi submits the maximum feasible contribution,
; any contribution gives IGi an expected payoff of zero. A1 requires that an indifferent IG maximize the probability of having its policy implemented. This probability is maximized at a value of 1 when IGi submits the maximum feasible contribution, 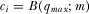 . For all
. For all 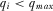 , A1 means that IGi over contributes since
, A1 means that IGi over contributes since 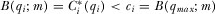 .
.
Other proofs and analysis of the extensions can be found in the online appendix.
Biography
Christopher Cotton, Department of Economics, Queen's University, Kingston, Ontario K7L 3N6, Canada ([email protected]).
References
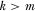 , and show that the policymaker can still become fully informed by selling access through an all-pay auction. However, when
, and show that the policymaker can still become fully informed by selling access through an all-pay auction. However, when 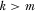 , there does not exist a payment-maximizing full-information equilibrium. Because of this, it is reasonable to expect that the policymaker would never allocate more than m access slots.
, there does not exist a payment-maximizing full-information equilibrium. Because of this, it is reasonable to expect that the policymaker would never allocate more than m access slots.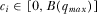 is a best responses for IGi, each giving an expected payoff of zero. Therefore, each IG is willing to contribute
is a best responses for IGi, each giving an expected payoff of zero. Therefore, each IG is willing to contribute 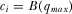 , but we see no reason why it would do so. Unlike in the earlier sections, here such a contribution does not stand out from the other contributions over which an IG is indifferent. Because of this, we impose Assumption 1, putting some structure on the choice of contribution by an indifferent IG, and therefore ruling out any full-information equilibrium when there are no reviews.
, but we see no reason why it would do so. Unlike in the earlier sections, here such a contribution does not stand out from the other contributions over which an IG is indifferent. Because of this, we impose Assumption 1, putting some structure on the choice of contribution by an indifferent IG, and therefore ruling out any full-information equilibrium when there are no reviews.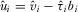 when its policy is implemented and
when its policy is implemented and 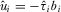 when it is not implemented. Here,
when it is not implemented. Here, 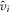 is the weight on policy and
is the weight on policy and 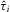 is the weight on payments. Any positive affine transformation of
is the weight on payments. Any positive affine transformation of 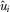 maintains preferences. We therefore define
maintains preferences. We therefore define 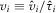 and
and 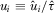 , and rewrite agent i's preferences as we defined them in the body of the paper. An increase in
, and rewrite agent i's preferences as we defined them in the body of the paper. An increase in 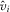 and a decrease in
and a decrease in 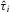 are indistinguishable in the model.
are indistinguishable in the model.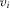 . Additionally, we could incorporate differences in quality distribution,
. Additionally, we could incorporate differences in quality distribution, 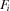 , allowing IGs to, for example, differ in the expected quality of their proposals. Allowing such differences complicates the analysis, particularly the functions for
, allowing IGs to, for example, differ in the expected quality of their proposals. Allowing such differences complicates the analysis, particularly the functions for 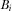 , without providing additional insight. The main results continue to hold.
, without providing additional insight. The main results continue to hold. for
for 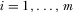 . It is an equilibrium under such an alternative mechanism for the m highest value IGs to contribute
. It is an equilibrium under such an alternative mechanism for the m highest value IGs to contribute  , and such a mechanism results in the maximum feasible expected sum of payments. It does not, however, guarantee the first best policy outcome.
, and such a mechanism results in the maximum feasible expected sum of payments. It does not, however, guarantee the first best policy outcome.



