Advancing loss reserving: A hybrid neural network approach for individual claim development prediction
Abstract
Accurately estimating loss reserves is critical for the financial health of insurance companies and informs numerous operational decisions. We propose a novel neural network architecture that enhances the prediction of incurred loss amounts for reported but not settled claims. Moreover, differing from other studies, we test our model on proprietary datasets from a large industrial insurer. In addition, we use bootstrapping to evaluate the stability and reliability of the predictions and Shapley additive explanation values to provide transparency and explainability by quantifying the contribution of each feature to the predictions. Our model shows superiority in estimating reserves more accurately than benchmark models, like the chain ladder approach. Particularly, our model exhibits nuanced performance at the branch level, reflecting its capacity to effectively integrate individual claim characteristics. Our findings emphasize the potential of using machine learning in enhancing actuarial forecasting and suggest a shift towards more granular data applications.
1 INTRODUCTION
A fundamental aspect of operations within an insurance company is loss reserving. It is mandated by regulatory frameworks such as Solvency II in Europe or ORSA in North America to maintain the financial health and solvency (EIOPA, 2019; NAIC, 2022) of the insurance company. Traditional loss reserving methods, like the chain ladder method, are based on aggregating claims into a homogeneous portfolio structured in a triangular shape which captures claims development over time. Besides its original purpose of risk management, information on loss reserves and thereby a good prediction of the ultimate claim amount is used in areas such as pricing, portfolio management, and strategic business planning (Taylor, 2019). This need arises because accurate financial forecasting and decision-making depend on knowing the full extent of liabilities and not just current ones. By ensuring that the final claim amounts are correctly estimated, companies can more effectively set premia, assess portfolio health, and develop future growth strategies. This can improve overall financial stability and operational efficiency across various functions. The traditional aggregated view treats all claims in a portfolio as homogeneous, while unique characteristics of the claim are ignored. Thus, it relies on the assumption that past patterns will continue in the future. This can be problematic with changing external factors like inflation, which is usually not included in the predictions. However, this information is vital to provide granular insights on the claim developments and allow for an up-to-date handling of processes within the insurance. The importance of loss reserving within the insurance, coupled with new advances in data collection and computational efficiency, call for more granular and flexible approaches for loss reserving based on individual claims. Such methods can offer the flexibility and adaptability to effectively respond to evolving market conditions and emerging risk patterns.
Our paper adds to this discussion by developing a new machine learning-based model architecture, which maintains a level of complexity comparable to recently proposed models. We test this model on two real claim portfolios of a large industrial insurance company. Although a few studies have used machine learning techniques, a notable challenge is the limited availability of public individual claims data. Hence, empirical studies on loss reserving often refer to the stochastic simulation machine by Gabrielli and Wüthrich (2018). Therefore, our datasets offer a particularly interesting perspective on investigating advanced machine learning techniques for loss reserving.
Typically, newer models which consider richer data on individual claims are either parametric or use machine learning techniques. However, none have become a gold standard, and advances are still needed. The approach proposed by Kuo (2020), while not surpassing chain ladder estimates at an aggregate level for a specific simulated dataset, offers insightful individual claims forecasts, although without benchmark comparisons at the granular level. Gabrielli (2020) reports individual claims reserves within 2% of true payments across all lines of business (LoB) considered, yet without benchmarking against other models. Chaoubi et al. (2023) find that, depending on the dataset, their long short-term memory (LSTM) model either slightly overestimated reserves compared to the chain ladder method or, in real data scenarios, provided closer approximations to actual reserves; this highlights the machine learning potential for capturing claim trends more accurately than traditional methods. However, their comparisons are limited to the chain ladder model. These studies emphasize the ongoing need for advances in loss reserving methodologies. To the best of our knowledge, no proposed model consistently outperforms the chain ladder approach when considering a broad spectrum of scenarios.
Central to the task of loss reserving is predicting two claim types: claims incurred but not reported (IBNR) to the insurance, and those reported but not settled (RBNS). This study focuses on RBNS claims and suggests a machine learning algorithm tailored to the dynamic nature of the task at hand and demand for more detailed analysis incorporating diverse granular claim characteristics. We consider incurred losses as payments plus individual case reserves; here, expert information on case reserves works as latent information, which is included in the machine learning algorithm to predict the cumulative incurred losses of the unknown periods. By leveraging standard deep learning techniques for static features and a LSTM model with an added attention mechanism for dynamic features, our model efficiently processes and combines these diverse inputs. The final predictions are made through a straightforward decision-making process based on the predicted probability of changes in cumulative losses by utilizing a composite loss function to optimize for both classification and regression tasks. We benchmark our model against traditional methods, like the chain ladder approach1 and a standard econometric model. In addition, we test against our machine learning algorithm but based on incremental claim amounts, which is commonly employed as outlined by Kuo (2020) and Gabrielli (2021), and the model proposed by Chaoubi et al. (2023). We assess the predictive performance of the model by analyzing the percentage error of the estimated reserves for the entire portfolio and sub-portfolios. Additionally, we compare models using the normalized mean absolute error (NMAE) and normalized root mean squared error (NRMSE) for the regression tasks, and balanced accuracy for the classification tasks. Our comparative analysis shows that the neural network model, especially when processing cumulative data, consistently outperforms traditional methods like the chain ladder and linear regression models in estimating reserves for both property and liability lines. This granular approach treats each claim individually. Hence, accounting for unique characteristics and specific risk factors. As a consequence, it provides a more detailed understanding of risk at the individual claim level, which enhances risk mitigation strategies. Moreover, this methodology enables detailed portfolio analysis and optimization, improving our insights into portfolio performance and profitability within the insurance sector. The model also enhances pricing accuracy by facilitating more precise and tailored pricing strategies and supports a better alignment with actual risk by incorporating individual claim details.
In addition, we employ a bootstrap aggregation technique (bagging) to improve the stability and accuracy of both regression and classification tasks. Additionally, we thereby reduce variance and avoid overfitting. We show that the neural network model, particularly when based on cumulative data, consistently demonstrates superior accuracy and reliability than other models.
For any machine learning application, especially in the insurance domain, transparency and explainability of the driving features are crucial. For this, we provide Shapley additive explanation (SHAP) values for the top 10 features in both datasets for the regression and classification tasks. Additionally, we present SHAP values for each time point (i.e., every development period). This illustrates the benefits of our granular approach to loss reserving and highlights the complex interplay of various features over time.
The remainder of this article is organized as follows: Section 2 presents the context and process of loss reserving and provides an overview of the literature on loss reserving models. Section 3 discusses the used datasets. Section 4 introduces the proposed neural network architecture to estimate the outstanding claim amounts. Section 5 presents the benchmark models. Section 6 discusses the results and adds insights on the robustness and explainability of the neural network model for loss reserving. Finally, Section 7 presents the conclusions of the study.
2 LOSS RESERVING AND LITERATURE OVERVIEW
2.1 Loss reserving: An economic perspective
Loss reserving is a crucial and economically significant task within every insurance company (Radtke et al., 2016). As depicted in Figure 1, the loss reserving process can be described as follows2: First, a claim occurs. After a certain delay, the policy holder reports the claim to the insurance company. Based on the knowledge of the company at the time of reporting, parts of the claim might be settled immediately or partially until the claim is closed. Before the final closure, the claim may be reopened, and further payments and recoveries may happen. In nonlife insurance, actuaries go beyond analyzing raw claim payments by focusing on incurred losses, which are defined as the sum of raw claim payments and case reserves. Case reserves are usually set by experts and represent their current estimate of the outstanding loss on individual claims. The process involving payments, case reserves, and recoveries upon closure or final closure is referred to as incurred loss adjustments.
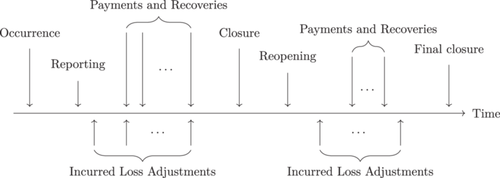
Incurred losses change dynamically over time. Payments and case reserves are not necessarily adjusted simultaneously. However, the incurred losses remain unaffected in scenarios where case estimates automatically adjust with claim payments while keeping the overall incurred loss constant. Additionally, for industrial insurance, incurred loss amounts may not change in every period, especially for complex claims characterized by long settlement horizons. Ultimately, the total paid amount aligns with the ultimate incurred loss amount, ensuring a balance in the final assessment. Our subsequent analyses considers these specifics of industrial insurance, and our machine learning methods are tailored to address these characteristics.
At the evaluation date, denoted by and representing the starting point of our prediction task, insurance companies distinguish between RBNS and IBNR claims. An IBNR claim was occurred before the evaluation date but is reported and settled afterwards. For an RBNS claim, the claim's occurrence and reporting before the evaluation date, while the settlement takes place afterward. Our model is specifically designed to leverage individual claim characteristics. As IBNR claims' characteristics are not observable at the time of evaluation, we exclusively focus on predicting RBNS claims.
We consider a portfolio comprising reported claims, indexed by . Each claim is reported after a specified time point. We use discrete points in time with development periods of equal length; that is, each development period spans 1 year. We also assume that each claim in the portfolio is fully settled within a fixed number of development periods. Therefore, for each claim, we have development periods indexed by . Our objective is to predict the incurred losses for the unknown periods , for each claim . Thus, at the evaluation date , each claim is in its specific development period. Our task is to estimate the remaining development periods until settlement. Each claim's development period at is defined by the number of discrete time points before .
Theoretically, there is a modeling equivalence between cumulative and incremental losses, making both approaches valid. However, incremental losses are more commonly predicted in the literature. By exploring both approaches, our model provides a robust and versatile tool for reserve estimation.
2.2 Loss reserving: A methodological perspective
Traditional loss reserving methods, such as the chain ladder method, rely on aggregating claims into a homogeneous portfolio, structured in a triangular format that captures the development of claims over time. These methods have been extensively employed and studied. For example, Mack (1993) introduces a distribution-free stochastic framework for the chain ladder method to quantify uncertainty in reserve estimates. Additionally, Verrall (2000) explores various stochastic models that align with chain ladder reserve estimates. Moreover, England and Verrall (2002), Pinheiro et al. (2003), and England and Verrall (2006) introduce bootstrapping techniques, which help in integrating expert judgments within a general linear model framework. For a comprehensive overview of traditional methods, see Wüthrich (2008).
New advances in data collection and increasing dataset complexity have led to extensions of traditional approaches, evolving the univariate chain ladder method into multivariate extensions (Merz & Wüthrich, 2008; Pröhl & Schmidt, 2005; Shi, 2017; Zhang, 2010). The multivariate extensions can aid in developing a portfolio of several correlated sub-portfolios by accounting for both contemporaneous correlations and structural relationships. However, the methods require strong structural assumptions on the relation between sub-portfolios and the aggregate portfolio, which are often rather ad hoc. We emphasize that this presents a huge advantage of machine learning methods, whereby nonlinear dependencies are captured without strong ad hoc assumptions. While using aggregated data for the chain ladder method is still the most popular approach, it has some limitations (Antonio & Plat, 2014): the inadequacy in handling outliers (Verdonck et al., 2009), parameter overfitting (Wright, 1990), and the presence of the chain ladder bias (Taylor, 2003). Antonio and Plat (2014) provide a comprehensive overview of these limitations. They argue that the existence of these problems, along with extensive literature on the topic, suggests that using aggregate data with the chain ladder method is not always suitable, especially when individual claims data are available.
Early contributions towards granular modeling on loss reserving are based on parametric models (Buhlmann et al., 1980; Norberg, 1986). Arjas (1989) and Norberg (1993, 1999) model individual claims development to compute reserves based on Position Dependent Marked Poisson Processes (PDMPP). Larsen (2007) refines their approach by decomposing the complex stochastic process of claim developments into independent segments corresponding to calendar years. By treating these as independent segments, Larsen's method allows the overall likelihood function to be separated into individual components, which can be maximized separately. This decomposition simplifies the stochastic reserving model's estimation process. Zhao and Zhou (2010) extend this idea by accounting for the dependence of claim event times and covariates. Furthermore, Huang et al. (2015, 2016) develop a stochastic model based on individual claim data that considers factors such as each claim's occurrence, reporting, and settlement times. Their model demonstrates a significant reduction in the mean squared error loss compared to classical models based on aggregated data. Thus, their findings support the use of models that leverage individual claim data.
In their review article, Wüthrich (2018) summarizes the benefits of machine learning in individual claims reserving. Pigeon and Duval (2019) explore these ideas by using different tree-based approaches, like the XGBoost algorithm, to predict the total paid amount of individual claims. Meanwhile, Baudry and Robert (2019) use another tree-based ensemble technique, ExtraTrees, to compute individual-level IBNR and RBNS claims reserves. A survey of recently developed claims reserving techniques can be found in Taylor (2019), emphasizing that research in this area remains highly relevant.
While loss reserving models have significantly evolved, including the adoption of machine learning techniques, the limited availability of publicly accessible individual claims data remains a notable challenge. To address this, Gabrielli and Wüthrich (2018) develop a stochastic simulation machine based on neural networks to synthesize claims data and provide back-testing capabilities. Using this stochastic simulation machine, Gabrielli (2020) and Gabrielli et al. (2020) integrate classical loss-reserving models into neural networks. They initially align the network with a traditional model, such as the over-dispersed Poisson, and then refine it through training to reduce prediction errors, effectively leveraging a boosting-like method. Gabrielli (2021) presents an individual claims reserving model for reported claims, which uses summarized past information to predict expected future payments. Instead, Kuo (2020) again focuses on the aggregated losses but considers the underlying time series nature of the data. The author's framework facilitates the joint modeling of paid losses and claims outstanding, adapting to incorporate various data types. The author then tests their model on aggregated datasets and demonstrates the potential for broader application with more detailed data. Furthermore, Kuo (2020) introduces an individual claims model for RBNS claims incorporating an encoder LSTM for past payments and a decoder LSTM for generating paid loss distribution, augmented by a Bayesian neural network for uncertainty quantification. However, none of these proposed models consistently and systematically outperform the classical chain ladder method for the used datasets. Chaoubi et al. (2023) suggest a different model architecture using a LSTM network followed by two fully connected layers to jointly predict the probability of a payment or recovery and the corresponding amount. Their model focuses on predicting incremental payments and treats static features as dynamic within the network. While their model seemingly has an advantage over the chain ladder method, an extensive set of benchmark models and large samples of actual data are missing.
3 DATA
We first detail the underlying datasets used here and describe the different claim features. Subsequently, we outline how we use the data for training and testing purposes.
3.1 Data description
Our data comprise proprietary claims data provided by a large industrial insurance company covering both short-tail and long-tail LoBs, which are the property and liability lines.3 The scarcity of publicly available individual claims data in empirical studies of insurance loss reserving means that simulated claims datasets are often used to enable the back-testing of the proposed models. For instance, Baudry and Robert (2019), Kuo (2020), and Gabrielli (2021) all use synthetically generated data on individual claims for their analysis. Moreover, when real claim data are utilized, the focus tends to be narrowly on a single LoB, predominantly examining general liability insurance for private individuals.4 Thus, the use of real-world, individual claim data from two distinct LoBs within the industrial insurance domain is particularly interesting for analyzing the use of machine learning methods for insurance loss reserving.
The property claim dataset contains a total of 66,208 claims arising from 16,713 distinct policies reported from January 1, 2011 to December 31, 2016, where observations are available until the end of 2021. The long-tailed liability claims dataset includes 403,461 claims from 24,084 distinct policies, reported from January 1, 2000, to December 31, 2011, where observations are available until the end of 2022. Thus, our data ensure a comprehensive analysis framework with at least six and twelve discrete annual observation periods for property and liability claims, respectively. This timeframe aligns with the assumption that claims are fully settled within the specified periods—6 years for property and twelve years for liability—corresponding to the internal reserving practices of the insurance company. This extensive dataset allows to thoroughly analyze each claim's development trajectory, providing a critical advantage for back-testing our model against real-world outcomes.
The data can be dissected into two types of data. The first type includes static features, which are fixed and do not change over time. The second type of data is dynamic; that is, these features may vary over time.
The property dataset contains the following static features: the Contract category, which identifies whether an insurance policy is part of an international program or a local policy; Contract type, which is differentiated into standard, primary, layer, and master policies; Business type, segmented into sole, lead, coinsurance, and indirect business, the Policy share, which captures the share of the overall insured risk (ranging from 0% to 100%); Risk category, which classifies each claim into one of 12 distinct risk categories5; Risk class, with values ranging from 1 to 10, with 10 signifying a higher risk; Coverage, which is detailed with three different coverages; Covered perils, which include three classes; Claim type, differentiated into attritional losses, large losses, and natural catastrophes; Notification duration of the claim, measured in days; and Branch, indicating which of the 12 branches the corresponding policy belongs to. The dynamic features are the German real GDP (base year 2011) and an internal Inflation mixture indices, created internally by the insurance company to reflect inflationary trends relevant for the specific LoB.
The liability dataset comprises the following static features: the Contract category, Business type, Policy share, the Risk category containing seven categories, the Coverage detailed by 12 different coverages, the Notification duration, and the Branch. The dynamic features are the same as those for the property dataset. The features used in our model for the two datasets are summarized in Appendix A.
We remove claims categorized at the reporting date as large losses. At the point of notification, a claims handler classifies each claim as either an attritional loss, a large loss, or a natural catastrophe. The classification is based on whether the expected ultimate loss amount exceeds a predetermined threshold specific to the LoB. Large losses, especially in the industrial insurance, can further increase the inherent volatility of the data. This may distort the predictions of the model aimed at more typical claim behavior. Therefore, it is usually analyzed and modeled separately (Denuit & Trufin, 2018; Riegel, 2014). In practice, reserving for large losses often involves a significant amount of expert judgment and adjustments. Due to this complexity and the unique handling required for these claims, we have excluded them from our analysis. Excluding large losses narrows our focus to attritional patterns, enhancing model precision for typical claims. Moreover, it highlights the necessity of separately addressing large losses for a holistic loss reserving approach. Notably, some claims may ultimately develop into large losses, although they were initially categorized as attritional losses. Hence, they remain a part of our datasets.
3.2 Training- and testing-setup
Grouping claims not only by their development period but also by their reporting year, indexed by , facilitates the structural organization of the data such that it aligns with traditional loss reserving methods based on loss triangles. This structure enables us to define the cumulative incurred loss amount for claim , in reporting year , and in development period as .
Figure 2 appropriately illustrates how the property dataset is organized in the form of a common loss triangle. Here, each cell represents , which is the sum of the incurred losses of all claims that were reported in year and are in their development period . This is helpful for visualizing the comparison between our individual loss reserving approach and the traditional aggregated methods. Moreover, we can visualize how we split our data into training, validation, and test sets.
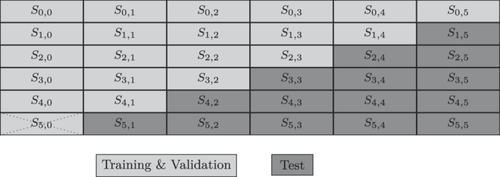
As our datasets contain the complete development trajectory of each claim up to their final development period , we first split the data into training and testing sets by setting the evaluation date to December 31, 2016, and December 31, 2011, for the property and liability datasets, respectively.6 The cumulative incurred loss amounts for are observable Up to these dates for each claim and serve as our training data (represented in light gray in Figure 2). The incurred loss amounts beyond this valuation date for , which are not observable as of , form the test set (represented in the dark gray in Figure 2).
That is, is the time point up to which data are considered known and used for training. Meanwhile, represents the final development period for any claim. Data observed up to are used for training, whereas those beyond are reserved for testing.
Further, we split the claims inside the training data randomly into the final training and validation sets.7 To be more precise, 80% of these data are used for model training, while the remaining 20% are used for model validation to evaluate the model's performance and generalizability.
4 METHODOLOGY
To model individual claims development, we propose a specific neural network architecture tailored to the claim settlement process. The key to our neural network model is two prediction goals: estimating the unknown cumulative incurred loss amounts per period and the probability of changes in these amounts within those periods. Neural networks, with their ability to discern complex patterns within large datasets, have become pivotal in various insurance applications, including fraud detection (Gomes et al., 2021), pricing (Wüthrich, 2019), and enhancing customer service interactions (Ansari & Riasi, 2016). Our approach integrates various deep learning building blocks that are particularly suited for modeling the sequential nature of claim developments while leveraging information stored in static features.
This section outlines our model architecture and introduces the benchmark methods and evaluation metrics used to assess predictive performance. The code for applying the proposed model to a synthetic dataset (due to the confidentiality of our actual data) is available online.8
4.1 Model architecture
The model architecture which is most similar to ours is introduced by Chaoubi et al. (2023). While inspired by this architecture, we introduce significant changes: We treat static and dynamic features individually within the network, include an attention mechanism besides our sequential model to further enhance the network's ability to focus on the input sequence's relevant parts, and use a decision rule for updating the predicted claim amounts.
Essentially, our model adopts a two-part approach: it separately processes static and dynamic features before integrating them to produce two task outputs. Consequently, the model can capture the unique characteristics of each type of feature. Furthermore, the final prediction is based on a simple decision rule that incorporates the two outputs: if the probability of a change in the cumulative incurred loss amount exceeds a predefined threshold, the model updates its forecast using the output of the regression task; otherwise, the current estimate is retained. The specific threshold is determined post-training by analyzing the validation set, ensuring that the forecast over the next period depends on a substantial probability of change.9 This approach mitigates the risk of over-adjustment during periods of claim stability, thereby implicitly optimizing operational efficiency. This strategy contrasts with the method proposed by Chaoubi et al. (2023), wherein the output of the regression task is weighted by the predicted probability through the multiplication of these two quantities.
In summary, the model operates under the following assumptions: (1) Claim development patterns are assumed to be consistent across reporting years. However, time dependence is introduced through dynamic factors such as GDP and inflation, which change over time and impact the claims process. These factors ensure that the model adapts to varying economic conditions while maintaining the assumption of underlying structural consistency in claim development. (2) Claims are fully settled within predefined periods (six and twelve for property and liability claims, respectively). (3) The final output is produced by combining the results of the regression and classification task, utilizing a decision rule to update predictions based on the probability of change in the incurred loss amount.
In our network, the first step is processing the static features, which contain both quantitative and categorical types. All static quantitative features are standardized. Each static categorical feature is initially indexed and then processed by embedding layers, as introduced by Bengio et al. (2000). According to Kuo (2020) and Gabrielli (2021), we embed categorical variables into two-dimensional vectors. The processed static features are concatenated into a single vector, denoted by and fed into a fully connected (FC) layer10 with a rectified linear unit (ReLU) activation function. This yields the output vector .
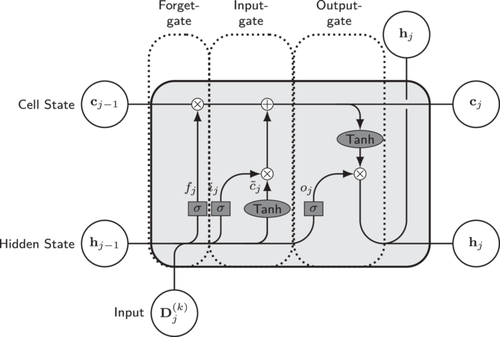
Dynamic features, denoted by , are processed within our model by a LSTM layer, introduced by Hochreiter and Schmidhuber (1997). This architecture is designed to handle sequential data by maintaining a memory of past information. This is particularly useful for modeling the time-dependent behavior in the claims reserving process. The LSTM operates on a sequence of dynamic features, updating two crucial components at every time step: the cell state and hidden state . These states integrate new information provided by the current input, and are essential for the model to remember and forget information through a process involving three gates. Specifically, the forget gate controls the extent to which the previous cell state is retained. The input gate updates the cell state by adding new information. The output gate decides which information from the cell state will be used to generate the output hidden state, which is further used for predicting the next development period. These operations allow the LSTM to maintain and manipulate its internal state over time, providing the ability to remember information across sequences of variable lengths. We refer to Figure 3 for a visual representation of a single LSTM cell, which delineates the workflow through its various gates. As the LSTM processes the sequence of dynamic features up to the last observed period, it outputs a series of hidden states. The last hidden state is particularly important as it encapsulates the information from the entire input sequence. This state is used for making the one-step-ahead prediction for the coming unknown period.
To further refine the focus of the model on relevant temporal patterns, we introduce an attention mechanism besides the set of hidden states. Attention mechanisms, initially popularized in the context of neural machine translation (Bahdanau et al., 2014; Luong et al., 2015), allow a model to dynamically focus on different parts of the input sequence to generate the output sequence's each element. They work by assigning weights to different input elements, indicating their relative importance for the task at hand. This approach can significantly improve the performance of time series tasks, as demonstrated by Lai et al. (2018), who empirically show improved performance across various time series domains. It is also effective in financial time series predictions, where attention mechanisms have been successfully used in conjunction with LSTMs (Kim & Kang, 2019; Zhang et al., 2019). This demonstrates this approach's adaptability and efficiency in diverse applications. Our dot product attention mechanism is identical to that used by Lai et al. (2018) and is designed such that the hidden states can only be influenced by their predecessors without affecting them in return. The mechanism also maintains the temporal ordering of the sequences.
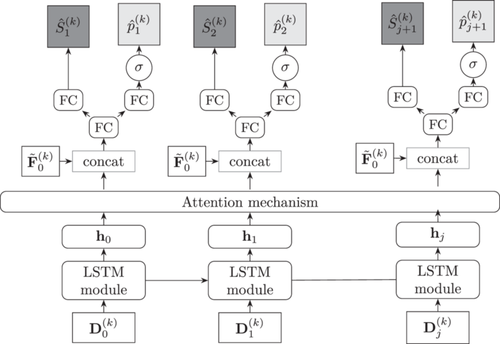
Finally, the processed static feature vector is replicated and concatenated with the attended hidden states to form a comprehensive feature set for each period. The resulting feature vector is then fed into another FC layer using the ReLU activation function, followed by two separate pathways to produce the one-step ahead prediction. One pathway involves an FC layer with the identity activation function to produce the regression output for the cumulative incurred loss amount of the next period, defined as . The second pathway utilizes an FC layer with a sigmoid activation function to get the probability of a change in the cumulative incurred loss amount in the next period . The proposed architecture is illustrated in Figure 4.
To optimize the hyperparameters of the network, we perform a two-staged approach. Initially, Random Search is utilized to broadly explore the hyperparameter space, followed by a refinement process using Bayesian Search. Our training methodology and hyperparameter tuning strategy, including the two-staged approach's specifics, are described in detail in Appendix B. Notably, the training process of our model, particularly during hyperparameter tuning, does demand considerable computational resources (e.g., up to 9.25 hours for Random Search and 11.07 h for Bayesian Search on an Amazon-EC2-G5.8xlarge instance). However, such computational demands should not be a limiting factor for modern insurance companies. The potential for more accurate and flexible predictions, which advanced methods like ours aim to achieve, can justify these resources when the model outperforms classical methods.
5 BENCHMARK MODELS
To assess our proposed model's predictive performance, we compare the results, based on the test sets to several benchmark models, including aggregated and individual ones.
We apply the chain ladder method to our two aggregated datasets from the property and liability LoBs. This helps in establishing a foundational comparison for our model, particularly given its wide acceptance and usage in the industry for reserve estimation.
Furthermore, we utilize the simplest form of econometric modeling: linear regression. This choice allows us to emphasize the difference in predictive performance between a straightforward econometric approach and complex neural network architecture at the individual claim level. Instead of using the complete feature set, which may introduce noise and lead to overfitting, we employ a stepwise backward elimination based on the Akaike Information Criterion (AIC) for feature selection. Starting with the full model, which includes all predictors, we sequentially drop predictors while incorporating fixed effects for both the reporting years and development periods to account for their temporal dynamics (Friedman, 2009).
We also include the model architecture proposed by Chaoubi et al. (2023) for comparison. For this benchmark, while we utilize incremental data following the modeling strategy used by the aforementioned authors, we also adapt the training process to mirror that of our model. Chaoubi et al. (2023) suggest a method where the final prediction arises from the product of a non-zero loss predicted probability and the regression task's outcome. This approach contrasts with our use of a decision rule, where we separately evaluate the two tasks before making a prediction. This inclusion is particularly insightful as it allows us to directly assess the impact of the modifications we introduced.
Lastly, we extended the application of our model to incremental data. The training process remained largely analogous to that used for cumulative data, with a change in setting up the classification task and the final decision rule. In the context of incremental data, our classification objective transformed to predicting the probability that the incurred loss amount in the upcoming period is non-zero. The final prediction of the model is therefore given by the decision rule: If the probability of a non-zero incurred loss amount exceeds the threshold, we use the regression task output, and otherwise, we predict a zero amount.
In summary, these benchmark models—the chain ladder method, linear regression, the model proposed by Chaoubi et al. (2023), and the adaptation of the model to incremental data—provide a robust foundation for evaluating our novel approach. To compare the models, we assess the predictive performance using the percentage error of the estimated reserve for the complete portfolio and sub-portfolios. We also evaluate the individual cumulative loss forecasts' accuracy by comparing the normalized NMAE and NRMSE for our model's regression task, and balanced accuracy for the classification task. By normalizing the error metrics by the standard deviation, we account for the potentially decreasing variability in claims as they get settled over time, ensuring that the error metrics do not artificially change simply due to reduced variability. Therefore, the normalization also facilitates a fair comparison across different development periods. In the early development periods, claims are often more volatile and less predictable due to the initial uncertainty. As time progresses and more claims are settled, overall variability reduces. Normalizing the errors helps distinguish whether the error reduction is genuinely due to better model performance or merely a consequence of the natural claim settlement.
We use the normalized mean absolute error because it is inherently less sensitive to outliers. Conversely, the normalized mean squared error provides a complementary perspective as it penalizes larger errors more and, thus, provides insights into the predictions' variability. Together, these metrics provide a holistic view of the model performance, encompassing the average accuracy and distribution of the prediction error. Furthermore, the balanced accuracy is used to evaluate the classification task of the models. Balanced accuracy is especially informative in the insurance claim context, as the number of claim adjustments and non-claim adjustments may not be evenly distributed over all claims. This metric helps adjust for any imbalances by considering both the True Positive (sensitivity) and True Negative Rates (specificity), thus providing a more accurate measure of the model's ability to correctly identify periods with and without changes in claim amounts. Balanced accuracy is the average of sensitivity and specificity. Hence, it provides a more equitable evaluation by giving equal weight to the performance on both the majority and minority classes. Consequently, it helps ensure that the model is not biased towards the more frequent class, and can effectively and accurately identify changes in the loss amounts.
6 RESULTS
Here, we present the empirical results obtained from applying the proposed models to our datasets. Additionally, we include the outcomes of a bootstrap analysis to assess therobustness and sensitivity of the model. Finally, we identify the features that most significantly influence the predictions of the neural network.
6.1 Model performance
We first examine each model's overall performance, quantifying this via the estimated reserves' percentage error, shown in Table 1.
| Line of business | ||
|---|---|---|
| Model | Property | Liability |
| Chain Ladder | −14.36 | −16.32 |
| Neural Network | −1.37 | −1.18 |
| Neural Network (Incr) | 7.59 | −16.28 |
| C-LSTM | 11.34 | −18.58 |
| Linear Regression | −20.73 | −61.37 |
- Note: Bold values indicate the model with the lowest percentage error for each line of business.
We find a significant heterogeneity in performance across the models. Our neural network models demonstrate superior accuracy, with the model based on cumulative data yielding the lowest percentage errors: −1.37% for property and −1.18% for liability. This is better than the chain ladder method, which exhibits larger negative errors, indicating an underestimation of the reserves. Interestingly, the neural network model applied to incremental data shows a notable deviation from the cumulative data-based network. It exhibits a positive percentage error of 7.59% for property, suggesting overestimation and comparable underestimation to the chain ladder method for liability with a −16.28% error.
The C-LSTM model, following the methodology proposed by Chaoubi et al. (2023), exhibits a similar pattern to our models but with larger percentage errors. With an 11.34% error for property, it slightly outperforms the chain ladder model but still overestimates the underlying claims portfolio. Conversely, for the liability line, the C-LSTM model shows an −18.58% error, indicating greater underestimation than traditional approaches. Clearly, our modifications in the model architecture and reserve estimation strategy are beneficial.
Lastly, the performance of the linear regression model highlights its limitations in handling claim data complexity, significantly underestimating property by −20.73% and liability by −61.37%. Thus, the simplicity of the model is inadequate for capturing the complex, possibly nonlinear patterns present in the data.
To provide deeper insights into the predictive performance of our model at the individual claim level, we present each development period's NMAE, NRMSE, and balanced accuracy. These metrics are detailed in Tables 2–4 for property and Tables 5–7 for liability. These tables show the final prediction errors of the neural network and isolate the NMAE and NRMSE for the regression task alone (, and ). This allows to distinguish the classification task's impact on prediction accuracy.
| NMAE | |||||||
|---|---|---|---|---|---|---|---|
| Development period | NN | NN-incr | C-LSTM | LR | |||
| 0 | - | - | - | - | - | - | - |
| 1 | 0.0459 | 0.0540 | 0.0475 | 0.0582 | 0.0717 | 0.0860 | 0.1589 |
| 2 | 0.0318 | 0.0439 | 0.0334 | 0.0495 | 0.0729 | 0.0886 | 0.1601 |
| 3 | 0.0252 | 0.0441 | 0.0281 | 0.0478 | 0.0598 | 0.0721 | 0.1588 |
| 4 | 0.0213 | 0.0479 | 0.0244 | 0.0458 | 0.0465 | 0.0609 | 0.1832 |
| 5 | 0.0188 | 0.0497 | 0.0225 | 0.0441 | 0.0448 | 0.0456 | 0.1760 |
- Note: Bold values indicate the model with the lowest normalized mean absolute error for each development period.
| NRMSE | |||||||
|---|---|---|---|---|---|---|---|
| Development period | NN | NN-incr | C-LSTM | LR | |||
| 0 | - | - | - | - | - | - | - |
| 1 | 0.4686 | 0.6130 | 0.6601 | 0.6632 | 0.6876 | 0.7083 | 0.7652 |
| 2 | 0.3685 | 0.4186 | 0.4533 | 0.4628 | 0.6332 | 0.6516 | 0.8200 |
| 3 | 0.3322 | 0.3609 | 0.3940 | 0.4122 | 0.5087 | 0.5233 | 0.8721 |
| 4 | 0.3145 | 0.3336 | 0.3480 | 0.3796 | 0.4483 | 0.4564 | 0.9605 |
| 5 | 0.2985 | 0.3451 | 0.3289 | 0.3726 | 0.3673 | 0.3793 | 0.9588 |
- Note: Bold valued indicate the model with the lowest normalized root mean squared error for each development period.
| Balanced accuracy | ||
|---|---|---|
| Development period | NN | NN-incr |
| 0 | - | - |
| 1 | 66.63 | 67.60 |
| 2 | 69.17 | 67.55 |
| 3 | 71.53 | 70.98 |
| 4 | 73.86 | 72.34 |
| 5 | 79.44 | 77.45 |
- Note: Bold values indicate the model with the lowest balanced accuracy for each development period.
| NMAE | |||||||
|---|---|---|---|---|---|---|---|
| Development period | NN | NN-incr | C-LSTM | LR | |||
| 0 | - | - | - | - | - | - | - |
| 1 | 0.0862 | 0.0961 | 0.1001 | 0.1170 | 0.1640 | 0.1792 | 0.2329 |
| 2 | 0.0889 | 0.0888 | 0.1144 | 0.1142 | 0.1544 | 0.1714 | 0.2381 |
| 3 | 0.0806 | 0.0811 | 0.1029 | 0.1091 | 0.1466 | 0.1545 | 0.2186 |
| 4 | 0.0749 | 0.0764 | 0.0951 | 0.0973 | 0.1464 | 0.1455 | 0.2055 |
| 5 | 0.0622 | 0.0647 | 0.0810 | 0.0909 | 0.1249 | 0.1220 | 0.1802 |
| 6 | 0.0601 | 0.0676 | 0.0825 | 0.0843 | 0.1195 | 0.1213 | 0.1869 |
| 7 | 0.0579 | 0.0762 | 0.0781 | 0.0840 | 0.1160 | 0.1158 | 0.1872 |
| 8 | 0.0504 | 0.0789 | 0.0695 | 0.0802 | 0.1057 | 0.1076 | 0.1754 |
| 9 | 0.0447 | 0.0798 | 0.0630 | 0.0732 | 0.0972 | 0.0986 | 0.1684 |
| 10 | 0.0397 | 0.0769 | 0.0575 | 0.0647 | 0.0893 | 0.0926 | 0.1626 |
| 11 | 0.0359 | 0.0736 | 0.0550 | 0.0679 | 0.0858 | 0.0917 | 0.1568 |
- Note: Bold values indicate the model with the lowest normalized mean absolute error for each development period.
| NRMSE | |||||||
|---|---|---|---|---|---|---|---|
| Development period | NN | NN-incr | C-LSTM | LR | |||
| 0 | - | - | - | - | - | - | - |
| 1 | 1.0546 | 1.0806 | 1.0737 | 1.0851 | 1.1971 | 1.1993 | 1.1947 |
| 2 | 0.8638 | 0.8880 | 0.8810 | 0.8980 | 0.9574 | 0.9690 | 1.0071 |
| 3 | 0.6518 | 0.6772 | 0.6721 | 0.6829 | 0.8127 | 0.8526 | 0.9908 |
| 4 | 0.6930 | 0.7165 | 0.7315 | 0.7336 | 0.7989 | 0.7983 | 0.9973 |
| 5 | 0.8301 | 0.8322 | 0.8596 | 0.8671 | 0.9121 | 0.9197 | 0.9743 |
| 6 | 0.8975 | 0.9200 | 0.9381 | 0.9663 | 0.9888 | 1.0209 | 1.1084 |
| 7 | 0.9338 | 0.9339 | 0.9829 | 1.0206 | 1.0260 | 1.0145 | 1.1208 |
| 8 | 0.8943 | 0.8942 | 0.9345 | 0.9365 | 0.9648 | 0.9720 | 1.0519 |
| 9 | 0.8441 | 0.8681 | 0.9228 | 0.8912 | 0.9730 | 0.9308 | 1.0108 |
| 10 | 0.7915 | 0.8156 | 0.8259 | 0.8257 | 0.8709 | 0.8887 | 0.9744 |
| 11 | 0.7504 | 0.7518 | 0.7823 | 0.8071 | 0.8407 | 0.8429 | 0.9739 |
- Note: Bold values indicate the model with the lowest normalized root mean squared error for each development period.
| Balanced accuracy | ||
|---|---|---|
| Development period | NN | NN-incr |
| 0 | - | - |
| 1 | 66.61 | 64.13 |
| 2 | 66.63 | 63.93 |
| 3 | 66.94 | 62.24 |
| 4 | 67.45 | 65.34 |
| 5 | 67.12 | 65.85 |
| 6 | 67.89 | 67.34 |
| 7 | 67.57 | 66.75 |
| 8 | 70.20 | 68.21 |
| 9 | 73.75 | 70.88 |
| 10 | 75.18 | 72.43 |
| 11 | 76.12 | 73.81 |
- Note: Bold values indicate the model with the lowest balanced accuracy for each development period.
Importantly, for the C-LSTM model, the final prediction is the product of the predicted claim amount and predicted probability of a non-zero amount. This approach inherently differs from ours, as it directly integrates the probability into the regression output to refine the prediction. This distinction is crucial as it highlights the significance of the classification task in enhancing the performance of the model, particularly when it accurately predicts periods without a change in the incurred claim amount. This accuracy effectively reduces the error for those instances, which may even go to zero if the last state is known.14
For the property line, the NMAE and NRMSE for all models, except for the linear regression, decline over the development periods. This indicates the increasing accuracy of the models as they gain more information about the trajectories of the claims over time. Notably, the neural network models' (NN, NN-incr, and C-LSTM) final predictions consistently outperform the regression-only predictions (, and ). This highlights the significance of the classification task in the prediction process, as it enables the model to identify periods where the incurred claim amounts remain unchanged, potentially reducing the NMAE and NRMSE in those instances.
Moreover, for the C-LSTM model, the differences between the final predictions and regression outputs are smaller than those observed in our proposed models. This may be attributable to the C-LSTM's approach, wherein the classification task is primarily used to scale the regression results subtly rather than drastically altering them, which improves the prediction.
The balanced accuracy results, calculated for our neural networks (NN and NN-incr) and presented in Table 4, follow a similar pattern. Accuracy generally increases over time, indicating the improving capability of the model to correctly classify changes in claim amounts as claims progress. Notably, not all claims follow the same settlement pattern. While our models assume a fixed number of periods for full settlement, some claims may settle earlier. As the model adapts to these settlement patterns over time, the classification task potentially becomes simpler with each passing period.
As the model progresses through successive periods, it becomes more proficient at identifying patterns and anomalies within the claims data, refining predictions, and thus, likely resulting in the observed decrease in NMAE and NRMSE. This trend reflects the growing adeptness of the model in predicting claim closure timings and adapting to the data's evolving nature over the development periods.
When examining the liability line, we observe patterns similar to those seen in the property line. The models reveal a consistent decrease in NMAE over the development periods, as shown in Table 5. This trend is corroborated by increasing balanced accuracy scores, provided in Table 7. The NRMSE, detailed in Table 6, also diminishes over time, albeit with less uniformity, hinting at the influence of outliers in the reserving process. In industrial insurance, outliers are generally more prevalent in the liability than in the property line. Liability claims often involve complex legal issues and long-tail liabilities. This increases the likelihood of large, unpredictable claims that result in outliers. Despite initially excluding claims marked as large losses, some claims evolve into large losses during their lifecycle. This evolution can partially explain the observed variability in NRMSE values, revealing areas where our model's performance can be improved in predicting these evolving large-loss claims within the liability line.
Next, we focus on a distinct advantage of our neural network model: its ability to perform runoff analysis at various granular levels, such as the branch level. This is a particularly relevant aspect for practical actuarial applications. Table 8 presents the percentage error in estimated reserves for the property line across branches. The neural network models (NN, NN-incr, and C-LSTM) generally exhibit improved accuracy than the chain ladder method, with notably precise estimates in certain branches. Interestingly, for branch 300, the neural networks based on incremental data (NN-incr and C-LSTM) show a lower percentage error than the cumulative model. This may be attributed to the tendency of the former model to overpredict; in the context of large claims that disproportionately affect reserve estimates, this may result in closer alignment with actual incurred losses. The cumulative model's underprediction of −10% suggests that it may not be effectively capturing the volatility associated with such large claims. This demonstrates that different models may be appropriate for large claims and can lead to improved performance. Overall, the performance across branches is heterogeneous. Despite this variability, the neural network model based on cumulative data generally delivers better performance than its incremental counterpart.
| % Error | |||||
|---|---|---|---|---|---|
| Branch | CL | NN | NN-Incr | C-LSTM | LR |
| 100 | −16.09 | 11.70 | 16.18 | 17.83 | −18.34 |
| 130 | −15.55 | −2.64 | 3.07 | 7.24 | −45.75 |
| 200 | −13.40 | 9.65 | 29.21 | 34.48 | −37.48 |
| 300 | −18.20 | −10.00 | 1.91 | 3.24 | −43.11 |
| 400 | −31.14 | 0.88 | 19.95 | 20.01 | −65.97 |
| 430 | −3.51 | −2.43 | 3.43 | 7.11 | −21.55 |
| 460 | −14.58 | −2.49 | 7.22 | 8.13 | −58.61 |
| 650 | −20.08 | 1.80 | 9.74 | 9.18 | −41.03 |
| 700 | −33.34 | 12.65 | 33.78 | 40.05 | −77.50 |
| 800 | −56.46 | −3.70 | 10.06 | 15.33 | −68.05 |
| 850 | 55.28 | 38.25 | 98.61 | 97.12 | −98.79 |
- Note: Bold values indicate the model with the lowest percentage error for each branch.
Table 9 presents the percentage error of the estimated reserves by branch for the liability dataset. The liability line results exhibit a similar pattern to the property lines, as the neural network models generally demonstrate more accurate performance than the chain ladder and linear regression methods across several branches. Particularly, the incremental data-based model (NN-Incr) shows a lower absolute percentage error in branches 430 and 650, indicating more precise estimates in these cases. However, the difference in performance compared to the cumulative model (NN) is not notably large, suggesting that both models possess their strengths in handling the data for these specific branches.
| % Error | |||||
|---|---|---|---|---|---|
| Branch | CL | NN | NN-Incr | C-LSTM | LR |
| 100 | −56.90 | −20.65 | −43.05 | −51.48 | −87.47 |
| 130 | −10.37 | 0.42 | −33.51 | −34.12 | −89.12 |
| 200 | −54.28 | 6.45 | 13.13 | −16.79 | −69.04 |
| 300 | −23.11 | 12.49 | −21.14 | −22.55 | −64.98 |
| 400 | −38.46 | −3.79 | −19.77 | −325.74 | −59.26 |
| 430 | −16.89 | 16.16 | −16.00 | −17.12 | −71.83 |
| 460 | −22.13 | −15.90 | −25.37 | 26.42 | −36.77 |
| 650 | −38.78 | −3.99 | 1.70 | 4.91 | −55.39 |
| 700 | −32.48 | −15.34 | −29.56 | −33.23 | −51.03 |
| 800 | −18.62 | 17.71 | −20.54 | −22.38 | −64.78 |
| 850 | 15.23 | −16.61 | −28.95 | −30.01 | −57.39 |
- Note: Bold values indicate the model with the lowest percentage error for each branch.
Clearly, our neural network model, particularly when employing cumulative data, has consistently outperformed traditional actuarial methods, such as the chain ladder, and simple econometric models, like linear regression, across both property and liability lines. Although the performance across branches demonstrates some variability, the overall trend suggests that the neural network's sophisticated architecture is more adept at capturing the claims data's complexities than the benchmark models. The incremental neural network model also shows promise in certain segments, indicating its potential applicability under specific conditions. The deviations observed in the cumulative data model can be attributed to the incremental claims data's inherent variability. Incremental data, which captures changes in claims from period to period, may exhibit a more erratic trajectory than the cumulative data's smoother progression. This complexity can lead to increased prediction errors. These results highlight the neural network's versatility and superior predictive capabilities, affirming its value as a powerful tool for actuarial forecasting and reserve estimation.
6.2 Bootstrap analysis
Here, we provide a more comprehensive statistical overview of the forecast performance of our neural network and benchmark methods, including their capacity to estimate the impact of the uncertainty related to the initial conditions. We utilize a bootstrapping technique to assess the quality and reliability of our predictions. This method helps us generate a distribution over the predictions rather than providing a single value for the estimated reserve (Efron & Tibshirani, 1994). The following outlines the key steps and presents the corresponding results.
We first generate 100 bootstrapped datasets from our original training and validation dataset. Each bootstrapped dataset is created by randomly sampling with replacement claim sequences; that is, a time series of claim developments. Thus, each bootstrapped dataset retains the same size (i.e., the same number of claims) as the original dataset. Subsequently, we divide each bootstrapped dataset into training and validation sets using the same ratio as described in Section 3.2.15
Each neural network model (NN, NN-Incr, and C-LSTM) is trained on all 100 bootstrapped datasets using the best hyperparameters identified by Random Search. Initially, we used the final optimal hyperparameters obtained by Bayesian Search. However, this extended approach allows to further test the robustness and sensitivity of the model to different hyperparameter configurations, providing a comprehensive evaluation of their performance. Meanwhile, the linear regression model used the set of predictors identified from the original training dataset. After training each model on the bootstrapped datasets, we obtain an ensemble of reserve predictors, enabling us to provide insights into model confidence.
For the chain ladder method, we calculate predictors directly from each of the 100 bootstrapped samples. The chain ladder method cannot be applied in the same manner as the neural network models, which can use the trained models to make predictions based on the original dataset. This is because the chain ladder method calculates development factors specific to the data it is applied to. These factors cannot be directly used to predict another dataset. Instead, for each bootstrapped sample, we use the reserve estimates generated by the chain ladder method, which is similar to the bootstrapped chain ladder approach suggested by England and Verrall (2002).
Note that we could have also predicted the reserves for the neural networks based on the 100 bootstrapped samples. Ultimately, our methodology introduces an additional layer of uncertainty into the neural networks' predictions, making it more challenging for them to outperform the chain ladder method.
Next, we discuss the reliability and performance of the different models based on the percentage error of the ensemble point estimates across the 100 bootstrapped samples; that is, the point estimates are obtained as the average reserve prediction across all individual predictions. This bootstrap aggregation (bagging) technique improves the stability and accuracy of the classification and regression task, reducing the variance and avoiding overfitting. Additionally, we use box plots to illustrate the distribution of each model's percentage errors' distribution.16 The generated point predictions are presented in Table 10 for the property and liability LoBs, revealing similar patterns to those observed in the original estimates.
| Line of business | ||
|---|---|---|
| Model | Property | Liability |
| Chain Ladder | −13.44 | −15.53 |
| Neural Network | −2.47 | −1.03 |
| Neural Network (Incr) | 9.91 | −15.06 |
| C-LSTM | 11.71 | −16.57 |
| Linear Regression | −19.29 | −58.19 |
- Note: Bold values indicate the model with the lowest percentage error for each line of business.
Crucially, the neural network models maintain their superior accuracy, with the cumulative neural network model (NN) showing a slight increase in percentage error for property claims but still outperforming all other models. The neural network models based on incremental data (NN-Incr and C-LSTM) continue to overestimate (underestimate) property (liability) data, with a slight increase (decrease) in percentage error. Both the chain ladder and linear regression models exhibit slight improvements for both datasets, indicating increased stability.
Figures 5 and 6 show box plots illustrating the error distributions, highlighting the median, quartiles, and potential outliers in the predictions.
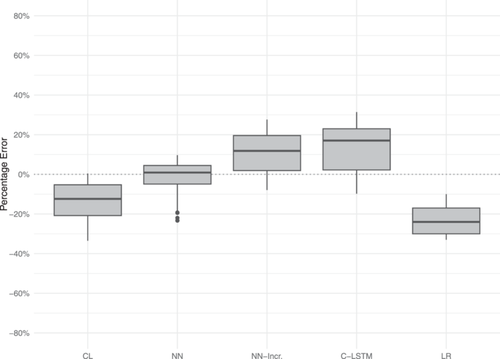
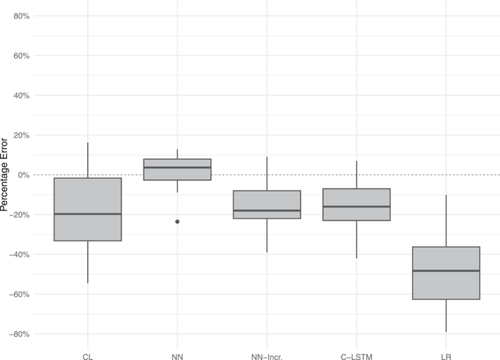
For both property and liability LoBs, the cumulative neural network model (NN) demonstrates the smallest interquartile range (IQR) and least variability, indicating a high level of consistency and accuracy across all model predictions. Consistently, for both LoBs, the neural network models based on incremental data (NN-Incr and C-LSTM) exhibit greater variability, reflecting the higher dispersion of percentage errors observed in the bootstrap analysis. Overall, the error distribution is higher for these models compared to the cumulative model.
For the property line, the chain ladder method shows moderate variability but tends to underestimate reserves, resulting in an overall negative distribution of errors. Conversely, for the liability line, the chain ladder method shows substantially higher variability. The linear regression model provides generally inaccurate predictions, highlighting its limitations in accurately predicting reserves and leading to a negative distribution of percentage errors.
Overall, the bootstrapping analysis offers valuable insights into the practical implications of utilizing different models for loss reserving in the insurance sector. The neural network models, particularly the cumulative data ones (NN), demonstrate superior accuracy and consistency. This makes them highly suitable for practical applications. The low variability and narrow IQR indicate reliable performance, which is crucial for making informed decisions regarding reserve estimation.
6.3 Explainability
While we have examined the performance of the different reserving models, we have not yet addressed a crucial aspect of using machine learning methods in insurance applications: the driving features' transparency and explainability. For this, we rely on a state-of-the-art explainability technique used for applications like ours: SHAP values (Lundberg & Lee, 2017). SHAP values offer insights into each feature's contribution to a specific prediction, enabling us to evaluate the importance and impact of various variables in the dataset. To determine this impact, each feature is systematically omitted to observe the resulting change in the output of the model. This process is repeated across all possible feature combinations, ensuring that each feature's importance is evaluated within every possible feature set's context (Lundberg & Lee, 2017). We calculate SHAP values for a randomly sampled 10% of our data. This helps ensure that we capture a comprehensive picture of feature importance without overwhelming computational resources. After computing SHAP values, we aggregate them to summarize each feature's overall contribution to the predictions of the model. This aggregation helps us identify which features are consistently influential and which have less impact. As a further advantage this provides us with a clear understanding of the driving factors behind the behavior of the model.
Figures 7 and 8 display the mean absolute SHAP values for the top 10 features in the property and liability datasets, respectively, for both regression and classification tasks. The left panel of Figure 7 shows that for the regression task, Losses Incurred is the most important feature. This is unsurprising, as the incurred loss directly relates to the amount to be predicted. In particular, we consider incurred losses as payments plus individual case reserves. This expert information is critical because it reflects the claims handler's current estimate of the outstanding loss. Moreover, this information provides a robust basis for future loss predictions. Interestingly, all other features, such as Business Type, Risk Category, and Branch, only play a minor and do not significantly contribute to the regression task. Thus, although these features provide additional context, the incurred losses predominantly drive the model's predictive accuracy for estimating future claim amounts.
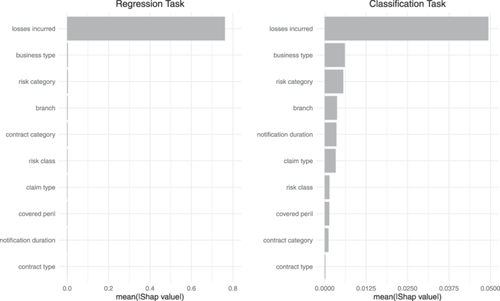
The right panel of Figure 7 illustrates the importance of different features for the classification task. Here, we observe a different picture than that for the regression task. Although Losses Incurred remains the most important feature, its relative importance is reduced compared with the regression task. Other features, such as Business Type, Risk Category, and Branch, also show considerable importance, highlighting their relevance in predicting changes in the cumulative incurred loss amounts. These features capture various dimensions of risk and policy characteristics that can influence the probability of changes in incurred losses. For instance, different business types and risk categories are likely to exhibit distinct patterns in claim development and settlement, thereby affecting the likelihood of adjustments in the incurred amounts.
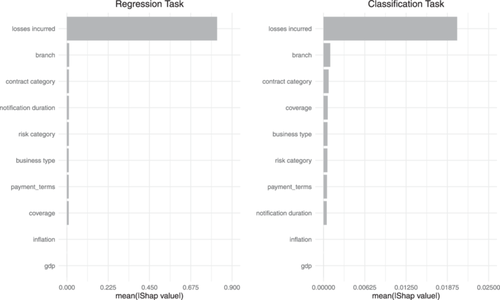
For the liability dataset's regression task (Figure 8), insights from the SHAP values are nearly the same as for the property line. However, for the classification task, the magnitude and order of the features besides Losses Incurred differ compared to the property dataset. Other features, such as Branch, Contract Category, and Coverage, only show slightly higher importance. Thus, while these additional features contribute to predicting changes in the cumulative incurred loss amounts, their impact remains relatively minor for liability claims.
To further illustrate the benefits of our granular machine learning approach to reserve prediction, we provide SHAP values for the property dataset for each point in time (i.e., every development period).17 The left (right) panel of Figure 9 presents the regression (classification) task's 10 most important features at each development period. This temporal analysis offers a more detailed understanding of how features' importance evolves as additional information becomes available over the claim development periods.
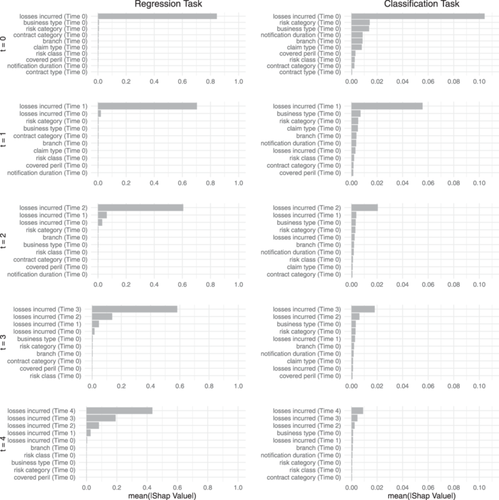
In the regression task, Losses Incurred consistently emerges as the most important feature across all development periods, reaffirming its importance in predicting future claim amounts. This consistent prominence underscores the direct relationship between the incurred losses and the final amounts to be predicted. As the development periods progress, the importance of Losses Incurred from previous time points increases. Thus, earlier assessments of incurred losses accumulate valuable information, enhancing the ability of the model to make accurate predictions. As additional information about the incurred losses becomes available over time, initial estimates are continually updated and improved throughout the claim's lifecycle.
For the classification task, the picture is slightly different. While information about the loss amounts remains the primary driver, other variables such as Business Type, Risk Category, and Branch also play crucial roles, particularly in the earlier development periods. As the claim evolves, these features' relative importance changes, highlighting the dynamic nature of the factors influencing the likelihood of changes in incurred loss amounts.
For instance, Notification Duration and Contract Category exhibit varying importance across different stages. Thus, the timeliness of claim reporting and specific policy terms can significantly impact the classification of claim developments at different points in time.
This temporal analysis highlights the complex interplay of various features over time, deepening our understanding of how different factors influence reserve predictions throughout the claim lifecycle. By examining these dynamics, we can achieve greater transparency and accuracy in the reserving process, ensuring that predictions are informed by the most relevant and timely information.
7 CONCLUSION
Today, loss reserving is not just important for regulatory compliance and financial solvency. Besides its original purpose of risk management, information on loss reserves and, thereby, a good prediction of ultimate claim amounts is used in areas such as pricing, portfolio management, and strategic business planning. This expansion of the application scope requires granular and flexible approaches for loss reserving based on individual claims data. While the extant literature often assesses synthetic data to facilitate the back-testing of such models, applications to real claim data are often limited to general liability claims.
We propose a novel model architecture for predicting the development of incurred loss amounts for RBNS claims. The key feature to our model is predicting the cumulative incurred loss amount for the upcoming periods and the probability of a change in this amount. Our model offers a refined approach to loss reserving by using a data-driven decision rule: the forecast is updated based on a predefined probability threshold. We further conduct a comparative analysis with established models, including the chain ladder method, the proposed model by Chaoubi et al. (2023), and a simple linear regression model, as well as the proposed model trained on incremental data. To test the models, we utilize two proprietary datasets stemming from the short- and long-tail LoB from a large industrial insurance. This is a sector, which to our knowledge, has not previously been explored using individual loss reserving.
We find superior performance for our proposed model based on the aggregated data, measured by the estimated reserve's percentage error. Interestingly, the neural network model applied to incremental data exhibits a notable deviation from the network based on cumulative data and underperforms compared with the latter. At the individual level, integrating the classification task emerges to be important, as it progressively decreases the NMAE across successive development periods. We further illustrate the model's adeptness at conducting runoff analysis across diverse granularity levels, particularly at the branch level. This versatility underscores the model's adaptability to varied informational needs and organizational structures within the insurance sector.
Moreover, we challenge our model by introducing uncertainty based on bootstrapping. The bootstrap analysis shows that the cumulative neural network model (NN) consistently outperforms traditional methods, demonstrating superior accuracy and consistency in reserve estimation for both property and liability lines. This method exhibits the least variability, indicating high reliability in its predictions. This is critical for effective risk management and pricing strategies in the insurance sector. Overall, the bootstrapping technique confirms neural network models' robustness and suitability for practical applications in loss reserving. We also address the importance of transparency and explainability in machine learning models for insurance applications by utilizing SHAP values (Lundberg & Lee, 2017). SHAP values provide insights into each feature's contribution to a prediction, allowing us to evaluate the importance and impact of various variables in the dataset. By calculating SHAP values for a randomly sampled 10% of our data, we identify the key drivers behind our model's behavior for both regression and classification tasks. We find that while Losses Incurred is the most critical feature, other variables such as Business Type, Risk Category, and Branch also play significant roles, especially in the classification tasks and at different development periods.
While our results focus on the predictive modeling of RBNS claims, a comprehensive approach to claims reserves should also address IBNR reserves and the treatment of large losses, highlighting some future research directions. To address claims that may evolve into large losses, we suggest investigating the incorporation of predictive indicators and ensemble techniques to improve prediction accuracy. Although this approach adds complexity, it may offer a nuanced understanding and management of large loss claims. Furthermore, integrating or developing an additional model tailored to handle the unique challenges posed by IBNR claims, which lack the detailed claim features available for RBNS claims, is another crucial research area.
ACKNOWLEDGMENTS
We thank the two anonymous referees, the Senior Editor, and the Editor for their valuable comments and support during the publication process. We also would like to thank Alexander Szimayer and Johannes Kriebel for reading an early draft of this manuscript. Open Access funding enabled and organized by Projekt DEAL.
APPENDIX A: DATA DESCRIPTION
Tables A1 and A2 describe the set of features for the two datasets used in our model.
| Feature | Datatype | Static/Dynamic (s/d) | # of categories |
|---|---|---|---|
| Contract category | Categorical | s | 2 |
| Contract type | Categorical | s | 4 |
| Business type | Categorical | s | 4 |
| Policy share (%) | Numerical | s | - |
| Risk category | Categorical | s | 12 |
| Risk class | Categorical | s | 10 |
| Coverage | Categorical | s | 3 |
| Covered peril | Categorical | s | 4 |
| Claim type | Categorical | s | 2 |
| Notification duration (days) | Numerical | s | - |
| Real GDPa | Numerical | d | - |
| Internal inflation mixture indicesa | Numerical | d | - |
| Branch | Categorical | s | 11 |
- a Forecast values were used for unknown periods to prevent data leakage.
| Feature | Datatype | Static/Dynamic (s/d) | # of categories |
|---|---|---|---|
| Contract category | Categorical | s | 2 |
| Business type | Categorical | s | 4 |
| Policy share (%) | Numerical | s | - |
| Risk category | Categorical | s | 12 |
| Coverage | Categorical | s | 13 |
| Claim type | Categorical | s | 2 |
| Notification duration (days) | Numerical | s | - |
| Real GDPa | Numerical | d | - |
| Internal inflation mixture indicesa | Numerical | d | - |
| Branch | Categorical | s | 11 |
- a Forecast values were used for unknown periods to prevent data leakage.
APPENDIX B: HYPERPARAMETERS
The objective of the learning process is to optimize the network weights to minimize a loss function tailored to the specific tasks—regression and classification. In our setting, the model weights are updated after each mini batch using the Adaptive Moment Estimation (Adam) optimization algorithm, introduced by Kingma and Ba (2014). We use its default parameters, recommended by the authors, and only tune the learning rate. Additionally, we adapt the learning rate throughout the training process by implementing a decay strategy, which helps the network converge to a local minimum (You et al., 2019). Specifically, we use the default settings and apply a learning rate decay every 10 epochs, using a multiplicative factor set to 0.1.
A mini batch refers to a subset of the training data consisting of a predefined number of claim sequences, each of varying lengths. We denote the lengths of the sequence for claim as . Thus, periods for claim are known. The claim sequences within a batch are processed and evaluated together in one iteration of the training algorithm. The learning rate and the batch size are, therefore, hyperparameters and are fine-tuned.
For each claim sequence within the batch, we adopt a one step ahead prediction strategy. This means, for a claim sequence of length , we only feed the first periods into the model to ensure we always have a target value available for prediction. Therefore, for each period of the claim sequence, the model receives the static feature vector and the set of dynamic features , to predict the values for period .
The predictions are evaluated using two distinct loss functions suitable for the two learning tasks. For the regression task, we use the mean squared error (MSE) loss function.18 In parallel, for the binary classification task, we use the binary cross-entropy loss function.
-
The learning rate is sampled from a log-uniform distribution, defined over the interval . Here, the log-uniform distribution is used to explore candidate values that vary over several orders of magnitude.
-
The hidden sizes , and are sampled from the discrete set .
-
The batch size is sampled from the discrete set .
-
The dropout rate is uniformly sampled from the interval .
After running the Random Search process with a total of 32 configurations, we refined our hyperparameter tuning using Bayesian Opimization (Snoek et al., 2012). Based on the outcomes of the Random Search, we identified the top three configurations and used their parameter ranges to define the search space for Bayesian Search. In constructing the search space for Bayesian Optimization, we took into consideration the parameter ranges observed in the top configurations from the Random Search. The upper and lower bounds for each parameter in the Bayesian search space were set based on the extremities of these ranges, ensuring a focused yet comprehensive exploration in the subsequent optimization phase. To thoroughly explore the refined search space, we evaluated 32 further configurations. The results of this two-stage hyperparameter tuning approach, including the top three configurations from the Random Search and the final optimal configurations identified, are detailed in Tables B1, B2, and B3 for both data sets analyzed in our study.
| Cumulative | ||||||
| 1. | 0.004 | 64 | 128 | 128 | 1024 | 0.429 |
| 2. | 0.001 | 32 | 64 | 128 | 1024 | 0.315 |
| 3. | 0.003 | 128 | 64 | 64 | 1024 | 0.442 |
| Incremental | ||||||
| 1. | 0.00025 | 256 | 32 | 256 | 1024 | 0.1245 |
| 2. | 0.00022 | 256 | 128 | 128 | 1024 | 0.3971 |
| 3. | 0.00215 | 128 | 256 | 256 | 1024 | 0.2467 |
| Cumulative | ||||||
| 1. | 0.0935 | 128 | 128 | 128 | 1024 | 0.4854 |
| 2. | 0.0439 | 64 | 128 | 128 | 1024 | 0.4081 |
| 3. | 0.0043 | 128 | 256 | 64 | 1024 | 0.0.3854 |
| Incremental | ||||||
| 1. | 0.0296 | 64 | 32 | 32 | 1024 | 0.2516 |
| 2. | 0.00088 | 128 | 64 | 64 | 1024 | 0.2487 |
| 3. | 0.0273 | 128 | 64 | 32 | 1024 | 0.2340 |
| Property | Liability | |||
|---|---|---|---|---|
| Cumulative | Incremental | Cumulative | Incremental | |
| 0.004 | 0.00043 | 0.0851 | 0.0273 | |
| 128 | 256 | 128 | 64 | |
| 128 | 128 | 128 | 128 | |
| 128 | 128 | 128 | 128 | |
| 1024 | 1024 | 1024 | 1024 | |
| 0.378 | 0.338 | 0.458 | 0.2509 | |
To integrate the two learned tasks into the proposed decision rule for making predictions on unseen data, the threshold is determined based on the predicted probabilities obtained from the validation set. These probabilities were generated by the model trained on the training set with the best hyperparameter configuration identified through the tuning process. Specifically, we stored the predicted probabilities of a change in the cumulative incurred loss amounts and the corresponding true labels of the classification task and used a receiver operating characteristic (ROC) curve to choose the threshold , which maximizes the difference between the True Positive Rate and the false positive rate.21 This threshold is crucial for translating the outputs of the regression and classification tasks into actionable predictions.
Finally, we trained the model with the best hyperparameters on both the training and validation sets to predict the test set. For predicting future data points in the test set, we employed a recursive multi-step forecasting approach. In this method, the model uses its own predictions from previous time steps as input to forecast subsequent time steps. The time required for this training on a Amazon-EC2-G5.8xlarge instance is given in Table B4 for for both data sets, separated by Random and Bayesian Search.
| Property | Liability | |||
|---|---|---|---|---|
| Cumulative | Incremental | Cumulative | Incremental | |
| Random Search | 11,764 | 12,759 | 29,460 | 33,289 |
| Bayesian Search | 14,521 | 16,632 | 36,235 | 39,854 |
REFERENCES
- 1 Despite its simplicity, the chain ladder method remains one of the most commonly used methods for loss reserving (Wüthrich, 2018).
- 2 A similar description can be found in Pigeon et al. (2014) and Pigeon and Duval (2019).
- 3 Short-tailed means that the claims are generally reported and settled more quickly. Meanwhile, long-tailed means that a significant proportion of total claims payments take a long time to be settled by the insurer.
- 4 See, for example, Pigeon et al. (2014), Pigeon and Duval (2019), or Chaoubi et al. (2023).
- 5 The risk category classification for each claim is determined based on the industry sector in which the insured company operates.
- 6 Notably, with a greater observation timeline, a rolling window approach can be used to further test the model's stability over time.
- 7 Claims reported at the most recent reporting year are excluded from the training process because here, only one development period is known.
- 8 https://github.com/brandonschwab/advancing_loss_reserving.
- 9 For a detailed description of the threshold determination, see Appendix B.
- 10 For an in-depth understanding of deep learning principles, including dense layer functionalities, see Goodfellow et al. (2016) and Chollet and Allaire (2018).
- 11 We provide a detailed explanation on how is optimally determined in Appendix B.
- 12 Meanwhile, the prediction method used by Chaoubi et al. (2023) is based on the product of the two model outputs and can be described as: .
- 13 Note that this form of linear regression allows the prediction of negative values, which can be interpreted as recoveries occurring in practice.
- 14 In the modeling strategy proposed by Chaoubi et al. (2023), the predicted probability or predicted loss amount must be exactly zero for the prediction to be zero.
- 15 The division into training and out-of-sample prediction sets occurs naturally by combining data and claim closure in practice. Clearly, a longer time series with a rolling window can enable further robustness.
- 16 Given the sensitive nature of the data, we focus on showing the percentage errors of the point estimates and these errors' distribution across all predictions. This approach allows us to assess the model estimates' variability and uncertainty without revealing any sensitive information.
- 17 Due to the extensive number of development periods in the liability dataset, a similar figure can be excessively large and hard to read. Hence, this detailed temporal analysis is focused solely on the property dataset. The results are qualitatively similar and can be obtained from the authors upon request.
- 18 Note that in the reserve process, recoveries can also occur. We therefore use the MSE loss function which allows for negative values.
- 19 For a detailed explanation of GradNorm, we refer to Zhao Chen et al. (2018).
- 20 Dropout randomly sets a predefined percentage of neurons to zero during training, which helps prevent overfitting by ensuring that the network does not become overly reliant on any specific neuron (Srivastava et al., 2014).
- 21 For a comprehensive explanation of ROC curves, see Fan et al. (2006).




