The effect of subsidized flood insurance on real estate markets
Abstract
Subsidized insurance against extreme weather events improves affordability among households in at-risk areas but it can weaken the risk signal via property prices. Leveraging a granular data set of all property transactions and flood events in England, we study the effects of a reinsurance scheme that lowers insurance premiums for at-risk properties. We document that the introduction of this scheme increases prices and transaction volumes of flood-prone properties. This fully offsets the negative direct effects of flooding on property prices, with high-income areas and high-value properties benefiting relatively more. Our findings speak to the debate on climate adaptation policies and their consequences for wealth distribution.
1 INTRODUCTION
Housing is vulnerable to extreme weather events related to climate change (Gourevitch et al., 2023).1 At the same time, it is one of the major vehicles of household wealth accumulation (Bach et al., 2020; Benjamin et al., 2004; Bhatia, 1987; Bin et al., 2008) and one of the major types of collateral in the financial system (Chaney et al., 2012; Ramcharan, 2020). The literature on the effect of extreme weather events on property values is extensive (e.g., Beltrán et al., 2018; Hallstrom & Smith, 2005). Less is known about the role in property markets of public policies against extreme weather events.
To address this gap, we exploit a novel empirical setting, the introduction of a UK public scheme, Flood Re, which provides insurers with an option to reinsure the flood risk element of their policies at a predetermined (not risk-based) price. Flood Re was introduced in April 2016 with the aim of improving the affordability of flood insurance in flood-prone areas (Flood Re, 2016), and it is estimated to halve the average annual insurance premium of flooded properties.2 The scheme is financed by a levy on all UK home insurance policies, resulting in a small increase in premiums in areas not exposed to flood risk.3
Beyond the introduction of Flood Re, the UK residential real estate market offers an appealing setting to study the introduction of a public flood reinsurance scheme for several reasons. First, homeownership rates in the UK are high (about two-thirds of households own a property, Campbell, 2013). Second, mortgage lenders require building insurance to extend a loan, and as a result take-up rates of home insurance, which also covers flood risk, are high, reaching over 95% in England, also in risky areas (DEFRA, 2018; Surminski, 2018). The high take-up rate allows us to estimate the effect of Flood Re on property prices without explicitly looking at the level of insurance coverage. Third, information on flood risk is publicly available to all participants in the real estate market. The UK EA has been publishing granular flood maps since 2004 (Belanger & Bourdeau-Brien, 2018).
In this setting, we study the effect of Flood Re on property prices. To isolate the effect of the policy from other confounding factors driving property prices, we leverage a comprehensive data set of all property transactions (including the full address) in England.4 To control for local factors and unobservable but time-invariant property characteristics, we compare price changes for individual properties in a small area. The data set also allows us to control for observable property characteristics, such as property type, on transaction prices. To measure flood risk we use both flood risk maps as well as maps with the outlines of actual flood events, published by the EA. We focus on properties built before 2002, when tighter building standards were introduced for new developments in flood-prone areas.
We find that flood events reduce property values before the introduction of Flood Re (by 1.6% in our preferred specification). After the introduction of Flood Re, we do not observe a reduction in the values of flooded properties. On average, the introduction of Flood Re increases the value of flooded properties by 4083.5
The high insurance take-up rate means that properties damaged by floods are likely to be repaired before being sold, mitigating concerns about differences in the physical state of buildings. We further address this concern by using flood risk maps, which provide an ex ante measure of flood risk. Compared with no-risk properties, at-risk properties are sold at discount before the introduction of Flood Re. The discount (before Flood Re) on at-risk properties (0.4%) is lower than on flooded properties (1.6%). This result aligns with recent findings by Niu et al. (2023), which indicate that ex ante flood risk has a smaller impact on property prices due to its lower salience. The discount vanishes after introduction of Flood Re, implying that our findings are related to the expectation of future flood risk.
We conduct a set of placebo tests based on a temporary extension of an agreement between the government and insurance providers shortly before the introduction of Flood Re. We do not find any effect of the extension (which did not involve any policy change) on property values. We also conduct simulations by testing the placebo effect of flood events and Flood Re on properties that are not actually flooded. These simulations confirm that our findings are unlikely to be driven by factors other than flood events and Flood Re. Additionally, our results are consistent in a series of robustness test, such as excluding flats from the sample (flats above the ground floor are not exposed to direct flood damage) and controlling for the change in hedonic price function after flood (flood events may increase demand for newer properties with stronger flood defenses, relative to older properties in the same areas).
The mitigating effects of Flood Re on prices of properties exposed to flood risk are stronger in areas with higher average income, education level, and age. The net housing wealth effect (measured as a percentage of average household annual income) is about 14.2% in high-income areas compared with 3.8% in low-income areas. These results highlight possible unintended distributional implications of Flood Re, with benefits concentrated in areas with higher socioeconomic status. We do not find any differences in the effect of Flood Re in terms of beliefs about climate change (proxied by the share of votes to the Green Party).
Finally, we explore the mechanisms through which Flood Re affects property prices. First, we find that Flood Re increases transaction probabilities for properties in at-risk areas. The combination of more transactions and higher prices following Flood Re suggests that buyers increase their demand for properties in at-risk areas (rather than potential sellers reducing their supply). Second, flood events have a larger negative effect on property prices when they hit at-risk areas, which seems consistent with the idea that ex post flood events reinforce existing information about ex ante flood risk. Third, our results suggest that properties built after 2002 do not benefit from the introduction of Flood Re, given their stronger resilience against flood risk.
Our paper contributes to the growing literature examining the linkage between climate risks and government interventions. Several papers consider the effect of public policies, including public information on flood risk (Hu, 2022) and improving flood risk classifications (Mulder, 2021), on flood insurance take-up. However, contrasting findings by Ragin et al. (2021) suggest that information disclosure alone has a limited effect on influencing flood insurance demand. Wagner (2022) finds that homeowners' willingness to pay for natural disaster insurance is inefficiently low in the absence of government intervention, and flood insurance mandates could increase social welfare. Oh et al. (2022) study the effect of regulated homeowners' insurance prices across US states, and find that insurers overcome pricing frictions by cross-subsidizing insurance across states. Our paper shows the effect of a subsidized public flood reinsurance scheme on prices and liquidity in the real-estate market, providing a link to the literature on climate risks and property markets (Baldauf et al., 2020; Bernstein et al., 2019; Murfin & Spiegel, 2020; Nguyen et al., 2022).
We also highlight the distributional impact of flood insurance scheme, contributing to the literature on the distributional impact of environmental policies, for example, Bento et al. (2015), da Silva Freitas et al. (2016), Grainger (2012), and Isen et al. (2017). Studies on the distributional effects of flood insurance schemes focus on the National Flood Insurance Program (NFIP) in the United States. The evidence suggests that the NFIP mitigates the adverse financial impact of flooding better than ex post disaster assistance (Billings et al., 2022), but also that its net premiums (premiums minus payouts) are regressive, implying that the NFIP disproportionally benefits wealthier segments of population (Bin et al., 2017). These distributional impacts however do not translate to the county level, suggesting that subsidized flood insurance does not contribute to regional inequalities (Bin et al., 2012). We study the distributional effect of public flood insurance schemes in a novel setting (the UK Flood Re scheme), in terms of property values rather than insurance premiums, and document that the mitigating effect of a public flood reinsurance scheme on at-risk properties are much stronger in richer areas.
The rest of the paper is structured as follows. Section 2 summarizes the policy background, Section 3 details the data of our analysis, Section 4 presents the empirical strategy, and Section 5 discusses the results. We further explore the heterogeneous effects of Flood Re and examine the mechanisms by which Flood Re influences property prices, respectively, in Sections 6 and 7. Section 8 evaluates housing wealth net effects, and Section 9 concludes.
2 POLICY BACKGROUND
Flood Re was established by the UK government in April 2016 to lower the cost of flood insurance in high-risk areas. The scheme offers reinsurance at a subsidized price linked to the council tax band of the property, rather than its flood risk. Insurance firms can transfer the flood risk component of home insurance policies to Flood Re, which must accept all eligible policies. There is no threshold for claims payout. Properties built after 2009 are excluded to discourage new developments in flood-prone areas.6 The scheme is financed through a 180 million annual levy on insurers, which is proportional to their share in the home insurance market, along with premium and investment income. Flood Re is scheduled to be phased out in 2039, allowing the flood insurance market to transition to risk-based pricing.
According to Flood Re's (2020) annual report, 80% of households with previous flood claims found quotes that are more than 50% cheaper after the reinsurance scheme started operating (Flood Re, 2020). The average annual insurance premium for flooded properties was roughly halved from around 650 (DEFRA, 2013) to less than 325. Before the introduction of Flood Re, none of the households with prior flood claims received quotes from more than four insurers. However, 94% of them can receive quotes from five or more insurers after the introduction of Flood Re. Since Flood Re's reinsurance nature does not offer insurance policies directly to households, they do not have to be aware of Flood Re to benefit from it. Around half of households in at-risk areas are aware of Flood Re, while only a quarter of households in no-risk areas are familiar with Flood Re (DEFRA, 2018). We outline the relationship between Flood Re, government and industry in Figure A.1 in our Supporting Information Appendix (based on Crick et al., 2018).
Before the introduction of Flood Re, the supply of flood insurance in the UK was subject to a “Statement of Principles on the Provision of Flood Insurance” (SoP) agreed in 2002 between the UK government and the insurance industry, represented by the Association of British Insurers.7 Under the SoP, insurers agreed to offer flood insurance to all residential properties without any restrictions on insurance premiums.8 However, the development of more accurate flood risk models during the 2000s, the publication of public flood maps by the EA in 2004, and the increasing frequency of extreme floods raised concerns about the affordability of flood insurance (Belanger & Bourdeau-Brien, 2018). In 2013, the insurance industry and the government agreed to create a nonprofit reinsurance scheme, Flood Re, to replace the SoP in 2016. As an interim solution, they extended the SoP for another 3 years.
In Section A.1 of the Supporting Information Appendix, we compare Flood Re with the NFIP, which has been the subject of several studies (e.g., Ge et al., 2022; Georgic & Klaiber, 2022, see also Introduction). Here we summarize the main differences. First, the NFIP provides subsidized flood insurance to households, while Flood Re provides reinsurance. Second, the NFIP provides insurance only in designated at-risk areas, where flood insurance is mandatory for mortgage borrowers, while UK insurers are free to pick which policies to cede to Flood Re. Third, the NFIP is funded by central government borrowing, while the main funding source for Flood Re is a levee on private insurers. Finally, Flood Re is designed to phase out.
3 DATA AND SAMPLE
3.1 Data
To understand the effect of Flood Re on property prices, we employ four data sets. The first data set includes property transactions, the second and third contain the measures of flood risk, and the fourth data set includes the characteristics of local-authority districts.9
3.1.1 HM land registry price paid data (PPD)
PPD from HM Land Registry covers the universe of transactions of residential properties in England since 1995, and it has been used in several studies on the UK property market (e.g., Bracke & Tenreyro, 2021; Giglio et al., 2015). For each property, the data set contains information on the exact address, the transaction date and the price, and characteristics such as property type (detached, semidetached, and flat), whether the property is a new-built, and ownership type (leasehold vs. freehold).
3.1.2 Recorded flood outlines
Our first measurement of flood risk is based on the Recorded Flood Outlines produced by the EA, which document historic flooding since 1946 as Geographic Information System (GIS) (accepted for publication) layers. To match the layers with the property transaction data set, we map them to six-digit postcode units, which cover a small area (15 properties on average). The data records the exact dates of the start and end of each flood outline, allowing us to calculate the duration of each flood event and the time interval between each property transaction and the latest flood event to affect the property.
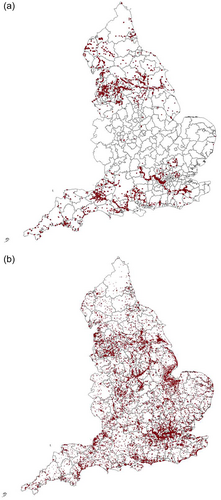
We classify a property as “flooded” if at least one flood event lasting for more than a day is recorded in the 4 years before the transaction.10 To isolate minor flood events, we identify a property as “flash-flooded” if only flood events lasting for up to a day are recorded in the 4 years before the transaction. The geographic distribution of “flooded” properties is depicted in Panel A of Figure 1.
3.1.3 Flood map
Our second measure of flood risk is extracted from flood maps published by the EA. Compared with actual flood events, our ex post measure, flood maps provide an estimate of the ex ante flood risk of properties. This measure is then aggregated at six-digit postcode level, and provides information on the number of properties classified in four flood-risk categories.11 To simplify the analysis, we calculate the average flood risk for the six-digit postcode and then classify all properties in six-digit postcodes with an average annual flood probability of more (less) than 0.1% as an “at-risk” (“no-risk”) property. The locations of the at-risk properties are shown in Panel B of Figure 1, showing that at-risk properties are clustered in areas that have been exposed to flood events (in Panel A).
The ex ante flood risk measure is less related to physical damage from actual floods, while the ex post measure could, at least in part, also reflect differences in the physical state of the building. The limitation of the ex ante risk data is that they barely change over time. Although the Flood Map is updated annually, the variations across the year are rather limited, apart from a major update in 2013–2014 (Garbarino & Guin, 2021). For our analysis, we use the 2016 version of this flood map. Comparing the ex ante risk measure in 2016 with the latest measure in 2023, only 0.98% of the no-risk properties in 2016 are now classified as at-risk properties.
3.1.4 Local-authority characteristics
To examine the heterogeneous effects of Flood Re, we employ the English Indices of Deprivation which provide: an overall measure of the deprivation level; the proportion of population with National Qualifications Framework level 4 or above qualification, for example, degree with honors and postgraduate certificate; average income; age; percentage of rental properties of local authorities; rural–urban classification. We also use general election results recorded by the House of Common to measure the percentage of votes for the Green Party in local authorities in the 2019 United Kingdom general election, and EU referendum results as recorded by Data.gov.uk.
3.2 Sample construction
To construct our sample, we start with the universe of all property transactions in England between 1995 and 2020. The first step of sample filtering addresses concerns over the change in the planning process for new buildings after the publication of the Planning Policy Guidance Note 25 (PPG25) (DTLR, 2001). PPG25 required local planning authorities to employ a set of decision rules accounting for flood risk, and to consult with the EA on permissions to build in flood-risk areas. As a result, the rejection rate of building permissions on flood risk grounds increased from 10% in 2001 to 33% in 2004 (Porter & Demeritt, 2012). Properties built after the publication of the PPG25 are therefore likely to be more resilient to flood risk. To alleviate this concern, our sample excludes properties built after 2002.
In the second step, we select a subsample of properties that were transacted at least twice since 1995, with at least one transaction in the sample period which covers the 4 years before and after Flood Re. The relatively short sample period around the introduction of Flood Re mitigates the concern that our findings are driven by the improvement in flood defenses over time.
We then convert the data into a panel structure by identifying the series of transactions of the same property, using the full address. After taking first differences of the transaction price, the sample comprises 1,754,067 observations of 1,563,062 properties. We then match this repeat-transactions sample with the two flood risk measures using the six-digit postcode, and with the local-authority-level data using the local-authority identifier.
3.3 Summary statistics
Table 1 shows summary statistics for our sample.12 In Panel A, we present summary statistics for property-level variables. The average property price in our sample is 226,840 with a growth rate of 42.4% between transactions. The appreciation of properties is rather large because of the long time interval between transactions, which is around 8 years and 4 months. A small proportion of properties are newly built at the time of the first transaction in our sample. The majority of properties in the sample is detached, semidetached, or terraced, and around 15% of them are flats. The large majority of the properties are freehold and the remaining are leasehold. In Panel B, we show summary statistics for flood risk measures. Around 0.3% of the properties experience at least one severe flood event (lasting more than a day) in the 4 years before a transaction, and 0.1% experience flash floods (lasting less than a day) in the 4 years before a transaction. About 11% of the properties are classified as at-risk properties in terms of the annual probability of being flooded. In Panel C, we summarize the eight local-authority level characteristics used for heterogeneity analysis.
| Variable | N | Mean | SD | p5 | p95 |
|---|---|---|---|---|---|
| Panel A: Property variables | |||||
| ln (Property price) | 1,754,067 | 12.332 | 0.618 | 7.313 | 19.163 |
| D.ln (Property price) | 1,754,067 | 0.424 | 0.33 | −0.019 | 1.249 |
| 1,754,067 | 0.029 | 0.169 | 0 | 1 | |
| Property type | |||||
| Detached | 1,754,067 | 0.233 | 0.423 | 0 | 1 |
| Semidetached | 1,754,067 | 0.288 | 0.453 | 0 | 1 |
| Terraced | 1,754,067 | 0.319 | 0.466 | 0 | 1 |
| Flat | 1,754,067 | 0.153 | 0.36 | 0 | 1 |
| Other | 1,754,067 | 0.008 | 0.087 | 0 | 1 |
| Tenure | |||||
| Freehold | 1,754,067 | 0.801 | 0.399 | 0 | 1 |
| Leasehold | 1,754,067 | 0.199 | 0.399 | 0 | 1 |
| Panel B: Flood risk variables | |||||
| Flooded | 1,754,067 | 0.003 | 0.059 | 0 | 1 |
| Flash-flooded | 1,754,067 | 0.001 | 0.031 | 0 | 1 |
| Duration of flood (100 days) | 1,754,067 | 0.001 | 0.031 | 0 | 0 |
| At-risk | 1,754,067 | 0.109 | 0.312 | 0 | 1 |
| Annual flood probability (%) | 1,754,067 | 0.153 | 0.604 | 0 | 0.639 |
| Panel C: Local-authority characteristics | |||||
| Annual household income | 324 | 42,745.470 | 8270.216 | 32,338.461 | 57,644.445 |
| Index-of-multiple-deprivation | 308 | 19.777 | 8.012 | 8.500 | 34.300 |
| Age | 308 | 42.144 | 5.094 | 33.300 | 50.500 |
| Urban | 330 | 0.727 | 0.446 | 0.000 | 1.000 |
| Education level (%) | 324 | 27.212 | 7.903 | 16.900 | 41.000 |
| Percentage of rental property (%) | 300 | 34.746 | 9.321 | 24.475 | 53.855 |
| Votes for the Green Party (%) | 316 | 2.970 | 2.007 | 0.000 | 5.637 |
| Votes for Brexit (%) | 330 | 54.504 | 9.963 | 32.540 | 68.860 |
- Note: This table provides descriptive statistics for the variables used in the empirical analysis. Summary statistics of property-level variables are presented in Panel A. Panel B summarizes statistics of the measurements of flood risk. Summary statistics of local authorities level variables are shown in Panel C. ln denotes that a variable is measured in natural logarithm.
4 EMPIRICAL STRATEGY
indicates flood risk of property and the related coefficient captures the effects of flood risk on property prices before the introduction of Flood Re. We employ different flood risk indicators. The primary measurement is a dummy variable, , which indicates whether the property experiences at least one flood event lasting for more than a day in the 4 years before the transaction in year . The dummy variable equals one if the property only experiences flood events lasting up to a day in the 4 years before the transaction in year . For both and , we use the 4-year cut-off to reflect on Beltrán et al. (2019), who find that prices of properties affected by flooding decline for merely 4 years. In Figure A.2 in the Supporting Information Appendix, our pre-Flood Re observations show a similar pattern, confirming that the negative effect of flooding on property prices vanishes after 4 years. Flood events are an ex post measure of flood risk and could, at least in part, also reflect differences in the physical state of the building due to flood damage. The high penetration rate of flood insurance in the UK (see Section 2) limits concerns that owners of damaged properties might sell before the damage from flooding has been rectified. An alternative, ex ante risk measure that is less likely to reflect flood damages come from the EA's flood risk maps. We use the 2016 version to construct a dummy variable, . It indicates if the property has, according to the EA risk classification, an annual flood risk probability larger than 0.1%. Whilst this measure mitigates concerns about flood damage, it comes with the limitation of barely changing over time.14 Overall, the two measures are correlated, since the ex ante risk measure reflects the probability of flooding.15 We therefore present the ex post and ex ante variables as complementary measures in the main results of our paper.
is a dummy variable indicating whether the property transaction in year happened after the implementation of Flood Re. The interaction term, , is our variable of interest and the related coefficient, , captures the effect of Flood Re on the prices of flooded/at-risk properties. The impact of flood risk on property prices after Flood Re is therefore measured by the sum of and in Equation (1). A negative and a positive with similar magnitude support the conjecture that Flood Re mitigates the negative effect of flood risk on property prices. is a vector of control variables, reflecting property characteristics, that is, property type, year of construction and form of tenure (freehold vs. leasehold).
and are fixed effects for each combination of three-digit postcode and transaction year, where is the year of the last transaction, and the year of the previous transaction. and capture further confounding factors, such as the supply of new properties, affecting property values in the three-digit postcode areas in the years of the latest and previous transactions.16 The interaction allows us to isolate the effects of flood risk and Flood Re on flood-prone properties from other confounding factors and price trends that might influence the value of properties in the same postcode and transact in the same years. In an alternative specification, we use additive (instead of interacted) fixed effects to relax the condition that the transactions must happen in exactly the same 2 years. As a result, the fixed effects are less demanding in the time dimension whilst we keep the geographical dimension constant. Finally, is the error term. We cluster standard errors at the local-authority level.
Equation (1), with ex post and ex ante risk measures, is also the basis for robustness checks and heterogeneity analyses. Most of the analysis focuses on property prices, but in Section 7.1 we look at the effect of Flood Re on transaction probabilities. The specification for transaction probabilities is similar to the one used for property prices but the outcome variable is a dummy indicating whether a property was transacted in a specific year.
An alternative to using the first difference of the natural logarithm of the property prices as the dependent variable, which accounts for time-invariant characteristics, is to use the level of house prices while incorporating property fixed effects. In Section A.3 of the Supporting Information Appendix, we discuss this approach in detail and show that our results remain consistent with this alternative specification.
Our empirical strategy follows a Difference-in-Difference (DiD) framework. Properties exposed to flood risk—based on either ex post or ex ante measures—form the treatment group whilst those that are not exposed form the control group. In our empirical analyses, we examine their change in housing prices relative to the timing of Flood Re. Identification relies on the assumption that properties not exposed to flood risk serve as an appropriate control group, comparable to those that are at risk. To assess the extent to which differences between treatment and control groups could be a concern for identification, we compare observable property characteristics based on their exposure to flood risk. Panel A of Table 2 presents mean values according to ex post flood exposure. Similarly, Panel B compares properties in at-risk areas to those in no-risk areas using our ex ante measure of flood risk. In both panels, we compute normalized differences between groups across various property-level and local-authority-level characteristics. The normalized differences for all characteristics are below the critical threshold of 0.25, as suggested by Imbens and Wooldridge (2009) and Imbens and Rubin (2015). The only exception is the rental rate, which is lower in flooded areas compared with nonflooded areas. Overall, the results indicate that our findings are unlikely to be driven by heterogeneous property and demographic characteristics across areas with varying levels of flood risk.17 We also address potential self-selection of properties in our house price sample. In Section 7.1 we show that flooded properties are more likely to be transacted after Flood Re, which is consistent with Flood Re reducing buyers' concerns about flood insurance premiums.18
| Flooded | Nonflooded | ||||
|---|---|---|---|---|---|
| Panel A | Mean | SD | Mean | SD | ND |
| Property variables | |||||
| Detached | 0.233 | 0.423 | 0.233 | 0.423 | 0.000 |
| Flat | 0.160 | 0.367 | 0.153 | 0.360 | 0.014 |
| Other | 0.015 | 0.123 | 0.008 | 0.086 | 0.052 |
| Semidetached | 0.233 | 0.423 | 0.288 | 0.453 | −0.088 |
| Terraced | 0.358 | 0.479 | 0.319 | 0.466 | 0.058 |
| Freehold | 0.787 | 0.410 | 0.801 | 0.399 | −0.025 |
| Leasehold | 0.213 | 0.410 | 0.199 | 0.399 | 0.025 |
| New | 0.035 | 0.183 | 0.029 | 0.169 | 0.021 |
| Local-authority characteristics | |||||
| Annual-household-income | 43,737.466 | 8874.595 | 42,662.365 | 7983.373 | 0.090 |
| Index-of-multiple-deprivation | 17.625 | 7.552 | 20.234 | 8.109 | −0.235 |
| Age | 42.915 | 4.915 | 41.485 | 5.184 | 0.200 |
| Urban | 0.711 | 0.453 | 0.761 | 0.426 | −0.080 |
| Education-level | 28.724 | 6.149 | 27.303 | 7.427 | 0.147 |
| Rental-rate | 32.143 | 5.778 | 35.052 | 8.960 | −0.273 |
| Vote-for-the-Green-Party | 2.721 | 1.214 | 3.060 | 2.310 | −0.130 |
| Vote-for-Brexit | 52.983 | 7.319 | 53.722 | 9.805 | −0.060 |
| At-risk | No-risk | ||||
|---|---|---|---|---|---|
| Panel B | Mean | SD | Mean | SD | ND |
| Property variables | |||||
| Detached | 0.224 | 0.417 | 0.234 | 0.424 | −0.017 |
| Semidetached | 0.248 | 0.432 | 0.293 | 0.455 | −0.072 |
| Terraced | 0.338 | 0.473 | 0.316 | 0.465 | 0.033 |
| Flat | 0.182 | 0.386 | 0.149 | 0.356 | 0.062 |
| Other | 0.009 | 0.092 | 0.007 | 0.086 | 0.009 |
| Freehold | 0.786 | 0.410 | 0.803 | 0.398 | −0.030 |
| Leasehold | 0.214 | 0.410 | 0.197 | 0.398 | 0.030 |
| New | 0.038 | 0.191 | 0.028 | 0.166 | 0.037 |
| Local-authority characteristics | |||||
| Annual-household-income | 43,243.491 | 8745.510 | 42,594.894 | 7885.373 | 0.055 |
| Index-of-multiple-deprivation | 19.726 | 7.978 | 20.288 | 8.123 | −0.049 |
| Age | 42.123 | 5.498 | 41.411 | 5.138 | 0.095 |
| Urban | 0.689 | 0.463 | 0.770 | 0.421 | −0.129 |
| Education-level | 27.609 | 8.831 | 27.271 | 7.230 | 0.030 |
| Rental-rate | 35.416 | 10.342 | 34.994 | 8.760 | 0.031 |
| Vote-for-the-Green-Party | 2.852 | 1.716 | 3.085 | 2.369 | −0.080 |
| Vote-for-Brexit | 54.383 | 11.327 | 53.638 | 9.590 | 0.050 |
A further identification concern is that the introduction of Flood Re might have been anticipated by home buyers, and reflected in transaction prices, already before its official start in 2016. To that end, we examine the effect of the extension of the SoP in 2013. This extension coincided with the announcement that the SoP would be replaced by Flood Re in 2016. Our findings, presented in Section 5.1, do not suggest announcement effects on property prices. To assure us of the validity of the DiD parallel trends assumption, we also provide estimates of the annual treatment effects over time. House price trends appear parallel before the introduction of Flood Re, which we discuss in Section A.4 of the Supporting Information Appendix.
5 EFFECT OF FLOOD EVENTS AND FLOOD RE ON PROPERTY PRICES
Panel A of Table 3 summarizes the estimation results of the main specification in Equation (1). Columns 1–3 show results using the ex post measure of flood risk based on actual flood events (Flooded), and Columns 4–6 present results using the ex ante measures based on EA risk flood maps (At-risk).
| D.ln(Property price) | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Panel A: Dependent variable | ||||||
| Flooded | −0.009** | −0.015*** | −0.016*** | |||
| (−2.21) | (−2.70) | (−2.97) | ||||
| Flooded × Post-Flood Re | 0.014** | 0.018*** | ||||
| (2.15) | (2.68) | |||||
| Flash-flooded | 0.002 | 0.004 | 0.004 | |||
| (0.34) | (0.57) | (0.49) | ||||
| Flash-flooded × Post-Flood Re | 0.000 | 0.001 | ||||
| (0.02) | (0.08) | |||||
| At-risk | −0.003*** | −0.004*** | −0.004*** | |||
| (−3.49) | (−3.24) | (−3.11) | ||||
| At-risk × Post-Flood Re | 0.004*** | 0.004*** | ||||
| (3.67) | (3.45) | |||||
| 3 dig plc × Year FE (latest transaction) | Yes | Yes | No | Yes | Yes | No |
| 3 dig plc × Year FE (previous transaction) | Yes | Yes | No | Yes | Yes | No |
| 3 dig plc × Year FE (latest) × Year FE (previous) | No | No | Yes | No | No | Yes |
| Built year FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Property controls | No | Yes | Yes | No | Yes | Yes |
| Observations | 1,754,067 | 1,754,067 | 1,754,067 | 1,754,067 | 1,754,067 | 1,754,067 |
| R2 | 0.761 | 0.766 | 0.792 | 0.761 | 0.766 | 0.792 |
| Panel B: Dependent variable | ||||||
| Flood duration (in 100 days) | −0.015** | −0.023*** | −0.024** | |||
| (−2.55) | (−2.82) | (−2.59) | ||||
| Flood duration × Post-Flood Re | 0.020* | 0.023** | ||||
| (1.90) | (2.04) | |||||
| Flood risk midpoint | −0.001 | −0.001** | −0.001** | |||
| (−1.34) | (−2.50) | (−2.45) | ||||
| Flood risk midpoint × Post-Flood Re | 0.001*** | 0.002*** | ||||
| (2.82) | (2.61) | |||||
| 3 dig plc × Year FE (latest transaction) | Yes | Yes | No | Yes | Yes | No |
| 3 dig plc × Year FE (previous transaction) | Yes | Yes | No | Yes | Yes | No |
| 3 dig plc × Year FE (latest) × Year FE (previous) | No | No | Yes | No | No | Yes |
| Built year FE | Yes | Yes | Yes | Yes | Yes | Yes |
| Property controls | No | Yes | Yes | No | Yes | Yes |
| Observations | 1,754,067 | 1,754,067 | 1,754,067 | 1,754,067 | 1,754,067 | 1,754,067 |
| R2 | 0.766 | 0.766 | 0.792 | 0.792 | 0.766 | 0.792 |
- Note: The dependent variable in this table is . In Columns 1–3 (4–6) of Panel A, the measurements of flood risk in this table is and (). Columns 1 and 4 in Panel A present estimation results of Equation (1) with the additive fixed effects (FE) and without the interaction variable, . Columns 2 and 5 of this table present estimation results of Equation (1) with the additive fixed effects. Columns 3 and 6 of this table presents estimation results of Equation (1). Panel B mirrors Panel A with continuous measurements of flood risk, namely, and . Property control variables include sets of dummy variables indicating property types, types of tenure and whether the property is newly built in the previous transaction. Definitions of variables are detailed in Table A.1 in the Supporting Information Appendix. Standard errors are clustered at local-authority district level and the corresponding t − statistics are reported in parentheses.
- *, **, and *** indicate statistical significance at the 10%, 5%, and 1% levels, respectively.
We first provide a benchmark for the effect of flood risk on property prices: In Column 1, we present results of a simplified version of Equation (1) using only the ex post measure of flood risk, , but not yet interacting it with our Flood Re indicator, . We use simple, additive fixed effects but we do not employ any property-level control variables. The results confirm previous findings (Bernstein et al., 2019; Kousky, 2010; Lamond & Proverbs, 2006), indicating that flooded properties experience a 0.9% (t − statistics −2.21) decrease in property prices, while there is no effect for less severe flash floods. Similarly, Column 4 presents the estimation results with the ex ante flood risk measure, . At-risk properties are sold at a discount of 0.3% (t − statistics −3.49). The effect is lower than actual flood events, a result that is consistent with recent findings in Niu et al. (2023) showing that ex ante flood risk is less reflected on property prices due to its low salience.
We then introduce the variable into the estimations to differentiate the effect of flood risk after the introduction of Flood Re. The interaction term, (), indicates whether Flood Re plays a role in mitigating the negative effect of flood risk, with a positive coefficient suggesting that it mitigates the effect of flood risk on property values. We also expect the introduction of the interaction term to change the magnitude of the coefficient of , increasing it compared with the results in Columns 1 and 4, as it now reflects the effect of flood risk before the introduction of Flood Re. Estimation results are presented in Columns 2 (using flood events) and 5 (using our ex ante flood risk measure). In these specifications, we also add property controls, but the fixed effects are still additive. In Column 2, flood events longer than a day reduce property values by 1.5% (t − statistics −2.70) before Flood Re, mitigated by 1.4% with the introduction of Flood Re. The net negative effect of flood events on prices (calculated by adding these two coefficients) is only 0.1% after the introduction of Flood Re. Consistent with the findings in Column 1, there is no evidence that flash floods affect property prices in either periods (before and after the implementation of Flood Re). In Column 5, we find that at-risk properties are sold at a 0.4% (t − statistics −3.24) discount before the introduction of Flood Re but the discount disappears after the introduction of Flood Re. In short, the introduction of Flood Re completely offsets the negative pricing effect of flood risk, irrespective of the risk measure we employ.
Columns 3 and 6 show the estimation results with our preferred specification in Equation (1), with interacted postcode year fixed effects for each transaction ( and ). The results are similar to those presented Columns 2 and 5. Column 3 (6) shows that flooded (at-risk) properties experience a 1.6% (0.4%) drop in value. The estimated coefficient of the variable, (), is 1.8% (0.4%), suggesting that flood events (ex ante flood risk) do not reduce property values after the implementation of Flood Re. In short, the results with interacted fixed effects are similar to those with additive fixed effects (Columns 2 and 5), addressing concerns that interacted fixed effects might be too demanding and thereby over-controlling. In the remainder of the paper, we will present the specification using interacted fixed effects.19
In Panel B of Table 3 we replace the binary risk variables with continuous measurements for flood risk, namely, flood duration (for the ex post measure) and the annual probability of flooding (for the ex ante measure). We conjecture that the negative effects on property prices increases with the level of flood risk, and, as a result, properties that are more prone to flooding are expected to benefit more from Flood Re. The specifications in Panel B mirror the respective columns in Panel A. The negative effects on property prices indeed increase with the duration of flood events and the ex ante flood risk. Importantly, the mitigating effects of Flood Re on property values also increase with the level of flood risk. Results presented in Column 3 of Panel B suggest that before the introduction of Flood Re, a 100-day increase in the duration of the flood reduces property prices by an additional 2.4%.20 For ex ante risk, we use the midpoint flood probability in each risk bucket. Before the introduction of Flood Re, a 1 percentage point increase in ex ante flood risk reduced property prices by an additional 0.1%.21 In both cases, the negative effects of flood risk are offset after the introduction of Flood Re.
5.1 Falsification tests
To examine whether property prices are indeed affected by Flood Re, we conduct two sets of falsification tests. The first test relates to the introduction of Flood Re and implicitly also tests whether there are announcement effects. We redefine the sample to property transactions from April 2010 to April 2016 and use the extension of the SoP, briefly described in Section 2, in July 2013 as a placebo treatment to flooded properties. As the extension did not change the terms of SoP, it should not affect the price of flooded properties. We replace the variable in Equation (1) with , which equals to 1 if the transaction is after July 2013 (0 otherwise). This specification estimates how the SoP extension affects flooded property prices. Columns 1 and 2 in Panel A of Table 4 show that the interaction term is not different from zero, suggesting that value of flooded properties is unaffected by the placebo treatment. Since the extension of the SoP coincided with the announcement that Flood Re would become fully operational in 2016, these results also suggest that there was no effect of the announcement on property prices.
| D.ln(Property price) | ||
|---|---|---|
| Dependent variable | 1 | 2 |
| Panel A: Extension of the SoP in July 2013 | ||
| Flooded | −0.012** | −0.014** |
| (−1.97) | (−2.01) | |
| Flooded × Post SoP extension | 0.002 | 0.003 |
| (0.28) | (0.30) | |
| Flash-flooded | 0.001 | 0.007 |
| (0.09) | (0.58) | |
| Flash-flooded × Post SoP extension | 0.006 | 0.001 |
| (0.45) | (0.09) | |
| 3 dig plc × Year FE (latest transaction) | Yes | No |
| 3 dig plc × Year FE (previous transaction) | Yes | No |
| 3 dig plc × Year FE (latest) × Year FE (previous) | No | Yes |
| Built year FE | Yes | Yes |
| Property controls | Yes | Yes |
| Observations | 933,566 | 933,566 |
| 0.801 | 0.822 | |
| D.ln(Property price) | ||
|---|---|---|
| Dependent variable | 1 | 2 |
| Explanatory variable | Pseudo-flooded | Pseudo-flooded × Post-Flood Re |
| Panel B: Monte Carlo simulations of floods and Flood Re | ||
| Rejection rate at the 10% level (2-tailed test) | 13.60 | 11.40 |
| Rejection rate at the 5% level (2-tailed test) | 7.30 | 7.40 |
| Rejection rate at the 1% level (2-tailed test) | 2.60 | 1.80 |
| Coefficient (t − statistics) | −0.002 (−0.50) | 0.003 (0.60) |
- Note: Column 1 in Panel A of this table present estimation results of Equation (1) with the additive fixed effects (FE) and the placebo treatment, the extension of the Statement of Principle (SoP). Column 2 in Panel A of this table presents estimation results of Equation (1) with the placebo treatment Post SoP extension. Definitions of variables are detailed in Table A.1 in the Supporting Information Appendix. Standard errors are clustered at local-authority district level and the corresponding t − statistics are reported in parentheses. Column 1 (2) of Panel B shows the rejection rates of the null hypothesis of the estimated coefficient of being equal to zero at the 10%, 5%, and 1% levels. The last row of Panel B presents the corresponding coefficients and t − statistics of these two variables.
- *, **, and *** indicate statistical significance at the 10%, 5%, and 1% levels, respectively.
In the second falsification test, we verify the effect of the flood treatment. We constrain the sample to properties that are not being flooded in the past 4 years of transactions. We employ the genuine Flood Re introduction date but we randomly assign properties to be “flooded” properties and replicate the estimation Equation (1). We then run Monte Carlo simulations with 1000 replications of Equation (1) to check whether nonflooded properties are affected by Flood Re. As Flood Re should not affect properties that are not at flood risk, the null of zero effect is true. Thus, we should only reject the null by making Type 1 errors. Panel B of Table 4 shows that the rejection rates are in line with those that would occur through Type 1 errors. In most cases, the average value the coefficients of and are close to 0, suggesting that non flooded properties are unaffected by Flood Re.
5.2 Robustness tests
We perform four robustness tests, shown in Table 5. First, the estimated coefficients could be biased if flood events change the hedonic price function of property. For example, flood events may induce buyers to buy newer properties with better protection against flooding. To account for such possibility, we follow Kuminoff and Pope (2014) to control for the interactions of flood event indicators and various property characteristics. The results in Column 1 show that the inference of our estimated coefficients of interest is the same as the baseline results.
| D.ln(Property price) | ||||
|---|---|---|---|---|
| Dependent variable | Full sample | At least 1 flooded | No flats | |
| Sample | 1 | 2 | 3 | 4 |
| Flooded | −0.014* | −0.015*** | −0.016*** | −0.013** |
| (−1.66) | (−2.69) | (−3.08) | (−2.26) | |
| Flooded × Post-Flood Re | 0.018*** | 0.016** | 0.019*** | 0.019*** |
| (2.63) | (2.39) | (2.82) | (2.94) | |
| Flash-flooded | −0.007 | 0.005 | 0.004 | 0.005 |
| (−0.46) | (0.70) | (0.53) | (0.53) | |
| Flash-flooded × Post-Flood Re | −0.007 | −0.001 | 0.001 | 0.000 |
| (−0.51) | (−0.07) | (0.07) | (0.02) | |
| At-risk | −0.003*** | |||
| (−2.96) | ||||
| At-risk × Post-Flood Re | 0.004*** | |||
| (3.22) | ||||
| 3 dig plc × Year FE (latest) × Year FE (previous) | Yes | Yes | Yes | Yes |
| Built year FE | Yes | Yes | Yes | Yes |
| Property controls | Yes | Yes | Yes | Yes |
| Built year FE × Flooded | Yes | No | No | No |
| Built year FE × Flash-flooded | Yes | No | No | No |
| Property controls × Flooded | Yes | No | No | No |
| Property controls × Flash-flooded | Yes | No | No | No |
| Observations | 1,754,067 | 1,754,067 | 57,444 | 1,477,458 |
| R2 | 0.792 | 0.792 | 0.790 | 0.798 |
- Note: This table shows a set of robustness tests. The dependent variable in this table is . Column 1 presents estimation results of Equation (1) with additional controls, the interaction of property characteristics with the indicators of flooding events. Column 2 presents estimation results of Equation (1) employing both flood events and ex ante flood risk indicators. Column 3 shows the estimation results with the sample includes only postcodes with at least one flooded property. Column 4 presents estimation results of Equation (1) but excluding flats from the sample. Property control variables include sets of dummy variables indicating property types, types of tenure and whether the property is newly built in the previous transaction. Definitions of variables are detailed in Table A.1 in the Supporting Information Appendix. Standard errors are clustered at local-authority district level, and the corresponding t − statistics are reported in parentheses.
- *, **, and *** indicate statistical significance at the 10%, 5%, and 1% levels, respectively.
Second, to address the correlation between ex ante flood risk and flood events, we replicate our estimation with both the ex ante flood risk and flood events as explanatory variables. The results (shown in Column 2) are consistent with the literature which suggests that flood events are more salient and has stronger negative impact on house price than long run flood risk, for example, Atreya et al. (2013) and Zhang and Leonard (2019). The results highlight that recently-flooded properties benefit more from the mitigating effect of Flood Re.
Third, in Column 3 we implement a robustness test that includes only postcodes with at least one flooded property. The estimated coefficients are similar to those in our main results in Table 3. To further address concerns that our location-by-time fixed effects might be overly specific and rely on a limited number of observations, we conducted two additional analyses, with results presented in Table A.8 of the Supporting Information Appendix. First, we estimate the fixed effects separately, including observations excluded by the original location-by-time model. Second, we relax the regional dimension of our fixed effects by using a broader two-digit postcode level. The results from these analyses show that the estimated coefficients and sample size remain consistent with the original specification, alleviating concerns about the potential specificity of the sample when using more demanding fixed effects.
Finally, in our sample, about 16% of the properties are flats. Flood events might have different impact on flats, because some flats are above ground floor. To alleviate such concerns, we replicate the estimation in a sample excluding flats. The results are shown in Column 4. The inference of our estimated coefficients of interest stays the same, suggesting that the estimation of our key coefficients is not biased by the inclusion of flats.
6 HETEROGENEOUS EFFECTS OF FLOOD RE
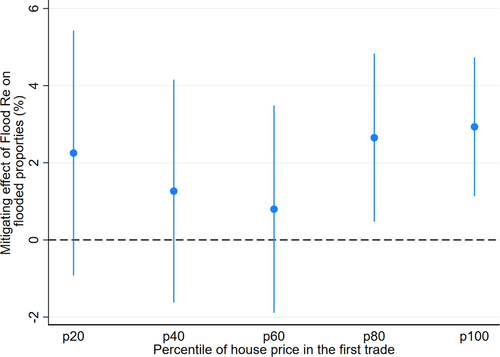
Flood Re might exert heterogeneous effects on different subpopulations as they might react differently to the risk of flooding. In this section, we examine whether Flood Re has different effects in subsamples that reflect heterogeneity in property values and in the socioeconomic characteristics of local areas. First, we replicate the estimation in Column 3 of Table 3 with subsamples constructed using the distribution of property prices in the first transaction. Figure 2 shows the estimated coefficient and 95% confidence interval of the variable for each quintile of the distribution of property prices. Flood Re has a stronger effect on more expensive properties (properties whose value is higher than the 60th percentile (p60) of property prices in the sample) and has a limited effect on lower-value properties (properties whose value is lower than or equals to the p60 of property prices).
To provide a richer picture of the heterogeneous effects of Flood Re, we complement our property transaction data with a number of local-authority level indicators on income, deprivation, age, education, urban versus rural location, and the share of rental properties. We split the sample based on the median value of each indicator (apart from the urban/rural indicator) and replicate the estimation of Equation (1). Table 6 shows results using the ex post measure of flood risk.22 Columns 1 and 2 present estimation results for properties in local authorities with average income above and below the median, respectively. The results suggest that (a) the negative effect of flood events on property prices is stronger in local authorities that have higher average income, (b) households in higher income areas benefit more from Flood Re. The Chow test F statistics verify that the coefficients of the two groups are significantly different at a 5% significance level.
| D.ln(Property price) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Annual household income | Index of multiple deprivation | Age | Education | Urban/rural area | Rental property | |||||||
| Dependent variable | Urban | Rural | ||||||||||
| Sample split | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Flooded | −0.024*** | −0.001 | −0.010* | −0.021*** | −0.021** | −0.017** | −0.023*** | −0.004 | −0.022*** | −0.003 | −0.016** | −0.019** |
| (−3.44) | (−0.12) | (−1.76) | (−2.99) | (−2.57) | (−2.37) | (−3.14) | (−0.56) | (−3.54) | (−0.36) | (−2.56) | (−2.58) | |
| Flooded × Post-Flood Re | 0.019** | 0.007 | 0.004 | 0.027*** | 0.029*** | 0.009 | 0.023** | 0.008 | 0.022** | 0.008 | 0.008 | 0.027*** |
| (2.38) | (0.70) | (0.43) | (3.46) | (3.29) | (0.78) | (2.47) | (0.88) | (2.57) | (0.91) | (0.75) | (3.00) | |
| Flash-flooded | 0.024* | −0.004 | −0.001 | 0.014 | 0.009 | −0.005 | 0.007 | 0.005 | 0.002 | 0.005 | −0.008 | 0.017 |
| (1.91) | (−0.43) | (−0.12) | (1.22) | (0.88) | (−0.36) | (0.67) | (0.41) | (0.14) | (0.56) | (−0.69) | (1.28) | |
| Flash-flooded × Post-Flood Re | −0.015 | 0.007 | 0.000 | 0.002 | 0.002 | −0.002 | 0.000 | −0.004 | −0.000 | 0.010 | −0.006 | 0.004 |
| (−0.83) | (0.39) | (0.02) | (0.11) | (0.14) | (−0.07) | (0.01) | (−0.19) | (−0.02) | (0.53) | (−0.28) | (0.20) | |
| 3 dig plc × Year FE(latest) × Year FE (previous) | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Built year FE | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Property controls | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| Chow test F statistics | 2.44 | 2.71 | 2.85 | 1.21 | 3.50 | 5.64 | ||||||
| Observations | 878,670 | 842,721 | 880,974 | 790,351 | 742,261 | 928,234 | 882,770 | 835,253 | 1,330,189 | 413,634 | 858,243 | 780,637 |
| 0.796 | 0.790 | 0.788 | 0.801 | 0.791 | 0.795 | 0.795 | 0.793 | 0.793 | 0.795 | 0.790 | 0.796 | |
| Power | 0.999 | 0.248 | 0.249 | 0.999 | 0.989 | 0.826 | 0.997 | 0.145 | 0.995 | 0.284 | 0.759 | 0.999 |
| No. of flooded and flash-flooded properties | 3381 | 4204 | 3156 | 4156 | 4230 | 3034 | 4384 | 3115 | 5399 | 2303 | 2991 | 4281 |
- Note: This table presents estimation results of Equation (1) based on different subsamples. The subsample in Column 1 (2) includes property transactions in local-authority districts with higher (lower) average annual income. The subsample in Column 3 (4) includes property transactions in local-authority districts with higher (lower) Index of multiple deprivation. The subsample in Column 5 (6) includes property transactions in local-authority districts with higher (lower) age. The subsample in Column 7 (8) includes property transactions in local-authority districts with higher (lower) education level. The subsample in Column 9 (10) includes property transactions in local-authority districts in urban (rural) area. The subsample in Column 11 (12) includes property transactions in local-authority districts with higher (lower) percentage of rented properties. The measurements of flood risk in this table are Flooded and Flash-flooded. The dependent variable in this table is D.ln(Property price). Property control variables include sets of dummy variables indicating property types, types of tenure and whether the property is newly built in the previous transaction. Definitions of variables are detailed in Table A.1 in the Supporting Information Appendix. The Chow test F statistic is the F statistic from a Chow test for equality of the estimated coefficients between the two respective subsamples. Standard errors are clustered at local-authority district level, and the corresponding t − statistics are reported in parentheses.
- *, **, and *** indicate statistical significance at the 10%, 5%, and 1% levels, respectively.
Income alone is, however, an incomplete measure of local living standards (Ringen, 1987, 1988). Columns 3 and 4 show results with sample splits using an index of multiple deprivation that, in addition to income, takes into account six other domains, including employment, education, health, crime, barriers to housing and local services, and living environment.23 The negative effect of flood events on property prices is stronger in less deprived local authorities, and these areas benefit more from Flood Re. The Chow test F statistics indicates that the coefficients of the two groups are significantly different at 5% significance level.
We also look at heterogeneity according to demographic characteristics of the local authority, including average age, average education level, urban/rural location and the share of rented properties. Detailed results are shown in Columns 5–12 in Table 6. Here, we summarize them briefly. The effect of flood events is similar across areas with above versus below average age, but the effect of Flood Re is stronger in areas with older populations (Columns 5 and 6). The Chow test F statistics verifies that the coefficients of the two groups are significantly different at 5% significance level. Areas with a more educated population have a stronger effect of Flood Re on flooded properties value (Columns 7 and 8). However, the Chow test F statistics suggests that the difference is statistically insignificant at 10% level. The effects of flood events and of Flood Re are stronger in urban areas (Columns 9 and 10). The Chow test F statistics suggests that the coefficients of the two groups are significantly different at 1% significance level. Finally, the effect of flood is similar in areas with high versus low share of rental properties (Columns 11 and 12), but Flood Re only mitigates the negative effect on property price in areas with a lower share of rental properties. The Chow test F statistics suggests that the coefficients of the two groups are significantly different at a 1% significance level.
Together, these results suggest that Flood Re has distributional implications. It appears to disproportionately benefit (in terms of the appreciation of flood-prone properties' values) owners of more expensive properties living in areas with higher income and lower deprivation. One possible interpretation for this result is that socioeconomic differences capture differences in financial sophistication and awareness of climate risks (Fielding & Burningham, 2005; Fielding, 2012; Lambregts & Schut, 2024).24 Older households with higher education levels and living in urban areas might be more aware of the implications of flood risk and Flood Re for property prices. Some support for this interpretation is provided by survey data indicating that older households living in flood-prone areas are more likely to be aware of Flood Re.25 The heterogeneity results also appear consistent with previous findings sowing that the value of rural properties is less affected by flood events (Beltrán et al., 2019), and that renters are less sensitive to future inundation risk than homeowners (Bernstein et al., 2019).
Previous studies have also shown that heterogeneous beliefs about risks from climate change affect property values. Baldauf et al. (2020) find that the value of properties exposed to climate risks are more likely to sell at a discount if they are located in areas with more climate change “believers.” However, beliefs in climate risks may play a limited role in our analysis if insurance premium discounts from Flood Re are salient to households. To examine these two opposing hypotheses, we employ the percentage of votes for the Green Party in the 2019 United Kingdom general election as a proxy for the differences in belief of climate change risk across local authorities. If awareness of climate risks is the driver of the heterogeneous effects, the effect of flood and Flood Re is expected to be stronger in local authorities with a higher share of votes for the Green Party. Columns 1 and 2 in Table 7 present the estimation results. The Chow test suggests that there is no significant difference across local authorities with Green Party votes above versus below the median, and the coefficients of the two key variables, and , are similar across the two groups.26
| D.ln(Property price) | ||||
|---|---|---|---|---|
| Percentage of vote | Percentage of | |||
| for the Green Party | vote for Brexit | |||
| Dependent variable | 1 | 2 | 3 | 4 |
| Sample split | ||||
| Flooded | −0.016* | −0.017*** | −0.007 | −0.022*** |
| (−1.80) | (−2.75) | (−0.84) | (−2.99) | |
| Flooded × Post-Flood Re | 0.016 | 0.020** | 0.012 | 0.022** |
| (1.30) | (2.41) | (1.07) | (2.37) | |
| Flash-flooded | −0.005 | 0.016 | 0.004 | 0.004 |
| (−0.43) | (1.42) | (0.36) | (0.36) | |
| Flash-flooded × Post-Flood Re | 0.012 | −0.012 | −0.002 | 0.003 |
| (0.59) | (−0.70) | (−0.10) | (0.22) | |
| Chow test F statistics | 0.50 | 1.15 | ||
| 3 dig plc × Year FE (latest) × Year FE (previous) | Yes | Yes | Yes | Yes |
| Built year FE | Yes | Yes | Yes | Yes |
| Property controls | Yes | Yes | Yes | Yes |
| Observations | 889,755 | 850,770 | 782,499 | 961,677 |
| 0.798 | 0.791 | 0.796 | 0.791 | |
| Power | 0.762 | 0.868 | 0.227 | 0.986 |
| No. of flooded and flash-flooded properties | 3162 | 4447 | 3292 | 4374 |
- Note: This table presents estimation results of Equation (1) based on different subsamples. The subsample in Column 1 (2) includes property transactions in local-authority districts with higher (lower) percentage of vote for the Green Party. The subsample in Column 3 (4) includes property transactions in local-authority districts with higher (lower) percentage of vote for Brexit. The measurements of flood risk in this table are Flooded and Flash-flooded. The dependent variable in this table is D.ln(Property price). Property control variables include sets of dummy variables indicating property types, types of tenure and whether the property is newly built in the previous transaction. Definitions of variables are detailed in Table A.1 in the Supporting Information Appendix. The Chow test F statistic is the F statistic from a Chow test for equality of the estimated coefficients between the two respective subsamples. Standard errors are clustered at local-authority district level and the corresponding t − statistics are reported in parentheses.
- *, **, and *** indicate statistical significance at the 10%, 5%, and 1% levels, respectively.
We use the voting results in the 2016 “Brexit” referendum on UK membership in the European Union as an alternative measurement of local views on climate change. Survey findings indicate that “Leave” voters are much less likely to believe in climate change risks than “Remain” voters.27 The results in Columns 3 and 4 in Table 7 show a stronger impact of Flood Re in areas with a higher share of “Leave” vote, yet the differences in coefficients among the two subgroups are statistically insignificant at 10% significance level. Overall, these results imply that differences in concerns about climate risks do not help explaining the heterogeneous effects of Flood Re.
7 MECHANISMS
In this section, we enhance the interpretation of the effect of Flood Re on the property market by assessing three potential mechanisms. First, we use transaction data to disentangle demand versus supply-side interpretations of price changes. Second, we interact ex ante and ex post measures of flood risk to evaluate surprise versus confirmation effects. Third, we consider properties built after 2002 to provide evidence on the role of tightening building standards in flood-prone areas.28
7.1 Demand versus supply of properties
The price discount for flood-prone properties could be related to buyers' reluctance to purchase at-risk properties (a reduction in demand) or current owners' desire to sell and move out of risky areas (increasing the supply of properties in the market). In the former case, we should observe a decrease in property transactions in flooded areas. In the latter, we expect to see an increase. In either case the effect of flood risk on transactions should be mitigated by the introduction of Flood Re.
In Column 1 of Table 8, we show the estimation results for Equation (2). Flooded properties are 3.6% less likely to be transacted in the following 4 years (from a base transaction rate of 15.3%). Flood Re not only mitigates the negative effect but it increases the transaction probability by 2.4%. The results plausibly reflect the sales of the accumulated properties that were flooded before the introduction of Flood Re. We also find that flooded properties are being traded later than nonflooded properties, and Flood Re completely mitigates this effect. The results are shown in Column 2 of Table 8. We interpret this result with caution, as it plausibly suffers from reverse causality, that is, longer time interval between transactions increase the likelihood of being flooded. Overall, lower transaction probabilities in the period before Flood Re suggest that the price discount for flood-prone properties is driven by a reduction in demand. A more in-depth analysis of demand and supply behavior would require data on property listings (Genesove & Mayer, 2001) or on price expectations (Armona et al., 2019; Bakkensen & Barrage, 2022).
| 1 | 2 | |
|---|---|---|
| Dependent variable | Trade | Days since last trade (ln) |
| Flooded | −0.036*** | 0.076*** |
| (−9.97) | (19.92) | |
| Flooded × Post-Flood Re | 0.060*** | −0.131*** |
| (9.69) | (−13.43) | |
| Flash-flooded | −0.002 | 0.070*** |
| (−0.25) | (13.27) | |
| Flash-flooded × Post-Flood Re | 0.008 | −0.115*** |
| (0.85) | (−9.26) | |
| 3 dig plc × Year FE (latest transaction) | Yes | Yes |
| 3 dig plc × Year FE (previous transaction) | No | Yes |
| Built year FE | Yes | Yes |
| Property controls | Yes | Yes |
| Observations | 14,446,899 | 1,754,067 |
| 0.014 | 0.939 |
- Note: Column 1 of this table presents estimation results of Equation (2). The dependent variable in this table is a dummy variable that indicates whether the property is traded in the year of observation. Column 2 of this table presents estimation results of Equation (1) with the dependent variable measuring the natural logarithm of the number of days since the last transaction. The measurements of flood risk in this table are Flooded and Flash-flooded. Property control variables include sets of dummy variables indicating property types, types of tenure, and whether the property is newly built in the previous transaction. Definitions of variables are detailed in Table A.1 in the Supporting Information Appendix. Standard errors are clustered at local-authority district level and the corresponding t − statistics are reported in parentheses.
- *, **, and *** indicate statistical significance at the 10%, 5%, and 1% levels, respectively.
The results in Table 8 also help address potential concerns with regard to selection in the sample of transacted properties. In theory, the price effect could be explained by differences in unobserved risk characteristics between the pre- and post-Flood Re periods. If properties transacted after Flood Re are lower risk, then we should expect higher relative prices. But we find that flooded properties are more likely to be transacted after Flood Re, suggesting that the selection effect goes in the opposite direction, with riskier properties more likely to be transacted after Flood Re. This result is consistent with Flood Re reducing buyers' concerns about flood insurance premiums.
7.2 Surprise versus confirmation effects
Flood events can have different effects on house prices depending on properties' risk exposure. The negative price effect of floods events could be stronger in no-risk areas (as floods are more surprising) or in at-risk areas (as new floods reinforce existing information about flood risk). We examine the interaction between ex ante and ex post indicators for flood risk in Table 9. In Columns 1 and 2, we run the specification with ex post flood indicators but split the sample between at-risk and no-risk areas. The effect is concentrated in at-risk areas, where flooding reduces prices by 2.5% before the introduction of Flood Re, and we see a positive coefficient (3.4%) on the interaction term for the Post-Flood Re period. In no-risk areas, the negative effect is small and statistically insignificant in the pre-Flood Re period, and so is the coefficient on the interaction term for the Post-Flood Re period. Columns 3 and 4 show similar results for trade probabilities. The negative effect of flooding on trading is larger in high ex ante risk relative to low ex ante risk areas (−5.2% vs. −3.1%), both in both cases the effect is statistically significant. The positive offsetting effect of Flood Re for flooded properties is larger in at-risk relative to no-risk areas (8.9% vs. 5.2%).
| D.ln(Property price) | Trade | |||
|---|---|---|---|---|
| Dependent variable | 1 | 2 | 3 | 4 |
| Sample | At-risk | No-risk | At-risk | No-risk |
| Flooded | −0.025*** | −0.001 | −0.052*** | −0.031*** |
| (−3.14) | (−0.21) | (−10.91) | (−6.63) | |
| Flooded × Post-Flood Re | 0.034*** | 0.003 | 0.089*** | 0.052*** |
| (3.72) | (0.40) | (8.61) | (6.41) | |
| Flash flooded | 0.016 | 0.006 | −0.002 | 0.003 |
| (1.24) | (0.36) | (−0.22) | (0.38) | |
| Flash flooded × Post-Flood Re | 0.012 | 0.006 | 0.019 | 0.001 |
| (0.56) | (0.28) | (1.19) | (0.05) | |
| 3 dig plc × Year FE (latest) × Year FE (previous) | Yes | Yes | Yes | Yes |
| Built year FE | Yes | Yes | Yes | Yes |
| Property controls | Yes | Yes | Yes | Yes |
| Observations | 151,624 | 1,555,018 | 1,574,118 | 12,872,223 |
| R2 | 0.829 | 0.795 | 0.023 | 0.014 |
- Note: Columns 1 and 2 of this table present estimation results of Equation (1) based on different subsamples. Columns 3 and 4 of this table present estimation results of Equation (2) based on different subsamples. Subsamples in Columns 1 and 3 (2 and 4) include property transactions in at-risk (no-risk) areas. The dependent variable in Columns 1 and 2 (3 and 4) of this table is D.ln(Property price) (Trade, a dummy variable indicating the property is transacted in a given year). Property control variables include sets of dummy variables indicating property types, types of tenure, and whether the property is newly built in the previous transaction. Definitions of variables are detailed in Table A.1 in the Supporting Information Appendix. Standard errors are clustered at local-authority district level, and the corresponding t − statistics are reported in parentheses.
- *, **, and *** indicate statistical significance at the 10%, 5%, and 1% levels, respectively.
Flooding in at-risk areas seems to lead to a larger reassessment of property prices than in no-risk areas. In other words, the ‘confirmation’ effect of flooding in at-risk areas appears stronger than the ‘surprise’ effect in no-risk areas. This could be because flood risk becomes more salient, or because of an actual increase in premiums, or a combination of the two.
7.3 Building standards
As described in Section 3.2, so far we have excluded from the sample properties built after 2002, when tighter building standards were introduced for new developments in flood-prone areas. We expect these properties to be more resilient to flooding, and to benefit less from the introduction of Flood Re. To test this, we reintroduce properties built after 2002 in our sample. There are about 250,000 such properties, compared with about 1,750,000 properties built pre-2002. In Table 10, we compare results for properties built up to 2002 (Column 1), our baseline results, against results for properties built after 2002 (Column 2). For properties built after 2002, we observe neither a decrease in prices as a result of flooding before the introduction of Flood Re nor an offsetting positive effect afterwards.30 To limit incentives to build new properties in flood-prone areas, Flood Re does not cover properties built after 2009. In Column 3 of Table 10 we show results for the post-2009 subset of properties. The coefficients for flooded properties and the interaction term are similar to those for the whole subset of post-2002 properties, and are also not statistically significant.
| D.ln(Property price) | |||
|---|---|---|---|
| Dependent variable | 1 | 2 | 3 |
| Built year of properties | Up to 2002 | From 2002 | From 2009 |
| Flooded | −0.016*** | 0.025 | 0.020 |
| (−2.97) | (0.91) | (0.60) | |
| Flooded × Post-Flood Re | 0.018*** | −0.009 | −0.004 |
| (2.68) | (−0.25) | (−0.09) | |
| Flash-flooded | 0.004 | −0.044 | 0.000 |
| (0.49) | (−0.80) | (0.00) | |
| Flash-flooded × Post-Flood Re | 0.001 | 0.006 | 0.055 |
| (0.08) | (0.06) | (0.72) | |
| 3 dig plc × Year FE (latest) × Year FE (previous) | Yes | Yes | Yes |
| Built year FE | Yes | Yes | Yes |
| Property controls | Yes | Yes | Yes |
| Observations | 1,754,067 | 252,885 | 137,408 |
| R2 | 0.792 | 0.585 | 0.580 |
- Note: This table presents estimation results of Equation (1) based on different subsamples. The subsample in Column 1 includes property built until 2002. Subsamples in Column 2 (3) include property built in 2002 (in 2009) and all following years. Standard errors are clustered at the local-authority district level, and the corresponding t − statistics are reported in parentheses.
- *, **, and *** indicate statistical significance at the 10%, 5%, and 1% levels, respectively.
Overall, these results are consistent with the idea that properties built after 2002 are more resilient to flood risk, and that this is reflected in their pricing. The exclusion of properties built after 2009 from the Flood Re cover does not affect their pricing. From a policy perspective, these results also suggest that tighter building standards might limit the need for reinsurance schemes for new properties.
8 HOUSING WEALTH EFFECTS
It is not the aim of this paper to offer a comprehensive assessment of the costs and benefits of the Flood Re. We can however provide a back-of-the-envelope comparison of the scheme's costs with its overall effects on housing wealth. First, we assume that the average property price is 226,840 (as in our sample) and that there are about 5.2 millions at-risk properties in England (as estimated by the EA). In our baseline calculation, we use the coefficient of the interaction term in our preferred specification in Panel A of Table 3, which indicates a 1.8% increase in the price of flooded properties after the introduction of Flood Re. In monetary terms, the average price effect is . Assuming that all 5.2 m at-risk properties are on a 100-year flood plain (i.e., 1% annual flood probability), this translates to a net wealth effect of 5.2 m properties at risk 1% risk m.31 This estimate of net wealth effect of Flood Re is in a similar order of magnitude but above the annual costs of the Flood Re scheme, which is a levy of 180 for the UK, broken down to about 151 m in England.32
We can construct a stock measure for the housing wealth effects of Flood Re, assuming that flood probabilities are independent over time. The resulting benefit of Flood Re is 4382 m, compared with a cost of 4140 over the lifetime of Flood Re.33 The primary mechanism behind the price effect seems to be related to salience: flooding highlights the underlying risk, but only for directly affected properties (see Section 7.2). In a hypothetical scenario flood risk could become equally salient for all at-risk properties, for example, as a result of government policies that made premiums prominent in the purchase process or of a series of large flood events. To explore this scenario, we can apply the price effect of floods to all at-risk properties. The true economic benefit of Flood Re could be as high as 21.23 bn, or five times the cost of Flood Re over its lifetime.34
We can also employ our estimates to compare the net housing wealth effect in high-income versus low-income areas. Therefore, we calculate the average perhousehold wealth benefit of Flood Re relative to the average income per area (in %). To that end, we use the estimates of subsample analyses shown in Columns 1 and 2 of Table 6, which indicate a price effect of 1.9% (0.07%) for high-income (low-income) areas. Similarly, we know that the average property price is 364,712 (195,943) and average income is 48,812 (36,248), respectively. These numbers suggest a relative housing wealth effect in high-income areas of % of the average income. Similarly, we obtain a relative housing wealth effect in low-income areas of 3.78% of average income. Even taking into account average costs per household relative to income, around 0.02% (0.03%) in high-income (low-income) areas, the net benefits of Flood Re appear to be concentrated in high-income areas.35
Beyond the housing wealth effects, there are other potential benefits from Flood Re that we cannot take into account. Flood Re results in lower insurance premiums, which may mitigate adverse selection among at-risk homes, addressing market frictions and improving insurance accessibility (Einav & Finkelstein, 2023). This can lead to enhanced postdisaster recovery and reduced strain on public finances (Philippi & Schiller, 2024; Unterberger, 2018; You & Kousky, 2024). Moreover, insurance is often expensive for correlated tail risks like flooding, which can justify a centralized reinsurer with lower funding costs (Kousky & Cooke, 2012). These positive externalities may be not be reflected in house prices.
9 CONCLUSION
In this paper, we examine how the introduction of a public, subsidized, reinsurance scheme affects the values of properties exposed to flood risk. Our results suggest that public reinsurance mitigates the negative effect of flood risk on property prices. Surprisingly, Flood Re has a weak impact in lower income and more deprived areas. These results have relevance for the debate on public flood insurance schemes beyond our specific UK setting, and are related, for example, to research on the capitalization of insurance subsidies under US NFIP (Ge et al., 2022; Georgic & Klaiber, 2022; Nyce et al., 2015). Our results suggest that such subsidies may matter for higher income areas and households, and the reason may be that they are more aware of the implications of climate risks for property prices.
Public reinsurance schemes such as Flood Re do not sell policies directly to households, and their ultimate impact on the price and coverage of flood insurance will depend on the functioning of private markets. Recent research on flood insurance contracts has focused on risk-sharing in centralized insurance markets (Boonen et al., 2024), in multiperiod contexts (Abdikerimova et al., 2024), considering also the role of government disaster relief (Hinck, 2024). While public policies are usually concerned about low flood insurance coverage, industry practices can also lead to overinsurance (Collier & Ragin, 2020; Collier et al., 2022). These important interactions between public interventions and private markets are not directly addressed in this paper and warrant future research.
ACKNOWLEDGMENTS
The authors express their gratitude to the editor and the two anonymous reviewers for their thorough reviews and valuable feedback. For comments and discussions, we would like to thank Allan Beltrán, Laura Ballester, Erik Benrud, Martin Brown, Celso Brunetti, Stefan Claus, Piotr Danisewicz, Julian Gray, Eleanor Hammerton, Sinem Hacioglu Hoke, Zhongchen Hu, Huyen Nguyen, Jose A Poncela, Klaus Schaeck, Paolo Siciliani, Mike Steel, Swenja Surminski, an anonymous referee of the Staff Working Paper Series and staff of Flood Re, the EA and DEFRA. We also thank seminar participants at the Bank of England, the Green Seminar at the European Central Bank, the European System of Central Banks, the 2022 Meeting of the EFMA and the 27th Conference of the EAERE, the 2023 World Finance Conference, and the third Annual Conference of the ASFAAG. We are grateful to Zahid Amadxarif for his research assistance. Any views expressed are solely those of the authors. They should not be taken to represent those of the Bank of England or as a statement of Bank of England policy. This paper should not be reported as representing the views of members of the Monetary Policy Committee, Prudential Regulation Committee, or Financial Policy Committee. Nicola Garbarino's contribution was partially supported by the German Ministry of Education and Research (BMBF) under the project “Klimawandelanpassung auf regionaler Ebene: ansteigende Starkregenrisiken am Beispiel des bayerischen Oberlandes” (KARE; grant number 01LR2006A).
REFERENCES
- 1 For the United Kingdom, the Environment Agency (EA) estimates that one in every six properties, in total 5.2 millions properties, across England are at risk of flooding. In the United States, the National Oceanic and Atmospheric Administration estimates that $106 billion worth of coastal property will be below sea level by 2050.
- 2 From around 650 to less than 325, based on survey data from DEFRA (2013).
- 3 The increase is estimated at around 10.5 annually (Surminski, 2018).
- 4 See Lustig and Van Nieuwerburgh (2005) and Piazzesi et al. (2007) for other drivers of property prices.
- 5 The average property price is 226,840. The calculation is based on the estimates of our preferred specification shown in Column 3 of Table 3: .
- 6 Despite that, a large number of properties are still being built in flood-prone areas, particularly in deprived neighborhoods (Rözer & Surminski, 2021).
- 7 In turn, the SoP replaced previous, similar, informal arrangements between government and industry.
- 8 The agreement did not cover properties in the highest flood risk categories and properties built after 2009.
- 9 Local-authority district is a level of administrative division in England. There are a total of 343 local-authority districts in England, comprising five types of local authority: county councils, district councils, unitary authorities, metropolitan districts, and London boroughs.
- 10 We motivate the 4-year cut-off in Section 4.
- 11 The categories are very low (1-year ahead flood probability less than 0.1%), low (between 0.1% and 1%), medium (between 1% and 3.3%), and high (greater than 3.3%).
- 12 Definitions of variables are detailed in Table A.1 in Supporting Information Appendix.
- 13 In Section A.2 in the Supporting Information Appendix, we provide a simple conceptual framework which motivates the empirical strategy discussed in this section.
- 14 Comparing the ex ante risk measure in 2016 with the latest measure in 2023, only 0.98% of the no-risk properties in 2016 are now classified as at-risk properties.
- 15 Within our sample 1.9% of the properties classified as ex ante high risk were flooded, compared with 0.2% of properties classified as low ex ante risk.
- 16 Each three-digit postcode contains on average around 6000 properties.
- 17 Concerns about the selection of households or properties in high flood-risk areas are less relevant in our regression analyses. Whilst Table 2 presents property and local-authority characteristics across different local authorities, our regression framework does not exploit cross-local-authority level variation but it leverages even more granular, within three-digit postcode variation by employing geographic fixed effects. Therefore, in our regressions using ex post flood events, we effectively control for the ex ante risk that is constant in a small geographic scope. The flood events variable captures mainly the unanticipated effect of flooding.
- 18 Selection of properties into treatment and control groups is not possible. The properties in our sample were built several years before the introduction of Flood Re, and the risk measures can only change with local area, not individual property, characteristics.
- 19 In Section A.4 and Figure A.3 of the Supporting Information Appendix, we shed light on the dynamic impact of Flood Re by employing the event-study approach.
- 20 The mean duration of a flood in our sample is 20 days.
- 21 The mean ex ante risk of at-risk properties in our sample is 1.4%.
- 22 Results with the ex ante measure are similar and are available in the Supporting Information Appendix in Table A.6. The correlation matrix between the socioeconomic indicators is shown in Table A.2.
- 23 See Payne and Abel (2012) for more details of the background and computation method of the English indices of deprivation.
- 24 While the difference in renovation rate could probably explain the heterogeneous effects of Flood Re in different social classes, Garbarino and Guin (2021) show that flood events in the UK do not affect the renovation rate of residential properties. Therefore, renovation after flooding may not be a major factors driving our results. Also, the UK has number of home renovation subsidization programs for low-income households, such as the Green Homes Grant Support and Support for Mortgage Interest for home improvement. The availability of these programs mitigate the possibilities that the properties of low-income households being severely underrenovated.
- 25 We employ the survey data from the 2018 Availability and Affordability of Insurance report conducted by DEFRA to examine the correlation between different demographic characteristics and the awareness of Flood Re (DEFRA, 2018). The results are presented in Table A.3 in the Supporting Information Appendix.
- 26 Results using the ex ante measure are available in Table A.7 of the Supporting Information Appendix.
- 27 Details of the survey, conducted by Savanta ComRes, can be found at https://comresglobal.com/polls/assaad-razzouk-eu-referendum-and-science-poll/
- 28 We also test whether Flood Re has a differential effect on properties with water amenities by incorporating a triple interaction term, which captures the specific impact of Flood Re on flooded and at-risk properties. The results, presented in Table A.9 in the Supporting Information Appendix, do not indicate that properties closer to water (and hence may have additional water amenities) benefited more from the introduction of Flood Re.
- 29 The sample still includes the same properties used to model price effects, that is, properties that were transacted at least twice since 1995 and at least one transaction is in the sample period which covers the 4 years before and after Flood Re.
- 30 In Table A.10 of the Supporting Information Appendix, we show that employing ex ante risk measure do not affect the inference of the results.
- 31 The EA does not specify the average annual flood probability for properties in flood plains. A more conservative assumption on flood risk would result in higher net wealth effects. For example, taking the average property price of at-risk properties, which is 293,514, or employing the average risk in the data, which 1.4% based on our midpoint measure, the net wealth effect increases.
- 32 Assuming that about 84% of all dwellings are located in England, the pro-rata levy for England would be 151 m. These estimations are based on population in 2011, which is included in the sample period. Source: https://www.ons.gov.uk/peoplepopulationandcommunity/populationandmigration/populationestimates/bulletins/annualmidyearpopulationestimates/mid2022
- 33 The probability of never being flooded over the life time of Flood Re (23 years, from 2016 to 2039) is , assuming that flood probabilities are independent over time. The probability of at least one flood event is then 0.21 and the total effect is 5.2 m properties at risk 21% risk m. The total cost of Flood Re is calculated as 180 m 23 years = 4140, assuming zero discount rate.
- 34 5.2 m properties at risk bn. We abstract from the fact that properties might be flooded several times, and that owners might decide not to sell to avoid a discount.
- 35 To calculate the average costs per household, we divide the levy per policy, which is estimated to be 10.5 (Surminski, 2018), by average household income in high-income (low-income) areas.




