Grain-scale pressure variations and chemical equilibrium in high-grade metamorphic rocks
Abstract
In the classical view of metamorphic microstructures, fast viscous relaxation (and so constant pressure) is assumed, with diffusion being the limiting factor in equilibration. This contribution is focused on the only other possible scenario – fast diffusion and slow viscous relaxation – and brings an alternative interpretation of microstructures typical of high-grade metamorphic rocks. In contrast to the pressure vessel mechanical model applied to pressure variation associated with coesite inclusions in various host minerals, a multi-anvil mechanical model is proposed in which strong single crystals and weak grain boundaries can maintain pressure variation at geological time-scales in a polycrystalline material. In such a mechanical context, exsolution lamellae in feldspar are used to show that feldspar can sustain large differential stresses (>10 kbar) at geological time-scales. Furthermore, it is argued that the existence of grain-scale pressure gradients combined with diffusional equilibrium may explain chemical zoning preserved in reaction rims. Assuming zero net flux across the microstructure, an equilibrium thermodynamic method is introduced for inferring pressure variation corresponding to the chemical zoning. This new barometric method is applied to plagioclase rims around kyanite in felsic granulite (Bohemian Massif, Czech Republic), yielding a grain-scale pressure variation of 8 kbar. In this approach, kinetic factors are not invoked to account for mineral composition zoning preserved in rocks metamorphosed at high grade.
Introduction
Mineral reactions are accompanied by volume and/or shape changes as well as changes in the chemical composition. In previous studies, emphasis has been placed on the separate roles of diffusion (e.g. Fisher, 1973; Joesten, 1977; Brady, 1983; Carlson & Johnson, 1991; Markl et al., 1998; Milke & Heinrich, 2002; Keller et al., 2008; Caddick et al., 2010) or mechanics (Lee et al., 1980; Morris, 1992, 2002; Fischer et al., 1994; Liu et al., 1998; Zhang, 1998; Mosenfelder et al., 2000; Barron, 2003). However, stress and diffusion in solid phases are coupled (e.g. Stephansson, 1974; Fletcher, 1982; Wheeler, 1987; Schmid et al., 2009) and, therefore, both the mechanical and the chemical responses of a system should be considered together. Only limited information exists on the interplay between mineral reactions, chemical transport and pressure variations (Rutter, 1976; Ferguson & Harvey, 1980; Fletcher, 1982; Wheeler, 1987; Fletcher & Merino, 2001; Milke et al., 2009; Schmid et al., 2009). To address this shortcoming, the geological applicability of mechanical closure to account for petrographic observations of chemical zonation in high-grade metamorphic rocks is investigated, in the case of zonation, which cannot be explained fully by conventional, diffusion-based approaches (i.e. by sluggish kinetics).
During the pressure–temperature (P–T) evolution of a rock, mineral assemblages and compositions evolve until the process of equilibration becomes closed. There are two common mechanisms of reaction closure, thermal closure (Dodson, 1973) and mechanical closure (e.g. Chopin, 1984). As mentioned above, the role of mechanical closure in the interpretation of petrographic observations has only recently been recognized as being important (e.g. Schmid et al., 2009). The classical thermal closure mechanism assumes that differences in chemical potentials are responsible for mass transport via diffusion, with diffusivities for each component generally being different. Diffusion rates then increase with temperature and even if equilibration volumes vary between different elements, mineral assemblages should be relatively well equilibrated on at least a millimetre scale at high temperature (say, above 750 °C) at common geological time-scales (Ma). Chemical equilibrium is realized when chemical potentials are equalized and diffusion stops. Thermal conduction and viscous stress relaxation are analogous to diffusion. At temperatures above 750 °C, systems reach thermal equilibrium within seconds on a grain scale; thus, rapid thermal relaxation is generally assumed in petrological analysis (Fig. 1). Components like H2O and Na2O, K2O and BaO have relatively high diffusivities, whereas the main constituents of most rock-forming minerals FeO, MgO, MnO, CaO and particularly SiO2 and Al2O3 have relatively slow diffusivities (Fig. 1). Given the small grain size of metamorphic matrix minerals, the question arises as to why the chemical zonation in minerals at temperatures >750 °C can be preserved in exhumed rocks.
Recent cooling or exhumation rate estimation based on diffusion modelling of chemical profiles has implied that these processes occur in bursts that are so short that they cannot even be resolved by traditional geochronological methods (Camacho et al., 2005; Ague & Baxter, 2007), even if these rates appear to be geodynamically unrealistic, i.e. inconsistent with the regional geological context. Was the metamorphic process really so rapid with respect to diffusion that chemical equilibrium could not occur (the sluggish kinetics explanation)? Is it appropriate to use constant–pressure diffusion modelling for high-grade rocks with preserved chemical heterogeneities on a grain scale? Or is there another mechanism or controlling factor relating to the preservation of chemical zonation?
In classical diffusion modelling, which involves only chemical equilibration, the system is assumed to behave isobarically, i.e. that mechanical relaxation is infinitely fast. This assumption cannot be strictly valid in rocks with finite strength and viscosity. The behaviour of a system can approach the isochoric or isobaric limit, depending on whether strength and viscosity are high or low respectively (Connolly, 1990, 2009). This might allow an explanation for the preservation of zonation at high temperature where diffusion is fast; under such conditions, the system is controlled mechanically. Considering this, stress relaxation, which is dependent on the viscosity of the rock, could potentially be calculated, but given how little is known about effective viscosities (Karato, 2003), the time for stress relaxation is indeterminate (Fig. 1a).
The present study addresses the effect of pressure variation in high-grade metamorphism. The focus is on accounting for the preservation of chemical zoning in crustal minerals at high-temperature conditions (>750 °C) where diffusional equilibration is expected to be rapid. An alternative model is built, which is complementary to the idea of classical thermal closure. The only other possible scenario for reaction control is followed as already suggested by Schmid et al. (2009), in which chemical diffusion is fast compared with viscous relaxation, with the strength of the minerals mechanically controlling maintenance of pressure variations. Then it is shown that grain-scale pressure variations can develop and that these pressure variations allow compositional zoning in minerals to be preserved at geological time-scales. The results yield new insights into the preservation of mineral assemblages, mineral compositions and microstructures during high-temperature metamorphism.
Pressure variations and mechanical equilibrium
Pressure variation in metamorphic rocks – a classical pressure vessel example
The preservation of coesite and diamond in a host mineral like garnet (Chopin, 1984), clinopyroxene (Smith, 1984) or zircon (Carswell et al., 2003) indicates well-known examples where a high-pressure inclusion is preserved during decompression (Rosenfeld, 1969; Zhang, 1998). The difference in pressure between the inclusion and the environment outside the host has been shown by Parkinson & Katayama (1999) to be 20 kbar for coesite inclusions in garnet. The preservation of such a high-pressure phase as an inclusion is controlled by the strength of the host mineral (the pressure vessel model), which prevents the inclusion from transforming into the higher volume lower pressure polymorph (Gillet et al., 1984; Van der Molen & van Roermund, 1986; Morris, 1992; Liu et al., 1998; Zhang, 1998; Mosenfelder et al., 2000; Ye et al., 2001; Barron, 2003; Chopin, 2003; Guiraud & Powell, 2006; O'Brien & Ziemann, 2008). However, the pressure vessel model is inappropriate for a polycrystalline rock involving weak grain boundaries and relatively strong single crystals. For these cases, a different mechanical representation of the system is needed.
Pressure variation in polycrystalline material – a multi-anvil model
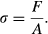(1)Therefore, the force balance does not require a balance of stresses due to area variations. For example, in a piston cylinder apparatus, stress in the thinner part of the pillar (smaller area) is significantly amplified while maintaining force balance (Fig. 2a). Similarly, in an effectively spherical multi-anvil apparatus (Fig. 2b), the inner stress is amplified proportionally to the radius squared while maintaining radial force balance. At every point in solids, the value of the normal stress depends on its orientation and ranges between maximum and minimum stresses, σmax and σmin respectively. For example, in a piston cylinder apparatus, the vertical stress is different from the horizontal stress at every point of the system. In general, the difference between σmax and σmin controls deformation (change of shape), whereas mean stress is associated with volume change of the solids. Thermodynamic (metamorphic) pressure must lie between σmax and σmin (i.e. σmin < P < σmax). The difference between σmax and σmin is commonly assumed to be negligible (Fig. 3a).
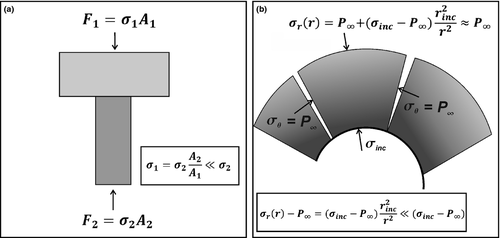
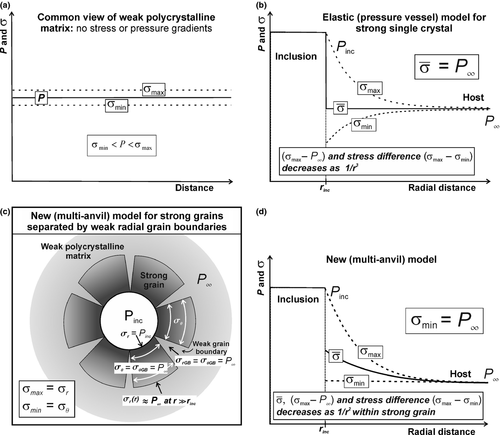
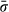is a mean stress being constant across the host in the elastic regime. σmax − σmin is differential stress in the host and r is a radial coordinate. (c) A mechanical model for a high-pressure inclusion surrounded by a polycrystalline rim composed of strong grains separated by weak grain boundaries (multi-anvil model). σrGB and σθGB are radial and circumferential stresses at weak grain boundaries. σθ, σrGB and σθGB are equal to low pressure in the matrix due to the weakness of the grain boundaries. (d) A cross-section through the mechanical model in (c).
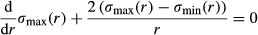(2)Different stress and pressure profiles arise for two possible end-member rheologies, namely pre-failure linear elastic or linear viscous rheology (the pressure vessel model) and a post-failure rheology with weak radial grain boundaries (the multi-anvil model). These end-members are illustrated for a spherical inclusion–host system with radial coordinate r in Fig. 3b–d. For the elastic or viscous rheology, the differential stress in the host (σmax − σmin) can be large, but, interestingly, the mean stress (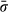
) distribution is constant across the host (Fig. 3b). The stress difference, σmax − σmin, in the host decreases with distance towards the matrix as 1/r3 (Fig. 3b). The maximum value of the differential stress in the host next to the inclusion is 1.5 times higher than the pressure difference between the inner and outer part. If the pressure difference is high (>10 kbar), the maximum differential stress would be 1.5 times higher, leading to a failure, i.e. the development of radial cracks. The fully disintegrated end-member assumes complete failure of the grains adjacent to the inclusion along radial grain boundaries, while the radial stress gradients inside the grains are still maintained. This configuration of strong crystals with weak grain boundaries is referred to as the multi-anvil model (Fig. 3c and d). In this case, circumferential force balance requires σmin = P∞ = const. (see Fig. 3c) and radial force balance satisfies
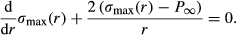(3)
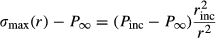(4)
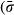) decreases from the inclusion towards the matrix as 1/r2 (Fig. 3d). The stress dependence on the radius can be rearranged to a more intuitive expression of force balance:
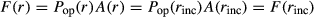(5)Materials can be strong or weak depending on composition and fluid/melt presence (Robertson, 1955; Brace et al., 1970; Ji et al., 2000; Rybacki & Dresen, 2000, 2004; Mancktelow, 2008; Moghadam et al., 2010). Resistance of a rock to deformation is also dependent on the geometric configuration of a system. In the multi-anvil model, maintaining pressure variation is mechanically feasible for any rheology of the grain boundary (e.g. reaction rims). Furthermore, if the anvils are solid solutions, then the mechanically maintained variation in thermodynamic pressure (bounded by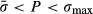 
; Fig. 3d) results in radial chemical zoning. In this model, the radial quasi steady-state pressure variation is likely to cause a redistribution of components, with higher density end-members diffusing towards the high-pressure (inner) side of the anvil. At chemical equilibrium, a chemical zonation is present as long as the pressure gradient is maintained.
An alternative approach – unconventional barometry
The preservation of composition and pressure variations is a consequence of how both the diffusional and the mechanical closure are attained. The quantification of a pressure profile from the foregoing mechanical model is impractical, given the uncertainties related to the strength constraints mentioned above. Therefore, an alternative approach to the prediction of pressure profiles in single grains that is independent of the rheology parameters is required. Here, such an approach is developed, based on equilibrium thermodynamics, which accounts for chemical heterogeneities in solid solutions mutually connected with high-pressure minerals observed in thin section such as coesite or kyanite.
Under general conditions including the presence of pressure gradients, chemical equilibrium within a phase is represented by the assumption of zero net flux across the microstructure. Considering a binary system involving two components, A and B, i.e. with only one independent component, the difference between the chemical potentials of the two components is constant in space (Loomis, 1978)
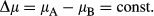(6)
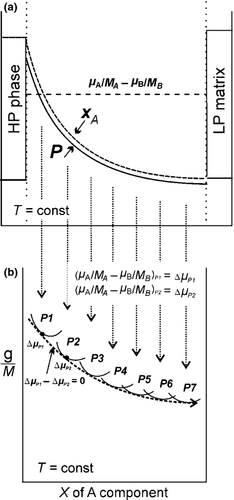
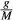–X diagram (X = xA/(xA − xB)) for constant temperature portraying the equilibrium situation with varying pressure, represented as a series of pressure steps (P1–P7). Each step is represented by a parabola portraying the path of a point traversing a 3D 
–P–X surface for the mineral.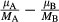 
and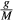 
stand for the chemical potentials and a Gibbs free energy converted to molar mass respectively.The approximate equilibrium relation 6 is converted from molar to the exact mass form to satisfy the mass conservation, involving the ∆μ written in terms of chemical potentials normalized to molar mass, Mi, following, for example, Gibbs (1906), Truesdell (1962), Landau & Lifshitz (1987), De Groot & Mazur (1962), Kuiken (1994) and Müller & Weiss (2012)
(7)
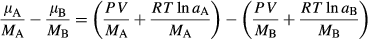(8)If the chemical potential difference is constant across a zoned rim or porphyroblast (Fig. 4a), in the sense of Eq. 7, a pressure change imitating the compositional change across the grain is required to maintain the force balance (Fig. 4a). The assumption is that each compositional step in the zoned profile across the grain can be taken as a point on a parabola for which Gibbs free energy (chemical potential) is known at given pressure and temperature. Under pressure gradients at constant temperature, chemical potentials are changing and thus different points on a parabola will be stable at each pressure step following the compositional changes across the grain (Fig. 4b). Each step on the G surface involves the phase at P1 being in equilibrium with its neighbour at P2, with zero flux
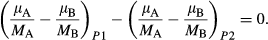(9)
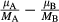for one pressure, equal to 
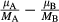for another, the difference in pressure is
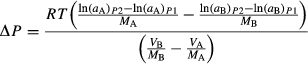(10)
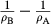), the prediction that the higher density end-member occurs at the higher pressure (inner) side of the anvil is satisfied.Examples
Two examples of high-grade microstructures, which can be found within a single thin section, were chosen to discuss the evidence for preserved pressure variations on a grain-scale (Fig. 5). The first example of exsolution lamellae in alkali feldspar documents that feldspar can sustain stresses up to 20 kbar at geological time-scales. The second example of plagioclase rims on kyanite illustrates that pressure variation is a valid explanation for microstructures involving preserved composition zoning commonly ascribed to disequilibrium.
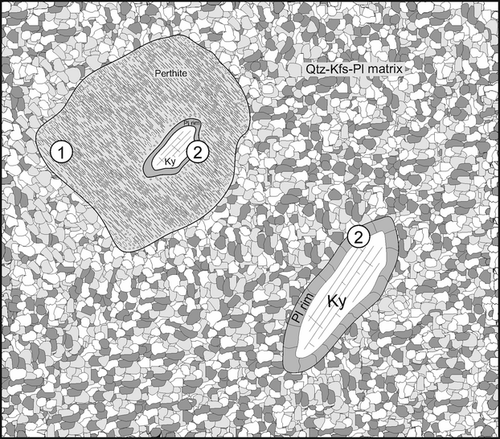
Figure 5 is a sketch based on the observations of microstructures in high-pressure felsic granulites from the Bohemian Massif (Variscan belt of Central Europe) described in detail by Štípská et al. (2010), Franěk et al. (2011) and Tajčmanová et al. (2011). These rocks are mostly characterized by a Grt–Ky±Bt–Pl–Kfs–Qtz mineral assemblage corresponding to peak P–T conditions of 16–18 kbar and 850–900 °C followed by nearly isothermal decompression (Franěk et al., 2011; Tajčmanová et al., 2011). The description of the compositions of the phases involved, and discussion of the details of the P–T evolution is beyond the scope here. They can be found in the works referred to above.
Exsolution lamellae in alkali feldspar
A simple example of pressure variation on a grain scale is provided by coherent exsolution lamellae. They are a typical microstructure in alkali feldspar that is generated by precipitation of a more albite-rich phase from alkali feldspar or ternary feldspar of an intermediate composition during cooling, producing at the same time a more orthoclase-rich host (Fig. 6). Already in the 1970s, transmission electron microscope observations documented coherent lamellae in alkali feldspar in which the lamellae maintain full continuity of their lattices across the lamellar interfaces (Willaime & Gandais, 1972; Brown & Willaime, 1974; Robin, 1974). In particular, Robin (1974) documented that coherency causes elastic strains in the individual lamellae affecting the lattice parameters. For a very small proportion of pure coherent albite lamellae within an orthoclase grain, the values for stress correspond to 6 kbar parallel to the b–axis and 23 kbar orthogonal to the b-axis (Robin, 1974). Values of 9 and 20 kbar were obtained for a coherent albite precipitate in microcline (Pryer & Robin, 1996). Moreover, the coherency stresses in alkali feldspar may be even higher when updated elastic constants are used (Brown et al., 2006; Neusser et al., 2012). These results are not surprising if the volume difference between the orthoclase-rich feldspar and albite-rich precipitate (up to 10 vol.%) is taken into account. These nanometre-scale pressure variations due to the volumetric change at the precipitate–host interface are comparable to the case of coesite inclusions in garnet.
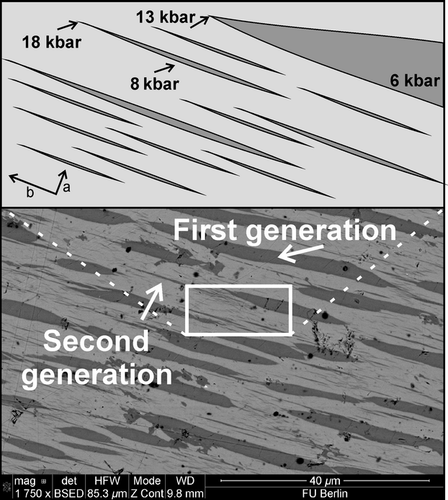
In slowly cooled rocks, the exsolution lamellae are often incoherent, most likely a consequence of stress relaxation (the partial or complete release of the induced pressure variations) involving destruction of an original coherent perthitic microstructure. In Example 1 (Figs 5 & 6), where two generations of exsolution lamellae are present, the first generation of lamellae, corresponding to higher temperature exsolution (800 °C; Tajčmanová et al., 2012) is already incoherent, but the lower temperature (680 °C; Tajčmanová et al., 2012) second generation is still coherent (Fig. 6). Given the elastic constants for alkali feldspar and the coordinate system used in Robin (1974), the stress was calculated for directions parallel (13–18 kbar) and orthogonal (6–8 kbar) to the b-axis based on the chemical composition of the precipitate (Fig. 6). The fact that the perthitic microstructure is still preserved reflects the fact that even feldspar as a representative of an apparently weak material can sustain large stresses internally at geological time-scales.
Plagioclase rims on kyanite
The second example offers an alternative explanation of a reaction rim microstructure around a high-pressure phase, which is a very common feature in high-grade kyanite-bearing rocks. Plagioclase rims around kyanite grains have a radial thickness from 50 up to 200 μm depending on their microstructural position. They are present both in the polycrystalline matrix and in large perthite grains (Figs 5 & 7). The plagioclase rim may either comprise a single grain or it can be polycrystalline with grains of different crystallographic orientation (Tajčmanová et al., 2011). Regardless of this, the plagioclase rims show identical continuous outward decrease of the anorthite content (Ca/(Ca+Na); mol.%) from An35 at the contact with kyanite to An20 at the contact with the surrounding matrix. Such a zonation has been explained by sluggish kinetics involving the slow diffusion of Al (Tajčmanová et al., 2007; Štípská et al., 2010). Taking into account the high-grade P–T conditions during which the plagioclase rim grows, about 800 °C, and the scale on which the microstructure is preserved, all components should have been already equilibrated within a few hundred thousand years (see Discussion and Conclusions below). However, this interpretation conflicts with the duration of the decompression event estimated at around 10 Ma from geochronology (details in Franěk et al., 2011).
The plagioclase rim can be described by the binary albite–anorthite chemical system. For such a system at constant temperature, zero fluxes can be calculated at given pressures using Eq. 10 with the feldspar activity model of Holland & Powell (2003), based on the compositional changes across the plagioclase rim (Fig. 9a). The result based on the direct data indicates that the overall equilibrium is satisfied only when pressure variations are considered. If the isobaric assumption is made, the Δμ (Eqs 7-8) is never constant (Fig. 8). Therefore, following the alternative explanation described above based on the assumption of overall chemical equilibrium and force balance, the preserved chemical zonation within the rim is inferred to be the result of pressure variation. Pressure changes progressively across the plagioclase rim from higher pressure in the kyanite to lower pressure in the matrix (Fig. 9a and c). This is also supported by the fact that more anorthite-rich compositions at the kyanite interface have higher density (and thus indicate higher pressure) than the more albitic ones at the matrix interface (Fig. 9b). The surrounding matrix, being composed of quartz and K-feldspar, shows little or no compositional zonation, and thus documenting of any pressure variation into the matrix is not possible. The compositional profile can be used as a barometer and the total pressure difference between both interfaces of the rim corresponds to around 8 kbar (Fig. 9c). This means that, after the decompression of the rock, say to 10 kbar, the pressure in the kyanite is still at 18 kbar, with pressure decrease across the plagioclase rim from 18 to 10 kbar.
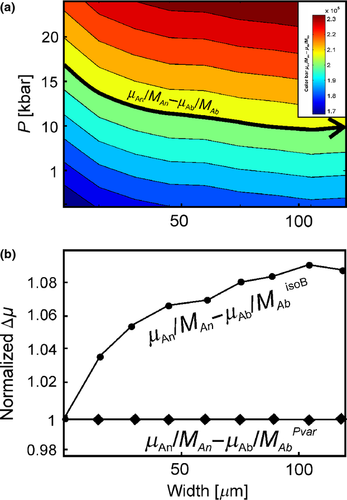
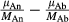) chemical potential differences across the plagioclase rim at isobaric conditions of 10 kbar (isoB) and under the inferred pressure variations (Pvar).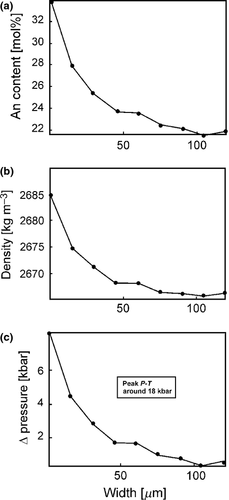
Discussion and conclusions
Microstructure diversity – the limits of the application of the present model
An alternative explanation for chemical zoning in porphyroblasts and reaction rims preserved in high-grade rocks has been outlined. An alternative model is required because the classical approach based on thermal closure does not fully explain the petrographic observations described above. Furthermore, a model based on fast diffusion and slow viscous relaxation, which would be complementary to the classical view as suggested by Schmid et al. (2009), had not been applied to natural samples. The approach used here avoids invoking the sluggish kinetics interpretation commonly used in accounting for preserved mineral zonation in high-grade rocks. Also, the approach accounts for local chemical heterogeneities which, based on regional geology data, are unlikely to be connected with very fast geological processes such as exhumation or local short thermal pulses that have been proposed to account for them (e.g. Camacho et al., 2005; Ague & Baxter, 2007).
The alternative approach does not attempt to account for the mechanisms that are responsible for the growth of the precipitates in perthitic feldspar or the growth of the plagioclase rim. These require a consideration of the rheology of the developing microstructure and its surrounding with time, and are beyond the scope of this paper. Because the approach used here is an inverse model, it only focuses on explaining why a microstructure or a compositional zonation is preserved at high temperature. Therefore, the thermodynamic approach is applicable to all petrographic observations where a high-pressure assemblage/phase is separated from a low-pressure assemblage/phase by a zoned mineral, independent of any rheology parameters.
Two different microstructures were described to discuss pressure heterogeneity on the thin section scale. The exsolution lamellae from Example 1 vary from nanometre scale to a maximum of a few micrometres, thus the size of the confined space here is mostly on a lattice scale, which is very stiff. The most evident are precipitates in feldspar from volcanic rocks that were cooled very quickly allowing preservation of coherent lamellae (e.g. Robin, 1974). However, exsolution lamellae in feldspar also provide a very important documentation of pressure variation in regionally metamorphosed rocks at geological time-scales. Considering the two generations of exsolution outlined above in slowly cooled samples, large stress variations in exsolution lamellae were obtained for the second coherent generation (Fig. 6), as similarly documented by Robin (1974). Assuming the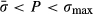 
, the values of stresses in albitic precipitates (Fig. 6) would imply metamorphic pressure variations between 13 and 18 kbar. In contrast, pressure variations for the incoherent generation should have diminished, even though the shape of the first-generation lamellae is still preserved. The elastic constants used for the calculation of induced stresses are for alkali feldspar. However, the first generation of precipitates was developed in the system involving CaO. Given that the content of anorthite component in the integrated composition of the feldspar is very low (5 mol.% anorthite; Tajčmanová et al., 2012), its effect on elastic properties and hence the resulting stress values is assumed to be negligible. The metamorphic pressure variation for the first generation of precipitates is estimated at around 10 kbar.
These results show that the induced pressure variations inside the large feldspar grains were enormous on the nanometre to micrometre scale and were sustained over geological time-scales. Furthermore, it is interpreted here that the reason why the spatially well-organized microstructure was not immediately fully transformed into a new coarse-grained phase with lower Gibbs energy is that it is mechanically maintained, preventing it from being completely recrystallized.
The plagioclase rims around kyanite grains were also developed at high temperature during decompression (800 °C; Štípská et al., 2010; Tajčmanová et al., 2011). No matter which mechanism was responsible for their growth, the chemical zonation is still well preserved. There are two different thicknesses of the rims connected with different microstructural positions in the same thin section, 50 and 150 μm, respectively, in the samples studied by Tajčmanová et al. (2011). Taking into account the coefficient for CaAl–NaSi interdiffusion in plagioclase for dry systems at 800 °C (10−22 m2 s−1; Yund, 1986; Liu & Yund, 1992; Korolyuk & Lepezin, 2009; Cherniak, 2010), the removal of such zoning in plagioclase (in a layer with a thickness of 100 μm) should have been complete in ≪0.5 Ma. This duration is unlikely from a tectonic point of view for this region, so the survival of the zoning needs to be explained. Moreover, if classical diffusion theory was applied here (with no pressure variation), given different thicknesses of the rims and same compositional differences within one thin section, different durations of equilibration would be inferred.
The suggested incorporation of mechanical equilibrium provides a more elegant and physically defensible explanation than the speculative mechanism of sluggish kinetics. The plagioclase rim then reflects a steady-state long duration process, based on the whole microstructure being in mechanical and chemical equilibrium. If there is a pressure gradient across the profile, the equilibrium conditions are reflected in a trend of isopleths with constant difference in chemical potentials (Fig. 8a). If an isopleth is followed, the way that pressure varies across the profile is given.
The multi-anvil model (strong single crystal and weak grain boundaries) leads to the preservation of the chemical zonation inside the single crystal as long as it survives against processes such as deformation, fluid infiltration or a sudden increase in temperature. Survival may be for a long time, e.g. millions of years, which would then be consistent with results from conventional geochronology for the region studied. The identical chemical zonation is not only for different thicknesses of the plagioclase rim but also for different crystallographic orientations in either the single crystal or the polycrystalline rim. This supports the multi-anvil mechanical concept allowing for maintaining pressure variations also in polycrystalline material and not only for homogeneous grains such as garnet (as for coesite inclusions).
As a comparison, pressure variation in the coesite/garnet example can correspond to 20 kbar (e.g. Parkinson & Katayama, 1999; O'Brien & Ziemann, 2008). In the example of the plagioclase rims around kyanite, a smaller pressure variation (8 kbar) is obtained. This pressure difference is significantly less than those retrieved from inclusion–host relationships in UHP rocks based on the classical pressure vessel model, but it is feasible regarding the rheology studies on stress relaxation and strength of feldspar (Rybacki & Dresen, 2000, 2004) and in polyphase rock aggregates (Ji et al., 2000). Regardless of the rheology data, perthite with incoherent exsolution lamellae can be considered as a polycrystalline material (two different phases, dislocations). Then the preservation of a second generation of coherent exsolution lamellae in one feldspar grain already weakened by the first generation of incoherent exsolution lamellae documents directly a minimum feldspar strength of 10 kbar at geological time-scales and temperatures around 650–700 °C.
Implications for estimation of P–T and rates of metamorphic processes
There are several potentially important implications of the proposed mechanical point of view. Estimation of the rates of metamorphic processes via diffusion modelling without considering the consequences of a mechanical equilibrium is likely to be misleading, especially for high-temperature rocks. Also the corollary, using microstructures to deduce diffusion coefficients when the thermal story is known, may seriously underestimate coefficient values. As shown above, taking into account mechanical equilibration suggests that pressure variations correspond to chemical variations (Fig. 4). The rate-controlling factor is always the slowest (Schmid et al., 2009) and, at high temperatures, diffusion is fast. This new view regarding what is preserved in high-grade rocks is unlikely to mean that the evolution of the rock, such as burial or exhumation, must have been so fast that it did not have time to chemically equilibrate. However, below 650 °C, at conditions typical, for example, for Barrovian metamorphism, the possibility that conventional rate estimates are valid cannot be excluded.
In phase equilibria calculations, the application of equilibrium thermodynamics requires a careful estimate of equilibration volume because of the apparent limited scale of equilibration especially at fluid-deficient conditions. Clearly, the possibility of grain-scale pressure variations affects how rocks should be considered using a phase equilibria modelling approach. If pressure variations are present, they should preclude the use of P–T diagrams calculated for a bulk rock composition where those variations are deduced to occur, unless the whole microstructure in which pressure variation is involved is excluded from the bulk composition. In many studies, small chemical and by interference possible pressure variations in the thin section are commonly neglected. However, the observation of such local chemical variations is very important for understanding all processes that took place in the sample and should not be ignored. For the phase relationships, which involve large volumetric changes, the V–T diagram at constant pressure can be informative in understanding the chemical equilibrium processes (e.g. Connolly, 1990, 2009; Powell et al., 2005). Such diagrams are helpful in a qualitative way in studies of, for instance, melting processes, but they cannot portray the pressure variations transparently as the mechanical equilibrium is not included in the approach.
In thermobarometry, chemical zoning in minerals is generally believed to be inappropriate for use in determining P–T estimates due to the apparent incomplete equilibration. However, the new interpretation of such zoning presented here does not rule out the application of barometric methods. All compositions across a zoning profile can be used, potentially, for pressure estimation, although not, for example, with the matrix mineral assemblage. It is of utmost importance that before the use of any thermobarometric method, the compositions and compositional variations in all phases in the rock should be carefully measured, rather than measuring only a few random points for use in calculating the P–T conditions.
Acknowledgements
Financial support for this project came from the European Commission (the Marie Curie Intra–European Fellowship Program) to LT. RP acknowledges support from ARC DP0987731. E.M. acknowledges the Alexander S. Onassis Public Benefit Foundation for financial support. We thank T. Gerya, D. Schmid, M. Dabrowski and five anonymous reviewers for their constructive comments, which improved to clarify the overall aim and mechanical part of the manuscript. M. Brown is acknowledged for careful editorial handling and patience.
