Social effects of territorial neighbours on the timing of spring breeding in North American red squirrels
Funding information
Funding for this study was provided by the Natural Sciences and Engineering Research Council, the Northern Scientific Training Program, the National Science Foundation and the Ontario Ministry of Research and Innovation.
Abstract
Organisms can affect one another's phenotypes when they socially interact. Indirect genetic effects occur when an individual's phenotype is affected by genes expressed in another individual. These heritable effects can enhance or reduce adaptive potential, thereby accelerating or reversing evolutionary change. Quantifying these social effects is therefore crucial for our understanding of evolution, yet estimates of indirect genetic effects in wild animals are limited to dyadic interactions. We estimated indirect phenotypic and genetic effects, and their covariance with direct effects, for the date of spring breeding in North American red squirrels (Tamiasciurus hudsonicus) living in an array of territories of varying spatial proximity. Additionally, we estimated indirect effects and the strength of selection at low and high population densities. Social effects of neighbours on the date of spring breeding were different from zero at high population densities but not at low population densities. Indirect phenotypic effects accounted for a larger amount of variation in the date of breeding than differences attributable to the among-individual variance, suggesting social interactions are important for determining breeding dates. The genetic component to these indirect effects was however not statistically significant. We therefore showcase a powerful and flexible method that will allow researchers working in organisms with a range of social systems to estimate indirect phenotypic and genetic effects, and demonstrate the degree to which social interactions can influence phenotypes, even in a solitary species.
1 INTRODUCTION
An individual's phenotype is influenced by both its genotype and the environment it experiences. As organisms mate, compete and cooperate with conspecifics (Frank, 2007), an important component of the environment they experience is social, and partly made up of the phenotypes of other individuals. This can allow an individual to influence others, and if their influence is partly genetic-based, then a portion of any organism's phenotype will be influenced by the genes of those with whom it interacts (Griffing, 1967). These are known as indirect genetic effects (“IGEs”), of which maternal genetic effects are the best known example (McAdam, Garant, & Wilson, 2014; Moore, Brodie, & Wolf, 1997; Wolf, Brodie, Cheverud, Moore, & Wade, 1998). With maternal genetic effects, the genes of a mother influence the traits of her offspring beyond those directly inherited (e.g. a mammal's genes affecting milk production may influence the growth rate of her offspring; Koch, 1972; María, Boldman, & Van Vleck, 1993). In the same way, the genes affecting the aggression level of an individual (so a direct genetic effect, “DGE”) may influence the aggression of any rival in a dominance contest (an IGE, e.g.: Wilson, Gelin, Perron, & Réale, 2009). Additionally, when competing for limited resources, the genes for resource acquisition of one individual are expected to negatively influence the resource acquisition, and so resource-dependent traits, of individuals with which it competes (Wilson, 2014). Therefore, IGEs can be expected in almost any system where conspecifics interact with each other (McAdam et al., 2014).
Indirect genetic effects contribute additional heritable variation within a population alongside DGEs (Bijma & Wade, 2008; Moore et al., 1997). Similar to a genetic correlation between any two traits (Kirkpatrick, 2009; Lande, 1979), an individual's own phenotype for some focal trait and its indirect effect on that trait expressed by neighbours can be genetically correlated (a DGE-IGE correlation). When IGEs are positively correlated with DGEs, such as the example with aggression above, IGEs can enhance that trait's response to directional selection. This happens because the standard response of the focal trait to selection results in a correlated evolutionary change in the social environment. This in turn causes further change in focal trait mean—in the same direction—through a plastic response to the social environment (Moore et al., 1997).
Conversely, if IGEs are negatively correlated with DGEs, then the population response to selection can be reduced, removed or even reversed (Bijma & Wade, 2008; Wilson, 2014). Negative correlations are expected for focal traits that are themselves dependent on the outcome of competition for limited resources (Wilson, 2014). For instance, Wade (1976) observed a decrease in mean reproductive output across generations in flour beetles (Tribolium castaneum) that were under individual selection for increased reproduction. This was presumably due to a negative IGE-DGE correlation that caused each subsequent generation to be composed of individuals that more strongly suppressed the reproduction of others through competitive interactions. Similarly, Costa e Silva, Potts, Bijma, Kerr, and Pilbeam (2013) observed a strong negative DGE-IGE covariance for diameter at breast height in eucalyptus trees (Eucalyptus globulus). This meant that, despite tree growth rates being heritable in the traditional sense (i.e. subject to DGEs), the total heritable variation in the population was near zero, preventing a response to selection. Estimates of DGEs alone might, therefore, provide a poor measure of the potential for a trait to respond to natural selection, yet most estimates of response to selection or evolvability in the wild only consider DGEs (Houle, 1992). More specifically, to the extent to which resources are limited in nature, we might expect DGEs to consistently overestimate the adaptive potential of resource-dependent traits because of negatively covarying IGEs (Wilson, 2014). As such, IGEs arising from competition represent one possible explanation for the “paradox of stasis,” in which natural selection on heritable traits often leads to stasis rather than evolutionary change (Merilä, Sheldon, & Kruuk, 2001), yet IGEs are very rarely quantified in the wild.
To date, empirical studies of IGEs in animals have focused on scenarios in which within-group interactions can be considered (approximately) uniform, and among-group interactions are absent. This allows IGEs to be estimated from the covariance between phenotypes of group mates, provided pedigree data spanning groups are available (Bijma, 2010a). This approach is well suited not only to dyadic interactions, but also to larger discrete groups (n > 2) of captive animals, where all individuals within a pen are assumed to interact equally, but no interactions occur between individuals in different pens. It has now been applied in a variety of taxa, such as mussels (Mytilus galloprovincialis; Brichette, Reyero, & Garcı́a, 2001), flour beetles (T. castaneum; Ellen et al., 2016), Nile tilapia (Oreochromis niloticus; Khaw, Ponzoni, Yee, Bin Aziz, & Bijma, 2016), domesticated chickens (Gallus domesticus; Muir, 2005; Brinker, Ellen, Veerkamp, & Bijma, 2015), mink (Neovison vison; Alemu, Bijma, Møller, Janss, & Berg, 2014) and domestic rabbits (Oryctolagus cuniculus; Piles et al., 2017). This work has helped establish the importance of IGEs for trait evolution (see: Ellen et al., 2014, for a review in livestock) and has led to growing interest in studying IGEs in wild populations.
Studies of IGEs in free-living animal populations, however, have thus far been confined to dyadic interactions. For example, Wilson et al. (2011) demonstrated that the tendency to win one-on-one fights in wild red deer (Cervus elaphus) is subject to both DGEs and IGEs that are perfectly negatively correlated, resulting in a total heritable variation of zero. This reconciles quantitative genetic predictions with a common sense approach that sees that the tendency to win cannot evolve at the population level, as each contest must always have one winner and one loser (see also: Wilson et al., 2009; Sartori & Mantovani, 2013). Other estimates for IGEs have focused on maternal genetic effects (McAdam & Boutin, 2004; McFarlane et al., 2015) or influences of male partner on female bird laying dates (Brommer & Rattiste, 2008; Caro et al., 2009; Germain, Wolak, Arcese, Losdat, & Reid, 2016; Liedvogel, Cornwallis, & Sheldon, 2012; Teplitsky, Mills, Yarrall, & Merilä, 2010). Studies on social interactions in groups of wild animals larger than two are, however, absent.
For social processes in wild populations, it is often problematic to identify and define discrete groups when individuals interact with multiple individuals but not all at equal intensity. Some interactions are frequent or strong whereas other interactions are brief or weak, and interactions may be indirect, for example competition for resources (Croft, James, & Krause, 2008; Croft, Krause, & James, 2004; Lusseau et al., 2003). Organisms interacting in larger groups may have generally weaker indirect effects on each of their group mates, as a consequence of their phenotype being “diluted” among more group members (Bijma, 2010b; Hadfield & Wilson, 2007; Muir, 2005). However, within a continuous population (i.e. one in which distinct groups cannot be identified) the net effect of one individual on the phenotype of any other may depend on distance or other factors (e.g. time associating) that mediate interaction intensity or frequency (Cappa & Cantet, 2008; Muir, 2005). To model these situations, variation in interaction strengths can be incorporated as “dilution” or “intensity of competition” factors in IGE models (Bijma, 2010b; Cappa & Cantet, 2008; Muir, 2005). Here, we refer to “intensity of association” factors, since social interactions are not always competitive. In eucalyptus trees, the inverse of the distance between pairs of trees was used as the intensity of association factors to estimate DGEs, IGEs and their covariance, on growth traits in Costa e Silva et al. (2013) and Costa e Silva, Potts, Gilmour, and Kerr (2017). The important premise here is that each focal individual has a potential indirect genetic effect on the phenotype of all its social partners, but the degree to which each partner experiences that effect depends on its distance from the focal individual. Incorporating intensity of association factors should be equally useful for animal-focused IGE models, as this allows us to account for animals interacting with multiple different individuals, in groups of varying sizes, and with different individuals at different strengths; a realistic representation of social interactions in the natural world (Fisher & McAdam, 2017).
Here, we used intensity of association factors to model IGEs among multiple neighbours for the first time in a wild animal (but see Formica et al., 2011 and; Farine & Sheldon, 2015 who weighted interacting phenotypes by distance to estimate social selection). We applied this framework to a population of North American red squirrels (Tamiasciurus hudsonicus, hereafter “red squirrels”) that have been continuously studied since 1987. We looked at a resource-dependent, but also heritable (h2 = 0.14; Lane et al., 2018) life-history trait: parturition date (the date in the spring on which a female squirrel gives birth to a litter; Réale, Berteaux, McAdam, & Boutin, 2003; Boutin et al., 2006; Kerr, Boutin, LaMontagne, McAdam, & Humphries, 2007; Lane et al., 2018), which could depend on competition for limited resources and, therefore, incorporate IGEs. Red squirrels of both sexes in this population live on individual exclusive territories based around a central cache of white spruce (Picea glauca) cones called a “midden.” The seeds from stored spruce cones represent their main food source during reproduction in the spring (Fletcher, Landry-Cuerrier, et al., 2013). Individuals make territorial calls (“rattles”) to delineate territory boundaries (Lair, 1990) and deter intruders (Siracusa et al., 2017) from stealing cached resources (Donald & Boutin, 2011; Gerhardt, 2005). Previous analyses have shown that selection favours earlier parturition dates (Réale et al., 2003), while a food supplementation experiment advanced the timing of spring breeding (Kerr et al., 2007). Note, however, that females can upregulate reproduction prior to a resource pulse (Boutin et al., 2006), and so typically are reproducing below capacity (Boutin, McAdam, & Humphries, 2013). Therefore, although reproduction is food-dependent, they can still increase reproductive output if necessary (see also: Dantzer et al., 2013). Still, if neighbours compete for food resources, we expect superior competitors to have access to more food and breed earlier. Conversely, competitively inferior individuals are expected to acquire less food and so breed later.
Population density is a key demographic parameter that we expect will influence the magnitude of IGEs. Selection on birth dates is particularly strong in years of high density (Williams, Lane, Humphries, McAdam, & Boutin, 2014; Fisher et al., 2017; although not found in Dantzer et al., 2013). Furthermore, red squirrels respond behaviourally to both real and perceived increases in density (Dantzer, Boutin, Humphries, & McAdam, 2012), while mothers adaptively increase the growth rates of their offspring under high-density conditions (Dantzer et al., 2013). Taken together, these findings are consistent with the expectation that, all else being equal, high density means increased competition.
In the light of the above, we had the following predictions:
- We expected individuals to have indirect effects on the parturition dates of their neighbours, and that the covariance between direct and indirect effects would be negative. That is, superior competitors will both breed earlier and cause their neighbours to breed later (following Costa e Silva et al., 2013; see also: Piles et al., 2017).
- Parturition dates depend on resource acquisition and possess direct genetic variance, so we expected the indirect effects to possess genetic variance (i.e. to be an IGE; McAdam et al., 2014; Wilson, 2014).
- Increased competition in years of high density should result in stronger indirect effects in high-density years, both in the magnitude of the indirect effects and the in strength of the negative covariance (Fisher & McAdam, 2019).
2 MATERIALS AND METHODS
2.1 Data collection
All data were collected as part of the Kluane Red Squirrel Project (KRSP) in the south-west Yukon, Canada. Since 1987, we have monitored two adjacent and unmanipulated 40-ha. study areas (“Kloo” and “Sulphur”), bisected by the Alaska highway. Red squirrels of both sexes defend exclusive resource-based territories of around 0.3 ha (LaMontagne et al., 2013), centred around a midden, an aggregation of discarded white spruce cone scales underneath which red squirrels cache intact white spruce cones. Each study area is staked at 30-m intervals in a grid system, and we recorded the x- and y-coordinates of the centre of each midden (to the nearest tenth of a coordinate point, giving distances to the nearest 3 m). In the spring of each year, we live-trapped (Tomahawk Live Trap, Tomahawk, WI, USA) new individuals and gave them unique ear tags in each ear. We also located females (based on vocalizations at known and new territory locations), monitored them for signs of pregnancy and ear tagged their pups once they were born. Based on the previously identified stages of female pregnancy and the body mass of the pups once they were located, we then estimated the female's parturition date. We analyse this date as the number of days since the 1st January in the calendar year. We also conducted censuses twice yearly (once in spring and once in autumn) using complete enumeration to ascertain the location of all individuals holding a territory, and so estimate population density. See McAdam, Boutin, Sykes, and Humphries (2007) for further details on the study system.
Red squirrels collect food throughout the summer and autumn, cache it in their middens and rely on it to survive over winter (Fletcher, Landry-Cuerrier, et al., 2013). The number of cached cones is positively associated with overwinter survival (juveniles: Larivée, Boutin, Speakman, McAdam, & Humphries, 2010; juveniles and adults: LaMontagne et al., 2013). Squirrels primarily forage close to their midden, with occasional forays further afield, including small amounts of theft from other red squirrels’ hoards (Donald & Boutin, 2011). We define the individuals a red squirrel potentially competes with as its n nearest neighbours (n was set at 6 for the majority of this analysis, but see below for explorations with different numbers of neighbours). We defined neighbourhoods and population densities based on our autumn census (August) rather than our spring census (May), because autumn is when squirrels are potentially competing for resources to hoard, and conception occurs well before May in most years. Gestation varies little around 35 days (Lair, 2014), and hence, parturition dates cannot be influenced by conditions after conception. Squirrels occasionally defend a second adjacent midden, but as they rarely store food in secondary middens we considered each squirrel's location to be the location of its primary midden. We then analysed each female's parturition date the following spring as influenced by her own genes (the DGE), and the identities and genotypes (the IGE) of those competing individuals as identified in the autumn census. Some females gave birth in multiple years, in which case they were included each year they did so, with an updated set of nearest neighbours as necessary. Females may attempt multiple litters in years of high resources, or if their first litter fails (Boutin et al., 2006; McAdam et al., 2007; Williams et al., 2014), but we limited our analyses to each female's first litter of each year (e.g. Dantzer et al., 2013).
We tagged pups while they were still on their mother's territory, so maternity was known for all nonimmigrants. Male red squirrels provide no parental care. From 2003 onwards, paternities were, therefore, assigned by collecting tissues samples from the ears of adults and neonatal pups. We used these tissue samples to genotype all adults and pups since 2003 at 16 microsatellites (Gunn et al., 2005) analysed with 99% confidence using CERVUS 3.0 (Kalinowski, Taper, & Marshall, 2007; see Lane, Boutin, Gunn, Slate, & Coltman, 2007, 2008 for further details). This method gives an estimated error rate of paternities, based on mismatches between known mother–offspring pairs, of around 2% (Lane et al., 2008), which we consider acceptable. Approximately 90% of yearly pups are assigned paternities with known males whereas the remaining 10% are analysed further in Colony 2.0 (Jones & Wang, 2010) to determine whether they might still be full or half siblings from unknown sires using 95% confidence in maximum likelihoods.
2.2 Data analysis
Data on the locations of squirrel territories were available from the autumns in 1991–2015, and so we looked at parturition dates in the following springs (i.e. 1992–2016). All squirrels identified as holding a territory in an autumn census were included in this analysis, including females that did not attempt a litter in the following spring, and males. These individuals had missing values entered for their parturition dates. As all males have missing values, we did not include an effect of sex. Their inclusion was nonetheless necessary as they acted as potential competitors during the autumn for those squirrels that did have a litter.
We initially fitted two mixed-effects linear models to our data, the first to estimate indirect effects (the “phenotypic model”) and second to split these indirect effects into genetic and nongenetic components (the “genetic model”). All models we fitted in the software “ASReml” ver 4.1; (Gilmour, Gogel, Cullis, Welham, & Thompson, 2015). We divided raw parturition dates by the standard deviation of all observations, giving a sample with a variance of 1, making the variance components easier to interpret (Schielzeth, 2010). In each model, we included the fixed effects of study area (a two-level factor), year (to test for a continuous linear trend), whether or not the spruce trees “masted” (produced a super-abundance of cones; Silvertown, 1980; Kelly, 1994; LaMontagne & Boutin, 2007) in the year of the autumn census (a two-level factor), age and age2 of the squirrel, and the separate random effects of year and squirrel identity, to account for repeated measures within each year and within each squirrel, respectively. If the age of the squirrel was not known, the mean age of all other squirrels in that breeding season was entered. Estimating the squirrel identity random effect allowed the calculation of the (conditional) repeatability of individual squirrel parturition dates (Nakagawa & Schielzeth, 2010). Additionally, while we predicted a negative covariance between neighbours due to competition for resources (especially during high-density conditions), this could be masked by positive spatial autocorrelation in resource availability within a study area. This would generate a net signal of positive phenotypic covariance among neighbours (Regan et al., 2017; Stopher et al., 2012; Thomson, Winney, Salles, & Pujol, 2018). To avoid this, we fitted a term (hereafter referred to as the “square term” or differences among “squares”) to control for spatial autocorrelation (see Supplementary materials for details, and Table S1 for results of varying the scale at which we modelled this).
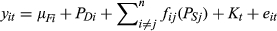(1)
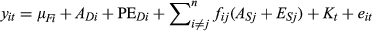(2)Where individual i's parturition date in year t, is comprised of the fixed effect mean, a direct additive genetic effect (ADi), a direct permanent environmental effect (PEDi), both the additive genetic (ASj) and nonadditive genetic (ESj) indirect effects of all the n neighbours (j) that i interacts with, a year term (Kt) and an individual by year specific residual term (eit).
This model has not been applied to wild animals before, and we fully acknowledge that our choice to consider only the six nearest neighbours here is somewhat arbitrary, as indeed is the scaling of fij. Therefore, we also explored different numbers of neighbours and different methods for defining our fij terms. We then monitored how this influenced the estimates of the variance parameters, to determine whether the model was particularly sensitive to altering these factors (see also: Costa e Silva et al., 2017). We present results using fij = 1/(1 + distance2) in the supplementary materials (Table S1). In the supplementary materials, we also present results where we defined the competitors as all those within 60, 130 or 200 m, without weighting by distance, up to 24 competitors (Table S1), and investigations with varying numbers of neighbours 1–5, 9, 12, 15, 18 and 24; Table S2). Neither changing the number of neighbours nor rescaling intensity of association terms changed the number of model parameters estimated (either a single indirect phenotypic effect, or both genetic and permanent environmental indirect effects, and their respective covariances). Therefore, information criteria-based approaches for comparing model fits were not appropriate as biological complexity (e.g. number of neighbours) changed but the degree of penalization did not (i.e. still one neighbour variance estimated). Additionally, we were primarily interested in our ability to estimate, and the magnitude and significance of, certain parameters (our indirect effects), hence finding the most parsimonious model of parturition date was not a goal of ours. Instead, we simply assessed the change in variance components, noting the size of the parameter estimates and size of the standard errors. We focus on the results with the six closest neighbours, as this seemed the median result among the variations we tried. Using the inverse of distance2 squared led to a large increase in the standard errors of the DGE estimate, which only occurred in this model, hence we considered simply the inverse of distance as more appropriate. Nevertheless, we direct readers to the supplementary material to view the range of possible results depending on the model specification.
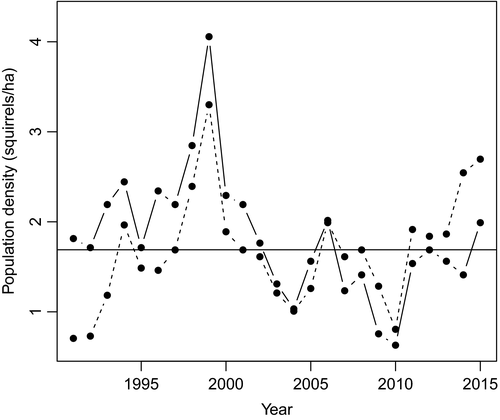
We tested the significance of the direct–indirect phenotypic covariance in the phenotypic model using a likelihood ratio test (LRT) between a model with the covariance freely estimated and one with it fixed to zero, and tested the significance of the indirect phenotypic effect using a LRT between the model with the indirect effect (and a zero covariance) and a model without it. With the genetic model, we tested the significance of the DGE-IGE covariance, and the IGE variance, in the same way, in models that still estimated the full direct–indirect phenotypic covariance matrix. We assumed the LRT statistic was distributed as a 50:50 mixture of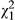 
and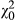 
when testing single variance components (following Self & Liang, 1987) but as 
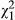when testing covariances. We report correlations, although if the variance of either the direct or indirect effect was very small (<0.0001), then we assumed it was essentially zero, and so then we report the correlation as “undefined.” Although they were not directly relevant to the biological hypotheses being tested, the statistical significance of the fixed effects in the genetic model was tested using conditional Wald tests (see: Gilmour et al., 2015). This approach to testing the significance of fixed effects in mixed linear models performs well in situations with limited sample sizes (Kenward & Roger, 1997). We then calculated partial R2 for each fixed effect, following Edwards, Muller, Wolfinger, Qaqish, and Schabenberger (2008), using the residual degrees of freedom as calculated by ASReml (1174 for the genetic model).
2.3 Influence of population density on indirect effects
We consider population density during the resource caching period to be key to resource acquisition. Consequently, for any given year of parturition the relevant measure of density was obtained from the census in the autumn of the year prior to parturition, that is at the same time as when the territory ownership was defined. As the study area has grown marginally since the start of the project, we restricted counts to individuals holding a territory within a defined 38-ha area that has been constant throughout the entire study period. Across both study areas in all years, the median population density in the autumn was 1.69 squirrels/ha (Figure 1). We, therefore, labelled each study area within each year with a density higher than this as “high density” (1994, 1998–2000, 2006 and 2015 for both study areas, 1991–1993, 1995–1997, 2001 and 2002 for Sulphur only and 2011–2014 for Kloo only), and so the remainder as “low density.” There were, therefore, 26 instances of low-density conditions and 24 instances of high-density conditions. There are several instances of study areas having exactly the median density, hence why there are more low- than high-density conditions.
For both the phenotypic and the genetic models, we fitted an interaction between population density (low or high) and each random effect. This gave us separate density-specific estimates of each of the variances (DGEs, IGES and nongenetic versions) and covariances, the among-year variances and the among-square variances for low- and high-density study areas. To obtain stable model convergence in the genetic model, we were required to fix the direct permanent environment effect in low-density years to 0.1 × 10−4, but since this term was estimated to be very small in the model across all years, this is likely not problematic. There was a single residual variance in each model. We also included density as two-level factor in the fixed effects, and an interaction between this term and each of the other fixed effects, to allow them to vary between low- and high-density conditions. We tested for significance of indirect effects in both low- and high-density conditions in the same way as for the full models. When testing the significance of terms for low-density, we maintained the full model structure (e.g. IGEs and their covariance with DGEs, and the equivalent permanent environmental effects in the genetic model) for high-density conditions, and vice versa for when testing the significance of terms for low density.
2.4 Calculating total variance parameters
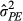, incorporating both consistent direct and indirect phenotypic effects; for the phenotypic model) and the total variance in individuals’ heritable influence on the population mean parturition date (
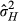; for the genetic model, commonly referred to as the “total heritable variance”). Following Bijma (2011) and Costa e Silva et al. (2013), these are as follows:
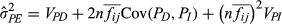(3)
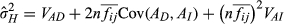(4)Where n is the number of neighbours (excluding the focal individual, so 6), 
is the mean intensity of association factor, VPD and VAD are the direct phenotypic and additive genetic variances, respectively, Cov(PD, PI) and Cov(AD, AI) are the phenotypic and genetic direct–indirect covariances, respectively, and VPI and VAI are the indirect phenotypic and additive genetic variances, respectively. The 
was calculated as 0.330 across the whole data set, 0.298 at low densities and 0.352 at high densities, which means a squirrel's six nearest neighbours were on average, 60.9 m, 70.7 m and 55.2 m from it across the whole data set, at low densities, or at high densities, respectively. Note that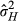 
, unlike traditional heritability, can exceed 1; see Bijma (2011) for the mathematical demonstration of this and Ellen et al. (2014) for empirical examples in livestock.
3 RESULTS
In total, 1862 unique red squirrels were recorded a total of 4362 times in autumn censuses as holding territories and so were included in the analysis. There were 555 unique females that had at least one litter, with a mean of 2.1 (range = 1–8, standard deviation = 1.3) recorded parturition dates each. The median date of first litters was 23rd April, with interquartile ranges of 6th April to 11th May. There were 364 females that had no recorded parturition dates and 943 males. 1196 squirrels had a known mother, and 498 had a known father, with 481 of those having both parents known.
Parturition dates differed greatly among years and less so among squares, with variance among years accounting for 32.0% of the variance in the genetic model, whereas variance among squares accounted for 4.0% of the total variance (all variance component estimates are shown in Table 1, with fixed effect estimates shown in Table 2). While there was no linear trend across years, parturition dates were significantly earlier following mast years by approximately 40 days.
| Model | V AD | V AI | Cov(AD, AI) | V PD | V PI | Cov(PD, PI) | V Y | V S | V R |
|---|---|---|---|---|---|---|---|---|---|
| Whole dataset | |||||||||
| Phenotypic model | NA | NA | NA | 0.038 (0.012) | 0.076 (0.023) | −0.005 (0.014) | 0.317 (0.098) | 0.038 (0.014) | 0.197 (0.017) |
| Genetic model | 0.048 (0.012) | <0.001 (-) | 0.005 (0.015) | <0.001 (-) | 0.063 (0.023) | −0.018 (0.020) | 0.320 (0.099) | 0.040 (0.014) | 0.192 (0.016) |
| Low- vs. high-density comparison | |||||||||
| Phenotypic model split by density | |||||||||
| Low density | NA | NA | NA | 0.043 (0.022) | 0.031 (0.046) | 0.027 (0.024) | 0.316 (0.123) | 0.040 (0.024) | 0.205 (0.019) |
| High density | NA | NA | NA | 0.040 (0.019) | 0.078 (0.030) | −0.001 (0.022) | 0.380 (0.150) | 0.028 (0.178) | |
| Genetic model split by density | |||||||||
| Low density | 0.047 (0.020) | <0.001 (-) | 0.027 (0.030) | <0.001 (-) | 0.021 (0.045) | −0.003 (0.036) | 0.322 (0.126) | 0.042 (0.024) | 0.189 (0.017) |
| High density | 0.053 (0.018) | 0.038 (0.037) | −0.018 (0.023) | <0.001 (-) | 0.033 (0.046) | −0.001 (0.026) | 0. 384 (0.151) | 0.031 (0.018) | |
| Term | Estimate | SE | df_d | F-statistic | p-value | R 2 |
|---|---|---|---|---|---|---|
| Intercept | −6.684 | 32.355 | 23.3 | 0.06 | 0.810 | NA |
| Study area (SU) | 0.176 | 0.054 | 5.72 | 10.68 | 0.002 | 0.009 |
| Year | 0.006 | 0.016 | 23.1 | 0.16 | 0.693 | <0.001 |
| Following a mast (yes) | −1.71 | 0.288 | 22 | 35.57 | <0.001 | 0.029 |
| Age | −0.002 | <0.001 | 1091.5 | 145.85 | <0.001 | 0.111 |
| Age2 | <0.001 | <0.001 | 1164.0 | 95.59 | <0.001 | 0.075 |
Alongside these environmental effects, individuals showed some degree of consistency in their parturition dates, with the direct variance among individuals in parturition date in the phenotypic model accounting for 3.8% of the phenotypic variance. Indirect phenotypic effects of neighbours were significant (VPI = 0.076, LRT, χ0, 12 = 13.755, P < 0.001), but the covariance between the direct and indirect phenotypic effects was not (cor = −0.094, LRT,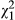 
= 0.111, P = 0.739), indicating that individuals that give birth earlier do not influence their neighbours in any particular direction relative to their own parturition date. Individuals’ consistent differences in their own phenotypes and consistent effects on neighbours (
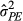from eq. 3) were calculated as 31.4% of the phenotypic variation, much larger because each individual affects multiple neighbours and indicating that social effects account for a large amount of the variation in parturition date. Alongside this consistency, individuals showed a degree of plasticity, with older squirrels having earlier parturition dates, whereas the positive quadratic effect indicates a nonlinear effect of age in which squirrels began to breed later at older ages.
Parturition date showed direct heritability, with VAD in the genetic model accounting for 4.8% of the phenotypic variance (note this differs from previous estimates of h2 for this trait in this system as here we include the among-year variation and the variance attributable to fixed effects in VP, see also Wilson (2008)). The estimate for the IGEs was not different from zero (VAI < 0.001, LRT, χ0, 12 = 0.003, P = 0.480), as was the DGE-IGE covariance (cor = undefined, LRT,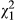 
= 0.119, P = 0.729). We calculated the total heritable variance of parturition date, 
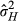from eq. 4, as 6.8%, a modest increase over VAD. The very small DGE-IGE covariance indicated that genotypes for early parturition dates did not affect their neighbours in any consistent direction relative to their own parturition date.
3.1 Low- vs high-density comparison
In low-density conditions, both the variance in indirect phenotypic effects (VPI = 0.031, LRT, χ0, 12 = 0.808, P = 0.184) and the direct–indirect phenotypic covariance (cor = 0.737, LRT,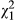 
= 0.1.206, P = 0.272) were not significantly different from zero. At high densities, there were significant phenotypic indirect effects (VPI = 0.078, LRT, χ0, 12 = 9.523, P = 0.001), although the covariance was not different from zero (cor = −0.023, LRT, 
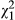= 0.004, P = 0.952). We note here that size of the standard errors suggests that the indirect phenotypic effects at low and high densities are not different from each other, but we did not test this formally.
Given that we detected no phenotypic indirect effects in low-density conditions, it is unsurprising that the IGEs (VAI < 0.001, LRT, χ0, 12 = 0.000, P = 0.500) and the DGE-IGE covariance in these conditions were also not different from zero (cor = undefined, LRT,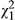 
= 0.566, P = 0.452). For high densities, IGEs were considerably stronger than across the whole data set, and more than one standard error from zero, although still not significantly different from zero (VAI = 0.038, LRT, χ0, 12 = 0.607, P = 0.218). The covariance between DGEs and IGEs was negative but not different from zero (cor = −0.401, LRT, 
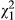= 0.688, P = 0.407). Although we reiterate that neither covariance was statistically significant, based on our parameter estimates in low-density conditions, 
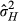was 14.3%, which was higher than VAD, as this calculation includes the positive DGE-IGE covariance estimate (despite the lack of variance in IGEs rendering the correlation undefined). In high-density conditions,
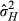was 14.2%, much higher than with direct genetic effects alone due to the additional genetic variance from IGEs. We stress that, as the estimates for the IGEs and their covariances with the DGEs were not significantly different from zero, the estimates of 
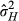should be interpreted with caution.
Variation attributable to spatial location accounted for 4.2% of the variation in parturition dates in low-density and 3.1% in high-density conditions (from the genetic model split between low and high densities). Finally, there was also substantial among-year variance in both conditions, accounting for 32.2% and 38.4% for the observed variance in low- and high-density conditions, respectively. We present estimates for fixed effects at low and high densities from the genetic model in the supplemental materials (Table S3); for the calculation of partial R2s, we calculated the residual degrees of freedom to be 1169.
4 DISCUSSION
4.1 Indirect effects are present and change with population density
Red squirrels live in territories surrounded by conspecifics, with whom they engage in social interactions through vocalizations, competition for resources and mating interactions. Our analyses show that these interactions can lead to substantial indirect effects on female squirrel reproductive traits. These are detected here as a repeatable influence of competitor identity on the parturition date of focal individuals—which accounted for a much greater amount of variation in parturition date than direct effects of individual identity alone. Our results also suggest that these indirect effects are significant determinants of focal phenotypes at high densities, but they are not at low densities. Specifically, at high densities, there is significant variation in the extent to which squirrels influence each other's parturition dates, but this is not the case at low densities.
The social effects on parturition date we documented indicate that much more of an individual's phenotype is under the control of those it socially interacts with than is determined by its own identity (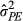
was large compared to within-individual repeatability), even in a solitary and territorial species. Work on eucalyptus trees (Costa e Silva et al., 2013) implicated competition for limited resources as the source of indirect effects, and our results are broadly consistent with this idea. Highly competitive red squirrels may acquire larger amounts of resources from the environment, leaving less for other individuals. Earlier studies have shown that red squirrel females may be food-limited to some degree, aside from in years following a mast event. For example, earlier parturition dates and lower levels of oxidative protein damage and higher levels of antioxidants were found when food was supplemented (Fletcher, Selman, et al., 2013; Kerr et al., 2007; Williams et al., 2014), and individuals are more likely to survive over winter with a larger food cache (LaMontagne et al., 2013; Larivée et al., 2010), suggesting that not all individuals have enough stored food. However, female squirrels appear to reproduce below capacity in nonmast years, and upregulate their reproduction before pulsed resources are available (Boutin et al., 2006, 2013), and so they are likely not completely food-limited. The additional insight from the current study is that, for focal individuals, competitive effects on phenotype depend not simply on high density, but also on the identities—and so phenotypes—of their nearest neighbours.
Our analysis did not explore the specific mechanism (or trait(s)) that mediate indirect phenotypic effects from competition, hence we have not confirmed that red squirrels are competing for limited food resources, although this explanation seems likely. While direct physical interactions are rare (Dantzer et al., 2012) and thus an unlikely mechanism, red squirrels might instead influence each other's parturition dates through acoustic territorial interactions. Red squirrels give territorial calls (“rattles”), to which neighbours behaviourally respond (Shonfield, Taylor, Boutin, Humphries, & Mcadam, 2012; Wilson et al., 2015) and which function to maintain their territory from conspecifics (Lair, 1990; Siracusa et al., 2017; Smith, 1978). Additionally, red squirrels rattle more when they have a higher local population density (Dantzer et al., 2012; Shonfield et al., 2012), whereas red squirrel mothers increase the growth rate of their pups when playback of territorial vocalizations leads to the perception of higher local population density (Dantzer et al., 2013). This is through upregulation of maternal glucocorticoids (Dantzer et al., 2013), part of the stress axis. Other life-history traits, such as parturition date, may be influenced by rattles at high densities, allowing individuals to influence each other's parturition dates. Therefore, acoustic interactions among neighbours, which enable neighbours to influence each other's reproduction, may be a source of indirect effects, particularly in high-density conditions.
4.2 Indirect effects with a limited heritable basis
Although our analyses provide statistical support for considerable indirect effects of competitors on a focal individual's parturition date, we did not conclusively demonstrate that these indirect effects were underpinned by genetic variation. Estimated effect sizes were larger at high densities, in line with our predictions and the phenotypic effects, but standard errors remained quite wide. Therefore, while the point estimates of predicted change indicate IGEs are potentially strong enough to make a meaningful difference to evolutionary dynamics, they were estimated with high uncertainty so should be interpreted with caution.
Previous work on livestock has shown that IGEs negatively correlated with DGEs can reduce or even reverse the expected response to selection (Costa e Silva et al., 2013; Ellen et al., 2014; Muir, Bijma, & Schinckel, 2013). The evolutionary stasis of heritable traits under directional selection is a well-known observation in need of an explanation in the study of trait evolution in wild populations (Kokko et al., 2017; Merilä et al., 2001; Pujol et al., 2018). The negative DGE-IGE covariance found here at high densities would counteract selection responses (compared to a DGE-only scenario) and so reduce evolutionary change. Whether this is a general explanation for evolutionary stasis remains to be explored (Wilson, 2014). In our study population, despite phenotypic selection on parturition dates (which as noted above are heritable), we have observed no evolution in this trait over 20 years (Lane et al., 2018). However, Lane et al. (2018) found that the association between parturition date and fitness was entirely a residual correlation, rather than a genetic one, so no alternative explanation for evolutionary stasis (such as IGEs) is required.
If IGEs are not different from zero and so all social effects are solely phenotypic, then the expected response to selection will not differ from that predicted by the breeder's equation (Bijma & Wade, 2008). We note that the nonsignificance of our IGE variance estimates may have been driven by a high degree of uncertainty (large standard errors), rather than the magnitude of the effect, as in high-density years the VAI was quite close in absolute size to VAD, and their contribution to total heritable variance was large. By demonstrating this possibly important but uncertain effect, we hope to stimulate others to estimate more precisely these parameters, and so help the field achieve a general understanding of their importance.
4.3 Altering association factors and neighbourhood size
Varying the intensity of association factors (i.e. how strongly we weighted neighbours at different distances) and the size of the neighbourhood did alter the balance between the estimated direct and indirect effects, as well as estimated relative contribution of genetic and environmental influences (see Tables S1–S2 in the supplementary materials). Weighting the closest individuals more strongly, by only including the one to three nearest neighbours, or using the inverse of distance or distance2, or by only including individuals within 60 m, gave similar results. In all these versions, the variance arising from DGEs increased marginally compared to the model where all neighbours were weighted equally. This effect was more pronounced when using the inverse of distance2 to define the intensity of association factors. We note that the standard errors of estimates for direct additive genetic variance (VAD) in the model using the inverse of distance2 were greatly increased, causing the estimate to be within two standard errors of zero (i.e. nominally nonsignificant). This was the only model explored where this occurred. Weighting farther individuals as strongly as close individuals, either by not including any intensity of association factors for the six closest individuals, or by including all individuals within 200 m and weighting them equally, gave very low estimates for the IGEs. This could suggest that individuals at greater distances do not influence their neighbours as much as close individuals.
Increasing the number of neighbours considered in the analysis beyond six led to larger estimates for the variance arising from the nongenetic indirect effects (VPI). A larger estimate for the VPI was also present in the model before the square term was added (not shown). This suggests the apparent nongenetic influence of neighbours at large spatial scales, as indicated by VPI, may be driven by shared environmental factors at the larger scale causing sets of neighbours to be consistently different from other sets, rather than by social interactions of the focal individual causing their neighbours to be consistently different. Decreasing the number of neighbours tended to increase the variance attributed to the DGE, while IGEs showed a nonlinear trend, peaking in magnitude with four neighbours and then falling back down towards zero. At these neighbourhood sizes, VPI was typically estimated near zero, but grew in size once five or more neighbours were considered. Overall, these results do not indicate that inferences from our model with the six closest neighbours, weighted by the inverse of distance, are inappropriate for the system.
The approach we used, based on the work of Muir (2005) and Cappa and Cantet (2008), can be applied to organisms in a range of social structures. Due to the relatively recent increase in usage of techniques such as social network analysis (Croft et al., 2008; Krause, Croft, & James, 2007; Krause, James, Franks, & Croft, 2014), estimates of pairwise associations within populations of animals have been made in many systems. These values can be used as the intensity of association factors, as we used the inverse of distance, to scale indirect effects (Fisher & McAdam, 2017). To estimate IGEs, this must be twinned with information on the phenotypes and relatedness of the individuals in the population. We had a large data set with good information on phenotypes and relatedness of individuals, yet high uncertainty around moderately large estimates of IGEs did not distinguish them from zero. The requirement to phenotype, genotype and assess the social relationships of many individuals within a population may well limit the range of study systems this approach can be used in (Kruuk & Wilson, 2018). Simulations to provide guidelines for sample sizes may well be useful. However, with decreases in the cost of tracking technologies and in the cost of assessing the genetic relatedness of animals (Bérénos, Ellis, Pilkington, & Pemberton, 2014), more study systems will begin to be able to apply this and similar models, increasing the number of estimates for these difficult-to-estimate quantitative genetic parameters, which could then be aggregated in a meta-analysis to detect general patterns (Reid, 2012), such as that by Wilson and Réale (2006) for the direct-maternal genetic correlation.
4.4 Conclusions
Previous to this study, IGEs had only ever been estimated for wild animals in the context of pairwise (dyadic) social interactions. We extended this to estimate IGEs on a life-history trait with links to fitness in a population of wild animals that do not interact in discretely defined groups. We also incorporated varying strengths of closeness of association between individuals to more accurately represent the heterogeneous and complex nature of social interactions in the natural world. We found that indirect effects of neighbours were a significant contributor to parturition dates at high densities, and this effect may have a heritable component. However, the point estimates for genetic parameters are characterized by high uncertainty and, as noted, we cannot exclude the possibility that the indirect effects have a nongenetic basis. Nonetheless, significant indirect phenotypic effects were detected and appear to increase in importance at high density. This is consistent with competition for limited food resources being the source of neighbour influences on focal life-history traits. Exactly how this competition is mediated remains to be determined. The estimation of indirect effects, and IGEs specifically, should be extended to more systems where densities and resource availabilities vary (either naturally or artificially) to determine whether the patterns we have observed are general. While we did not conclusively demonstrate IGEs are present, we think wider estimation of effect sizes is useful even if power is limiting to make strong inferences in any single case. The method we have used is flexible enough to be applied to alternative systems, and hence, we look forward to the accumulation of more estimates of IGEs in the wild to detect general patterns.
ACKNOWLEDGMENTS
We thank Agnes MacDonald for long-term access to her trapline, and the Champagne and Aishihik First Nations for allowing us to conduct work on their traditional territory. We thank all the volunteers, field assistants and graduate students whose tireless work makes the KRSP possible. We thank the Centre for the Genetic Improvement of Livestock, University of Guelph, for providing computing resources, and Bill Szkotnicki and Piter Bijma for assistance with the analyses. We also thank an editor and five anonymous reviewers for helpful comments that improved the manuscript. We have no conflicts of interest. This is KRSP paper number 98.
AUTHOR CONTRIBUTIONS
AGM, AJW and DNF conceived the research question. SB initiated the long-term study, and all authors contributed to field logistics, data collection and the writing of the manuscript. DNF drafted the manuscript and conducted the data analysis, with guidance from AJW and AGM. All authors approved the final manuscript for submission.
DATA ACCESSIBILITY
Data has been archived in FigShare: https://doi.org/10.6084/m9.figshare.7763564.v1
