The evolutionary response of mating system to heterosis
Abstract
Isolation allows populations to diverge and to fix different alleles. Deleterious alleles that reach locally high frequencies contribute to genetic load, especially in inbred or selfing populations, in which selection is relaxed. In the event of secondary contact, the recessive portion of the genetic load is masked in the hybrid offspring, producing heterosis. This advantage, only attainable through outcrossing, should favour evolution of greater outcrossing even if inbreeding depression has been purged from the contributing populations. Why, then, are selfing-to-outcrossing transitions not more common? To evaluate the evolutionary response of mating system to heterosis, we model two monomorphic populations of entirely selfing individuals, introduce a modifier allele that increases the rate of outcrossing and investigate whether the heterosis among populations is sufficient for the modifier to invade and fix. We find that the outcrossing mutation invades for many parameter choices, but it rarely fixes unless populations harbour extremely large unique fixed genetic loads. Reversions to outcrossing become more likely as the load becomes more polygenic, or when the modifier appears on a rare background, such as by dispersal of an outcrossing genotype into a selfing population. More often, the outcrossing mutation instead rises to moderate frequency, which allows recombination in hybrids to produce superior haplotypes that can spread without the mutation's further assistance. The transience of heterosis can therefore explain why secondary contact does not commonly yield selfing-to-outcrossing transitions.
1 INTRODUCTION
Secondary contact between previously isolated populations is a dramatic event with a variety of potential evolutionary repercussions, including genetic rescue (Richards, 2000), the exposure of epistatic incompatibilities evolved in isolation (Bateson, 1909; Dobzhansky, 1937; Muller, 1942), and the release of selfish genetic elements (Fishman & Willis, 2005). A particularly common consequence of secondary contact is heterosis, an increase in fitness of the offspring of interpopulation crosses relative to within-population crosses. Heterosis is especially likely to accumulate between highly inbred and self-fertilizing (selfing) populations. Their small effective population sizes allow deleterious alleles to reach high frequencies locally, a phenomenon called local drift load (Whitlock, Ingvarsson, & Hatfield, 2000). The part of the local drift load attributable to recessive alleles is masked in hybrids, resulting in heterosis. Empirical heterosis estimates in populations of different census sizes (Heschel & Paige, 1995), levels of isolation (Richards, 2000) and breeding systems (Busch, 2006) generally support the proposition that isolated or predominantly selfing populations accumulate greater heterosis than effectively large, connected populations (but see Ouborg & van Treuren, 1994). Here, we explore the evolutionary consequences of the exposure of heterosis upon secondary contact between selfing populations that have each incurred their own genetic load. Specifically, we ask if such heterosis allows diverged populations to shed their genetic load and if such heterosis favours the invasion and fixation of a mutation that increases the rate of cross-fertilization (outcrossing).
Whereas the potential for heterosis increases as isolated populations inbreed, individuals can only exploit this advantage through outcrossing. Heterosis therefore provides an advantage of outcrossing in historically selfing populations, in which the advantage of outcrossing is usually low. The reduced advantage of outcrossing within selfing populations stems from the purging of inbreeding depression: the removal or fixation of deleterious recessive alleles in highly homozygous selfing populations. Purging may determine the long-term trajectory of mating system evolution: transitions to predominant selfing are traditionally expected to be irreversible because an increase in the selfing rate tends to purge deleterious alleles, reducing inbreeding depression, which then allows the evolution of even greater selfing in a positive feedback loop (Lande & Schemske, 1985). But heterosis provides an alternative advantage that might be sufficient to favour the evolution of greater outcrossing even in predominantly selfing populations (Igić & Busch, 2013).
Could this heterosis favour the secondary evolution of outcrossing? Although inferred patterns of trait evolution suggest selfing-to-outcrossing transitions are indeed rare (Barrett, Harder, & Worley, 1996; Escobar et al., 2010; Stebbins, 1974), some reversions to outcrossing have been hypothesized (Armbruster, 1993; Barrett & Shore, 1987; Bena, Lejeune, Prosperi, & Olivieri, 1998; Olmstead, 1990). Indeed, it has been suggested that heterosis in the face of secondary contact has favoured the secondary evolution of outcrossing (Igić & Busch, 2013). Since purging only eliminates segregating variants within a population, heterosis caused by differentiation among populations is a logical route to the evolution of greater outcrossing. In contrast with the rich body of theory on the conditions for outcrossing-to-selfing transitions (Fisher, 1941; Kimura, 1959; Lande & Schemske, 1985; Lloyd, 1979; Nagylaki, 1976), there is a dearth of theory on selfing-to-outcrossing transitions. Their relative rarity is not a sufficient reason to neglect them: by examining exceptions to typical patterns, theory can explain why the exceptions are rare.
Theory predicts that heterosis will indeed be favourable to outcrossing (Theodorou & Couvet, 2002), but since previous models focused on heterosis maintained at equilibrium among connected populations, the effects of the potentially larger heterosis accumulated among long-isolated populations remain unknown. In one way, secondary contact among long-isolated populations should be more favourable to outcrossing because arbitrarily large levels of heterosis could have accumulated (limited only by the accumulation of incompatibilities or other isolating barriers in the interim). But this elevated heterosis is also transient: once secondary contact unites alleles into the same population, selection will reduce the frequencies of inferior alleles and will thus undermine the genetic differentiation underlying heterosis. There is thus a limited period in which outcrossing is highly favourable, after which heterosis declines. If high levels of outcrossing evolve during this window, the remaining deleterious alleles may be masked, ensuring a more lasting disadvantage of selfing. Alternatively, heterosis may be depleted before outcrossing mutations reach high frequencies, returning the populations to a highly selfing equilibrium. The final effects of secondary contact are thus unclear, and they require an explicit population genetic model.
To investigate the conditions under which heterosis may allow greater outcrossing to evolve from predominant selfing, we simulated the invasion of a modifier mutation that increases the rate of outcrossing in a pair of completely selfing populations that have recently come into secondary contact. Our results verify that local drift load initially favours outcrossing, but they also show that in most cases, this advantage is lost too quickly for an outcrossing allele to fix. The benefit of an outcrossing mutation depletes so quickly that only unrealistically great levels of initial heterosis are sufficient to propel it to fixation with any regularity. We find that even these demanding conditions were very generous compared to those in several more realistic variant scenarios, suggesting that secondary contact should rarely result in a reversion to outcrossing. Heterosis alone may never be sufficient. If heterosis contributes to reversions to outcrossing, it is likely only in conjunction with additional advantages of outcrossing such as unpurged inbreeding depression.
2 MODEL
We first outline the general structure of the model, then use a simple version of the model to derive the invasion condition for an outcrossing allele analytically and finally describe in detail the specific simulation steps for the main study. All simulations and numerical iterations were performed using custom R scripts (provided as Supporting Information; R Core Team, 2016).
2.1 General model description
2.1.1 Population history
We began with two selfing populations generated perhaps by a vicariance event that split an ancestral population in half. The two populations’ highly selfing mating system could have been inherited from their common ancestor or it could have evolved in both populations after they split. We assume that each of these parental populations had been selfing long enough to become monomorphic, with unique sets of fixed alleles at L total viability loci. Any differences in the frequencies of deleterious alleles can contribute to heterosis (Whitlock et al., 2000), but we focus on the conceptually simple extreme case of fixation versus absence. One population possessed the inferior allele at LA viability loci, whereas the other population possessed the inferior allele at the remaining LB loci (LA + LB = L). Such a pattern could be caused by unique beneficial mutations fixed by selection in each population (in which case the superior alleles are derived) or by unique deleterious mutations fixed by chance in each population (in which case the inferior alleles are derived). The same pattern could also be caused by alternative fixation of segregating alleles in each population, either because the inferior allele fixed by chance in one population or, perhaps more realistically, the currently inferior allele was temporarily superior in one population's local environment. Whatever the populations’ historical environments were, we assume that they currently occupy identical environments in which one allele is unambiguously superior. However realistic monomorphism may be, it is convenient for isolating the effects of heterosis because fixed differences only contribute to heterosis, whereas segregating deleterious recessives at different frequencies would contribute both to heterosis and to inbreeding depression. We consider segregating alleles separately in a variant model.
The two parental populations then came into secondary contact, forming a daughter population composed of NA individuals from one of the contributing populations and NB individuals from the other (NA + NB = N). In the most general case, we assume that, each generation, a fraction ν of seeds produced by residents in the daughter population were replaced by seed migrants drawn equally from the two parental populations. However, we assume in our focal case (described later) that the daughter population is formed by a single event and receives no additional migrants thereafter (ν = 0). Any F1 individuals produced by outcrossing within the daughter population would be heterozygous at all loci at which their parents were fixed for divergent alleles.
Our model describes evolution from the time of secondary contact onwards. Selection acts directly on viability and indirectly on mating system, which determines the viability of offspring. Selfing confers a transmission advantage (Fisher, 1941), whereas outcrossing confers the potential advantage of producing heterozygous offspring. Viability selection was chosen so that selection would occur after mating, and so the modifier's effects on progeny genotypes would be exposed to selection in a single generation. This allows us to use the change in allele frequency between two consecutive generations of adult cohorts as an invasion criterion because it reflects the effects of both offspring fitness and transmission advantage. The inferior alleles must be at least partially recessive to cause heterosis, and we assumed them to be completely recessive for convenience. If the deleterious alleles were only partially recessive, heterosis would decrease because they would be only partially masked, and they would also be more rapidly removed by selection. Deleterious alleles, especially strongly deleterious ones, also tend to be more recessive in nature (Caballero & Keightley, 1994; Mackay, Lyman, & Jackson, 1992). Thus, in our model, each inferior allele was recessive and conferred a viability of 1 − s, where s is the selection coefficient against any inferior allele. Viability was multiplicative across loci, so an individual had fitness (1 − s)l, where l is the number of loci at which the individual was homozygous for the inferior allele. Fitness effects at multiple loci are multiplicative if the loci have independent effects on the probability of survival or reproduction (Charlesworth & Charlesworth, 2010, p. 166). However, we assumed viability selection to be soft so that the population size remained constant whatever the average viability was. Strictly speaking, therefore, the viability calculated from the product of viability effects across loci was not itself the survival probability, which was determined by the viability relative to competing genotypes under soft selection. It can nevertheless be imagined as some trait which is the sole basis of viability selection.
2.1.2 Mating system
We considered a rare outcrossing allele, M, at a modifier locus unlinked to any of the L viability loci under direct selection. The outcrossing allele is initially rare because it could not have been maintained at high frequency in the purged ancestral populations, although recurrent mutation could have kept it at a low-frequency mutation–selection balance. The common selfing allele at this locus is denoted m. We assume throughout that mm homozygotes are completely selfing and that MM homozygotes are completely outcrossing, but we consider both additive and dominant versions of M. An outcrossing allele of large effect maximizes the probability that outcrossing will take place, whereas a more biologically realistic small-effect allele would require many additional simulations in which the outcrossing phenotype was never expressed. The outcrossing phenotype we modelled best corresponds to a morphological trait that prevents self-pollination, rather than to self-incompatibility, because it caused random rather than disassortative mating. In the terminology of Lloyd (1992), seed discounting was complete: every selfed seed came at an opportunity cost of not producing one outcrossed seed. Of the different modes of selfing Lloyd (1992) defined, ours was similar to prior selfing in that the fraction of ovules selfed was independent of the supplies of self and outcross pollen. However, each of Lloyd's modes of selfing assumed a limited supply of ovules for each dam, whereas ours did not.
The modifier genotype only controlled mating, and it had no direct effect on viability or fecundity. Therefore, selfing in our model lacked the advantage of reproductive assurance Lloyd (1992) and the disadvantage of pollen discounting (Holsinger, Feldman, & Christiansen, 1984; Lloyd, 1992; Nagylaki, 1976). Our model does have Fisher's (1941) automatic advantage of selfing: self-fertilization transmits more gametes than outcrossing because the additional siring success on selfed ovules does not detract from outcross siring success.
2.2 Invasion condition
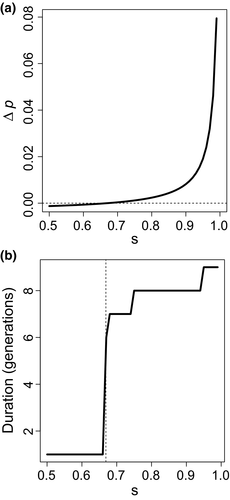
We analytically obtained the condition under which an outcrossing allele was expected to increase in frequency initially, for a simple case of the model. The population size was infinite, and there was no ongoing migration (ν = 0). The genome consisted of three unlinked loci: one modifier locus controlling the outcrossing rate and two viability loci. The daughter population initially had equal frequencies of the two parental genotypes: homozygous for the superior allele at one viability locus and for the inferior allele at the other viability locus. Thus, all individuals initially had fitness 1 − s. The Appendix contains the invasion condition (Inequality 1) and its derivation. Essentially, the selfing allele m always increases in frequency in the seed pool before selection because of its transmission advantage. For the outcrossing allele M to increase in frequency by the next generation, M-carrying offspring must have sufficiently greater average viability such that m decreases in frequency among adults despite having increased in frequency among seeds. However, numerical iteration showed that, at least in the deterministic case, two viability loci were too few to allow M to reach fixation even for extremely large s (Figure 1). In contrast, recombination would take longer to break up the repulsion-phase linkage disequilibrium among greater numbers of loci, which could delay the purging of the load. We therefore proceeded to a model that could accommodate more viability loci.
2.3 Simulation model
We used a simulation model to investigate the dynamics and fixation probability of the outcrossing allele. In contrast to deterministic numerical iteration, stochastic simulations allowed us to identify trajectories that differed from the expected outcome. We were interested in possible transitions to greater outcrossing rates even if outcrossing was not a guaranteed consequence of initial heterosis. In particular, we investigated whether increased outcrossing was substantially more probable with more initial heterosis, using simulations to estimate the probability of fixation of a new mutation that increases outcrossing. Additionally, simulations allowed us to incorporate the disadvantages of reduced recombination (and thus of selfing) caused by stochasticity in the haplotypes that are produced and survive (Hill & Robertson, 1966; Muller, 1964). These stochastic effects could play a major role in the evolution of outcrossing. We conducted these simulations under multiple models of the magnitude and genetic architecture of heterosis, and of population history. Our simulation model was identical to the analytic model used above to obtain the invasion condition, except that we simulated with finite population size and more than two viability loci, which were not necessarily unlinked.
2.3.1 Genetic architecture
We assumed that the viability loci were evenly spaced along nchrom chromosomes. Each chromosome except the first carried the same number of loci. The first chromosome took the remainder if the number of loci was not divisible by the number of chromosomes. In each region between viability loci, recombination occurred with probability r independently of recombination elsewhere in the genome. Viability loci on separate chromosomes assorted independently. The relative positions of the superior alleles allotted to each genotype were randomized at the beginning of each simulation. We neglected ongoing mutation during the invasion process because it would be dwarfed by the heterosis built up before contact. Instead, the only mutation was the original one giving rise to the outcrossing allele M at frequency 1/2N in a population composed of N diploid individuals. The outcrossing modifier locus was unlinked to any of the viability loci.
2.3.2 Mating
Each generation, we created a seed pool 10 times as large as the number of adults in the daughter population (i.e., 10N). For each seed to be generated, a dam was chosen at random to outcross or self with a probability determined by its genotype at the modifier locus. If the dam selfed, it was also the sire. If the dam outcrossed, a sire was chosen at random from the population. One offspring was then produced as the product of a recombinant gamete from each parent.
2.3.3 Selection
Soft viability selection among seeds generated the next adult generation. Such a scenario is similar to competition among seeds or seedlings in a small plot: although all individuals would be physically capable of survival on their own, competition eliminates the worse competitors. Ten per cent of seeds were sampled without replacement to survive to adulthood, so that each generation had N adults. Seed i's probability of being sampled was weighted by its viability,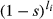 
, where s is the selection coefficient at each viability locus, and li is the number of viability loci homozygous for the inferior allele in individual i. Because we assumed viability selection in the deterministic model, we also assumed viability selection in the simulation so that we could fairly compare their results.
2.3.4 Duration
Each simulation was terminated when the outcrossing allele reached fixation, when the selfing allele reached fixation, or when 1,000 generations had passed, whichever came first. We found that 1,000 generations were usually more than sufficient to allow the outcrossing allele to run its course to fixation or extinction in preliminary simulations. If a parameter combination resulted in one or more simulations that failed to reach fixation or loss of the outcrossing allele before 1,000 generations had passed, all simulations for that parameter combination were discarded. Two parameter combinations (s = 0.1, r = 0.5, LA = LB = 50 and s = 0.7, r = 0.1, LA = LB = 14) were discarded, and all simulations for these parameter combinations were rerun.
2.3.5 Constant parameters
We held some parameters constant for all simulations. We chose a small population size of N = 100 because the simulation scaled poorly with N, but we compensated by performing enough replicates to observe the diversity of outcomes. We chose 2,000 trials per parameter combination so that a new neutral mutation would fix 10 times on average, allowing us to observe deviations below this expectation. Fixations of M more or less frequent than the neutral expectation imply positive or negative selection on M, respectively.
2.3.6 Simulation scenarios
Our primary question is whether heterosis can allow outcrossing to evolve. Because the answer seemed to be “no” in most cases, as we detail below, we pushed our simulation efforts towards parameters chosen to be generally favourable to outcrossing even if they strained the boundaries of realism. We call the scenario using this set of parameters the focal scenario and devote most of our description to it. But in order to extend our conclusions to more realistic scenarios, we also conducted additional tests. Some were expected to be more favourable to outcrossing than the focal scenario, whereas others were expected to be less favourable.
We assumed equal sizes of the parent populations in the focal scenario (NA = NB = 50). This postponed the eventual loss of either genotype, an outcome that would eliminate the advantage of outcrossing. In follow-up Test 1, we relaxed this assumption and examined population size ratios of 1:9, 1:4, 3:7, and 2:3 (NA ≠ NB), and 1:1 (NA = NB), all with total population size N = 100. We distinguished cases where M arose on the rarer or the more common background. For this test, we assumed M was dominant, nchrom = 2, r = 0.5, s = 0.1 and LA = LB = 5, 25 or 50.
We assumed equal fitnesses of the two parental genotypes in the focal scenario so that neither could simply outcompete the other before M had a chance to invade. We therefore set the number of loci with deleterious alleles to be the same in the two parental populations, LA = LB, and varied this number from 5 to 50 in increments of 1. In follow-up Test 2, we allowed the populations to have unequal numbers of fixed deleterious alleles. We examined LA: LB ratios of 1:9, 1:4, 3:7, and 2:3 (LA ≠ LB), and 1:1 (LA = LB). For this test, we assumed M was dominant, nchrom = 2, r = 0.5, s = 0.1 and NA = NB = 50.
The focal scenario assumed that there was no ongoing migration after formation of the daughter population (ν = 0). We thought this could favour outcrossing because M would not be swamped out by migration. However, it is also possible that migration of inferior parental genotypes could regenerate the segregating load and thus the advantage of outcrossing. In follow-up Test 3, we allowed the initial parental populations to continue to contribute migrant seeds to the focal daughter population (ν = 0). We varied the migration rate ν from 0.1 to 0.5 in increments of 0.1. We further set LA = LB = 25 and s = 0.3 because these parameters resulted in an intermediate fixation probability in the focal case, and we assumed M was dominant, nchrom = 2, r = 0.5 and NA = NB = 50.
At the modifier locus, we set M to be completely dominant in the focal scenario. This ensured that the outcrossing allele was expressed even when rare. In follow-up Test 4, we instead made the outcrossing allele additive. In this test, ovules from Mm dams were equally likely to be selfed or outcrossed. The other parameters in this test were nchrom = 2, r = 0.5, s = 0.3, NA = NB = 50 and LA = LB = 5, 25 or 50.
The central conceit of the focal scenario was that the load was oligogenic, with few enough loci that all were either unlinked or only loosely linked. The parameters chosen to represent this scenario were a small (s = 10−5, 10−4, 10−3 and 10−2) or large (s = 0.1–0.9 in increments of 0.1) selection coefficient for all loci, LA = LB = 5–50 viability loci in increments of 1 and a recombination frequency of r = 0.5 or 0.1. We examined large selection coefficients because they produced large magnitudes of initial heterosis, favouring outcrossing. But in nature, such strongly deleterious alleles could not have fixed in the first place. Large levels of local drift load would only be plausible if composed of many alleles of small effect. In follow-up Test 5, we considered more polygenic heterosis. In this test, we assumed a large number of individually weakly deleterious alleles, LA = LB = 2,500 and s = 10−5 or 10−3. With this many loci, many of them would certainly be tightly linked in nature, so we lowered the value of r. We set nchrom = 10 chromosomes and r = 0.002, which gave each chromosome of 500 loci a map length slightly <1 morgan (slightly less because there were only 499 inter-locus regions with a 1/500 recombination probability each). The other parameters were NA = NB = 50 and dominant M.
We assumed in the focal model that all deleterious alleles in the ancestral populations had either been purged or fixed. This idealized endpoint of the purging process generated substantial heterosis from the large differences in allele frequencies but also eliminated inbreeding depression in the ancestral populations. However, purging need not be complete in nature, and inbreeding depression may contribute more to the evolution of outcrossing than heterosis does. In follow-up Test 6, we allowed the ancestral populations to retain some unpurged inbreeding depression. In each ancestral population, 25 loci were segregating for a low-frequency inferior allele and a high-frequency superior allele. Each ancestral population was segregating for different loci: the 25 loci segregating in one population were fixed for the superior allele in the other. Each individual in the first generation was homozygous for the inferior allele at 5 loci randomly selected out of the 25 segregating loci in the ancestral population from which that individual originated. These segregating alleles only affected the initial genotype composition of the daughter population, and the ancestral populations were not tracked afterwards. The selection coefficient against each deleterious allele was 0.14. Collectively, these parameters result in an inbreeding depression of approximately 0.46 within each parental population, equal to the level of unpurged inbreeding depression that Willis (1999) found to remain after artificial inbreeding of Mimulus. For this test, we varied the total number of viability loci diverging between the ancestral populations (including the 25 segregating sites plus additional fixed sites) from 25 (all segregating) to 50 (half segregating, half fixed). The fixed sites functioned identically to those in the focal scenario. For each parameter combination in this test, we ran a control in which the 25 segregating sites were replaced with 25 fixed differences.
2.3.7 Model outputs
For each parameter combination, we recorded the proportion of simulations resulting in the fixation of the outcrossing allele. This was our estimate of the fixation probability. For the subset of parameter combinations in which s = 0.3 and LA = LB = 5, 25 or 50, we ran an additional 2,000 trials per parameter combination to track the outcrossing allele frequency through time, as well as recording the population mean fitness and the duration of the simulation in generations. Previous simulations showed these parameter combinations to result in a wide range of fixation proportions. We also tracked the dynamics for Test 4, with an additive outcrossing allele. We did not track evolution in the ancestral populations, so heterosis between them could not evolve. However, inbreeding depression in the daughter population did evolve, and, much like heterosis, this metric captured the advantage of crossing with unlike genotypes. In a sense, the initial heterosis between parental populations was converted to inbreeding depression by introducing segregating deleterious recessives into the daughter population. We therefore tracked inbreeding depression in the daughter population through time, along with duration and mean fitness, for a new set of simulations with s = 0.3, LA = LB = 5, 25 or 50, and a dominant outcrossing allele. Inbreeding depression was estimated each generation by generating 5,000 selfed and 5,000 outcrossed offspring from random dams irrespective of modifier genotype, calculating the mean fitness of these two sets of offspring and substituting the resulting fitnesses into the formula for inbreeding depression, δ = 1 − wi/wo, where wi and wo are the mean fitness of inbred (selfed) and outcrossed offspring.
3 RESULTS
We first briefly report results for the deterministic model. Then, we report the main results from our focal simulation model, including both fixation probabilities and transient dynamics. We conclude with results from our follow-up tests of more general model assumptions.
3.1 Outcrossing mutation never fixed in a three-locus deterministic model
Our analysis of the invasion condition (Inequality 1) showed that the outcrossing allele, M, was expected to increase in frequency when the selection coefficient, s, was slightly below 0.67 for an initial frequency of M of 0.005. The threshold for s approached 2/3 as the frequency of M approached zero. This result comports with the 1/2 inbreeding depression threshold calculated by Kimura (1959) because inbreeding depression is 1/2 when the two initial genotypes are at equal frequencies and s = 2/3. Numerical iteration for a single generation confirmed that M was lost in a single generation below the threshold and was lost after six or more generations above it (Figure 1). Thus, the outcrossing allele never fixed in the deterministic model.
3.2 Outcrossing mutation could fix under restricted circumstances in stochastic simulations
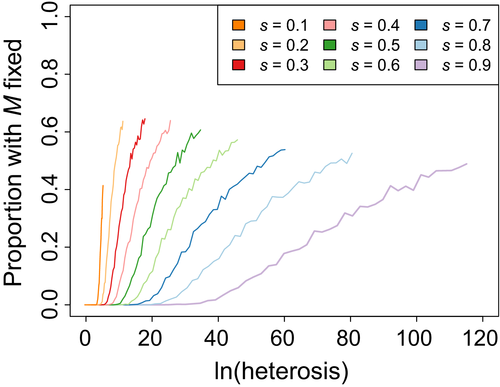
A rare outcrossing mutation fixed in some of the simulations (Figure 2). For many parameter combinations we considered, the mutation fixed more often than the expectation (0.005) for a neutral allele. However, M never fixed when L ≤ 100 for the small coefficients of s < 0.1. All further results for the focal scenario are reported for s ≥ 0.1 (results for Test 5, in which s < 0.1 but L = 5,000, are reported later). Across all of parameter space that we examined, the outcrossing allele only fixed more often than the neutral expectation when the F1s had a fitness of at least 29.12 times that of individuals in either parental population, which translates to an initial heterosis of 2812%. The outcrossing allele fixed when many loci were under selection and/or when there was strong selection at each locus.
3.3 Intermediate selection favoured outcrossing
The fixation proportion was greater for larger values of the selection coefficient, s, than for the smallest values (Figure 2). However, the relationship was not monotonic. Fixation proportion increased sharply going from s = 0.1 to s = 0.2. Fixation proportion reached a maximum somewhere in the range from s = 0.2 to 0.4, but the exact value depended on the number of viability loci. At LA = LB = 50, fixation was maximized at s = 0.3.
3.4 No effect of loose linkage
There was no qualitative difference between the results of simulations with free recombination between viability loci (r = 0.5) and those with reduced recombination (r = 0.1; Figure 2). The outcrossing allele fixed more often than the neutral expectation in five more parameter combinations when r = 0.1 (303 parameter combinations) than when r = 0.5 (298 parameter combinations). The maximum difference in fixation proportion for any parameter combination was 0.06. The maximum fixation proportions were 0.6545 and 0.6455 for r = 0.1 and r = 0.5, respectively. Differences showed no consistent pattern with respect to s or L. All further results of the focal scenario are reported for r = 0.5.
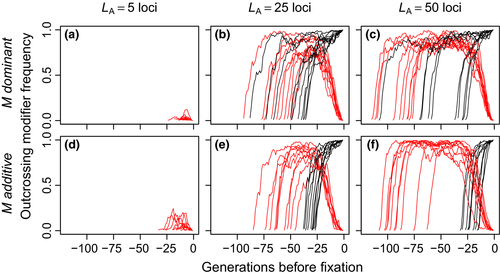
3.5 Outcrossing was sometimes lost after initially invading
The outcrossing allele, M, often ultimately went extinct even when it initially increased in frequency (Figure 3). There was a qualitative difference between parameter combinations in which M sometimes fixed and those in which it never fixed. In parameter combinations in which M never fixed, the initial increase in frequency was much smaller (Figure 3, left column). Loss was rapid when it occurred, regardless of the frequency of M before the decrease in frequency began.
3.6 Ultimate mean fitness and time to extinction were bimodal
All simulation durations and final mean fitnesses are summarized in Supporting Information Figures S1–S3 and Figure 4. Simulations resulting in fixation of M most often ended with high but not maximal mean population fitness. Simulations resulting in loss of M showed a bimodal pattern, with the largest number eventually ending with very high fitness and a smaller number rapidly ending with very low fitness (Figure 4). The shortest and longest runs resulted in extinction of M, whereas runs resulting in fixation lasted an intermediate duration (Figure 4). Purging was more complete in the longer runs than in the shorter ones (Supporting Information Figure S4): the mean of the final mean fitnesses of all simulations with LA = LB = 50 was 0.81, while the mean for the subset with below-average duration was 0.69. The modal duration was one generation for all six of the parameter combinations that were tracked through time (s = 0.3, LA = LB = 5, 25 or 50, dominant or additive M). Two parameter combinations were exceptions to the general pattern. At LA = LB = 5, no fixations were observed and the ultimate fitness had one mode concentrated near zero (Supporting Information Figure S1), and in the additive model with LA = LB = 50, most extinctions of M were rapid (Supporting Information Figure S3).
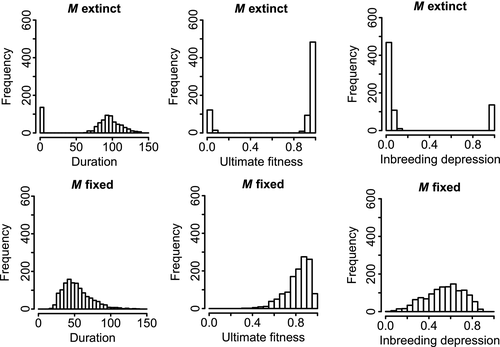
3.7 Purging was incomplete when the outcrossing allele fixed
Inbreeding depression was gradually purged in all simulations but to a lesser degree in simulations in which the outcrossing allele reached fixation (Figure 4). In contrast, purging was often nearly complete when the outcrossing allele was lost. There was no obvious difference in the rate of purging between runs in which M fixed and those in which it was lost, assuming the same parameter values (Supporting Information Figure S5). However, runs in which M was destined to fix were shorter and thus had less time to purge.
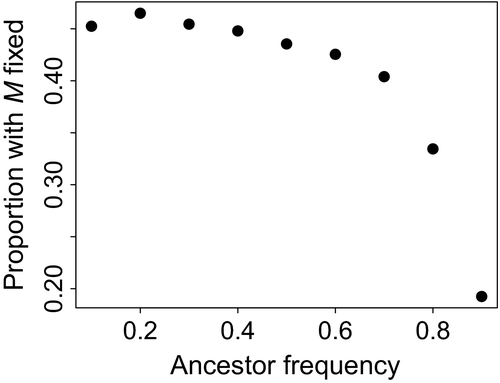
3.8 Test 1: Rare genetic background favoured outcrossing mutation
We initially assumed that the two parental populations contributed exactly the same number of individuals to the daughter population. The frequencies of the two initial genotypes determined the probability of an F1 cross because outcross matings were at random, and we varied those initial frequencies partly to determine the effect of this probability. Compared to when the initial genotypes were at equal frequencies, the outcrossing allele fixed slightly more often when it arose on the rarer background, but much less often when it arose on a very common background (Figure 5). However, this effect was only visible when there were many viability loci (LA = LB = 50) because no fixations occurred at LA = LB = 5 or 25 when s = 0.1.
3.9 Test 2: Unequal fitness reduced fixation proportion
The assumption that individuals from the two parent populations were of equal fitness conveniently prevented one from simply outcompeting the other before mating system could change. We relaxed this assumption to test whether it was essential for outcrossing to evolve. For a given total load, the fixation proportion was greater when the two initial genotypes carried equal numbers of deleterious alleles (LA = LB) than when one genotype carried more (LA ≠ LB) (Supporting Information Figure S6). In many cases, smaller but more equal numbers of deleterious alleles per population resulted in a greater fixation proportion: for example, LA = LB = 35 (0.4555 fixation proportion) vs. LA = 30, LB = 45 (0.4255 fixation proportion).
3.10 Test 3: Continuous migration reduced fixation proportion
Continuous migration of less fit genotypes from the parent populations into the daughter population could swamp out M or slow the purging process but was not modelled in the focal case. We therefore tested its effects by increasing the migration rate, ν. When ν > 0, the fixation proportion was always lower than when ν = 0, and it generally decreased as ν increased. The fixation proportions were 0.1855 (ν = 0.0), 0.1655 (ν = 0.1), 0.1565 (ν = 0.2), 0.1510 (ν = 0.3), 0.1515 (ν = 0.4) and 0.1300 (ν = 0.5).
3.11 Test 4: Additive modifiers fixed more often
When dominant outcrossing alleles invaded, they often segregated at high frequencies and then declined to extinction instead of reaching fixation (Figure 3). We tested whether this pattern was due to dominance. Compared to dominant outcrossing alleles, alleles that additively increased the outcrossing rate did not slow their invasion at high frequencies before reaching fixation. Such additive alleles spent less time segregating, and their allele frequency trajectory less often reversed direction. This resulted in an increased fixation probability for additive alleles. At LA = LB = 5, M never fixed. At LA = LB = 25, M fixed in 343 (M dominant) or 598 (M additive) of 2,000 trials. At LA = LB = 50, M fixed in 1,292 (M dominant) or 1,599 (M additive) of 2,000 trials.
3.12 Test 5: Polygenicity was insufficient to favour outcrossing under reasonable parameters
In the focal scenario, the outcrossing allele fixed more often when the ancestral populations differed by many fixed viability loci. Holding the selection coefficient constant, the fixation proportion generally increased with the number of viability loci (Figure 2). Fixation was maximized at the greatest number of viability loci modelled (LA = LB = 50). This effect was not due simply to initial heterosis being stronger with more loci, though. The outcrossing allele fixed more often under a polygenic initial heterosis than an oligogenic initial heterosis of comparable magnitude (Figure 6). Based on this observation, we tested whether more reasonable loads could favour outcrossing if they were even more polygenic. However, the effect of polygenicity was not sufficient to favour M unless the total magnitude of initial heterosis was also extremely large. The highly polygenic loads (L = 2,500) resulted in either no fixations of M for a small selection coefficient (s = 10−5) or a fixation proportion of 0.006 for a larger selection coefficient (s = 10−3).
3.13 Test 6: Unpurged inbreeding depression was more favourable to outcrossing than local drift load
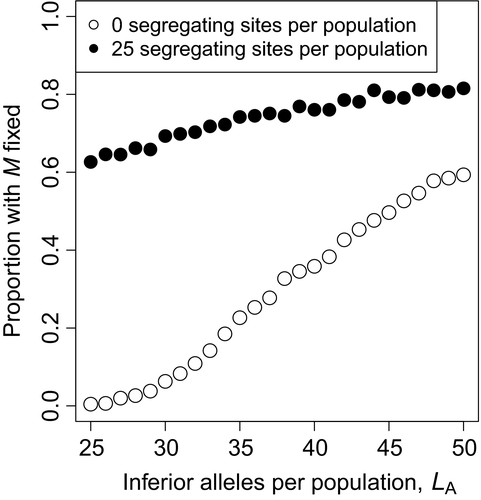
We assumed in the focal scenario that all deleterious alleles had reached fixation or loss in the purged ancestral populations. In this test, we instead assumed that 25 loci in each ancestral population retained a low-frequency segregating deleterious allele unique to that population. The fixation probability was greater when there were both fixed and segregating differences than in controls in which all differences were fixed (Figure 7). The difference in fixation proportion was greatest when there were few total diverging sites (0.6265 with 25 segregating sites per population; 0.0045 with 25 pairs of fixed differences per population) and decreased as the total number of diverging sites increased (0.6265 with 25 segregating sites and 25 fixed differences per population; 0.5935 with 50 fixed differences per population).
4 DISCUSSION
When two previously selfing populations come into secondary contact, initial heterosis is immediately favourable to outcrossing. We find that an allele that confers complete outcrossing invades an otherwise completely selfing population and rapidly reaches a moderate frequency for many parameter combinations. We further find, however, that the initial allele frequency differentiation underlying heterosis is eventually eliminated by selection among the now-segregating alleles. This loss of heterosis removes the advantage of outcrossing. The outcrossing mutation is then usually lost, and only for extremely large initial heterosis can it reach fixation before it becomes obsolete. Even when selfing ultimately prevails, the bout of recombination in the outcrossed hybrids and backcrosses sorts the superior alleles from each population to produce fit new haplotypes. Secondary contact thus promotes a transient increase in outcrossing, followed by removal of inferior alleles originally fixed in the donor populations, an increase in population mean fitness and finally a return to selfing. In this sense, adaptive introgression of superior alleles from each population is parallel to purging of inbreeding depression within a population with respect to its effects on the advantage of outcrossing.
Although some parameter combinations allowed the outcrossing allele to fix more often than expected by chance, it was still often rapidly lost after reaching high frequencies (red lines in Figure 3, middle and right columns). This is because recombination in outcrossed individuals generated lightly loaded haplotypes that suffered less from selfing. These haplotypes were introduced into the selfing subset of the population because individuals heterozygous for the outcrossing allele produced some seeds homozygous for the selfing allele when they received pollen carrying the selfing allele. Competition between the less and more heavily loaded selfing haplotypes resulted in purging and an increase in the mean fitness of selfed offspring. That is, selfing generated linkage disequilibrium between the selfing allele and high-fitness haplotypes, in a manner similar to the way in which the “reduction principle” (Feldman & Liberman, 1986) favours alleles that decrease the recombination rate because they generate LD with high-fitness haplotypes.
4.1 Implications for mating system evolution
The smallest initial heterosis that allowed the outcrossing allele to fix more often than the neutral expectation was 2812%, a level almost 40-fold larger than the highest heterosis we found in the literature (73.6% heterosis in a self-compatible population of Leavenworthia alabamica; Busch, 2006) and over 60-fold larger than the 42.6% heterosis for total survival documented in Scabiosa columbaria (van Treuren, Bijlsma, Ouborg, & van Delden, 1993). The extent of initial heterosis required for the adaptive fixation of an outcrossing allele not only surpasses levels observed to date, but also likely exceeds any theoretically reasonable level. Surprisingly, we find more frequent fixation at intermediate selection coefficients than at larger ones (Figure 2a,b). The transition from a positive to a negative effect of s on the fixation probability may be because purging was ineffective in the lower range of s. Glémin (2003) showed that purging by nonrandom mating is mostly ineffective below a population size threshold on the order of N = 10/s. For the smallest selection coefficients in our focal model, the population size of N = 100 is right in the vicinity of this threshold. Below the threshold, more deleterious alleles should increase the magnitude of initial heterosis without being exposed to purging. Above the threshold, more deleterious alleles are more effectively purged, and the advantage of outcrossing is reduced.
However, the coefficients at which the fixation probability is maximized (s ≈ 0.3) are unrealistically large. Even a disadvantage for a given deleterious allele of s = 0.1 is large enough that its fixation would be effectively impossible in nature. Polygenic loads did favour outcrossing more than oligogenic loads of equal magnitude (Figure 6). A possible explanation is that, since it takes more generations for recombination to unite the best alleles at many loci, purging will be impeded and outcrossing will remain advantageous for longer. However, polygenicity does not appear to be a sufficient substitute for strong per-locus selection: 2,500 unique fixed deleterious alleles per population with s = 10−3 only resulted in a fixation proportion of 0.006, and the same number of alleles with s = 10−5 resulted in no fixations of the outcrossing allele. The rarity of permanent selfing-to-outcrossing transitions, despite the possibility of secondary contact, can thus be attributed partly to the transience of heterosis.
The transience of heterosis is well known, though we did not initially appreciate what a strong barrier it would be to the evolution of outcrossing. Like inbreeding depression, heterosis becomes more depleted the more it is exposed. The equilibrium level of heterosis is lower when migration is greater because migration eliminates the allele frequency differences underlying heterosis (Whitlock et al., 2000). That is, gene flow depletes heterosis and with it the advantage of outcrossing. In fact, deleterious mutations accelerate genetic homogenization. This is because they provide a relative advantage to superior alleles from the other population, thereby increasing the frequency of migrant alleles through selection and thus increasing the effective migration rate through adaptive introgression (Bierne, Lenormand, Bonhomme, & David, 2002). We only modelled gene flow from the ancestral populations into a focal population, not between the ancestral populations themselves. In nature, however, superior alleles could adaptively introgress between the ancestral populations, further reducing heterosis.
But even transient increases in outcrossing rate could affect the distribution of mating systems in the biota. Despite the theoretical prediction that outcrossing rate should be bimodal (Lande & Schemske, 1985; Schemske & Lande, 1985), a substantial fraction of species examined are estimated to outcross at intermediate rates: so-called mixed-mating species (Goodwillie, Kalisz, & Eckert, 2005). Mixed mating has been interpreted as either a stable equilibrium or as a transient step in the trajectory from predominant outcrossing to selfing (Igić & Busch, 2013). Our model suggests a third possibility: mixed mating as a temporary hiatus from predominant selfing. It was not unusual for an outcrossing allele to segregate for over a hundred generations in our model. This is certainly short on a macroevolutionary timescale, but it could produce a constantly rotating class of mixed-mating populations. If so, populations in which mixed mating is observed should have a recent history of secondary contact. Furthermore, assuming secondary contact occurs on a per-population basis rather than species-wide, species with mixed-mating populations should also contain predominantly selfing populations that have not undergone secondary contact.
4.2 Robustness of model conclusions
Our focal scenario was designed to be very favourable to outcrossing. If outcrossing cannot evolve in this case, it cannot evolve under more stringent and realistic conditions. But since we had no reason to believe that the focal scenario was absolutely optimal for the evolution of outcrossing, we had to examine variants directly. We therefore relaxed the focal case's assumptions (equal initial genotype frequencies, equal initial genotype fitnesses, no continuous migration, a dominant outcrossing mutation, an oligogenic load and completely purged ancestral populations) one by one. First, the outcrossing allele fixed more often when it arose on an uncommon genetic background (Figure 5), which could represent an outcrossing individual that arrived in a selfing population through a rare migration event. Second, the outcrossing allele fixed much less often when the two initial genotypes had unequal fitnesses, likely because the fitter haplotype was able to outcompete the less fit before the outcrossing allele could fix. Third, continuous migration from selfing donor populations slightly reduced the fixation probability for the outcrossing allele, possibly because migrant selfing alleles swamped out the mutation. Fourth, an additive outcrossing mutation was more likely to fix than a dominant one because its competitor, the selfing allele, was not masked when the additive outcrossing allele reached high frequencies. Fifth, polygenicity increased the fixation probability, but weakly deleterious fixed differences did not greatly favour outcrossing even if there were many of them. Sixth, segregating deleterious alleles underlying unpurged inbreeding depression favoured outcrossing much more than did an equal number of fixed differences between populations.
A major point of departure between our model and others was that we assumed that heterosis had long accumulated in allopatry but was re-exposed en masse upon secondary contact. Other models of the evolution of heterosis (Bierne et al., 2002; Whitlock et al., 2000) or mating system (Theodorou & Couvet, 2002) assume some level of continuous migration. Sudden secondary contact is more favourable to outcrossing in some ways but less favourable in others. If migration is continuous, heterosis is limited by the amount of drift load that can stably persist in mutation-selection-migration-drift balance (Whitlock et al., 2000), whereas upon secondary contact after isolation, heterosis could start at a large but unstable level. Even our model of continuous migration assumed that heterosis began at an unstably high level, implying that migration only became continuous after a long initial period of isolation. Our model of unequal starting frequencies of the ancestral genotypes, however, showed that the outcrossing allele benefited slightly from being on a rare background. It seems that a small finite pulse of migration after long isolation combines the best of both worlds: the migrants can reap substantial heterosis from crossing with the residents, but since the deleterious alleles that the migrants bring are rare in the population, there is a more stable benefit for the migrants’ descendants to continue outcrossing.
In the focal scenario, we assumed that the highly inbred mating systems of the parent populations would have eliminated the genetic variation underlying inbreeding depression. In nature, however, moderately or even highly selfing populations show inbreeding depression (Winn et al., 2011), which may sometimes be large (Herlihy & Eckert, 2002, 2004). We found that the outcrossing mutation fixed far more often when there was unpurged inbreeding depression than when there was only local drift load composed of fixed differences (Figure 7). This was likely because the main advantage of heterosis occurs in the first generation, when there is an opportunity to mask common recessive inferior alleles with dominant superior alleles from the other ancestral population. However, since these recessive deleterious alleles continue to be masked, they remain relatively common. Carriers for these alleles now receive relatively little advantage from outcrossing because a random mate is also likely to be a carrier. This contrasts with the architecture of inbreeding depression in which, since each deleterious allele is at low frequency, a random mate is unlikely to carry another copy. So long as it remains unpurged, inbreeding depression therefore provides a more lasting advantage to outcrossing. Heterosis may contribute to the advantage of outcrossing, but its effect seems to be marginal compared to that of inbreeding depression.
Inbreeding depression can remain unpurged if individual deleterious alleles have weak enough effects to escape selection even after selfing exposes them (Charlesworth, Morgan, & Charlesworth, 1990). Also, inferior recessive alleles at loci in repulsion-phase linkage disequilibrium (pseudo-overdominance) resist purging because the superior double homozygote cannot be generated until the linkage disequilibrium is broken by recombination (Charlesworth & Willis, 2009). An outcrossing population of Mimulus guttatus retained most of its inbreeding depression (0.46 remaining of 0.57 initial) for lifetime fitness from germination to gamete production after five generations of artificially enforced selfing (Willis, 1999). We used this magnitude estimate in our test of unpurged inbreeding depression. The oligogenic architecture we used (25 strongly deleterious loci, s = 0.14) likely could not have survived purging in the first place, but it does illustrate the essential difference between genetic loads composed of low- versus high-frequency alleles. It should also be kept in mind that this large magnitude of inbreeding depression is close to the 0.5 threshold above which outcrossing is favoured (Kimura, 1959) if inbreeding depression is static (but see Holsinger, 1988). Some outcrossing populations like the one used for this example may retain so much unpurgeable inbreeding depression that, even if they underwent purging, they would not evolve towards predominant selfing. Comparisons among species, among populations and among families within populations sometimes showed a negative relationship between selfing rate and inbreeding depression but showed no consistent overall pattern in one meta-analysis (Byers & Waller, 1999). However, a subsequent meta-analysis focusing on experimental inbreeding studies did find reduction in inbreeding depression (Crnokrak & Barrett, 2002). Overall, it appears that predominantly inbreeding populations have purged much of their inbreeding depression (which therefore cannot contribute to a reversion), but mixed-mating populations have retained it (Winn et al., 2011).
Although we considered some variant models, we have not been exhaustive. The omission that most plausibly could favour a reversion is pollen discounting: a decrease in pollen success associated with a selfing phenotype. Greater pollen discounting reduces the transmission advantage, and complete pollen discounting totally eliminates it (Nagylaki, 1976). Furthermore, since pollen discounting is simply a physical side effect of a particular selfing phenotype, it is not dependent on genotype frequencies. Therefore, unlike heterosis, it will not be depleted by selection. We suspect our model without pollen discounting is nevertheless representative of at least some cases in nature. Zero or even negative pollen discounting has been observed in multiple studies of Ipomoea purpurea and Eichhornia paniculata, though other species (particularly those possessing multiple morphological correlates of selfing) showed positive pollen discounting (reviewed in Busch & Delph, 2011). A model incorporating pollen discounting would be similar to our own, except that the baseline advantage of outcrossing in the absence of heterosis would be greater. The same temporal pattern, a spike in the advantage of outcrossing followed by a return to the status quo, should occur regardless.
We have also ignored outbreeding depression, the phenomenon in which inbred offspring (or within-population crosses) are fitter than outcrossed offspring (or among-population crosses) instead of the reverse. Outbreeding depression can be caused by local adaptation, negative epistasis or underdominance. If outbreeding depression occurs, one or several of these factors has overwhelmed heterosis, and greater outcrossing is unlikely to evolve. Local adaptation contributes to outbreeding depression because, if each family or population is locally adapted to its own environment, crossing with distant genotypes maladapted to the local environment is a form of deleterious gene flow. Local adaptation occurs when the populations occupy different environments and is a strong predictor of outbreeding depression (Frankham et al., 2011). Reversion should therefore be most likely when an initial vicariance event cuts off gene flow between the populations but does not otherwise alter their environments. Deleterious epistasis can also contribute to outbreeding depression. Each population can accumulate alleles that are neutral or beneficial on that population's genetic background but deleterious on the other population's background. An alternative phrasing is that each population accumulates coadapted gene complexes that break down in hybrids or admixed individuals: this is equivalent to negative epistasis because the non-coadapted alleles interact negatively relative to the coadapted alleles. It is easy to imagine deleterious epistasis accumulating with no limit short of complete hybrid inviability, and this process is hypothesized to beget speciation (Bateson, 1909; Dobzhansky, 1937; Muller, 1942). Heterosis should evolve as a function of the antagonistic effects of deleterious epistasis and local drift load, which should accumulate simultaneously. If deleterious epistasis gets too great relative to drift load, the populations will become permanently isolated. Since species do exist, reproductive isolation has apparently often overwhelmed heterosis in the long run, though heterosis may have won out in cases in which ephemeral species merged with the population from which they originated (Rosenblum et al., 2012).
5 CONCLUSION
Selfing-to-outcrossing transitions are expected to be rare because predominantly selfing populations lack much of the allelic diversity that normally favours outcrossing. Heterosis from local drift load circumvents this barrier because within-population variation is regenerated from among-population divergence. Outcrossing allows adaptive introgression, which increases offspring fitness but also eliminates the advantage of further outcrossing by homogenizing the originally differentiated allele frequencies. However, this advantage alone is ultimately too transient to allow reversions from predominant selfing to outcrossing in nature, consistent with the estimated rarity of such events. It may, however, marginally increase the probability of reversion if unpurged inbreeding depression is already great. Reversions, if possible, most likely occur in mixed-mating populations that have retained substantial unpurged inbreeding depression.
APPENDIX A: Condition for increase in the outcrossing modifier allele with two viability loci
Here, we derive the values of the selection coefficient, s, for which the frequency of the outcrossing allele, M, initially increases in frequency. We assume here two viability loci, which, when combined with the three mating system genotypes, yields 27 genotypes to track.
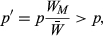
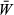is the mean fitness in the population. Multiplying both sides by 
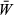and expanding pWM into a weighted average of genotype frequencies, this condition becomes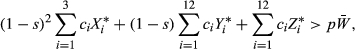
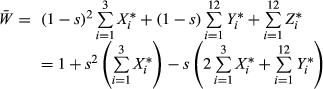
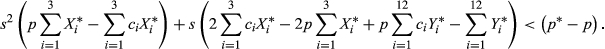
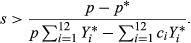
The numerator in this expression is the decrease in the frequency of the outcrossing allele due to the transmission advantage of selfing. The denominator is a quantity that increases as the proportion of outcrossing individuals homozygous for neither deleterious allele increases.
