1 Introduction

Understanding causal factors in the distribution of species across scales is of great relevance to the development of theory and practice in conservation biogeography and related fields. Much recent research into this question has focused on the role of habitat fragmentation on biodiversity (Hanski 2015; Fletcher Jr et al. 2018; Fahrig et al. 2019). With origins in species-area relationships, island biogeography and the SLOSS (single large or several small) literature, the debate as to whether fragmentation has an overall positive or negative influence on ecological communities has become known as the fragmentation-biodiversity debate (Valente et al. 2023). Multiple theoretical and methodological standpoints can be applied to this question, but all are predicated on the delineation of habitat patches, which typically informs subsequent analyses where comparisons are made at the patch (e.g., patch size) or landscape (e.g., mean patch size) level. A foundational concern that is often overlooked in the associated literature relates to the confidence with which researchers can accurately and appropriately measure habitat patches. A great deal of discussion and analysis has been invested in improving our knowledge of fragmentation effects (Fahrig 2017; Fletcher Jr et al. 2018; Watling et al. 2020; Dennis, Huck, Holt et al. 2024; Dennis, Huck, Holt, and McHenry 2024), but within the fragmentation-biodiversity literature, less effort has been devoted to the pursuit of a functional understanding of the object of that fragmentation. Here, we articulate the central problem of defining habitat as a spatial phenomenon that exhibits both discrete (e.g., contained within a defined boundary that separates it from non-habitat) and overlapping (e.g., where habitat can grade into non-habitat) characteristics, which we refer to as the continuity-contiguity problem. These characteristics have been explored through a large body of literature within the ecological and geographical sciences (Fortin 1994; Hall, Krausman, and Morrison 1997; Csillag et al. 2001; Fortin 2005; Fortin et al. 2005; Fisher et al. 2006; Comber et al. 2012). However, this problem, we argue, continues to be largely ignored amidst the heated dialogue around the fragmentation-biodiversity debate, likely due to the challenges of operationalising both sets of characteristics within common landscape ecology methods and metrics. The aim of this paper is therefore to articulate the continuity-contiguity problem and its relevance to key debates in conservation science, before providing recommendations for incorporating and leveraging its implications in fragmentation studies.

The study of biodiversity is an inherently spatial pursuit. Whichever way we measure biodiversity and its determinants, we are faced with decisions related to space. For example, one of the most fundamental measures of biodiversity is species richness, which consists of the number of species in a defined sampling area. The inseparability of species observations and the spaces that they occupy have filtered into debates concerning fragmentation effects. For example, meta-population ecology is predicated on the notion that a given species can maintain a meta-population across (fragmented) patches at the landscape scale if dispersal between habitat patches is possible at a rate such that immigration offsets extinction (Hanski 1997; Levins 1969). The parameterisation of models seeking to quantify this process is dependent on the assumption that local populations are bounded within the limits of habitat patches normally implemented through a binary scheme of ‘habitat’ versus ‘non-habitat’. Fahrig's (2013) Habitat Amount Hypothesis (HAH) challenges this assumption. Fahrig rightly identifies the difficulty of delineating habitat patches in a functional way, which relates to the composition and configuration of habitat in the landscape. For example, should patches positioned in close proximity be regarded as one patch (the ‘gap-crossing’ problem)? Should patches be subdivided according to different kinds of resources within their boundaries (the problem of multi-variate habitat delineation)? Should patches be considered as a whole, or only as the core, or the edge, according to different species specialisms (the problem of delineating interior-edge habitat transitions)? Notwithstanding this ambivalence around patch delineation, the HAH presents a paradoxical situation in which it theoretically removes the need to delineate patches at all, but can only be tested based on a binary model of habitat patches in a non-habitat matrix (because of the need to differentiate between resources and habitat associations relevant to different species). This is an example of how the habitat patch concept continues to ensnare landscape research and is an instance of the continuity-contiguity problem.

A related criticism of the patch concept states that the patch-matrix viewpoint is not consistent with the observation that matrix quality influences population and community persistence (Gallé et al. 2022). If this is the case, then it follows that, from a functional perspective, landscapes represent a heterogeneous distribution of resources along gradients, rather than a crisp delineation between habitat and non-habitat. Nonetheless, research on the fragmentation-biodiversity debate has consistently used a binary formulation to determine habitat amount (e.g., Evju and Sverdrup-Thygeson 2016; Lindgren and Cousins 2017; Melo et al. 2017; Watling et al. 2020). Research into habitat configuration therefore remains focused on the concept of the habitat patch. Another example can be seen in the SLOSS comparison approach (Fahrig 2017), which requires knowledge on the size and number of patches for a given area of habitat. Here, three key assumptions are made: (1) a habitat patch can be delineated effectively from the matrix, (2) the size of the patch is an absolute measure and (3) the amount of habitat in a patch is commensurate with its area (i.e., the patch comprises a homogenous distribution of resources). These assumptions also rely on a binary formulation of habitat which, as others have demonstrated (Dennis and Hardy 2007), may be unfounded. We do not believe this shortcoming to be the result of a logical contradiction within the arguments set out in the associated debates (e.g., SLOSS or HAH), but of a conceptual and methodological impasse based on an incomplete understanding of the continuity-contiguity problem. Neither do we suggest that a binary representation is always inferior to one that is continuous. The ability to delineate habitat patches is important for the development of theory around the role of heterogeneity and habitat structure. For example, Holling's landscape textural discontinuity hypothesis (TDH) explains the role of discontinuities in habitat structure in the generation of keystone processes that entrain cycles of change in ecosystems (Holling 1992). This relates to the body size distributions of animals which tend to be discontinuous (clumped) in response to the ‘clumpiness’ of habitat structure at different scales (Holling 1992). If upheld (and multiple lines of evidence support the hypothesis: Holling and Allen 2002; Fischer, Lindenmayer, and Montague-Drake 2008; Peterson 2008), this means that the tendency of habitat to aggregate in space (i.e., form patches) has an ecological consequence. Again, as highlighted by others (e.g., Gagné, Proulx, and Fahrig 2008), the difficulty of successfully identifying such clumping in space (i.e., functionally delineating patches) prevents the TDH from being comprehensively tested at large scales. Hence, in addition to the three problems highlighted by Fahrig (2013), summarised above, a fourth, over-arching, issue relates to the need to acknowledge that habitat tends towards aggregation (i.e., the formation of contiguous patches) whilst appreciating that real-world landscapes do not follow a Boolean scheme of habitat and non-habitat.

It is clear, therefore, that the concept of the habitat patch continues to play a central role in biogeographical research. Despite its tendency to defy definition and attempts to lessen its relevance, the development of methods for habitat patch delineation remains an active field (Watts and Handley 2010; Halstead et al. 2019; Dennis, Huck, Holt, and McHenry 2024). Researchers operating in complex landscapes typically use biotopes (i.e., land-cover) to classify study regions (usually from satellite imagery), broadly equating these with habitat (e.g., Watts et al. 2010; Moua et al. 2021; Chang et al. 2022). This is problematic for two reasons. Firstly, biotopes have been criticised for not adequately describing the multiple resource types that comprise a species-oriented definition of habitat (Dennis and Hardy 2007). Secondly, the classification of imagery into discrete classes prohibits the quantification of transitional zones, which may disproportionately contribute to biodiversity (Arnot et al. 2004; Kark 2012). The search for a more mechanistic parameterisation of habitat edge has been pursued in recent research into functional connectivity. For example, the Edge-weighted Habitat Index (EHI: Dennis, Huck, Holt et al. 2024; Dennis, Huck, Holt, and McHenry 2024) incorporates information on interior-edge-matrix transitions achieved using spatial kernels, a technique that allows for the strength of interaction between features in the landscape to be a function of the distance between them. However, a complete solution to the continuity-contiguity problem is still missing, as existing methods rely on a single crisp boundary for summarising habitat area after accounting for dispersal and continuous habitat-matrix transitions (e.g., Dennis, Huck, Holt et al. 2024). To navigate this duality, it is necessary to understand the implications of adopting either position. Below, we argue that we should neither dismiss the patch concept as an unwieldy heuristic nor should we settle for a limited view of the world that can stem from a naive binary-versus-gradient representation of the patch concept. Rather, we suggest a useful way to approach the issue is through the notion of continuity-contiguity.

2 The Continuity-Contiguity Problem

The continuity-contiguity problem arises as a function of the degree to which information is retained or lost in representations of space, the degree to which we accept that loss of information and the implications for complexity and uncertainty in the computation of landscape metrics. In the case of habitat, this information relates to the degree to which a given location contains one or more of the biotopes required by a particular species. To illustrate, we take the example of a continuous landscape representation from which boundaries (i.e., contiguous patches) can be derived. Such an instance is suited to our discussion because, from a landscape research perspective, this is a common way of representing study areas in fragmentation-biodiversity studies (Evju and Sverdrup-Thygeson 2016; Lindgren and Cousins 2017; Melo et al. 2017; Watling et al. 2020). Given the preponderance of studies of this type in research on fragmentation-biodiversity outcomes, we limit our discussion from here to landscape-scale studies that employ land-cover classification methods.

The problem of delineating habitat is, generally speaking, one of classification. In a complex world, researchers are forced to use classification to make sense of their study systems. In the context of landscape ecology, this typically involves assigning locations to one biotope or another. Increasingly, this is achieved using classification algorithms trained on examples supplied by the researcher, resulting in each location being assigned to the biotope for which it shows highest probability. In practice, this means that a location can exhibit a degree of membership (probability) to multiple classes and that this information is then lost at the classification stage when this probabilistic classification is replaced with a binary one. Take for example a location that is given 0.45 probability of being woodland, 0.25 scrub, 0.2 heath and 0.1 grassland and so receives a final binary classification of woodland (i.e., 1 woodland, 0 scrub, 0 heath and 0 grassland). In assigning this location to the woodland class, the associated uncertainty is lost and the location will contribute to the size, shape and isolation of a resulting woodland patch, despite a 0.55 probability of belonging to non-woodland cover types. Therefore, at the scales at which fragmentation effects are usually tested, the confidence with which researchers delineate habitat from non-habitat becomes a limiting factor. Operationally, this implies a loss of information and oversimplification of resource availability.

Previous research has been carried out with the aim of achieving a realistic delineation of habitat from non-habitat. For example, moving-window-based techniques for boundary detection have provided continuous representations of ecosystems (Jacquez, Maruca, and Fortin 2000; Fortin et al. 2000). In addition, kernel density estimates and geo-statistical techniques have been employed to achieve a gradient-based view of species ranges (Fortin et al. 2005). However, though Jacquez, Maruca, and Fortin (2000) highlight the propagation of fuzziness into statistical procedures as a research priority, such representations have not been fully integrated into subsequent fragmentation-related workflows. McGarigal, Tagil, and Cushman (2009) proposed the use of ‘surface metrics’ instead of landscape metrics to characterise landscape heterogeneity, relying on continuous landscape characteristics (such as information on terrain and vegetation indices) to avoid a reliance on patches. Again, this falls short of a complete framework for fragmentation analysis as, by removing the patch concept entirely, fragmentation-relevant methods such as graph-theoretic connectivity metrics that require information on patch size and isolation cannot be computed. Similarly, though studies exploring alternative species–area curves (e.g., Guilherme and Pereira 2013) comprise examples of research on fragmented landscapes that do not depend on patch delineation but shed light on species-habitat relationships, they do not directly address the effects of increasing fragmentation. We argue that a comprehensive approach to habitat delineation that supports the computation of a wide range of fragmentation metrics at the landscape scale requires that the patch concept (contiguity) model be reconciled with the gradient (continuity) model. This reconciliation presents a considerable challenge given the observation that habitat represents a heterogeneous component of complex systems that does not comply with the notion of binary classification but which nevertheless exhibits the tendency to aggregate in space. Though this problem persists in biogeographical research, much more attention has been paid to the development of more flexible approaches to patch delineation in the field of geographical information science. Much promise has been shown by approaches to land-cover representation based on fuzzy sets (Zadeh 1965), whereby membership to each class is represented using a real number in the range $\left[0,1\right]$, with the membership values for all classes summing to 1 (Arnot et al. 2004; Fisher et al. 2006; Comber et al. 2012). Fuzzy methods provide a means to represent uncertainty in the classification process and so retain a greater level of information about the landscape compared with a binary classification. However, implementations of such approaches are generally less concerned with (and hence less informed by) ecological theory, being principally focused on spatial representation rather than landscape processes. For example, the classification probabilities listed above could be alternatively interpreted as a degree of membership to each different biotope, known as a type-1 fuzzy set. This is depicted in the example in Figure 1A where each cell has a membership to the woodland biotope. In Figure 1B, a binary approach, patches are determined as contiguous cells for which membership to ‘woodland’ is higher than for any other class. Both results are derived from a Random Forest classification of a 9 m resolution colour infra-red image (Planet Labs 2024) into five classes, trained on ~4500 sampling points and exhibiting an overall accuracy of 95%. The loss of information between 1A and 1B is clear, as the continuous surface in Figure 1A retains more information on the variation of woodland habitat provision. Cells of intermediate membership values are preserved in this surface, likely representing transitional zones between biotopes. A clear limitation of this approach, however, is that it cannot provide an estimate of patch size or location without resorting to the application of a function to ‘crisp’ the fuzzy set back to a binary representation of the landscape. A common approach to this is the use of a membership threshold, in which case all cells above a chosen membership value, known as an alpha-cut (or α-cut), are assigned to the habitat class.

An alternative approach to these contiguous models is to weight the area of the cell by the membership such that, for example, a cell whose membership to the habitat class is 0.5 contributes half of its area to the total. We refer to this as a continuous approach to habitat amount, and it can be performed with or without an α-cut (i.e., only including cells with a membership value $>$ α). As a continuous model without a threshold is equivalent to $\alpha =0$, these forms do not need to be formally distinguished.

These two different perspectives imply very different estimates of habitat provision, with the difference being sensitive to the choice of α-cut used. This effect is shown in Figure 2 for the landscape in Figure 1, with the continuous, contiguous (α) and contiguous (α-Max) inversely related to α whereas contiguous (Max) remains stable. Figure 2B shows the effect of threshold selection on mean patch area (MPA), where patches are based on the area of groups of adjacent cells above the α-cut.

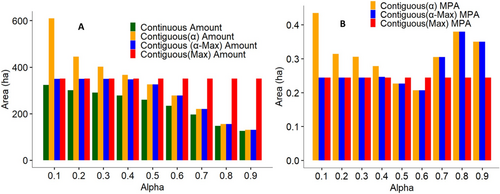
Figures 1 and 2 demonstrate the large amount of variance in the estimation of habitat amount and patch size implied by the adoption of different perspectives on habitat delineation. Moreover, contiguous approaches to habitat amount exhibit a non-linear response to increasing values for α, with mean patch size exhibiting a bimodal response. This bimodal response reflects the initial fragmentation of larger patches into smaller ones, resulting in a smaller mean patch size (e.g., α $=\left[\mathrm{0.1,0.5}\right]$), followed by the removal of smaller patches, resulting in an effective increase in mean patch size (e.g., α $=\left[\mathrm{0.7,0.8}\right]$). Clearly, attempts to combine the use of contiguous and continuous positions by applying alpha-cuts to habitat memberships do little to resolve the continuity-contiguity problem, as estimates relating to habitat amount and patch size are highly sensitive to the choice of threshold. Nevertheless, existing work exploring the implications of using a fuzzy approach to computing landscape metrics has generally made comparisons across a series of alpha cuts. This has served to demonstrate variability in habitat availability and related metrics resulting from the choice of threshold, but these studies do not clarify the implications of such variability on the modelling of landscape processes, nor do they offer guidance on its operationalisation in landscape analysis.

Moreover, even when adopting a continuous, fuzzy approach to habitat delineation, the concept of the patch cannot be dismissed. This is because regions dominated by smaller patches are more likely to contain cells with intermediate membership values reflecting edge habitat (due to the higher edge-area ratio). It follows that more of these cells will be included as habitat as the membership threshold reduces, with substantial implications for any study attempting to explain biodiversity outcomes with measures of habitat amount or patch size. Such associations should therefore be understood and reported in fragmentation-biodiversity studies. Looking forward, overcoming the use of unsatisfactory arbitrary values in patch delineation should be a key priority towards more functional methods in landscape research.

3 Moving the Continuity-Contiguity Problem Forward

The continuity-contiguity problem persists in landscape research on biodiversity distributions. If we concede, however, that the patch concept will likely also persist, future work must find a way to either reconcile or leverage the value ranges produced by different perspectives on habitat delineation. The search for a solution to this problem, if both contiguous and continuous viewpoints are to be valued, will require an approach capable of leveraging all of the information available to the researcher. From a methodological perspective, a potential solution to the tension between contiguous and continuous representations of habitat lies in the representation of higher-order uncertainty in landscape classifications. For example, whereas type-1 fuzzy sets capture first-order uncertainty, whereby uncertainty in the classification is represented by the membership function, a type-2 fuzzy set represents second-order uncertainty, whereby uncertainty is represented not only in the classification but in the membership function itself (Zadeh 1975; Arnot and Fisher 2007). The use of a type-2 fuzzy set means that the membership value for each class is therefore represented as a ‘fuzzy number’ (i.e., a set of possible values, each with their own secondary membership value, analogous to a probability distribution). Taking the output in Figure 1A as an example, the type-1 membership value is simply the mean prediction of all Decision Trees in a Random Forest classifier. Accordingly, the set of individual estimates from each Decision Tree can be used to create a continuous distribution representing the uncertainty in this membership. This approach permits an assessment of the confidence with which we can assess cell membership to each class and hence allow the researcher to build multiple scenarios reflecting a range of landscape possibilities. Here we use the example of Random Forest as an efficient algorithm that is widely used in land cover classification tasks, but our approach can be generalised to any classifier that permits the extraction of uncertainty from the modelling process. For example, Figure 3 shows (A) the membership and (B) the variance around the membership values of each cell to the woodland class. We can estimate a distribution of habitat provision calculated as the range of probability point values computed based on 10,000 draws taken from a Beta distribution (representing the type-2 membership value) for each cell. If we take an $\alpha$-cut of 0.5 and calculate the continuous habitat amount, this returns the range of values depicted in Figure 3C. Note that this effectively removes the need for patches to have a single crisp boundary where, for each scenario, we can delineate patches as adjacent cells with values above the $\alpha$-cut. This allows for a distribution of estimates of both patch size and habitat amount. We suggest here that the amount is parameterised based on membership values on the basis that this reflects most closely the degree to which each cell belongs to woodland.

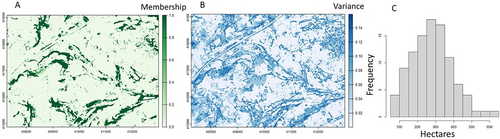
Note that although (continuous) membership values are summed to estimate habitat amount, adopting a distribution-based approach allows for an analysis that reflects both the contiguous and continuous perspectives. This is because the distribution describes a fuzzy (or gradient)-oriented measure (i.e., incorporating multiple potential values) whilst the distribution itself is generated from the delineation of habitat patches (i.e., based on an α-cut) for each realisation of the landscape. Theoretically then, this approach can be applied to a wide range of subsequent metrics whether at the patch (e.g., patch size, edge length) or landscape (e.g., mean patch size, total edge length) level, revealing a comprehensive range of possible values that are empirically derived.

More research is needed to clarify how uncertainty can be more formally incorporated into existing fragmentation-relevant methods, particularly those that involve patch-matrix interactions and effective distances (e.g., functional connectivity metrics). Here we suggest some promising avenues for investigation that draw on existing work in spatial ecology, principally the use of spatial kernels and the leveraging of continuous membership (type-1 fuzzy sets) and higher-order uncertainty (type-2 fuzzy sets). To illustrate, Figure 4 presents four common challenges with respect to the habitat patch concept and describes potential approaches that, in combination, should be the subject of future work on habitat delineation in fragmentation-biodiversity studies. Figure 4i refers to the gap-crossing problem highlighted by Fahrig (2013). Here the question of whether to allow two resource patches in close proximity to be allowed to comprise a single patch, or delineate them as two patches, can be addressed through the application of spatial kernels and the notion of continuous habitat amount. Spatial kernels involve characterising a given location based on the characteristics of neighbouring features, the influence of which is a function of their distance to the focal location. An example of this can be seen in functional connectivity models where spatial kernels are parameterised according to the dispersal distance of the focal species (e.g., Saura and Pascual-Hortal 2007; Watts and Handley 2010). Here, the degree to which patches are ‘connected’ is a function of the distance between them and the kernel function used. In connectivity studies, a negative exponential function is commonly used, such that increasing distance between patches leads to an exponential decrease in the probability that they are connected. In such a case, the ‘gap’ can be effectively closed if the dispersal capacity of the species is sufficiently large. For example, the two patches in 4(i) become functionally ‘joined’ for species b which has a high dispersal capacity relative to the distance between the two patches (here we suppose Euclidean distance, but this could also relate to effective distance based on landscape resistance). Note that this implies a total patch area that includes both ‘patches’ and the gap in between. From a functional perspective, however, habitat amount should be determined as a reflection of the available habitat (i.e., excluding the gap). For this, a continuous habitat approach (i.e., the sum of fuzzy membership values before a binary scheme is applied) should be preferred. Removing the requirement that patch size and habitat amount are equivalent is consistent with a functional view of habitat, and is already implicit in recent functional connectivity measures (e.g., Dennis, Huck, Holt, and McHenry 2024). As pointed out by Fletcher Jr et al. (2023) the parameterising of such methods, and assessments of fragmentation in general, is sensitive to the scale at which habitat is sampled and subsequently analysed. For example, the sampling grain can significantly influence, if not reverse, our interpretation of results, owing to the Modifiable Area Unit Problem (Jelinski and Wu 1996). Equally, for two patches in close proximity, they may be determined as one patch or two separate patches simply as a result of the resolution at which information on the landscape is detected which, again, can influence interpretation (Connor et al. 2019). Therefore, consideration of scale related to both sampling and study design cannot be ignored when implementing neighbourhood analysis.

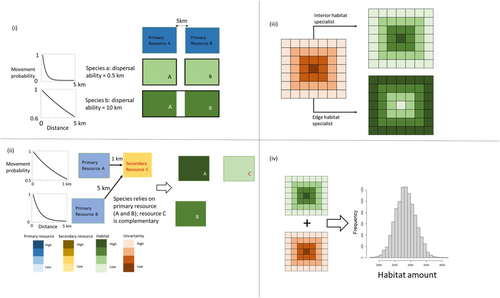
The situation in 4(ii) describes a multi-variate habitat delineation scenario where complementary resources are spatially distant. Here, the use of spatial kernels can again be employed to weight locations as a function of their membership to primary resources and their proximity to nearby complementary resources to give a final measure of habitat amount. In addition, resource types (biotopes) can be weighted according to the focal species' affinity towards them. Hence, membership and suitability related to different biotopes can be incorporated into a multi-variate delineation of habitat. Methods for leveraging spatial kernels to assess negative edge effects are already in use (e.g., Dennis, Huck, Holt, and McHenry 2024), and their application to the positive effects of nearby biotopes is a logical extension. Note that the same logic can be applied for a single cell where membership values relating to different classes that represent complementary resources can be summed directly, or according to a weighting scheme. Figure 4iii refers to the situation where interior and edge habitat associations may contribute to patch definitions. In this case, a continuous assessment of membership allows for a measure of uncertainty that can be used to differentiate areas of ‘core’ and ‘edge’ habitat, where higher (type-2) uncertainty is a function of intermediate membership values that occur at the transition between one or more biotopes. Finally, Figure 4iv describes the leveraging of Type-1 membership and the Type-2 uncertainty described in 4(iii) to achieve a distribution of possible values for habitat amount. The scaling of this process to the landscape scale is simply a case of summing values for all patches as in the example in Figure 3.

The challenge for conservation science is to leverage the uncertainty inherent in classification schemes and link this to ecologically relevant processes. The continuity-contiguity problem, if it is to be resolved, may well be clarified through the treatment of habitat as a spectrum of possibility that emerges as a function of the perception and requirements of individual species. The idea of a species-oriented definition of habitat has been articulated before (e.g., Dennis and Hardy 2007; Tellería 2016), and species distribution modelling approaches to habitat suitability may present a more functional, species-specific approach (e.g., Halstead et al. 2019). However, they do not circumvent the problem of delineation in space and typically rely on crisp land-cover classification schemes as input data (e.g., Duff, Bell, and York 2014; Romero et al. 2016) or the use of thresholds based on predictions of species presence (Halstead et al. 2019). Incorporating higher-order uncertainty from the beginning of the modelling process could therefore be an interesting line of future research into habitat suitability modelling. This proposition does not escape, however, the challenge of scaling up from a species-specific to a community-level delineation of habitat, which is a problem for fragmentation-biodiversity studies in general. A promising approach with respect to incorporating uncertainty in the modelling of multi-species responses is the use of a focal generic species (Watts et al. 2010; Eycott, Marzano, and Watts 2011) to simulate outcomes for groups with similar habitat requirements (e.g., woodland specialists). Leveraging uncertainty may be particularly useful in this context as different positions along a distribution of results may reflect outcomes for species with similar requirements but with greater or lesser sensitivity to habitat amount or quality.

Hence, a mature framework for operationalising a functional view of habitat remains absent in biogeographical research, largely due to the absence of a resolution to the continuity-contiguity problem. Moving towards a pluralistic appreciation of habitat that acknowledges uncertainty in land cover classification and habitat definition will be an important field of future inquiry if the goal is to apply, rather than ignore, the continuity-contiguity dichotomy in conservation science. We suggest that working with a distribution of estimates of habitat availability (whether measured as amount, size or connectedness), driven by uncertainty in landscape characterisation, is a more empirically justified proposal than existing classification methods. We give three recommendations for future work exploring fragmentation-biodiversity outcomes: (1) uncertainty in habitat measurements (of amount, size, isolation) should be reported where possible and captured throughout the research process (e.g., from habitat delineation through to area-based metrics and statistical inferences); (2) the assumption that habitat area is commensurate with habitat amount should be relaxed; and (3) higher-order uncertainty should be leveraged towards a more comprehensive assessment of habitat distributions and a more complete understanding of associated processes.

Author Contributions

M.D. and J.J.H. conceived the continuity-contiguity problem together. M.D. and J.J.H. contributed equally to the writing of the manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.