A comparison of methods to estimate genomic relationships using pedigree and markers in livestock populations
Summary
Accurate prediction of breeding values depends on capturing the variability in genome sharing of relatives with the same pedigree relationship. Here, we compare two approaches to set up genomic relationship matrices for precision of genomic relationships (GR) and accuracy of estimated breeding values (GEBV). Real and simulated data (pigs, 60k SNP) were analysed, and GR were estimated using two approaches: (i) identity by state, corrected with either the observed (GVR-O) or the base population (GVR-B) allele frequencies and (ii) identity by descent using linkage analysis (GIBD-L). Estimators were evaluated for precision and empirical bias with respect to true pedigree IBD GR. All three estimators had very low bias. GIBD-L displayed the lowest sampling error and the highest correlation with true genome-shared values. GVR-B approximated GIBD-L's correlation and had lower error than GVR-O. Accuracy of GEBV for selection candidates was significantly higher when GIBD-L was used and identical between GVR-O and GVR-B. In real data, GIBD-L's sampling standard deviation was the closest to the theoretical value for each pedigree relationship. Use of pedigree to calculate GR improved the precision of estimates and the accuracy of GEBV.
Introduction
In traditional pedigree-based evaluation, the numerator or additive relationship matrix (Henderson 1976), which is equal to twice the matrix of pairwise kinship (or coancestry) coefficients, has been widely used to estimate genetic covariances and breeding value of individuals. Additive relationships carry information on genetic resemblance from common inheritance and are based on probabilities that gene pairs are identical by descent or IBD (Wright 1922). In animal breeding, and throughout this paper, it is assumed that there is an accepted founder population relative to which IBD is to be measured, consisting of the founder members of a defined pedigree, with the implication that more remote coancestry of current gametes is ignored (Thompsom 2013). Therefore, individuals whose genes are copies from an ancestral one in the base population are likely to share on average the same causal loci, so that phenotypic data from related individuals are informative for the prediction of the breeding value of either animal. Inbreeding and kinship coefficients, and more generally probabilities of any IBD state, are expectations of random variables that indicate IBD at a given point in the genome (Thompsom 2013). In the absence of inbreeding, additive relationships (Wright 1922) represent the expected proportion of genome-shared IBD.
Finite size of the genome and recombination introduce randomness and variation on the amount of genome-shared IBD for any particular type of relatives (Risch and Lange, 1979; Guo, 1996; Hill & Weir 2011), which makes actual relationships to differ from their expected value. The availability of dense panels of SNP markers in livestock species allows estimating these actual relationships using marker data. The genomic relationship matrix (G) calculated with markers has a paramount role in the prediction of breeding values from animal models, when using best linear unbiased predictors. Elements of G are estimates of the actual proportion of the genome that two individuals share (realized relationships), whereas the pedigree-based relationship matrix is the expectation of this proportion (expected relationships) (Goddard et al. 2011). The use of realized relationships is responsible for the gain in accuracy while predicting breeding values in genomic selection schemes. This gain in accuracy can be shown to be due to the reduction in the variance of Mendelian residuals of the genomic breeding values (Cantet & Vitezica 2014). The efficiency of the BLUP (accuracy) depends on how well marker-derived genomic relationships capture the patterns of realized genetic relationships at causal loci (VanRaden 2007, 2008; De los Campos et al. 2013).
VanRaden (2007, 2008) proposed a calculus of genomic relationships by adding cross-products of marker data deviated from mean gene frequencies and divided by the total heterozigosity at the markers. These relationships reflect the actual proportion of marker alleles shared by identity by state (IBS), as a deviation from the expected proportion of alleles shared in the population (Vela-Avitúa et al. 2015). As a result, likeness among alleles at all markers constitutes the information on which genetic resemblance among animals is carried to G. An alternative way of using marker information to estimate realized relationships is to trace IBD inheritance of haplotypes within the known pedigree (Thompson 2013). The efficiency of either method depends on how well they can capture the signals from the true IBD process in the genome continuum, which in turn is affected by linkage disequilibrium, incomplete pedigree information and inbreeding. VanRaden's estimates of genomic relationships require accurate estimates of the true allele frequencies of the unselected base population, which can be difficult to obtain. Simple frequency estimates obtained as means of only the subset of known genotypes either from the current or from the base population (founders), or even base frequency estimates using the algorithm of Gengler et al. (2007), can lead to biased relationship coefficients. If base allele frequencies are unknown, incorporating pedigree information into these calculations could be a strategy when dealing with large families with a small number of genotyped animals.
The purpose of this research was to compare two approaches to estimate the true pairwise-realized relationships between genotyped animals, in terms of the precision of the relationships, by analysing real and simulated data. We define the true realized relationship as the proportion of total genome that two individuals share IBD relative to the specified founders of a pedigree. The first one is the IBS-derived approach that is widely employed in genomic BLUP (GBLUP) methods (VanRaden 2008) and uses only markers to infer genome sharing across individuals. The second approach (IBD) infers relationships tracing transmission of markers throughout the pedigree (linkage analysis) even if there are many ungenotyped family members, while accounting for population linkage disequilibrium or background sharing beyond the pedigree. We further illustrate the consequences of using either approach on accuracy of genomic estimated breeding values (GEBV).
Materials and methods
Two approaches to estimate genomic relationships were evaluated using both simulated and real pig data. To ascertain the precision of these estimates, the true relationships – or realized proportion of genome shared by relatives of a given degree – need to be known. These are available only for simulated data, yet unknown with real data (it is impossible to know without error which of the alleles from the founder allele set an individual has inherited at every genome location). Still, for real data, we can compare the mean and variance of the true relationships, which can be calculated using theoretical formulae (Hill & Weir 2011) that depend only on map length and on the pedigree relationship between the individuals, with the corresponding estimated mean and variance. Thus, we used an existing real pig data set from an F2 cross, in which pedigree relationships were precisely defined and had many pairs of individuals within each type of pedigree relationship. The simulated data are a more conventional population.
Simulated data set
Data were simulated using QMSim (Sargolzaei & Schenkel 2009), by considering a simplified scenario for the breeding programme of a pig nucleus. The simulated genome consisted of 5 autosomal chromosomes of 160 cM each. Bi-allelic markers (35 000) were distributed randomly across the genome, with equal allele frequency in the first historical generation. A mutation rate of 2 × 10−4 per locus per generation was applied, assuming a recurrent model. The historical population was simulated by considering an equal number of males and females, discrete generations, random mating, no selection and no migration. Offspring were produced by the union of gametes randomly sampled from the male and female gametic pools. Recombination was modelled at a rate of 1 cM/Mb assuming a Poisson distribution. After 2500 generations with a constant size of 500, followed by a severe bottleneck during 30 generations with a constant size of 75, a historical population at mutation-drift equilibrium that produced realistic level of linkage disequilibrium was established. Sex ratio was constant across historical generations, except for the last generation, in which 20 males and 200 females were generated by random choice of two gametes from the male and female gametic pools. These animals constituted the founders for the recent population (G0). Among the marker loci with MAF >0.01 in G0, 16 000 SNPs (spaced on average every 0.05 cM) were randomly chosen. A polygenic trait with heritability (h2) of 0.25 and phenotypic variance of 1 was simulated by assigning to each founder an additive effect sampled from a normal distribution with mean 0 and variance 0.25. Then, the following selection scheme was followed for five generations. In each generation, 20 boars were mated with 200 sows to produce 2000 offspring (half of them males). Mating design was optimized to minimize inbreeding (Sonesson & Meuwissen 2000) using the ‘minf’ option in QMSim. For the next generation, the 20 boars with the highest estimated BV were selected based on best linear unbiased prediction (BLUP) via an animal model, whereas 200 sows were randomly selected. Pedigree was available for all 5 generations (10 220 animals). For estimation purposes, it was assumed that 140 animals (i.e. G0 boars, the 20 selected boars from generations 1 to 4, and 40 boars randomly chosen from the selection candidates from generation 5) were genotyped. The rest of animals in the pedigree were assumed non-genotyped. The whole simulation process was replicated 50 times.
Real data set
Pedigree and genotypic data used in our analyses were collected on 411 animals from an outbred resource pig population Duroc × Pietrain elapsing three generations (F0, F1 and F2) that was raised at Michigan State University Swine Teaching and Research Farm (Edwards et al. 2008). Animal protocols were approved by the Michigan State University All-University Committee on Animal Use and Care. The population was established from 4 F0 Duroc sires and 15 F0 Pietrain dams. From the F1 progeny, 50 females and 6 males were selected as parents of the F2 generation while avoiding full- or half-sib matings. A total of 1259 F2 pigs were born alive in 141 litters across 11 farrowing groups. All animals were produced through the artificial insemination. From the F2 animals, 336 pigs were selected for genotyping to represent all full-sib families (Gualdrón Duarte et al. 2013). A total of 411 pigs (19 F0, 56 F1 and 336 F2) out of 1334 were genotyped with the Illumina PorcineSNP60 chip (Ramos et al. 2009). Genotyping was performed at a commercial laboratory (GeneSeek, a Neogen Company, Lincoln, NE, USA). Of 62 163 SNPs, 38 263 were employed for all analyses after quality-control procedures, which involved removing non-autosomal SNPs (15 298), SNPs with MAF <0.01, call rate <90% or Mendelian inconsistencies >2%.
Computation of Pairwise identical-by-descent (IBD) genome sharing in simulated data
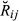 be the ‘true’ realized relationship or proportion of the total genome individuals i and j share IBD, with respect to the specified founders of a pedigree (i.e. starting from G0 in the simulated data and from F0 in the real data). We will call
be the ‘true’ realized relationship or proportion of the total genome individuals i and j share IBD, with respect to the specified founders of a pedigree (i.e. starting from G0 in the simulated data and from F0 in the real data). We will call 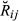 shortly hereafter the pedigree IBD genome sharing. Assume initially that, at any genome location, it can be determined which of the 2n alleles from the founder set an individual inherited (this is not possible with real data). Furthermore, let
shortly hereafter the pedigree IBD genome sharing. Assume initially that, at any genome location, it can be determined which of the 2n alleles from the founder set an individual inherited (this is not possible with real data). Furthermore, let 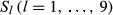 be an indicator variable for the event of observing the condensed identity state l (Jacquard 1974). Thus, Sl is equal to 0 or 1, depending on the observed IBD pattern among the four alleles present in two individuals. Then, the realized coancestry or kinship coefficient between a pair of individuals i and j at location t is
be an indicator variable for the event of observing the condensed identity state l (Jacquard 1974). Thus, Sl is equal to 0 or 1, depending on the observed IBD pattern among the four alleles present in two individuals. Then, the realized coancestry or kinship coefficient between a pair of individuals i and j at location t is 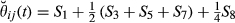 . This directly provides that the realized additive relationship coefficient at location t is
. This directly provides that the realized additive relationship coefficient at location t is 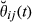 and that the actual relationship
and that the actual relationship 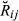 , considering a genome of length L, is as follows (Guo 1995)
, considering a genome of length L, is as follows (Guo 1995)
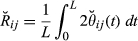 (1)
(1)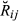 for each pair of animals and also computed the overall mean and variance of
for each pair of animals and also computed the overall mean and variance of 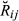 across the whole set of analysed pairs (10 220) for each replicate. For the real data set, we cannot compute the value of
across the whole set of analysed pairs (10 220) for each replicate. For the real data set, we cannot compute the value of 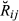 as we cannot observe
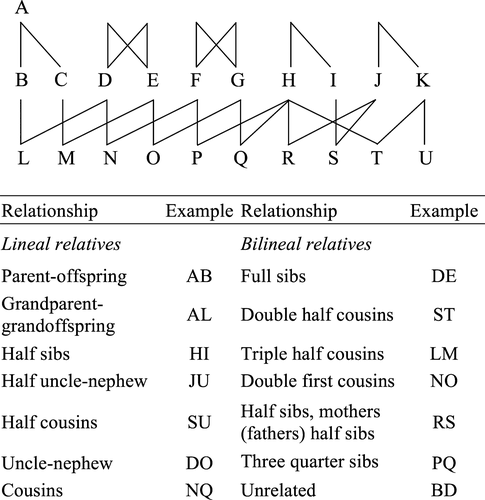
as we cannot observe  , but we can compute theoretically its mean and variance. All pairs of animals in the real data set (1334 animals) were classified into 14 different pedigree relationships (e.g. half-sibs, full-sibs, see Fig. 1). For each relationship, the mean of
, but we can compute theoretically its mean and variance. All pairs of animals in the real data set (1334 animals) were classified into 14 different pedigree relationships (e.g. half-sibs, full-sibs, see Fig. 1). For each relationship, the mean of 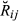 , E(
, E(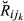 ) (k = 1, …, 14), was obtained from the pedigree, and the variance, Var(
) (k = 1, …, 14), was obtained from the pedigree, and the variance, Var(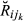 ), was computed using the theoretical formulae derived by Hill & Weir (2011) (formulae are for non-inbred individuals, as is the case for the real data set), which depends only on the number of chromosomes and their map length. Sex-averaged map length (cM) was taken from recombination rates reported by Tortereau et al. (2012). The overall mean and variance of
), was computed using the theoretical formulae derived by Hill & Weir (2011) (formulae are for non-inbred individuals, as is the case for the real data set), which depends only on the number of chromosomes and their map length. Sex-averaged map length (cM) was taken from recombination rates reported by Tortereau et al. (2012). The overall mean and variance of 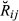 across the whole real set of analysed pairs can be derived from the theory of finite mixture distributions (Frühwirth-Schnatter 2006). Let
across the whole real set of analysed pairs can be derived from the theory of finite mixture distributions (Frühwirth-Schnatter 2006). Let 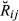 denotes the IBD genome sharing for a pair of animals from a mixture distribution whose probability density function is as follows:
denotes the IBD genome sharing for a pair of animals from a mixture distribution whose probability density function is as follows:
 (2)
(2)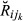 ) denotes the conditional probability density function of
) denotes the conditional probability density function of 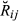 given relationship class k (k = 1, …, 14) (Fig. 1), and ηk is the mixture coefficient for class k such that
given relationship class k (k = 1, …, 14) (Fig. 1), and ηk is the mixture coefficient for class k such that 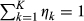 . Then,
. Then,
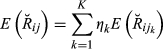 (3)
(3)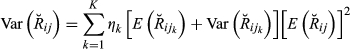 (4)
(4)
Estimated IBD genome sharing between genotyped animals
Two approaches to estimate pairwise relationships based on markers, using or not pedigree information, were compared. These estimates will constitute the elements of the genomic relationship matrix for genotyped animals, G, of order 140 (411) for the simulated (real) data set.
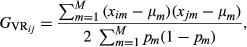 (5)
(5)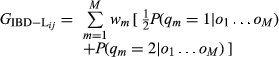 (6)
(6)Matrix GIBD-L may be indefinite showing (small) negative eigenvalues. The reason for this is that elements of GIBD-L (the genomic relationships) are computed on a pairwise basis instead of globally. Thus, the ‘nearPD’ function in the R package ‘Matrix’ was used to compute the nearest positive definite matrix to the original GIBD-L (Cheng & Higham 1998; Higham 2002). These estimates were retained for the statistical analysis.
Statistical analysis
For the real data, the mean and variance of the estimated genome sharing (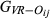 ,
,
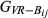 or
or
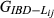 >) within each class of relationship (Fig. 1) and for all the pedigrees were calculated and compared against the theoretical values. Correlations between the estimated relationship or genome sharing values and their corresponding additive relationship coefficients obtained from pedigree were also calculated.
>) within each class of relationship (Fig. 1) and for all the pedigrees were calculated and compared against the theoretical values. Correlations between the estimated relationship or genome sharing values and their corresponding additive relationship coefficients obtained from pedigree were also calculated.
For each replicate of simulated data, estimators were evaluated for precision by means of mean square error (MSE) and the Pearson correlation coefficient, ρ, between the estimated (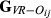 ,
,
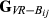 or
or
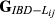 ) and the true values of genome sharing (
) and the true values of genome sharing (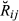 ). The estimators were also evaluated for empirical bias, which was calculated by taking the difference Gij –
). The estimators were also evaluated for empirical bias, which was calculated by taking the difference Gij – 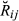 for each pair of animals and averaging them across pairs. Finally, the regression of true values of genome sharing on the estimated values was calculated as a measure of the closeness between estimators and the true relationships.
for each pair of animals and averaging them across pairs. Finally, the regression of true values of genome sharing on the estimated values was calculated as a measure of the closeness between estimators and the true relationships.
Consequences of using different G on accuracy of breeding values
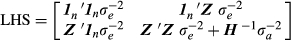 (7)
(7)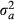 is the additive genetic variance and
is the additive genetic variance and 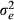 is the residual variance. Accuracy of GEBV for each animal was taken to be equal to the following:
is the residual variance. Accuracy of GEBV for each animal was taken to be equal to the following:
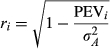 (8)
(8)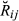 with elements
with elements  obtained using Equation 1. In the ‘true’ model (i.e.
obtained using Equation 1. In the ‘true’ model (i.e.  ), PEV can be computed based on the inverse of LHS. When the covariance matrix of BV is misspecified, PEV can be calculated as in Henderson (1975):
), PEV can be computed based on the inverse of LHS. When the covariance matrix of BV is misspecified, PEV can be calculated as in Henderson (1975):
 (9)
(9)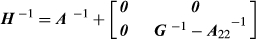 (10)
(10)Scheffé's multiple comparison procedure was used to test the significance of differences in accuracies between the covariance matrix estimators. Accuracies (accijk) of selection candidates (k = 1, …, 2000) were analysed using the mixed model (Proc Mixed SAS version 9.3.1, SAS Institute, Cary, NC, USA) accijk = τi + rj + εijk, where the relationship matrix estimator was treated as fixed (τi, i = 1, …, 4 for A22, GVR-O, GVR-B and GIBD-L, respectively), and the replicate (rj, j = 1, …, 50) was treated as a random effect. A banded main diagonal covariance matrix was used for errors εijk, in which all observations having the same level of the fixed effect (τi) have the same variance parameter or component.
Estimating accuracy using 9, we assume that IBD relationships are a perfect description of genetic covariances across individuals (i.e. they correspond to the ‘true’ model), which in turn implies the hypothesis that all base alleles are different. This is wrong in the presence of large QTLs, but seems a reasonable assumption for most cases, as most genomic information comes from close relatives (i.e. Habier et al. 2013).
Results
Real data
In the real data, the estimated genome sharing was computed for a total of 84 254 pairs of genotyped animals. The mean and standard deviation of the absolute difference between the observed and the base allele frequency were 0.083 and 0.074, respectively. The observed pattern for the three estimators of genome sharing (GVR-O, GVR-B and GIBD-L) within each pedigree relationship was similar: the estimated mean decreased as relationships become more distant (Table 1). However, the mean of GIBD-L was closer to its theoretical value on nine of fourteen pedigree relationships; GVR-O was the closest to the theoretical value for the grandparent–grand offspring and half-cousin relationships. The latter relationship involves the former one, as half-cousins have one grandparent in common. Besides, the mean of the estimated relationship between half-cousins followed the same pattern as the overall mean, and it was computed with the highest number of pairs. The estimators GVR-B for uncle–nephew, half-uncle–nephew and double half-cousins were closest to the true means. Note that uncle–nephew can be regarded as a two-way half-uncle–nephew relationship, whereas double half-cousins can be viewed as descendants of four half-uncle–nephew pairs.
 ) and sample mean of estimated genome sharing (G) using three different estimators for a real pig data set for specific types of relatives
) and sample mean of estimated genome sharing (G) using three different estimators for a real pig data set for specific types of relatives| Relationship | N | Expected | Mean | ||
|---|---|---|---|---|---|
|
G IBD-L | G VR-O | G VR-B | ||
| Parent–offspring | 784 | 0.5000 | 0.5000 | 0.4299 | 0.4824 |
| Full-sibs | 639 | 0.5000 | 0.5046 | 0.4286 | 0.4886 |
| Three-quarter sibs (horizontal) | 816 | 0.3750 | 0.3730 | 0.3126 | 0.3588 |
| Half-sibs, mothers’ (fathers) half-sibs | 2848 | 0.3125 | 0.3231 | 0.2522 | 0.2997 |
| Grandparent–grand offspring | 1344 | 0.2500 | 0.2067 | 0.2299 | 0.2709 |
| Half-sibs | 7061 | 0.2500 | 0.2537 | 0.2185 | 0.2811 |
| Uncle–nephew | 1716 | 0.2500 | 0.2282 | 0.2279 | 0.2468 |
| Double first cousins | 544 | 0.2500 | 0.2343 | 0.2193 | 0.3150 |
| Triple half-cousins | 2912 | 0.1875 | 0.1754 | 0.1533 | 0.2197 |
| Double half-cousins | 5408 | 0.1250 | 0.1313 | 0.1076 | 0.1229 |
| Half-uncle–nephew | 6800 | 0.1250 | 0.1344 | 0.1216 | 0.1266 |
| First cousins | 6960 | 0.1250 | 0.1169 | 0.1097 | 0.1780 |
| Half-cousins | 22 944 | 0.0625 | 0.0735 | 0.0585 | 0.1019 |
| Unrelated | 23 478 | 0.0000 | 0.0000 | 0.0444 | 0.0599 |
Table 2 reports the theoretical standard deviations (SD) of actual relationships and the sampling SD of the estimated genome sharing for each type of relatives. The IBD-based values of estimated SD were always smaller than their IBS-based counterparts, whether the observed or base allele frequencies were used: on average, GIBD-L, GVR-O and GVR-B were 7.50, 60.37 and 174.07% higher than the theoretical SD, for each pedigree relationship, respectively. Thus, the overlapping in the amount of IBD sharing from quite different pedigree relationships was higher for the IBS-based estimates.
 ) and estimated genome sharing (G) using three different estimators for a real pig data set for specific types of relatives
) and estimated genome sharing (G) using three different estimators for a real pig data set for specific types of relatives| Relationship |
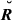
|
G IBD-L | G VR-O | G VR-B |
|---|---|---|---|---|
| Parent–offspring | 0.0000 | 0.0000 | 0.0573 | 0.1188 |
| Full-sibs | 0.0527 | 0.0578 | 0.0826 | 0.1317 |
| Three-quarter sibs (horizontal) | 0.0476 | 0.0478 | 0.0711 | 0.1180 |
| Half-sibs, mothers’ (fathers) half-sibs | 0.0447 | 0.0438 | 0.0641 | 0.1086 |
| Grandparent–grand offspring | 0.0456 | 0.0465 | 0.0993 | 0.1454 |
| Double first cousins | 0.0419 | 0.0472 | 0.0581 | 0.1017 |
| Half-sibs | 0.0373 | 0.0344 | 0.0609 | 0.0895 |
| Uncle-nephew | 0.0348 | 0.0361 | 0.0512 | 0.1204 |
| Triple half-cousins | 0.0386 | 0.0420 | 0.0560 | 0.1038 |
| Double half-cousins | 0.0350 | 0.0385 | 0.0504 | 0.0862 |
| Half-uncle–nephew | 0.0335 | 0.0375 | 0.0465 | 0.1110 |
| First cousins | 0.0297 | 0.0321 | 0.0535 | 0.0793 |
| Half-cousins | 0.0248 | 0.0279 | 0.0495 | 0.0709 |
| Unrelated | 0.0000 | 0.0000 | 0.0651 | 0.0854 |
For the real data set with pig records, the overall mean and standard deviation (SD) of the estimated genome sharing were compared against their theoretical values (Table 3) calculated using Equations 3 and 4 and based on pedigree and porcine genetic maps. The mean of genomic relationships was equal to the theoretical value when GVR-O was used, as this estimator was scaled based on A so that the means of diagonals and off-diagonals are the same as in the pedigree relationship matrix (Vitezica et al. 2011). The overall mean of GIBD-L was very close to the theoretical value. The estimator that differed most from the overall theoretical mean was GVR-B. With respect to the overall SD of the estimated genome sharing, the value for GIBD-L was closer to the theoretical value than GVR-O or GVR-B.
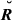 ) and estimated genomic relationships (G) across all pairs of genotyped individuals in a real pig data set
) and estimated genomic relationships (G) across all pairs of genotyped individuals in a real pig data set
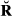
|
G IBD-L | G VR-O | G VR-B | |
|---|---|---|---|---|
| Mean | 0.1062 | 0.1087 | 0.1062 | 0.1416 |
| SD | 0.1100 | 0.1090 | 0.0985 | 0.1273 |
The Pearson correlation coefficients between the estimated values of genome sharing and their corresponding pedigree-based additive relationship coefficient were 0.959, 0.797 and 0.702 for GIBD-L, GVR-O and GVR-B respectively.
Simulation
In the simulated data, the estimated genome sharing was computed for a total of 9730 pairs of genotyped animals. For the simulated data set, the mean and standard deviation of the absolute difference between the base and the observed allele frequency were 0.072 and 0.068, respectively. Table 4 summarizes the precision and bias averaged over replicates that were achieved by the three different estimators (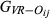 ,
,
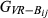 and
and
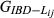 )
of the pairwise pedigree IBD genome sharing between simulated genotypes (
)
of the pairwise pedigree IBD genome sharing between simulated genotypes (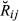 ). All three estimators had very low empirical bias, being GVR-O the least unbiased. GIBD-L displayed lower sampling MSE and higher correlation with true values of genome sharing than GVR-O. When allele frequencies in the base population were used, the correlation between GVR-B and the true value approximated the corresponding correlation for GIBD-L, while having lower MSE than GVR-O. The GVR-B estimator, although not always feasible to calculate (as the frequencies from the base population are not always available), assured a better scenario. The last column in Table 4 displays the regression of the true genomic relationships on the estimated genomic relationships. The regression coefficient was close to 1 for GIBD-L, being significantly lower for both GVR estimators.
). All three estimators had very low empirical bias, being GVR-O the least unbiased. GIBD-L displayed lower sampling MSE and higher correlation with true values of genome sharing than GVR-O. When allele frequencies in the base population were used, the correlation between GVR-B and the true value approximated the corresponding correlation for GIBD-L, while having lower MSE than GVR-O. The GVR-B estimator, although not always feasible to calculate (as the frequencies from the base population are not always available), assured a better scenario. The last column in Table 4 displays the regression of the true genomic relationships on the estimated genomic relationships. The regression coefficient was close to 1 for GIBD-L, being significantly lower for both GVR estimators.
| MSE(×100) | Pearson correlation | Bias | b 1 a | |
|---|---|---|---|---|
| G VR-O | 0.9352 ± 0.2847 | 0.678 ± 0.048 | −0.0086 ± 0.0095 | 0.7483 |
| G VR-B | 0.5703 ± 0.2059 | 0.876 ± 0.022 | 0.0180 ± 0.0185 | 0.7285 |
| G IBD-L | 0.1886 ± 0.0535 | 0.946 ± 0.008 | 0.0122 ± 0.0091 | 0.9723 |
- a b1 is the regression coefficient of the true genomic relationship on the estimated genomic relationships.
To analyse the consequences of using different G matrices in the accuracy of prediction of BV, the accuracy of GEBV for selection candidates was computed under two heritability scenarios: h2 = 0.25 and h2 = 0.15 (Table 5). As expected, the use of any of the genomic matrices resulted in greater accuracy of GEBV for selection candidates when compared to the pedigree-only-based relationship matrix. Accuracy of GEBV for selection candidates was statistically higher when matrix GIBD-L was used. In fact, differences were larger for genotyped animals. The differences among the IBS-based estimators were not statistically significant. The accuracies dropped in the same magnitude when h2 = 0.15 for the three estimators.
| h 2 | A | G VR-O | G VR-B | G IBD-L | |
|---|---|---|---|---|---|
| 0.25 | Genotypeda | 0.498a (0.002) | 0.538b (0.002) | 0.538b (0.002) | 0.559c (0.002) |
| Alla | 0.497a (0.001) | 0.518b (0.001) | 0.518b (0.001) | 0.521c (0.001) | |
| 0.15 | Genotypeda | 0.460a (0.003) | 0.501b (0.003) | 0.501b (0.003) | 0.528c (0.003) |
| Alla | 0.458a (0.002) | 0.481b (0.002) | 0.481b (0.002) | 0.486c (0.002) |
- a Different letters in the same row indicate a statistically significant difference between the covariance matrices (p < 0.0001)
- A: pedigree-based relationship matrix; GVR: IBS-based genomic relationship matrix constructed with either the observed allele frequencies (GVR-O) or the frequencies of all base population animals (GVR-B); GIBD-L: IBD-based genomic relationship matrix.
Discussion
De los Campos et al. (2013) found that ‘the effectiveness of GBLUP depends critically on the extent to which marker-derived genomic relationships reflect the patterns of realized genetic relationships at causal loci’. The current research attempted to compare two approaches to estimate true realized relationships to be used in the set-up of genomic relationship matrices. One was the widely used VanRaden (2008) approach, which estimates relationships using only markers (GVR). The second was an approach that uses genomic data to estimate realized relationships based on IBD sharing of marker alleles relative to the known pedigree (GIBD-L).
The real data set allowed comparing the empirical variation in genome sharing of relatives with the same pedigree relationship, from either IBD- or IBS-based estimators. The SD of the estimated genome sharing for GIBD-L was notably closer to the theoretical value than GVR-O or GVR-B. In contrast, it was extremely difficult to distinguish different pedigree relationships from the actual fraction of the genome shared estimated by GVR. Although GVR is an estimate of the realized proportion of genome-shared IBD, it does not take either the parent–offspring transmission or the segmental nature of inheritance of DNA into account (Thompson 2013). Indeed, permutation of the genotypes for each SNP will result in the same IBS-based G matrix. The mean of GIBD-L was extremely close to its theoretical value for most pedigree relationships. GVR-O was unbiased for the overall mean, yet it did not behave as well as GIBD-L when comparisons were made on a relationship basis. The most biased estimator was GVR-B (Table 3), which tended to overestimate pedigree IBD genome sharing. This can be explained in part by the fact that base allele frequencies were computed from a small number of animals that belonged to two different breeds (4 Duroc sires and 15 Pietrain dams) so that estimates of true base allele frequencies suffered from a lack of precision. In fact, GVR-B was the most biased for the half-cousins and unrelated relationships, which account for 27.2 and 27.9% of the pairwise estimated relationships, respectively, and are expected to have the lowest (or zero) theoretical mean pedigree IBD genome sharing (Table 1).
Results from our simulation allowed us to compare the precision and bias achieved by the different estimators of the true pedigree IBD genome sharing between genotyped animals. GIBD-L displayed higher precision than GVR-O. This can be because GVR-O could not capture the unobserved history of relatedness within a small livestock population as the one simulated when dealing with a small number of genotyped animals. A better scenario was assured when allele frequencies in the base population were used, allowing the precision of GVR-B to approximate that of GIBD-L. This result also agrees with the fact that GVR-B was nearly unbiased in our simulation, in contrast to the results from real data, where base allele frequencies were not well represented by frequencies of F0 genotyped animals. A solution, as in VanRaden (2008), could be to estimate base allele frequencies with a linear model that solves for gene content of non-genotyped ancestors and descendants using pedigree (Gengler et al. 2007).
Vela-Avitúa et al. (2015), in a simulated aquaculture breeding scheme, showed that differences in accuracies of GEBVs among G estimators depend on marker density: IBS-based GEBVs were slightly more accurate than their IBD-based counterparts using dense markers, but also considerably more sensitive to a reduction in density. Yet, these authors found that accuracy of IBD-based GEBV was stable across marker densities and, in fact, greater at low densities (≤100 SNP/M) than that achieved using the IBS-based G matrix. In our simulation using dense markers, accuracy of GEBV for selection candidates was statistically higher when matrix GIBD-L was used. This slight superiority in accuracy could be explained by the fact that our IBD-based approach differs from that used in the above-mentioned article in that it models LD information. This is achieved by adding a background IBD state to fit the hidden relatedness beyond the relatedness that is observed through the available pedigree structure. Yet, this comes at the expense of using HMM methods that are computationally intensive (~4 hours per chromosome on a computer having a Quad-core 2.7 GHz AMD Opteron 8384 processor with 128 GB of memory).
Characterizing actual relationships in animal, human and agricultural populations is a key aspect in genetic analysis. QTL detection models in association analysis generally correct for structure and relatedness between individuals using a relationship matrix (either genomic or pedigree-based) or even using the methods of estimating genome-wide pairwise IBD within families (Kennedy et al. 1992; Kang et al. 2010; Legarra et al. 2015). Legarra et al. (2015) obtained similar results when comparing methods to detect QTL in four livestock species using markers, whether a genomic or a pedigree-based numerator relationship matrix was used. Yet, no further investigation on the subject has been carried out so far. A more precise genomic relationship matrix such as the one proposed in our research (GIBD-L) may potentially imply higher power to detect QTL in livestock populations, where pedigree is (up to some extent) known.
With respect to the differences in accuracy of GEBVs among the IBS-based estimators, these were not statistically significant. Strandén & Christensen (2011) showed that changes in the numerator of GVR (as can the allele frequencies used to centre genotypes) do not change relative differences between the estimated GEBVs, because they are just shifted by a constant. However, modifying the denominator that scales GVR is like dividing or multiplying G by a constant and will, in principle, change results, although in our case this did not affect the results greatly.
Conclusion
Incorporating pedigree data to trace IBD inheritance in the calculation of genomic relationships improved the precision of estimates of actual relationships or proportion of genome shared between individuals in livestock populations. Moreover, the IBD-based method presented here better captures the extent of the variation in the actual proportion of genome shared by relatives that have the same kind or degree of pedigree relationship. When dealing with small numbers of genotyped animals, marker-only-based methods could be good estimators of G as well, provided that accurate inferences of allele frequencies in the base population were available. Using pedigree and markers, the gain in accuracy in elements of G was translated into higher accuracies in genomic breeding value predictions for selection candidates.
Acknowledgements
This project was supported by Agriculture and Food Research Initiative Competitive Grant no. 2010-65205-20342 from the USDA National Institute of Food and Agriculture and by funding from the National Pork Board Grant no. 11-042. Partial funding was also provided by the US Pig Genome Coordination Program. Computer resources were provided by the Michigan State University High Performance Computing Center (HPCC) and by Toulouse Midi-Pyrénées bioinformatic platform. NSF and RJCC were funded by grants of CONICET (PIP 2013-00833) and ANPCyT (PICT 2013-1661) from Argentina. Part of this work was made possible by a visit of NSF to INRA, Toulouse, France, financed by the Saint-Exupéry Scholarship Program 2013–2014 (MinCyT Argentina–French Embassy).




