Endogenous preferential treatment in centralized admissions
We wish to thank the editor, Chaim Fershtman, and two referees for useful comments that have significantly improved the article. We also wish to thank Atila Abdulkadiroğlu, Kalyan Chatterjee, Steve Ching, Eric Chou, Kim Sau Chung, Al Roth, Wing Suen, and seminar participants at Academia Sinica, Central University of Economics and Finance, National Tsing Hua University, Renmin University of China, Tsing Hua University, Shanghai University of Economics and Finance, University of Hong Kong, the 2008 HKU Summer Microeconomics Conference, and the Second Singaporean Economic Theory Conference for their comments. Any remaining errors are our own. Financial support from the Hong Kong Research Grants Council (HKU742407H) is gratefully acknowledged.
Abstract
We study a model of centralized admissions in which schools are allowed to pre-commit to admitting qualified applicants who rank them as their top choices over more qualified applicants who do not. A less popular school may use the pre-commitment to steal applicants who otherwise would not choose it as their top choice (the stealing motive); a popular school may use the pre-commitment to prevent its own applicants from being stolen (the preemptive motive). We identify the conditions for these two motives to exist. We also clarify the relationship of this phenomenon with that of pre-arrangement of school places.
“We want the students that want us most!”
—A New York City educator(New York Times, November 29, 2004)
1. Introduction
▪ A significant number of school and college places in the world are allocated through centralized admissions schemes. Instead of filing separate applications to different schools, students need to file only a single application (a rank-order list) through which they indicate their preferences for schools; schools then allocate their places in accordance with a strict protocol, taking into account applicants' rank-order lists as well as all other available information. We are interested in a phenomenon in which a school gives preferential treatment to applicants who rank it as their top choice over more qualified applicants who do not.
Such preferential treatment may be an intrinsic feature of the admissions scheme being used. For instance, in the so-called Boston admissions scheme, first discussed by Abdulkadiroğlu and Sőnmez (2003), school places are first assigned according to applicants' top choices. This means that an applicant failing to get into her top-choice school will also fail in getting into her second-choice school if the second-choice school has already filled up its places with applicants ranking it as their top choice, even though the applicant may be a much better student than many of the accepted applicants. (Regarding the old Boston scheme, also see Ergin and Sőnmez, 2006; Pathak and Sőnmez, 2008; Abdulkadiroğlu, Pathak, Roth, and Sőnmez, 2005, 2006.)
Our article, however, is concerned about preferential treatment that is a deliberate choice made by the school. One notable example is the system used in New York City prior to its reform in 2003 (see Abdulkadiroğlu, Pathak, and Roth, 2005). The emphasis of preferential treatment by some New York City schools is succinctly summarized by the complaint quoted at the beginning of this article by an administrator that the new admissions scheme no longer contained information on how each school was ranked by each applicant.1
There are two potential reasons for such a phenomenon, which we call endogenous preferential treatment. First, a school may want to admit those who are genuinely more enthusiastic about it, because presumably students' motivations and commitments are important to success in their studies. In contrast with this motivational consideration, a school may adopt the policy out of a strategic consideration. If preferential treatment helps sway applicants to rank a school as their top choice and if this effect is strong enough, the school may turn out admitting a better group of students. Thus, it is in the interest of the school to adopt the practice despite no intrinsic interest in each applicant's ranking of schools. In this article, we explore under what circumstances this latter strategic consideration is sensible.
In Section 2, we present our baseline model with two schools. Starting with the Gale-Shapley mechanism (Gale and Shapley, 1962), we allow schools to pre-commit to admitting qualified applicants who rank them as their top choices. We call this policy the immediate acceptance (IA) policy, in contrast with the deferred acceptance (DA) policy inherent in the Gale-Shapley mechanism. More specifically, we consider a three-stage game. First, schools—or school place offering units—announce publicly whether they pre-commit to an IA policy. Then, applicants submit their rank-order lists, followed by the assignment of places in accordance with the Gale-Shapley mechanism subject to constraints of schools' pre-commitments. Throughout the article, we assume that, albeit strategic, schools are honest and trustworthy.
Section 2 ends with a neutrality result, which roughly says the following. So long as the outcome in the game in which all schools have DA policies is deterministic and commonly known, no schools would gain from adopting IA. Exactly the same outcome, in terms of who enters what school, would result. Simple as it seems, this result suggests that uncertainty is essential for understanding the role of IA behind its strategic use. In light of this, we study in Sections 3 and 4 two types of uncertainty: demand uncertainty and ranking uncertainty.
In the demand uncertainty model, applicants are uncertain about others' genuine demands, that is, others' preferences for places at different schools. This captures scenarios in which applicants may not be certain of the latest fads regarding whether computer science or business studies, say, is popular this year. In the ranking uncertainty model, applicants do not know how well they are ranked among themselves. This model captures the scenario in which applicants are required to apply before learning their examination results or even before taking examinations.
Throughout the analysis, we identify two motives for pre-commitment. A school may use IA to steal applicants who otherwise would not have made it their top choice (the stealing motive). A less popular school is more likely to have a stealing motive when it is not too inferior to a more popular school in terms of the utility that enrolled students can obtain. On the other hand, rarely will a popular school have this motive. Under more restricted conditions, the popular school does have a motive to use IA. Although not helping to steal applicants, IA is attractive because it can prevent the less popular school from using IA and thereby protecting the popular school from being hurt (the preemptive motive). We show the conditions for such motives to exist and relate them to school popularity, differences in schools' preferences, and relative school size. We also find that being able to influence applicants' behaviors need not imply an improvement in the school's average student quality. IA can be influential yet self-defeating.
Our article falls into the literature that studies manipulation in matching and market design. Despite the very desirable property of stability, later work shows that the deferred acceptance mechanism introduced by Gale and Shapley is susceptible to manipulations prior to and during the match. In the mechanism in which students propose, schools may have an incentive to misrepresent their preferences (Dubins and Freedman, 1981; Roth, 1982; Roth and Sotomayor, 1990), to misreport their capacities (Sőnmez, 1997), or to have pre-arrangements with students prior to the admissions exercise (Sőnmez, 1999).
The new manipulation of admissions policy that we identify differs from the pre-arrangement policy in that it takes place during the matching exercise, rather than prior to it. As will be clear below, pre-arrangement does replicate the effect of the IA policy that we study, provided that the school engages in unrestrained pre-arrangement, ready to fill up all its places for this purpose—a condition unlikely to occur in many real-world applications. This suggests that the studies of pre-arrangement given the extent of its use that we actually observe are no substitute for the studies of manipulation that takes place during the centralized admissions exercise. Focusing on the existence of stable matching rules that are free of manipulation of pre-arrangement, Sőnmez (1999) assumes that in the centralized exercise, agents report their preferences truthfully. In the present article, however, we focus on equilibrium behavior subsequent to admissions policy choices. As such we are able to obtain the neutrality result, implying that a similar neutrality result also holds under unrestrained pre-arrangement and that, for pre-arrangement to matter, some kind of uncertainty is essential. There is a counterpart literature for decentralized markets, known as early contracting (see Li and Rosen, 1998; Roth and Xing, 1994; Suen, 2000). One market in which there was a great deal of endogenous preferential treatment was the decentralized market for clinical psychologists (Roth and Xing, 1997). And, of course, many American colleges have what is called “binding early decision.” So it may be as big an issue in decentralized as in centralized markets.
Section 5 extends our analysis to a framework of three schools, generating additional insights. As most of our analysis is conducted in an environment of a few schools, however, how likely a school may benefit from endogenous preferential treatment is an open question. Generalizing Roth and Peranson (1999) and Immorlica and Mahdian (2005), Kojima and Pathak (forthcoming) argue that under reasonable assumptions, the fraction of schools that can benefit from manipulations in the form of misreporting of preferences, misreporting of capacities, or pre-arrangement will become negligible as the matching market grows larger. A similar result may apply to the type of manipulation that we identify, although it needs to be proved. Thus, our contribution is to identify, manipulation motives rather than to assess their likelihood in large markets. By analyzing endogenous preferential treatment that was a feature of the old New York City system, our article complements the literature that attempts to understand real-world school choice mechanisms and their reforms.2
Our study is also relevant to other places where centralized admissions systems are being used. It is common for commonwealth countries to assign university places using such centralized systems.3 China's national college admissions system allocates a few million college places every year (Table 21-2, China Statistical Yearbook, 2006). At present, more than half of the provinces are still using the traditional hierarchical choice ranking scheme (dengji zhiyuan). In each such province, the provincial admissions office sends to each university—within or without the province—a short list of students exceeding by 20% the university's quota allotted to the province. These 120% students are strictly chosen, in accordance with public exam scores, among those students ranking the university, or some of its programs, as their top choice. Short-listed students who are declined by the university may be subsequently declined by universities that they ranked as their second choice, third choice, and so forth, simply because their places have all been filled up. This is a case of intrinsic preferential treatment similar to that found in the old Boston system. Notice that, in the case of insufficient first-choice students, the short list provided by the provincial admissions office will contain students who ranked the university, or some of its programs, as their second choice (and likewise third choice, fourth choice, etc.). These students are often treated disadvantageously: the university typically deduces some points from their public exam scores simply because they have not ranked the university as their top choice. Such deliberate policy of a university is a practice of endogenous preferential treatment that our article is concerned about.4 All in all, we have the feeling that, in the real world, concerns about endogenous preferential treatment are not unwarranted.
2. The model
▪ A mass of applicants of size N is competing to enter two schools. Each applicant is indexed by an ability attribute pair (y1, y2), where y1 may be her math score and y2 her language score, for example. (y1, y2)s are distributed over 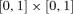 with a cumulative function which is continuous and has no mass point. Each applicant's ability pair, as well as the cumulative function, is commonly known, and as such she knows her exact ranking vis-à-vis other applicants. Given attribute pair (y1, y2), a fraction μ1 of applicants views school 1 as the better school: the utility to these applicants of attending the two schools is, respectively, u1 and u2, where u1 > u2 > 0; a fraction, μ2= 1 −μ1, of applicants views school 2 as better: the utility to these applicants of attending the two schools is v1 and v2, where 0 < v1 < v2. We call the former group of applicants type-1 applicants and the second group type-2 applicants.
with a cumulative function which is continuous and has no mass point. Each applicant's ability pair, as well as the cumulative function, is commonly known, and as such she knows her exact ranking vis-à-vis other applicants. Given attribute pair (y1, y2), a fraction μ1 of applicants views school 1 as the better school: the utility to these applicants of attending the two schools is, respectively, u1 and u2, where u1 > u2 > 0; a fraction, μ2= 1 −μ1, of applicants views school 2 as better: the utility to these applicants of attending the two schools is v1 and v2, where 0 < v1 < v2. We call the former group of applicants type-1 applicants and the second group type-2 applicants.
 (1)
(1)A centralized admissions scheme in the fashion of Gale and Shapley is in place; each applicant is required to submit a rank-order list of schools—indicating whether she regards school 1 as her first choice and school 2 as her second choice or vice versa.5 Before the centralized admissions scheme actually operates, schools publicly announce which policy they use: a deferred acceptance (DA) policy or an immediate acceptance (IA) policy. Under the former, the school ranks applicants based solely on their quality attributes and processes the applications strictly in accordance with the Gale-Shapley mechanism. Under the latter, whereas still using the centralized admissions scheme, the school is committed to admitting applicants who specify it as their top choice up to its capacity. We assume that schools are honest so that the commitment is genuine and credible; this is so perhaps because schools are honest, or simply because reputation concerns are a strong enough enforcement device.6 The game is identical to the Gale-Shapley mechanism except that schools may pre-commit to an IA policy. We do not consider other kinds of preferential treatment because the IA policy that we study, the most extreme kind, presumably gives the sharpest insight.7
We use a pair (p1, p2), where p1, p2=DA, IA, to represent the admissions policies used by the two schools. Under (DA,DA), there exists an equilibrium in which all type-1 applicants report school 1 as their top choice and all type-2 applicants report school 2 as their top choice. The two schools then admit according to the standard Gale-Shapley procedure. We call the strategies the truthful strategies, the equilibrium the truthful equilibrium, and the outcome (in terms of who goes to what school) the truthful outcome. Making use of (1), we use AQi(p1, p2) to denote school i's equilibrium average quality under policy pair (p1, p2), where i= 1, 2, and p1, p2∈{DA, IA}. Payoffs and the structure of the game are commonly known.
The truthful outcome is easy to characterize. For i= 1, 2, school i will set a cutoff standard, ci, so that all type-i applicants satisfying y1+αiy2≤ci are admitted and all type-j≠i applicants satisfying this criterion yet not admitted by j are also admitted. Because school 2 is less popular, it always admits some type-1 applicants who fail to get into school 1. On the contrary, being more popular, school 1 may or may not admit any type-2 applicants.
□ A neutrality result We first report a neutrality result (all proofs are relegated to Appendix A).
Proposition 1 Under any policy pair (p1, p2) where at least one school uses IA, the equilibrium outcome is unique and is the same as the truthful outcome.
Foreseeing the impact of the IA policy, every applicant who would be adversely affected will strategically rank the school that she would enter in the truthful outcome as her top choice; she knows what the school is under the complete information assumption. As such, she succeeds in getting into the school, and the effect of the IA policy is completely neutralized. It is clear that this constitutes an equilibrium. The uniqueness result is less straightforward. The following heuristic example, in which both school places and applicants are measured in discrete numbers, illustrates that uniqueness may not hold in general.
Example 1 s 1=s2= 2 and there are four type-1 applicants and four type-2 applicants, denoted as a1, a2, a3, a4 and b1, b2, b3, b4, where the subscripts denote the quality of the student (the lower the number the better, and ai and bi are equally qualified for all i). In the truthful outcome, school 1 admits a1 and a2 and school 2 admits b1 and b2. This is still an equilibrium outcome under (IA,IA). Provided that u2/u1 > 0.5, v1/v2 > 0.5 and that an equal-choice tie-breaking rule is used, there also exists an equilibrium outcome in which school 1 admits a1 and b2 and school 2 admits b1 and a2, supported by strategies in which a1 and b2 report school 1 as their top choice and b1 and a2 report school 2 as their top choice.
In Example 1, whereas there is a unique equilibrium outcome under (DA,DA), there are multiple equilibrium outcomes under (IA,IA): there exists another equilibrium outcome characterized by a coordination failure between a2 and b2. There are two points to notice. First, the new equilibrium outcome is sustained because of schools' weak preferences over applicants (not satisfied in Proposition 1). Second, despite schools' weak preferences, the outcome non-uniqueness is restricted to the two borderline applicants, but not more qualified ones. By ranking it as her top choice, a1 can enter school 1 and she surely will in any equilibrium; similarly, by ranking it as her top choice, b1 can enter school 2 and she surely will in any equilibrium. In general, through an iteration process—which will be frequently used in the later analysis—one can narrow down the set of equilibrium outcomes, and may obtain a unique outcome under favorable conditions.
Here we report a more general neutrality result, in which we allow more than two schools and impose no restrictions on the number of types of applicants in terms of their preferences.
Proposition 2 Consider an environment with complete information, strict preferences, discrete agents, and a number of schools greater than or equal to two. Suppose that all agents on one side are acceptable for all agents on the other side (better assigned than not) and that there are more applicants than school places. Let p′ be any policy profile in which at least one school uses IA, and p be the one in which all schools use DA. Then all Nash equilibrium (NE) outcomes under p are NE outcomes under p′. If NE outcomes under p′ are all stable, then the two sets of NE outcomes under p and p′ coincide, equal to the set of all stable matchings.8
That the truthful outcome, itself a stable matching, continues to be an equilibrium outcome when IA is used suggests that, without uncertainty, applicants are able to replicate the same outcome by optimally misreporting their preferences. We will next turn to two models of uncertainty that make IA relevant.
3. Demand uncertainty
 (2)
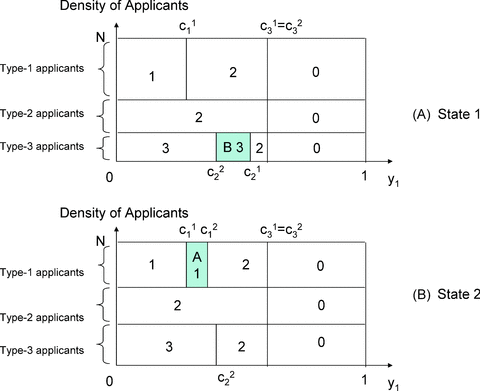
(2)□ Unilateral incentive We now illustrate how demand uncertainty may enable IA to matter. To see this, we focus on the simplest case in which α1=α2= 0: the two schools have identical preferences and do not care about the y2 attribute. Denote by F(.) the cumulative distribution function of y1. The truthful equilibrium under (DA,DA) is characterized as follows. Type-i applicants specify school i as their top choice, i= 1, 2. Because of (2), school 1 will only admit type-1 applicants, setting cutoff values c11 and c21 in the two states, where c11=F−1(s1/μ11N) < c21=F−1(s1/μ21N). School 2 sets the same cutoff value, c2=F−1((s1+s2)/N) > c21, in both states, admitting all type-2 applicants satisfying this condition as well as all type-1 applicants satisfying this condition who have been declined by school 1. Figure 1 illustrates these cutoffs, using a uniform distribution of y1. We now study school 2's incentive to use IA.
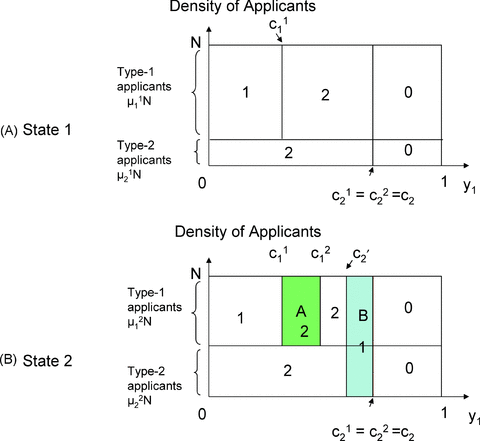
UNDER (DA,DA), THE TWO SCHOOLS SET CUTOFFS, ck1 AND ck2, IN STATE k, k= 1, 2
Provided that u2 > π2u1, the number in each region indicates the school the applicant enters in equilibrium in (DA,IA). In state 2, school 2 succeeds in stealing type-1 applicants in region A, in lieu of those in region B (no change in state 1).
Lemma 1 Under (DA,IA), in any equilibrium, (i) the reporting strategies of those applicants with y1≤c11 are the same as under the truthful equilibrium, and (ii) all type-2 applicants have truthful reporting as their (at least weakly) dominant strategy.
Point (i) in the lemma is shown by iterative elimination of dominated strategies, in much the same way whereby we showed the neutrality result in Proposition 1; point (ii) is straightforwardly true. Despite the lemma, those type-1 applicants with y1 > c11 are not immune to school 2's use of IA. One can show that, provided that u2 > π2u1, a non-truthful equilibrium exists in which (i) all type-1 applicants with y1≤c11, as well as all type-2 applicants, report truthfully, and (ii) all type-1 applicants with y1∈ (c11, c21] specify school 2 as their top choice (strategies of other applicants being inconsequential). In this equilibrium, whereas the state 1 outcome is exactly the same as in the truthful equilibrium, the state 2 outcome is not. Under state 2, those type-1 applicants with y1∈ (c11, c21] now are admitted by school 2 and their mass is equal to |A| =s1(1 −μ21/μ11) (the area in region A in Figure 1). To accommodate it, school 2 sets a more stringent cutoff of c′2=F−1((s1+s2− |A|)/N) < c2, releasing less qualified applicants with y1∈ (c′2, c2] for school 1's admission (region B in Figure 1). School 2 is strictly better off by stealing students from school 1.
One can show that this equilibrium is indeed unique—there does not exist any other equilibrium that corresponds to a different outcome. The key point is that those type-2 applicants with y1 > c2 reporting school 2 as their top choice act as a threat, forcing those type-1 applicants with y1∈ (c2−ɛ, c2] to rank school 2 as their top choice, where ɛ is a small positive number. But this in turn implies that those type-1 applicants with y1∈ (c2−ɛ−ɛ′, c2−ɛ] are forced to rank school 2 as their top choice, where ɛ′ is a small positive number. This process continues to apply to all type-1 applicants with y1∈ (c11, c2].9
The stealing effect of school 2 does not always exist, however. When u2 < π2u1, school 2's IA policy is unable to persuade type-1 applicants with y1∈ (c11, c2] to make school 2 their top choice. As a result, these students are neither stolen by school 2 in state 2, because of the pre-commitment, nor are they admitted by school 2 in state 1. School 2 has to admit poorer applicants to fill the vacancies. School 2 is thereby worse off as a whole, and the IA policy is self-defeating.10
The analysis of the effect of (IA,DA), the regime in which only school 1 uses IA, is more straightforward. Because under (DA,DA), school 1 already sets a more stringent admissions requirement, those type-2 applicants whom school 1 is interested in stealing must be good enough to enter school 2—their preferred school—and they have no incentive to change their behavior under (IA,DA). As a result, the truthful outcome prevails under (IA,DA), and school 1 never benefits from using IA when the other school does not use it. This asymmetry between school 1 and school 2 with respect to the stealing effect appears repeatedly in the article.
So far, we have assumed that α1=α2= 0. But it is clear that the same argument holds true as long as α1=α2, which need not exactly equal zero. We summarize our results as follows.
Proposition 3 (unilateral incentive) Suppose that α1=α2.
- (i)
Suppose that u2 > π2u1(u2 < π2u1). Under (DA,IA), there exists a unique equilibrium outcome, in which school 2's admitted applicants' average quality is improved (worsened) compared with under (DA,DA).
- (ii)
(IA,DA) and (DA,DA) are outcome equivalent.
A few comments are in order here. First, given μ11 and starting from μ21=μ11, the number of applicants who are affected by school 2's IA increases as μ21 decreases. That is, starting with no demand uncertainty, an increase in the difference between μ11 and μ21 always increases the number of applicants whose behavior is affected. Second, because the two schools have identical preferences, whenever school 2 experiences an improvement of its average quality through using IA, school 1 experiences a worsening thereby. Third, some applicants are better off under (DA,IA) than under (DA,DA). Those type-1 applicants in region B now get into school 1 in state 2 under (DA,IA), whereas they can only get into school 2 under (DA,DA). (Thus, it is not the case that school 2's IA policy will be universally opposed by all applicants.) Relatedly, we also note that these type-1 applicants have a higher expected utility compared with their slightly more qualified counterparts (with slightly lower y1), who also adopt the same strategy. Somewhat ironically, just because the latter group is of better quality and is selected by school 2—their top choice but less-preferred school—the former group is able to get into school 1.
Our last comment concerns the relationship between IA and pre-arrangement identified in Sőnmez (1999) (see also Kojima and Pathak, forthcoming; see also Li and Rosen, 1998; Roth and Xing, 1994, 1997; and Suen, 2000 for pre-arrangement in decentralized markets).11 Consider an alternative game in which the two schools are committed to (DA,DA) in the centralized admissions exercise. Suppose, prior to the exercise, school 2 is allowed to pre-arrange with applicants. If it is allowed to use up all its places s2 for pre-arrangement and is committed to admitting every applicant subject only to its capacity constraint, then the same outcome prevails as under our model of (DA,IA): provided that u2 > π2u1, those type-1 applicants stolen by school 2 under (DA,IA) will aim at and succeed in pre-arranging with school 2. The intuition is exactly the same: the possibility of all of school 2's places being taken up in the pre-arrangement stage compels the aforementioned type-1 applicants to pre-arrange. However, if the number of places available for pre-arrangement is limited, the outcome under (DA,IA) need not be fully replicated by pre-arrangement followed by a centralized admissions exercise with (DA,DA). To be more precise, consider the scenario in which α1=α2= 0. Suppose the total number of places that school 2 allots for pre-arrangement is less than F(c2) −F(c21) < s2. Even though these places are completely used up, there are still enough remaining places to admit all type-2 applicants with y1≤c21 and all type-1 applicants with y1∈ (c11, c21]. Therefore, it is the dominant strategy for the latter group to not pre-arrange but to participate in the centralized procedure under (DA,DA).
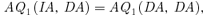 (3)
(3)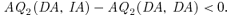 (4)
(4)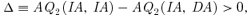 (5)
(5)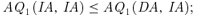 (6)
(6)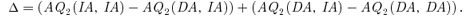 (7)
(7)Under (DA,IA), applicants with y1≤c′2 are admitted by the same school under both states and they are admitted by their top-choice schools. They are admitted as though both schools were using IA. Therefore, they could not do better by a unilateral deviation under (IA,IA). In fact, one can show that—using iterative elimination of the strictly dominated strategy that we used earlier—adopting the same strategies as under (DA,IA) constitutes the unique equilibrium. This also implies that to study the difference, AQ2(IA, IA) −AQ2(DA, IA), one only needs to focus on the state 1 change.
- (i)
In equilibrium, applicants with y1≤c′2 have the same reporting behavior under (IA,IA) as under (DA,IA).
- (ii)
In state 2, school 2's student intakes under (IA,IA) are the same as under (DA,IA).
Proof Omitted.
By contrast, applicants with y1∈ (c′2, c2] need to choose between being admitted by school 2 in state 1 and not being admitted by any school in state 2, on one hand, and being admitted by school 1 in state 2 and not being admitted by any school in state 1, on the other. As the respective utilities from the two choices are π1u2 and π2u1 for type-1 applicants and π1v2 and π2v1 for type-2 applicants, to understand these applicants' optimal strategies, we need to consider three cases: (i) π1u2 > π2u1 (implying π1v2 > π2v1), (ii) π1v2 < π2v1, and (iii) u1/u2 > π1/π2 > v1/v2.
Case (i). π1u2 > π2u1 It is easy to show that all applicants with y1∈ (c′2, c2] now specify school 2 as their top choice. School 2's student intakes under (IA,IA) are just the same as under (DA,IA). Substituting AQ2(IA, IA) −AQ2(DA, IA) = 0 and (4) into (7), we find that (7) is negative and, as a result, there does not exist any preemptive equilibrium.
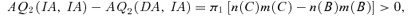 (8)
(8)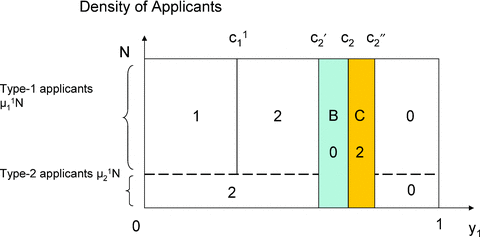
THE NUMBER INSIDE EACH REGION SHOWS THE PLACEMENT OF APPLICANTS IN THE REGION IN STATE 1 UNDER (IA,IA)
Applicants in region B will report school 1 as their top choice. There is no change in placement from (DA,IA) to (IA,IA) in state 2, which is not depicted.
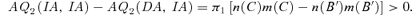 (9)
(9)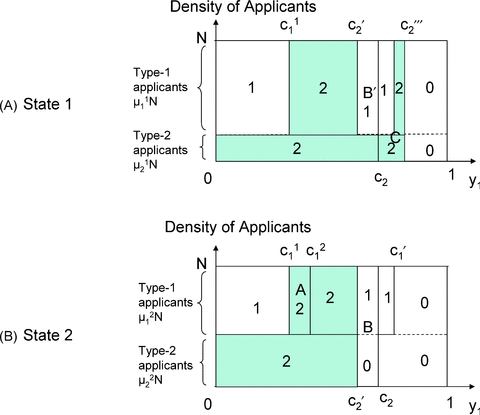
THE NUMBER INSIDE EACH REGION SHOWS THE PLACEMENTS OF THE APPLICANTS IN THE REGION UNDER (IA,IA)
Proposition 4 (Competition) Suppose that α1=α2.
- (i)
If π2u1 > u2, there are only two pure-strategy equilibria: (DA,DA) and (IA,DA). They both lead to the same truthful outcome.
- (ii)
If π2u1 < u2 and π1u2 > π2u1, there is a unique equilibrium of (DA,IA).
- (iii)
If π2u1 < u2 and π1v2 < π2v1, there is a unique equilibrium: either (DA,IA) or (IA,DA). If α1=α2= 0 and y1 is uniformly distributed, then (IA,DA) is an equilibrium if and only if s2/s1 < 2π1/π2.
- (iv)
If π2u1 < u2 and u1/u2 > π1/π2 > v1/v2, (DA,IA) is an equilibrium, and there may exist another equilibrium, (IA,DA). If α1=α2= 0 and y1 is uniformly distributed, then (IA,DA) is an equilibrium if
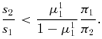 (10)
(10)
For result (iii), there are two ways to understand the condition s2/s1 < 2π1/π2. First, given that the other parameters are unchanged and given s1, the greater s2, the less likely that a preemptive equilibrium exists. Comparing (IA,IA) with (IA,DA), we find that school 2's loss in state 1 is invariant to s2 but its gain in state 2 is increasing in s2. Hence, when s2 is sufficiently large, IA is so attractive to school 2 that its use is never thwarted. Second, π1/π2 has to be sufficiently large for Δ > 0. The reason is that the greater the likelihood of state 1, the greater weight we put on state 1's effect, which is favorable for Δ > 0. For result (iv), the intuition behind the roles of s2/s1 and of π1/π2 is analogous to that of point (iii) and is not repeated. Note that unlike in point (iii), (10) is only a sufficient condition, and its violation does not necessarily mean the nonexistence of a preemptive equilibrium.
□ Heterogeneous school preferences Thus far, our results are obtained under the assumption of identical school preferences. It is useful to see how the insights may be generalized under heterogeneous school preferences. Our working article (Chiu and Weng, 2007) discusses this in more detail; here we only want to highlight a few points. We argue that Proposition 3 still holds so long as α1 and α2 do not differ too much so that school 1 will not admit type-2 applicants under state 1. In particular, provided that school 1 does not use IA, school 2 benefits (worsens) from using IA if u2 > π2u1 (u2 < π2u1). On the other hand, when α1 and α2 differ so much that in the truthful outcome, school 1 will admit type-2 applicants under both states, the difference between school 1 and school 2 blurs. As some type-2 applicants enter school 2 in state 1 and enter school 1, their less preferred school, in state 2, school 1 now has the incentive to steal this group of applicants using IA. If the utility from being admitted by school 1 for certainty exceeds the utility from being admitted by school 2 in state 1 and not by any school in state 2 (i.e., v1 > π1v2), these applicants will be successfully swayed and school 1 is better off. Of course, if v1 < π1v2, school 1's IA is self-defeating. A new question is what the equilibrium is like when school preferences differ sufficiently and both schools have a stealing motive. Through simulation using two specifications for the distributions of (y1, y2), we find that there are ample scenarios in which both schools using IA can be an equilibrium outcome. It also generates some comparative statics, which are found in the working article.
4. Ranking uncertainty
▪ Here we argue that applicants' uncertainty about their relative rankings among all applicants might also make IA relevant. We call this a model of ranking uncertainty. To make the point, we focus on a very simple version. Like in the previous model, there are two schools with places, s1 and s2, for which a mass of applicants of size N is competing. The two schools' preferences are represented by α1= 0 and α2≥α1. Each applicant is characterized by an attribute pair (y1, y2) uniformly distributed over [0, 1]×[0, 1]. The distribution function is commonly known, and schools know each applicant's attribute pair when evaluating applicants. Despite this, each applicant does not know her own attribute pair (nor the attribute pair of any other applicants) and is ex ante identical. This is the quintessential case of ranking uncertainty. We also assume that applicants have identical preferences. For each applicant, the utility of attending school i is ui, i= 1, 2, so that u1 > u2; the utility of not attending any school is zero.
□ Identical school preferences
Unilateral incentive We first study the case of identical school preferences, that is α1=α2= 0, and as such we can represent each applicant's attribute simply by her first attribute, y1. Under (DA,DA), the equilibrium is such that all applicants make school 1 their top choice. It follows immediately that school 1 never has the stealing motive. This is not the case for school 2, however. Suppose under (DA,IA) that all other applicants report truthfully. By reporting truthfully, an applicant obtains an expected payoff of (s1u1+s2u2)/N; by reporting school 2 as her top choice, she obtains a payoff of u2 for certain. If u2/u1 is sufficiently high, such a unilateral deviation is beneficial and the truthful equilibrium is infeasible. This means that, in equilibrium, a nonnegligible fraction of applicants will specify school 2 as their top choice, and if this fraction (denoted by b) is large enough, school 2 will indeed benefit from the IA policy. The equilibria under (DA,DA) and (DA,IA) are shown in Figure 4, where a and b, respectively, are the corresponding number of applicants who specify school 1 and school 2 as their top choice.
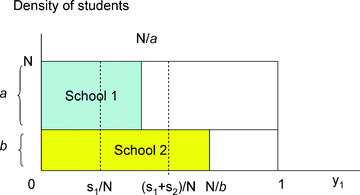
RANKING UNCERTAINTY
The two dotted lines show the cutoffs under (DA,DA). The two shaded regions show the admitted students under (DA,IA).
Proposition 5 (Unilateral incentive) Suppose that α1=α2= 0 and that y1 is distributed uniformly over the [0,1] interval.
- (i)
(IA,DA) and (DA,DA) are outcome equivalent.
- (ii)
Under (DA,IA), if u2/u1 < s1/(N−s2), there exists a truthful equilibrium.
- (iii)
Under (DA,IA), if u2/u1 > s1/(N−s2), then (a) there does not exist a truthful equilibrium, but (b) there exists an equilibrium in which b∈ (s2, N) and, in this equilibrium, AQ2(DA, IA) < AQ2(DA, DA), if and only if u2/u1 > 1/2.
According to point (iii), the condition for school 2's IA to influence the applicants' behaviors is different from the condition for it to benefit from the policy. For instance, consider the parameter values s1=s2=N/4 and u2/u1= 0.4. Then, school 2's IA is able to influence the applicants' behaviors but its average applicant quality will worsen. More generally, provided that 2s1+s2 < N, there exists a nonvanishing range of u2/u1∈ (s1/(N−s2), 1/2) such that school 2's IA is influential yet self-defeating.13
Competition Given that u2/u1 > s1/(N−s2), the equilibrium under (DA,IA) has the following simple but powerful feature: relative to school 2's, school 1's cutoff value must be more stringent. (Or else, each applicant would strictly prefer to make school 1 her top choice, contradicting the claim that school 1's cutoff value is less stringent.) This implies that school 1 admits only among those who specify it as their top choice. Taking into account the property that b > s2 (part [iii] of Proposition 5), we reckon that neither school will admit any applicant not specifying it as her top choice. In other words, the outcome under (DA,IA) is exactly the same as that under (IA,IA). Noting the outcome equivalence of (DA,DA) and (IA,DA), we conclude that, regardless of school 2's policy choice, school 1 cannot worsen school 2 through using IA. School 2's IA is non-preemptable.
Proposition 6 (Competition) Suppose that α1=α2= 0 and that y1 is distributed uniformly over the [0,1] interval.
- (i)
If u2/u1 > max{s1/(N−s2), 1/2}, then there is a unique equilibrium outcome, which is the same as under (DA,IA).
- (ii)
If u2/u1 < max{s1/(N−s2), 1/2}, then there is a unique equilibrium outcome, which is the same as under (DA,DA).
Proof Omitted.
According to the first result, when u2/u1 is high enough, school 2 will gain from using IA, and its use of IA is not deterred by school 1. In fact, school 2's student intake is invariant to whether or not school 1 adopts IA. There are two pure-strategy equilibria: (DA,IA) and (IA,IA), and they are outcome equivalent. According to the second point, when u2/u1 is not high enough, school 2 will not gain from using IA and will not use it. There are two pure-strategy equilibria: (DA,DA), and (IA,DA), and they are outcome equivalent. To conclude, we have found not only an asymmetry between the two schools regarding the stealing effect but also the lack of preemptive ability on the part of the popular school.
□ Heterogeneous school preferences Despite its absence under homogeneous preferences, a preemptive equilibrium by school 1 may exist if school preferences are sufficiently heterogeneous. To see this, we assume that α1= 0 and α2→∞ such that school 1 cares about the applicants' first attribute, y1, and school 2 cares only about their second attribute, y2. This is the most extreme case of heterogeneous preferences. Under (DA,DA), applicants still report truthfully, and school 1 admits applicants whose y1≤c1=s1/N and school 2 admits applicants whose (y1, y2) satisfies y1 > c1 and y2≤c2=s2/(N−s1), where c1 and c2 are the two cutoffs on y1 and y2 that the two schools, respectively, set in equilibrium. We have the following proposition regarding the unilateral incentive to use IA.
Proposition 7 (Unilateral incentive) Suppose α1= 0, α2→∞, and (y1, y2) is distributed uniformly over the [0,1] square.
- (i)
(IA,DA) and (DA,DA) are outcome equivalent.
- (ii)
Under (DA,IA), if u2/u1 < s1/(N−s2), there exists a truthful equilibrium; if u2/u1 > s1/(N−s2), then (a) there does not exist a truthful equilibrium, but (b) there exists a unique equilibrium, in which b=N and AQ2(DA, IA) < AQ2(DA, DA).
The first result is derived from the fact that school 1 has no incentive to use IA given that school 2 does not use it. The bandwagon phenomenon in result (ii)b is a joint outcome of school 1's DA and the two schools' orthogonal preferences. Because of school 1's DA, those applicants who did not specify school 1 as being as their top choice are not discriminated against by school 1 when they become available for its selection. Because of the schools' orthogonal preferences, these applicants are viewed by school 1 as being as good as those who specified school 1 as their top choice. As a result, they will be admitted with the same probability by school 1 as though they chose it as their top choice. Foreseeing this, they find it optimal to make school 2 their top choice provided that u2 is sufficiently high. In the identical school preferences case, on the contrary, those specifying school 2 as their top choice and subsequently declined by school 2 are of inferior quality from school 1's point of view and will not be admitted. This difference leads to a very significant difference in terms of the applicants' behaviors.
Given that b=N, school 2 has all the applicants to select from, and it is not surprising to see that the average quality of its intakes will improve. We note in passing that, under (DA,IA), the two schools will have cutoffs c1=s1/(1 −c2)N and c2=s2/N, with average qualities AQ1(DA, IA) =s1/2(N−s2) and AQ2(DA, IA) =s2/2N. Compared with their counterparts under (DA,DA), we know that school 1 is worse off whereas school 2 is better off. Therefore, the ability to influence applicants' behavior is equivalent to gaining from the IA policy.
We next note that, if u2/u1 > s1/(N−s2) and both schools are allowed to pre-commit to IA, there are two asymmetric equilibria: (IA,DA) and (DA,IA). The policy pair (IA,IA) is not an equilibrium because given that the other school uses IA, each school finds it optimal not to use it, that is, we have AQ1(DA, IA) < AQ1(IA, IA) and AQ2(IA, DA) < AQ2(IA, IA).
Proposition 8 (Competition) Suppose that α1= 0, α2→∞, (y1, y2) is distributed uniformly over the [0,1] square, and u2/u1 > s1/(N−s2). There are two pure-strategy equilibria: (IA,DA) and (DA,IA).
(IA,DA) is a preemptive equilibrium. Not directly benefiting from the use of IA, school 1 can deter school 2 from using IA. Thus, the asymmetry between the two schools that we have seen under homogeneous preferences is somewhat diluted.
□ Discussion As in the demand uncertainty model, we have found both stealing and preemptive incentives in this ranking uncertainty model. Regarding the preemptive motive, we have new results. There is little the popular school can do to prevent the less popular school from choosing IA when the two schools have like preferences. When they are sufficiently different, however, the popular school can successfully use IA as a defensive policy. More importantly, universally seen as a less preferred school, school 2 is still able to steal students from school 1. This is a unique feature of the ranking uncertainty model.
Despite our focus on the quintessential case, we maintain that the general insights still hold when applicants have more information about the rankings among themselves. We illustrate this with a simple variant. Assume that, whereas still not knowing her y1, each applicant observes a signal 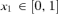 of it. We assume that x1 and y1 are affiliated and distributed according to a cumulative function that is continuous and has no mass point. In this case, the lower her signal x1, the more confident is an applicant that her y1 is low. Under (DA,DA), applicants report truthfully. As a result, school 1 admits all applicants with y1≤c1 and school 2 admits all applicants with y1∈ (c1, c2], where c1 and c2 are the equilibrium cutoffs set by the two schools.
of it. We assume that x1 and y1 are affiliated and distributed according to a cumulative function that is continuous and has no mass point. In this case, the lower her signal x1, the more confident is an applicant that her y1 is low. Under (DA,DA), applicants report truthfully. As a result, school 1 admits all applicants with y1≤c1 and school 2 admits all applicants with y1∈ (c1, c2], where c1 and c2 are the equilibrium cutoffs set by the two schools.
Under (DA,IA), provided that u2/u1 is high enough, one can show that there exists a critical value, x*1, such that applicants with x1 < x*1 (x1 > x*1) write school 1 (school 2) as their first choice, that school 1 and school 2 are both oversubscribed, and that each school admits only from those who report it as their top choice. Denote their cutoffs by c′1 and c′2 > c′1. As u2/u1 approaches unity, in the limiting case, c′1=c′2=c2, and exactly the same set of applicants admitted under (DA,DA) is admitted under (DA,IA). Because now school 2 gets better students than under (DA,DA), it clearly benefits from using IA. When u2/u1 is lower, it is conceivable that the stealing effect will become detrimental. Using this framework, we thus are able to replicate the main results in Propositions 4 and 5 (see Appendix B for details).
5. Multiple schools
▪ We now explore a framework of three schools, denoted by q1, q2, and q3, to check whether the basic insights found still hold and whether additional insights will emerge. We assume that α1=α2=α3= 0 (i.e., schools have the same preferences). We first study demand uncertainty, assuming that all applicants who share the same ordinal preferences share the same cardinal preferences, and that their proportions are different under different states of the world. A full model for a three-school case will consist of six types of applicants, classified by their preferences. To illustrate the point, however, it suffices to focus on a smaller number of types. We next study ranking uncertainty and conclude.
□ Multiple stealing Unlike in our earlier model, in general a school may steal more than one type of applicants from more than one school in more than one state. Suppose there are three types of applicants, 1, 2, and 3, with the following strict preferences: q1≻1q2≻1q3, q2≻2q3≻2q1, and q3≻3q1≻3q2. Denote by ui(θ) the utility a type θ applicant obtains from entering school i. Suppose there are two states, π1 and π2≡ 1 −π1, such that the truthful outcome is depicted in Figure 5.
THE TRUTHFUL OUTCOME IN EACH STATE
School 2's IA policy may be able to steal some type-1 applicants (region A) in state 2 and some type-3 applicants (region B) in state 1.
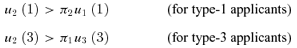
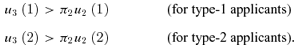
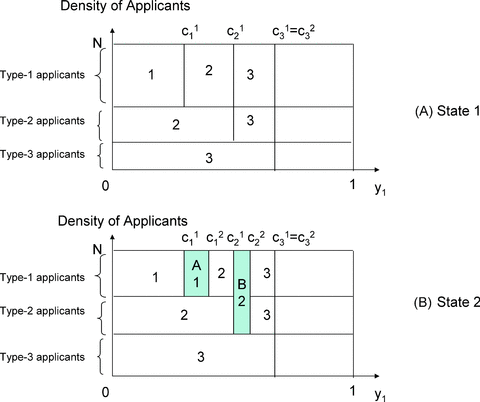
A SCHOOL'S LACK OF THE STEALING EFFECT HINDERS ITS PREEMPTION
School 3's IA may want to steal type-1 and type-2 applicants from school 2 (region b), and School 2's IA may want to steal type-1 applicants from school 1 (region A). The lack (presence) of a beneficial stealing effect by school 2 hinders (enhances) its preemption against school 3's IA.
□ Horizontal competition versus vertical competition We note that IA has no such strategic value for a school in its competition with another school if under no states do any applicants consider it as the better school. Imagine a model in which there are two types of applicants with preferences: q1≻1q2≻1q3 and q1≻2q3≻2q2. There are two states of the world so that the proportions of the two types are μi1 and μi2≡ 1 −μi1 in state i, i= 1, 2. Despite the uncertainty about the proportion of each type, the cutoff standard set by school 1 under the truthful outcome is known and invariant across states. Hence, school 1 is insulated from any stealing attempt by school 2 or school 3. A generalization is that a school generally known to be superior to other schools will not be affected by use of IA by the latter schools. We may say that the school competition studied in Section 3 is horizontal competition: for each school, there are applicants who find it the best, whereas the competition between q1, on the one hand, with q2 and q3, on the other, that we study here is vertical competition. Our discussion suggests that in the case of demand uncertainty, the IA policy matters only for schools that engage in horizontal competition.
□ Ranking uncertainty This model with affiliated signals (introduced in the second half of Section 4) is extendable to a multiple-school framework. Suppose there are three schools that give admitted students the utilities of u1, u2, u3, where u1 > u2 > u3. Suppose u3/u2 and u2/u1 are sufficiently high. Then it is conceivable that under the policy regime (DA,DA,IA) there exists a critical value x*1 so that those applicants with higher, hence worse signals will be swayed to rank school 3 as their top choice and as a result school 3 is better off using IA. It is interesting to note that school 3 steals students not only from school 2 but also from school 1, which is two places better. It is also conceivable that under (DA,IA,IA) there exists x′1 and x″1 so that those with signals x1 < x′1 rank school 1 as their top choice, those with x1∈ (x′1, x″1] rank school 2 as their top choice, and those with x1 > x″1 rank school 3 as their top choice.
□ Large number of schools The previous exploration suggests that, in a multiple-school setting, conditions can be found under which some school has the motive to steal applicants using IA. We have not, however, addressed the question as to what fraction of schools will be expected to have such a motive or how likely it is a beneficial use of IA may occur.
It is worth noting the recent work of Kojima and Pathak (forthcoming) on the incentive to manipulate in large markets. Generalizing Roth and Peransonate (1999) and Immorlica and Mahdian (2005), they show that the fraction of schools that can benefit from manipulations in the form of misreporting of preferences, misreporting of capacities, or pre-arrangement will become negligible as the matching market grows larger. They also show that no manipulation is an ɛ-equilibrium between schools and applicants when the market is getting large and the sequence of markets has the property of being sufficiently thick. It is a question whether scenarios that do not satisfy their assumptions may still be interesting.15 Moreover, the model they consider is very different from ours. For instance, in their game of equilibrium analysis, schools submit their preference lists prior to applicants knowing their preferences and submitting their rank-order lists. That said, we do have the feeling that a similar result may apply to the type of manipulation that we identify, although it needs to be formally analyzed. We leave this for future research.
6. Concluding remarks
▪ We have been interested in a phenomenon in which a school deliberately gives preferential treatment to applicants who rank it as their top choice over more qualified applicants who do not. We have explored a particular form of preferential treatment in which a school uses the so-called immediate acceptance policy, committing to admitting applicants who rank it as their top choice as long as places are available. We have identified two motives of doing so. A less popular school may use the pre-commitment to steal applicants who otherwise would not choose it as their top choice (stealing motive); a popular school may use the pre-commitment to prevent its own applicants from being stolen (preemptive motive).
What can we do to reduce the scope and effects of endogenous preferential treatment? One natural answer is to reduce the scope of uncertainty. Demand uncertainty can be reduced by a more thorough survey of applicants' preferences prior to application, whereas ranking uncertainty can be reduced by providing finer examination grades and scores or postponing the application period until applicants know their examination scores.
Should endogenous preferential treatment be banned? In our model, we assumed that schools adopted preferential treatment simply out of a strategic consideration, and the motivational consideration was completely neglected. When students' motivations and commitments are important to success in their studies, schools naturally want to admit students who like them most, other things being equal.16 There is nothing wrong with it and banning preferential treatment does not seem justifiable. To answer the question satisfactorily, therefore, requires studying a model that also takes into account the motivational consideration. We hope that this issue can be tackled in the future.
Footnotes
Appendices
Appendix A
▪ Proofs of Lemma 1 and Propositions 1–5, 7, and 8 follow.
Proof of Proposition 1: Existence Partition applicants into three groups according to where they end up under the truthful outcome: those who get admitted to school 1 (with measure s1), those who get admitted to school 2 (with measure s2), and the rest. Call them group 1, group 2, and group 0 applicants, respectively. Given the policy pair in which at least one school uses IA, consider the following strategies: each group 1 applicant specifies school 1 as her top choice, and each group 2 applicant specifies school 2 as her top choice. (It does not matter what the rest will do.) We first note that school k considers every group k applicant strictly better than every group 0 applicant, k= 1, 2. (Otherwise, it should have given a place to some group 0 applicant under (DA,DA).) Therefore, in the first round of the Gale-Shapley mechanism, school k will keep all group k applicants. Each school that uses IA will simply admit this group of applicants and will not proceed to the second round. The school, if any, that uses DA will find the applicants it retained in the first round to be strictly better than any applicant whom the school can newly consider in the second round. As a result, the mechanism terminates with school k admitting all group k applicants, k= 1, 2. Given the aforementioned prescription for applicants, it is clear that no applicant can benefit from a unilateral deviation; otherwise, she would have benefitted from a unilateral deviation under (DA,DA). Thus, the truthful outcome is still feasible as an equilibrium outcome under the said policy pair. It is clear that this same result holds for a general setting with multiple schools.
Uniqueness For i= 1, 2, let Qi be the set of all type-i applicants. Let Ri be the set of applicants admitted by school i in the truthful outcome and Si be the set of type-i applicants among them. Given any policy regime (p1, p2) where at least one school uses IA, we construct a recursive process that determines the equilibrium. Essentially, the recursive process helps us clarify the following equation. Suppose school i happens to have received the applications from all type-i and type-j applicants, j≠i. What is the cutoff, denoted by γi(1), so that an applicant with (y1, y2) satisfying y1+αiy2≤γi(1) can surely enter school i? Thus those type-i applicants satisfying this criterion, denoted by the set Ti(1), can enter school i despite the most fierce competition from type-j applicants (this is the case whether the school uses DA or IA). Hence, there cannot exist another equilibrium in which any of them is not assigned to school i. Now that we know in equilibrium type-i applicants in Ti(1) will enter school i (and type-j applicants in Tj(1) will enter school j), we proceed to the next round to deal with the remaining unassigned applicants. In this round, we ask a similar question: suppose school i happens to have received, along with the applications from Ti(1), the applications from all remaining unassigned applicants (of both types). What is the cutoff, denoted by γi(2), so that an applicant with (y1, y2) satisfying y1+αiy2≤γi(2) can surely enter school i? Those type-i applicants satisfying this criterion can thus enter school i despite the most fierce competition from type-j applicants (this is the case whether the school uses DA or IA). Hence, there cannot exist another equilibrium in which any of them is not assigned to school i. We argue that when we continue this process, at the end, in any equilibrium each school is assigned the same set of applicants under the truthful equilibrium, and the equilibrium outcome is unique.
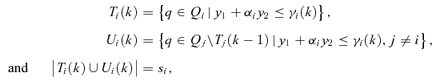
It is easy to show that for all k, Ti(k) ⊇Ti(k− 1) and γi(k) ≥γi(k− 1). That is, the set of type-i applicants who get assigned to school i is larger and the cutoff the school adopts is more lenient as k increases. Next we observe the following two facts:
- Claim 1
.
School i must admit any member in Ti(k), for all k, in any equilibrium.
- Claim 2
.
As k→∞, Ti(k) →Si and γi(k) →ci, where ci is school i's cutoff in the truthful outcome.
We first show Claim 1. Note that, as explained earlier, school i must admit any member in Ti(1) in any equilibrium. Assume that it is also true that school i must admit any member in Ti(k− 1) in any equilibrium. We now show the validity of the claim for Ti(k). By definition, Ti(k)\Ti(k− 1) is the group of remaining unassigned type-i applicants who can get assigned to school i when competing with the remaining unassigned type-j applicants. In other words, each applicant in Ti(k)\Ti(k− 1) can surely enter school i by specifying it as her top choice. As entering school i is most ideal for her, she must enter school i in any equilibrium. Hence, by mathematical induction, Claim 1 is shown.
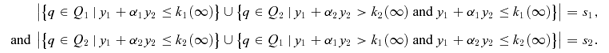
It follows that under policy regime (p1, p2), in any equilibrium, members in Si get admitted by school i. Given this result, one can show that members in Ri\Si—type-j applicants who get into school i in the truthful outcome—will indeed enter school i in any equilibrium. Note that these applicants are clearly qualified to enter school i in any equilibrium (they satisfy the same cutoff, limk→∞γi(k) =ci, that allows all members in Si to enter school i) and the only possible source of non-uniqueness is that some of them turn out to enter school j. This latter possibility could not occur, however. The basic point is that there exist type-j applicants who are more qualified than members in Ri\Si from school j's viewpoint and who eventually do not enter any school. A formal proof would require an iterative process similar to the ones that have been used.
Note that what is essential to the unique equilibrium outcome is the assumption that schools have strict preferences. To illustrate this, we apply to Example 1 the recursive process studied here. Given (p1, p2) = (IA, IA), in the first round, we have T1(1) ={a1}, U1(1) ={b1}, T2(1) ={b1}, and U2(1) ={a1}. In the second round, however, for i= 1, 2, Ti(2) is undefined because school i is selecting for the remaining single place between a2 and b2, which it is indifferent between them. The argument used in this proof thus fails to work. Q.E.D.
Proof of Proposition 2 Call the game under p as game 1 and the game under p′ as game 2. For j= 1, 2, consider any Nash equilibrium in game j that yields a stable matching π. Denote as π (i) the assigned school for applicant i. Now consider game k≠j and the strategy profile where applicant i ranks π(i) as her top choice (the strategies of applicants who are unassigned under j are inconsequential). We argue that, given this strategy profile, these applicants will be admitted by their top-choice schools, hence replicating π. To see this, notice that in the first round, each school s has two sets of applicants for its selection: those who are assigned to s under game j, and those who are unassigned any school under game j. Notice that every member in the former group is more preferred to every member in the latter group (implied by stability of π under game j) and the former group's size is just equal to the number of places that s has. Therefore, the latter group of applicants is declined and made available for other schools' selection in the second round. However, also because of the stability of π under game j, they are less preferred to those applicants who their second-choice schools have kept (in case of DA schools) or admitted (in case of IA schools) in the first round. Therefore, they are also declined in the second round. These applicants are made available for the next round and are declined for the same reasons. The process stops until all applicants who are unassigned according to π are rejected by all schools. Because the set of Nash equilibrium outcomes under game 1 is the set of all stable matchings (each stable matching can be replicated as a Nash equilibrium outcome under game 1 using the aforementioned algorithm), the proposition is thus immediate. Q.E.D.
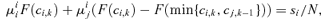 ((A1))
((A1))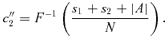
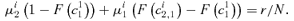
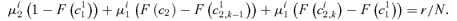
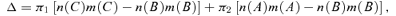 ((A2))
((A2))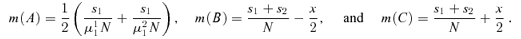
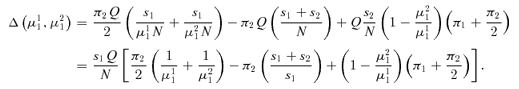
Step 2: ∂Δ (μ11, μ21)/∂μ21 < 0.
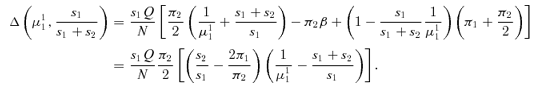
Step 4: Using Steps 2 and 3, as well as continuity, we establish that there exist parameters in which Δ(μ11, μ21) > 0 if s2/s1 < 2π1/π2 and there do not if s2/s1≥ 2π1/π2.
Step 5: In the above derivation, as well as the exposition in the main text, we assumed that the right boundary of region A is on the left-hand side of the left boundary of region B. This may not be the case, and there may be “overlapping” of the two regions. However, it can be easily shown that all the calculations in this proof, as well as the proposition, still hold. The trick is that we can add the overlapping region to both the gain and loss in state 2 so that the specifications of regions A and B that we used in defining Δ remain the same. It is thus without loss of generality that we assume no overlapping of the two regions. Q.E.D.
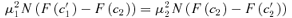
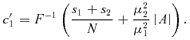
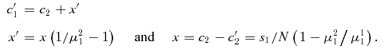
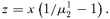
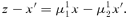
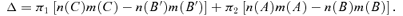 ((A3))
((A3))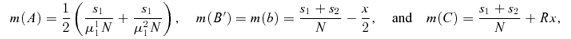
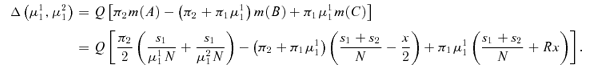
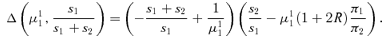
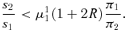 ((A4))
((A4))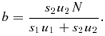
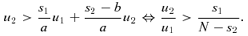
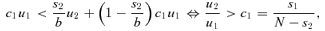
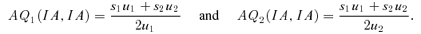
Appendix B
▪ Regarding the noisy signal model introduced in Section 4, we can establish the following claim.
Claim 2 Suppose that α1=α2= 0, that each applicant's attribute (y1, y2) is unknown to her, and that she has a signal x1 which is affiliated with her attribute y1.
- (i)
Under (DA,IA), there exists
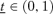 such that if
such that if 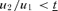 , there exists a truthful equilibrium.
, there exists a truthful equilibrium. - (ii)
Under (DA,IA), there exists
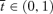 such that if
such that if 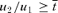 , then (a) there does not exist a truthful equilibrium, and (b) there exists an equilibrium in which applicants with x < x*(x > x*) rank school 1 (school 2) as their top choice and, in this equilibrium, AQ2(DA, IA) < AQ2(DA, DA) (beneficial stealing).
, then (a) there does not exist a truthful equilibrium, and (b) there exists an equilibrium in which applicants with x < x*(x > x*) rank school 1 (school 2) as their top choice and, in this equilibrium, AQ2(DA, IA) < AQ2(DA, DA) (beneficial stealing). - (iii)
(IA,DA) is outcome equivalent to (DA,DA).
- (iv)
Suppose that both schools are allowed to choose IA simultaneously. If
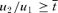 , the equilibrium outcome is exactly the same as (DA,IA).
, the equilibrium outcome is exactly the same as (DA,IA).
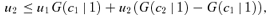
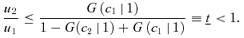
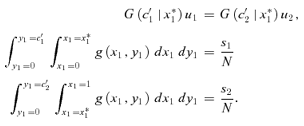 ((A5))
((A5))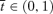 with the claimed properties.
with the claimed properties.Point (iii) is straightforward.
Point (iv). If 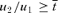 and under (DA,IA), both schools are oversubscribed and school 1 has a more stringent cutoff than school 2 has. This implies that no applicants choosing school 2 as their top choice who get turned down will ever be admitted by school 1. Thus (DA,IA) is de facto (IA,IA), and applicants' behaviors would be the same under the two regimes. Thus, school 2's optimal admissions policy is independent of school 1's policy and the equilibrium outcome is the same as (DA,IA). Q.E.D.
and under (DA,IA), both schools are oversubscribed and school 1 has a more stringent cutoff than school 2 has. This implies that no applicants choosing school 2 as their top choice who get turned down will ever be admitted by school 1. Thus (DA,IA) is de facto (IA,IA), and applicants' behaviors would be the same under the two regimes. Thus, school 2's optimal admissions policy is independent of school 1's policy and the equilibrium outcome is the same as (DA,IA). Q.E.D.




