Reproductive Allocation Patterns in Different Density Populations of Spring Wheat
Supported by the National Natural Science Foundation of China (30730020, 90102015), 863 project (2006AA100202) and Cooperation Project Between China and Greece (2003DFB00034).
Abstract
The effects of increased intraspecific competition on size hierarchies (size inequality) and reproductive allocation were investigated in populations of the annual plant, spring wheat (Triticum aestivum). A series of densities (100, 300, 1 000, 3 000 and 10 000 plants/m2) along a gradient of competition intensity were designed in this experiment. The results showed that average shoot biomass decreased with increased density. Reproductive allocation was negatively correlated to Gini coefficient (R2 = 0.927), which suggested that reproductive allocation is inclined to decrease as size inequality increases. These results suggest that both vegetative and reproductive structures were significantly affected by intensive competition. However, results also indicated that there were different relationships between plant size and reproductive allocation pattern in different densities. In the lowest density population, lacking competition (100 plants/m2), individual reproductive allocation was size independent but, in high density populations (300, 1 000, 3 000 and 10 000 plants/m2), where competition occurred, individual reproductive allocation was size dependent: the small proportion of larger individuals were winners in competition and got higher reproductive allocation (lower marginal reproductive allocation; MRA), and the larger proportion of smaller individuals were suppressed and got lower reproductive allocation (higher MRA). In conclusion, our results support the prediction that elevated intraspecific competition would result in higher levels of size inequality and decreased reproductive allocation (with a negative relationship between them). However, deeper analysis indicated that these frequency- and size-dependent reproductive strategies were not evolutionarily stable strategies.
In plant populations, increasing density can intensify plant–plant competition directly (Pianka 1981). Competition among plants is an important factor in affecting size hierarchies (Weiner 1985; Bonan 1988; Pan et al. 2003a, b), growth rate (Ehleringer 1984; Weiner and Thomas 1992), survivorship (White 1981; Tanner 1997; van Kleunen et al. 2001), and reproductive output (Ehleringer 1984; Weiner and Thomas 1992; Soto-Pinto et al. 2000; van Kleumen et al. 2001). Among these components, size hierarchies and reproductive output have been mostly investigated because they are of tremendous ecological and evolutionary significance.
It has long been recognized that size inequality always increases with increasing density (Weiner 1985). The increase of size inequality may affect total reproductive output (Weiner 1985; Sugiyama and Bazzaz 1997; Pan et al. 2003a, b). Weiner (1988) presented a simple linear model of size-dependent reproductive output to explain the decrease in reproductive allocation (RA) in plants grown at high densities. It has also been reported that, in water deficit and mulching with clear plastic film conditions in spring wheat (Triticum aestivum) populations, there is a negative correlation between RA and Gini coefficient (G) (Pan et al. 2003a, b). It was suspected that this negative correlation would exist along an elevated intraspecific competition gradient. Unfortunately, direct evidence is still lacking to prove this prediction. Therefore, in the present experiment, we designed a wide range of densities for further analysis.
The purpose of this study was to explore (1) the relationship between size inequality and RA in a wide range of densities from no competition to intensive competition (in which plants underwent self-thinning) and (2) size-dependent reproductive allocation patterns in different densities.
Results
Size inequality
Average shoot biomass per plant decreased with increasing density at 20 June (Figure 1), which means the increased strength of intraspecific competition suppressed plant growth.
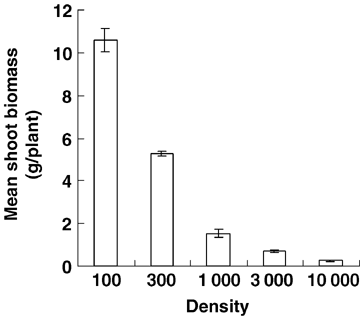
Mean plant biomass (above-ground) in different density treatments at 20 June.
RA was negatively correlated to G of the population (R2 = 0.927, Figure 2). The negative correlation suggests that RA is inclined to decrease as size inequality increases. This result supports the theory that stand uniformity of field crops is an important aspect of high yield formation (Glenn and Daynard 1974).

Relationships between Gini coefficients of spring wheat populations and reproductive allocation (RA) (data at 20 June). The regression line is y = –1.464x + 0.5221, R2 = 0.927.
Size-dependent reproductive allocation
To investigate the relationships between RA and plant size and between spike size and plant size, data from 20 June were analyzed, when spring wheat is at the grain filling stage and no individuals have died because of ripening. For all five populations, spike size increased linearly with plant size (above-ground biomass) (Figure 3, Table 2). Meanwhile, RA increased inversely with plant size in the four competitive densities (300, 1 000, 3 000, and 10 000 plants/m2) (Figure 4, Table 3). Apparently, individual spike size and RA in competitive populations in spring wheat were size-dependent. However, at a density of 100 plants/m2, RA kept constant in different plant sizes (Figure 4, Table 3). So, when the population lacks competition, individual RA is size-independent.
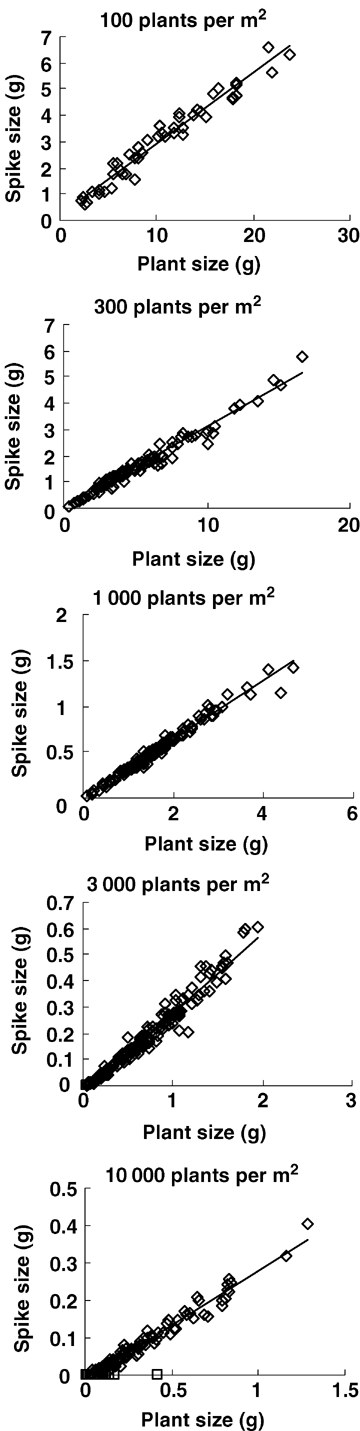
Linear relationship between spike size and plant size (above-ground biomass) in different spring wheat populations at 20 June.⋄ indicates individuals with spikes which were used in fitting the line; □ indicates barren individuals which were excluded in fitting the line. See Table 2 for regression coefficients.
| Density of sowing (plants/m2) | Density at 20 June | Slope (a1) | y-intercept (b1) | x-intercept (-b1/a1) | R2 | Sample size |
|---|---|---|---|---|---|---|
| 100 | 101 ± 2 | 0.271 ± 0.009 | 0.206 ± 0.103 | –0.760 | 0.958 | 46 |
| 300 | 279 ± 6 | 0.312 ± 0.005 | −0.021 ± 0.033 | 0.067 | 0.973 | 100 |
| 1 000 | 952 ± 24 | 0.321 ± 0.004 | −0.005±0.007 | 0.016 | 0.977 | 148 |
| 3 000 | 2 288 ± 164 | 0.308 ± 0.005 | −0.030 ± 0.004 | 0.097 | 0.960 | 151(2**) |
| 10 000 | 5 424 ± 620 | 0.290 ± 0.005 | –0.011 ± 0.002 | 0.038 | 0.970 | 150(39**) |
- * The model is y=a1x+b1
- ** Number of barren individuals in the sample. To fit the model, the barren individuals were excluded.
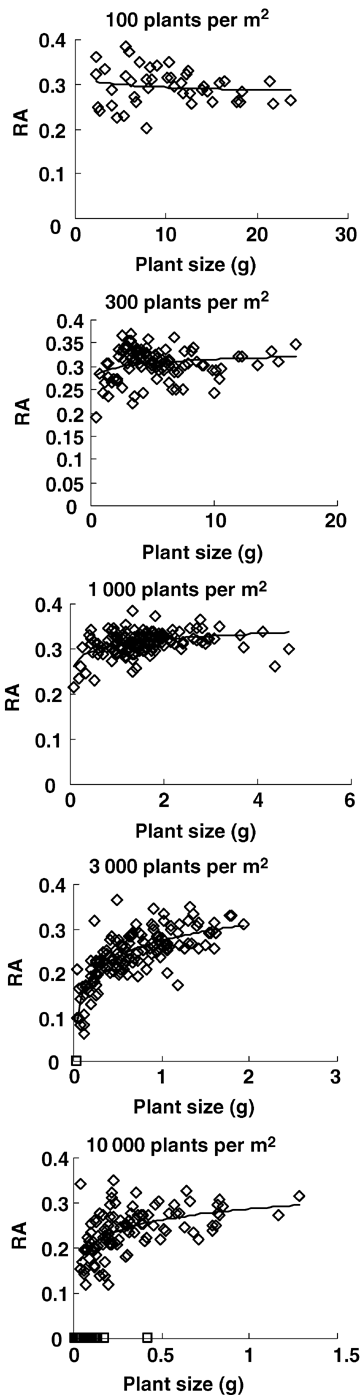
Inverse relationship between RA and plant size (above-ground biomass) in different spring wheat populations at 20 June.⋄ indicates individuals with spikes which were used in fitting the line; □ indicates barren individuals which were excluded in fitting the line. See Table 3 for regression coefficients.
| Density of sowing (plants/m2) | Density at 20 June | Slope b2 | y-intercept a2 | R2 | Sample size |
|---|---|---|---|---|---|
| 100 | 101 ± 2 | 0.032 ± 0.058 | 0.290 ± 0.010 | 0.007 | 46 |
| 300 | 279 ± 6 | –0.044 ± 0.010 | 0.319 ± 0.004 | 0.153 | 100 |
| 1 000 | 952 ± 24 | –0.008 ± 0.001 | 0.323 ± 0.002 | 0.218 | 148 |
| 3 000 | 2 288 ± 164 | –0.009 ± 0.001 | 0.264 ± 0.004 | 0.376 | 151(2**) |
| 10 000 | 5424 ± 620 | −0.005 ± 0.001 | 0.264 ± 0.006 | 0.225 | 150(39**) |
-
* The model is
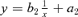
- ** Number of barren individuals in the sample. To fit the model, the barren individuals were excluded.
Discussion
Four competition levels were investigated in this study: (1) no competition (population sown at 100 plants/m2); (2) slight competition (population sown at 300 plants/m2); (3) intermediate competition (population sown at 1 000 plants/m2); and (4) intensive competition (population sown at 3 000 plants/m2 and 10 000 plants/m2 which underwent self-thinning in the growth period). The results indicated that the relationship between plant size and RA of these populations developed in different ways.
Reproductive allocation and size structure
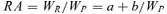
In competitive populations, large individuals are strong competitors and they have the chance to utilize all their potential reproductive ability. The diminished MRA means that large individuals have higher individual fitness, and can generate offspring more successfully. Small individuals are weak competitors with high MRA. If other individuals give up competition, they will improve their RA. However, in dense populations, small individuals risk density-dependent mortality more than large individuals (Weiner 1985). Moreover, spring wheat is an annual semelparous species, and this determines that small individuals with high MRA have little chance to improve their RA. So, in this experiment, the diminished MRA is not bad for large individuals and high MRA is not good for small individuals. That is, trade-off between plant size and MRA is invalid.
A strategy or strategy mixture that cannot be invaded by novel strategies is called an evolutionarily stable strategy (ESS or ESS mixture; Falster and Westoby 2003). So we can test a population for ESS by whether it has the capacity to exclude alternative strategies from invading. Potential invading strategies can be thought of as rare mutants within the existing population, or as initially rare species colonizing from elsewhere. It has been widely recognized that modern seed crops, which are seeking maximum population yield, are evolutionarily unstable, and require ongoing artificial selection to maintain the evolutionarily unstable strategy (Zhang et al. 1999; Falster and Westoby 2003). In this study, the frequency- and size-dependent reproductive strategies in dense spring wheat populations are evolutionarily unstable too, because neither large plant size with high reproductive capacity nor small plant size with low reproductive capacity is a successful strategy. Furthermore, in self-thinning populations, the latter strategy will be eliminated from seriously competitive populations, and the former strategy will fail when it faces a more competitive strategy such as a mutant that has developed large plant size and low RA. So these strategies are not stable against invasion by rare mutant or deviant strategies. In fact, without artificial management, most crop populations will be replaced by other wild species, or will be replaced by more competitive mutants.
Size-dependent reproductive allocation patterns in different densities
In this study, different size-dependent reproductive patterns are shown among the different densities. In populations without competition (100 plants/m2), all members (large ones and small ones) can develop their maximum potential reproductive ability, so MRA is equal to zero (Figure 4, Table 3) and their reproductive patterns are size-independent. This implies that plant RA is determined by intrinsic properties when competition is lacking. In the higher density populations (300, 1 000, 3 000, and 10 000 plants/m2) with competition, as found by Weiner (1988) and Pan et al. (2003a, b), there are significant correlations between plant size and reproductive structure (Figure 3, Table 2) and between plant size and RA (Figure 4, Table 3). Among the higher density treatments, the increased size inequality suggests the proportion of small plants increased and the proportion of large plants decreased. So it is the small ones that mainly contribute to the great growth redundancy, for the small ones had relatively lower RA in the higher density treatments. Furthermore, the increasing proportion of small plants (with lower RA) caused the average RA to decrease along the density gradient. So it can be concluded that there are negative correlations between size inequality (as measured by Gini coefficient) and RA (Figure 2) within these competitive populations.
In conclusion, this study supported the prediction (Pan et al. 2003a) that elevated intraspecific competition would result in higher levels of size inequality and decreased RA. There were also inverse correlations between plant size and RA in competitive populations. These facts imply that reproductive strategies in competitive populations are frequency- and size-dependent. However, we are not yet certain that they are evolutionarily stable, because there was no evidence to prove that they can exclude other competitive strategies, especially in artificially managed populations.
Materials and Methods
Field experiments were conducted in the year of 2003 at Yuzhong experimental station of Lanzhou University (36° 03′ N, 103° 53′ E and 1517 m in altitude). The main climatic conditions are presented in Table 1. The soil is a loess-like loam, with a bulk density of 1.37 g/cm3, and a field water-holding capacity (FWHC, maximum capillary-held water) of 25% (gravimetrically). High organic fertilizer inputs were added to the experimental plot before sowing.
| Year | Annual mean temperature (°C) | Annual mean precipitation (mm) | Precipitation during growing season (mm) | Annual mean evaporation (mm) | Evaporation during growing season (mm) | Relative humidity (%) |
|---|---|---|---|---|---|---|
| Mean annual | 9.1 | 328 | 158 | 1365 | 938 | 59 |
| 2003 | 10.8 | 376 | 229 | 1113 | 703 | 58 |
Seeds of spring wheat (Triticum aestivum L., cv. Longchun No.15) were sprinkled in plots each 50 cm × 50 cm at five densities (three replicates were used in each density): 100, 300, 1 000, 3 000 and 10 000 seeds/m2. The total irrigation was 50 mm × 5. Rainfall during the period from sowing to the last harvest was 229 mm (Table 1). Sowing occurred on 18–20 March 2003, and harvest was taken on 20 June. The plots were surrounded by supports of wire netting to prevent the plants from lodging (especially in high densities) and 25 cm guard rows were planted to avoid marginal effects. Plants were sprayed with chlorpyriphos (Dow Agrosciences, USA) against pest attack and streptomycin solution against bacteria. High fertilizer inputs (irrigated with 500 mL solution containing 1% urea and 0.2% potassium dihydrogen phosphate per plot every two weeks) were added during the growth stage.
Plants grown in the central plot were harvested at ground level. 100–150 live individuals were randomly collected from the three plots. The individuals were put in paper bags separately, dried (65 °C, 48 h), and weighed. Dry shoot biomass per plant was calculated for each plot (total sample size 100–150 in each treatment for calculating Gini coefficient, but 40–70 in 100 plants/m2 plots). Shoot biomass and spike biomass (for calculating RA which is equal to spike biomass/shoot biomass) of each plant were weighed separately.
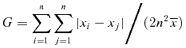
(Handling editor: Da-Yong Zhang)




