Economic efficiency in farm households: trends, explanatory factors, and estimation methods
Due to the confidentiality expectations we have in working with the members of the associations from which we obtained the data for this study, we are unable to provide open access to a data appendix. However, Olson, the corresponding author, is willing to discuss this confidentiality expectation, other uses that may be considered, and the possibility of further joint work that could be done on site at the University of Minnesota.
Abstract
Factors explaining differences in economic efficiency between farms are of major interest to owners, managers, and other stakeholders as they strive to improve earnings and improve the chances of firm survival. This study is undertaken to improve our understanding of interfarm differences in, and opportunities to improve, farm household efficiency in utilizing their land, labor, and capital resources to achieve household objectives. The technical, allocative, and scale efficiencies of farm households are estimated using a nonparametric, output-based data envelopment analysis (DEA) of a panel data set from 1993 to 2006. Single and double bootstrapping procedures are used to estimate technical efficiency. Initial technical efficiency assuming variable returns to scale (TEV) is estimated to be 0.83. Using single bootstrapping, the average bias-corrected TEV estimate is 0.70; using double bootstrapping, the TEV estimate is 0.72. Allocative efficiency is estimated to be 0.81. Scale efficiency is estimated to be 0.93. The only factor that is consistently associated with higher technical efficiency across analysis methods and years is larger farm size (as measured by the log of farm income). The significance of other factors changes with analysis methods.
Economic efficiency, especially interfirm differences in efficiency, is one of the major factors explaining differences in firm survival and growth and changes in industry structure. Thus, factors explaining and determining differences in economic efficiency and changes in efficiency between firms are of major interest to owners, managers, and other stakeholders as they strive to improve earnings and improve the chances of firm survival. This study is undertaken to improve our understanding of the interfarm differences in, and opportunities to improve, farm efficiency in utilizing their land, labor, and capital resources to achieve their objectives.
In the last 10 years, the total number of farms in Minnesota has declined from 80,000 in 1998 to 79,000 in 2007, a 1% decrease (Table 1). This change in total numbers tells only part of the story during the last 10 years. The mix of farm sizes has changed tremendously also. The number of farms with sales of $100,000 or more has decreased 5% from 21,000 to 19,700. However, the number of farms with sales of $500,000 or more has increased almost 50% since 1998. The number of farms with sales of $100,000 up to $250,000 has decreased 21%; the number of farms with sales between $250,000 and $500,000 has remained basically the same. While a rise in prices will push farms into higher sales categories even though the size does not change physically, a quick review of prices received indices show that this price effect does not adequately explain the change in the mix of farms. The number of farms with milk cows and hogs has shown a steady and rapid decrease while the number of farms with beef cows has a slower but still steady decrease. Total production of cattle and calves has remained quite stable while milk production has decreased slightly and hog and pig production has increased by almost 50%. These changes in farm numbers, sizes of farms, and farms with livestock also motivated our interest in whether changes in economic efficiencies could be associated with these changes.
| 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Farms by economic size class | ||||||||||
| $1,000–9,999 | 29,600 | 30,500 | 32,100 | 33,900 | 35,400 | 35,200 | 34,800 | 34,800 | 34,500 | 34,000 |
| $10,000–99,999 | 29,400 | 29,500 | 28,400 | 27,100 | 26,200 | 25,500 | 25,500 | 25,400 | 25,200 | 25,000 |
| $100K–249,999 | 12,600 | 12,400 | 11,600 | 10,900 | 10,000 | 10,000 | 9,900 | 9,900 | 9,900 | 10,000 |
| $250K–499,999 | 5,500 | 5,500 | 5,500 | 5,400 | 5,400 | 5,400 | 5,400 | 5,500 | 5,600 | 5,600 |
| $500,000 + | 2,900 | 3,100 | 3,400 | 3,700 | 3,900 | 3,900 | 4,000 | 4,000 | 4,100 | 4,300 |
| Total | 80,000 | 81,000 | 81,000 | 81,000 | 80,900 | 80,000 | 79,600 | 79,600 | 79,300 | 79,000 |
| Farms with the following livestock | ||||||||||
| With milk cows | 9,700 | 9,100 | 8,500 | 7,800 | 7,200 | 6,600 | 6,100 | 5,800 | 5,400 | 5,200 |
| With beef cows | 15,800 | 15,800 | 15,800 | 15,500 | 15,500 | 15,300 | 15,200 | 15,000 | 14,600 | 14,600 |
| With hogs | 8,500 | 7,500 | 7,300 | 6,500 | 5,800 | 5,700 | 5,000 | 4,900 | 4,800 | 4,700 |
| Production (million pounds) | ||||||||||
| Cattle and calves | 1,070 | 1,083 | 1,157 | 1,134 | 1,150 | 1,096 | 1,053 | 1,076 | 1,050 | 1,085 |
| Milk produced | 9,275 | 9,478 | 9,493 | 8,812 | 8,458 | 8,258 | 8,102 | 8,195 | 8,370 | 8,656 |
| Hogs and pigs | 2,403 | 2,461 | 2,515 | 2,774 | 2,786 | 3,016 | 3,109 | 3,238 | 3,329 | 3,543 |
| Prices received index, U.S., 1990–1992 = 100 | ||||||||||
| All farm products | 102 | 96 | 96 | 102 | 98 | 107 | 119 | 115 | 115 | 136 |
| All crops | 107 | 97 | 96 | 99 | 105 | 111 | 115 | 111 | 120 | 142 |
| All livestock & products | 97 | 95 | 97 | 106 | 90 | 103 | 122 | 120 | 111 | 130 |
- Sources: Farm numbers and production: USDA, Minnesota agricultural statistics service, accessed on February 9, 2009; Prices received index: USDA, NASS, Agricultural prices, 2006 Summary and 2007 Summary and agricultural prices, accessed on February 9, 2009.
This study estimates the technical, allocative, and scale efficiencies of farms in southern Minnesota using a nonparametric, output-based data envelopment analysis (DEA) with single and double bootstrapping of a panel data set of individual farm and household financial records from southern Minnesota from 1993 to 2005.
This study extends current research in several ways. First, it uses a true panel data set versus the pseudo panel used by Morrison Paul et al. (2004). Second, it applies and compares bootstrapping procedures to correct the bias generated by the deterministic DEA approach.
Technical efficiency (TE) measures the firm's ability to use the best available practices and technology in the most effective way. Allocative efficiency (AE) is dependent on prices and measures the firm's ability to make optimal decisions on product mix and resource allocation. Combining measures of technical and allocative efficiency yield a measure of economic efficiency. Scale efficiency (SE) measures the optimality of the firm's size, so a change in size will not improve output or revenue.
Estimation of efficiency using nonparametric linear programming has its origin with Farrell (1957). Seitz (1970) used linear programming techniques to calculate measures of Farrell-type efficiencies for the single-output case. However, not until Charnes et al. (1978) has the generalized linear programming method, known as DEA, been applied widely to estimate technical efficiency, at first within operating research and management science and later, within the economics community. In U.S. agriculture, Morrison Paul et al. (2004) used survey data collected by the USDA to estimate technical and scale efficiency in U.S. agriculture and found family farms to be both scale and technically inefficient. Wu et al. (2003) computed technical and scale efficiency for Idaho sugar beet farms and concluded that improper scale operation and input overutilization are the main sources of inefficiency. Tauer (1993) calculated technical and allocative efficiency indices of 395 dairy farms in New York and found that dairy farms in his sample were more technically efficient but less allocatively efficient in the long run than in the short run.
Not many studies using DEA pay much attention to its statistical properties. In the context of the multi-output, multi-input case, the only currently feasible method to establish statistical properties for DEA estimators is by bootstrapping (Simar and Wilson, 1998, 2000, 2007). Simar and Wilson (1998, 2000) proposed a smoothed bootstrapping method to derive the statistical properties of technical efficiency. This bootstrapping method had been applied empirically to several studies. In agriculture, Latruffe et al. (2005) used bootstrapping in estimating the technical efficiency of crop and livestock farms in Poland. Brümmer (2001) applied it to establish confidence intervals for technical efficiency among private farms in Slovenia. The method is also used in Ortner et al. (2006) for dairy farms in Austria.
Many of the studies on efficiency also use a two-stage approach, where efficiency is estimated in the first stage, and then the estimated efficiencies are regressed on the environmental variables (or nondiscretionary inputs) in the second stage1. Simar and Wilson (2007) criticize the two-stage method because the DEA efficiency estimates are biased and serially correlated, therefore invalidating conventional inferences in the second stage. Simar and Wilson propose a procedure, based on a double bootstrap, which provides both confidence intervals for efficiency estimates and consistent inferences for factors explaining efficiency.
The specific objectives of this study are to: (1) estimate technical, allocative, and scale efficiencies of farms using an output based approach; (2) use both bootstrapping procedures to correct the bias generated by the deterministic DEA method and compare the two bootstrapping methods; and (3) identify factors that are significant in explaining differences in both levels of technical efficiency and differences in technical efficiency among farms by using the double bootstrapping method.
1. Methods and models
Efficiency can be estimated in two ways: parametric and nonparametric. The parametric approach includes specifying and estimating a parametric production frontier (cost or profit function). The main strength of the parametric or stochastic frontier function approach (SFA) is its incorporation of stochastic error, and therefore permitting hypothesis testing. The disadvantage of this approach is the imposition of an explicit functional form and distribution assumption of the error term. Therefore, stochastic frontier method is sensitive to the parametric form chosen.
In contrast, the nonparametric approach, or DEA, has the advantage of no prior parametric restrictions on the technology and thus is less sensitive to misspecification. It is also not subject to assumptions on the distribution of the error term. However, because DEA is a deterministic approach, all deviations from the frontier are considered as inefficiencies, making it sensitive to measurement errors and data noises. Furthermore, DEA is known to be sensitive to outliers. To overcome the deterministic and outlier problems, we use bootstrapping methods (as described below) to estimate stochastic error and allow hypothesis testing.
Following Chavas et al. (2005), Morrison Paul et al. (2004), and others, we first used nonparametric (DEA) methods to estimate output-based technical, allocative, and scale efficiencies. While others have chosen input-based models (e.g., Morrison Paul et al. (2004), Morrison Paul and Nehring (2005)) based on farmers’ abilities to control inputs in the short run more than outputs, we chose an output-based model on the assumption that farmers are revenue maximizing given a level of inputs that are fixed in the short run (especially land and operator and family labor.) The output-based model allowed us to study the allocative efficiency of farmers based on output price signals since the data contained considerable variability in the outputs selected per farm per year. Of the five outputs included in the model, the average number of outputs per farm per year was 2.6 with a standard deviation of 0.7. Some farms had only one output; some had all five. The output-based model was also more feasible to estimate since the output price data were also more reliable and available than the input price data. The choice of the output-based model can also be defended by looking at the results, which, as will be seen, indicate high average scale efficiency (0.93 with a standard deviation of 0.11) and indicating the assumption of constant returns to scale (CRS) was not an invalid approximation for this data. And, since the output- and input-based measures are equivalent under CRS, the choice between the output- and input-based techniques is relatively harmless. We use both the double bootstrap method proposed by Simar and Wilson (2007) and the smoothed bootstrap procedure for DEA estimators as in Simar and Wilson (2000) to estimate the bias and confidence intervals for efficiency estimates. We use the package FEAR developed by Wilson (2005) in the R platform and STATA software in the process.
1.1. Technical efficiency
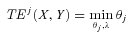 (1)
(1)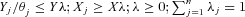 where θ is a scalar and λ is a vector of constant λj (j = 1, … , n).
where θ is a scalar and λ is a vector of constant λj (j = 1, … , n).TE measures the distance between the observed input-output mix and the production frontier. In general, 0 ≤ TE ≤ 1; when TE = 1, the farm is producing on the production frontier, and hence, technically efficient. When TE < 1, the farm is technically inefficient.
The DEA model above is a variable returns to scale (VRS) DEA model, implying it permits the production frontier to have increasing, constant, or decreasing return to scale. In the case of constant returns to scale, one can find TE easily by deleting the convexity constraint 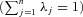 .
.
1.2. Allocative efficiency
 (2)
(2)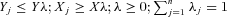 where p is a vector of output prices and other variables are as defined previously. Equation (2) only assumes a well-functioning output market and remains valid despite factor market imperfections. After obtaining maximal revenue Rj (p, X, Y) from this problem, we can derive allocative (AE) and economic efficiency (EE) from the equation
where p is a vector of output prices and other variables are as defined previously. Equation (2) only assumes a well-functioning output market and remains valid despite factor market imperfections. After obtaining maximal revenue Rj (p, X, Y) from this problem, we can derive allocative (AE) and economic efficiency (EE) from the equation
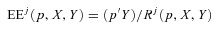
Thus, EE is the ratio of observed output revenue to maximum revenue for the farm. AE is the economic efficiency after taking out the effect of technical inefficiency. In other words, allocative efficiency is the ratio of the revenue from the hypothetical technically efficient farm to maximal revenue obtained by allocating resources in the “right way.” In general, 0 ≤ AE ≤ 1, where AE = 1 represents a farm that is allocatively efficient in output.
1.3. Scale efficiency
Scale efficiency (SE) can be estimated by dividing the technical efficiency estimates under CRS to the technical efficiency estimates under VRS. In general, 0 ≤ SE ≤ 1, with SE = 1 representing efficient economy of scale. SE < 1 implies that the inputs are not efficient in scale, which can be either increasing returns to scale (IRS) or decreasing returns to scale (DRS). We can decide among farms with scale inefficiency, which farms are “too large” (DRS) or “too small” (IRS) by running a DEA problem with nonincreasing returns to scale (NIRS) imposed. This can be done by replacing the convexity constraint 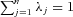 in Eq. (1) with
in Eq. (1) with 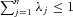 .
.
Then we compare the NIRS and VRS efficiency scores. For a particular farm, if the two scores are unequal and SE < 1, the farm is increasing returns to scale. On the other hand, if they are equal and SE < 1, the farm exhibits decreasing returns to scale.
1.4. Bootstrapping the DEA estimators
Simar and Wilson (2007) noted many papers that have regressed DEA estimates on environmental variables in a two-stage approach to account for factors that might affect the firm's efficiency. The Tobit analysis is the most common method used in this two-stage approach so far. However, Simar and Wilson (2007) criticized all the papers using the two-stage approach as being invalid because they did not describe the underlying data-generating process (DGP) in their models and their methods suffer from serial correlation among the estimated efficiencies. Simar and Wilson (2007) proposed a procedure based on a double bootstrap that is consistent with a sensible DGP and permits valid inferences in the efficiency estimates as well as in explaining the efficiency estimates. The double bootstrap also improves statistical efficiency in the second stage. This method would greatly improve the theoretical as well as practical aspects in DEA models. However, there are only a few studies so far that apply this method (Afonso and St. Aubyn, 2006; Latruffe et al., 2008).
Bootstrapping is based on the idea that by resampling the data with replacement, we can mimic the DGP characterizing the true data generation. The procedures for double bootstrapping used in this article are based on Algorithm 2 in Simar and Wilson (2007) which is described in the Appendix. In addition, we also estimate the single bootstrap as in Simar and Wilson (2000) to compare the estimated efficiencies between the two methods.
The truncated bias corrected maximum likelihood method is used to identify those environmental variables that have significant explanatory effect on differences in efficiencies using the double bootstrap estimates. Following Simar and Wilson (2007), the dependent variable is the inefficiency index, which is the reciprocal of the technical efficiency. Therefore, a positive relationship between an environmental factor and efficiency exists if the sign of the coefficient is negative, and negative if the coefficient is positive.
We also use standard and weighted Tobit analyses to identify significant factors explaining differences in efficiencies. As with the truncated bias corrected maximum likelihood method, the dependent variable is the reciprocal of the initial estimates of technical efficiency so the predicted impact is the opposite of the signs on the estimated coefficients.
We also perform both standard and weighted Tobit analyses using single bootstrap results with pooled data from all years. The weighted Tobit combines the initial estimates with the results from the single bootstrap to minimize the measurement error by applying a weight equal to the reciprocal of the width between higher and lower bounds of the estimated technical efficiency obtained in stage one. Thus, farms with less variable efficiency estimates have a higher weight than farms with more variable estimates. The idea of the weighted Tobit is to minimize measurement error by “punishing” farms with less precise estimates with a lower weight due to higher widths between higher bounds and lower bounds.
2. Data
For this analysis, we used data from the Southeastern and Southwestern Minnesota Farm Business Associations collected by the Department of Applied Economics at the University of Minnesota. After dropping some farms with missing or suspicious data, the complete data contain financial and farm characteristic records from about 400 farms that had been members of either Association in at least one year from 1993 through 2006, and had records of sufficient quality to be included in at least one year. The number of records per year averaged 216 and ranged from a high of 252 in 1999 to a minimum of 137 in 2005. Membership in the Associations is not stable; farms have differing frequencies of years in the data. There are 49 farms with only one year of data and 54 farms with 14 years of data. Eighty-three percent of the observations are from 211 farms (53% of the total) with 8–14 years of data.
To understand the results better, farms are also grouped according to farm size and type of output mix based on reported farm income.2 For this grouping, farm income includes income from all products (except nonfarm income) not just those products identified as outputs for the estimation of efficiencies in this study. To be consistent with the class boundaries used in USDA's definitions, large farms are defined as farms with total gross farm income higher than or equal to $250,000. We also divide the sample into subsamples of farms that mostly grow crops, mostly raise livestock, and those that produce both crops and livestock using a 70% rule on the source of sales. That is, if crop sales constitute 70% or more of total sales, the farm is classified as a crop farm. Based on these criteria, 54% of the farm observations are classified as large; 46% as small (Table 2). Forty-eight percent of the farm observations are classified as crop farms, 31% as livestock, and 21% as diversified.
| Definition | Percentage (%) | Gross farm income ($,000) | Labor (hours) | Capital ($,000) | Nonfarm ratio | |
|---|---|---|---|---|---|---|
| Large farms | Gross farm income ≥$250,000 | 54.4 | 575 | 5,530 | 46 | 0.041 |
| Small farms | Gross farm income < $250,000 | 45.6 | 156 | 3,914 | 13 | 0.156 |
| Crop farms | Crop income ≥ 70% farm income | 47.9 | 286 | 3,723 | 27 | 0.122 |
| Livestock farms | Livestock income ≥ 70% farm income | 31.2 | 570 | 6,669 | 39 | 0.055 |
| Diversified farms | Neither crop farms or livestock farms | 20.9 | 393 | 5,019 | 28 | 0.073 |
The model includes four inputs: land, labor, capital, and immediate expenditures (Table 3). Data come directly from the database. Land input is the total crop and pasture land used in production. Labor is the total hours worked on the farm by the operator and unpaid family labor; it is estimated by the farm operator. Capital is calculated as the flow of interest and depreciation expense, measured in dollars. Immediate expenditures include all the immediate expenses for livestock, crop, and operating purposes, measured in dollars.
| Variable | Mean | Std. Dev. |
|---|---|---|
| Inputs | ||
| Land (acres) | 709 | 518 |
| Labor (hours) | 3,773 | 3,660 |
| Capital1 | 30.7 | 46.5 |
| Immediate expenditures1 | 217.3 | 290.2 |
| Outputs | ||
| Corn income1 | 79.7 | 99.0 |
| Soybean income1 | 70.0 | 68.5 |
| Milk income1 | 54.8 | 197.1 |
| Beef income1 | 47.3 | 197.4 |
| Hog income1 | 63.5 | 244.4 |
| Prices | ||
| Corn price ($/bu) | 2.17 | 0.46 |
| Soybean price ($/bu) | 5.64 | 1.00 |
| Milk price ($/cwt) | 13.73 | 1.27 |
| Hog price ($/cwt) | 43.33 | 7.03 |
| Beef price ($/cwt) | 63.69 | 7.08 |
| Environmental variables | ||
| Gross farm income1 | 385.9 | 414.5 |
| Debt asset ratio | 0.50 | 0.23 |
| Years of farming | 24.71 | 11.28 |
| Nonfarm ratio | 0.09 | 0.13 |
| Tenancy ratio: rented land/total land | 0.60 | 0.33 |
| Ratio of hired labor/total farm labor | 0.13 | 0.23 |
| Land/labor ratio | 0.25 | 0.18 |
| Herfindahl index | 0.56 | 0.18 |
- Note: 1Thousand dollars.
The model includes five outputs: two crops (corn and soybean) and three livestock products (milk, beef, and hog). Corn and soybean are the most important crop outputs in Minnesota. They are produced in more than 90% of our sample. Hogs and milk are the main livestock products and account for 84% of total livestock production value.
Annual output price data are taken from National Agricultural Statistics Service (2006a, 2006b) assuming farms in the region faced the same prices for their outputs in a given year. Physical crop production for a specific crop on an individual farm in a specific year is calculated by dividing that farm's gross production value by that year's price of that crop. Physical livestock production for a specific livestock enterprise on an individual farm in a specific year is calculated by dividing the total livestock value by the price of livestock.
The environmental variables used in the second stage to determine factors explaining differences in farm efficiencies include financial condition, farm characteristics, labor characteristics, land tenure, and the relative importance of different outputs. Financial condition and farm characteristics are measured by gross farm income, debt-asset ratio, land-labor ratio, and nonfarm income ratio. Labor characteristics are measured by the main operator's years of farming and the hired labor ratio. Land tenure is measured by the tenancy ratio. The relative importance of different outputs is measured by the nonfarm income ratio and the Herfindahl index. The nonfarm income ratio is the farm household's nonfarm income expressed as a proportion of the sum of gross farm income and nonfarm income. The Herfindahl index measures the degree of output concentration and is defined as 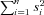 in which si is the share or ratio of each farm's output of the ith output to the total of that farm's six outputs in this study.
in which si is the share or ratio of each farm's output of the ith output to the total of that farm's six outputs in this study.
3. Results
Efficiency estimates obtained from the DEA analysis are presented with technical efficiency first followed by allocative and then scale efficiency. Significant explanatory factors are then identified.
3.1. Technical efficiency
Over all years and farms, the initial estimate of average technical efficiency is 0.77 assuming CRS and 0.83 assuming VRS (TEV; Table 4). There is no clear upward or downward trend of technical efficiency over the years. The average highest technical efficiency is 0.87 (TEV) in 1997 and the lowest is 0.67 (TEC) in 2001. These initial estimates showed that 22% of farms have an estimated TEC score of 1, and 32% have an estimated TEV score of 1.
| Year | Initial TEC | Initial TEV | % of farms with TEV = 1 | Corrected TEV single | Higher bound single | Lower bound single | Corrected TEV double | Higher bound double | Lower bound double | AE | SE |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1993 | 0.79 | 0.83 | 31.4 | 0.70 | 0.82 | 0.66 | 0.72 | 0.81 | 0.64 | 0.81 | 0.95 |
| 1994 | 0.79 | 0.84 | 37.1 | 0.71 | 0.83 | 0.66 | 0.72 | 0.82 | 0.63 | 0.79 | 0.94 |
| 1995 | 0.72 | 0.86 | 33.6 | 0.76 | 0.85 | 0.70 | 0.76 | 0.84 | 0.69 | 0.79 | 0.83 |
| 1996 | 0.79 | 0.83 | 26.5 | 0.71 | 0.82 | 0.67 | 0.74 | 0.81 | 0.67 | 0.75 | 0.95 |
| 1997 | 0.84 | 0.87 | 34.8 | 0.77 | 0.86 | 0.72 | 0.77 | 0.85 | 0.69 | 0.88 | 0.96 |
| 1998 | 0.81 | 0.85 | 32.0 | 0.74 | 0.84 | 0.69 | 0.75 | 0.84 | 0.68 | 0.84 | 0.96 |
| 1999 | 0.77 | 0.80 | 28.2 | 0.68 | 0.80 | 0.64 | 0.70 | 0.79 | 0.64 | 0.82 | 0.95 |
| 2000 | 0.77 | 0.82 | 30.0 | 0.70 | 0.82 | 0.66 | 0.72 | 0.81 | 0.64 | 0.84 | 0.94 |
| 2001 | 0.67 | 0.78 | 26.1 | 0.64 | 0.78 | 0.62 | 0.69 | 0.77 | 0.61 | 0.77 | 0.85 |
| 2002 | 0.77 | 0.81 | 34.7 | 0.67 | 0.80 | 0.64 | 0.70 | 0.80 | 0.62 | 0.81 | 0.95 |
| 2003 | 0.77 | 0.79 | 27.8 | 0.65 | 0.78 | 0.62 | 0.68 | 0.78 | 0.61 | 0.85 | 0.97 |
| 2004 | 0.78 | 0.82 | 32.7 | 0.69 | 0.81 | 0.65 | 0.69 | 0.79 | 0.61 | 0.86 | 0.96 |
| 2005 | 0.80 | 0.84 | 33.6 | 0.72 | 0.84 | 0.67 | 0.73 | 0.83 | 0.65 | 0.83 | 0.96 |
| 2006 | 0.76 | 0.80 | 34.7 | 0.65 | 0.80 | 0.62 | 0.67 | 0.79 | 0.60 | 0.81 | 0.95 |
| Average | 0.77 | 0.83 | 31.5 | 0.70 | 0.82 | 0.66 | 0.72 | 0.81 | 0.64 | 0.81 | 0.93 |
| Median | 0.79 | 0.86 | 0.72 | 0.85 | 0.68 | 0.75 | 0.84 | 0.66 | 0.83 | 0.98 | |
| Std. dev. | 0.20 | 0.18 | 0.14 | 0.18 | 0.13 | 0.15 | 0.18 | 0.13 | 0.14 | 0.11 | |
| Skewness | −0.59 | −0.90 | −0.94 | −0.90 | −0.96 | −1.00 | −0.86 | −0.92 | −0.89 | −2.65 | |
| Kurtosis | 2.69 | 3.30 | 4.12 | 3.30 | 4.33 | 3.84 | 3.28 | 4.13 | 4.35 | 11.82 | |
| Farm size | |||||||||||
| Small | 0.73 | 0.79 | 28.2 | 0.67 | 0.79 | 0.63 | 0.68 | 0.78 | 0.61 | 0.80 | 0.92 |
| Large | 0.81 | 0.85 | 34.1 | 0.73 | 0.85 | 0.68 | 0.75 | 0.84 | 0.67 | 0.83 | 0.94 |
| Farm type | |||||||||||
| Crop | 0.72 | 0.78 | 25.2 | 0.67 | 0.78 | 0.64 | 0.68 | 0.77 | 0.62 | 0.81 | 0.92 |
| Livestock | 0.86 | 0.90 | 47.2 | 0.74 | 0.89 | 0.69 | 0.78 | 0.88 | 0.68 | 0.84 | 0.96 |
| Diversified | 0.79 | 0.83 | 26.6 | 0.72 | 0.83 | 0.68 | 0.74 | 0.82 | 0.67 | 0.80 | 0.94 |
From these initial estimates, we apply both methods of bootstrapping to correct for the bias of TEV: the single bootstrap in Simar and Wilson (2000) and the double bootstrap in Simar and Wilson (2007). The two bootstrapping methods produce similar results. The average bias-corrected estimate for the single bootstrap is 0.70 while the one for the double bootstrap is 0.72. The correlation between the two bias-corrected estimates (i.e., single and double bootstrap) is 0.94; the Spearman rank correlation is 0.90.
The biases in the uncorrected initial results are quite considerable. The initial TEV estimates suggest that with a given input, an “average” farm could expand its output by 20%= (((1/0.83) − 1) * 100%) if technical efficiency were improved to 1.0.3 The bias-corrected TEV estimates, however, suggest an expected output expansion of 43%= (((1/0.70) − 1) * 100%) for the single bootstrap estimate and 40%= (((1/0.72) − 1) * 100%) for the double bootstrap estimate.
The lower and upper bounds of the 95% confidence interval for the bias-corrected TEV in the double bootstrap are 0.64 and 0.81, respectively, which suggests that the amount an “average” farm could expand its output by increased technical efficiency ranged from 23.5% to 56.3%.
The width of the 95% confidence intervals is 0.16 for TEV using the single bootstrap method and 0.17 for TEV using the double bootstrap method. This indicates a high statistical variability of DEA efficiency estimates. Similar results are found in Brümmer (2001) and Latruffe et al. (2005) for single bootstrap and Latruffe et al. (2008) for double bootstrap.
Over time the average bias-corrected TEV estimates follow a trend similar to, but lower and more accentuated than, that of the average initial TEV estimate (Fig. 1). When farms are ranked by their bias-corrected TEV (from lowest to highest), the quantitative disparities between the initial and corrected TEV estimates are obvious (Figs. 2 and 3). These graphs show the initial TEV estimates do not provide the same ranking of individual farms since they do not form a smooth line following the corrected TEV. Also visible is the variability in the lower and upper bounds of the corrected TEV, even between farms with similar expected values of corrected TEV. This variability is greatest for those farms with initial TEV estimates of 1.0. The Spearman rank correlation between initial TEV and single bootstrap estimates is 0.73 while that between initial TEV and double bootstrap is 0.86. This result is expected since the single bootstrap method is based only on the input and output information while the double bootstrap adjusts the estimates, based on not only this information but also the environmental variable information.
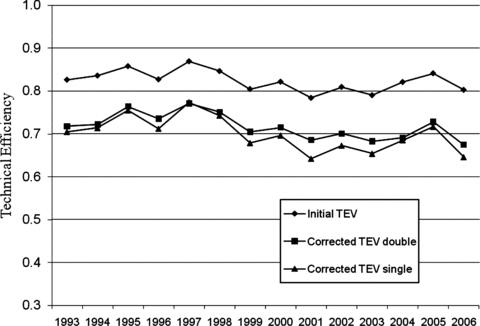
Initial and corrected estimates TEV, 1993–2006.
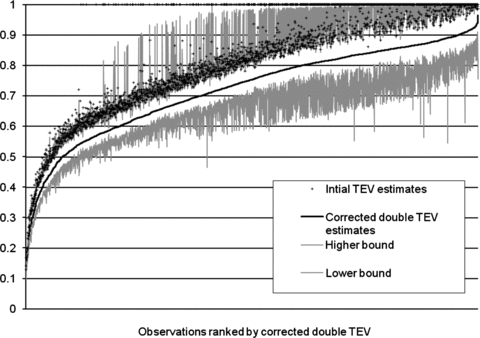
Distribution of technical efficiency with confidence intervals (double bootstrap).
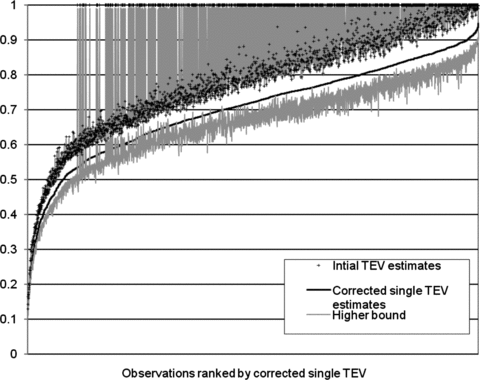
Distribution of technical efficiency with confidence intervals (single bootstrap).
When the farms are classified by size using gross farm income, larger farms are on average more technically efficient than smaller farms. Both size groups have patterns in the lower and upper bounds that are similar to the patterns for the overall averages.
When the farms are classified by type of farm based on source of gross farm income, livestock farms tend to be the most technically efficient on average over all years followed by diversified farms and then crop farms.
3.2. Allocative efficiency
In terms of allocative efficiency (AE), a majority of the farms in this study are not efficient, that is, these farms did not make the correct allocation of inputs to produce the correct set of outputs to maximize revenue based on the prices received. Over all years, average AE is 0.81 (Table 4). Only 13% of the farms had a score of 1. Annual average AE ranges from a low of 0.75 in 1996 to a high of 0.88 in 1997. The average farm is estimated to have the ability to potentially increase revenue by 23% if price signals had been responded to perfectly. No trend in allocative efficiency is noted over time (Fig. 4). As seen with technical efficiency, large farms and livestock farms tend to be more efficient than other farms although the group averages are closer than with technical efficiency.
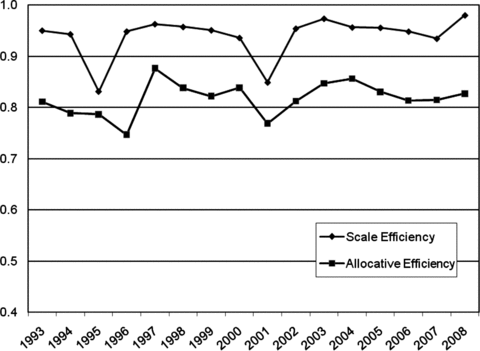
Scale and allocative efficiency, 1993–2006.
3.3. Scale efficiency
Average SE is 0.93 over all years. Only 24% of the farms had an SE score of 1; however, many farms had an SE score of close to 1. Almost 66% of farms had an SE score higher than or equal to 0.95, and 42% of farms had an SE score higher than or equal to 0.99. The annual average SE score is quite stable over time with a low of 0.83 in 1995 and a high of 0.97 in 2003. Among the farms being scale inefficient (i.e., SE <1), the distribution between farms that are “too large”[having decreasing returns to scale (DRS)] and farms that are “too small”[increasing returns to scale (IRS)] are sharply different. Using the procedures described earlier, 46% of farms are found to be “too large” compared with 30% being “too small”; 24% are at an optimal scale of operation. Large farms have a slightly higher average SE compared to small farms. Livestock farms have slightly higher SE followed by diversified farms that are closely followed in SE by crop farms.
In summary, farms tended to be very scale efficient, followed by allocative efficiency with technical efficiency being the lowest on average.
3.4. Factors explaining differences in technical efficiencies
Using the methods described earlier, environmental variables are used to explain differences in technical efficiencies. We first evaluate the factors by year and then pool the data over years.
Using the double bootstrap method, farm size (as measured by the log of farm income) is the only explanatory variable that has a significant coefficient in more than 7 of the 14 years (Table 5). Farm size has a significant positive effect on levels in every year except 2006 when it is negative and 2001, 2002, 2003, and 2005 when the effect is not significant. This may explain, at least partly, the trend of increasing farm size in Minnesota farms during the last decades.
| Constant | Log income | Debt/asset ratio | Log of farming years | Nonfarm ratio | Tenancy ratio | Hired rate | Land to labor ratio | Herfindahl index | |
|---|---|---|---|---|---|---|---|---|---|
| 1993 | 16.7 | −5.19 | −1.01 | −0.15 | −0.43 | 0.4 | 0.54 | 9.83 | 2.84 |
| (3.2)** | (4.9)** | (0.4) | (0.3) | (0.9) | (2.2)** | (1.4) | (2.0)** | (1.1) | |
| 1994 | −0.55 | −2.97 | 3.45 | 1.29 | 0.3 | 0.34 | 0.61 | 10.1 | 4.23 |
| (0.1 | (3.1)** | (1.6) | (1.5) | (0.6) | (2.4)** | (2.8)** | (2.5)** | (1.8) | |
| 1995 | 13.11 | −2.75 | 0.6 | 0.15 | −0.11 | 0.15 | 0.14 | 0.08 | −1.9 |
| (2.5)** | (2.2)** | (0.7) | (0.5) | (0.5) | (1.8)* | (1.1) | (0.6) | (1.2) | |
| 1996 | 5.96 | −0.86 | 0.35 | −0.03 | −0.18 | 0.00 | 0.12 | 0.13 | −1.16 |
| (5.9)** | (4.3)** | (1.3) | (0.4) | (2.5)** | (0.2) | (3.1)** | (2.3)** | (2.6)** | |
| 1997 | −9.86 | −2.54 | 4.67 | 1.04 | 0.03 | 0.76 | 0.94 | 6.24 | 8.93 |
| (1.5) | (2.6)** | (2.9)** | (2.1)** | (0.1) | (7.3)** | (3.7)** | (1.5) | (3.0)** | |
| 1998 | 3.51 | −0.44 | 0.06 | −0.13 | 0.00 | 0.03 | −0.01 | −1.32 | 0.22 |
| (2.9)** | (1.8)* | (0.1) | (1.1) | (0.0) | (0.9) | (0.2) | (1.5) | (0.4) | |
| 1999 | 4.9 | −0.73 | −0.3 | −0.02 | 0.04 | 0.06 | 0.05 | −0.04 | −1.47 |
| (2.7)** | (2.1)** | (0.5) | (0.1) | (0.4) | (1.2) | (0.6) | 0.0 | (1.6) | |
| 2000 | 2.08 | −4.14 | −1.64 | 2.48 | −0.57 | 0.85 | 0.06 | −5.28 | 8.54 |
| (0.3) | (3.5)** | (0.5) | (2.6)** | (1.1) | (4.2)** | (0.2) | (1.0) | (2.3)** | |
| 2001 | 8.15 | −4.1 | 9.04 | 1.43 | −0.74 | 0.02 | −0.01 | −3.93 | 1.79 |
| (0.9) | (1.1) | (1.1) | (0.9) | (0.8) | (0.1) | (0.0) | (0.7) | (0.4) | |
| 2002 | 4.94 | −2.27 | 3.22 | 0.76 | 0.15 | 0.11 | 0.08 | −3.0 | −0.83 |
| (0.6) | (0.9) | (0.8) | (0.5) | (0.3) | (0.5) | (0.2) | (0.6) | (0.2) | |
| 2003 | −3.01 | −1.42 | 2.24 | 0.41 | 0.46 | 0.21 | −0.01 | 3.92 | 6.35 |
| (0.5) | (1.2) | (1.0) | (0.5) | (1.1) | (1.2) | (0.1) | (1.5) | (1.8)* | |
| 2004 | 15.8 | −5.59 | −3.5 | 0.42 | 0.03 | 1 | −0.24 | −8.9 | 4.8 |
| (1.7)* | (4.0)** | (0.8) | (0.4) | 0.0 | (3.9)** | (0.5) | (1.9)* | (1.0) | |
| 2005 | −3.56 | −0.06 | −0.11 | 0.62 | 0.31 | 0.27 | −0.59 | −10.08 | 2.3 |
| (0.5) | (0.1) | 0.0 | (0.7) | (0.7) | (1.9)* | (1.8)* | (3.7)** | (0.8) | |
| 2006 | −17.2 | 2.65 | 4.38 | −0.87 | 1.68 | 0.17 | 0.32 | −4.32 | −6.22 |
| (3.1)** | (3.2)** | (1.4) | (1.0) | (6.1)** | (1.0) | (1.0) | (1.0) | (1.8)* |
- Note: Since the dependent variable is the inefficiency index that is the reciprocal of the technical efficiency, a positive relationship between an environmental factor and efficiency exists if the sign of the coefficient is negative and negative if the coefficient is positive. The absolute t-statistics are in the parentheses.
- * Significant at 10%.
- ** Significant at 5%.
The debt/asset ratio has a significant impact on technical efficiency in only 1 of the 14 years. The only significant impact is negative in 1997. This result for this group of farms runs counter to the agency theory by Jensen and Meckling (1976) which states that since higher-indebted borrowers are more risky to bankers, they have to bear higher costs in obtaining funds. Due to the increasing costs, these farmers would be less technically efficient since they are not able to borrow sufficient funds to make investments that would increase their efficiency. These current results suggest lenders are not imposing additional borrowing costs on most of these farms due to high debt.
The other factors have significant effects only in a few years. Farmers’ experience, as measured by the log of years farming, has a significant but negative effect in only two years. The nonfarm income ratio is positively related with better technical efficiency only in 1996 and negatively in 2006; it is not significant in other years. The tenancy ratio has a significant but negative effect in 7 of the 14 years. A higher hired labor rate has a significant effect in only four years: three negative effects in earlier years and a positive effect in 2005. The land to labor ratio also has a significant effect in five years with three negative effects in earlier years and two positive effects in 2004 and 2005. Specialization, as measured by the Herfindahl index, has an indeterminate effect with significant but mixed effects in five of the 14 years.
Using weighted Tobit analysis and the results from the single bootstrapping procedure, we find farm size to be associated with better technical efficiency levels in 13 of the 14 years (Table 6). In 10 of the 14 years, farms with higher tenancy ratios are associated with lower technical efficiency. Other explanatory variables have significant coefficients in seven or fewer years. Except for the increase in years in which the debt/asset ratio has a significant negative effect, these results are similar to those estimated using truncated regression in the double-bootstrapping procedure.
| Constant | Log income | Debt/asset ratio | Log of farming years | Nonfarm ratio | Tenancy ratio | Hired rate | Land to labor ratio | Herfindahl index | |
|---|---|---|---|---|---|---|---|---|---|
| 1993 | 4.73 | −0.72 | 0.09 | −0.10 | −0.10 | 0.05 | 0.08 | 0.55 | 0.47 |
| (7.4)** | (6.0)** | (0.4) | (1.6) | (1.6) | (2.9)** | (2.1)** | (1.3) | (1.8)* | |
| 1994 | 2.49 | −0.55 | 0.85 | 0.22 | −0.01 | 0.03 | 0.12 | 1.19 | 0.25 |
| (3.3)** | (4.5)** | (3.1)** | (2.2) | (0.1) | (1.5) | (3.7)** | (2.3)** | (0.9) | |
| 1995 | 3.35 | −0.47 | 0.45 | 0.06 | 0.01 | 0.03 | 0.02 | 0.01 | −0.35 |
| (6.3)** | (5.6)** | (2.5)** | (0.9) | (0.1) | (2.4)** | (1.1) | (0.0) | (1.5) | |
| 1996 | 3.73 | −0.40 | 0.26 | −0.02 | −0.10 | −0.01 | 0.05 | 0.44 | −0.64 |
| (10.7)** | (6.4)** | (2.1)** | (0.6) | (3.2)** | (1.1) | (3.5)** | (1.9) | (3.8)** | |
| 1997 | 1.28 | −0.32 | 0.80 | 0.11 | −0.07 | 0.07 | 0.12 | 0.59 | 0.62 |
| (1.7)* | (2.4)** | (2.9)** | (1.3) | (1.2) | (3.5)** | (3.3)** | (1.2) | (1.6) | |
| 1998 | 2.47 | −0.16 | 0.18 | −0.05 | −0.03 | 0.01 | 0.00 | −0.43 | −0.33 |
| (6.8)** | (2.7)** | (1.4) | (1.1) | (1.0) | (0.7) | (0.2) | (2.0)** | (1.8)* | |
| 1999 | 3.30 | −0.35 | 0.23 | 0.03 | −0.01 | 0.03 | 0.00 | −0.36 | −0.54 |
| (6.7)** | (4.4)** | (1.2) | (0.5) | (0.3) | (2.2)** | (0.2) | (1.3) | (2.3)** | |
| 2000 | 2.73 | −0.62 | 0.36 | 0.30 | −0.06 | 0.11 | 0.00 | −1.14 | 1.25 |
| (2.7)** | (3.9)** | (0.9) | (2.1)** | (0.7) | (4.0)** | (0.0) | (2.0)** | (2.9)** | |
| 2001 | 1.49 | −0.33 | 1.47 | 0.32 | −0.08 | 0.03 | −0.04 | −1.10 | 0.59 |
| (1.8)* | (2.2)** | (4.5)** | (2.5)** | (1.1) | (1.4) | (1.0) | (2.3)** | (1.4) | |
| 2002 | 2.96 | −0.45 | 0.43 | 0.30 | 0.03 | 0.05 | −0.03 | −0.82 | −0.57 |
| (3.2)** | (2.9)** | (1.3) | (1.9)* | (0.4) | (2.0)** | (0.9) | (1.8) | (1.2) | |
| 2003 | 1.47 | −0.51 | 0.75 | 0.33 | 0.17 | 0.07 | 0.02 | 0.54 | 1.39 |
| (1.8)* | (3.5)** | (2.2) ** | (2.5)** | (2.5)** | (2.9)** | (0.6) | (1.4) | (3.4)** | |
| 2004 | 4.87 | −0.92 | −0.13 | 0.20 | 0.04 | 0.18 | 0.02 | −1.38 | 0.85 |
| (2.9)** | (3.4)** | (0.2) | (0.9) | (0.3) | (4.0)** | (0.3) | (1.5) | (1.1) | |
| 2005 | 2.78 | −0.30 | −0.08 | 0.14 | −0.08 | 0.05 | −0.03 | −0.82 | −0.18 |
| (3.1)** | (2.1)** | (0.2) | (1.0) | (1.2) | (2.4)** | (0.9) | (2.0)** | (0.4) | |
| 2006 | 0.80 | 0.29 | 0.96 | −0.16 | 0.45 | 0.14 | 0.05 | −2.70 | −3.16 |
| (0.6) | (1.2) | (1.4) | (0.7) | (6.3)** | (3.1)** | (0.6) | (3.2)** | (3.6)** |
- Note: Since the dependent variable is the inefficiency index that is the reciprocal of the technical efficiency, a positive relationship between an environmental factor and efficiency exists if the sign of the coefficient is negative and negative if the coefficient is positive. The absolute t-statistics are in the parentheses.
- * Significant at 10%.
- ** Significant at 5%.
Results using the initial efficiency estimates and standard Tobit analysis show the same significant positive effect of farm size, but an increase in the years with a significant but negative effect of the debt/asset ratio and a decrease in the years with a significant tenancy ratio (Table 7). Other variables show results similar to double and single bootstrapping.
| Constant | Log income | Debt/asset ratio | Log of farming years | Nonfarm ratio | Tenancy ratio | Hired rate | Land to labor ratio | Herfindahl index | |
|---|---|---|---|---|---|---|---|---|---|
| 1993 | 3.35 | −0.43 | 0.43 | −0.07 | −0.09 | 0.03 | 0.05 | −0.19 | 0.03 |
| (6.7)** | (4.7)** | (2.5)** | (1.4) | (1.8)* | (2.2)** | (1.7)* | (0.6) | (0.2) | |
| 1994 | 2.27 | −0.40 | 0.66 | 0.12 | −0.06 | 0.02 | 0.09 | 0.78 | −0.04 |
| (4.0)** | (4.3)** | (3.2)** | (1.5) | (1.2) | (1.3) | (3.3)** | (1.9)* | (0.2) | |
| 1995 | 2.36 | −0.27 | 0.46 | 0.06 | −0.01 | 0.01 | 0.01 | −0.07 | −0.44 |
| (6.3)** | (4.4)** | (3.5)** | (1.4) | (0.2) | (0.7) | (0.4) | (0.3) | (2.5)** | |
| 1996 | 3.17 | −0.30 | 0.31 | −0.02 | −0.09 | −0.01 | 0.02 | 0.24 | −0.61 |
| (10.9)** | (6.0)** | (2.9)** | (0.5) | (3.5)** | (1.7) | (1.9)* | (1.2) | (4.2)** | |
| 1997 | 1.68 | −0.22 | 0.65 | 0.05 | −0.06 | 0.03 | 0.08 | 0.58 | −0.36 |
| (3.3)** | (2.6)** | (3.6)** | (0.8) | (1.5) | (2.2)** | (3.0) | (1.7)* | (1.3) | |
| 1998 | 2.29 | −0.13 | 0.27 | −0.07 | −0.04 | 0.00 | 0.00 | −0.34 | −0.48 |
| (7.0)** | (2.4)** | (2.2)** | (1.5) | (1.4) | (0.4) | (0.0) | (1.9)* | (3.0)** | |
| 1999 | 2.86 | −0.27 | 0.28 | 0.00 | −0.02 | 0.02 | 0.01 | −0.33 | −0.54 |
| (7.1)** | (4.1)** | (1.8)* | (0.1) | (0.6) | (1.5) | (0.4) | (1.6) | (2.8)** | |
| 2000 | 1.99 | −0.29 | 0.45 | 0.16 | −0.04 | 0.03 | −0.01 | −0.41 | 0.08 |
| (3.3)** | (3.0)** | (1.9)** | (1.9)* | (0.9) | (1.6) | (0.3) | (1.3) | (0.3) | |
| 2001 | 3.04 | −0.38 | 1.09 | 0.12 | −0.07 | −0.01 | −0.01 | −0.31 | −0.55 |
| (6.0)** | (4.5)** | (5.3)** | (1.6) | (1.5) | (0.6) | (0.4) | (1.1) | (2.1)** | |
| 2002 | 2.54 | −0.31 | 0.83 | 0.16 | −0.04 | 0.00 | −0.02 | −0.48 | −0.56 |
| (4.4)** | (3.2)** | (3.7)** | (1.6) | (0.9) | (0.1) | (1.1) | (1.7)* | (1.8)* | |
| 2003 | 1.63 | −0.31 | 0.83 | 0.22 | 0.06 | 0.03 | 0.01 | 0.21 | 0.01 |
| (2.8)** | (3.0)** | (3.2)** | (2.2)** | (1.2) | (1.7) | (0.4) | (0.8) | (0.0) | |
| 2004 | 3.59 | −0.56 | 0.74 | 0.10 | −0.07 | 0.04 | 0.00 | −0.48 | 0.08 |
| (3.5)** | (3.3)** | (1.7)* | (0.7) | (0.9) | (1.4) | (0.1) | (0.9) | (0.2) | |
| 2005 | 2.49 | −0.24 | 0.35 | 0.11 | −0.11 | 0.01 | −0.02 | −0.42 | −0.49 |
| (3.8)** | (2.3)** | (1.3) | (1.0) | (2.1)** | (0.6) | (0.7) | (1.5) | (1.6) | |
| 2006 | −0.08 | 1.09 | −0.06 | 0.14 | 0.05 | 0.01 | −1.10 | −1.37 | 1.86 |
| (0.6) | (2.4)** | (0.4) | (2.8)** | (1.8)* | (0.2) | (2.0)** | (2.4)** | (2.0)** |
- Note: Since the dependent variable is the inefficiency index that is the reciprocal of the technical efficiency, a positive relationship between an environmental factor and efficiency exists if the sign of the coefficient is negative and negative if the coefficient is positive. The absolute t-statistics are in the parentheses.
- * Significant at 10%.
- ** Significant at 5%.
Using Tobit analysis with initial, single, and double bootstrap estimates pooled over all years, almost all variables are significant at the 10% significance level (Table 8). Farm size and land to labor ratio have positive effects on technical efficiency estimated by all three methods. All other variables in the weighted Tobit analyses have a negative effect except specialization, as measured by the Herfindahl index, which has an insignificant effect. Thus, compared to the earlier results, factors such as years farming, nonfarm income, hired labor ratio, and land to labor ratio have significant impacts on technical efficiency when the data are pooled over years, but when their impact is assessed within an individual year, these factors appear not to have strong impacts on efficiency. Particularly interesting is specialization, as measured by the Herfindahl index. Specialization has mixed effects and is often insignificant in individual years (Tables 5–7). When the data are pooled over years, specialization is significant in the standard Tobit but insignificant in the weighted Tobit analyses. The dummy variables for years show a trend toward lower technical efficiency among farms starting in 1999.
| Standard Tobit | Weighted Tobit (single) | Weighted Tobit (double) | ||||
|---|---|---|---|---|---|---|
| Log income | −0.28 | (11.6)** | −0.40 | (10.5)** | −0.40 | (10.8)** |
| Debt/asset ratio | 0.59 | (10.3)** | 0.53 | (6.1)** | 0.55 | (6.3)** |
| Log of farming years | 0.04 | (2.1)** | 0.08 | (2.9)** | 0.07 | (2.4)** |
| Nonfarm ratio | −0.02 | (1.6)* | 0.05 | (2.9)** | 0.05 | (2.6)** |
| Tenancy ratio | 0.01 | (3.4)** | 0.05 | (8.5)** | 0.05 | (8.7)** |
| Hired ratio | 0.01 | (1.8)* | 0.03 | (3.2)** | 0.03 | (3.1)** |
| Land/labor ratio | −0.21 | (2.7)** | −0.40 | (3.1)** | −0.46 | (3.6)** |
| Herfindahl index | −0.35 | (5.0)** | 0.11 | (1.1) | 0.06 | (0.6) |
| Constant | −0.05 | (0.9) | −0.03 | (0.3) | −0.05 | (0.5) |
| 1994 | −0.11 | (1.9)* | −0.13 | (1.5) | −0.14 | (1.6) |
| 1995 | 0.01 | (0.1) | −0.02 | (0.2) | −0.02 | (0.2) |
| 1996 | −0.11 | (1.9)* | −0.07 | (0.8) | −0.06 | (0.7) |
| 1997 | −0.05 | (0.9) | −0.10 | (1.2) | −0.09 | (1.0) |
| 1998 | 0.07 | (1.3) | 0.06 | (0.7) | 0.07 | (0.8) |
| 1999 | 0.07 | (1.2) | 0.16 | (1.8)* | 0.17 | (1.9)* |
| 2000 | 0.19 | (3.2)** | 0.30 | (3.5)** | 0.32 | (3.7)** |
| 2001 | 0.09 | (1.4) | 0.16 | (1.8)* | 0.16 | (1.7)* |
| 2002 | 0.23 | (3.7)** | 0.36 | (3.9)** | 0.37 | (3.9)** |
| 2003 | 0.19 | (2.8)** | 0.37 | (3.7)** | 0.35 | (3.5)** |
| 2004 | 0.11 | (1.5) | 0.14 | (1.3) | 0.14 | (1.3) |
| 2005 | 0.27 | (3.9)** | 0.55 | (5.3)** | 0.57 | (5.4)** |
| 2006 | 2.41 | (16.8)** | 2.58 | (11.5)** | 2.63 | (12.0)** |
- Note: Since the dependent variable is the inefficiency index that is the reciprocal of the technical efficiency, a positive relationship between an environmental factor and efficiency exists if the sign of the coefficient is negative and negative if the coefficient is positive. The absolute t-statistics are in the parentheses.
- * Significant at 10%.
- ** Significant at 5%.
4. Conclusions
The results of the analysis of technical, allocative, and scale efficiency show the degree of inefficiency in Minnesota farms to be considerable. Farms tend to be more scale efficient, followed by allocative efficiency, and then by technical efficiency. Estimates of TEV using bootstrapping methods are lower than the initial TEV estimate.
The study employed both the double and single bootstrapping methods to determine the variability of DEA technical efficiency estimates and to correct for the bias inherent in the deterministic measurement. Using the double bootstrap, the bias-corrected point estimate of technical efficiency is 0.72 and the average width of the confidence intervals is estimated to be 0.17. The results from the single bootstrap are very similar.
From this study of technical efficiency, farm size (as measured by the log of farm income) is the only explanatory variable consistently associated with higher technical efficiency. Its positive sign and significance is robust across analysis methods as well as years.
The significance of other explanatory variables varies between analysis methods. The tenancy ratio has a significant negative effect in 7 of 14 years using truncated maximum likelihood regression in the double bootstrap method, and in 9 of 14 years using a weighted Tobit analysis and the single bootstrap method. However, using initial estimates of technical efficiency in standard Tobit analysis, the tenancy ratio effect is significant in only two years, whereas the debt/asset ratio effect is significant but negative in 12 of the 14 years. When the data are pooled over years, all explanatory variables are significant except for specialization.
These trends in efficiencies and the factors explaining differences between farms help explain some of the trends in farm numbers discussed earlier. When sorted by farm sales, only two groups of farms have increased in numbers in the last 10 years: those with sales less than $10,000 and those with sales greater than $250,000, and especially those with sales greater than $500,000. The robust finding that efficiency is positively associated with larger farms can help explain the continued increase in the number of large farms. The increase in smaller farms is not explained by changes in efficiency, but other data point toward the importance of off-farm jobs, rather than farm income for these farms.
The decrease in the number of livestock farms does not follow the same argument on efficiency though. Our analysis shows that livestock farms are more efficient than diversified and crop farms. The decrease in the number of livestock farms must be explained by other factors. The opposite relationship may be the explanation. That is, other forces in the livestock industry are forcing farms to increase the number of head per farm and to do so require more efficient operations. Thus, as the smaller farms are forced out of production, the larger, more efficient operations are left, although fewer in number. This is supported by the trends in total production (except milk) as the number of livestock farms has decreased.
This article is one of the first applications of the double bootstrap method. From our application, there are several conclusions. First, the method is straightforward and not very computationally demanding. Therefore, the method should be employed more in the empirical studies on efficiency that account for environmental variables. Second, a comparison between the truncated regression used in the double bootstrap method and the standard Tobit analysis shows that, while results from both methods are not substantively different, differences can be seen. This suggests that the findings of previous studies using two-stage Tobit analysis should be reassessed and reestimated to obtain a more accurate picture of significant factors explaining differences in efficiency. As noted earlier, these results need to be extended to include the economies of scope and the differences between types of farms when each type is analyzed independently.
Footnotes
Acknowledgment
The authors thank Jeffrey Apland, Vernon Eidman, Rodney Smith, and Loren Tauer for helpful discussions; two anonymous reviewers for their very helpful comments and suggestions; and Greg Kimmet for help with the data.
Appendix
Algorithm for double bootstrapping as in Simar and Wilson (2007).
- 1
Using the original data, compute the technical efficiency
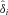 that satisfy the following program
where yi and xi are the original output and input vectors of the ith farm; Y and X are the output and input matrices of the sample; λ is a n × 1 vector of constants and
that satisfy the following program
where yi and xi are the original output and input vectors of the ith farm; Y and X are the output and input matrices of the sample; λ is a n × 1 vector of constants and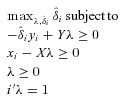 ((A.1))
((A.1)) is the DEA estimate, which is bounded by one on the left
is the DEA estimate, which is bounded by one on the left  for i = 1 , … , n.
for i = 1 , … , n.
- 2
Use the method of maximum likelihood to estimate
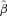 of β as well as
of β as well as 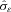 of σɛ in the truncated regression of
of σɛ in the truncated regression of  on zi when
on zi when 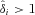 , in which zi is the vector of environmental factors.
, in which zi is the vector of environmental factors. - 3
For each farm i = 1 , … , n, loop over the next four steps L1 times to obtain n set of bootstrap estimates
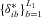 :
: - 4
For each i = 1 , … , n, compute the bias-corrected estimator
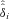 as follows
as follows 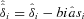 where
where 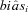 is the bootstrap estimator of bias obtained as in Simar and Wilson (2000) by the formula
is the bootstrap estimator of bias obtained as in Simar and Wilson (2000) by the formula 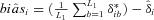 .
. - 5
Use the maximum likelihood method to estimate the truncated regression of
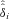 on zi to obtain an estimate
on zi to obtain an estimate 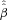 of β and
of β and  of σɛ.
of σɛ. - 6
Loop over the next three steps L2 times to provide a set of bootstrap estimates
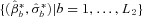
- a.
For each i = 1 , … , n, draw ɛi from the
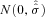 distribution with left- truncation at
distribution with left- truncation at 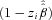 .
. - b.
Compute
 .
. - c.
Maximum likelihood method is used to estimate the truncated regression of δ**i on zi, yielding
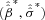 .
.
- a.
- 7
Use the bootstrap values
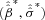 from step 6 and the original estimates
from step 6 and the original estimates 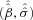 to construct (1 −α) confidence intervals for each element of β and for σɛ as follows:
where Lowerα,j and Upperα,j are calculated using the empirical intervals obtained from the bootstrap values
to construct (1 −α) confidence intervals for each element of β and for σɛ as follows:
where Lowerα,j and Upperα,j are calculated using the empirical intervals obtained from the bootstrap values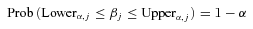 And
And
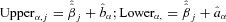 .
.



 distribution with left truncation at
distribution with left truncation at  .
.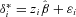 .
. .
.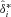 by replacing Y, X in
by replacing Y, X in 
