ADAPTIVE POPULATION DIFFERENTIATION IN PHENOLOGY ACROSS A LATITUDINAL GRADIENT IN EUROPEAN ASPEN (POPULUS TREMULA, L.): A COMPARISON OF NEUTRAL MARKERS, CANDIDATE GENES AND PHENOTYPIC TRAITS
Abstract
A correct timing of growth cessation and dormancy induction represents a critical ecological and evolutionary trade-off between survival and growth in most forest trees (Rehfeldt et al. 1999; Horvath et al. 2003; Howe et al. 2003). We have studied the deciduous tree European Aspen (Populus tremula) across a latitudinal gradient and compared genetic differentiation in phenology traits with molecular markers. Trees from 12 different areas covering 10 latitudinal degrees were cloned and planted in two common gardens. Several phenology traits showed strong genetic differentiation and clinal variation across the latitudinal gradient, with QST values generally exceeding 0.5. This is in stark contrast to genetic differentiation at several classes of genetic markers (18 neutral SSRs, 7 SSRs located close to phenology candidate genes and 50 SNPs from five phenology candidate genes) that all showed FST values around 0.015. We thus find strong evidence for adaptive divergence in phenology traits across the latitudinal gradient. However, the strong population structure seen at the quantitative traits is not reflected in underlying candidate genes. This result fit theoretical expectations that suggest that genetic differentiation at candidate loci is better described by FST at neutral loci rather than by QST at the quantitative traits themselves.
Gene flow is normally expected to impede local adaptation by homogenizing the genetic composition of local populations (Slatkin 1985). However, if selection is strong enough to overcome the counteracting effects of gene flow, local adaptation can still evolve and may result in clinal (e.g., Endler 1977) or ecotypic variation (e.g., Turesson 1922) across a spatially heterogeneous environment. For instance, many plants show strong genetic differentiation over very short distances at boundaries between regular and heavy metal contaminated soils (Antonovics 1968; Antonovics and Bradshaw 1970; Linhart and Grant 1996; Brady et al. 2005). Over greater geographic scales there is often a more gradual change in the environment and clines have been documented in a wide variety of organisms (Endler 1977). It has been shown that selection can rapidly differentiate populations along an environmental gradient as a species is expanding its range (Gilchrist et al. 2001).
A classic example of clinal variation in plants is the adaptive response to the steep latitudinal gradient in the length of growing season that characterizes boreal environments (Rehfeldt et al. 1999; Howe et al. 2003). Perennial plants often show clines in important phenological traits, such as bud set (BS) and growth cessation, representing local adaptation to latitudinal changes in the length of the growing season. Increased tolerance of harsher climates imposes trade-offs between cold tolerance and enhanced growth. Artificial selection for enhanced growth results in trees with a longer growing season mimicking trees from milder climates and trees are thus more likely to experience frost damage in late spring and early autumn (Rehfeldt 1992). However, adaptive population differentiation in many wide-ranging forest trees appears to have occurred despite substantial gene flow, as genetic differentiation at putatively neutral genetic markers is usually low, consistent with long-distance pollen and seed dispersal that is commonly observed in many boreal forest trees (Dvornyk et al. 2002; Garcia-Gil et al. 2003; Waldmann et al. 2005; Cole 2005).
Comparing genetic differentiation at putatively adaptive traits with those of neutral markers could be indicative of the relative influence of selection versus purely demographic processes, such as gene flow, in shaping the underlying population genetic structure (Spitze 1993). Comparisons between genetic differentiation at quantitative traits, measured as QST (Spitze 1993; Whitlock 1999), and genetic differentiation at neutral marker loci, measured as FST (Wright 1951), can thus yield important insights into which quantitative traits that are under diversifying selection.
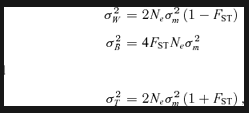(1)
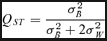(2)Therefore, when QST and FST differ significantly from each other, genetic differentiation among populations in quantitative traits cannot solely be explained by drift and natural selection is usually invoked. Divergent or disruptive selection results in adaptive population divergence and hence the expectation QST > FST (Spitze 1993; Whitlock 1999). The opposite pattern (QST < FST) occurs when a trait is under stabilizing selection that constrains population divergence (Spitze 1993; Whitlock 1999; Merilä and Crnokrak 2001; McKay and Latta 2002).
What is less clear is how natural selection affects patterns of genetic differentiation at the loci that directly control quantitative variation (quantitative trait loci or QTLs). Theoretical models suggest that genetic differentiation at QTLs is better predicted by FST than by QST, because selection generates covariance between individual QTL that act to reinforce the total effect of the QTLs, even if allele frequencies change little between populations (Latta 1998; Le Corre and Kremer 2003). It is important to realize that this covariance, or linkage disequilibrium, that is generated by selection occurs among populations and can occur between loci that are not physically linked. Simulations also indicate that diversifying selection often will result in substantial heterogeneity among loci, with a few QTLs showing strong allelic differentiation among populations (paralleling the patterns of QST) whereas a large number of QTLs appear no more differentiated than neutral markers (Le Corre and Kremer 2003). This among-locus variation implies that only a subset of QTLs affecting a quantitative trait can be expected to show signals of diversifying selection and are therefore possible to detect using methods that identify outlier loci with unusually high genetic differentiation (e.g., Beaumont 2005). Nevertheless, empirical studies that have estimated genetic differentiation across neutral markers, QTLs, and quantitative traits are scarce but are clearly needed to test theoretical predictions (Latta 1998; Le Corre and Kremer 2003).
In this article we compare population differentiation at several types of genetic markers and quantitative traits related to phenology in European aspen (Populus tremula) across a latitudinal gradient spanning 10 latitudinal degrees (56°N to 66°N). This gradient representing growing seasons (number of days with an average temperature above +5°C) ranging from less than three months to over five months. We estimate FST using a set of 18 neutral microsatellite markers and compare this to estimates of FST from seven microsatellite markers that were chosen to be close to candidate genes regulating phenology in P. tremula. We also scored single nucleotide polymorphisms (SNPs) in five candidate genes for phenology and estimate FST. Finally, we used common garden experiments replicated at two sites to estimate population differentiation (QST) at several phenology traits. Our main focus was to determine whether P. tremula show evidence for adaptive divergence in phenology across the latitudinal gradient and to determine whether this was also reflected in genetic variation at candidate genes of phenology regulation.
Material and Methods
PLANT MATERIAL AND COMMON GARDEN TRIALS
The trees that constitute the Swedish Aspen Collection (SwAsp) have been described in detail elsewhere (Ingvarsson et al. 2006; Luquez et al. 2007). Briefly, root cuttings from a total of 116 trees were sampled in the spring of 2003 from 12 localities (populations) in Sweden. Ten trees were sampled from each locality except from locality 12 in which only six trees were sampled. Root cuttings were allowed to produce suckers and these were planted in two common gardens at the Skogforsk stations in Ekebo (55.9°N, Svalöv district) and Sävar (63.4°N, Umeå district) in June 2004. At least four replicate clones of each tree were planted in four (Ekebo) or eight (Sävar) randomized blocks.
During the spring, summer, and autumn of 2005 we measured several phenology traits scored as the number of days since 31 December 2004, as well as height and diameter. Bud flush (BF) was scored every two days from the flush of the first tree in the spring until all trees had flushed and BS was scored twice a week starting in mid-July and was continued until all trees had set terminal buds. The length of the growing season (LGS) was calculated as the time between days to BF and days to BS. Leaf abscission (ABS) was scored as the day when a tree had lost 90% of its leaves and was surveyed twice weekly until all trees had dropped their leaves. The estimated leaf area duration (ELAD) was calculated as the difference between the days to leaf abscission and the days to BF. Total height and the diameter of each tree were recorded at the beginning and end of the season. Seasonal height increase (SHI) and seasonal diameter increase (SDI) was expressed as the differences between the initial and final values of height and diameter, and standardized by the initial measurement.
GENETIC ANALYSES
One hundred thirteen single sequence repeat markers (SSRs), also known as microsatellites, were chosen from a list of over 4000 potential SSRs that have been identified in the Populus Genome Program from the genome sequence of Populus trichocarpa (Tuskan et al. 2006, the list of SSR repeats is publicly available at http://www.ornl.gov/sci/ipgc/Links.htm). Seventy-one of these markers produced PCR products of the predicted size when tested in P. tremula and a preliminary screening with eight individuals suggested that about 50% of these markers were variable. We choose 18 SSR markers that either produced high-quality PCR fragments and were found to be variable in our initial screen (ORPM and GCPM markers) or markers that had previously been found to work in the closely related species P. tremuloides and that had been optimized for P. tremula (PTR markers, Dayanandan et al. 1998; Rahman et al. 2000; modifications from Suvanto and Latva-Karjanmaa 2005).
We also developed a set of SSR markers that were located close to candidate genes involved in regulating phenology. We scanned genome regions from the P. trichocarpa genome sequence (Tuskan et al. 2006) surrounding 12 candidate genes using the program Tandems Repeat Finder (Benson 1999, available at http://tandem.bu.edu/trf/trf.html). Initially, exons and introns from the gene itself and 5-kb upstream and downstream of the genes were scanned for putative repetitive sequences that could be developed into SSR markers. In a few instances in which we did not find a suitable SSR we expanded our search to 10-kb upstream and downstream of the gene. When a suitable repetitive sequence was identified, primers were designed to amplify a fragment between 100 and 300 bp containing the putative SSR. These primers were tested for amplification and polymorphism using eight P. tremula individuals. We succeeded in getting polymorphic SSR markers from six candidate genes phyB2, FLC1B, TFL6, FT1, FY-2, and FLC1A. We also included an SSR located in the coding region of the candidate gene COL2B that was discovered during sequencing of this gene (see below).
Amplification of all PTR loci followed Rahman et al. (2000). All other loci were amplified with an initial denaturing of 95°C for 1 min then 40 cycles of 20 sec 95°C denaturing, 20 sec for annealing at 54–60°C depending on primer pair, 20 sec of 72°C for elongation, and a final step of 5 min at 72°C for elongation.
SSR fragments were labeled with florescent dyes using a tagged universal forward primer approach (Boutin-Ganache et al. 2001). Briefly, the method employs PCR amplification with three primers: a gene-specific forward primer with an M13 universal tail (18 bp, 5′-TGTAAAACGACGGCCAGT-3′.), a gene specific reverse primer and a fluorescently labeled M13 universal primer. PCR reactions were performed in 10–12 μl reactions using 1.5 pmol M13-labeled primer, 1.5 pmol reverse primer, and 0.1 pmol tagged forward primer, with 1.5 μM template DNA. All SSRs were analyzed on a Beckman-Coulter CEQ8000 capillary sequencer (Beckman-Coulter, Fullerton, CA) and before fragments were applied to the capillary sequencer, samples were prepared by mixing 1.5 μl PCR product with 38 μl sample loading buffer and fluorescently label size marker. The resulting chromatograms were visualized and analyzed using the CEQ 8000 Fragment Analysis software.
We scored SNPs in a set of five candidate genes thought to be involved in regulating phenology in Populus. We have no a priori knowledge about whether these candidate genes have functional variation segregating across the specific latitudinal cline studied in this article. These are putative candidate genes that are known or suspected to be involved in regulating BS based on information from other species or from laboratory experiments. These candidate genes include a photoreceptor protein (phyB2,Frewen et al. 2000; Ingvarsson et al. 2006); a gene involved mediating signals in the photoperiodic pathway (COL2B, Böhlenius et al. 2006), and two genes involved in phytohormone signaling pathways (GA20ox1,Eriksson and Moritz 2002 and ABI1B,Frewen et al. 2000; Garcia and Ingvarsson 2007). In addition we included data from a gene of unknown function (hypO312). The start codon of this gene is located approximately 150-bp downstream of one of the SSR markers (ORPM_312). We decided to include this gene as preliminary results suggested that alleles at ORPM_312 showed clinal variation with latitude. We scored between 2 and 30 SNPs in these five candidate gene using a variety of methods, including screening of polymorphisms using restriction enzymes (Ingvarsson et al. 2006), single base-pair primer extension on a Beckman-Coulter CEQ8000 Genetic Analyzer or by complete sequencing of PCR-amplified fragments from genomic DNA that contained the SNPs of interest. In total we scored 52 SNPs from the five candidate genes. Previously unpublished sequences have been deposited in the EMBL database under accession numbers (COL2B: AM600696-AM600901, hypO312: AM600972-AM600996, ABI1B: AM690392-AM690435).
STATISTICAL ANALYSES
(3)We used a Bayesian approach to calculate point estimates and confidence regions of QST. A recent study by O'Hara and Merilä (2005) has shown that Bayesian methods yield the most precise estimates of the confidence intervals of QST. The model in equation (3) was fitted using the lmer function in the statistical package R (http://www.r-project.org). The mcmcsamp function was used to sample from the posterior density of the parameters of the fitted model using Markov Chain Monte Carlo (MCMC) methods. For each trait two independent MCMC chains of 20,000 steps were run, where the first 5000 steps were discarded as burn-in samples. Convergence of the chains was assessed using the coda package in R. The priors of the variances and covariances of the random effects in the model are locally noninformative priors taken from Box and Tiao (1973), as implemented in mcmcsamp. In a Bayesian analysis the full posterior distribution of a statistic of interest is estimated. It is therefore straightforward to calculate point estimates of the QST as the mode of the posterior density. This estimate is comparable to a maximum-likelihood estimate of the statistic of interest (O'Hara and Merilä 2005). Confidence intervals were calculated by 95% highest posterior density (HPD) regions. HPD is the region that contains 95% of the posterior probability mass (Gelman et al. 1995; O'Hara and Merilä 2005). We estimated QST independently for the two different common garden sites (Ekebo and Sävar).
The SSR data were checked with Microchecker version 2.2.3 that tests for null alleles and possible scoring errors (Van Oosterhout et al. 2004). For loci in which we suspected null-alleles to be present, we used the program FreeNA (Chapuis and Estoup 2007, http://www.montpellier.inra.fr/URLB/) to estimate frequencies of putative null alleles (
). Population genetic structure and genetic characteristics for each subpopulation were analyzed using FSTAT (ver. 2.9.3.2, Goudet 1995) and FreeNA for null alleles along with CI for FST, or were inferred using BAPS 4.13 (Corander et al. 2004) and STRUCTURE 2.1 (Pritchard et al. 2000). Correlations between genetic and physical distances were calculated using Mantel tests, implemented in the “vegan” package in R. To test the hypothesis that phenology clines were simply the byproduct of isolation-by-distance and neutral genetic drift we compared the overall explanatory power of latitude for phenology traits and molecular markers for isolation-by-distance. We employed the method of Gockel et al. (2001) to empirically obtain confidence limits for the coefficients of determination (R2) for phenology traits and the molecular markers by bootstrapping. Observed residuals from a regression of the variable of interest (trait values or allele frequencies) on latitude were drawn at random and used to calculate new regression coefficients (Venables and Ripley 2002, p. 163). This procedure was repeated 1000 times and the 95% confidence limits were obtained from the bootstrap samples. For molecular markers we generated samples consisting of 41 alleles (the number of SSR alleles with frequencies exceeding 0.1) and mean R2 values were calculated across these alleles. This procedure was repeated 1000 times and the 95% confidence intervals for R2 for the molecular markers were obtained from these 1000 mean R2 values (Gockel et al. 2001).
Results
GENETIC DIFFERENTIATION AT MOLECULAR MARKERS
The SSR markers were generally highly polymorphic, with the number alleles per locus ranging from 3 (ORPM_214, PTR1, and PTR4) to 23 (PFT1) and levels of heterozygosity were generally high (Table 1). We found no evidence for linkage disequilibrium in pairwise tests of all SSR loci (data not shown). Several of the SSR loci show an excess of homozygotes as indicated by a significant departure from Hardy–Weinberg expectations (i.e., significantly positive FIS values, Table 1). When primers designed from a different species are used to amplify SSR loci, point mutations in the flanking region can prevent annealing of primers during the PCR reaction, resulting in a failed amplification. Unamplified alleles will occur as heterozygotes in some individuals but will not be detectable and heterozygosity is hence underestimated. As P. tremula is a highly polymorphic species (Ingvarsson 2005) it is likely that the observed deficit of heterozygotes we see at some of the SSR loci is caused by null alleles. We therefore estimated null-allele frequencies (
, Table 1) at loci showing heterozygote deficiencies and recalculated FST values accounting for null alleles (Table 2).
), HObs, HExp, and F-statistics for SSR loci.| Locus | Repeat motif | Linkage group | NA |  |
HObs | HExp | FIT | FST | FIS |
|---|---|---|---|---|---|---|---|---|---|
| ORPM_86 | (CTT)5 | XVI | 4 | 0.012 | 0.276 | 0.271 | −0.001 | 0.011 | −0.012 |
| GCPM_1831 | (AG)2 | VI | 8 | 0.043 | 0.743 | 0.800 | 0.079 | 0.012 | 0.069 |
| ORPM_60 | (AAT)5 | VI | 6 | 0.053 | 0.311 | 0.378 | 0.180 | −0.003 | 0.183 |
| ORPM_214 | (TC)11 | XVIII | 3 | 0.074 | 0.220 | 0.334 | 0.362 | 0.018 | 0.352 |
| ORPM_327 | (TC)6 | VIII | 14 | 0.123 | 0.496 | 0.753 | 0.340 | 0.011 | 0.332 |
| ORPM_344 | (TC)8 | X | 7 | 0.022 | 0.729 | 0.760 | 0.042 | 0.001 | 0.041 |
| ORPM_26 | (CA)8 | VI | 6 | 0.019 | 0.056 | 0.077 | 0.268 | −0.012 | 0.276 |
| ORPM_20 | (CTTT)4(CTT)2TT | scaffold_127 | 10 | 0.018 | 0.839 | 0.758 | −0.103 | −0.001 | −0.101 |
| ORPM_16 | (CTT)15 | XIII | 6 | 0.028 | 0.641 | 0.575 | −0.131 | −0.013 | −0.117 |
| ORPM_312 | (CCT)6 | VII | 9 | 0.027 | 0.645 | 0.667 | 0.067 | 0.042 | 0.026 |
| ORPM_276 | (TA)6 | XIX | 6 | 0.048 | 0.500 | 0.538 | 0.069 | 0.005 | 0.064 |
| PTR4 | (TC)17 | III | 3 | 0.052 | 0.482 | 0.534 | 0.108 | 0.026 | 0.085 |
| PTR8 | (A)11(CT)8 | VIII | 12 | 0.163 | 0.389 | 0.760 | 0.498 | 0.001 | 0.498 |
| PTR14 | (TGG)5 | III | 5 | 0.052 | 0.632 | 0.698 | 0.078 | −0.003 | 0.081 |
| PTR3 | (TC)11 | IX | 8 | 0.044 | 0.439 | 0.525 | 0.150 | −0.010 | 0.158 |
| PTR2 | (TGG)8 | IX | 4 | 0.141 | 0.263 | 0.524 | 0.466 | −0.031 | 0.483 |
| PTR1 | (GGT)5N45(AGG)9 | IV | 3 | 0.051 | 0.262 | 0.312 | 0.128 | −0.006 | 0.135 |
| PTR6 | (AT)8 | scaffold_127 | 15 | 0.193 | 0.441 | 0.779 | 0.446 | 0.023 | 0.433 |
| PhyB2 | (AT)14 | X | 19 | 0.335 | 0.168 | 0.825 | 0.794 | 0.021 | 0.789 |
| FLC1B | (TA)16 | III | 13 | 0.025 | 0.763 | 0.827 | 0.110 | 0.037 | 0.076 |
| TFL6/PtCENL-1 | (TA)20 | scaffold_66 | 10 | 0.019 | 0.844 | 0.709 | −0.095 | 0.061 | −0.165 |
| PFT1 | (TA)13 | X | 23 | 0.081 | 0.695 | 0.910 | 0.235 | 0.010 | 0.227 |
| FY-2 | (TG)16 | III | 10 | 0.205 | 0.299 | 0.740 | 0.587 | −0.013 | 0.593 |
| FLC1A | (ATT)15 | III | 16 | 0.087 | 0.513 | 0.727 | 0.300 | 0.013 | 0.291 |
| Col2b | (GAG)5 | IV | 6 | 0.003 | 0.719 | 0.669 | −0.082 | 0.000 | −0.082 |
| 25 | Total | 226 | 0.078 | 0.495 | 0.618 | 0.205 | 0.010 | 0.197 |
| All | SSR | SSR accounting for null alleles | SNPs All | ||||
|---|---|---|---|---|---|---|---|
| Random | Close to genes | All | Random | Close to genes | |||
| mean | 0.010 | 0.006 | 0.019 | 0.015 | 0.012 | 0.022 | 0.016 |
| 95% CI L | 0.002 | −0.002 | 0.003 | 0.008 | 0.005 | 0.009 | 0.007 |
| U | 0.018 | 0.014 | 0.036 | 0.023 | 0.020 | 0.039 | 0.026 |
Theoretically SSRs are expected to evolve in a stepwise manner as a result of replication slippage (the stepwise mutation model, SMM, Ohta and Kimura 1973). Theory has shown that when the tendency for SSR loci to evolve in a stepwise manner is ignored, genetic differentiation at these loci can be underestimated due to the high mutation rate often observed at SSRs (Charlesworth 1998) and methods have been developed to account for this when estimating population structure (Slatkin 1995; Rousset 1996). In our dataset, most of the loci did not behave in a stepwise manner; we observed single base pair differences between alleles at several loci and some loci also showed evidence for larger insertion or deletions. We did analyze the data using RST but did not find any systematic differences in the overall population differentiation compared to FST (data not shown). In addition, Balloux and Goudet (2002) have shown that genetic differentiation in large populations with high gene flow is better estimated using the infinite allele method (IAM, Kimura and Crow 1964). For the remainder of the article we will therefore use FST as our measure of genetic differentiation among populations.
Estimation of FST yielded similar results for all markers analyzed and global genetic differentiation over all loci is approximately 0.01 (Table 2). The comparison of randomly selected SSR markers and markers that were designed to be located close to candidate genes shows that the candidate gene SSRs have levels of genetic differentiation that are two to three times higher than the random SSRs (Table 2). Nevertheless, 95% confidence intervals of the two classes of SSR loci overlap (Table 2) and there is thus little evidence for increased genetic differentiation at loci that are located close to candidate genes for phenology.
The SNPs scored gave very similar levels of genetic differentiation as the SSRs did (Table 2). The SNPs had a broader distribution of FST values, reflecting the greater sampling variance expected at di-allelic loci compared to multi-alleic loci (Fig. 1). FST estimates obtained by excluding null alleles were slightly higher than when the presence of null alleles was ignored (Table 2). However, the 95% confidence intervals overlap and null alleles appear to have only modest effects on population differentiation in our sample. Again, this is not surprising, because most null alleles occur at relatively low frequencies (Table 1).
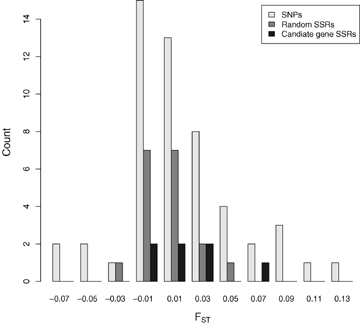
Distribution of FST values for individual loci at random SSRs, candidate gene SSRs and SNPs.
We assessed the genetic characteristics of the 12 populations and did not find any significant differences between them in terms of allelic richness (F= 0.217, df = 11, P= 0.99), gene diversity HE (F= 0.184, df = 11, P= 0.99), observed heterozygosity, HO (F= 0.300, df = 11, P= 0.99), estimated null allele frequencies (F= 0.489, df = 11, P= 0.911) and FIS (F= 0.545, df = 11, P= 0.87). In general, only a single population was identified when we attempted to infer population structure from the marker datasets using Structure or BAPS, showing no population structuring at the molecular level across the SwAsp collection (data not shown).
ADAPTIVE DIVERGENCE IN PHENOLOGY
All traits involved in phenology show significant genetic differentiation among populations and the results were similar at the two common garden sites (Fig. 2, and online Supplementary Table S1). BF showed the least amount of genetic differentiation among populations (QST= 0.175 for Sävar and QST= 0.275 for Ekebo). The remaining traits all had QST values that exceeded 0.6 (Fig. 2). Despite the fact there is a large degree of uncertainty associated with the estimates of QST, as evidence by the wide confidence regions, there is clear evidence for adaptive divergence in all phenology traits, as confidence intervals for QST estimates do not overlap with the confidence interval for FST. A more thorough analysis of the phenology trait data is available elsewhere (Luquez et. al. 2007).
Mean and confidence intervals for QST at several phenology traits. Data from the two common garden sites are shown separately, (S) Sävar and (E) Ekebo. The gray box marks the 95% confidence interval for FST derived from the molecular markers.
ISOLATION-BY-DISTANCE AND CLINAL VARIATION
Comparison of pairwise population differentiation at molecular markers shows a weak, but statistically significant pattern of isolation by distance, suggesting some degree of spatial limitation to gene flow across the sampled populations (Table 3). There is also a strong increase in pairwise QST values with distance for all traits except BF. This holds regardless of whether pairwise QST values are regressed on Euclidian distances or latitudinal distances between populations (Table 3).
| Site | Trait | Q ST versus latitudinal distance | Q ST versus Euclidian distance | Q ST versus genetic distance (FST) |
|---|---|---|---|---|
| Ekebo | ABS | 0.729*** | 0.723*** | 0.385** |
| ELAD | 0.716*** | 0.720*** | 0.338* | |
| BF | −0.119ns | −0.111ns | −0.109ns | |
| BS | 0.830*** | 0.817*** | 0.267* | |
| LGS | 0.823*** | 0.803*** | 0.338*** | |
| SDI | 0.448** | 0.455** | 0.280* | |
| SHI | 0.502** | 0.486** | 0.164ns | |
| Sävar | ABS | 0.772*** | 0.779*** | 0.324* |
| ELAD | 0.816*** | 0.830*** | 0.366** | |
| BF | −0.098ns | −0.127ns | 0.251ns | |
| BS | 0.627*** | 0.664*** | 0.100ns | |
| LGS | 0.680*** | 0.721*** | 0.080ns | |
| SDI | 0.488** | 0.458** | 0.269* | |
| SHI | 0.630*** | 0.597*** | 0.293* | |
| Genetic versus | Genetic versus | |||
| latitudinal distance | Euclidian distance | |||
| F ST | 0.242* | 0.178ns | ||
- nsnot significant, *P < 0.05, **P < 0.01, ***P < 0.001.
The increase in differentiation of phenology traits with distance is also reflected in the clinal patterns observed for most phenology traits. All traits, with the exception of BF, show significant latitudinal clines and latitude explains over 80% of the variation in the population mean of phenology traits (Fig. 3). Trees from the southernmost population had phenology trait scores that typically were two to three standard deviations greater than the northernmost population.
Latitudinal clines for the phenology traits. Population mean ± SE are plotted separately for the two common garden sites (E – Ekebo, open circles, S – Sävar, solid circles). Regressions of population mean versus latitude are shown as dashed lines and percent of variation explained by latitude is indicated in each plot. The pattern of clinal variation at SHI is very similar to SDI and is therefore not included in the plots.
We also looked for evidence of clinal variation at individual alleles of the molecular markers. We assessed clinal variation at all alleles that had frequencies exceeding 0.1 by regressing population frequencies on latitude. After Bonferroni correction, a single SSR allele (TFL6-241) and three SNPs showed evidence for clinal variation. The three SNPs are all located in the phyB2 gene and are three of the five SNPs for which we have already documented significant latitudinal clines in P. tremula (T608N, L789M, and L1078P, Ingvarsson et al. 2006). The proportion of variation explained by latitude was substantially less, however, for the molecular markers compared to phenology traits (mean R2SSR= 0.114, mean R2SNP= 0.100, mean R2phenology= 0.737).
To test the hypothesis that phenology clines were simply the byproduct of isolation-by-distance and neutral genetic drift we compared the overall explanatory power of latitude for phenology traits and molecular markers. The upper 95% CI for the SSR loci was 0.238 and for the SNP data 0.223. In contrast, the lower 95% CI for phenology traits was greater than 0.307 and generally exceeded 0.6. Again the notable exception was BF, which had an R2 value not significantly different from zero. There is thus strong evidence that natural selection has shaped the clines observed in all phenology traits except BF.
Discussion
We have earlier shown that the most important environmental cue regulating growth cessation and the initiation of dormancy in P. tremula is a shortening of the photoperiod (Ingvarsson et al. 2006; Luquez et al. 2007). Here we have documented strong adaptive population differentiation and latitudinal clines in all phenology traits that are related to growth cessation, with latitude explaining over 60% of the observed variation among populations (Fig. 3).
Our estimates of genetic variation within populations rely on clonal replication of trees and the QST estimates are hence partly confounded by nonadditive genetic variances and maternal effects (Lynch and Walsh 1998). Recent theoretical work by Goudet and Büchi (2006) suggests that nonadditive genetic effects generally deflate estimates of QST relative to FST. Therefore, provided that estimates of QST are derived from individuals originating from a reasonable number of populations, patterns of QST > FST are expected to be robust to the effect of nonadditive gene actions (Goudet and Büchi 2006). Our estimates of QST are therefore likely to represent lower bounds and are thus conservative with respect to finding evidence for adaptive population differentiation.
The strong genetic differentiation observed in phenology traits is in stark contrast to the lack of genetic structure observed at all classes of molecular markers, where about 99% of all genetic variation is found within local populations (FST≈ 0.01). The low level of population differentiation observed at the molecular markers is consistent with P. tremula being dioecious, and therefore obligately outcrossing as well as wind-pollinated and with very small wind-dispersed seeds. Our sampling is limited to 20 alleles per locus and population and it is thus possible that we have missed rare alleles that could act to increase FST. We believe, however, that missing low-frequency alleles will only have minor effects on estimating FST. This is exemplified by the effect of null-alleles, which are mostly occurring in low frequencies, and that yields only a small increase in FST when included.
The variation explained by latitude is also substantially less for molecular markers than for phenology traits (mean R2SSR= 0.114, mean R2SNP= 0.100, mean R2phenology= 0.737). Taken together, the strong population differentiation in phenology combined with the lack of population differentiation at the molecular level is consistent with strong adaptive population differentiation driven by local climatic conditions. Population differentiation in phenology is thus not simply a byproduct of neutral genetic drift and migration (Table 3, Figs. 2 and 3). The extensive gene flow among populations of P. tremula, shown by the lack of genetic differentiation at the molecular level, has thus not impeded adaptive differentiation in phenology, suggesting the natural selection acting on these traits must be strong.
We did observe significant clinal variation at a single SSR allele (TFL6-241) and in three of the 52 SNPs. The TFL6 SSR locus is located close to the PtCENL-1 gene (Centroradialis Like-1), which is one of two Populus homologs of the Terminal Flowering Locus 1 (TFL1) gene in Arabidopsis thaliana. This gene is known to promote the maintenance of the vegetative growth phase in A. thaliana and transgenic experiments suggest that PtCENL-1 is involved in regulating flowering and dormancy control in Populus (Mohamed 2006). The three SNPs that show significant clinal variation are all located in the phyB2 gene and are three of the five SNPs for which we have previously documented clinal variation with latitude (sites T608N, L789M, and L1078P from Ingvarsson et al. 2006). The fact that no other SNP shows clinal variation reduces the likelihood that the clines at phyB2 are caused by chance and provides circumstantial evidence for a causal relationship between the phyB2 SNPs and variation in phenology.
We find little evidence for a greater genetic differentiation at SNPs or SSRs sampled from phenology candidate genes than from the putatively neutral SSR markers (Table 2, Fig. 1). There are at least two explanations for this. First, candidate gene SSRs were generally located a few kb away from the coding regions of the candidate genes. LD is low in P. tremula, extending only a few hundred bps (Ingvarsson 2005), and sites located few kb away will therefore effectively be decoupled from a target locus under selection. The same also appears to be true for SNPs, despite the fact that these SNPs are located within the candidate genes themselves. We have previously documented the existence of independent clines at SNPs in the gene phyB2 (Ingvarsson et al. 2006), suggesting that sites separated by as little as a few hundred bps can respond independently to natural selection.
Second, and more interesting, is that the lack of population differentiation also holds for the three SNPs in which we could document significant clinal variation. These three SNPs are not more differentiated than a randomly chosen SNP or SSR marker (FST=−0.004, 0.006 and 0.045, Fig. 1). This result fit theoretical expectations that have shown that genetic differentiation at QTLs is better described by FST at neutral loci rather than by QST at the quantitative traits themselves (Latta 1998; Le Corre and Kremer 2003). The reason for this is that in the presence of high levels of gene flow, spatially variable selection generates covariances between individual QTLs (i.e., linkage disequilibrium) that act to reinforce their total phenotypic effect (Latta 1998; Le Corre and Kremer 2003). If these covariances are positive, they can result in large population differences in mean phenotypes despite small changes in frequencies of the underlying QTLs (Latta 1998; Le Corre and Kremer 2003). Note that these covariances refer to an among-population component of LD that develop in the face of selection and that is distinct from the low intrapopulation LD observed in Populus (Ingvarsson 2005). It is also interesting to note that none of the three SNPs that show clinal variation would have been detected by an approach that scans for genes under disruptive selection by identifying loci with unusually high genetic differentiation (cf. Beaumont 2005). Whether our data are in any way atypical or whether there is a general lack of power to detect QTLs with low-to-moderate phenotypic effects (<10–15%) using “FST outlier” methods remains to be investigated in further detail.
Growth cessation is a prerequisite for the development of dormancy and cold hardiness in trees and the developmental processes leading up to complete endodormancy take several weeks to complete, thereby reducing the period during which active growth can take place (Rehfeldt et al. 1999; Horvath et al. 2003; Howe et al. 2003). Once trees have achieved complete cold hardiness they are able to withstand very low temperatures. Cold damage to trees is therefore largely caused by an improper timing of cold acclimation rather than a failure to fully acclimate to low temperatures (Rehfeldt et al. 1999; Chen et al. 2002; Howe et al. 2003). Nevertheless, fast-growing trees are generally those that flush early in the spring and that enter dormancy late in the fall. A correct timing of growth cessation and dormancy induction hence represents a critical ecological and evolutionary trade-off between survival and growth in most forest trees (Rehfeldt et al. 1999; Horvath et al. 2003; Howe et al. 2003). In this study we have documented adaptive population differentiation and clinal variation over substantial geographic scales, suggesting a balance between gene flow and local selection (Endler 1977). We show that the clines in phenology traits of P. tremula are likely driven by latitudinal changes in the length of the growing season. The strong genetic differentiation at the phenotypic level is not matched by genetic differentiation at the molecular level, where markers suggest virtually no genetic drift and unconstrained gene flow across the sampled populations (Lewontin 1984; Reed and Frankham 2001). Nevertheless, the lack of genetic differentiation at putative QTLs, even for SNPs in which we can observe significant clinal variation, is in accordance with theoretical predictions (Latta 1998; Le Corre and Kremer 2003).
In conclusion, we have shown strong adaptive divergence in several quantitative traits related to phenology, across a latitudinal gradient in P. tremula. At the same time, molecular data suggest little population structure and in turn extensive gene flow. A major goal of plant genetics is to study the genetic basis of adaptive phenotypic variation in natural plant populations (Borevitz and Ecker 2004). In forest trees, progress has been hampered by the long generation times and need to establish segregating mapping populations (Neale and Savolainen 2004). Association mapping of candidate genes has therefore been hailed a way forward, but thus far few successful studies have been published on association mapping in forest trees. The low genetic differentiation observed at the molecular level in P. tremula, along with strong adaptive population differentiation in phenology; suggest that association mapping is a viable approach to investigate the genetic basis of these traits in P. tremula. This, combined with the availability of the genome sequence of black cottonwood, P. trichocarpa (Tuskan et al. 2006), allows for new possibilities to study genetic variation and the process of selection and local adaptation in a woody, perennial plant.
Associate Editor: R. Mauricio
ACKNOWLEDGMENTS
We would like to thank R. Mauricio, R. Latta, and two anonymous reviewers for valuable comments and suggestions that markedly improved this article. This study has been funded by grants from the Swedish Research Council (VR) and from the Research School in Forest Genetics and Breeding to PKI and by grants from Kempestiftelserna, Swedish Foundation for Strategic Research (SSF) and the Swedish Research Council (VR) to SJ.
