Logistic Regression: A Brief Primer
The author has no relevant financial information or potential conflicts of interest to disclose.
Supervising Editor: Craig D. Newgard, MD, MPH.
Abstract
Academic Emergency Medicine 2011; 18:1099–1104 © 2011 by the Society for Academic Emergency Medicine
Regression techniques are versatile in their application to medical research because they can measure associations, predict outcomes, and control for confounding variable effects. As one such technique, logistic regression is an efficient and powerful way to analyze the effect of a group of independent variables on a binary outcome by quantifying each independent variable’s unique contribution. Using components of linear regression reflected in the logit scale, logistic regression iteratively identifies the strongest linear combination of variables with the greatest probability of detecting the observed outcome. Important considerations when conducting logistic regression include selecting independent variables, ensuring that relevant assumptions are met, and choosing an appropriate model building strategy. For independent variable selection, one should be guided by such factors as accepted theory, previous empirical investigations, clinical considerations, and univariate statistical analyses, with acknowledgement of potential confounding variables that should be accounted for. Basic assumptions that must be met for logistic regression include independence of errors, linearity in the logit for continuous variables, absence of multicollinearity, and lack of strongly influential outliers. Additionally, there should be an adequate number of events per independent variable to avoid an overfit model, with commonly recommended minimum “rules of thumb” ranging from 10 to 20 events per covariate. Regarding model building strategies, the three general types are direct/standard, sequential/hierarchical, and stepwise/statistical, with each having a different emphasis and purpose. Before reaching definitive conclusions from the results of any of these methods, one should formally quantify the model’s internal validity (i.e., replicability within the same data set) and external validity (i.e., generalizability beyond the current sample). The resulting logistic regression model’s overall fit to the sample data is assessed using various goodness-of-fit measures, with better fit characterized by a smaller difference between observed and model-predicted values. Use of diagnostic statistics is also recommended to further assess the adequacy of the model. Finally, results for independent variables are typically reported as odds ratios (ORs) with 95% confidence intervals (CIs).
Regression analysis is a valuable research method because of its versatile application to different study contexts. For instance, one may wish to examine associations between an outcome and several independent variables (also commonly referred to as covariates, predictors, and explanatory variables),1 or one might want to determine how well an outcome is predicted from a set of independent variables.1,2 Additionally, one may be interested in controlling for the effect of specific independent variables, particularly those that act as confounders (i.e., their relationship to both the outcome and another independent variable obscures the relationship between that independent variable and the outcome).1,3 This latter application is especially useful in settings that do not allow for random assignment to treatment groups, such as observational research. With random assignment, one can generally exercise sufficient control over confounding variables because randomized groups tend to have equal or balanced distribution of confounders.4 In contrast, observational studies do not involve any experimental manipulation, so confounding variables can become a real problem if left unaccounted for—which is why regression analysis is very appealing in such settings.
Logistic Regression
There are different types of regression depending on one’s research objectives and variable format, with linear regression being one of the most frequently used. Linear regression analyzes continuous outcomes (i.e., those that can be meaningfully added, subtracted, multiplied, and divided, like weight) and assumes that the relationship between the outcome and independent variables follows a straight line (e.g., as calories consumed increases, weight gain increases). To assess the effect of a single independent variable on a continuous outcome (e.g., the contribution of calories consumed to weight gain), one would conduct simple linear regression. However, it is usually more desirable to determine the influence of multiple factors at the same time (e.g., the contribution of number of calories consumed, days exercised per week, and age to weight gain), since one can then see the unique contributions of each variable after controlling for the effects of the others. In this case, multivariate linear regression is the proper choice.
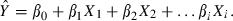
The components of this equation are as follows: 1) Ŷ is the estimated continuous outcome; 2) β0 + β1X1 + β2X2 + …βiXi is the linear regression equation for the independent variables in the model, where
•β0 is the intercept, or the point at which the regression line touches the vertical Y axis. This is considered a constant value.
•β1X1 + β2X2 + …βiXi is the value of each independent variable (Xi) weighted by its respective beta coefficient (β). Beta coefficients give the slope of the regression line or how much the outcome increases for each 1-unit increase in the value of the independent variable. The larger the beta coefficient, the more strongly its corresponding independent variable contributes to the outcome.
Despite its common usage, linear regression is not appropriate for some types of medical outcomes. For a binary event, such as mortality, logistic regression is the usual method of choice. Similar to linear regression, logistic regression may include only one or multiple independent variables, although examining multiple variables is generally more informative because it reveals the unique contribution of each variable after adjusting for the others. For instance, when evaluating 30-day mortality rates for septic patients admitted through the emergency department (ED), are patient characteristics (e.g., age, comorbidities) more important than provider practices, treatment protocols, or hospital variables such as ED sepsis case volume? If so, how much more do patient characteristics contribute compared with other variables? If not, which variables are better associated with sepsis-related mortality? Using this example, one can easily see the importance of assessing multiple independent variables simultaneously, rather than looking at each variable in isolation, since a condition such as sepsis obviously involves many different factors.
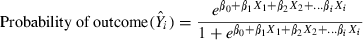
Readers will notice that this equation contains similar configurations for independent variables (X) and accompanying beta coefficients (β) found in linear regression. Indeed, a major advantage of logistic regression is that it retains many features of linear regression in its analysis of binary outcomes. However, there are some important differences between the two equations:
- 1
In logistic regression, Ŷi represents the estimated probability of being in one binary outcome category (i) versus the other, rather than representing an estimated continuous outcome.
- 2
In logistic regression,
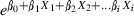represents the linear regression equation for independent variables expressed in the logit scale, rather than in the original linear format.
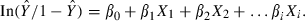
Within the context of these equations, logistic regression then identifies, through iterative cycles, the strongest linear combination of independent variables that increases the likelihood of detecting the observed outcome—a process known as maximum likelihood estimation.2,3
To ensure that logistic regression produces an accurate model, some critical factors that must be taken into account include independent variable selection and choice of model building strategy.
Independent Variables
1. Selection Criteria. Carefully selecting one’s independent variables is an essential step. While logistic regression is quite flexible in that it accommodates different variable types, including continuous (e.g., age), ordinal (e.g., visual analog pain scales), and categorical (e.g., race), one must always justify variable selection using well-established theory, past research, clinical observations, preliminary statistical analysis, or some sensible combination of these different options. As an example, one could start with a large number of potential independent variables based on previous studies as well as one’s own clinical experience in the ED and then analyze differences between groups using univariate statistics at a more relaxed Type I error rate (e.g., p ≤ 0.25) to determine which variables belong in the logistic regression model. Incorporating a less stringent p-value at this stage guards against exclusion of potentially important variables. Alternatively, one could choose to include all relevant independent variables regardless of their univariate results, since there may be clinically important variables that warrant inclusion despite their statistical performance. However, one must always keep in mind that too many independent variables in the model may lead to a mathematically unstable outcome, with decreased generalizability beyond the current study sample.2,3
A key part of the variable selection process is acknowledging and accounting for the role of potential confounders. As described previously, confounding variables are those whose relationship to both the outcome and another independent variable obscures the true association between that independent variable and the outcome.1,3 For instance, socioeconomic status (SES) could confound the relationship between race and annual ED visits because of its association with both race (i.e., some racial groups tend to be more heavily represented in certain SES categories) and ED visits (i.e., poorer patients may use the ED more frequently for basic health care). However, since these sorts of causal associations may not be readily apparent, one should consider formally assessing them during the variable selection process to ensure that they are being appropriately characterized and subsequently modeled. Path analysis diagrams can be particularly helpful in this regard.1
No matter how one goes about selecting independent variables, basic assumptions for conducting logistic regression must always be met. One assumption is independence of errors, whereby all sample group outcomes are separate from each other (i.e., there are no duplicate responses). If one’s data include repeated measures or other correlated outcomes, errors will be similarly correlated, and the assumption is violated.2 Other methods exist for analyzing correlated data using logistic regression techniques, but they are beyond the scope of this paper; for more information, readers may refer to Stokes et al.,5 Newgard et al.,6,7 and Allison.8
A second assumption is linearity in the logit for any continuous independent variables (e.g., age), meaning there should be a linear relationship between these variables and their respective logit-transformed outcomes. There are different ways to check this assumption, with a typical method being to create a statistical term representing the interaction between each continuous independent variable and its natural logarithm. If any of these terms is statistically significant, the assumption is violated.2,3 Solutions include dummy coding the independent variable,3 or statistically transforming it into a different scale.2,3
A third assumption is the absence of multicollinearity, or redundancy, among independent variables (e.g., since weight and body mass index [BMI] are correlated, both should not be included in the same model). A logistic regression model with highly correlated independent variables will usually result in large standard errors for the estimated beta coefficients (or slopes) of these variables.2,3 The usual solution is to eliminate one or more redundant variables.2
A final assumption is lack of strongly influential outliers, whereby a sample member’s predicted outcome may be vastly different from his or her actual outcome. If there are too many such outliers, the model’s overall accuracy could be compromised. Detection of outliers occurs by looking at residuals (i.e., the difference between predicted and actual outcomes) with accompanying diagnostic statistics and graphs.2,3 One would then compare the overall model fit and estimated beta coefficients with versus without the outlier cases. Depending on the magnitude of change, one could either retain outliers whose effect is not dramatic3 or eliminate outliers with particularly strong influence on the model.2,3
In addition to checking that the previous assumptions are met, one may want to consider including interaction terms that combine two or more independent variables. For instance, it is possible that the interaction of patients’ age and race is more important to explaining an outcome than either variable by itself3 (e.g., the association between age and trauma-related mortality is different for Asians, whites, and Hispanics). However, since interaction terms can needlessly complicate the logistic regression model without providing much, if any, benefit,2,3 one should think carefully about including them, getting guidance from statistical diagnostics (e.g., seeing how much the estimated beta coefficients, or slopes, change for one independent variable when the other is added to the model), and assessing whether the interactions make sense clinically.3
2. Number of Variables to Include. As part of selecting which independent variables to include, one must also decide on an appropriate number. The challenge is to select the smallest number of independent variables that best explains the outcome while being mindful of sample size constraints.2,3 For instance, if one selects 50 people for the study sample and includes 50 independent variables in the logistic regression analysis, the result is an overfit (and therefore unstable) model. Generally speaking, an overfit model has estimated beta coefficients for independent variables that are much larger than they should be, as well as higher-than-expected standard errors.3 This sort of scenario causes model instability because logistic regression requires that there be more outcomes than independent variables to iteratively cycle through different solutions in search of the best model fit for the data through the process of maximum likelihood estimation.2,3
What, then, is the correct number of outcomes for avoiding an overfit model? While there is no universally accepted standard, there are some common “rules of thumb” based in part on simulation studies. One such rule states that for every independent variable, there should be no fewer than 10 outcomes for each binary category (e.g., alive/deceased), with the least common outcome determining the maximum number of independent variables.9,10 For example, in a sepsis mortality study, assume that 30 patients died and 50 patients lived. The logistic regression model could reasonably accommodate, at most, three independent variables (since 30 is the smallest outcome). Some statisticians recommend an even more stringent “rule of thumb” of 20 outcomes per independent variable, since a higher ratio tends to improve model validity.11 However, the issue has not been definitively settled, and some would argue that fewer than 10 outcomes per independent variable may be appropriate in certain research contexts.3
Model Building Strategies
In addition to careful selection of independent variables, one must choose the right type of logistic regression model for the study. Indeed, selecting a model building strategy is closely linked to choosing independent variables, so these two components should be considered simultaneously when planning a logistic regression analysis.
There are three model building approaches that apply to regression techniques in general, each with a different emphasis and purpose: direct (i.e., full, standard, or simultaneous), sequential (i.e., hierarchical), and stepwise (i.e., statistical). These model building strategies are not necessarily interchangeable, since they may produce different model fit statistics and independent variable point estimates for the same data. Therefore, identifying the appropriate model for one’s research objectives is extremely important.
The direct approach is a default of sorts, since it enters all independent variables into the model at the same time and makes no assumptions about the order or relative worth of those variables.1,2 For example, in analyzing 30-day mortality in septic patients admitted through the ED, if one identifies 10 different independent variables for inclusion, all 10 variables would be placed into the model simultaneously and have equal importance at the start of the regression analysis.
The direct approach is best if there are no a priori hypotheses about which variables have greater importance than others. Otherwise, one should consider using sequential/hierarchical regression, whereby variables are added sequentially to see if they further improve the model based on their predetermined order of priority.1,2 As a hypothetical example, one might start by entering age into the model, assuming that it is the strongest predictor of 30-day mortality in septic patients admitted through the ED, followed by age plus comorbidities, then by age, comorbidities, and ED sepsis case volume, and so on. While the sequential/hierarchical approach is particularly useful in clarifying patterns of causal relationships between independent variables and outcomes, it can become quite complicated as the causal patterns increase in complexity, making it more difficult to draw definitive conclusions about the data in some cases.1
In contrast to the previous two methods, stepwise regression identifies independent variables to keep or remove from the model based on predefined statistical criteria that are influenced by the unique characteristics of the sample being analyzed.2,3 There are different types of stepwise techniques, including forward selection (e.g., age, comorbidities, ED sepsis case volume, and other independent variables are entered one at a time into the model for 30-day sepsis mortality until no additional variables contribute significantly to the outcome) and backward elimination (e.g., age, comorbidities, ED sepsis case volume, and other variables are entered into the model simultaneously, then those with a nonsignificant contribution to the outcome are dropped one at a time until only the statistically significant variables remain).1,3 Another model building strategy that is conceptually similar to stepwise regression is called best subsets selection, whereby separate models with different numbers of independent variables (e.g., age alone, age plus comorbidities, comorbidities plus ED sepsis case volume) are compared to determine the strongest fit based on preset guidelines.3
As a note of caution, although stepwise regression is frequently used in clinical research, its use is somewhat controversial because it relies on automated variable selection that tends to take advantage of random chance factors in a given sample.2 Additionally, stepwise regression may produce models that do not seem entirely reasonable from a biologic perspective.3 Given these concerns, some would argue that stepwise regression is best reserved for preliminary screening or hypothesis testing only,2 such as with novel outcomes and limited understanding of independent variable contributions.3 However, others point out that stepwise methods per se are not the problem (and may actually be quite effective in certain contexts); instead, the real issue is careless interpretation of results without fully appreciating both the pros and cons of this approach. Therefore, if one does choose to create a stepwise model, it is important to subsequently validate the results before drawing any conclusions. However, it should be noted that all model types need formal validation before they are considered definitive for future use, since models are naturally expected to perform more strongly with the original sample than with subsequent ones.3
Internal and External Model Validation When validating logistic regression models, there are numerous methods from which to choose, each of which may be more or less appropriate depending on study parameters such as sample size. To establish internal validity, or confirmation of model results within the same data set, common methods include: 1) the holdout method, or splitting the sample into two separate subgroups prior to model building, with the “training” group used to create the logistic regression model and the “test” group used to validate it;12,13 2) k-fold cross-validation or splitting the sample into k-number of separate and equally sized subgroups (or folds) for model building and validation purposes; 3) “leave-one-out” cross-validation, which is a variant of the k-fold approach in which the number of folds equals the number of subjects in the sample;13 and 4) different forms of bootstrapping (i.e., getting repeated subsamples with replacement from the entire sample group).13,14
In addition to internally validating the model, one should attempt to externally validate it in a new study setting as further proof of both its statistical viability and clinical usefulness.12,15 If the results of either internal or external validation raise any red flags (e.g., the model poorly fits a certain subgroup of patients), it is advisable to make adjustments to the model as needed, or to explicitly define any restrictions for the model’s future use.15
Interpreting Model Output
1. Assessing Overall Model Fit. After the logistic regression model has been created, one determines how well it fits the sample data as a whole. Two of the most common methods for assessing model fit are the Pearson chi-square and residual deviance statistics. Both measure the difference between observed and model-predicted outcomes, while lack of good model fit is indicated by higher test values signifying a larger difference. However, the accuracy of these measures is contingent upon having an adequate number of observations for the different patterns of independent variables.3,16,17
As another frequently used measure of model fit, the Hosmer-Lemeshow goodness-of-fit tests divide sample subjects into equal groups (often of 10) based on their estimated probability of the outcome, with the lowest decile comprised of those who are least likely to experience the outcome. If the model has good fit, subjects who experienced the main outcome (e.g., 30-day sepsis mortality) would mostly fall into the higher risk deciles. A poorly fit model would result in subjects being evenly spread among the risk deciles for both binary outcomes.2,3 Advantages of the Hosmer-Lemeshow tests are their straightforward application and ease of interpretation.3,16 Limitations include the tests’ dependence on how group cutoff points10,11 and computer algorithms are defined,17 as well as reduced power in identifying poorly fitting models under certain circumstances.3,16 Other less commonly used alternatives for measuring model fit are described by Hosmer et al.16 and Kuss.17
While model fit indices are essential components of logistic regression, one should also rely on diagnostic statistics before reaching any conclusions about the adequacy of the final model. These diagnostic statistics help determine whether the overall model fit remains intact across all possible configurations of the independent variables.3 Although a detailed overview of different diagnostic methods is beyond the scope of this paper, one may refer to Hosmer and Lemeshow3 for more information.
As a way to expand on the results of model fit and diagnostic statistics, one may also wish to evaluate the model’s ability to discriminate between groups. Common ways to do this include 1) classification tables, whereby group membership in one of the binary outcome categories is predicted using estimated probabilities and predefined cut-points,3 and 2) area under the receiver operating characteristic curve (AUROC), where a value of 0.5 means the model is no better than random chance at discriminating between subjects who have the outcome versus those who do not, and 1.0 indicates that the model perfectly discriminates between subjects. The AUROC is often used when one wants to consider different cut points for classification to maximize both sensitivity and specificity.3,18
2. Interpreting Individual Variable Results. Within the context of the logistic regression model, independent variables are usually presented as odds ratios (ORs).3 ORs reveal the strength of the independent variable’s contribution to the outcome and are defined as the odds of the outcome occurring (Ŷ) versus not occurring (1 – Ŷ) for each independent variable. The relationship between the OR and the independent variable’s estimated beta coefficient is expressed as OR = eβi. Based on this formula, a 1-unit change in the independent variable multiples the odds of the outcome by the amount contained in eβi.2,3
For a logistic regression model with only one independent variable, the OR is considered “unadjusted” because there are no other variables whose influence must be adjusted for or subtracted out. For illustrative purposes, assume that the outcome is in-hospital mortality following traumatic injury, and the single independent variable is patient age, classified into greater than or less than 65 years, with the latter category being the reference group (or the group to whom all other independent variable categories are compared). An OR of 1.5 means that for older patients, the odds of dying are 1.5 times higher than the odds for younger patients (the reference group). Expressed another way, there is a (1.5–1.0) × 100% = 50% increase in the odds of dying in the hospital following traumatic injury for older versus younger patients.
In contrast, if the logistic regression model includes multiple independent variables, the ORs are now “adjusted” because they represent the unique contribution of the independent variable after adjusting for (or subtracting out) the effects of the other variables in the model. For instance, if the in-hospital mortality scenario following trauma includes age category plus sex, BMI, and comorbidities, the adjusted OR for age represents its unique contribution to in-hospital mortality if the other three variables are held at some constant value. As a result, adjusted ORs are often lower than their unadjusted counterparts.
Interpreting ORs is also contingent on whether the independent variable is continuous or categorical. For continuous variables, one must first identify a meaningful unit of measurement to best express the degree of change in the outcome associated with that independent variable.3 Using the above in-hospital mortality illustration with age maintained in its original continuous scale and 10-year increments selected as the unit of change, one would interpret the results as follows: “For every 10 years a patient ages, the odds of in-hospital mortality following traumatic injury increase 1.5 times, or by 50%.”
Finally, 95% confidence intervals (CIs) are routinely reported with ORs as a measure of precision (i.e., whether the findings are likely to hold true in the larger unmeasured population). If the CI crosses 1.00, there may not be a significant difference in that population. For instance, if the OR of 1.5 for age has a 95% CI of 0.85 to 2.3, one cannot state definitively that age is a significant contributor to in-hospital mortality following traumatic injury.
Conclusions
Logistic regression is an efficient and powerful way to assess independent variable contributions to a binary outcome, but its accuracy depends in large part on careful variable selection with satisfaction of basic assumptions, as well as appropriate choice of model building strategy and validation of results. Also, it goes without saying that a well-constructed logistic regression model is not the sole determinant of high quality research—developing a clinically relevant and objectively measurable hypothesis, implementing an appropriate study design and statistical analysis plan, and accurately reporting both outcomes and conclusions are all important considerations. Therefore, readers who pay close attention to the parameters of their logistic regression analysis within the context of a well-designed and soundly executed study will make the most meaningful contribution to evidence-based emergency medicine. (For simple examples of syntax codes for conducting direct/standard logistic regression in SAS and SPSS, refer to the Appendix.)
Appendix
Sample Syntax Codes for Direct (Standard) Logistic Regression for Binary Outcomes
I) SAS
proc logistic data = samplefile descending;
/* the “descending” statement ensures that the probability of the outcome coded “1” will be modeled; otherwise, the code will model the probability of the smaller outcome value coded “0”*/
class Gender Age ISS logHLOS / param = ref;
/* the “class” statement is used for categorical covariates */
/* the “param = ref” statement sets up reference categories similar to dummy coding */
model Mortality = Gender Age ISS logHLOS / lackfit ctable waldrl;
/* the “lackfit” option requests the Hosmer-Lemeshow goodness-of-fit statistic */
/* the “ctable” option shows the model’s ability to correctly discriminate between outcomes coded “1” and “0”*/
/* the “waldrl” option requests 95% confidence intervals for covariates’ odds ratios */
title ‘DIRECT LOGISTIC REGRESSION SAMPLE CODE’;
output out = probs predicted = phat;
/* the “output” and “predicted” statements allow SAS to create an output dataset with predicted probabilities for each observation */
run;
II) SPSS
LOGISTIC REGRESSION Mortality
/METHOD = ENTER Gender Age ISS logHLOS
/PRINT = GOODFIT CI(95)
/CRITERIA = PIN(.05) POUT(.10) ITERATE(20) CUT(.5).
