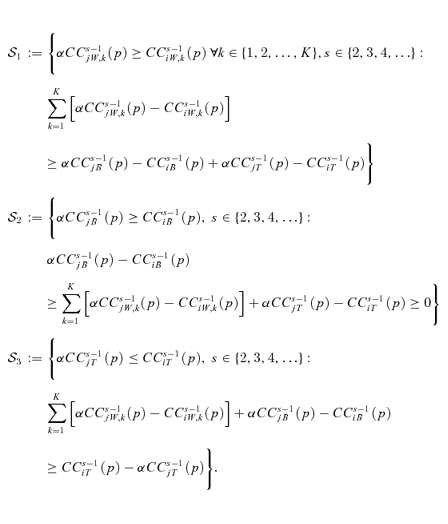Decomposition of s-concentration curves
Décomposition des courbes de concentration.
Mussard is also affiliated with GREDI, Université de Sherbrooke, and CEPS/INSTEAD, Luxembourg. This paper was done when Stéphane Mussard was post-doctoral researcher at CEPS/INSTEAD Luxembourg and when he visited the University of Sherbrooke and GRÉDI, which are gratefully acknowledged. He is also greatly indebted to the Minsitére de la Recherche du Luxembourg and GRÉDI for financial support. Email: [email protected]; [email protected]
Abstract
enAbstract. For any given order of inverse stochastic dominance, standard concentration curves are decomposed into three components, called contribution curves. Those components correspond to within-group inequalities, between-group inequalities, and transvariational inequalities. We prove, for all orders, that contribution curve dominance implies systematically welfare-improving tax reforms and conversely. Accordingly, as welfare expansions may be costly in terms of particular inequalities, we propose targeted fiscal reforms.
Abstract
esLes courbes de concentration sont décomposées, quel que soit l'ordre de dominance stochastique inverse considéré, en trois composantes appelées courbes de contribution. Ces composantes correspondent aux inégalités intragroupes, intergroupes et aux inégalités de transvariation. Nous montrons, pour chaque ordre, que la dominance des courbes de contribution implique systématiquement l'existence de réformes fiscales augmentant le bien-être, et inversement. Des réformes fiscales ciblées sont proposées dans la mesure où les augmentations de bien-être peuvent être coûteuses en termes d'inégalités particulières.
1. Introduction
Yitzhaki and Slemrod (1991) and subsequently Yitzhaki and Thirsk (1990) demonstrated that tax reforms, for pairs of commodities or multiple commodities, can be welfare improving with non-intersecting concentration curves for all additively separable social welfare functions and all increasing 
-concave social welfare functions. In 1991 they applied their technique on the extended Gini coefficient. Accordingly, if the concentration curve of good i dominates (lies above) that of good j – in other words, if there are less inequalities in good i than in good j – then an increasing tax on good j combined with a decreasing tax on good i enables decision makers to improve overall welfare or equivalently to decline overall inequalities.
When the population is partitioned into many groups, a usual way to analyze the structure of income inequalities, referring to the Gini index, is to decompose the overall inequality (see, e.g., Lerman and Yitzhaki 1991; Dagum 1997a,b; Aaberge, Steinar, and Doksum 2005) in a within-group index GW, an average between-group index GB, and a transvariational index GT.1 The latter, being different from a residual, gauges between-group inequalities issued from the groups with lower mean incomes.
In practical policies issues, the policy maker sometimes has constraints that are more stringent than simply increasing a social welfare function. For example, he may be constrained to find indirect tax reforms that decrease between-group inequality and/or increase transvariational inequalities (which may be interpreted as a decrease in polarization) and, in addition, that increase the social welfare function. This is precisely the aim of this note. We aim at using the subgroup decomposition technique of the Gini index initiated by Lambert and Aronson (1993) in order to show that standard welfare-improving marginal tax reforms, for pairs of commodities {i, j}, can be performed with fewer within-group inequalities, fewer between-group inequalities in mean, and more transvariational inequalities in good i than in good j. In other words, instead of looking for non-intersecting concentration curves, we provide stronger conditions allowing for welfare-improving tax reforms on goods {i, j} by introducing contribution curves for all determinants of overall inequality, namely: within-group, between-group, and transvariational contribution curves, which correspond respectively to within-group, between-group, and transvariational inequalities. Contrary to the results related to traditional concentration curves (see, e.g., Makdissi and Mussard 2008), we show that, for any order, it is sufficient but not necessary that all contribution curves of good j lie above those of good i, except for the transvariational contribution curve.2 The results shown in this paper capture the total effects for marginal tax reforms only. This fundamental assumption in our paper preserves the ordering of individuals and groups. It is worth mentioning that marginal criteria models of household consumption behaviour assume that households change behaviour even when a marginal change in the tax system takes place. This may be limited if households are constrained by quantity (and in the choice opportunities). However, although the obtained results disregard possible behavioural responses in the case of non-marginal tax reforms, they still might be interpreted as direct effects.
The article is organized as follows. Section 2 reviews Lambert and Aronson's (1993) Gini decomposition. Section 3 introduces notations and definitions. Section 4 explores welfare-improving tax reforms with the concept of contribution curves for all order of inverse stochastic dominance. Section 5 is devoted to the concluding remarks.
2. Subgroup decomposition of the Lorenz curve
In this section, we briefly summarize the results obtained by Lambert and Aronson (1993). Let a population Π of size n and mean income μ be partitioned into K groups: Π1, … , Πk, … , ΠK of size nk and mean income μk, k= 1, 2, … , K. The groups are ranked as follows: μ1≤⋯≤μk≤⋯≤μK. Assume the individuals are ranked within each Πk such that the richest person of Πk−1 is positioned just before the poorest one of Πk. It is important to note that the observations are not arranged in increasing order, as one would have expected in a regular Lorenz setting. Let 
be the rank of the ℓ-th individual belonging to Πk. His relative rank within Πk is given by: 
. Then, in the overall population Π, the relative rank of an individual belonging to Πk is given by: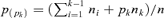 
. In this framework, Lambert and Aronson (1993) decompose the movement from the line of perfect equality to the observed Lorenz curves in three steps.
- •
First, they introduce between-group income inequality. The Lorenz curve between groups,
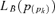, is obtained by considering that each individual within Πk earns the mean income of his group μk such that the total income 
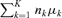is redistributed among the groups:
(1)
- •
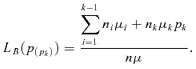
In the second step, they account for within-group income inequality, neglecting the overlappings. To account for those inequalities, they use the concentration curve for income with respect to the lexicographic income parade described in the above paragraph. This concentration curve,
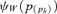is given by
where Lk(pk) is the Lorenz curve associated with group Πk.3
(2)
- •
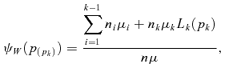
Finally, they take into account the overlappings between the groups, that is, the transvariational income inequality, which represents the inequality induced by the groups with lower mean income.
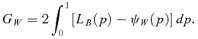
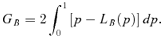
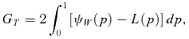
3. Subgroup decomposition of concentration curves
Let us remember the difference between the Lorenz curve and the concentration curve. The Lorenz curve gauges, for any given consumption good (say j), the proportion of total consumption of j received by the first np individuals ranked by ascending order of consumption. The concentration curve provides the proportion of total consumption of j received by the first np individuals ranked by ascending order of income. In the sequel, we use a decomposition technique related to concentration curves C2(p), (C2j(p) being that of good j ). For this purpose, we take recourse to the same lexicographic parade introduced by Lambert and Aronson (1993).
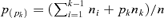, and μjk the kth group's average consumption of good j such as μj1≤⋯≤μjk≤⋯≤μjK. The between-group concentration curve and the within-group concentration curve of the jth commodity are expressed as, respectively: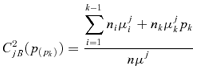
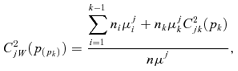
A subgroup decomposition technique exhibits both concentration indices related to each group and contribution indices, which are specified with population shares and income shares of each group. In our framework, we obtain three contribution indices, namely: within-group, between-group and transvariational contributions to the overall amount of the concentration index. These contribution indices are helpful to address issues in the design of indirect tax reforms. For this purpose, we formalize these contribution indices by initiating the concept of contribution curves. Note that a similar notion, used by Duclos and Makdissi (2005), enables contribution curves for poverty measures to be conceived.6
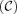. For instance, 
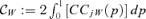yields the absolute contribution of the within-group concentration to the global amount of concentration in good j. In the same manner, one obtains the absolute contribution of between-group and transvariational concentrations, respectively, 
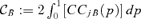and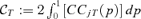 
, such as 
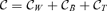.For the need of testing marginal tax reforms with s-order inverse stochastic dominance, s-order concentration curves are introduced.
Definition 3 The first-order concentration curve, defined as C1m(p) =xm(p)/Xm, is the consumption of good m for an individual at rank p divided by the average consumption of the good. The well-known concentration curve of order 2 is given by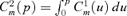 
. The s-concentration curve is then given by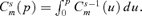 
In the sequel, we analyze the ethical properties underlying the non-negative and rank-dependent social welfare functions.
4. Measuring social welfare
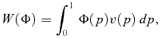
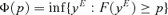is the left inverse continuous c.d.f. (cumulative distribution function), yE the equivalent income, F(yE) the c.d.f. of equivalent incomes, and v(p) ≥ 0 the frequency distortion function weighting an individual at the pth percentile of the distribution. The concept of equivalent incomes yE has been introduced by King (1983). To account for the effect of different prices across households/individuals, King (1983) uses the utility function of a reference household as a basis for defining equivalent incomes; that is, let Uℓ(yℓ, qℓ, t) represent the indirect utility of household ℓ, endowed with exogenous income yℓ, when facing prices qℓ and tax system t. Next, consider a reference household R that faces prices qR. Then King (1983) defines the equivalent income by the exogenous income yℓ,t that would allow the reference household facing prices qR and tax system t to reach utility Uℓ(yℓ, qℓ, t):
can be considered a money measure of the welfare change for household ℓ of changing the tax system from t1 to t2.Without loss of generality, we can restrict our attention to the class of social welfare functions for which v(p) ≥ 0 for all p∈[0, 1]. Those welfare functions are said to satisfy Pen's (1971) Parade principle defined as follows.
Principle 1 Pen's Parade (1971). If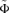 
lies nowhere belowΦ, that is, 
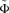weakly dominatesΦ, then 
.
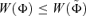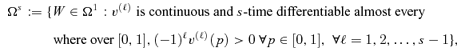
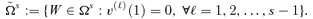
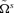is crucial to match the following ethical principles.Principle 2 Pigou-Dalton Transfers (Pigou 1912; Dalton 1920). An income distribution 
, whose left inverse cumulative distribution function is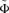 
, is obtained from the distribution Y (of left inverse c.d.f.Φ) by a progressive Pigou-Dalton transfer if a transfer of amount δ > 0 occurs from yi to yj such as yi > yj, letting their position be unchanged: yi−1≤yi−δ, yj+δ≤yj+1. A social welfare index satisfies the Pigou-Dalton principle if, and only if,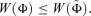 
A social welfare function W(Φ) ∈Ω1 satisfies this normative principle if, and only if, v(1)(p) ≤ 0, ∀p∈[0, 1].
In order to impose more structure on the social welfare function, let us expose the Positional Principle of Transfer Sensitivity (Mehran 1976; Kakwani 1980 have introduced this principle, building on Kolm's diminishing transfer principle, 1976, based on ‘utilitarian’ social welfare functions) and the underlying welfare variations.
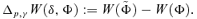
Principle 3 Principle of 1st-degree Positional Transfer Sensitivity. If a small transfer occurs from a higher-income person to a lower-income one, with a given proportion of the population between them, it is more valuable if it occurs at lower income levels; formally: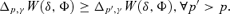 
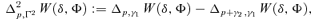
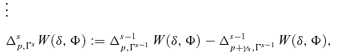
Principle 4 Principle of sth-degree Positional Transfer Sensitivity. A social welfare function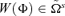 
satisfies the Principle of sth-degree Positional Transfer Sensitivity if,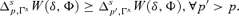 
Aaberge (2004) as introduced this Principle of sth-degree Positional Transfer Sensitivity building on Fishburn and Willig (1984), who have explored the relationship between the utilitarian-egalitarian framework and a particular generalized version of Kolm's (1976) Principle of Diminishing Transfers. Aaberge has shown that a social welfare function W(Φ) satisfies the Principle of (s− 2)th-degree Positional Transfer Sensitivity if, and only if,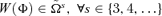 
.
It turns out that W(Φ) ∈Ω1 satisfies the Pen Parade Principle, W(Φ) ∈Ω2⊂Ω1 also satisfies the Pigou-Dalton Principle of Transfers,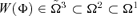 
also satisfies the Principle of 1st-degree Positional Transfer Sensitivity, and 
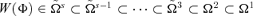for all s∈{3, 4, …} also satisfies the Principle of (s− 2)th-degree Positional Transfer Sensitivity.8
5. Inequality-reducing tax reforms
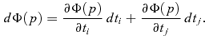
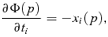
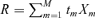and where Xm is the average consumption of the mth commodity: 
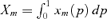. Yitzhaki and Slemrod (1991) prove that constant producer prices induce:
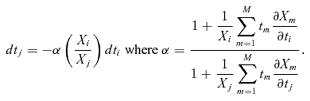
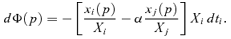
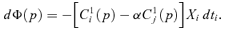
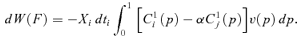
Theorem 1 An average-revenue-neutral marginal tax reform dtj=−α(Xi/Xj) ×dti > 0 implies the following equivalence:
- ı)
dW(Φ) ≥ 0 for all
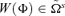
- ıı)
Csi(p) −αCsj(p) ≥ 0, ∀p∈[0, 1], s∈{1, 2, 3, …}.
Proof See Makdissi and Mussard (2008).▪
This result is appealing, since a marginal tax reform increasing the tax on the jth good and decreasing the tax on the ith good produces an increase of welfare if, and only if, the s-concentration curve of good i lies nowhere below that of good j, provided the latter is multiplied by α. This inverse stochastic dominance test enables one to compute the percentage of the population concerned with a positive welfare variation. Furthermore, it allows one to estimate a higher bound for α.9 Indeed, when α= 1, the marginal gain of increasing the tax on good j is the same as the marginal cost of decreasing the tax on good i. The lower α is, the greater the efficiency is; that is, the marginal cost is inferior to the marginal receipt.10 Finally, the methodology yields the ability to infer the behavior of the decision maker by computing s.11
Nevertheless, many questions arise. Imagine the population is composed of heterogeneous agents: are all individuals concerned with an increase of welfare? On the other hand, as the normative foundations of inequality measurement postulates that each social welfare function is associated with a particular inequality measure, the positive welfare variation may be seen as a decrease of income inequalities. But what is the nature of an inequality decline? The following results shed more light on these interrogations.
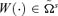, for any given s∈{2, 3, 4, …}, if and only if,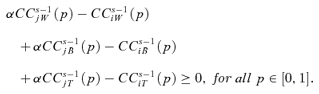
Proof The proof is based on the identity in equation (8). A complete proof can be found in Makdissi and Mussard (2006).▪
Theorem 2 gives many precisions on the duality between welfare and inequality. Indeed, a welfare-improving tax reform is equivalent to an inequality-reducing tax reform, for which overall inequality may be decomposed in within-group inequalities, between-group inequalities, and transvariational inequalities. It turns out that a welfare-improving tax reform potentially reduces within-group inequalities (if αCCs−1jW dominates CCs−1iW for α≤ 1), between-group inequalities (if αCCs−1jB dominates CCs−1iB for α≤ 1), and transvariational inequalities (if αCCs−1jT dominates CCs−1iT for α≤ 1).
Note that the specification of within-group contribution curves brings out the amount of within-group inequalities in mean. Subsequently, if we were able to construct within-group contribution curves for all groups Πk, k∈{1, 2, … , K} (say, CCs−1jW,k for the jth commodity), it would be possible to get a targeted fiscal reform, which would decrease inequality within each group. This result culminates in the following theorem.
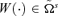, for any given s∈{2, 3, 4, …}, if and only if,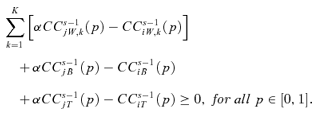
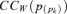represents the contribution of the within-group inequalities to the overall inequality. The within-group concentration index 
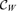is given by (see, e.g., Dagum 1997a,b for the Gini index case):
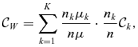
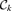is the concentration index of the kth group:
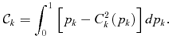
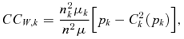
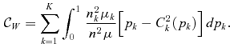
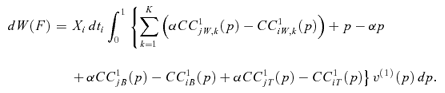
Consequently, welfare-improving tax reforms are compatible with inequality alleviation within each group of the population. Furthermore, following theorem 3, a wide range of tax programs are operational with different constraints.
Proof It is straightforward.▪
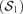This first solution postulates that all within-group contribution curves of good j dominate those of good i, provided the former is multiplied by α. The condition is that the dominance sum is sufficiently important compared with the remaining terms. Then, an increasing tax on good j, for which the repartition is favourable to rich people, coupled with a decreasing tax on good i produces systematically an overall welfare improvement with alleviation of inequalities within each group for any s-order inverse stochastic dominance.12
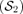If the between-group contribution curve of the jth commodity (multiplied by α) lies above that of the ith commodity, provided equation (23) remains positive, then an increasing tax on the jth commodity coupled with a decreasing tax on the ith commodity yields necessarily an increase of welfare with a between-group inequality reduction, for any s-order inverse stochastic dominance.
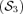The third case is an atypical one. Indeed, welfare-improving tax reforms might be performed with a reduction in transvariational inequalities. Nevertheless, as depicted in Figure 1, it is not a desirable issue.
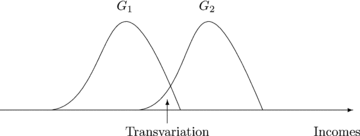
Inequalities of transvariation
Following figure 1, when two distributions overlap, inequalities of transvariation are recorded. This particular concept, inspired from Gini (1916) and subsequently developed by Dagum (1959, 1960,1961), characterizes the income differences between the group of lower mean income (G1) and that of higher mean income (G2). Remember that transvariation means that between-group differences in incomes are of opposite sign compared with the difference in the income average of their corresponding group. It is then closely connected with economic distances (see, e.g., Dagum 1980), stratification indices (see, e.g., Lerman and Yitzhaki 1991) or polarization measures (see, e.g., Duclos, Esteban, and Ray 2004). Therefore,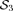 
suggests that welfare-improving tax reforms can be achieved with a growing transvariation (reduction of polarization) between the groups.
Finally, decision makers can contemplate doing welfare-improving tax reforms, subject to the reduction of within-group inequalities, subject to the decline of between-group inequalities or subject to the expansion of transvariational inequalities. These tax reforms may be performed as follows: αCCs−1jW dominates CCs−1iW, αCCs−1jB dominates CCs−1iB, and CCs−1iT dominates αCCs−1jT. This necessarily implies a welfare gain with alleviation of within-group and between-group inequalities and with transvariational expansion.
Proposition 2 A revenue-neutral marginal tax reform, dtj=−α(Xi/Xj) dti > 0 with α≤ 1, that increases Gini social welfare functions under the dominance conditions defined in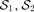 
, and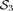 
enables decision makers to choose between a wide range of inequality aversion parametersν.
Proof The class of functions WSG(·), for which v(p) =ν(1 −p)ν−1, is the well-known family of Gini social welfare functions such as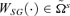 
. They are concave if 1 < ν < 2, convex if ν > 2, and consequently yield exactly the same results as in Theorem 3, for any given parameter of inequality aversion13. ▪
6. Concluding remarks
The employ of rank-dependent social welfare functions is welcome in respect of ethical properties such as Pen's parade, Pigou-Dalton transfers, or the principle of positionalist transfers (see, e.g., Zoli 1999; Aaberge 2004). For the latter, for all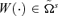 
, an income transfer from a higher-income individual to a lower-income one (say, a progressive transfer) yields a better impact on social welfare insofar as individuals' ranks are the lowest possible. For instance, when s= 2, a progressive transfer occurs. For s= 3, one gets composite transfers, that is, a progressive transfer arising at the bottom of the distribution combined with a reverse progressive transfer at the top. Higher-order principles can be illustrated with Fishburn and Willig's (1984) general transfer principle, for which composite transfers occur both at the bottom and at the top of the distribution. Accordingly, one should analyze, not independently, indirect tax reforms and the implication of the dominance ethical properties resulting from the social welfare function. Therefore, if the s-concentration curve of good i dominates that of good j, then s-order dominance and welfare-improving tax reforms may be interpreted as direct tax programs coupled with indirect ones. The former is interpreted as follows: the higher s is, the more attention is paid to lower-income persons. The latter is interpreted as follows: increasing the tax on the jth commodity (which may be favourable to lower-income earners) and decreasing the tax on the ith commodity imply an overall welfare expansion.
In a more general fashion, we point out targeted welfare-improving tax reforms and, equivalently, targeted inequality-reducing tax reforms. Indeed, by duality, as the welfare amplification possesses three inequality counterparts issued from concentration curves, it turns out that fiscal reforms may be proposed to increase overall welfare and additionally to reduce particular inequalities. Accordingly, it seems reasonable to perform welfare-increasing tax reforms, being aware of the underlying inequality entailments: variation of the inequalities within each group, variation of the inequalities between groups, and variation of the transvariational inequalities.
Finally, the methodology allows one to deal with Gini social welfare functions that depend on an inequality aversion parameter. This might contribute to sheddiag more light on the relationship between the power of the tax reform and the social planner's aversion towards inequality.
Footnotes
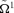and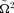 
is possible but not necessary.
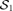. For instance, αCCs−1jB(p) −CCs−1iB(p) +αCCs−1jT(p) −CCs−1iT(p) ≥ 0, may be viewed as a stronger variant. This remark also holds for 
.
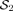