Asymmetric Information, Self-selection, and Pricing of Insurance Contracts: The Simple No-Claims Case
Abstract
This article presents an optional bonus-malus contract based on a priori risk classification of the underlying insurance contract. By inducing self-selection, the purchase of the bonus-malus contract can be used as a screening device. This gives an even better pricing performance than both an experience rating scheme and a classical no-claims bonus system. An application to the Danish automobile insurance market is considered.
Introduction
If one tells the truth, one is sure, sooner or later, to be found out.
Oscar Wilde
In a world with two levels of risk and asymmetric information, where the insurance company cannot distinguish between customers from the two risk groups, there is no pooling equilibrium and there may not be an equilibrium at all (Rothschild and Stiglitz, 1976). In a pooling equilibrium, the lower risk policyholders subsidize the higher risk policyholders. If the policyholders are aware of their risks and the difference is too large between risk and price, the lower risk individuals will not buy insurance. Thus, either the market for insurance breaks down or each type of policyholder buys an insurance contract with a payoff that caters to the specific riskiness of the policyholder. This idea of sufficiently tailor-made (i.e., differentiated) contracts may not fit exactly with what we see in current insurance markets. Insurance contracts offered by insurance companies are only to some extent differentiated, depending on the sophistication of the models, the available data, and regulations. However, Allard, Cresta, and Rochet (1997) show that pooling equilibria may exist if even the slightest distributional cost exists. Differences in risk aversion can also make policyholders with different risks accept pooling (at least to some extent), according to Rothschild and Stiglitz (1976).
Covariate-based regression is generally used to differentiate pricing and the most widely used models for this are generalized linear models (GLMs); see Pinquet (2001) for applications in actuarial science and McCullagh and Nelder (1989) for a general discussion of the statistical theory of GLMs. One way to improve the a priori pricing is to make use of a posteriori corrections based on experience rating, such as credibility theory and bonus-malus systems (BMS). Simple time-independent credibility models with extensions to both time-dependence and multivariate experience rating are found in Pinquet, Guillén, and Bolancé (2001) and Englund et al. (2009). Brouhns et al. (2003) provide a quick survey of different types of BMS. Unfortunately, these experience-based methods have a limited impact when individual claim information is rare, as for new policyholders, and it may take several years of observation before the precision is reasonable. However, Donnelly, Englund, and Nielsen (2013) find evidence of adverse selection within the Danish automobile insurance market, meaning that the degree of coverage chosen by the policyholder is based on the ex ante assessment that a policyholder makes of his riskiness and wealth. Therefore, we seek new ways to differentiate the policyholders by risk at the very outset, that is, at the time of purchase of the insurance product.
This article gives examples of an insurance contract that may induce self-selection within the existing risk classes of the rating scheme. The new type of insurance contract has some features that are not found in contracts of standard BMS. Similar to BMS, the payoff that is offered to policyholders depends on the actual number of experienced claims during each insurance period, but the contract has a more general form of payoff than a standard contract with bonus. The payoff can be tailor-made to individual policyholders’ needs or preferences. Implicit in this is the idea that insurance companies should offer a menu of contracts in such a way that self-selection is induced among the policyholders. Hence, we allow for an extended individual choice compared to standard BMS.
With such a contract the insurer will be able to differentiate the insurance premium for each period of time to an even greater extent, which makes it more competitive due to the separating effect. This is desirable since adverse selection can cause inefficiency in insurance contracts, reducing the benefit of taking an insurance for the lower classes of risk since the price will be too high in relation to the risk (Akerlof, 1970; Rothschild and Stiglitz, 1976; Stiglitz, 1977). For recent contributions on the subjects of asymmetric information, adverse selection, deductibles, and bonus systems, see Snow (2009), Spreeuw and Karlsson (2009), and Kim et al. (2009).
We use policyholder and claims data from a Danish insurance company to investigate the hypothesis that such a contract will in fact induce self-selecting behavior, in addition to the decision of buying the insurance, at the differentiated prices of the rating scheme. Other recent approaches to assessing individual customer risk and relating it to pricing are Guillén et al. (2012) and Thuring et al. (2012).
The article is arranged as follows. In the section titled “The New Insurance Contract,” a heterogeneity model for the data and the new insurance contract are defined. “Comparison of the Add-On to Other Pricing Methods” gives the first numerical study, as well as describing the data set and the pricing methods used to measure the pricing precision of the new insurance contract. In the section titled “Individual Choice and Self-Selection,” we investigate the effects of individual choice on the pricing precision, based on an expected utility representation and private information. We finish with “Conclusion.”
The New Insurance Contract
First, a model for insurance claims when policyholders are heterogeneous is presented. Second, the insurance contract is introduced to exhibit features useful for inducing self-selection among insurance customers. Finally, we illustrate the efficiency of the proposed insurance contact using Danish automobile insurance data.
The usual assumptions used in models on adverse selection are maintained in this article: individual information is costly to observe by the insurer, neither the frequency nor the claim size are functions of the actions of the policyholders, the provision of the insurance is costless, and the insurer is risk neutral while the policyholders are risk averse, having the same twice-differentiable, increasing, and strictly concave utility function 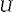 .
.
A Model for Heterogeneous Policyholders
Let us consider the number of claims, 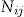 , for individual
, for individual 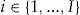 in insurance period
in insurance period 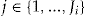 on one particular coverage (i.e., a product). We consider one coverage at a time and assume that the events in different coverages are independent. We assume that every policyholder has a latent individual risk profile
on one particular coverage (i.e., a product). We consider one coverage at a time and assume that the events in different coverages are independent. We assume that every policyholder has a latent individual risk profile 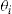 , which summarizes the informational asymmetry and is a realization of a positive random variable
, which summarizes the informational asymmetry and is a realization of a positive random variable 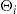 . The latent variable
. The latent variable 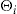 is considered to be a random effect for the insurer but known by the policyholder.
is considered to be a random effect for the insurer but known by the policyholder.
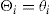 , the number of claims
, the number of claims 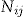 is assumed to be Poisson distributed with expectation
is assumed to be Poisson distributed with expectation 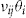 , in which
, in which 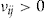 allows for the insurer's prior knowledge about the individual
allows for the insurer's prior knowledge about the individual 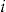 in time period
in time period 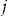 . Specifically, denoting by
. Specifically, denoting by 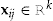 a column vector of covariates, such as age, sex, geographical area, or other relevant variables, and by
a column vector of covariates, such as age, sex, geographical area, or other relevant variables, and by 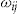 the duration of period
the duration of period 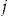 covered for policyholder
covered for policyholder 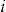 , then
, then
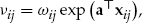
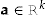 is a column vector of parameters and
is a column vector of parameters and 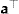 denotes the transpose of
denotes the transpose of 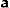 . When covariates are used to price insurance, it is assumed that individuals with the same characteristics have the same risk. However, the introduction of an individual risk profile into the model means that policyholders with the exact same set of covariates may differ in risk due to unobservable characteristics. Examples of these unobservable characteristics for automobile insurance may be aggressiveness while driving and the temperament of the driver.
. When covariates are used to price insurance, it is assumed that individuals with the same characteristics have the same risk. However, the introduction of an individual risk profile into the model means that policyholders with the exact same set of covariates may differ in risk due to unobservable characteristics. Examples of these unobservable characteristics for automobile insurance may be aggressiveness while driving and the temperament of the driver.The pairs 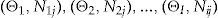 are independent random vectors, where
are independent random vectors, where 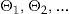 are independent and identically distributed (iid) random variables with
are independent and identically distributed (iid) random variables with 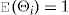 and
and 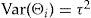 .
.
Since we will only consider full coverage insurances in what comes next, the cost of claims will not affect the individual decision rules or choices. Hence, we consider only the number of claims 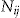 rather than the aggregate cost of the claims made by individual
rather than the aggregate cost of the claims made by individual 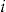 in insurance period
in insurance period 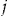 .
.
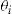 is observable by each policyholder and insurer, then we have symmetric information. In that case, the insurance contract is simple: in each period the insurer offers to cover all losses for each individual against an insurance premium
is observable by each policyholder and insurer, then we have symmetric information. In that case, the insurance contract is simple: in each period the insurer offers to cover all losses for each individual against an insurance premium
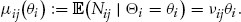
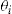 , the actuarially fair value of the insurance premium is
, the actuarially fair value of the insurance premium is
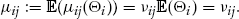
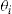 .
.The Add-On to the Standard Insurance Contract
Now we consider an add-on to the standard insurance contract, which allows for the policyholder's individual risk profile 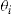 . To keep the discussion simple, we assume that the discount rate is zero.1
. To keep the discussion simple, we assume that the discount rate is zero.1
In addition to the premium 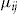 , policyholder
, policyholder 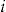 who accepts the add-on will pay an entrance fee
who accepts the add-on will pay an entrance fee 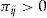 . If the policyholder makes no claims during the insurance period
. If the policyholder makes no claims during the insurance period 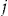 , the insurer will pay an amount
, the insurer will pay an amount 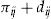 to the policyholder, in which the constant
to the policyholder, in which the constant 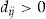 is called the dividend. In other words, a policyholder who makes no claims during the insurance period
is called the dividend. In other words, a policyholder who makes no claims during the insurance period 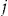 gets back his entrance fee plus a dividend at the end of the insurance period
gets back his entrance fee plus a dividend at the end of the insurance period 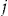 . If the policyholder makes one claim or more, then the insurer pays nothing to the policyholder in respect of the add-on (although the cost of the claims made under the standard insurance contract are covered as usual). The add-on to the standard insurance contract has a binary nature: either policyholder
. If the policyholder makes one claim or more, then the insurer pays nothing to the policyholder in respect of the add-on (although the cost of the claims made under the standard insurance contract are covered as usual). The add-on to the standard insurance contract has a binary nature: either policyholder 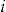 gets the payment
gets the payment 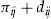 at the end of insurance period
at the end of insurance period 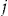 , or he does not.
, or he does not.
We focus our analysis on the simplest (one-period) setting in which the add-on is a one-period contract. Policyholders decide at the start of the insurance period whether or not to accept the add-on, and the contingent payment made at the end of the insurance period is distinct from the premium that would be paid in the next insurance period. Extensions of this simple setting are discussed in the following section, “Discussion of the Add-On.”
We assume that the contingent payment 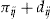 is made directly to policyholder
is made directly to policyholder 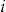 at the end of the insurance period
at the end of the insurance period 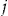 . In a more realistic setting, it may be tax efficient to reduce instead the insurance premium in the subsequent insurance period by the amount of the contingent payment.2
. In a more realistic setting, it may be tax efficient to reduce instead the insurance premium in the subsequent insurance period by the amount of the contingent payment.2
The payments in the add-on could be restructured so that the policyholder pays nothing at the start of the insurance period. Then if policyholder 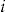 makes no claims, he would receive a payment of
makes no claims, he would receive a payment of 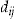 from the insurer at the end of the insurance period
from the insurer at the end of the insurance period 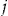 . Otherwise, policyholder
. Otherwise, policyholder 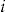 pays
pays 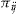 to the insurer at the end of the insurance period
to the insurer at the end of the insurance period 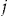 . All of the results in our simple setting are identical with this alternative payment structure. It also allows the identification of the payment
. All of the results in our simple setting are identical with this alternative payment structure. It also allows the identification of the payment 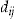 as a bonus and the payment
as a bonus and the payment 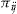 as a malus.
as a malus.
However, paying the entrance fee 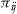 up front has the advantage of allowing us to bypass punishment rules in environments where they are forbidden, such as in some health insurance systems (e.g., see Riedel, 2006). The absence of a reward at the end of the insurance period in the case where no claims occur (i.e., receiving nothing) replaces the punishment decision of the alternative payment structure (i.e., having to pay a malus
up front has the advantage of allowing us to bypass punishment rules in environments where they are forbidden, such as in some health insurance systems (e.g., see Riedel, 2006). The absence of a reward at the end of the insurance period in the case where no claims occur (i.e., receiving nothing) replaces the punishment decision of the alternative payment structure (i.e., having to pay a malus 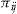 to the insurer). It may also be more attractive way of framing the add-on to the policyholder (see Johnson et al., 1993). Note that BMSs come in many variants in real life, as well as in the literature; for the latter, examples are Baione, Levantesi, and Menzietti (2002), Denuit et al. (2007), Lemaire and Zi (1994), Lemaire (2004), Moreno, Vázquez, and Watt (2006), and Pinquet (1997).
to the insurer). It may also be more attractive way of framing the add-on to the policyholder (see Johnson et al., 1993). Note that BMSs come in many variants in real life, as well as in the literature; for the latter, examples are Baione, Levantesi, and Menzietti (2002), Denuit et al. (2007), Lemaire and Zi (1994), Lemaire (2004), Moreno, Vázquez, and Watt (2006), and Pinquet (1997).
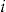 at the end of insurance period
at the end of insurance period 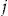 is represented by the random variable
is represented by the random variable
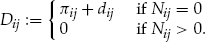
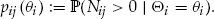
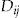 is
is
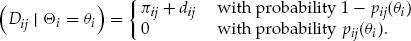
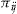 and the dividend
and the dividend 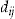 . The entrance fee,
. The entrance fee, 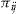 , can be set either individually or collectively. This will be a strategic decision of the insurer and something we discuss in the sequel.
, can be set either individually or collectively. This will be a strategic decision of the insurer and something we discuss in the sequel.The dividend 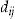 is calculated in this article via the actuarial net premium principle (see Young, 2006). The net premium principle is justifiable if we can assume that volatility is essentially nonexistent, that is, if the insurer sells enough iid policies so that the Law of Large Numbers applies. However, the dividend can be calculated via any other suitable principle, for example, the expected value premium principle:
is calculated in this article via the actuarial net premium principle (see Young, 2006). The net premium principle is justifiable if we can assume that volatility is essentially nonexistent, that is, if the insurer sells enough iid policies so that the Law of Large Numbers applies. However, the dividend can be calculated via any other suitable principle, for example, the expected value premium principle: 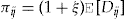 , for some
, for some 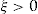 .
.
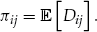 (1)
(1)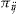 and
and 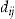 fixed at the start of insurance period
fixed at the start of insurance period 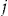 . The insurer cannot change
. The insurer cannot change 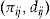 during insurance period
during insurance period 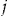 in light of the decision of policyholder
in light of the decision of policyholder 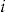 to accept the add-on or not. This does not preclude the insurer from changing the risk classification of policyholder
to accept the add-on or not. This does not preclude the insurer from changing the risk classification of policyholder 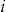 in subsequent insurance periods, based on his decision to accept the add-on in the current insurance period. We do not explore this interesting avenue of research in this article. Instead, our focus is on the pricing precision of the add-on within the current insurance period. This is important to know, to see if there is a cost to the insurer in offering the add-on. In fact, our results show that the insurer's pricing precision may be increased significantly by offering the add-on.
in subsequent insurance periods, based on his decision to accept the add-on in the current insurance period. We do not explore this interesting avenue of research in this article. Instead, our focus is on the pricing precision of the add-on within the current insurance period. This is important to know, to see if there is a cost to the insurer in offering the add-on. In fact, our results show that the insurer's pricing precision may be increased significantly by offering the add-on.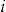 in insurance period
in insurance period 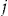
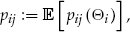
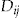 is
is
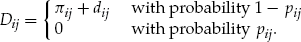
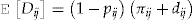 into Equation (1), we get
into Equation (1), we get
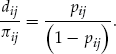 (2)
(2)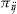 , the value of the dividend
, the value of the dividend 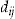 is fixed by the above equation. Note that the insurer sets the dividend based on
is fixed by the above equation. Note that the insurer sets the dividend based on 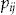 , the average probability of making a claim. In comparison, the policyholder evaluates the offered contract based on their individual probability of making a claim,
, the average probability of making a claim. In comparison, the policyholder evaluates the offered contract based on their individual probability of making a claim, 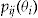 .
.Discussion of the Add-On
The add-on is a voluntary investment in addition to the original insurance contract. The add-on should be appealing to the customer who is a better-than-expected risk. Assuming this attractiveness is communicated to the customer, it is then for the customer to judge if he is a better-than-expected type. In this sense, there is a clear incentive from the customer's perspective to reveal his private knowledge. Consequently, the add-on is linked more directly to the economic discussion of asymmetric information than are classical BMSs.
Superficially, it seems that our simple no-claims example is similar to a “money-back” structure because money is paid out at the end of a claim-free year. Indeed, in the one-period case, the add-on clause has many similarities to a BMS. This can be seen by assuming a multiperiod setting in which the payments from the one-period add-on are paid only upon renewal of the insurance contract in the subsequent insurance period. In that case, the add-on is not very different from a BMS in the long run.
However, when generalizing the basic idea of paying money up front, that is, the entrance fee, to more complex pricing structures, such generalizations would differ fundamentally from other natural developments of a BMS. We could construct an add-on that is a 5-year or 10-year contract rather than a 1-year contract. A long-term contract gives the customer the full advantage of being a better-than-expected risk at the same time as providing a clear customer loyalty situation for the company. Furthermore, the add-on does not have to be restricted to the simple no-claims case. For example, one could introduce a threshold such the customers can have claims paid out up to some amount while still being in the class of customers getting a payout. Or one could simply say that the customer pays his own claims with the revenue from the add-on contract, as long as the revenue is large enough to pay the claims.
For example, suppose that the add-on is a 5-year contract. At the start of the 5-year period, the customer pays the standard insurance premium and the entrance fee. The entrance fee is calculated using the customer's expected experience over the 5-year period, rather than on observed experience data. During the 5 years, the standard insurance premium is adjusted using the emerging experience. The new idea is that we adjust also a historically already-paid premium. Aside from the initial entrance fee, the contract is structured so that the customer does not pay any more in premiums than if he had not bought the add-on. In other words, the buyer of the add-on cannot lose more than the entrance fee. That leaves the insurance company with a risk for which it charges an insurance premium in a similar way to the one-period case considered in this article. The distinction of moral hazard and dynamic selection on unobservables as analyzed in Abbring et al. (2003) and Abbring, Chiappori, and Pinquet (2003) based on observed data might be further developed and improved while incorporating future data in the consideration.
Comparison of the Add-On to Other Pricing Methods
We want to compare the insurance contract with a 1-year add-on against different pricing methods, using Danish automobile insurance data from 2001 to 2004. The accuracy of each pricing method is assessed by estimating the sum of squared errors (SSE) across all individual policyholders. Here, the error is defined as the net payment made by the insurer to the policyholder during an insurance period. The most efficient pricing method is the one that has the lowest SSE.
The idea behind using the SSE is that the insurer wants to break even on each contract. A premium that is too low will result in an economic loss. A premium that is too high will result in a loss of policyholders to another insurer that is offering a lower premium. More precisely, and since we only will investigate the product portfolio of one insurer, we assume that the insurer is a risk-neutral competitive specialist, whose expected profit for each policy is zero, as in Glosten and Milgrom (1985). The minimum SSE is expected in the theoretical situation where each customer pays exactly his own claim costs to the insurance company. Although the results below should clearly be interpreted in light of this, a low SSE seems to be a reasonable description of the insurance company's optimization problem (Bühlmann and Gisler, 2005).
Data Preparation and Model Validity
The data set that we analyze consists of 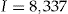 policyholders in the personal lines portfolio of a Danish insurance company. The data set contains the variables used by the pricing department at the insurance company for each of the years during the period. For example, the covariates are: policyholder's demographic characteristics such as age, gender, geography; policyholder's car characteristics: brand, size of engine, model year, initial value of the car, commercial vehicle or not, main vehicle or not.
policyholders in the personal lines portfolio of a Danish insurance company. The data set contains the variables used by the pricing department at the insurance company for each of the years during the period. For example, the covariates are: policyholder's demographic characteristics such as age, gender, geography; policyholder's car characteristics: brand, size of engine, model year, initial value of the car, commercial vehicle or not, main vehicle or not.
The data set was selected from more than 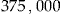 policyholders in the same portfolio. Policyholders with missing values and obvious outliers were removed. We chose the policyholders with exactly one automobile insurance policy, which has full coverage, full duration for each year of the period 2001–2004 and with no experience rating. In order to compare the classical no-claims bonus with the add-on as far as possible, each policyholder has to fulfill the criteria of the classical bonus, to the extent that the bonus is only dependent on the claim experience. Therefore, we further restricted our selection to policyholders who, in addition to the automobile insurance, have purchased a building and personal property insurance policy with full duration in the period 2001–2004.
policyholders in the same portfolio. Policyholders with missing values and obvious outliers were removed. We chose the policyholders with exactly one automobile insurance policy, which has full coverage, full duration for each year of the period 2001–2004 and with no experience rating. In order to compare the classical no-claims bonus with the add-on as far as possible, each policyholder has to fulfill the criteria of the classical bonus, to the extent that the bonus is only dependent on the claim experience. Therefore, we further restricted our selection to policyholders who, in addition to the automobile insurance, have purchased a building and personal property insurance policy with full duration in the period 2001–2004.
The actual number of claims experienced for policyholder 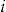 in year
in year 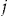 is denoted
is denoted 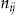 and, as all policies have full annual duration,
and, as all policies have full annual duration, 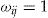 . By a covariate-based regression method (using GLM and maximum likelihood), we obtained the estimated expected number of claims
. By a covariate-based regression method (using GLM and maximum likelihood), we obtained the estimated expected number of claims 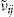 . However, in our data set there is a difference between the total expected and total experienced number of claims due to the pricing procedure, namely, the rating scheme is estimated on all policyholders of the automobile portfolio, while we use only a subset of these. One might suspect that policyholders with full duration in 4 consecutive years, and who have purchased at least three insurance products, have a better claim history than we expected, even though total duration (seniority) is not a significant variable in the rating scheme. Due to this difference and our interest to investigate the performance of various pricing methods, we scaled the original claim frequency estimates
. However, in our data set there is a difference between the total expected and total experienced number of claims due to the pricing procedure, namely, the rating scheme is estimated on all policyholders of the automobile portfolio, while we use only a subset of these. One might suspect that policyholders with full duration in 4 consecutive years, and who have purchased at least three insurance products, have a better claim history than we expected, even though total duration (seniority) is not a significant variable in the rating scheme. Due to this difference and our interest to investigate the performance of various pricing methods, we scaled the original claim frequency estimates 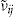 of the regression by multiplying each of them by a factor
of the regression by multiplying each of them by a factor 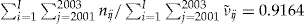 . These new claim frequency estimates
. These new claim frequency estimates 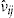 were then used to perform the analyses of this article.
were then used to perform the analyses of this article.
Table 1 summarizes the claim information for each year in the period 2001–2004 for the data set of 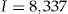 policyholders.
policyholders.
Year 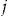 |
||||
|---|---|---|---|---|
| 2001 | 2002 | 2003 | 2004 | |
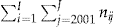 |
1,604 | 3,381 | 5,264 | 7,007 |
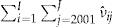 |
1,644 | 3,441 | 5,264 | 6,969 |
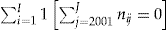 |
7,128 | 6,058 | 5,165 | 4,531 |
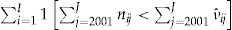 |
7,128 | 6,068 | 5,365 | 5,153 |
- Notes: Cumulative number of experienced claims, cumulative number of expected claims, the number of policyholders with no claims, and the number of policyholders with fewer claims than expected, for each year of the period 2001–2004 for the data set of
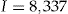 policyholders. The actual and expected number of claims by policyholder
policyholders. The actual and expected number of claims by policyholder 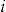 in year
in year 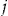 is denoted
is denoted 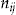 and
and 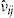 , respectively, and
, respectively, and 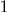 denotes the zero–one indicator function.
denotes the zero–one indicator function.
Empirically, we get a dispersion index of 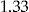 for the data set, which supports the correctness in assuming a conditional Poisson distribution, that is, assuming the existence of an individual latent risk profile.
for the data set, which supports the correctness in assuming a conditional Poisson distribution, that is, assuming the existence of an individual latent risk profile.
Pricing Methods
We investigated five pricing methods for the insurance contract. The premiums for the year 2004 were calculated based on the data in years 2001–2003. The premiums and the actual claims experience in 2004 were then used to calculate the SSE for each method.
-
1. Flat rate. The mean value estimator, or the flat rate, method with insurance premium
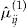 . For this pricing method, the premium charged is identical for all policyholders:
The flat rate method is the simplest possible estimator with an expected nonnegative profit. Based on the data in years 2001–2003, we find
. For this pricing method, the premium charged is identical for all policyholders:
The flat rate method is the simplest possible estimator with an expected nonnegative profit. Based on the data in years 2001–2003, we find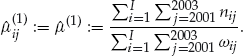
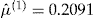 , meaning that, on average, there is approximately one claim every fifth year.
, meaning that, on average, there is approximately one claim every fifth year.
-
2. Regression. The covariate-based regression method with insurance premium
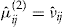 . It is the pricing method used by the Danish insurance company from whom we obtained the data and we use it as the baseline pricing method.
. It is the pricing method used by the Danish insurance company from whom we obtained the data and we use it as the baseline pricing method. -
3. Credibility. The experience rating method based on the one-dimensional homogeneous credibility estimator, with insurance premium
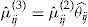 . Bühlmann and Gisler (2005) provide an excellent survey on credibility theory.
. Bühlmann and Gisler (2005) provide an excellent survey on credibility theory. -
4. No-claims BMS. The classical, market-based, no-claims BMS with premium
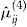 . In this case, if certain criteria are satisfied, the policyholder is granted a bonus expressed as a percentage of the premium. The bonus is given if the following criteria are fulfilled: the policy has a duration of at least 3 years, and no claims are reported during both the last 3 years and the current insurance period. For the given data set, the bonus is 10 percent. Normally, this requires that all policyholders pay 3–4 percent more of the original actuarial premium up front, in order that the portfolio is financially balanced. However, for the data subset of
. In this case, if certain criteria are satisfied, the policyholder is granted a bonus expressed as a percentage of the premium. The bonus is given if the following criteria are fulfilled: the policy has a duration of at least 3 years, and no claims are reported during both the last 3 years and the current insurance period. For the given data set, the bonus is 10 percent. Normally, this requires that all policyholders pay 3–4 percent more of the original actuarial premium up front, in order that the portfolio is financially balanced. However, for the data subset of 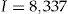 policyholders, the additional payment is 9.533 percent. The reason is due to the data selection: every policyholder in the data subset is in the bonus system and has the opportunity of getting a bonus. We lack the policyholders who subsidize the bonus system by not having the opportunity of getting one. Consequently, the additional payment is higher.
policyholders, the additional payment is 9.533 percent. The reason is due to the data selection: every policyholder in the data subset is in the bonus system and has the opportunity of getting a bonus. We lack the policyholders who subsidize the bonus system by not having the opportunity of getting one. Consequently, the additional payment is higher. -
5. Add-on. The standard insurance contract with an add-on. The premium charged for the standard insurance contract is
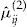 and the entrance fee for the add-on is
and the entrance fee for the add-on is 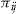 . In this section of the article, we assume that all policyholders buy the add-on, so that the total amount charged to policyholder
. In this section of the article, we assume that all policyholders buy the add-on, so that the total amount charged to policyholder 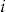 is
is 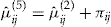 . This assumption will be removed in the section “Individual Choice and Self-Selection.”
. This assumption will be removed in the section “Individual Choice and Self-Selection.”The dividend of the add-on is calculated for each policyholder
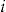 through Equation 10. This requires an estimator of
through Equation 10. This requires an estimator of 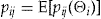 . First, we expanded
. First, we expanded 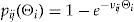 as a second-order Taylor series around
as a second-order Taylor series around 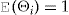 , with a remainder term. Based on the data set, the empirical mean value of the remainder term is negligible (it is less than
, with a remainder term. Based on the data set, the empirical mean value of the remainder term is negligible (it is less than 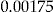 ). Hence, taking the expectation of the Taylor expansion, we assumed the expected value of the remainder term was zero. The resulting estimator is
). Hence, taking the expectation of the Taylor expansion, we assumed the expected value of the remainder term was zero. The resulting estimator is 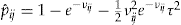 , in which
, in which 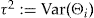 .
.Figure 1 shows the distribution of
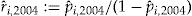 in the data set. The dividend is calculated as
in the data set. The dividend is calculated as 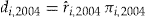 for each policyholder
for each policyholder 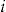 . Thus, each policyholder
. Thus, each policyholder 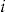 is offered an individually determined add-on, with entrance fee
is offered an individually determined add-on, with entrance fee 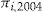 and dividend
and dividend 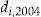 . We discuss below the choice of the entrance fee.
. We discuss below the choice of the entrance fee.
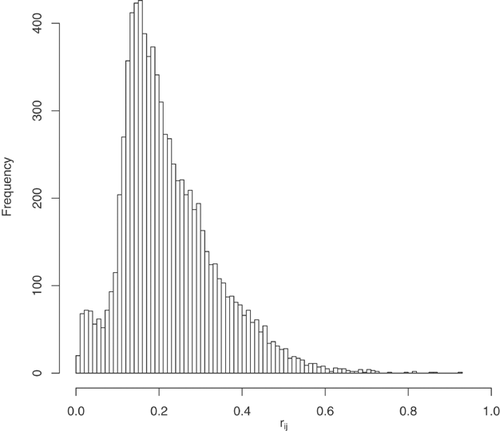
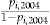
Notes: As we use Equation (2) to calculate the dividend 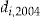 then, by Equation (4),
then, by Equation (4), 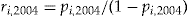 for policyholder
for policyholder 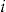 .
.
A First Numerical Study
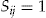 , the SSE for pricing methods
, the SSE for pricing methods 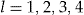 is defined as
is defined as
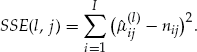
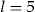 as
as
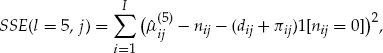
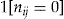 equals one if
equals one if 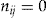 , and zero otherwise.
, and zero otherwise.Instead of reporting the absolute values of the SSE, we use the scaled SSE for each pricing method. It is calculated by dividing 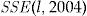 by
by 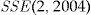 , that is, the SSE of the regression method, for each
, that is, the SSE of the regression method, for each 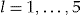 .
.
To fix the entrance fee 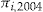 for the add-on, in this section we assume it is a constant multiple of the premium
for the add-on, in this section we assume it is a constant multiple of the premium 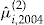 charged for the standard insurance contract to policyholder
charged for the standard insurance contract to policyholder 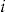 . Investigating the scaled SSE for the interval
. Investigating the scaled SSE for the interval 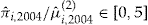 , we obtained Figure 2.
, we obtained Figure 2.
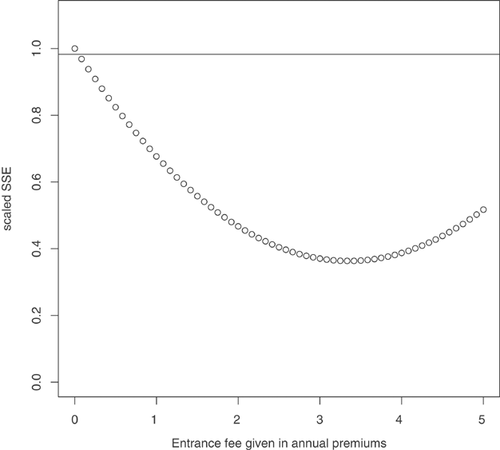
Notes: Here the entrance fee of policyholder 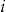 is calculated as
is calculated as 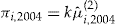 , for
, for 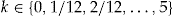 and all policyholders are assumed to accept the add-on. The circles in the figure show the scaled SSE of the add-on contract in the year 2004 for different values of
and all policyholders are assumed to accept the add-on. The circles in the figure show the scaled SSE of the add-on contract in the year 2004 for different values of 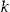 . The minimum scaled SSE occurs at
. The minimum scaled SSE occurs at 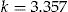 . The horizontal line is the scaled SSE of the no-claims BMS method. For an entrance fee of
. The horizontal line is the scaled SSE of the no-claims BMS method. For an entrance fee of 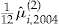 or more, the SSE is lower for the add-on than for the no-claims BMS method, in the investigated range.
or more, the SSE is lower for the add-on than for the no-claims BMS method, in the investigated range.
The minimum SSE for the add-on contract occurs at 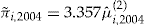 across the data set. We used this choice of the entrance fee to compare the pricing precision of the add-on contract with the other pricing methods. The results are shown in Table 2.
across the data set. We used this choice of the entrance fee to compare the pricing precision of the add-on contract with the other pricing methods. The results are shown in Table 2.
| Scaled SSE | Relative Improvement | ||
|---|---|---|---|
Pricing Method  |
Description | 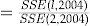 |
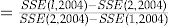 |
| 1 | Flat rate | 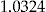 |
N/A |
| 2 | Regression | 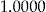 |
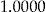 |
| 3 | Credibility | 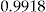 |
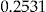 |
| 4 | No-claims BMS | 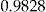 |
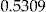 |
| 5 | Add-on | 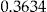 |
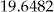 |
- Notes: Scaled SSE for each pricing method and the increase in the SSE over the regression method, relative to the improvement in the SSE by moving from the flat rate method to the regression method, for the year 2004. The actual
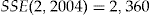 .
.
The difference in performance of the flat rate and the regression estimator is quite important since it illustrates why insurance companies have pricing departments. The credibility method, no-claims BMS method, and add-on method all use individual claim information. Therefore, they are expected to perform better than the other two ones, as is borne out by the numerical results.
Table 2 shows that the credibility method gives an additional improvement of 25 percent over the regression method relative to the improvement due to moving from the flat rate method to the regression method. Even so, it is not as good as we anticipated based on earlier studies, such as Englund et al. (2008) and Englund et al. (2009). However, the performance of a pricing method also depends on the type of coverage and data set. It may be that our data set is too limited; 4 years may be too few to fully benefit from the credibility approach.
In comparison, the performance of the no-claims BMS method is surprisingly good. It gives an additional improvement of 54 percent over the regression method compared to moving from the flat rate method to the regression method. It is also a rather simple method. These type of classical bonus systems are however afflicted with some drawbacks regarding fairness and stability aspects. Fairness: giving a fixed percentage in bonus is advantageous for the expected low-risk policyholders and disadvantageous for the expected high-risks compared to their probability of reporting claims. However, if the insurer has a strategy toward expected low risks, then it can be justified, or at least explained by, the insurer. Stability: if all customers qualify for the bonus system (e.g., they purchase the required number of products), then the system would not be stable, in the sense that the insurer will lose money if the initial extra payment is not re-estimated. Remember that one of the fundamental principles of insurance is that the policyholder should pay for the expected transferred risk, not the outcome.
The add-on deals with these fairness and stability aspects while retaining the advantages of simplicity and low requirements on information. It can perform even better than both the credibility method and the 10 percent no-claims BMS, depending on the choice of the entrance fee 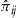 . The scaled SSE of the add-on with the optimal entrance fee
. The scaled SSE of the add-on with the optimal entrance fee 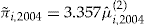 is exceptionally low, and it is almost 20 times the improvement of implementing the regression method over the flat rate method.
is exceptionally low, and it is almost 20 times the improvement of implementing the regression method over the flat rate method.
The drawback is that the optimal entrance fee is over three times the premium. It is doubtful that an average policyholder would pay the optimal entrance fee of more than three times his annual insurance premium up front and risk losing it all. For these reasons, and encouraged by the promising results in Table 2, we extend our study to allow for the policyholders to choose whether or not to buy the add-on.
Individual Choice and Self-Selection
In the previous section we saw that the pricing precision could be increased by setting individual risk-based bonuses. However, the analysis was under the assumption that all the policyholders bought the add-on, no matter how high the entrance fee. Here we relax the assumption.
Each policyholder buys the standard insurance contract, and then decides whether or not to buy the add-on. We expect that this will induce self-selection among policyholders within the same risk class of the rating scheme. The policyholders make their choice based on an expected utility decision rule; namely, they buy the add-on if it gives them a higher expected utility of wealth compared to not buying the add-on. Thus, we are introducing the individual risk preferences of the policyholders.
As we are interested in the performance of the add-on both as a pricing method and as a separating (self-selection) mechanism, we focus only on the decision to buy the add-on or not, and ignore the decision on whether to buy insurance or not. Moreover, for the numerical study below, the individuals in the data set have already decided to buy insurance. As before, we assume a null discount rate.
The Individual Decision Rule
Denote by 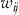 the wealth of individual
the wealth of individual 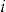 at the start of insurance period
at the start of insurance period 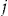 , that is, the initial wealth prior to the decision about insurance coverage. The initial wealth consists of all the policyholder's possessions including cash, financial assets, and the object that is insured. The policyholder is assumed to have more wealth than the insured object and enough cash to pay the premium
, that is, the initial wealth prior to the decision about insurance coverage. The initial wealth consists of all the policyholder's possessions including cash, financial assets, and the object that is insured. The policyholder is assumed to have more wealth than the insured object and enough cash to pay the premium 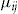 of the standard insurance contract and the entrance fee
of the standard insurance contract and the entrance fee 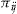 , that is,
, that is, 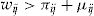 . Although there is no need to have the
. Although there is no need to have the 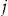 subscript in this section, we maintain it here for consistency with the notation in the rest of the article.
subscript in this section, we maintain it here for consistency with the notation in the rest of the article.
There are only two different outcomes for the terminal wealth depending on the binary decision on whether to buy insurance with or without an add-on. The outcomes are summarized in Table 3.
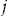
| Event | Conditional Probability | Decision | |
|---|---|---|---|
| Buy Insurance Without Add-On | Buy Insurance With Add-On | ||
 |
 |
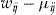 |
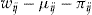 |
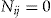 |
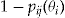 |
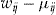 |
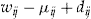 |
- Notes: The wealth at the end of insurance period
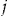 depends on the decision to buy the add-on or not, and whether the policyholder has no claims or not, assuming a null discount rate.
depends on the decision to buy the add-on or not, and whether the policyholder has no claims or not, assuming a null discount rate.
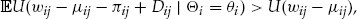
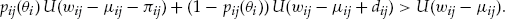 (3)
(3)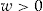 , the CRRA utility function is defined as
, the CRRA utility function is defined as
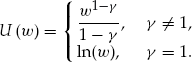
 , and investigate a number of alternative scenarios in which we alter the initial wealth and other parameters.
, and investigate a number of alternative scenarios in which we alter the initial wealth and other parameters.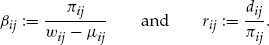 (4)
(4)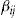 the investment ratio for policyholder
the investment ratio for policyholder 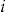 in insurance period
in insurance period 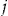 . Under the CRRA assumption, we can rewrite the decision rule (3) as3
. Under the CRRA assumption, we can rewrite the decision rule (3) as3
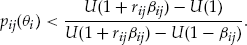
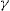 , his decision to buy the add-on depends on three things: his individual conditional probability of claim
, his decision to buy the add-on depends on three things: his individual conditional probability of claim 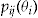 , the ratio
, the ratio 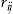 , and the investment ratio
, and the investment ratio 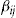 .
.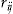 is determined by the insurer through Equation 10 and the relative risk aversion coefficient
is determined by the insurer through Equation 10 and the relative risk aversion coefficient 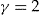 , the decision rule reduces to
, the decision rule reduces to
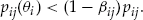 (5)
(5)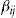 decreases, more policyholders will accept the add-on. Additionally, we see that as long as a policyholder's conditional probability of claim
decreases, more policyholders will accept the add-on. Additionally, we see that as long as a policyholder's conditional probability of claim 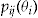 is less than the average probability of claim
is less than the average probability of claim 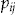 , it is possible to find an investment ratio at which the policyholder will buy the add-on. However, we do not explore further in this article precisely how the add-on can act as a screening device. Instead, we analyze the impact on the SSE of allowing the policyholders the choice to buy the add-on, and how the SSE varies with different investment ratios offered to the policyholders.
, it is possible to find an investment ratio at which the policyholder will buy the add-on. However, we do not explore further in this article precisely how the add-on can act as a screening device. Instead, we analyze the impact on the SSE of allowing the policyholders the choice to buy the add-on, and how the SSE varies with different investment ratios offered to the policyholders.A Second Numerical Study
On the Danish data set of  policyholders, we investigate three scenarios for the selection of the investment ratio using the decision rule (5). First, all policyholders are offered the same investment ratio
policyholders, we investigate three scenarios for the selection of the investment ratio using the decision rule (5). First, all policyholders are offered the same investment ratio 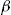 . Next, each policyholder is offered the investment ratio that maximizes his individual expected utility from the purchase of the add-on. Finally, the policyholders are offered an entrance fee that is the same constant multiple of their standard insurance premium across all policyholders.
. Next, each policyholder is offered the investment ratio that maximizes his individual expected utility from the purchase of the add-on. Finally, the policyholders are offered an entrance fee that is the same constant multiple of their standard insurance premium across all policyholders.
We use the regression method to calculate the premium for the standard insurance contract. As before, the parameters are estimated from the data in years 2001–2003. In particular, the (private) risk profile 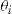 of each policyholder is taken to be his second-last credibility estimate, based on the information in years 2001–2003.
of each policyholder is taken to be his second-last credibility estimate, based on the information in years 2001–2003.
In the first scenario, all policyholders are offered the same investment ratio, that is, 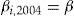 for all
for all 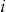 . Thus, policyholder
. Thus, policyholder 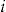 is offered an add-on with entrance fee
is offered an add-on with entrance fee 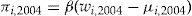 and dividend
and dividend 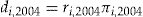 . Note that under the decision rule (5), each policyholder evaluates the add-on based on
. Note that under the decision rule (5), each policyholder evaluates the add-on based on 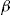 , and not directly on the entrance fee
, and not directly on the entrance fee 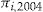 or his initial wealth
or his initial wealth 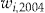 . Figure 3 shows how many policyholders would choose to buy the add-on at different levels of
. Figure 3 shows how many policyholders would choose to buy the add-on at different levels of 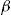 .
.
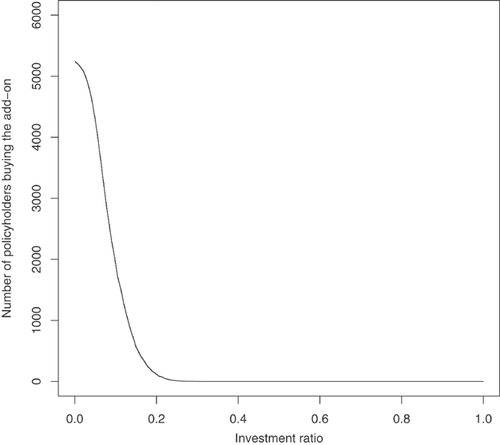
Notes: The number of policyholders who would buy the add-on, based on the decision rule (5), as the constant investment ratio 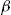 offered to all policyholders increases.
offered to all policyholders increases.
Under the first scenario, we find which investment ratio 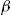 , offered to all the policyholders at the start of 2004, would have minimized the SSE at the end of 2004. Of course, this is not a method that an insurer could use a priori to select the investment ratio. However, it does give us some insight into the potential offered by add-on. Since we do not know the wealth of each policyholder, the analysis is done assuming that all policyholders start the year 2004 with the same amount of wealth. The results are summarized in Table 4.
, offered to all the policyholders at the start of 2004, would have minimized the SSE at the end of 2004. Of course, this is not a method that an insurer could use a priori to select the investment ratio. However, it does give us some insight into the potential offered by add-on. Since we do not know the wealth of each policyholder, the analysis is done assuming that all policyholders start the year 2004 with the same amount of wealth. The results are summarized in Table 4.
Initial Wealth 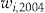 in DKK in DKK |
|||||
|---|---|---|---|---|---|
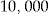 |
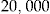 |
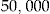 |
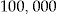 |
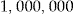 |
|
Optimal constant 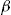 |
0.06203 | 0.06226 | 0.06188 | 0.05431 | 0.01395 |
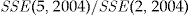 |
0.9735 | 0.9483 | 0.8804 | 0.7866 | 0.5534 |
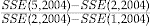 |
0.8179 | 1.5957 | 3.6914 | 6.5864 | 13.7840 |
| Number of buyers of add-on | 3,679 | 3,670 | 3,687 | 4,078 | 5,147 |
- Notes: Optimal investment ratio if all policyholders are proposed with the same investment ratio and are assumed to have the same risk aversion coefficient
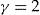 and the same initial wealth
and the same initial wealth 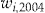 . The optimal investment ratio is the one that minimizes the SSE. The values of
. The optimal investment ratio is the one that minimizes the SSE. The values of 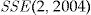 and
and 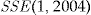 are derived from Table 2.
are derived from Table 2.
In Table 4, we see that the optimal constant investment ratio offered to the entire portfolio is decreasing as the initial wealth increases. The consequence is that the SSE decreases as wealth increases, since each policyholder is bearing more of his own risk. The increasing number of policyholders buying the add-on is due to the decreasing 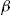 , under the assumption that the risk aversion coefficient remains constant. Notable is that for
, under the assumption that the risk aversion coefficient remains constant. Notable is that for 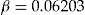 , the entrance fee is around DKK 620 (ignoring the premium for the standard insurance contract, as it varies between policyholders) and already we get an additional improvement in the SSE of 81.79 percent compared to going from the flat rate to the regression estimator. Just by adding individual choice!
, the entrance fee is around DKK 620 (ignoring the premium for the standard insurance contract, as it varies between policyholders) and already we get an additional improvement in the SSE of 81.79 percent compared to going from the flat rate to the regression estimator. Just by adding individual choice!
The average experienced claim frequency in year 2004 for the policyholders who buy an add-on at these portfolio optimal investment ratios is 18.84 percent, while it is 22.65 percent for those who do not buy the add-on. As 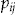 and
and 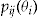 are estimated from the data in years 2001–2003, this means that the policyholders who decide to buy the add-on continue to show lower risk in the year 2004.
are estimated from the data in years 2001–2003, this means that the policyholders who decide to buy the add-on continue to show lower risk in the year 2004.
In the next scenario, we suppose that the insurer offers to each policyholder 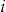 the investment ratio
the investment ratio 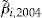 that maximizes his expected utility from the add-on (i.e., the
that maximizes his expected utility from the add-on (i.e., the 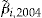 that maximizes the left-hand side of Equation 15). This means that policyholder
that maximizes the left-hand side of Equation 15). This means that policyholder 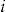 is offered an add-on with entrance fee
is offered an add-on with entrance fee 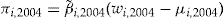 and dividend
and dividend 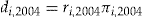 . If the decision rule (5) is satisfied for this choice of the investment ratio
. If the decision rule (5) is satisfied for this choice of the investment ratio 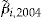 , then policyholder
, then policyholder 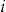 will buy the add-on. Figure 4 shows the distribution of the estimated values of the optimal individual investment ratios
will buy the add-on. Figure 4 shows the distribution of the estimated values of the optimal individual investment ratios 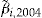 across the data set.
across the data set.
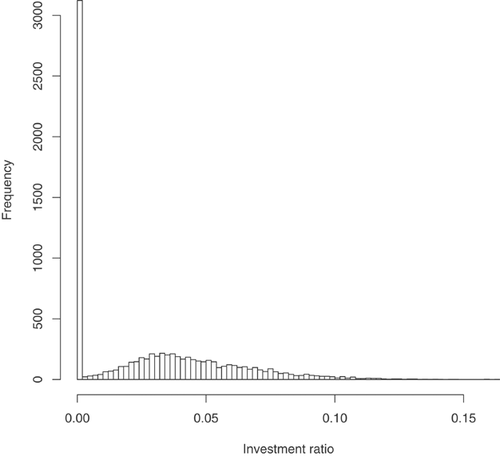
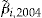
Notes: There are 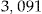 policyholders who will decide to not accept the add-on, regardless of the offered investment ratio, as the estimated value of their conditional probability of claims
policyholders who will decide to not accept the add-on, regardless of the offered investment ratio, as the estimated value of their conditional probability of claims 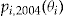 is greater than the estimated value of their unconditional probability
is greater than the estimated value of their unconditional probability 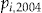 (recall decision rule (5)). The optimal investment ratio for these policyholders is set to zero.
(recall decision rule (5)). The optimal investment ratio for these policyholders is set to zero.
In total, 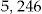 policyholders will choose to buy the add-on at their individually optimal
policyholders will choose to buy the add-on at their individually optimal 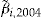 . Table 5 shows the scaled SSE under different assumptions on initial wealth, under this scenario.
. Table 5 shows the scaled SSE under different assumptions on initial wealth, under this scenario.
Initial Wealth 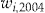 in DKK in DKK |
|||||
|---|---|---|---|---|---|
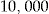 |
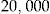 |
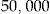 |
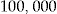 |
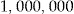 |
|
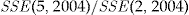 |
0.9707 | 0.9427 | 0.8659 | 0.7623 | 0.4125 |
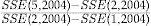 |
0.9043 | 1.7685 | 4.1389 | 7.3364 | 18.1327 |
| Number of buyers of add-on | 5,246 | 5,246 | 5,246 | 5,246 | 5,246 |
- Notes: Scaled SSE when the estimated value of the optimal investment ratio
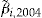 of each individual is used as entrance fee, and each policyholder is assumed to have the same initial wealth
of each individual is used as entrance fee, and each policyholder is assumed to have the same initial wealth 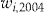 and risk aversion coefficient
and risk aversion coefficient 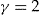 . The number of buyers of the add-on is constant, as their optimal investment ratio is independent of wealth. The values of
. The number of buyers of the add-on is constant, as their optimal investment ratio is independent of wealth. The values of 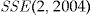 and
and 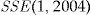 are derived from Table 2.
are derived from Table 2.
We get an even better pricing method than in the first scenario for all assumptions on initial wealth. However, in practice, for policyholders with large initial wealth, such as DKK 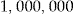 , there should be some restrictions for the entrance fee to be a good pricing method. For instance, a restriction could be that the net dividend
, there should be some restrictions for the entrance fee to be a good pricing method. For instance, a restriction could be that the net dividend 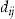 may not exceed the actuarial premium, or else the SSE will increase as the dividend increases. For implementational reasons, the insurer might offer the policyholder a stepwise function, instead of a continuum of eligible entrance fees. The precision of the function may depend on the precision of risk perception of the policyholders and the costs of implementation, systems maintenance, and so on.
may not exceed the actuarial premium, or else the SSE will increase as the dividend increases. For implementational reasons, the insurer might offer the policyholder a stepwise function, instead of a continuum of eligible entrance fees. The precision of the function may depend on the precision of risk perception of the policyholders and the costs of implementation, systems maintenance, and so on.
We find that the average experienced claim frequency in year 2004 for those policyholders who buy an add-on at their individually optimal investment ratio 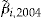 is 20.85 percent, while it is 21.00 percent for those who do not buy the add-on. Thus, while policyholders who decide to buy the add-on continue to show lower risk in the year 2004, the difference in risk is not as large as in the first scenario, in which all policyholders were offered the same constant investment ratio.
is 20.85 percent, while it is 21.00 percent for those who do not buy the add-on. Thus, while policyholders who decide to buy the add-on continue to show lower risk in the year 2004, the difference in risk is not as large as in the first scenario, in which all policyholders were offered the same constant investment ratio.
In the last scenario, each policyholder is offered an entrance fee that is a proportion of his individual standard insurance premium. It is the same scenario as in the subsection “A First Numerical Study,” except that now the policyholders make a decision to accept the add-on or not. For some constant 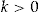 , policyholder
, policyholder 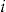 is offered an add-on with entrance fee
is offered an add-on with entrance fee 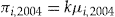 and dividend
and dividend 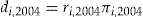 . The motivation is that it might be easier to relate to the insurance premium than the initial wealth, for both the policyholder and the insurer. The proportion
. The motivation is that it might be easier to relate to the insurance premium than the initial wealth, for both the policyholder and the insurer. The proportion 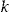 is chosen as the one that would have minimized the SSE at the end of year 2004. Table 6 shows the results, assuming all policyholders have the same initial wealth.
is chosen as the one that would have minimized the SSE at the end of year 2004. Table 6 shows the results, assuming all policyholders have the same initial wealth.
Initial Wealth 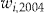 in DKK in DKK |
|||||
|---|---|---|---|---|---|
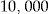 |
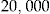 |
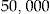 |
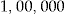 |
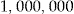 |
|
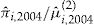 |
0.06366 | 0.2851 | 0.8576 | 1.605 | 3.566 |
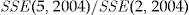 |
0.9837 | 0.9560 | 0.8948 | 0.8147 | 0.6046 |
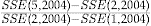 |
0.5031 | 1.3580 | 3.2469 | 5.7191 | 12.2037 |
| Number of buyers of add-on | 4,781 | 4,147 | 4,010 | 4,178 | 5,148 |
- Notes: Scaled SSE for different initial wealth
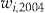 , when the entrance fee is a multiple of the individual annual insurance premium. The multiple is the same for each policyholder across the data set, while the annual insurance premium is individual. Here, the policyholders choose individually whether to accept the add-on or not. The values of
, when the entrance fee is a multiple of the individual annual insurance premium. The multiple is the same for each policyholder across the data set, while the annual insurance premium is individual. Here, the policyholders choose individually whether to accept the add-on or not. The values of 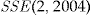 and
and 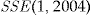 are derived from Table 2.
are derived from Table 2.
The scaled SSEs in Table 6 are less than under the no-claims BMS method (whose scaled SSE is 0.9828; see Table 2), except at an initial wealth 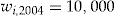 . The performance is improving as the initial wealth increases, but so is the entrance fee.
. The performance is improving as the initial wealth increases, but so is the entrance fee.
Generally, the SSE is somewhat higher than in the other two scenarios, for the same initial wealth (compare Table 6 with Table 4 and Table 5). In spite of this, the number of policyholders buying the add-on is larger than in the scenario in which all policyholders were offered the same investment ratio (compare Table 6 with Table 4).
The average experienced claim frequency in year 2004 for those policyholders who buy an add-on when the proportion 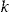 is chosen as the one that gives the lowest SSE is 18.79 percent, while it is 23.16 percent for those who do not buy the add-on. That is, the policyholders who decide to buy the add-on continue to show lower risk in the year 2004.
is chosen as the one that gives the lowest SSE is 18.79 percent, while it is 23.16 percent for those who do not buy the add-on. That is, the policyholders who decide to buy the add-on continue to show lower risk in the year 2004.
Conclusion
We have proposed an alternative way to turn a problem of asymmetric information into a solution of how to price insurance in groups with heterogeneous risk. The design of the proposed add-on can vary in many ways. Both the criterion of getting a dividend and the size of the dividend can easily be modified to suit a specific business line or area. For instance, no-claims are neither common nor relevant as a criterion for policyholders in areas with a high claim frequency, such as glass insurance within commercial transport. There, a criterion based on a bound on the number or cost of claims, either fixed or in relation to the expectation, might be more appropriate. However, as our intention has been to keep the model as simple and as descriptive as possible in this article, we kept the criterion of no-claims.
The size of the entrance fee will be a strategic decision based on either policyholder insight or the business strategy of the insurer, or by the policyholders themselves. We have showed that there might be both entrance fees and dividends that exist at realistic levels.
Under the assumptions made, we have found that each policyholder has an optimal entrance fee, depending on his initial wealth, individual risk profile, and risk aversion. Since the insurer usually does not know the initial wealth or risk aversion of each individual, the insurer may let the policyholder choose the size of the entrance fee in order to get the optimal effect of the self-selection mechanism when pricing insurance. The higher the number of choices offered to the individual, the larger becomes the price–coverage differentiation, thereby increasing the competitiveness of the insurance product, due to fair pricing. However, the add-on will become less effective as a screening device. The more the price is differentiated, the less the add-on separates the policyholders into groups of buyers or not, and vice versa.
Although the one-period add-on analyzed in this article is close to a classical BMS, its generalization to a multiperiod add-on opens up avenues for further developments. Our approach is an alternative to a BMS, rather than a reformulation of it, with a direct link to revealing a customer's asymmetric information. Exploring the pricing and efficiency of a multiperiod add-on contract is a topic for future research.
The main conclusion of this article is that the potential of the add-on increases with freedom of individual choice, while the efficiency is limited to the self-awareness of the individuals. But the most applicable conclusion is that by giving the policyholder an individually set contingent payment based on his expected risk, instead of a collective fixed bonus rate, we get a fairer and more competitive pricing system.




