Pricing Mortality Securities With Correlated Mortality Indexes
ABSTRACT
This article proposes a stochastic model, which captures mortality correlations across countries and common mortality shocks, for analyzing catastrophe mortality contingent claims. To estimate our model, we apply particle filtering, a general technique that has wide applications in non-Gaussian and multivariate jump-diffusion models and models with nonanalytic observation equations. In addition, we illustrate how to price mortality securities with normalized multivariate exponential titling based on the estimated mortality correlations and jump parameters. Our results show the significance of modeling mortality correlations and transient jumps in mortality security pricing.
INTRODUCTION
Over the last century, populations of different countries have been increasingly linked by flows of information, goods, transportation, and communication, and as a consequence the world has become more closely connected and interdependent. While the trend of globalization has substantially driven market growth and international trade, it has also helped to spread some of the deadliest infectious diseases across borders (Daulaire, 1999). Thus, it seems improper to forecast mortality for an individual national population in isolation from others. Indeed, in practice, intercountry mortality correlation has long been a serious concern for insurers that underwrite life insurance business.
Mortality forecast that takes into account a country's linkage to others is important in the sense that not only does it facilitate better understanding of mortality risk, but it also has enormous implications for pricing mortality securities. Recent financial innovation makes mortality securitization a viable option for insurers or reinsurers to transfer catastrophe mortality risk arising from the possible occurrence of pandemics or large-scale terrorist attacks. By segregating its cash flows linked to extreme mortality risk, an insurance firm is able to repackage them into securities that are traded in capital markets (Blake and Burrows, 2001; Lin and Cox, 2005; Cox and Lin, 2007). Since the first publicly traded mortality security issued by Swiss Re in 2003, almost all mortality transactions determine the coupons and principals based on three or more population mortality indexes, with the only exception—the Tartan mortality bond sold in 2006. This indicates that insurers or reinsurers are keenly interested in transferring potential country-correlated mortality risk embedded in their business. For instance, the mortality risk of the 2003 Swiss Re mortality bond was defined in terms of an index based on the weighted average annual population death rates in the United States, the United Kingdom, France, Italy, and Switzerland (Lin and Cox, 2008). As another example, the mortality bond issued by the Nathan Ltd. in 2008 depended on the annual population death rates of four countries, namely, the United States, the United Kingdom, Canada, and Germany. Given that the existing (and possible future) mortality securities bundle multination mortality risks, mortality correlation among countries merits serious consideration in mortality securitization pricing.
In the recent literature, a number of stochastic mortality models have been proposed. Despite the importance of mortality correlation, surprisingly very few papers treat correlation as an indispensable element. For example, in order to account for catastrophic mortality death shocks, Chen and Cox (2009) incorporate a jump-diffusion process into the original Lee–Carter model to forecast mortality rates and price the 2003 Swiss Re mortality bond. Yet, while the Swiss Re bond payments depended on five-country weighted mortality index, the authors price this bond only based on the U.S. mortality rates. Hence, it is not clear how to extend their method to multipopulation correlated mortality scenarios.
Beelders and Colarossi (2004) and Chen and Cummins (2010), on the other hand, use the extreme value theory to measure mortality risk of the 2003 Swiss Re bond. However, they simply model the combined index without considering the mortality correlations among different countries. So the question of how to model multipopulation mortality correlation remains open. Bauer and Kramer (2009) borrow a credit risk modeling approach introduced by Lando (1998) to describe stochastic force of mortality. To incorporate dramatic mortality changes that are crucial in measuring mortality risk (Lin and Cox, 2008), Bauer and Kramer (2009) propose a mortality model with an affine jump-diffusion process. Then they use their mortality model to price the Tartan transaction, which is the only publicly traded mortality bond to date solely based on one-country (i.e., United States) mortality experience. However, the authors acknowledge that their model misses correlations and diversification effects across genders and populations. Given the prevalence of multicountry combined mortality indexes in the mortality security markets, it is questionable whether their model is adequate for other mortality securities. Indeed, from a practical point of view, understanding the combined index as a function of various population death rates is at least as important, if not more so, than understanding it as a function of different age classes of a single country for mortality securitization.
Moreover, the existing mortality literature has demonstrated the significance of catastrophic death events in the pricing and tranche structure for a mortality risk bond (Cox, Lin, and Wang, 2006; Bauer and Kramer, 2009; Chen and Cox, 2009). While longevity risk modeling usually simplifies the analysis by ignoring dramatic mortality changes (Cairns, Blake, and Dowd, 2006; Schrager, 2006; Kogure and Kurachi, 2010; Wills and Sherris, 2010; Yang, Yue, and Huang, 2010; Cox et al., 2012), mortality jumps must be considered in order to successfully structure and price mortality-linked securities. Thus, in this article, as the first objective, we develop a tractable mortality model, which captures the mortality correlations among countries and incorporates mortality jumps. Specifically, we extend Cox, Lin, and Wang's (2006) model to a more general setting and disentangle transient jumps from persistent volatilities. As a departure from Cox, Lin, and Wang who model unanticipated mortality jumps as permanent shocks, we model them as transient jumps with a double-jump process. Since in most cases severe short-term events such as epidemics underlie mortality risk (Cox, Lin, and Petersen, 2010), our model provides a better fit for historical data.
A prominent calibration challenge for a model accounting for correlations is that the number of pairs grows quadratically with the number of countries of interests. To address this issue, as the second objective of this article, we employ a particle filtering approach for learning about unobservable mortality shocks and states from discretely observed population mortality rates. The particle filter algorithm is easy to implement and fast to compute, requiring only simulation from a proposal distribution. It is able to handle a large number of correlations with relatively low computation costs. Moreover, particle filters are highly adaptable and easy to be adjusted for various applications. In particular, they are able to deal with nonlinear, non-Gaussian systems, and variables in either continuous or discrete states as well as their combinations (Heijden et al., 2004). This property of particle filtering is important for mortality modeling because multivariate jump-diffusion processes are an indispensable component of a comprehensive mortality model, which is typically not Gaussian. In addition, the particle filtering approach is a Bayesian approach through which we can deal with estimation error and prediction uncertainty unaddressed in some mortality models. As highlighted in Cairns, Blake, and Dowd (2006), a model that takes into account parameter uncertainty is able to generate more reliable forecasts. So far the particle filtering approach has many practical applications in engineering and finance. Despite its usefulness, this technique has received little attention in the mortality literature.1 In this article, we show that it is useful to estimate variables related to mortality trend, volatility, correlation, and jump, which are crucial for mortality security pricing and risk management.
Aside from the question of how to appropriately model mortality stochastic process, there is an ongoing debate on how to price mortality-linked securities. If a security's payments are contingent on the correlation of mortality risks across countries, a common feature in mortality securitization, the pricing problem will become more challenging (Chen and Cox, 2009). Mortality securities, with only a limited number issued in financial markets, are not liquidly traded. As a result, to price a mortality risk linked security, the underlying mortality risk process needs to be risk adjusted (Wills and Sherris, 2010). Different mortality pricing methods have been proposed. Dahl (2004) applies financial risk models for mortality risk modeling and then uses market data to calibrate risk-adjusted probability measures. Lin and Cox (2005), Dowd et al. (2006), and Denuit, Devolder, and Goderniaux (2007) apply the Wang transform (Wang, 2000) to physical distributions in pricing distortion distributions. Bayraktar et al. (2009) propose to compensate a mortality risk taker according to an “instantaneous Sharpe ratio,” which is defined as the additional return in excess of the risk-free rate divided by the standard deviation of a mortality portfolio after all diversifiable risk is hedged away. In line with their Bayesian mortality models, Kogure and Kurachi (2010) present a Bayesian pricing approach, the entropy maximization principle, to risk neutralize the predictive distribution of future survival rates. However, while in these articles the transformed parameters are calibrated, they are built on a univariate setting or an independent assumption, ignoring the connections among different cohorts and populations. Thus, their pricing methods have limited implications for multivariate and correlated mortality cases. To address this pricing issue, we employ normalized multivariate exponential tilting to take into account correlations across countries for mortality securitization.
Exponential tilting is an incomplete market pricing method that neutralizes statistical distributions, which is consistent with the literature on nonarbitrage pricing of contingent claims (see Buhlmann, 1980; Gerber and Shiu, 1996; Madan and Unal, 2004; Kijima, 2006; Wang, 2007; and others). It can be applied in pricing risks embedded in loan defaults, mortgage refinancing, electricity trading, weather derivatives, catastrophic insurance, and insurance-linked securities (Duffie, 1992; Karatzas and Shreve, 1992; Heston, 1993; Gerber and Shiu, 1996; Cox, Lin, and Wang, 2006; Milidonis, Lin, and Cox, 2011). Kijima (2006) and Wang (2007) extend univariate exponential tilting to multivariate cases. The need for changing multivariate probability measures arises from pricing contingent claims on multiple underlying assets or liabilities. As noted earlier, the payoffs of the existing mortality securities are contingent on several population mortality indexes. To properly compensate investors for risk arising from mortality correlations among countries, as the last objective of this article, we apply the normalized multivariate exponential tilting to price mortality securities. Specifically, we first introduce the concept of normalized exponential tilting and then formulate probability distortions for the multivariate case. For demonstration, we utilize the normalized multivariate exponential tilting to make inference about the likely market prices of risk from the pricing information contained in the existing mortality securities. To the best of our knowledge, this is the first article that not only accounts for mortality correlations but also calibrates different market prices of risk for various mortality diffusions and jumps.
The article is organized as follows. In the next section, we introduce our proposed stochastic model for a set of correlated population mortality indexes with jumps. The “Estimation With Particle Filtering” section provides an overview on the particle filtering approach. The multivariate exponential tilting as an incomplete market pricing method is introduced in “Pricing Mortality Securities With Multivariate Exponential Tilting.” In “Empirical Applications,” we first estimate our proposed model by applying the particle filtering technique based on historical data. We show that mortality correlation and jump process play important roles in mortality securitization modeling. Then we price some mortality bonds issued in 2006 by applying normalized multivariate exponential tilting and compare our estimated market prices of risk to those when we do not consider mortality correlations and jumps. After a discussion of our findings, “Conclusions” concludes and provides an outlook on future research.
MODEL SPECIFICATION
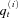 denote the observed population mortality index for country i at time t. The logarithm of
denote the observed population mortality index for country i at time t. The logarithm of 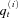 equals
equals
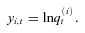
 (1)
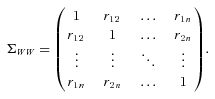
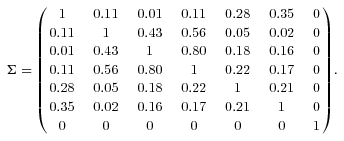
(1)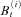 captures the correlation of yi,t's. We denote the correlation coefficient matrix of n countries, ΣWW = {rij}, as
captures the correlation of yi,t's. We denote the correlation coefficient matrix of n countries, ΣWW = {rij}, as
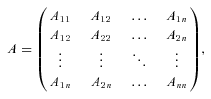
 of country i, is a linear combination of Aij's (Shrieve, 2000):
of country i, is a linear combination of Aij's (Shrieve, 2000):
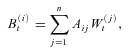
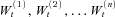 are n independent Brownian motions with mean 0 and variance t.
are n independent Brownian motions with mean 0 and variance t.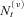 with intensity kc. The common jumps (e.g., the 1918 worldwide flu) act as a fundamental shock to mortality curves of all countries and decrease the expected lifetime of the population across countries. To model those jumps, we assume both positive and negative movements by applying a double-jump process. As customers in queues come and go, so does a pandemic. As such, the common double-jump process has two jump size parameters
with intensity kc. The common jumps (e.g., the 1918 worldwide flu) act as a fundamental shock to mortality curves of all countries and decrease the expected lifetime of the population across countries. To model those jumps, we assume both positive and negative movements by applying a double-jump process. As customers in queues come and go, so does a pandemic. As such, the common double-jump process has two jump size parameters 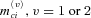 with opposite signs and two jump size volatilities
with opposite signs and two jump size volatilities 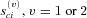 .
. 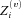 is the standard normal random variable:
is the standard normal random variable:
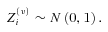
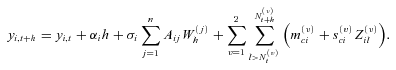 (2)
(2)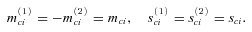
ESTIMATION WITH PARTICLE FILTERING
Why Use Particle Filtering?
The particle filtering approach has several advantages over other estimation methods. First, it is rooted in Bayesian statistics. In the spirit of recursive Bayesian estimation, particle filtering is an iterative application of Bayes rule to sequential parameter estimation. In each step, the particle filtering approach first uses all information up to the step to predict future values. Then, based on the differences between predicted values and realized values, the parameter estimates are modified and updated. This procedure, to some extent, is similar to our learning process as it does not assume stationary model parameters. So it is superior to non-Bayesian approaches, such as the maximum likelihood method, that require stationary model parameters.
Second, the particle filtering is more adaptable than other filtering methods like the Kalman filter, which is built on the linear and Gaussian assumptions. Instead, as mentioned earlier, the particle filtering approach combined with sequential Monte Carlo method is more flexible and provides a way to estimate nonlinear, non-Gaussian, and nonstationary models. To be shown later, the particle filter generates a set of “particles,” which are samples of the distribution from Monte Carlo simulations. Those particles are then used to forecast the future and are updated when new observations are available. Mortality shocks are rare events so typically the distribution of mortality rates is non-Gaussian. To properly handle this situation, we use the particle filtering to estimate our model.
Particle Filtering Estimation Procedure
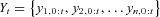 . The basis for the estimation is to specify state and measurement equations. Given the time-discrete observations of mortality indexes, we discretize Equation (1) using the Euler method:
. The basis for the estimation is to specify state and measurement equations. Given the time-discrete observations of mortality indexes, we discretize Equation (1) using the Euler method:
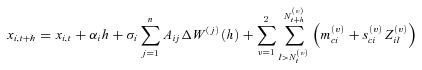 (3)
(3)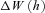 is a standard normal random variable, and h is the time discretization interval (1 year in this article, i.e., h = 1), during which there are
is a standard normal random variable, and h is the time discretization interval (1 year in this article, i.e., h = 1), during which there are 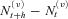 positive or negative jumps
positive or negative jumps 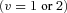 . That is, our latent state St is composed of unobservable mortality Brownian motions and double jumps. Equation (3) serves as the state equation in the particle filtering. The jump size of
. That is, our latent state St is composed of unobservable mortality Brownian motions and double jumps. Equation (3) serves as the state equation in the particle filtering. The jump size of 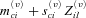 retains its normal distributional structure, with the mean
retains its normal distributional structure, with the mean 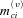 and the standard deviation
and the standard deviation 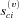 .
.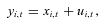 (4)
(4)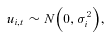
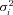 is the variance of ui,t.
is the variance of ui,t.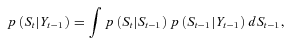 (5)
(5)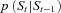 can be estimated using the state Equation (3). The probability
can be estimated using the state Equation (3). The probability 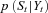 is updated by the Bayes rule,
is updated by the Bayes rule,
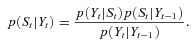 (6)
(6)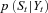 of our model cannot be determined analytically because of the mixture of diffusions and jumps in the model. Mixing diffusions with jumps makes analytic treatment of the filtering problem difficult. The particle filtering provides a solution to the problem in this setting. This technique makes two assumptions (Doucet et al., 2001):
of our model cannot be determined analytically because of the mixture of diffusions and jumps in the model. Mixing diffusions with jumps makes analytic treatment of the filtering problem difficult. The particle filtering provides a solution to the problem in this setting. This technique makes two assumptions (Doucet et al., 2001):
- The state evolution can be accurately simulated. In other words, accurate samples can be drawn from
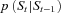 ;
; - The likelihood can be accurately evaluated as a function of state variables and observations.
With these two assumptions, we can estimate our model based on particle filtering with the Sampling-Importance-Resampling (SIR) algorithm. The key idea of particle filtering with the SIR algorithm is summarized in Appendix A.
PRICING MORTALITY SECURITIES WITH MULTIVARIATE EXPONENTIAL TILTING
A complete market is a market where any derivative security can be replicated and hedged by holding cash and the underlying asset. Mortality securities, contingent on mortality catastrophe events, are derivatives with mortality rates as their underlying indexes. Currently, there are only a limited number of mortality securities, which are illiquid. Furthermore, a catastrophic event can happen at a random time with a random size, which makes it impossible to create a hedge portfolio to replicate mortality jumps. This implies that mortality security markets are incomplete and contingent claims cannot be replicated by trading. Thus, it leaves open the problem of pricing securities in this situation.
One possibility of valuing mortality securities in an incomplete market is to apply exponential tilting. Given a statistical distribution of potential outcomes and their respective likelihoods from historical data, the exponential tilting risk neutralizes the statistical distribution. This technique, consistent with the existing literature on no-arbitrage pricing of contingent claims (Duffie, 1992; Heston, 1993; Karatzas and Shreve, 1992; Gerber and Shiu, 1996), has some popularity in pricing insurance-related risks (e.g., catastrophe property and mortality risks).
Another reason for us to apply the exponential tilting method in mortality securitization is that its multivariate version can account for multiple underlying assets or liabilities of a contingent claim and price the effect of their correlations accordingly (Cox, Lin, and Wang, 2006). This is important because the payoffs of existing mortality securities are typically determined by multiple population mortality indexes. By changing multivariate probability measures, the multivariate exponential tilting can capture the correlations of these indexes so as to properly disentangle different components of the risk premium and price such securities.
In the following discussion, we first present the basics of the exponential tilting approach. Then we adopt a normalization procedure proposed by Cox, Lin, and Wang (2006) and Wang (2007) to ensure a consistent interpretation of the risk-adjustment parameter. Next we formulate normalized multivariate exponential tilting that provides a general framework for pricing risks with respect to multiple reference risks. Later in “Empirical Applications,” we provide an example to show how to apply this approach to price mortality securities.
Normalized Univariate Exponential Tilting
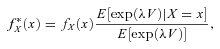 (7)
(7)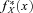 is the transformed probability density function after applying the exponential tilting. The ratio
is the transformed probability density function after applying the exponential tilting. The ratio
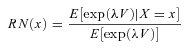 (8)
(8)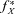 with respect to fX.
with respect to fX.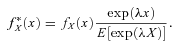 (9)
(9)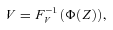 (10)
(10)Definition 1
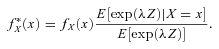 (11)
(11)For more details, see Wang (2007).
Normalized Multivariate Exponential Tilting
Consider n variables X1, X2, …, Xn with k references V1, V2, …, Vk in a probability space (Ω, P).
Definition 2
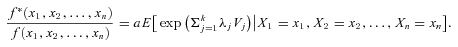 (12)
(12)The references V1, V2, …, Vk can be flexibly specified to fit a particular situation. For instance, the references can be the risks themselves, that is, (V1, V2, …, Vk) = (X1, X2, …, Xk) given n = k. In other cases, the references V1, V2, …, Vk represent a firm's specific financial variables or some industry aggregate indexes. In the context of this article, V1, V2, …, Vk refer to population mortality indexes of different countries.
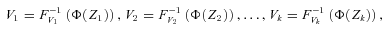 (13)
(13)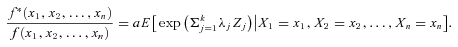 (14)
(14)With this setup, Wang (2007) proves the following theorem:
Theorem 1
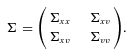 (15)
(15)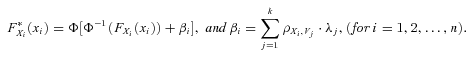 (16)
(16)In addition, Wang (2007) shows that the correlation matrix between X1, X2, …, Xn is unchanged after the normalized multivariate exponential tilting, 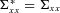 . This is a desirable property because it simplifies the pricing procedure.
. This is a desirable property because it simplifies the pricing procedure.
EMPIRICAL APPLICATIONS
In this section, an example is provided to illustrate how to apply the proposed methods. We first use particle filtering to estimate mortality stochastic of six countries (n = 6): United States, United Kingdom, France, Germany, Japan, and Canada. Then, based on the mortality rates forecasted from model (1) and the normalized multivariate exponential tilting introduced in “Pricing Mortality Securities With Multivariate Exponential Tilting,” we derive the market prices of risk for different mortality diffusion and jump processes. The same technique can be easily extended to more complicated situations where a greater number of countries are involved.
Data
Our U.S. data from 1900 to 1998 are obtained from the Vital Statistics of the United States (VSUS).2 The VSUS reports the U.S. age-adjusted death rates per 100,000 standard million population (2000 standard) for selected causes of death. Our mortality data for United States from 1999 to 2005 and United Kingdom and France from 1900 to 2005 are drawn from the Human Mortality Database.3 The Human Mortality Database reports the death and population size of country i for different ages. We divide the total number of deaths in different ages by the total population to get each population mortality index 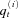 . Following the same procedure, we calculate the population mortality index for Canada using the cohort data from 1900 to 1920 and the period data from 1921 to 2005 from the Human Mortality Database.4 Our Japanese population mortality data are obtained from the Vital Statistics of the Ministry of Health, Labor and Welfare in Japan.5 The Japanese Vital Statistics database does not include the mortality data from 1944 to 1946. So we use the linear interpolation to generate the population mortality indexes for these 3 years. The German population mortality data from 1900 to 2005 are provided by the German Federal Statistical Office.6
. Following the same procedure, we calculate the population mortality index for Canada using the cohort data from 1900 to 1920 and the period data from 1921 to 2005 from the Human Mortality Database.4 Our Japanese population mortality data are obtained from the Vital Statistics of the Ministry of Health, Labor and Welfare in Japan.5 The Japanese Vital Statistics database does not include the mortality data from 1944 to 1946. So we use the linear interpolation to generate the population mortality indexes for these 3 years. The German population mortality data from 1900 to 2005 are provided by the German Federal Statistical Office.6
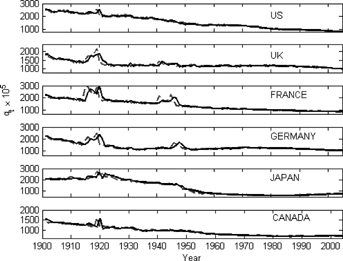
We plot our data as the change of log-mortality rate, 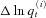 , from 1900 to 2005 in Figure 1, which shows a remarkable mortality fluctuation caused by the influenza breakout in 1918. Another visible fluctuation caused by influenza and pneumonia was around 1950 but its magnitude was much smaller as compared to that of the 1918 worldwide flu.
, from 1900 to 2005 in Figure 1, which shows a remarkable mortality fluctuation caused by the influenza breakout in 1918. Another visible fluctuation caused by influenza and pneumonia was around 1950 but its magnitude was much smaller as compared to that of the 1918 worldwide flu.
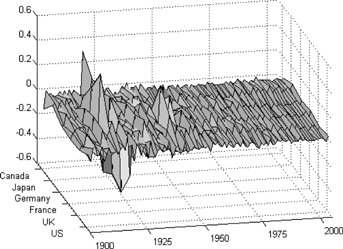
Note: The figure presents the change of log-mortality rate, 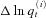 , for country i (i = 1, 2, …, 6) from 1900 to 2005. Country 1 is United States, country 2 is United Kingdom, country 3 is France, country 4 is Germany, country 5 is Japan, and country 6 is Canada.
, for country i (i = 1, 2, …, 6) from 1900 to 2005. Country 1 is United States, country 2 is United Kingdom, country 3 is France, country 4 is Germany, country 5 is Japan, and country 6 is Canada.
Parameter Estimation
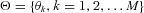 besides the state vector. One can achieve, in particle filtering, the joint estimation of states and parameters by the augmented state space
besides the state vector. One can achieve, in particle filtering, the joint estimation of states and parameters by the augmented state space 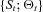 where each parameter is specified as a Gaussian random walk
where each parameter is specified as a Gaussian random walk
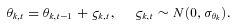
Estimation Results
Table 1 presents our parameter estimates after we apply the particle filtering approach. On average, the population mortality of the United States, United Kingdom, France, Germany, Japan, and Canada improves 0.91 percent, 0.32 percent, 0.77 percent, 0.58 percent, 0.55 percent, and 0.60 percent, per year, respectively. The six countries' mortality volatilities σi are comparable, with United Kingdom having the highest value of 0.0810. The common jump size volatility parameter sci for each country i is much larger than that of the Brownian motion volatility σi. It coincides with what we observe from Figure 1: mortality jumps have a much larger magnitude than mortality normal fluctuations. Moreover, our estimate of the Poisson parameter equals kc = 0.0120, implying that the worldwide mortality jump is approximately a one-in-eighty-three-year (1/kc ≈ 83) event.
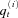 (t = 1900, …, 2005)
(t = 1900, …, 2005)| i | αi | σi | mci | sci | |
|---|---|---|---|---|---|
| United States | 1 | −0.0091 | 0.0404 | 0.1314 | 0.0602 |
| (0.0013) | (0.0085) | (0.0276) | (0.0178) | ||
| United Kingdom | 2 | −0.0032 | 0.0810 | 0.0001 | 0.1638 |
| (0.0006) | (0.0237) | (1.5× 10−5) | (0.0394) | ||
| France | 3 | −0.0077 | 0.0433 | 0.1947 | 0.1317 |
| (0.0013) | (0.0094) | (0.0514) | (0.0227) | ||
| Germany | 4 | −0.0058 | 0.0671 | 0.0001 | 0.1249 |
| (0.0011) | (0.0129) | (3.1 × 10−5) | (0.0347) | ||
| Japan | 5 | −0.0055 | 0.0218 | 0.1888 | 0.0562 |
| (0.0018) | (0.0034) | (0.0325) | (0.0142) | ||
| Canada | 6 | −0.0060 | 0.0336 | 0.1218 | 0.1711 |
| (0.0008) | (0.0076) | (0.0247) | (0.0265) |
- Note: The standard errors are reported in parentheses.
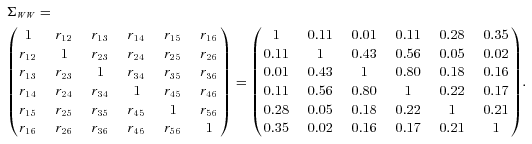 (17)
(17)Figure 2 provides a graphical depiction of the filter's performance with yearly sampling frequency. It displays the actual population death rate per 100,000  and the filtered posterior mean for country i from 1900 to 2005. On average, the posterior mean of each country tracks the actual observation nicely.
and the filtered posterior mean for country i from 1900 to 2005. On average, the posterior mean of each country tracks the actual observation nicely.
Note: The figure compares the actual and posterior means of the filtered population death rate per 100,000 (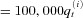 ) distribution for the United States (i = 1), United Kingdom (i = 2), France (i = 3), Germany (i = 4), Japan (i = 5), and Canada (i = 6) in years t = 1900, 1901, …, 2005. The dash line represents the historical data and the solid line plots the death rates estimated from the particle filtering.
) distribution for the United States (i = 1), United Kingdom (i = 2), France (i = 3), Germany (i = 4), Japan (i = 5), and Canada (i = 6) in years t = 1900, 1901, …, 2005. The dash line represents the historical data and the solid line plots the death rates estimated from the particle filtering.
Out-of-Sample Performance
Most of the existing papers on mortality risk modeling do not consider mortality correlations and temporary mortality common jumps in a single model. In “Model Specification,” we use the combination of Brownian motions and a double jump process to describe the dynamics of correlated mortality indexes of several countries. To justify this, we compare the prediction standard errors of our model, based on different prediction time horizons, with those of (1) a model with jumps but without correlations and (2) a model with neither common jumps nor correlations.
We first estimate these three models over the periods 1900 to 1950, 1900 to 1965, and 1900 to 1980, respectively.7 Then we conduct out-of-sample forecasting for each of them. In each sample period, we simulate 10,000 paths of the mortality indexes and measure prediction standard error across all six countries, prediction years, and paths. Mathematically, the prediction standard error is the square root of the prediction variance. In our case, the prediction variance is the variation associated with the difference between the true and predicted log-mortality rates, 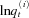 . A lower prediction standard error suggests a good prediction power. We compare the 3-, 4-, and 5-year prediction standard errors of the three models and the results are reported in Table 2.8 Table 2 shows that the model with correlations and common jumps consistently has the lowest prediction standard error in all specifications, which suggests that it has a better forecasting power than the other two models with less parameters.
. A lower prediction standard error suggests a good prediction power. We compare the 3-, 4-, and 5-year prediction standard errors of the three models and the results are reported in Table 2.8 Table 2 shows that the model with correlations and common jumps consistently has the lowest prediction standard error in all specifications, which suggests that it has a better forecasting power than the other two models with less parameters.
| Sample Period 1900 Through 1950 | ||||
|---|---|---|---|---|
| Correlation | Common Jump | Prediction Period | ||
| 3-Year | 4-Year | 5-Year | ||
| No | No | 0.1246 | 0.1415 | 0.1572 |
| No | Yes | 0.0889 | 0.0947 | 0.0975 |
| Yes | Yes | 0.0837 | 0.0893 | 0.0924 |
| Sample Period 1900 Through 1965 | ||||
| Correlation | Common Jump | Prediction Period | ||
| 3-Year | 4-Year | 5-Year | ||
| No | No | 0.1208 | 0.1363 | 0.1470 |
| No | Yes | 0.0837 | 0.0863 | 0.0899 |
| Yes | Yes | 0.0748 | 0.0791 | 0.0821 |
| Sample Period 1900 Through 1980 | ||||
| Correlation | Common Jump | Prediction Period | ||
| 3-Year | 4-Year | 5-Year | ||
| No | No | 0.1162 | 0.1284 | 0.1420 |
| No | Yes | 0.0825 | 0.0832 | 0.0851 |
| Yes | Yes | 0.0730 | 0.0770 | 0.0799 |
Pricing Mortality Securities
To illustrate how to apply the normalized multivariate exponential tilting on the multidimension mortality dynamics described by our proposed mortality model (1), we will use market data to calibrate risk-adjusted probability measures.9 In “Estimation Results,” we have obtained the parameters for six Brownian motions for United States, United Kingdom, France, Germany, Japan, and Canada, and a common jump process. To estimate the market prices of risk for these seven processes, we select the following seven mortality securities issued in 2006 that meet our needs: Vita II mortality bond Tranche B, Vita II mortality bond Tranche C, Vita II mortality bond Tranche D, Tartan mortality bond Tranche B, Osiris mortality bond Tranche B2, Osiris mortality bond Tranche C, and Osiris mortality bond Tranche D.
In the following discussion, we first briefly introduce these mortality securities and then show how to estimate the market prices of risk for different processes underlying these securities.
Mortality Securities Issued in 2006 for Our Calibration
Capital markets have grown increasingly important in recent years as a solution to deal with mortality risk and expand the capacity of paying catastrophic mortality losses. For instance, to transfer catastrophic death risk from events such as epidemics, earthquakes, hurricanes, and other natural or man-made disasters, Swiss Re launched its second mortality transaction in 2006, the Vita Capital II Ltd. mortality bond (Vita II) with three tranches (i.e., Tranches B, C, and D) after it issued the first pure mortality bond in December 2003.
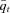 , which is the average of two annual index values over the period concerned:
, which is the average of two annual index values over the period concerned:
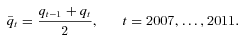
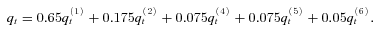
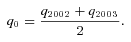
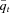 (t = 2007, …, 2011) exceeds id = 120 percent of the 2002/2003 index value, q0, the principal payment will be reduced. The principal will be forfeited when
(t = 2007, …, 2011) exceeds id = 120 percent of the 2002/2003 index value, q0, the principal payment will be reduced. The principal will be forfeited when 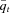 equals or goes above iu = 125 percent of q0. Specifically, the principal loss percentage, Lt in year t, is determined as follows:
equals or goes above iu = 125 percent of q0. Specifically, the principal loss percentage, Lt in year t, is determined as follows:
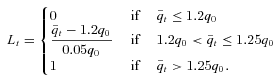
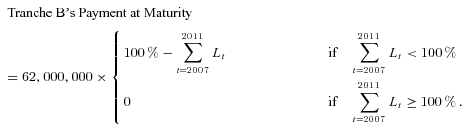 (18)
(18)The payment of Tranche C (Tranche D) of Vita II at maturity is similarly determined except that its size is $200 million ($100 million) and its attachment point id and detachment point iu are 1.15 and 1.2 (1.1 and 1.15), respectively. The above discussion on the three tranches of Vita II is summarized in Table 3. Table 3 also provides an overview on the other four 2006 mortality securities we use for calibrating market prices of risk.
| Vita II Tranche B | Vita II Tranche C | Vita II Tranche D | |
|---|---|---|---|
| Size | $62M | $200M | $100M |
| Issue date | April 2006 | April 2006 | April 2006 |
| Maturity | 5 years | 5 years | 5 years |
| Coupon (bps) | LIBOR+90 | LIBOR+140 | LIBOR+190 |
| Attachment | 1.2 × [(q2002 + q2003)/2] | 1.15 × [(q2002 + q2003)/2] | 1.1 × [(q2002 + q2003)/2] |
| Detachment | 1.25 × [(q2002 + q2003)/2] | 1.2 × [(q2002 + q2003)/2] | 1.15 × [(q2002 + q2003)/2] |
| Index | United Sates 62.5%, United Kingdom 17.5%, Germany 7.5%, Japan 7.5%, Canada 5% | ||
| Tartan Tranche B | |||
| Size | $80M | ||
| Issue date | May 2006 | ||
| Maturity | 3 years | ||
| Coupon (bps) | LIBOR+300 | ||
| Attachment | 1.1 × [(q2004 + q2005)/2] | ||
| Detachment | 1.15 × [(q2004 + q2005)/2] | ||
| Index | United States 100% | ||
| Osiris Tranche B2 | Osiris Tranche C | Osiris Tranche D | |
| Size | Euro 50M | $150M | $100M |
| Issue date | November 2006 | November 2006 | November 2006 |
| Maturity | 4 years | 4 years | 4 years |
| Coupon (bps) | LIBOR+120 | LIBOR+285 | LIBOR+500 |
| Attachment | 1.14 × [(q2004 + q2005)/2] | 1.10 × [(q2004 + q2005)/2] | 1.06 × [(q2004 + q2005)/2] |
| Detachment | 1.19 × [(q2004 + q2005)/2] | 1.14 × [(q2004 + q2005)/2] | 1.10 × [(q2004 + q2005)/2] |
| Index | United States 15%, Japan 25%, France 60% | ||
Pricing
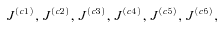
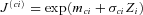 . The correlations between
. The correlations between 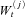 's are ΣWW as shown in (17). The common jump sizes J(ci)s are assumed to be independent of
's are ΣWW as shown in (17). The common jump sizes J(ci)s are assumed to be independent of 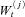 s. Further assume that
s. Further assume that
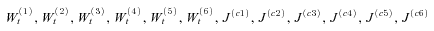
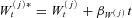 for j = 1, …, 6, and
for j = 1, …, 6, and 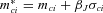 for i = 1, …, 6. Accordingly, we define a vector
for i = 1, …, 6. Accordingly, we define a vector 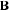 in such a way that it is composed of parameters for risk-adjusting physical distributions of various mortality Brownian motions and jump sizes:
in such a way that it is composed of parameters for risk-adjusting physical distributions of various mortality Brownian motions and jump sizes:
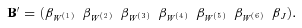 (19)
(19)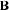 is given by
is given by
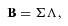 (20)
(20)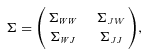
 (21)
(21)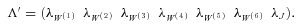 (22)
(22) as follows:
as follows:
 (23)
(23)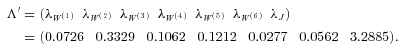 (24)
(24)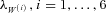 ). The high-risk premium of the common jump reflects the risk aversion of insurers or investors when they face unhedgeable catastrophe mortality risks (Froot and Stein, 1998; Lin and Cox, 2008).10 However, insurers pay a low premium to transfer their mortality diffusion risk. This can be explained by the fact that the insurers can predict mortality normal deviations from the trend to some extent. The regular mortality fluctuations are less likely to impose them a high financial distress cost so the risk premium is lower. Among all market prices of risk for various diffusions, the United Kingdom's Brownian motion has the highest market price of risk (
). The high-risk premium of the common jump reflects the risk aversion of insurers or investors when they face unhedgeable catastrophe mortality risks (Froot and Stein, 1998; Lin and Cox, 2008).10 However, insurers pay a low premium to transfer their mortality diffusion risk. This can be explained by the fact that the insurers can predict mortality normal deviations from the trend to some extent. The regular mortality fluctuations are less likely to impose them a high financial distress cost so the risk premium is lower. Among all market prices of risk for various diffusions, the United Kingdom's Brownian motion has the highest market price of risk (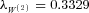 ). This is consistent with our parameter estimations in Table 1: the United Kingdom has a much higher volatility σ2 = 0.0810 than other sample countries. A higher volatility implies a higher risk so it requires a higher market price of risk.
). This is consistent with our parameter estimations in Table 1: the United Kingdom has a much higher volatility σ2 = 0.0810 than other sample countries. A higher volatility implies a higher risk so it requires a higher market price of risk. for different mortality securities. For example, the transformed annual CMI of Vita II equals
for different mortality securities. For example, the transformed annual CMI of Vita II equals
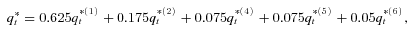
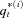 is the transformed country i's population mortality rate after applying normalized multivariate exponential tilting.
is the transformed country i's population mortality rate after applying normalized multivariate exponential tilting.As noted earlier, the payoffs of the Vita II mortality bond depend on (qt−1 + qt)/2 (t = 2007, …, 2011) where qt is a weighted average of the population mortality indexes of United States (62.5 percent), United Kingdom (17.5 percent), Germany (7.5 percent), Japan (7.5 percent), and Canada (5 percent). Figure 3 plots its transformed probability distribution of 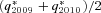 with the market prices of risk in (24). Figure 3 also compares the transformed distribution to its physical distribution (q2009 + q2010)/2.11 As what we expect, the transformed distribution lies on the right of the physical distribution. After transformation, we put more weight on catastrophic mortality events (i.e., the right tail). It implies that investors expect a higher probability of extreme mortality losses than what the physical distribution suggests.
with the market prices of risk in (24). Figure 3 also compares the transformed distribution to its physical distribution (q2009 + q2010)/2.11 As what we expect, the transformed distribution lies on the right of the physical distribution. After transformation, we put more weight on catastrophic mortality events (i.e., the right tail). It implies that investors expect a higher probability of extreme mortality losses than what the physical distribution suggests.
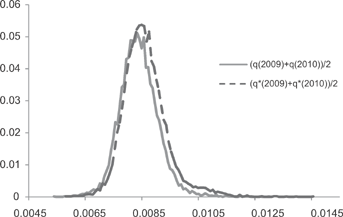
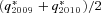 (Shown as Broken Line) and Physical Probability Distribution of (q2009 + q2010)/2 (Shown as Solid Line) Based on 10,000 Simulation Trials
(Shown as Broken Line) and Physical Probability Distribution of (q2009 + q2010)/2 (Shown as Solid Line) Based on 10,000 Simulation Trials
Note: The horizontal axis is the average of the weighted population mortality indexes in 2009 and 2010 defined in the Vita II bond (62.5 percent on U.S. population death rate, 17.5 percent on the U.K., 7.5 percent on Germany, 7.5 percent on Japan, and 5 percent on Canada) and the vertical axis stands for the probability.
Impact of Correlations and Jumps on Pricing
Do the correlations and common jumps play an important role in mortality security pricing? To answer this question, we compare the market prices of risk in (24) from the model with correlations and common jumps with those of (1) the model with common jumps but without correlations and (2) the model without common jumps and correlations.
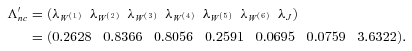 (25)
(25)| i | αi | σi | mci | sci | |
|---|---|---|---|---|---|
| United States | 1 | −0.0104 | 0.0386 | 0.1360 | 0.0576 |
| (0.0010) | (0.0037) | (0.0136) | (0.0057) | ||
| United Kingdom | 2 | −0.0035 | 0.0857 | 0.0001 | 0.1451 |
| (0.0004) | (0.0067) | (8.6 × 10−6) | (0.0147) | ||
| France | 3 | −0.0077 | 0.0421 | 0.2220 | 0.1194 |
| (0.0005) | (0.0091) | (0.0210) | (0.0128) | ||
| Germany | 4 | −0.0060 | 0.0689 | 0.0001 | 0.1417 |
| (0.0005) | (0.0070) | (9.9 × 10−6) | (0.0131) | ||
| Japan | 5 | −0.0061 | 0.0207 | 0.1784 | 0.0616 |
| (0.0007) | (0.0050) | (0.0174) | (0.0059) | ||
| Canada | 6 | −0.0059 | 0.0326 | 0.1105 | 0.1937 |
| (0.0006) | (0.0054) | (0.0112) | (0.0192) |
- Note: The standard errors are reported in parentheses.
Assuming zero correlations, the market prices of risk in (25) are all higher than those in (24) when we account for the correlations of six-country population death rates. According to our proposed model (1) with correlations and jumps, all six countries have positive correlations with each other (see the correlation matrix (17)). That is, an increase in a country's mortality rate will be coincident with mortality rate increases of the other five countries. As such, a CMI based on the model with positive correlations has a higher mortality risk since it is more likely to exceed the trigger level above which the principal will be reduced. Given the fixed par spreads of the seven mortality securities, the higher mortality risk from the real world model implies the lower market prices of risk when the positive mortality correlations are incorporated in pricing. In contrast, failing to model mortality correlations would overestimate market prices of risk and overprice a “new” mortality security based on these estimates, thus discouraging insurers from transferring catastrophe mortality risk to capital markets. High-risk premia at least partially explain the failure of some insurance-linked securities, such as the EIB longevity bond issued in 2004 (Lin and Cox, 2008).
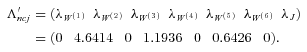 (26)
(26)| i | αi | σi | |
|---|---|---|---|
| United Sates | 1 | −0.0100 | 0.0373 |
| (0.0010) | (0.0039) | ||
| United Kingdom | 2 | −0.0038 | 0.0682 |
| (0.0004) | (0.0070) | ||
| France | 3 | −0.0046 | 0.0982 |
| (0.0005) | (0.0094) | ||
| Germany | 4 | −0.0045 | 0.0726 |
| (0.0005) | (0.0071) | ||
| Japan | 5 | −0.0071 | 0.0531 |
| (0.0007) | (0.0049) | ||
| Canada | 6 | −0.0058 | 0.0526 |
| (0.0006) | (0.0054) |
- Note: The standard errors are reported in parentheses.
CONCLUSIONS
Mortality correlations become an increasingly important consideration in life insurance business and mortality security pricing, because populations of different countries and cohorts are more interdependent than ever. Life insurers that operate in multiple countries have to evaluate the effect of massive catastrophic mortality events such as worldwide flu epidemics. In the mortality security markets, most transactions, albeit their difference in structure, have one thing in common: Based on mortality data reported by official agencies, they tend to calculate a weighted average mortality index of multiple underlying reference populations. Therefore, the payoffs of these mortality securities are dependent on the correlations among these population mortality indexes.
In this article, we propose a time-continuous model for describing mortality correlations among different countries. For each included country, the mortality model is composed of two parts: (1) a baseline component describes a country's mortality normal deviations from the trend and its correlation with other countries' mortality rates and (2) a common jump component is governed by a double-jump process. The double-jump process aims at capturing transient catastrophic death events.
Many existing papers ignore mortality correlations to simplify their calibration procedures because the correlations to be estimated grow quadratically with the number of countries of interests. However, as shown in the article, mortality correlation has a significant impact on parameter estimation and mortality security pricing, so it should not be ignored. To tackle this calibration challenge in correlation estimation, we apply the particle filtering approach. We describe its procedures and resulting parameterizations in the context of mortality stochastic modeling.
Finally, we utilize the normalized multivariate exponential tilting method to price some mortality securities issued in 2006 and calibrate market prices of risk for different mortality diffusion and jump processes. The market prices of risk derived from the normalized multivariate exponential tilting depend on intercountry mortality correlations and jumps. Our numerical example confirms that both mortality correlations and common jumps are important in pricing those securities.
In sum, this article contributes to the mortality literature in three ways. First, we develop a mortality dynamic model that captures both mortality correlation among countries and common jumps that affect all countries. Second, we propose to use a double-jump process to model transient mortality shocks. Third, we apply the particle filtering approach to estimate multicountry mortality models with correlations. While we apply the particle filtering approach in the context of multicountry population mortality indexes, we can extend the application of this technique to investigate cohort mortality dependency within a country or among countries. We leave this for future work.
APPENDIX A
The key idea of particle filtering with the SIR algorithm is briefly described in the following recursive steps.
Step 1. This step generates random samples from previous state variables and observations. Specifically, given the observation Yt−1 and the estimated St−1 at time t − 1, we simulate shocks {Δ Wj, Δ Nj, Zj} and draw 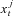 (j = 1, …, L) from p(St |St−1) by simulating the latent state vector forward using the state Equation (3). We draw L samples of
(j = 1, …, L) from p(St |St−1) by simulating the latent state vector forward using the state Equation (3). We draw L samples of 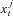 , from the prior probability density of (3) and approximate p(St |Yt−1) by using the set of L particles.
, from the prior probability density of (3) and approximate p(St |Yt−1) by using the set of L particles.
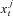 , set the importance weight equal to
, set the importance weight equal to 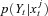 . Then we calculate the normalized importance weight
. Then we calculate the normalized importance weight 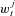 ,
,
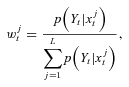
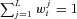 . The set of
. The set of 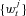 can be viewed as a discrete probability distribution of
can be viewed as a discrete probability distribution of 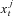 (j = 1, …, L), that is, an approximate density pL (St |Yt) to the true density
(j = 1, …, L), that is, an approximate density pL (St |Yt) to the true density 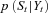 .
.Step 3. In this step the particle filter estimates an approximation, 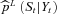 , using L unweighted particles, of the true filtering density
, using L unweighted particles, of the true filtering density 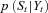 . The resampling step modifies the weighted density
. The resampling step modifies the weighted density 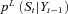 estimated previously to an unweighted density
estimated previously to an unweighted density 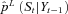 by eliminating particles with low importance weights and by multiplying particles with high importance weights. That is, the resampling procedure eliminates selectively over time those particles with very lower probability, replaces them with particles with higher probability, and at the same time, keeps the number of particles unchanged. This step generates a new set of L particles,
by eliminating particles with low importance weights and by multiplying particles with high importance weights. That is, the resampling procedure eliminates selectively over time those particles with very lower probability, replaces them with particles with higher probability, and at the same time, keeps the number of particles unchanged. This step generates a new set of L particles, 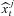
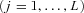 .12 As the number of particles, L, increases, the approximation converges to the true filtering distribution.
.12 As the number of particles, L, increases, the approximation converges to the true filtering distribution.
APPENDIX B
The process of the kernel smoothing approach (Doucet et al., 2001) is briefly described as follows:
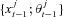 , first simulate shocks {Δ Wj, Δ Nj, Zj} for the time interval from t − 1 to t. Then sample the state variable
, first simulate shocks {Δ Wj, Δ Nj, Zj} for the time interval from t − 1 to t. Then sample the state variable 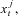 j = 1, …, L, using (3) and compute the mean of
j = 1, …, L, using (3) and compute the mean of 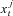
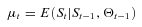
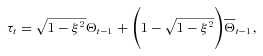
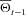 is the mean of the prior p(Θt−1 |Yt−1).
is the mean of the prior p(Θt−1 |Yt−1).Step 2. For j = 1, 2, …, L, sample a parameter vector 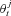 from the j th normal component of the kernel density,
from the j th normal component of the kernel density, 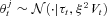 , where Vt is the variance/covariance matrix of p(Θt |Yt−1).
, where Vt is the variance/covariance matrix of p(Θt |Yt−1).
Step 3. Sample the values of the current state vector 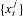 again. This time use the sampled parameter vector
again. This time use the sampled parameter vector 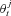 estimated in step 2. That is, step 3 draws samples
estimated in step 2. That is, step 3 draws samples 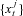 from the distribution p(St |St−1, Θt) compared to step 2 where we draw samples
from the distribution p(St |St−1, Θt) compared to step 2 where we draw samples 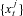 from the distribution p(St |St−1, Θt−1).
from the distribution p(St |St−1, Θt−1).
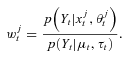
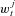 can be viewed as a discrete probability distribution of
can be viewed as a discrete probability distribution of 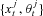 , that is, an approximation of the true density p(St, Θt |Yt).
, that is, an approximation of the true density p(St, Θt |Yt).Step 5. The resampling step modifies the weighted approximate density pL (St, Θt |Yt−1) to an unweighted density 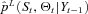 as in step 3 of Appendix A. The particles with low importance weights are eliminated and the particles with high importance weights are propagated so that the total number of particles remains constant. This step generates
as in step 3 of Appendix A. The particles with low importance weights are eliminated and the particles with high importance weights are propagated so that the total number of particles remains constant. This step generates 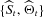 where
where 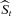 and
and 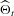 are the new set of unweighted particles. Their density approximates to the true filtering density p(St, Θt |Yt).
are the new set of unweighted particles. Their density approximates to the true filtering density p(St, Θt |Yt).
Repeat the above steps toward a final posterior estimation of states and parameters.
APPENDIX C
Based on the same data shown in the “Data” section, Table C1 shows the estimates when we assume zero mortality correlations between the six countries but with common jumps. Our estimate of the Poisson intensity in this model equals 0.0125, close to kc = 0.0120 when we model mortality correlations and common jumps. Table C2 shows the estimation results for the model without mortality correlations and common jumps.




