Mortality Heterogeneity and the Distributional Consequences of Mandatory Annuitization
The authors can be contacted via e-mail: [email protected] and [email protected], respectively. The authors would like to thank Jeffrey Brown for providing invaluable tables of relative mortality risk, and Irena Dushi and Cori Uccello for providing important data analyses. They would also like to thank Jeffrey Brown, Irena Dushi, Marjorie Flavin, Kathleen McGarry, Sara Rix, and Cori Uccello for very helpful comments.
Abstract
This article investigates the distributional consequences of mandatory annuitization. Using Health and Retirement Study (HRS) data and accounting for longevity risk pooling within marriage and preannuitized wealth, we find substantial redistribution away from disadvantaged groups in expected utility terms. Using HRS data on subjective survival probabilities, we construct a subjective life table for each individual in the HRS. We calculate the value each household would place on annuitization, based on the husband and wife's subjective life tables, and the household's degree of risk aversion and proportion of preannuitized wealth. A significant minority would perceive themselves as suffering a loss from mandatory annuitization.
Introduction
Mandatory annuitization on uniform terms, such as occurs in Social Security and most defined benefit pensions, redistributes wealth from those who die young and who are disproportionately male, less well educated, and black toward those with low mortality and who are disproportionately female, college educated, and white. But annuities provide insurance against outliving one's wealth that ought to be valued by risk-averse individuals facing an uncertain lifespan. It is possible that mandatory annuitization on uniform terms may make the average individual in each of the above groups better off in expected utility terms, even if the money's worth of their annuity, the income stream, discounted by an interest rate and group-average annual survival probabilities and divided by the premium paid, is considerably less than one.
Brown (2003) showed that for single individuals, and ignoring preannuitized wealth such as Social Security and defined benefit pensions, this was indeed the case. In expected utility terms, not only was the average individual in each group substantially better off as a result of mandatory annuitization, but there was also negligible redistribution from high to low mortality groups.
We first extend Brown's (2003) analysis to married couples, and then, using data from the Health and Retirement Study (HRS), further extend it to incorporate preannuitized wealth. We follow the literature by comparing the annuitization of all of a household's unannuitized wealth with an optimal decumulation of unannuitized wealth, solving the household's decumulation problem using numerical optimization techniques. We show that accounting for the above factors, mandatory annuitization would have substantial redistributive effects, although the average household in each group would still benefit, albeit by smaller amounts.
Married couples value the longevity insurance provided by annuities less highly than otherwise identical single individuals. The age of death of a surviving spouse is less uncertain than that of a single individual, so that the couple, in effect, pools longevity risk. Under plausible utility functions, preannuitized wealth will further reduce the value the household places on additional longevity insurance. The value the household places on annuitization is more affected by the household's survival probabilities, increasing between-group differences in annuity valuations.
But as Brown (2003) pointed out, group averages may conceal considerable household level variation in mortality beliefs, risk aversion, and proportion of preannuitized wealth, factors that economic theory indicates are important determinants of the value of annuitization. We therefore calculate the value each HRS household would place on annuitization of its unannuitized wealth, taking account of the above factors.
We recover subjective annual survival probabilities from each HRS individual's estimate of his probability of surviving to a specified age using Bayesian updating techniques applied by Gan, Hurd, and McFadden (2005) to the somewhat older Asset and Health Dynamics Among the Oldest Old cohort. Earlier work (Hurd and McGarry 1995, 2002) showed that these responses varied appropriately with known risk factors and have predictive power for actual mortality beyond that contained in a life table. We show that the subjective annual survival probabilities that we recover vary appropriately with socioeconomic status and that life expectancies derived from them are appropriately consistent with those obtained from life tables.
We find that when we take account of heterogeneity in household characteristics, a substantial 16.5 percent of the sample, and much larger percentages of low-socioeconomic-status households, would perceive themselves as being worse off under mandatory annuitization.
The remainder of the article is organized as follows. First, we discuss previous research and then explain our methodology. Next, we present our results. The final section concludes the article.
Previous Research
In this section, we review the literature on the impact of adverse selection on annuity prices, the value of annuities to risk-averse households facing an uncertain lifespan, and the distributional consequences of mandatory annuitization.
The Impact of Adverse Selection on Annuity Prices
An indication of the impact of adverse selection on annuity prices can be obtained by comparing the money's worth of an annuity to an individual with population mortality with its money's worth to an individual with annuitant mortality. Calculations by Mitchell et al. (1999) using 1995 data showed that this difference is about 8 percent. But this overstates the impact of adverse selection on households with annuitizable wealth because there is a strong and well-documented relationship between longevity and wealth (see Menchik, 1993; Attanasio and Hoynes, 2000; Hurd, McFadden, and Merrill, 2001); with many high mortality households having few annuitizable assets. Dushi and Webb (2006) estimate that the difference between the value of an annuity to someone with annuitant mortality and its value to someone with population mortality approximately halves when one weights population mortality by annuitizable wealth.
The Value of Annuities to Risk-Averse Households Facing an Uncertain Lifespan
Most of the literature uses numerical optimization techniques to calculate either the wealth equivalent of an annuity or annuity equivalent wealth (AEW). The wealth equivalent of an annuity is defined in the literature as the annuity money's worth at which a household would be indifferent between annuitizing its unannuitized wealth and undertaking an optimal decumulation of that wealth while continuing to hold it in unannuitized form. AEW equals the factor by which unannuitized wealth must be multiplied so that the household is indifferent between annuitizing its original wealth on actuarially fair terms and undertaking an optimal decumulation of an amount of unannuitized wealth equal to its original wealth multiplied by the above factor.1 When AEW is less than 1, the household is better off not annuitizing, and conversely, when AEW exceeds 1, the household is better off annuitizing.
Mitchell et al. (1999) calculated the wealth equivalent of an annuity for single individuals. Using 1995 U.S. data and assuming a real interest rate of 3 percent, an inflation rate of 3.2 percent, a rate of time preference of 1 percent, no bequest motive, no preexisting annuities, population mortality, and a coefficient of risk aversion equal to 1, they calculated that the before tax wealth equivalent of the typical nominal annuity was 0.659 for a single male. At a coefficient of risk aversion of 2, the wealth equivalent fell to 0.619. If half the individual's wealth was held in the form of a preexisting real annuity, the wealth equivalents increased to 0.730 and 0.695 under the same assumptions. As discussed above, only a very small proportion of single households have half or less of their financial wealth in annuitized form. These results are therefore representative only of the wealthiest households who may also have a stronger than average bequest motive.
 (1)
(1)Dushi and Webb (2004) examined the balance sheets of HRS households in which the older spouse turned 65 during the period 1994–2000. They calculated total wealth, inclusive of the present value of Social Security and employer pensions, sorted the households by total wealth, and then calculated the mean proportion of preannuitized to total wealth for households in each wealth decile. They found that in all but the top wealth decile, preannuitized wealth was greatly in excess of one half of total financial wealth.
Although the actuarial unfairness of annuities undoubtedly contributes to the low level of voluntary annuitization, the legal and institutional factors documented in Brown and Warshawsky (2001) may also contribute, as may the psychological biases described in Brown (2007). Households may perceive annuities as a gamble or may fear a loss of control of their wealth that extends beyond a mere desire for liquidity. Regret aversion by individuals who fear that they might learn after buying an annuity that they have a terminal illness might also contribute to the lack of demand. A bequest motive may also play a role, although it would not explain why households do not annuitize the part of their wealth they wished to consume.
There is also a literature, including work by Milevsky (1998, 2000), that examines the question of whether households might wish to postpone the purchase of a fixed annuity in order to obtain the benefit of the equity premium. But it is possible to purchase variable immediate annuities that offer the advantages of both annuitization and investment in equities, although they form only a small proportion of total annuity sales, despite a considerable body of literature demonstrating their attractiveness. We do not address the question of whether a program of mandatory annuitization should offer a variable annuity option and instead assume that there is a single risk-free asset in which households may invest and which the annuity provider uses to price the annuity. We refer the interested reader to Blake, Cairns, and Dowd (2003) for an analysis of optimal household portfolio allocations when variable annuities are available.
The Distributional Consequences of Mandatory Annuitization
There is a considerable literature that evaluates the distributional effects of the U.S. Social Security system in money's worth terms (e.g., Gustman and Steinmeier, 2001; Liebman, 2002; Coronado, Fullerton, and Glass, 2000). The literature finds that because households with high lifetime income have, on average, lower mortality, mandatory annuitization reduces, but does not eliminate, the overall progressivity of the system.
Brown (2003) is the only previous article that calculates the distributional consequences of mandatory annuitization in expected utility terms. He first calculated the money's worth of various types of annuities—real, nominal, and 20-year period certain—to various categories of individual and then calculated the AEW of the various types for each category. His methodology is described in detail in his article. To summarize, he made use of data from the National Longitudinal Mortality Study (NLMS), a nationally representative sample of over 600,000 individuals of all ages that was merged with National Death Index data for a period of 9 years during the 1980s. He sorted the NLMS data by gender and ethnicity (black, white, or Hispanic) and further sorted blacks and whites into three educational categories: less than high school, high school or some college, and at least 4 years of college. He then calculated an age-specific nonparametric mortality rate for each category, there being up to nine observations for each individual. Using nonlinear least squares, he estimated a survival function based on mortality rates for ages 25–84 and used the survival function to estimate mortality rates up to age 100.2 He then calculated mortality rates for each category and age, relative to the category average for that particular age. Assuming that relative mortality rates remain constant over time, he then combined these data with the 1978 birth cohort life table published by the Social Security Administration to calculate 1978 birth cohort life tables for each category of individual.
Brown (2003) then used these life tables to calculate the money's worth of an actuarially fair annuity to each category, assuming that the annuity is priced on uniform terms, using a combined male and female life table, and that the annuity is purchased at age 67. As one might expect, the money's worth of an annuity was higher for women than for men, for whites than for blacks, and for the better educated than the less well educated. The largest differences were between men and women, but the racial and educational differences were also substantial. His calculations show that in dollar terms, mandatory annuitization involves a substantial degree of redistribution from men to women and from traditionally disadvantaged groups toward the more advantaged.
Brown (2003) then calculated AEW for each class, using numerical optimization techniques. A completely different picture emerged. When evaluated in expected utility terms, the redistributive effect of mandatory annuitization is small to insignificant, particularly at higher degrees of risk aversion. He has kindly consented to us reproducing his calculations of AEW (Table 3 in his article), and they appear as our Table 1.
| Sample Size | Married Couples | Sample Size | Single Women | |||
|---|---|---|---|---|---|---|
| Annuitized as % of Financial Wealth | Annuitized as % of Total Wealth | Annuitized as % of Financial Wealth | Annuitized of Total as % Wealth | |||
| All | 1,418 | 0.775 | 0.615 | 519 | 0.816 | 0.678 |
| All whites | 1,142 | 0.760 | 0.598 | 311 | 0.764 | 0.621 |
| All blacks | 148 | 0.916 | 0.784 | 155 | 0.953 | 0.829 |
| All Hispanics | 96 | 0.947 | 0.795 | 44 | 0.955 | 0.768 |
| Whites: College+ | 253 | 0.660 | 0.509 | 36 | 0.593 | 0.452 |
| Whites: HS+ | 640 | 0.769 | 0.603 | 179 | 0.731 | 0.579 |
| Whites: <HS | 249 | 0.843 | 0.678 | 96 | 0.902 | 0.775 |
| Blacks: College+ | 7 | 0.944 | 0.868 | 17 | 0.923 | 0.812 |
| Blacks: HS+ | 67 | 0.893 | 0.731 | 63 | 0.929 | 0.787 |
| Blacks: <HS | 74 | 0.935 | 0.824 | 75 | 0.980 | 0.868 |
- Notes: (1) HRS household weights; (2) 32 husbands and 9 single women reported ethnicity other than white, black, or nonblack Hispanic; (3) top 1% of wealth distribution excluded.
| CRRA = 1 | CRRA = 2 | CRRA = 3 | CRRA = 4 | CRRA = 5 | |
|---|---|---|---|---|---|
| Men | |||||
| All | 1.350 | 1.449 | 1.497 | 1.527 | 1.546 |
| All whites | 1.352 | 1.450 | 1.498 | 1.528 | 1.546 |
| All blacks | 1.328 | 1.437 | 1.488 | 1.522 | 1.542 |
| All Hispanics | 1.362 | 1.449 | 1.495 | 1.523 | 1.543 |
| Whites: College+ | 1.361 | 1.452 | 1.498 | 1.527 | 1.546 |
| Whites: HS+ | 1.351 | 1.451 | 1.499 | 1.529 | 1.548 |
| Whites: <HS | 1.325 | 1.434 | 1.486 | 1.520 | 1.540 |
| Blacks: College+ | 1.343 | 1.443 | 1.492 | 1.523 | 1.542 |
| Blacks: HS+ | 1.328 | 1.437 | 1.488 | 1.523 | 1.543 |
| Blacks: <HS | 1.296 | 1.415 | 1.472 | 1.511 | 1.534 |
| Women | |||||
| All | 1.465 | 1.531 | 1.560 | 1.577 | 1.588 |
| All whites | 1.465 | 1.531 | 1.560 | 1.577 | 1.588 |
| All blacks | 1.459 | 1.529 | 1.560 | 1.577 | 1.588 |
| All Hispanics | 1.487 | 1.545 | 1.570 | 1.585 | 1.597 |
| Whites: College+ | 1.466 | 1.530 | 1.559 | 1.576 | 1.588 |
| Whites: HS+ | 1.465 | 1.531 | 1.561 | 1.577 | 1.588 |
| Whites: <HS | 1.463 | 1.531 | 1.562 | 1.578 | 1.589 |
| Blacks: College+ | 1.462 | 1.530 | 1.560 | 1.577 | 1.588 |
| Blacks: HS+ | 1.459 | 1.529 | 1.561 | 1.577 | 1.588 |
| Blacks: <HS | 1.453 | 1.526 | 1.560 | 1.577 | 1.587 |
- Source: Brown (2003), Table 1, p. 32. Calculations as described in the text.
All categories have AEWs well in excess of 1. At a coefficient of risk aversion of 5, women's AEWs are about 4 percent more than those of men, but black men valued annuitization only 0.4 percent less than white men, and black women have precisely the same valuation as white women. Education-related differences in AEW are similarly small. The intuition behind these results is that both high and low mortality groups wish to restrict their consumption by approximately equal amounts to self-insure against destitution in advanced old age, even though the risk of attaining advanced old age is much less for people in the high mortality groups.
Brown's (2003) calculations of AEW can be compared with Mitchell et al.'s (1999) calculations of the money's worth of annuities. When there is no preannuitized wealth, annuitization is advantageous when the reciprocal of AEW is less than the money's worth of the annuity. The above authors calculated that the money's worth of an annuity to a 65-year-old male was 75.6 percent, more when the more conservative Treasury strip interest rate was used. Comparing the money's worth of an annuity, calculated using even the corporate bond interest rate, with the reciprocals of AEW would lead one to predict substantial rates of voluntary annuitization whereas, of course, Poterba (1997) and many other authors have highlighted the rarity of its occurrence.
The Brown (2003) results are for single individuals and assume no preannuitized wealth. As previously mentioned, Brown and Poterba (2000) showed that for any given level of risk aversion, married couples will place a lower valuation on annuitization than single individuals, whereas Dushi and Webb (2004) showed that incorporating actual levels of preannuitized wealth further reduces of the value of annuitization.
Thus, it is clear that Brown's (2003) calculations represent an upper bound to the value of annuitization. However, it is difficult to tell ex ante whether, if we were to incorporate the above factors, we would still obtain his key findings, namely, that average AEW varies little from one household type to another and that in expected utility terms, the average household in each category would be better off under mandatory annuitization than it would be were it to undertake an optimal decumulation of its unannuitized wealth.
Furthermore, Brown's (2003) calculations are for the average individual in each household type. As he points out, the types are not monolithic, and averages may conceal considerable household level heterogeneity. It is possible that although the average household of each type may be better off under annuitization, substantial minorities may not be. We consider these questions further in the following section.
Methodology
Calculating Group Average AEW
When calculating category average AEW, we follow Brown (2003) by focusing on the 1978 birth cohort, using the utility function in Equation (1) with a value of λ of 0.5. We combine Brown's tables of relative mortality rates with Social Security Administration life tables for the 1978 birth cohort to construct 1978 birth cohort male and female mortality tables for all Hispanics, whites, and blacks, and for whites and blacks with less than a high school education, a high school education or some college, and at least 4 years of college.3, 4 We again follow Brown by constructing tables for all whites and all blacks by calculating a weighted average of the mortality rates of the three education categories using sample weights obtained from an analysis of the ethnicity and educational attainment of 30- to 34-year-olds in the March 1999 Current Population Survey. Our all male and all female mortality tables are simply the Social Security Administration mortality tables for the 1978 birth cohort.
We first use numerical optimization techniques to calculate AEW for each category of married couple, assuming no preannuitized wealth. We then calculate AEW for each category of married couples and single women, and for all single men, taking account of preannuitized wealth, there being insufficient single men in the sample to permit an analysis by category.5
Dushi and Webb (2004) showed that the mean proportion of preannuitized to total financial wealth varies with wealth decile and marital status. Given the strong relationship between wealth and socioeconomic status, it would be surprising if the proportion of preannuitized wealth did not also vary with ethnicity and education. We would ideally wish to forecast the balance sheets and proportions of preannuitized wealth of the 1978 birth cohort at retirement in 2045, taking account of changes in the structure of employer pensions and considering the potential impact of Social Security Individual Accounts. This task is well beyond the scope of this article. Poterba, Venti, and Wise (2002) projected 401(k) and Social Security wealth for households retiring in 2025 and 2035 but did not similarly project DB pension wealth, nonpension financial wealth, or the value of Social Security Individual Accounts and did not extend their analysis to 2045. We therefore adopt an alternative approach and assume that households have the mean proportion of each category's preannuitized to total financial wealth obtained from an analysis of the Dushi and Webb (2004) data for HRS households turning 65 between 1994 and 2000 (65 is the Social Security Normal Retirement Age for this cohort). To the extent that households retiring in 2045 will have smaller proportions of preannuitized wealth, for example, as a result of the displacement of annuitized DB by unannuitized defined contribution pensions, our results will understate the value of annuitization. The magnitude of the potential understatement can be gauged by comparing our results that exclude preannuitized wealth with those that include it.
The HRS oversamples black households, so the sample sizes for both blacks and whites are generally adequate, the principal exception being college-educated blacks.6 We refer the reader to Dushi and Webb (2004) for a description of the methodology used to calculate the expected present value of pension wealth, but in brief, they used self-reported data on actual or anticipated pension income, a 3 percent real interest rate, a 2.5 percent inflation rate, and population average mortality for the appropriate birth cohort.
Under any plausible utility function, the value of annuitization decreases with each dollar annuitized. We recognize that any plausible program of annuitizing either 401(k) plan balances, or Social Security Individual Accounts would result in only a proportion of the household's unannuitized wealth being annuitized. But it is difficult to say how large that proportion might be in 2045, as it will depend on the evolution of Social Security and the employer pension system, and households' responses to such changes. We therefore follow the literature referred to in the “Previous Research” section regarding all unannuitized wealth as potentially annuitizable. Our calculations will therefore understate the value of partial annuitization.
Brown's (2003) calculations assumed that the annuities being offered were actuarially fair or, alternatively, actuarially fair minus an 8 percent expense load. However, if wealthy and, on average, long-lived households have larger account balances, then the annuity provider must charge a higher than actuarially fair premium. We consider how large this effect might be, focusing on Social Security Individual Accounts, making use of analyses kindly provided by Cori Uccello using Urban Institute's DYNASIM microsimulation program. Uccello et al. (2003) used the program to calculate the money's worth of Social Security Individual Accounts for people in the 1978 birth cohort. It models individual level mortality risk and can be used to calculate equilibrium levels of actuarial unfairness resulting from mandatory annuitization of Social Security Individual Accounts under a number of policy options.
At our request, Uccello used DYNASIM to provide us with an estimate of the premium loading that would have to be applied to enable an annuity provider with zero administrative costs to break even under a system of mandatory annuitization of Social Security Individual Accounts. Her estimate of only about 1 percent reflects not only the very modest variation across socioeconomic classes in projected Individual Account balances but also the fact that women, who have lower mortality than men, have lower average lifetime earnings and lower projected Individual Account balances.7
For simplicity, and in view of the very small magnitude of Uccello's estimate, we follow Brown (2003) by assuming that the annuity is priced at an actuarially fair rate with zero administrative costs, using uniform pricing and a 3 percent real rate of interest. It is important to note that the annuity provider cannot simply use the average of the male and female mortality rates to price the annuity. Men have higher mortality rates than women, so women predominate at older ages, and at older ages, uniform mortality rates will be closer to female than to male rates.
Calculating Household-Level AEW
The above analyses have focused on the average household within each group. But AEW will vary within each group due to within-group variations in mortality risk, risk aversion, and proportion of preannuitized wealth. To obtain estimates of these variations, we calculate AEW for each HRS household in which the husband turned 65 between 1994 and 2000, taking account of the household's composition, proportion of preannuitized wealth, coefficient of risk aversion, and its members' subjective assessments of their annual survival probabilities. In the following paragraphs, we introduce the HRS data on subjective mortality beliefs and explain how we recover each individual's subjective life table and estimates of each household's coefficient of risk aversion.
HRS Data on Subjective Mortality Beliefs
Participants in the HRS and the Asset and Health Dynamics Among the Oldest Old (AHEAD) panel of somewhat older individuals born between 1890 and 1923 are asked to estimate their chances to surviving to ages 10–25 years hence. Hurd and McGarry (1995, 2002) analyzed the HRS data and found that these subjective survival probabilities contained important information. The responses aggregated quite closely to the predictions of life tables and varied appropriately with known risk factors and determinants of mortality. In panel, individuals modify their subjective survival probabilities in response to new information. The subjective survival probabilities also predict actual survival.
Hurd and McGarry (1995) analyzed data from Wave 2 of the HRS and found that after the inclusion of a variety of controls, nonwhite individuals reported significantly higher subjective survival probabilities. We find that both before and after controlling for age, education, and gender, black individuals report significantly higher survival probabilities.8 We consider the implications of this finding when discussing our results.
Constructing Subjective Life Tables for Each Individual in the HRS
In each wave, individuals were asked to assess their probabilities of surviving to ages 75 and 85, the Wave 1 question being evaluated on a scale of 1–10, and subsequent waves' questions being evaluated on a scale of 1–100. We restricted our analysis to the age 75 responses.9
Since we have wealth data at the wave the household attains age 65, we decided to calculate AEW at that age. We use the survival probability estimates given at the last wave before the husband turned 65.10 Our sample therefore consists of the 1,689 husbands who were aged 63–65 years old at Waves 1–4 of the HRS and their wives of any age. We do not use Waves 5–7 as only the first four waves can be matched to Dushi and Webb (2004) data on proportions of preannuitized wealth. We discard 79 households for whom we lack data on education or ethnicity, leaving 1,610.
Neither the subjective survival probability nor the risk-aversion questions were asked of proxy respondents, and responses are missing for some other individuals. We have subjective survival probability responses for both spouses in 1,255 of the above households, and responses to questions regarding risk aversion, discussed later, for 1,152 of the 1,255. We find that the nonrespondents to the survival questions had higher mortality than the remainder of the sample. Wave 1 of the HRS contains a total of 12,652 individuals, and subjective survival probabilities are missing for 944, or about 7 percent of the total. At Wave 6 the vital status of 8.45 percent of the 944 was unknown and 17.5 percent were known to be deceased, compared with 5.87 and 12.13 percent for those who provided data. Under the alternative assumptions that all of those who dropped out of the sample were either alive or dead at Wave 6, nonrespondents have a mortality rate about 44 percent higher than respondents.
We therefore imputed missing responses using hot-deck imputation, with gender, education, ethnicity, and self-reported health status as covariates.11Hurd and McGarry (1995) showed that self-reported health status is a highly significant predictor of self-assessed survival probabilities, even after controlling for many other variables that are likely correlated with health status. We also imputed the missing risk-aversion data, although the relationship between risk aversion and socioeconomic status is less clear.
Continuing with our analysis of sample attrition, we eliminated 65 households with wives aged less than 51, as these are unlikely candidates for immediate annuitization, leaving 1,545, and eliminated two households with a spouse over 75, leaving 1,543. We matched 1,229 of these households to Dushi and Webb's (2004) data on proportions of preannuitized wealth.12
We now explain how we recovered subjective annual survival probabilities from individuals' estimates of their survival probabilities. The difficulty faced by researchers in undertaking this task is that the data suffer from serious focal response problems; the tendency of individuals in this and similar surveys, when asked to respond on a scale of 0–100 percent, to give responses of either 0 or 100, or that are multiples of 25 or 10. These focal responses cannot be used directly as the measure of true subjective probabilities because the distribution of true probabilities should be continuous and the true probabilities cannot be literally either 0 or 1.
Gan, Hurd, and McFadden (2005, henceforth GHM) proposed a Bayesian updating method for recovering subjective annual survival probabilities from the AHEAD panel of somewhat older individuals born before 1924. More specifically, they assumed that an individual's true belief regarding his or her survival probability is unknown to the econometrician. However, the econometrician does know the distribution of those beliefs—the Bayesian “prior.” The individual reports a survival probability based on, but not necessarily equal to, his true beliefs. The difference between his true and his reported beliefs represents measurement error.
GHM used the self-reported survival probabilities to update the prior distribution and to obtain the posterior distribution. GHM then applied the mean of the posterior distribution as an individual's estimated subjective survival probability to the observed mortality data among the panel to estimate parameter values that best characterize each individual's belief as to his annual survival probabilities.
For each individual in the AHEAD data set, GHM estimated an “optimism” index. Compared to the life table survival probability, an individual may overestimate or underestimate his or her survival probability. The estimated “optimism” indices show significant individual heterogeneity and can be applied to derive individuals' subjective annual survival probabilities, their “subjective life tables,” without focal biases.
GHM considered four different optimism indices. Individuals may think of themselves as aging more or less rapidly than the average person of their age and gender, “age scaling,” or may think of themselves as facing an annual mortality risk that bears a fixed relationship to the average for persons of their age and gender, “hazard scaling.” The index can also be constrained so that the average belief coincides with the predictions of life tables or allowed to be unconstrained.

Calculating Households' Degrees of Risk Aversion
Individuals in the 1992 wave of the HRS were asked how they would choose between their present income for life and a 50:50 lottery in which their lifetime income would either increase or decrease by specified percentages. Under the assumption of constant relative risk aversion, one can use the responses to determine whether an individual's coefficient of risk aversion is less than 1, in the ranges 1–2 or 2–3.76, or is greater than 3.76. We follow Brown (2003) by assuming, dependent on the range in which the individual's coefficient of risk aversion lies, that his coefficient is 0.7, 1.5, 2.9, or 5.0. We assign each household a coefficient of risk aversion equal to the average of the husband's and the wife's coefficients.
Results
In the following sections, we first report calculations for the average household of each type. We start by reporting calculations for married couples with no preannuitized wealth, then married couples with preannuitized wealth, and finally, single individuals with preannuitized wealth. We then report our calculations of the entire distribution of AEW.
Utility-Based Calculations—Average Household in Each Category
We report AEWs for the 1978 birth cohort and, for consistency with Brown (2003), assume a retirement age of 67.13 We follow Brown by reporting results for all households; all whites, blacks, and Hispanics; and whites and blacks with less than a high school education, high school or some college, and at least 4 years of college. We report results only for married couples that are of the same ethnicity and have the same level of education. Our analysis of HRS couples turning 65 between 1994 and 2000 shows that 60.4 percent report the same ethnicity and education. We assume the constant relative risk-aversion utility function specified in Equation (1) and again follow Brown by considering coefficients of risk aversion of 1, 2, 3, 4, and 5. We assume that the real interest rate equals 3 percent and that households are required to purchase a real joint life and 2/3 survivor annuity that is priced using a uniform life table. This survivor benefit corresponds to that payable under Social Security when the widow's benefit is payable by reason of her husband's contributions.
Warner and Pleeter (2001) argued that many households might have quite high discount rates. We consider how the rate of time preference might affect AEW by also reporting results calculated at rates of time preference of 5 and 10 percent. These results might be applicable not only to households that are impatient but also to those that might prefer a decreasing consumption path during retirement because, for example, they fear that declines in health may limit their activities at older ages.
The top panel of Table 2 reports our calculations of AEW for married couples in each of the above categories, assuming a 3 percent interest rate and no preannuitized wealth. We find that longevity risk pooling very considerably reduces the value of annuitization, consistent with Brown and Poterba (2000). All ethnic and educational groups still have AEWs well in excess of one, even at low coefficients of risk aversion, but the between-group variations in AEW are much greater than those in Brown's (2003) calculations for single individuals.
| CRRA = 1 | CRRA = 2 | CRRA = 3 | CRRA = 4 | CRRA = 5 | |
|---|---|---|---|---|---|
| Time preference = 3% | |||||
| All | 1.190 | 1.245 | 1.284 | 1.316 | 1.345 |
| All whites | 1.196 | 1.250 | 1.288 | 1.320 | 1.348 |
| All blacks | 1.154 | 1.213 | 1.256 | 1.293 | 1.324 |
| All Hispanics | 1.222 | 1.271 | 1.306 | 1.335 | 1.359 |
| Whites: College+ | 1.215 | 1.265 | 1.301 | 1.331 | 1.360 |
| Whites: HS+ | 1.190 | 1.245 | 1.284 | 1.317 | 1.345 |
| Whites: <HS | 1.162 | 1.220 | 1.262 | 1.297 | 1.327 |
| Blacks: College+ | 1.190 | 1.244 | 1.283 | 1.316 | 1.344 |
| Blacks: HS+ | 1.159 | 1.217 | 1.260 | 1.296 | 1.327 |
| Blacks: <HS | 1.121 | 1.184 | 1.230 | 1.269 | 1.302 |
| Time preference = 5% | |||||
| All | 1.144 | 1.213 | 1.260 | 1.296 | 1.327 |
| All whites | 1.150 | 1.219 | 1.264 | 1.300 | 1.330 |
| All blacks | 1.104 | 1.180 | 1.230 | 1.271 | 1.306 |
| All Hispanics | 1.178 | 1.242 | 1.283 | 1.315 | 1.343 |
| Whites: College+ | 1.170 | 1.235 | 1.278 | 1.312 | 1.340 |
| Whites: HS+ | 1.144 | 1.214 | 1.260 | 1.296 | 1.327 |
| Whites: <HS | 1.114 | 1.188 | 1.237 | 1.276 | 1.309 |
| Blacks: College+ | 1.142 | 1.212 | 1.258 | 1.295 | 1.326 |
| Blacks: HS+ | 1.109 | 1.184 | 1.234 | 1.275 | 1.309 |
| Blacks: <HS | 1.070 | 1.150 | 1.204 | 1.247 | 1.283 |
| Time preference = 10% | |||||
| All | 0.993 | 1.108 | 1.177 | 1.227 | 1.266 |
| All whites | 1.000 | 1.114 | 1.182 | 1.231 | 1.270 |
| All blacks | 0.953 | 1.073 | 1.146 | 1.200 | 1.243 |
| All Hispanics | 1.025 | 1.136 | 1.201 | 1.247 | 1.284 |
| Whites: College+ | 1.018 | 1.130 | 1.196 | 1.243 | 1.280 |
| Whites: HS+ | 0.993 | 1.108 | 1.177 | 1.227 | 1.266 |
| Whites: <HS | 0.966 | 1.083 | 1.154 | 1.206 | 1.248 |
| Blacks: College+ | 0.989 | 1.105 | 1.175 | 1.225 | 1.265 |
| Blacks: HS+ | 0.958 | 1.077 | 1.150 | 1.204 | 1.247 |
| Blacks: <HS | 0.924 | 1.045 | 1.120 | 1.176 | 1.221 |
- Notes: r= 3%, λ= 0.5, 1978 birth cohort, retirement age = 67 years.
To illustrate, black couples with less than a high school education, the highest mortality group, have an AEW of 1.121 when their coefficient of risk aversion equals 1 and 1.302 when their coefficient of risk aversion equals 5, compared with Brown's (2003) results of 1.296 and 1.534 for black men and 1.453 and 1.587 for black women with the same level of education. In Brown's calculations, the difference between the AEW of a white college-educated male and a black male without a high school education was only 3.7 percent at a coefficient of risk aversion of 2, the corresponding difference for females being 0.4 percent. In contrast, the difference between the AEW of a white college-educated couple and a black couple with less than a high school education is 8.1 percent at the same degree of risk aversion. When the coefficient of risk aversion is 5, the comparable numbers are 1.2, 0.1, and 5.8 percent.
Why is the difference between AEW of high and low mortality groups lower for the more risk averse? Under constant relative risk aversion, the coefficient of risk aversion doubles as the reciprocal of the intertemporal elasticity of substitution. At high levels of risk aversion, a household that does not annuitize will optimally plan to enjoy a fairly high level of consumption in advanced old age, regardless of the probability of attaining that age. Both high- and low-mortality households will therefore place an almost equally high value on the longevity insurance provided by annuities.
The lower panels of Table 2 report our results calculated using rates of time preference of 5 and 10 percent. The AEWs of all household types are substantially reduced. At a rate of time preference of 10 percent and at low levels of risk aversion, high mortality groups may no longer be better off as a result of annuitization.14 These impatient households prefer to shift consumption from later in retirement to periods early in retirement. If they do not annuitize, they can do this very easily by increasing the rate at which they decumulate their wealth. In contrast, if they annuitize all their wealth, they face a binding liquidity constraint on the age profile of their consumption.
However, there is little change in the difference between the AEWs of high and low mortality groups. For example, assuming a rate of time preference of 10 percent and a coefficient of risk aversion of 5, the difference between the AEWs of white couples with a college education and black couples with less than a high school education is 5.9 percent, compared with 5.7 percent when the rate of time preference is 5 percent, and 5.8 percent when the rate of time preference is 3 percent.
We then consider how our results might be affected by the inclusion of preannuitized wealth. Table 3 reports the mean proportion of preannuitized to total financial wealth for various classes of HRS households turning 65 during the period 1994–2000.
Dushi and Webb (2004) showed that households with large amounts of unannuitized wealth also have small proportions of preannuitized wealth, and it is therefore not surprising, given the well-documented relationship between wealth, ethnicity, and socioeconomic class, that Table 3 shows that there is also a strong relationship between ethnicity, socioeconomic status, and the proportion of preannuitized wealth. The mean proportion of preannuitized wealth among married couples with a white college-educated husband is 66.0 percent, whereas the mean proportion of preannuitized wealth among married couples with a black husband with less than a high school education is 93.5 percent.15 Among single women, the respective proportions are 59.3 and 98.0 percent.
Table 4 reports AEW for each type of married couple, taking account of preannuitized wealth and again assuming rates of time preference of 3, 5, and 10 percent. AEW is reduced for all household types. For black couples with less than a high school education, AEW is now only 1.001 when the coefficient of risk aversion equals 1 and the rate of time preference equals 3 percent. The average household in this category would derive almost no benefit from mandatory annuitization.
| CRRA = 1 | CRRA = 2 | CRRA = 3 | CRRA = 4 | CRRA = 5 | |
|---|---|---|---|---|---|
| Time preference = 3% | |||||
| All | 1.092 | 1.117 | 1.117 | 1.153 | 1.168 |
| All whites | 1.101 | 1.125 | 1.144 | 1.160 | 1.174 |
| All blacks | 1.043 | 1.102 | 1.095 | 1.114 | 1.130 |
| All Hispanics | 1.135 | 1.157 | 1.175 | 1.189 | 1.203 |
| Whites: College+ | 1.125 | 1.148 | 1.165 | 1.181 | 1.194 |
| Whites: HS+ | 1.092 | 1.117 | 1.137 | 1.153 | 1.168 |
| Whites: <HS | 1.057 | 1.084 | 1.105 | 1.123 | 1.138 |
| Blacks: College+ | 1.090 | 1.116 | 1.137 | 1.154 | 1.169 |
| Blacks: HS+ | 1.049 | 1.078 | 1.101 | 1.119 | 1.136 |
| Blacks: <HS | 1.001 | 1.033 | 1.057 | 1.077 | 1.095 |
| Time preference = 5% | |||||
| All | 0.992 | 1.037 | 1.067 | 1.090 | 1.110 |
| All whites | 1.001 | 1.045 | 1.075 | 1.098 | 1.117 |
| All blacks | 0.941 | 0.988 | 1.020 | 1.046 | 1.068 |
| All Hispanics | 1.035 | 1.078 | 1.107 | 1.129 | 1.147 |
| Whites: College+ | 1.025 | 1.069 | 1.097 | 1.120 | 1.138 |
| Whites: HS+ | 0.993 | 1.037 | 1.067 | 1.090 | 1.110 |
| Whites: <HS | 0.958 | 1.003 | 1.034 | 1.058 | 1.079 |
| Blacks: College+ | 0.987 | 1.033 | 1.064 | 1.088 | 1.108 |
| Blacks: HS+ | 0.947 | 0.994 | 1.022 | 1.052 | 1.073 |
| Blacks: <HS | 0.903 | 0.950 | 0.983 | 1.010 | 1.032 |
| Time preference = 10% | |||||
| All | 0.740 | 0.809 | 0.859 | 0.898 | 0.931 |
| All whites | 0.746 | 0.816 | 0.866 | 0.905 | 0.938 |
| All blacks | 0.705 | 0.771 | 0.819 | 0.857 | 0.890 |
| All Hispanics | 0.767 | 0.839 | 0.891 | 0.931 | 0.965 |
| Whites: College+ | 0.762 | 0.833 | 0.884 | 0.924 | 0.957 |
| Whites: HS+ | 0.741 | 0.810 | 0.859 | 0.899 | 0.932 |
| Whites: <HS | 0.719 | 0.785 | 0.833 | 0.872 | 0.904 |
| Blacks: College+ | 0.735 | 0.804 | 0.853 | 0.893 | 0.926 |
| Blacks: HS+ | 0.709 | 0.775 | 0.823 | 0.862 | 0.894 |
| Blacks: <HS | 0.682 | 0.744 | 0.791 | 0.828 | 0.861 |
Recall that when there is no preannuitized wealth, the difference between the AEWs of white college-educated couples and black couples with less than a high school education is 8.1 percent at a coefficient of risk aversion of 2 and a rate of time preference of 3 percent. When one incorporates preannuitized wealth, the difference in AEW increases to 11.5 percent. At a coefficient of risk aversion of 5, the comparable figures are 5.8 and 9.9 percent.
The increase in the between group variation in AEW is partly because high mortality groups also have high proportions of preannuitized wealth. It also reflects the fact that at higher proportions of preannuitized wealth, the longevity insurance provided by an annuity becomes less important and its money's worth more important in determining its value to the household. When there is no preannuitized wealth, the difference between high and low mortality households' AEWs decreases substantially with increases in the coefficient of risk aversion, reflecting the higher value that risk-averse households place on longevity insurance. When one incorporates preannuitized wealth, the relationship is much less pronounced, reflecting the decreasing marginal value of further longevity insurance.
Table 5 reports similar results for each type of single women and all single men: there are insufficient single men in the sample to permit an analysis by education and ethnicity.
| CRRA = 1 | CRRA = 2 | CRRA = 3 | CRRA = 4 | CRRA = 5 | |
|---|---|---|---|---|---|
| Time preference = 3% | |||||
| All men | 1.024 | 1.082 | 1.123 | 1.156 | 1.184 |
| Women | |||||
| All | 1.245 | 1.295 | 1.329 | 1.357 | 1.379 |
| All whites | 1.267 | 1.320 | 1.356 | 1.385 | 1.408 |
| All blacks | 1.148 | 1.185 | 1.211 | 1.232 | 1.250 |
| All Hispanics | 1.192 | 1.214 | 1.230 | 1.244 | 1.255 |
| Whites: College+ | 1.322 | 1.383 | 1.424 | 1.455 | 1.481 |
| Whites: HS+ | 1.270 | 1.325 | 1.364 | 1.394 | 1.419 |
| Whites: <HS | 1.183 | 1.226 | 1.257 | 1.281 | 1.301 |
| Blacks: College+ | 1.207 | 1.247 | 1.276 | 1.299 | 1.318 |
| Blacks: HS+ | 1.172 | 1.214 | 1.244 | 1.268 | 1.288 |
| Blacks: <HS | 1.069 | 1.098 | 1.119 | 1.130 | 1.151 |
| Time preference = 5% | |||||
| All men | 0.776 | 0.838 | 0.883 | 0.920 | 0.950 |
| Women | 0.911 | 0.979 | 1.027 | 1.066 | 1.099 |
| All | 1.097 | 1.169 | 1.217 | 1.254 | 1.284 |
| All whites | 1.128 | 1.204 | 1.255 | 1.293 | 1.324 |
| All blacks | 0.974 | 1.019 | 1.052 | 1.079 | 1.102 |
| All Hispanics | 1.006 | 1.039 | 1.064 | 1.084 | 1.101 |
| Whites: College+ | 1.203 | 1.289 | 1.344 | 1.385 | 1.418 |
| Whites: HS+ | 1.135 | 1.214 | 1.267 | 1.307 | 1.339 |
| Whites: <HS | 1.023 | 1.081 | 1.122 | 1.155 | 1.183 |
| Blacks: College+ | 1.033 | 1.088 | 1.127 | 1.159 | 1.186 |
| Blacks: HS+ | 1.001 | 1.055 | 1.094 | 1.126 | 1.152 |
| Blacks: <HS | 0.901 | 0.933 | 0.957 | 0.978 | 0.995 |
| Time preference = 10% | |||||
| All men | 0.692 | 0.765 | 0.820 | 0.865 | 0.903 |
| Women | |||||
| All | 0.799 | 0.884 | 0.948 | 0.999 | 1.042 |
| All whites | 0.832 | 0.929 | 1.000 | 1.056 | 1.102 |
| All blacks | 0.681 | 0.724 | 0.757 | 0.785 | 0.810 |
| All Hispanics | 0.692 | 0.725 | 0.751 | 0.772 | 0.792 |
| Whites: College+ | 0.919 | 1.043 | 1.126 | 1.189 | 1.239 |
| Whites: HS+ | 0.844 | 0.947 | 1.021 | 1.078 | 1.126 |
| Whites: <HS | 0.730 | 0.792 | 0.839 | 0.878 | 0.912 |
| Blacks: College+ | 0.726 | 0.783 | 0.826 | 0.862 | 0.894 |
| Blacks: HS+ | 0.706 | 0.759 | 0.800 | 0.835 | 0.865 |
| Blacks: <HS | 0.630 | 0.659 | 0.681 | 0.700 | 0.717 |
Single women value annuitization more highly than similarly educated married couples because annuity rates are more favorable to them and they do not benefit from longevity risk pooling. Single men obviously have somewhat less favorable annuity rates, and at plausible degrees of risk aversion the effect of their higher mortality on AEW is approximately offset by the effect of the absence of longevity risk pooling.
Calculations of the Entire Distribution of AEW
We create a subjective life table for each HRS household, using the GHM methodology discussed previously. We first check that our subjective life tables represent “reasonable” beliefs. Our average optimism index, ψ, is 0.81. We expect it to be less than one because the sample excludes individuals institutionalized at baseline, who probably had higher than average mortality. We then calculate subjective life expectancies for each group and compare them with the predictions of life tables for the appropriate class of individual.
Table 6 reports our results. For whites, life expectancy varies appropriately with gender and education. Consistent with our estimate of ψ, subjective life expectancy is somewhat higher than the predictions of life tables. The education-related difference in subjective life expectancies is also slightly less than those shown by the life tables. A possible explanation for this is Perry's (2005) finding that the less well educated, who may also fail to understand the questions, are more likely to answer that they have a hundred percent chance of living to the target age.
| Life Table | Self-Assessed | |
|---|---|---|
| Men | ||
| All | 15.55 | 16.51 |
| All whites | 15.72 | 16.46 |
| All blacks | 13.35 | 17.26 |
| All Hispanics | 17.30 | 15.65 |
| Whites: College+ | 16.83 | 16.88 |
| Whites: HS+ | 15.63 | 16.48 |
| Whites: <HS | 14.39 | 15.95 |
| Blacks: College+ | 14.90 | 16.88 |
| Blacks: HS+ | 13.37 | 17.57 |
| Blacks: <HS | 12.97 | 17.00 |
| Women | ||
| All | 18.83 | 19.54 |
| All whites | 18.93 | 19.55 |
| All blacks | 17.28 | 20.07 |
| All Hispanics | 20.06 | 18.45 |
| Whites: College+ | 19.77 | 20.29 |
| Whites: HS+ | 18.93 | 19.65 |
| Whites: <HS | 18.00 | 18.59 |
| Blacks: College+ | 18.47 | 19.38 |
| Blacks: HS+ | 17.50 | 20.36 |
| Blacks: <HS | 16.42 | 19.93 |
- Notes: Sample size: 1,543 married couples with husband aged 63–65 at the date of any of the HRS Wave 1 to 5 interviews.
We find that, in contrast to whites who are more optimistic than the predictions of life tables, Hispanics are somewhat less optimistic. Turra and Goldman (2006) found that life table data may overstate Hispanic life expectancy, and Hispanics' subjective estimates of their life expectancy may therefore be closer the truth than calculations based on the NLMS. On the other hand, blacks are much more optimistic than the predictions of life tables, reflecting the optimism of their raw subjective survival probabilities, referred to previously.16 We considered estimating the model separately for blacks and nonblacks. We chose not to do this because, as mentioned previously, we have no evidence that differences in comprehension or interpretation of the question contributed significantly to the differences in responses. In the absence of evidence to the contrary, we take the responses at face value and conclude that black individuals really do believe they have greater longevity at older ages than nonblacks.
Figures 1 and 2 show the distribution of estimates of life expectancy at age 65 for all men and women, and for the three educational groups of white men and women. Life expectancy varies from 9 years 10 months for white men with less than a high school education to 25 years 3 months for white women with a college education. There is much greater education-related variation at the bottom of the distribution than at the top, suggesting that the educated are uniformly healthy, whereas there is a larger distribution of remaining life expectancy among the less well educated.
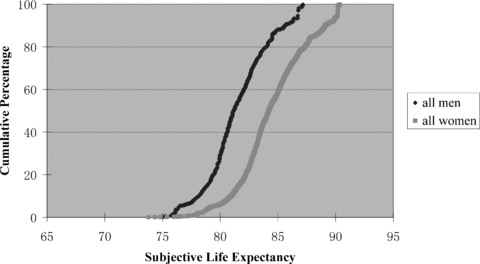
Distribution of Subjective Estimates of Life Expectancy at Age 65

Distribution of Subjective Estimates of Life Expectancy at Age 65—White Men and Women
Overall, 47.7 percent of households fall into the most risk-averse category. There was little variation in risk aversion with education or ethnicity, although it is possible that we are failing to identify socioeconomic differences in the proportions of households that are highly risk averse, given the high percentage of households falling into the most risk-averse category.
We calculate household level AEW at age 65 to correspond with the age at which Dushi and Webb (2004) calculated proportions of preannuitized wealth. Figure 3 shows the cumulative distribution of AEW for all married couples and Figure 4 shows the distributions for blacks, whites, and Hispanics. Among married couples, 16.5 percent have an AEW of less than 1 and would perceive themselves as being worse off under mandatory annuitization, given our assumptions about household preferences. The median AEW is 1.122, and the median coefficient of risk aversion is 4.17

Annuity Equivalent Wealth—All Couples

Annuity Equivalent Wealth—Black, White, and Hispanic Couples
The percentages reporting AEW of less than 1 vary little between black and white households, reflecting the relative optimism of black households about their life expectancy. Figure 5 shows that among white households, the percentages with AEW of less than 1 vary from 36.5 among those where both spouses have less than a high school education to 13.8 among those with high school or some college, and only 1.5 percent for those with 4 years of college education. The sample size is insufficient to permit a similar analysis of black and Hispanic households.

Annuity Equivalent Wealth—White Couples by Education
Conclusions
Previous research has shown that traditionally disadvantaged groups receive a lower “money's worth” from mandatory annuitization on uniform terms than more privileged groups. This same research has shown that, in expected utility terms, the average single individual with no preannuitized wealth in each of the educational and racial groups studied would reap substantial benefits relative to a counterfactual of no annuitization. The research also showed that there is almost no between-group difference in the magnitude of that benefit.
We show that if one takes account of preannuitized wealth and longevity risk pooling within marriage and retains the 3 percent rate of time preference used in previous research, the average household in each group now obtains only a small benefit from mandatory annuitization. However, in contrast to previous research, we find substantial between-group variation in AEW, a commonly used measure of the value of annuitization. This finding has important implications when considering whether households should be required to annuitize the balances accumulated in the Social Security individual accounts proposed by the President's Commission (2001).
Even within groups, there will be substantial heterogeneity not only in mortality beliefs but also in willingness to accept risk and proportions of preannuitized wealth, characteristics that economic theory indicates also affect the value households place on annuitization. Our analyses show that significant minorities of some groups may correctly perceive themselves as being net losers under mandatory annuitization even when the average household in the group perceives itself as being a net gainer. We follow the literature by assuming full annuitization of all unannuitized wealth but recognize that the value of partial annuitization will be somewhat greater, particularly if the proportion of household wealth held in preannuitized form declines in coming decades.
The low level of voluntary annuitization has long puzzled economists. The policy implications of our findings depend in part on whether we believe that the utility function in Equation (1) and our assumed coefficient of risk aversion and rate of time preference correctly describe household preferences. We note that the low level of voluntary annuitization is not inconsistent with our assumed preference parameters in that very few households have AEW in excess of the 125 percent that would be required to justify annuitization at a plausible 20 percent level of actuarial unfairness.18
If our assumed preference parameters are correct, then policymakers would need to weigh gains to the majority against losses to substantial proportions of traditionally disadvantaged groups. If they are not, then the policy implications would depend on the nature of the misspecification, the case for mandatory annuitization being particularly weak if households are choosing not to annuitize as a result of a strong bequest motive.




