Market Risk, Interest Rate Risk, and Interdependencies in Insurer Stock Returns: A System-GARCH Model
The authors can be contacted via e-mail: [email protected], [email protected], and [email protected], respectively. The authors thank participants of the 2006 ARIA meeting where the article was presented, two anonymous referees, and the editor for constructive comments and suggestions. Any remaining errors are ours.
Abstract
We examine market risk, interest rate risk, and interdependencies in returns and return volatilities across three insurer segments within a System-GARCH framework. Three main results are obtained: market risk is greatest for accident and health (A&H) insurers, followed by life (Life) and property and casualty (P&C) insurers; interest rate sensitivity is negative and greatest for Life insurers; and interdependencies in returns are significant with the magnitude being strongest between P&C and A&H insurers. The implication is that greatest diversification benefits arise between Life and the other segments of the insurance industry. Market risk and interest rate risk for diversified firms are smaller than those for nondiversified firms for both product and geographic diversification.
Introduction
The literature on the stock return behavior of banks and insurers demonstrates that these institutions are exposed to time-varying market and interest rate risks (Brewer et al., 2007). In examining risk–return relationships for insurers, Staking and Babbel (1995) identify a trade-off between the increasing probability of financial distress and the tax benefits due to leverage, and another trade-off between protecting franchise value and the expropriation of value through increases in exposure to interest rate risk. Through these trade-offs, the authors show why “insurers manage both capital structure (leverage) and interest rate risk (surplus duration) as part of their effort to maximize value” (p. 711).
In addition to research that has examined market and interest rate risks, interdependencies (spillover effects) of stock returns within the banking sector or across the banking and insurance sectors have received considerable attention (e.g., Elyasiani et al., 2007). However, the literature does not provide a direct comparison of interest rate risk between property and casualty (P&C), accident and health (A&H), and life (Life) insurers within the same analytical framework, and fails to examine the direction and the magnitude of the spillover effects across these three insurance sectors. This study provides the first examination of market risks, interest rate sensitivities, and interdependencies in stock returns across the P&C, A&H, and Life segments of the insurance industry for a common time period, in the aggregate as well as disaggregated small and large size, and diversified and nondiversified insurers.
Intraindustry spillovers or interdependencies constitute an important question for regulators, insurer managers, and investors. Just as bank regulators are concerned with bank runs and possible contagion effects, insurance regulators are interested in intersectoral interdependencies because shocks to one sector may be transmitted to other sectors, resulting in the collapse of the entire industry.1 Insurer decisions concerning the optimal avenue for product diversification through acquisition are also dependent on the extent of interdependence among different sectors of the industry; the more strongly these sectors move together, the smaller the diversification gains will be. This issue has implications on insurer decisions for entering single versus multiple lines of insurance activity and mergers and acquisitions across these lines. Similarly, from the viewpoint of investors in insurer stocks, high interdependence among different segments of the industry will translate into small gains in terms of risk diversification.
As De Nicola and Kwast (2002) have discussed, interdependencies may be direct or indirect. Direct interdependencies may arise, e.g., through counterparty credit exposures on derivative instruments such as futures, options, and swaps. Indirect interdependencies arise from exposures to the same or similar assets, and from other sources such as underwriting similar types of events. Common positions in these instruments can tie different segments of the insurance industry to a common fate.2, 3
If stock return variations are relatively independent across the P&C, A&H, and Life insurers, shocks affecting one segment will have little impact on the return distributions of the firms in the other segments. However, stock returns and risks in different insurer segments are linked through several channels. First, some insurers offer products in multiple segments and often reallocate resources among these segments, engendering comovements as a result. Some insurers in one segment of the industry may also make investments in affiliates in the other segments. If the size of such investment is large, comovement will be expected.4
Second, regulatory decisions for different segments of the insurance industry are made with similar objectives in terms of safety and consumer service and tend to affect these segments similarly. Third, industry segments operate within the same economic and financial environments and, consequently, would be expected to move in the same direction. Fourth, insurer assets primarily comprise bonds, regardless of the type of insurer (P&C, A&H, or Life), and movements in different bond categories are typically well correlated. Finally, the advent of risk-based capital requirements has led to the employment of similar risk assessment and risk management models on the part of a growing number of insurance providers in managing capital, often subjecting these insurers to similar destinies.
We introduce a System-GARCH model of stock return movements to simultaneously estimate and contrast the systematic market risk and interest rate sensitivity of P&C, A&H, and Life insurance companies and to examine the return and risk spillover among these segments of this industry. We make four primary contributions. First, we provide the first examination of market risks, interest rate sensitivities, and interdependencies in stock returns across three segments of the insurance industry for a common time period and within a common theoretical framework. Our empirical results show that market and interest rate risk measures (betas) differ significantly across the three segments. Market risk is greatest for A&H, followed by Life and then P&C insurers, whereas interest rate sensitivity is greater for Life insurers than for A&H and P&C insurers.5 When the sample is disaggregated by size, we find that interest rate sensitivity is negative and highly significant for large Life and P&C insurers but insignificant for the smaller firms. Between diversified and nondiversified insurers, market and interest rate risks are smaller for the diversified firms for both geographic and product-wise diversification.
Second, we find that the impact of changes in the stock returns in one insurance segment on another is always positive, indicating a direct comovement of returns across different insurance activities. Third, unlike findings for banks, volatilities of returns across the three insurance segments are not found to be highly interdependent (weak linkages do exist), suggesting less risk of volatility transmission from one category of insurers to the other categories. This feature highlights the presence of stronger return-related codependence and weaker risk codependence of different segments of the insurance industry. When the sample is disaggregated by size or degree of diversification, the disaggregate results show strong volatility interdependence within each segment. Finally, results show that stock return volatility increased significantly for A&H and P&C (but not for Life) insurers following the Gramm–Leach–Bliley Act (GLBA) of 1999. The next section describes the methodology, hypotheses, sample, and data. The third section discusses the empirical results, and the final section summarizes and concludes.
Methodology, Hypotheses, Sample, and Data
Methodology
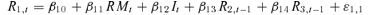 (1)
(1)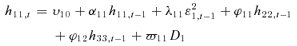 (2)
(2)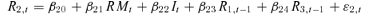 (3)
(3)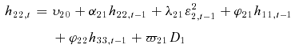 (4)
(4)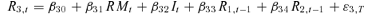 (5)
(5)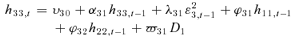 (6)
(6)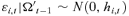 (7)
(7)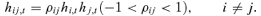 (8)
(8)The multivariate GARCH specification offers several advantages. First, it accounts for intraindustry transmission of stock returns and stock return volatilities.7 Second, this specification allows the asymmetry of the spillover effects across insurer categories to be investigated and tests of linear relationships among the parameters within and across the model equations to be carried out.8 Finally, the joint estimation of a multivariate system has an advantage, over the univariate GARCH, as it permits the errors in the mean equations to interact, and allows a more efficient set of estimates to be obtained. The Berndt et al. (1974) (BHHH) algorithm, a nonlinear maximum likelihood technique, is used to carry out the estimation.9
Hypotheses
Several sets of hypotheses, formulated and described in more detail in the “Empirical Results” section, are tested within the model developed above. These include the following hypotheses:
- •
H1i: equality of systematic risk across insurer segments
- •
H2i: significance of interest rate sensitivity of insurers
- •
H3i: equality of interest rate sensitivity across insurer segments
- •
H4i: prevalence of return spillover across insurer segments
- •
H5i: symmetry of return spillover effects across insurer segments
- •
H6i: prevalence of volatility spillover across insurer segments
- •
H7i: symmetry of volatility spillover across insurer segments
- •
H8i: significance of the effects of GLBA (1999) on insurer volatility.
Sample and Data
Based on the SIC values, firms are classified as Life, A&H, or P&C insurers, and are used to form three equally weighted portfolios. The sample for each trading day includes only those firms whose stocks were actively traded on that particular day. Due to factors such as mergers and acquisitions, spin-offs, and IPOs, the sample membership (size) for each portfolio varies over time. The sample size for the portfolios is between 17 and 37 for Life, 5 and 11 for A&H, and 21 and 46 for P&C portfolios.10 This procedure limits survivorship bias by allowing the use of all available data in each period and, thus, maximizes the sample size for each portfolio.
Daily data are obtained from the Center for Research in Security Prices (CRSP). All insurers traded on the NYSE, ASE, and NASDAQ are included for the sample period from January 2, 1991, to December 31, 2001. The choice of the sample period avoids the tumultuous conditions of the insurance industry in the post-911 era and keeps the period short enough to limit the effects of technological and regulatory changes.11 The S&P 500 index, also obtained from CRSP, is utilized as the market index. Finally, the 10-year Treasury constant maturity bond yield is used as the long-term interest rate and is obtained from the Federal Reserve Bank of St Louis website. Summary statistics for the data appear in Table 1. Results of stationarity tests (available on request) indicate that all return series are stationary as they follow an integrated order zero, I(0), process. The interest rate series follows an integrated of order 1, I(1), but the first difference of interest rate series reverts to an I(0) process.12 The explanatory variables in the return equations are also checked for multicollinearity using the conditional index measures.13
| Panel A: All Institutions | Panel B: Life Insurance | Panel C: Property and Casualty | Panel D: Geographic Diversification | Panel E: Product Diversification | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Life | A&H | P&C | Large | Small | Large | Small | Yes | No | Yes | No | |
| No. of observations | 2,869 | 2,869 | 2,869 | 2,869 | 2,869 | 2,869 | 2,869 | 2,869 | 2869 | 2,869 | 2,869 |
| Mean | 0.0012 | 0.0004 | 0.0006 | 0.0005 | 0.0013 | 0.0007 | 0.0005 | 0.0008 | 0.0009 | 0.0009 | 0.0007 |
| SD | 0.0097 | 0.0120 | 0.0081 | 0.0073 | 0.0115 | 0.0116 | 0.0082 | 0.0103 | 0.0112 | 0.0102 | 0.0114 |
| Minimum | −0.0513 | −0.0878 | −0.0698 | −0.0595 | −0.0543 | −0.0763 | −0.0750 | −0.0944 | −0.0687 | −0.0828 | −0.0665 |
| Maximum | 0.0619 | 0.0631 | 0.0523 | 0.0528 | 0.0716 | 0.0907 | 0.0516 | 0.0846 | 0.0994 | 0.0919 | 0.0873 |
| Skewness | 0.227*** | −0.116** | 0.049 | 0.284*** | 0.444*** | 0.406*** | −0.120*** | 0.048 | 0.258*** | 0.013 | 0.386*** |
| Kurtosis | 2.389*** | 5.174*** | 4.856*** | 7.042*** | 2.575*** | 4.947*** | 5.062*** | 7.487*** | 6.267*** | 7.037*** | 4.577*** |
| J-B (MSL) | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Q(5) | 6.767** | 6.248** | 26.210*** | 5.833* | 7.270** | 13.003*** | 25.800*** | 17.674*** | 9.219*** | 21.004*** | 10.226*** |
| Q(10) | 9.248 | 8.417 | 31.351*** | 10.663 | 9.537 | 16.578** | 34.022*** | 26.180*** | 13.591** | 26.602*** | 13.596** |
| Q(20) | 28.913** | 17.441 | 39.420*** | 19.743 | 33.520*** | 25.805* | 51.413*** | 32.513*** | 27.446** | 38.709*** | 24.370 |
| Q2(5) | 18.522*** | 24.535*** | 24.890*** | 40.008*** | 9.797*** | 27.615*** | 36.458*** | 73.793*** | 14.112*** | 40.268*** | 27.022*** |
| Q2(10) | 26.677*** | 28.625*** | 31.320*** | 73.415*** | 15.040** | 46.417*** | 50.831*** | 83.434*** | 69.097*** | 56.174*** | 55.124*** |
| Q2(20) | 43.463*** | 34.670*** | 57.569*** | 92.011*** | 35.849*** | 134.444*** | 69.282*** | 129.388*** | 140.675*** | 89.276*** | 139.154*** |
- Notes: Summary statistics for life, accident and health, and property and casualty insurance portfolios are provided below. J-B is the Jarque–Bera joint normality test statistic. MSL refers to the marginal significance level. Q(n) and Q2(n) are the Ljung–Box test for the 5th-, 10th-, and 20th-order serial correlation in return and squared return series.
- ***, **, and * represent significance at the 1%, 5%, and 10% levels, respectively.
Empirical Results
The coefficient estimates based on the System-GARCH model and the related t-statistics are displayed in Table 2. The hypothesis test results are presented in Tables 3 through Table 5. We will discuss the results in terms of the hypotheses stated earlier.
| Coefficients | Variables | Life Insurance (i= 1) | Accident and Health (i= 2) | Property and Casualty (i= 3) |
|---|---|---|---|---|
| βi0× (10−3) | Intercept | 1.324 | 0.023 | 0.035 |
| (5.591)*** | (0.078) | (0.258) | ||
| βi1 | Market beta | 0.714 | 0.866 | 0.508 |
| (28.688)*** | (29.549)*** | (33.733)*** | ||
| βi2 | Interest rate beta | −0.879 | −0.132 | −0.198 |
| (−37.867)*** | (−3.134)*** | (−10.882)*** | ||
| βi3 | Return spillover | 0.004 | 0.025 | 0.071 |
| (0.183) | (0.691)*** | (4.692)*** | ||
| βi4 | Return spillover | 0.050 | 0.120 | 0.046 |
| (1.515) | (2.868)*** | (3.690)*** | ||
| νi0× (10−3) | Volatility intercept | 0.048 | 0.123 | 0.030 |
| (3.891)*** | (4.896)*** | (6.316)*** | ||
| αi1 | GARCH | 0.617 | 0.123 | 0.140 |
| (7.816)*** | (1.688)* | (1.865)* | ||
| λi1 | ARCH | 0.114 | 0.178 | 0.171 |
| (5.171)*** | (6.538)*** | (6.300)*** | ||
| ϕi1 | Volatility spillover | −0.061 | −0.029 | 0.007 |
| (−4.317)*** | (−0.252) | (0.316) | ||
| ϕi2 | Volatility spillover | 0.101 | 0.041 | −0.019 |
| (0.548) | (0.123) | (−1.053) | ||
| ϖi1× (10−3) | GLBA binary | 0.026 | 0.105 | 0.069 |
| (1.548) | (2.779)*** | (6.915)*** |
- Notes: The model described in the “Methodology” section is the basis for the results presented here. Asymptotic t-values are in parentheses. i= 1, 2, and 3 represent Life, A&H, and P&C insurer portfolios, respectively. The log likelihood value is 35,844.54. Error diagnostic results are available upon request.
- *** and * represent significance at the 1% and 10% levels, respectively.
| Hypothesis Description | D.F. | χ2 Values |
|---|---|---|
| H1i: Hypothesis concerning the equality of systematic risk across segments | ||
| Joint test of the equality of systematic risk across groups: H11: β11=β21; β11=β31; β21=β31 | 2 | 143.49*** |
| Equality of systematic risk between Life and A&H: H12: β11=β21 | 1 | 16.73*** |
| Equality of systematic risk between Life and P&C: H13: β11=β31 | 1 | 51.52*** |
| Equality of systematic risk between A&H and P&C: H14: β21=β31 | 1 | 124.06*** |
| H2i: Hypothesis concerning interest rate sensitivity | ||
| No interest rate sensitivity for any insurer category: H21: β12=β22=β32= 0 | 3 | 1,494.89*** |
| No interest rate sensitivity for Life and A&H: H22: β12=β22= 0 | 2 | 1,450.02*** |
| No interest rate sensitivity for Life and P&C: H23: β12=β32= 0 | 2 | 1,475.53*** |
| No interest rate sensitivity for A&H and P&C: H24: β22=β32= 0 | 2 | 123.59*** |
| No interest rate sensitivity for Life: H25: β12= 0 | 1 | 1,433.91*** |
| No interest rate sensitivity for A&H: H26: β22= 0 | 1 | 9.82*** |
| No interest rate sensitivity for P&C: H27: β32= 0 | 1 | 118.41*** |
| H3i: Hypothesis concerning the equality of interest rate sensitivity across segments | ||
| Joint test of equality of IR sensitivity across segments: H31: β12=β22; β12=β32; β22=β32 | 2 | 702.95*** |
| Equality of IR sensitivity between Life and A&H: H32: β12=β22 | 1 | 287.95*** |
| Equality of IR sensitivity between Life and P&C: H33: β12=β32 | 1 | 601.73*** |
| Equality of IR sensitivity between A&H and P&C: H33: β12=β32 | 1 | 2.23 |
- *** represents significance at the 1% level.
| Hypothesis Description | D.F. | χ2 Values |
|---|---|---|
| H4 i: Hypothesis concerning the prevalence of return spillover across segments | ||
| No return spillover: H41: β13=β14=β23=β24=β33=β34= 0 | 6 | 95.54*** |
| No spillover between Life and A&H: H42: β13=β14=β23=β24= 0 | 4 | 19.03*** |
| No spillover between Life and P&C: H43: β13=β14=β33=β34= 0 | 4 | 73.33*** |
| No spillover between A&H and P&C: H44: β23=β24=β33=β34= 0 | 4 | 90.65*** |
| No spillover from A&H and P&C to Life: H45: β13=β14= 0 | 2 | 2.88 |
| No spillover from Life and P&C to A&H: H46: β23=β24= 0 | 2 | 16.67*** |
| No spillover from Life and A&H to P&C: H47: β33=β34= 0 | 2 | 67.63*** |
| No spillover from Life (to P&C and A&H): H48: β23=β33= 0 (Life not a leader) | 2 | 56.49*** |
| No spillover from A&H (to P&C and Life): H49: β13=β34= 0 (ACH not a leader) | 2 | 13.63*** |
| No spillover from P&C (to Life and A&H): H410: β14=β24= 0 (P&C not a leader) | 2 | 9.65*** |
| H5i: Hypothesis concerning symmetry of return-spillover effects across segments | ||
| Symmetric return spillover between Life and A&H: H51: β13=β23 | 1 | 0.22 |
| Symmetric return spillover between Life and P&C: H52: β14=β33 | 1 | 0.32 |
| Symmetric return spillover between A&H and P&C: H53: β24=β34 | 1 | 2.71* |
- *** and * represent significance at the 1% and 10% levels, respectively.
| Hypothesis Description | D.F. | χ2 Values |
|---|---|---|
| H6i: Hypothesis concerning the prevalence of volatility spillover across segments | ||
| No volatility spillover: H61: ϕ11=ϕ12=ϕ21=ϕ22=ϕ31=ϕ32= 0 | 6 | 36.75*** |
| No volatility spillover between Life and A&H: H62: ϕ11=ϕ21= 0 | 2 | 19.37*** |
| No volatility spillover between Life and P&C: H63: ϕ12=ϕ31= 0 | 2 | 0.38 |
| No volatility spillover between A&H and P&C: H64: ϕ22=ϕ32= 0 | 2 | 1.12 |
| H7i: Hypothesis concerning symmetry of volatility-spillover effects across segments | ||
| Volatility spillover is symmetric between Life and A&H: H71: ϕ11=ϕ21 | 1 | 0.07 |
| Volatility spillover is symmetric between Life and P&C: H72: ϕ12=ϕ31 | 1 | 0.25 |
| Volatility spillover is symmetric between A&H and P&C: H73: ϕ22=ϕ32 | 1 | 0.03 |
| H8i: Hypothesis concerning the effect of GLBA on volatility | ||
| GLBA had no effects on volatilities: H81: ϖ11=ϖ21=ϖ31= 0 | 3 | 70.39*** |
| GLBA had no effects on volatility of Life: H82: ϖ11= 0 | 1 | 2.39 |
| GLBA had no effects on volatility of A&H: H83: ϖ21= 0 | 1 | 7.72*** |
| GLBA had no effects on volatility of P&C: H84: ϖ31= 0 | 1 | 47.82*** |
- *** represents significance at the 1% level.
Systematic Risk (Market Betas) and Interest Rate Sensitivity
As shown in Table 2, systematic risk in all three portfolios (β11, β21, and β31) is positive and highly significant. In terms of magnitude, the market betas are all below unity with A&H insurers having a higher market beta (0.866) than the Life (0.714) and the P&C (0.508) insurers. Using these betas as measures of systematic risk, the insurers in the sample, considered collectively, are less risky than the average market portfolio. Tests of equality of systematic risk across the three portfolios of insurers, as well as tests of pair-wise equality of systematic risk between each pair of insurance segments, are also carried out. Based on the test statistics reported in Table 3, the null hypothesis of equal systematic risk (H1i) is rejected in all cases, providing empirical evidence that market beta does vary across the three insurance segments examined. By comparison, Hoyt and Trieschmann (1991) have reported market betas of 0.52 for Life–Health insurers and 0.95 for P&C insurers for the 1973 to 1987 period. Thus, as measured by beta, the relative risk of Life insurers has increased and the relative risk of P&C insurers has decreased since the earlier time period.
The interest rate sensitivities of the three portfolios (β12, β22, and β32) are found to be negative, as expected, and significant in all cases (Table 2). Simple and composite tests of insignificance of the interest rate sensitivities (H2i) are all rejected, confirming the prevalence of insurer exposure to interest rate risk. Based on the discussion of leverage in Staking and Babbel (1995), we would expect Life insurers, which have greater leverage than P&C and A&H insurers, to exhibit greater interest rate sensitivity. Our results support such a theoretical expectation, with Life insurers showing a stronger sensitivity (−0.879) to interest rates than the P&C (−0.198) and the A&H insurers (−0.132). This finding is also consistent with empirical solvency analyses in Browne et al. (1995 and 1999, respectively) for P&C and Life insurers.
Tests are also carried out to determine whether the differences in the magnitudes of the interest rate coefficients across insurance segments do indeed reflect statistically significant differences between them (H3i). Tests of equality of interest rate betas across all insurers and on a pair-wise basis are all rejected at the 1 percent level, except the pair-wise test between A&H and P&C. This further supports the statistical dissimilarity of interest rate risk exposure between Life insurers and the other two segments. Differences in interest rate sensitivity across segments of the insurance industry are likely to stem not only from dissimilarity in asset composition but also from the greater leverage of Life insurers and possibly the differential use of hedging products such as interest rate derivatives. In addition, our analysis supports the economic, as well as the statistical, significance of the market, interest rate changes, and the spillover effects.14
Return Spillover
An interesting result is the evidence in favor of the prevalence of stock return comovement (transmission) among the insurers in the Life, A&H, and P&C segments of the industry. The coefficients for the spillover of returns from other lines of activity are always positive, indicating a direct comovement of returns across different activities. It is notable, however, that although the effect of Life insurers on the other two categories is strongly significant, the latter do not exert a statistically significant effect on Life insurance companies. In pair-wise tests, A&H and P&C insurers are also found not to exert a significant impact on one another. Formal statistical tests of prevalence of return spillover (H4i) in Table 4 confirm these basic estimation results on the asymmetry of the spillover effects. The joint test of the null hypothesis of no spillover of returns from A&H and P&C to Life cannot be rejected. In contrast, however, all tests of the hypotheses postulating no spillover from Life to the A&H and P&C insurers are strongly rejected. This finding establishes a leadership position for the Life insurers versus a follower position for the latter two segments of the industry. The prevalence of intersegment mean spillover found here is consistent with but weaker than those found among banks, brokerages, and life insurers (Elyasiani et al., 2007).
In terms of magnitudes of the effects, the coefficient estimates of return spillover, reported in Table 2, indicate that P&C insurers have a larger effect on A&H insurers (0.120) than Life insurers do (0.025), whereas Life insurers have a bigger effect on P&C insurers (0.071) than A&H insurers do (0.046). A pair-wise comparison between P&C and A&H insurers shows a bigger effect running from P&C to A&H (0.120) than the effect in the reverse direction (0.046), providing P&C insurers a more dominant position between the two. Asymmetry of the spillover effects is also confirmed by the statistical tests in Table 4, but only partially. The hypotheses of symmetry in spillover of returns (H5i) cannot be rejected between Life insurers and the other two categories whereas symmetry in spillover of returns is rejected between A&H and P&C. In sum, it is notable that return interdependencies are found when interest rate and market factors are already accounted for. Hence, the findings of interdependencies are not due to joint exposure of the firms to the interest rate and market factors.
Volatility Spillover
The coefficient estimates for the parameters of volatility equations, presented in Table 2, demonstrate that a GARCH specification is indeed the appropriate model for describing the stock return behavior of the insurers. All ARCH and GARCH parameters for the three portfolios have the theoretically expected positive signs, are statistically significant, and satisfy the stability condition of adding up to less than the unit value. The persistence of volatility, captured by the sum of ARCH and GARCH parameters, is the highest for Life (0.73) compared to A&H and P&C that are around 0.30. The longer term asset–liability structure and the relatively higher level of return volatility for Life insurers contribute to this elevated level of volatility persistence. Confirmation of the GARCH functional form indicates greater reliability of the results reached here relative to those from the traditional constant variance asset pricing models.
Volatility spillover prevails in the industry but is limited in scope. Coefficient estimates in Table 2 for volatility spillover across lines of insurance activity are found to be significant only from A&H to Life. Based on this result, volatility spillover prevails only between A&H and Life insurers, and it is unidirectional. No volatility spillover is found between Life and P&C, or between A&H and P&C (H6i). Life insurers may be holding shares of the A&H companies, and this channel may have contributed to the volatility transmission between these institutions. The direction of the effect from A&H to life insurers is negative, indicating that increased uncertainty in the A&H market leads to a decline in volatility in the Life insurer returns. This may be an indication that disquiet in A&H markets drives the A&H customers to seek the same products from Life insurers when offered, enhancing the latter's risk profile as a result.
The lack of spillover of volatility between Life and P&C and between P&C and A&H is an indication of nonsubstitutability of the products and services that these institutions provide, or it may be due to the aggregate nature of the data that pools firms of all sizes and levels of geographic and product diversification, masking the true relationships. By virtue of their businesses, the P&C policies are short term in nature whereas the Life policies are long term. In addition, P&C insurers insure events that are varied in scope and more difficult to predict than mortality risks. The potential losses arising from P&C events are also difficult to predict compared to the losses in life insurance. These characteristics lead P&C insurers to hold more liquid assets than their Life counterparts. The divergence in the underlying risk characteristics of these assets impedes significant volatility comovement between these firms. Spillover within insurance segments disaggregated by size or level of diversification will be examined below.
We also test whether the spillover in volatility across lines of activity is symmetric in nature. Formal test results of the symmetry hypotheses are reported in Table 5 (H7i). The null of symmetry in volatility transmission between different segments of the insurance industry cannot be statistically rejected. In other words, although the t-tests of coefficient significance in Table 2 indicate that volatility of the A&H stock returns affects Life insurers, while the reverse fails to be true, symmetry tests lack the power to confirm these findings. Thus, volatility transmission across Life, A&H, and P&C can be said to be statistically similar (symmetric). Overall, these results show a weak risk linkage across insurers and point to sources of risk that are more idiosyncratic in nature. Volatility spillovers across banking, brokerage, and life insurance industries, reported in the literature, are similar to the findings here, but those found among the largest firms in these industries are much stronger and more stringent (Elyasiani et al., 2007).
The Effect of GLBA
The passage of GLBA (1999) had the potential to alter the return and/or volatility of insurer stock returns because it allowed banks, investment banks, and insurers to combine into a single entity in the form of a financial services holding company (FSHC). Theoretically, GLBA had the potential to decrease or increase riskiness of those insurers not forming FSHCs. This is because in the post-GLBA period these insurers face a new source of competition from some giant rivals such as Citigroup, but they may also be left alone to enjoy their particular niche of activity. Insurers forming FSHCs with other financial institutions may become safer due to diversification, but this may embolden them to seek riskier projects, especially in the areas in which they lack extensive knowledge and expertise.
We test the effect of GLBA on risk by including a binary variable in the volatility equation. This variable takes the unit value after the passage of the GLBA and zero otherwise.15 As shown in Table 5, the GLBA binary variable for the effect on volatility is found to be positive and significant for A&H and P&C insurers, and insignificant for Life insurers (H8i). This indicates that stock return volatility increased significantly for A&H and P&C insurers following the GLBA (1999), at least partially, due to the higher level of competition from FSHCs.
Size-Based and Diversification-Based Disaggregation
Large and small insurers may not respond to shocks similarly for many reasons including differences in access to financial markets, leverage, capital cushions, and differential affiliation structures that can serve as a source of strength. Similarly, insurers having greater geographic diversification and/or product diversification may not behave in the same manner because of their differential scope of activity and access to differential resources and product markets.16
To examine the size effect, we divide the sample into large and small entities based on market capitalization and investigate the behavioral dissimilarities between large and small firms within the same segments of the industry. Along the same lines, we divide the sample in terms of the extent of geographic and product diversification and examine the sensitivities of these subsamples as well as their interdependencies. Insurers with over 30 percent of their revenue coming from outside their main activity are classified as product-wise diversified, whereas those with over 20 percent of their revenues coming from outside the United States are classified as geographically diversified.
Summary statistics for the disaggregated subsamples are reported in Table 1. According to the figures in this table, there is no clear superiority for large Life and P&C insurers relative to their smaller counterparts in the same segment of the industry, in terms of mean return, standard deviation of returns, and range of fluctuations. Geographically diversified insurers are found to have a smaller mean and a smaller standard deviation of returns, indicating that geographic diversification may be a vehicle for achieving a trade-off between risk and return. Product diversification, however, is found to lead to both a higher return and a lower risk, making it a superior avenue to geographic diversification, for improving performance. It is noteworthy, however, that the differences between the two subsamples are small in magnitude in all cases.
The estimation results are provided in Table 6. Panels A and B of this table display the disaggregated sized-based results for Life and P&C insurers, respectively.17 Panels C and D show the results based on diversified versus nondiversified firms for geographic and product diversification. The main findings based on the aggregate sample, reported in Table 2 and discussed earlier, are found to be robust to portfolio disaggregation and to remain valid for the subsamples considered. Market beta values (βi1) are found to be lower for smaller sized P&C firms, compared to their larger counterparts, but rather identical between small and large Life companies. Interest rate sensitivity is negative and highly significant for large Life and P&C insurers but insignificant for the smaller firms (possibly reflecting greater leverage among larger insurers). It also appears that the significance of the interest rate risk exposure found in the aggregate sample is driven by that of the large firms.
| Coefficients | Variables | Panel A: Life Insurance | Panel B: Property and Casualty | Panel C: Geographic Diversification | Panel D: Product Diversification | ||||
|---|---|---|---|---|---|---|---|---|---|
| Large (i= 1) | Small (i= 2) | Large (i= 1) | Small (i= 2) | Yes (i= 1) | No (i= 2) | Yes (i= 1) | No (i= 2) | ||
| βi 0 | Intercept | 0.029 | 0.097 | 0.033 | 0.039 | 0.052 | 0.059 | 0.064 | 0.032 |
| (3.223)*** | (5.719)*** | (2.319)** | (3.667)*** | (4.107)*** | (4.671)*** | (5.226)*** | (2.402)** | ||
| βi1 | Market beta | 0.370 | 0.384 | 0.657 | 0.408 | 0.598 | 0.651 | 0.607 | 0.695 |
| (37.198)*** | (26.519)*** | (45.861)*** | (35.660)*** | (49.066)*** | (48.184)*** | (47.722)*** | (50.720)*** | ||
| βi2 | Interest beta | −0.587 | 0.047 | −0.633 | −0.107 | −0.569 | −0.708 | −0.436 | −0.597 |
| (−3.535)*** | (0.167) | (−2.279)** | (−0.534) | (−2.563)** | (−3.000)** | (−2.051)** | (−2.336)** | ||
| βi3 | Return spillover | 0.010 | 0.058 | 0.071 | 0.080 | 0.035 | 0.053 | 0.074 | 0.051 |
| (1.443) | (2.574)** | (3.454)*** | (7.461)*** | (2.820)*** | (3.978)*** | (6.583)*** | (3.417)*** | ||
| νi0 | Volatility intercept | 0.006 | 0.018 | 0.043 | 0.001 | 0.025 | 0.009 | 0.010 | 0.036 |
| (4.668)*** | (4.631)*** | (1.064) | (0.243) | (4.765)*** | (2.716)*** | (0.613) | (1.028) | ||
| αi1 | GARCH | 0.911 | 0.918 | −0.008 | 0.711 | 0.859 | 0.895 | 0.482 | 0.152 |
| (99.216)*** | (131.43)*** | (−0.075) | (11.098)*** | (42.000)*** | (75.856)*** | (4.270)*** | (1.287) | ||
| λi1 | ARCH | 0.067 | 0.069 | 0.110 | 0.038 | 0.082 | 0.069 | 0.080 | 0.086 |
| (9.865)*** | (11.589)*** | (5.745)*** | (7.743)*** | (7.474)*** | (8.351)*** | (7.625)*** | (5.975)*** | ||
| ϕi1 | Volatility spillover | −0.001 | −0.002 | 1.517 | 0.134 | 0.007 | 0.017 | 0.346 | 0.828 |
| (−0.583) | (−0.546) | (7.060)*** | (3.593)*** | (1.032) | (1.962)** | (3.587)** | (6.148)*** | ||
| ϖi1 | GLBA binary | 0.008 | −0.007 | −0.110 | 0.034 | 0.012 | 0.014 | −0.113 | 0.337 |
| (2.724)*** | (−1.895)* | (−1.154) | (2.210)** | (2.103)** | (2.270)*** | (−2.269)** | (20.404)*** | ||
| LL value | −6418.05 | −6271.37 | −6255.30 | −6298.20 | |||||
- Notes: The models estimated are as follows:
- Asymptotic t-values are in parentheses. In Panels A and B, i= 1 and 2 represent Large Life (Large P&C), and Small Life (Small P&C), respectively. Similarly, in Panels C and D, i= 1 and 2 represent Geographical Diversification—Yes (Product Diversification—Yes) and Geographical Diversification—No (Product Diversification—No), respectively. LL represents the log of the likelihood function.
- ***, **, and * represent significance at the 1%, 5%, and 10% levels, respectively.
Return spillover between large and small insurers is found to be bidirectional for P&C but unidirectional from large to small for Life companies. The large Life insurers appear to be insulated from the influence of their smaller counterparts because of their sheer size or broader geographic and product diversification. The volatility spillover does hold between small and large P&C but not between small and large Life insurers. These subsectors of the life insurance industry are somewhat segmented in this regard. The ARCH and GARCH parameters are in all cases, except one, positive and significant and have reasonable magnitudes. The persistence of shocks, measured by the sum of the ARCH and GARCH parameters, is larger for small insurer firms than their larger counterparts, and much more durable for Life than P&C insurer firms.
Results based on geographic and product diversification (Panels C and D) show that the market and interest rate risks for diversified firms are smaller than those for nondiversified firms for both types of diversification. These results are intuitive and consistent with portfolio theory. Return spillover is found to be positive, significant, and bidirectional between diversified and nondiversified firms, for both geographic and product diversification. Volatility spillover is also positive, significant, and bidirectional for product diversification but unidirectional from diversified to nondiversified firms for geographic diversification. These findings indicate that returns and volatilities of diversified and nondiversified firms always move in the same direction tying their destinies to one another. Geographically diversified firms, however, are rather immune to shocks from geographically nondiversified firms.
The effect of the passage of GLBA is larger in magnitude for the nondiversified than the diversified firms for both geographic and product diversification categories. These results are compatible with theory because the less diversified the firms are, the bigger the opportunities for them to diversify in response to GLBA through commingling with commercial and investment banking firms. This effect is manifested in the higher returns enjoyed by these insurer firms in the post-GLBA period. It is notable that the effect of GLBA on product-diversified firms is negative. This indicates that the market considers these firms as having lost a great opportunity to diversify into other lines of activity outside the insurance industry because they were already diversified across different insurance products.
Summary and Conclusions
We model the stock return behavior for P&C, A&H, and Life insurers based on a System-GARCH specification. Our empirical results show that market and interest rate risk measures (betas) differ significantly across the three segments, and vary by insurer size and diversification. Interest rate sensitivity is negative and highly significant for large Life and P&C insurers but insignificant for the smaller firms, whereas market and interest rate risks for diversified firms are smaller than those for nondiversified firms for both geographic and product diversification.
We find that the impact of changes in the stock returns in one insurance segment on another is always positive, indicating a direct comovement of returns across different insurance activities. Unlike findings for banks, volatilities of returns across the three insurance segments are not found to be highly interdependent (weak linkages do exist), suggesting less risk of volatility transmission from one category of insurers to the other categories. When the sample is disaggregated by size or the degree of diversification, the disaggregated results show strong volatility interdependence within each segment. Findings also indicate that stock return volatility increased significantly for A&H and P&C (but not for Life) insurers following the GLBA (1999).
The findings are important for regulatory efforts in the areas of contagion containment and risk-based capital, mergers and acquisitions, insurer expansion into new segments of insurance business, and investor risk diversification. Knowledge of spillover and the direction of flow can be used by regulators and insurer managers in addressing potential contagion effects, decisions to enter new segments through acquisition, and determining the gains from diversification. The finding of direct comovement of returns across the three insurance sectors suggests limited diversification gains for investors and for insurer managers considering entry into new sectors. Areas that offer the most gains from diversification are the areas in which return interdependence is weakest, i.e., between Life insurers and the A&H and P&C segments. The finding of higher interest rate risk among larger Life and P&C insurers versus smaller insurers suggests that one-size-fits-all regulatory schemes may be inappropriate. Future research is needed to provide greater insight in the relationships between insurer interest rate exposure, asset risk, leverage, size, and other firm characteristics.