Methods for Assessing Uncertainty in Fundamental Assumptions and Associated Models for Cancer Risk Assessment
Abstract
The distributional approach for uncertainty analysis in cancer risk assessment is reviewed and extended. The method considers a combination of bioassay study results, targeted experiments, and expert judgment regarding biological mechanisms to predict a probability distribution for uncertain cancer risks. Probabilities are assigned to alternative model components, including the determination of human carcinogenicity, mode of action, the dosimetry measure for exposure, the mathematical form of the dose-response relationship, the experimental data set(s) used to fit the relationship, and the formula used for interspecies extrapolation. Alternative software platforms for implementing the method are considered, including Bayesian belief networks (BBNs) that facilitate assignment of prior probabilities, specification of relationships among model components, and identification of all output nodes on the probability tree. The method is demonstrated using the application of Evans, Sielken, and co-workers for predicting cancer risk from formaldehyde inhalation exposure. Uncertainty distributions are derived for maximum likelihood estimate (MLE) and 95th percentile upper confidence limit (UCL) unit cancer risk estimates, and the effects of resolving selected model uncertainties on these distributions are demonstrated, considering both perfect and partial information for these model components. A method for synthesizing the results of multiple mechanistic studies is introduced, considering the assessed sensitivities and selectivities of the studies for their targeted effects. A highly simplified example is presented illustrating assessment of genotoxicity based on studies of DNA damage response caused by naphthalene and its metabolites. The approach can provide a formal mechanism for synthesizing multiple sources of information using a transparent and replicable weight-of-evidence procedure.
1. INTRODUCTION
In a recent report, Cohen(1) outlines the key steps in cancer risk assessment, including: (1) a determination of whether the agent is carcinogenic in humans, (2) estimation of the agent potency within the range of dosage used in an animal study, (3) quantitative extrapolation of risk from the test species to humans, and (4) high- to low-dose extrapolation to estimate risks for the dose range experienced in the exposed human population. In this article, these and other factors are considered as part of a general methodology for addressing fundamental uncertainties in the underlying biological mechanisms and model assumptions used in a cancer risk assessment. The methodology is based on a “distributional approach” to uncertainty analysis. In the distributional approach the risk analyst builds probability trees that allow calculation of risk estimates and associated probabilities for different plausible combinations of model assumptions. Software platforms for influence diagrams and “Bayesian belief networks” (BBNs) are shown to greatly facilitate model construction and evaluation. The method enables evaluations of the effect of complete or partial reductions in the uncertainty of different elements of the risk model, providing a first characterization of the value of information for specific studies that target these elements.
The distributional approach for characterizing uncertainty in cancer risk assessment was developed by Evans, Sielken, and co-workers beginning in the 1990s(2–10) and has also been referred to as information analysis, weight-of-evidence analysis, the comprehensive methodology, and comprehensive realism.(8–10) The method has since been acknowledged in a number of reviews of cancer risk assessment practice and research needs,(11–13) and applied in various forms for risk assessment of different chemical compounds.(14–19)
The motivation for the distributional approach is the recognition that the use of a single set of assumptions for the components of a cancer risk assessment, whether default, conservative, or otherwise, fails to capture the full range of plausible or likely relationships, how these relationships depend upon our current state of knowledge, the implications for computed values of potency or unit risk, and the opportunities for improved estimates. The distributional approach thereby enables consideration of a “portfolio-of-mechanisms” that may contribute to carcinogenesis.(20)
1.1. Methodological Context
Uncertainty may be considered and characterized at various stages of a cancer risk assessment. Traditionally, this has occurred first in the fitting of models to the experimental bioassay data. In the absence of toxicodynamic models (discussed further below), a functional relationship is fit between the experimental dose and the observed incidence of tumor occurrence or a related precursor endpoint, by statistically estimating the parameters of the dose-response equation. Different empirical functional forms may be fit to the bioassay results, often with only minor differences in their statistical goodness of fit to the experimental data. However, the predicted risks from these alternative models are often very different when extrapolated from high experimental doses, where risks of 10−2–1 must be achieved in order to detect effects and fit a dose-response relationship with a limited number of laboratory animals tested at each dose level (typically ∼50 animals per group), to the much lower dosage rates typically received by the human population, where expected risks of 10−10–10−3 are generally determined. The uncertainty involved in choosing a dose-response model, its associated low-dose extrapolation, and the dependence of these on the mode of action are key elements of the distributional method described in this article.
In addition to the “between-model” uncertainty inherent in the consideration of alternative dose-response equations, “within-model” uncertainty is reflected in the statistical uncertainty of the fitted parameters of any given equation. This parameter uncertainty is translated into uncertainty in a benchmark dose (BMD), in particular, the point of departure (POD) dose. The PODX is chosen as the effective dose that results in an X percentage increase in the observed cancer endpoint relative to the control group. A PODX estimated for cancer risk assessment is sometimes denoted as a BMDX (both of these terms also apply to dose metrics used for noncancer effects), a tumorigenic dose (TDX, especially in Europe, with the TD25 often referred to simply as the T25), or an effective dose (EDX). The latter is the most common terminology used for cancer risk assessment in the United States, with the ED10 the most commonly applied POD.
Statistical methods allow for the determination of a central, or “best,” point estimate for the EDX. This estimate is usually determined from the parameter values that make the observed experimental results most likely to have occurred (relative to other possible parameter values) and is referred to as the maximum likelihood estimate (MLE). In addition, statistical bounds can be determined for the estimated EDX. These bounds can be calculated using classical statistical methods—the interval for the EDX estimate is then referred to as a confidence interval, and the upper and lower values of the interval are referred to as the upper confidence limit (UCL) and the lower confidence limit (LCL), respectively. The latter, commonly referred to as the LEDX (or BMDLX), is of particular interest in health risk assessment, since it is the lower statistical bound of the effective dose that determines the upper statistical estimate of the cancer potency or risk for a given exposure. UCL and LCL estimates are now typically provided as part of the output from software packages used for fitting dose-response relationships and estimating BMDs (see, for example, the EPA Benchmark Dose Software at: http://cfpub.epa.gov/ncea/cfm/recordisplay.cfm?deid=164443). Additional guidance for calculating confidence intervals for dose-response relationships is found in References 21–23.
Bayesian statistical methods have been used increasingly in recent years to fit dose-response models and to estimate the uncertainty in model parameters and derived ED and risk values (e.g., References 24–27). Bayesian methods begin with a prior probability distribution for the model parameters and associated risk estimates and update these estimates using the likelihood function for the experimental results (the same function that is maximized to determine the MLE) to derive the posterior distribution of the model parameters and associated risk metrics. The prior distribution may be chosen to reflect expert knowledge regarding the model, or diffuse or informationless priors may be assumed. Statistical bounds determined using Bayesian methods are referred to as credible intervals.1
When reporting statistical bounds, typically a 90% confidence (or credible) interval is reported, ranging from the 5th percentile LCL to the 95th percentile UCL. As noted above, the conservative, health-protective estimate of risk is associated with the LCL for the POD (e.g., the 5th% LED10), which yields the corresponding UCL for the risk estimate, in this case, the 95th% UCL risk. Drawing on the advice of the EPA Science Advisory Board,(28) the current EPA guidance notes that “risk assessors should calculate, to the extent practicable, and present the central estimate and the corresponding upper and lower statistical bounds (such as confidence limits) to inform decisionmakers” (Reference 29, pp. 1–14).
Consistent with this recommendation, the distributional approach presented here (and in References 2–10) considers multiple risk metrics, including a central estimate (the MLE) and statistical bounds (here the 95th% UCL). Consideration of both is assumed to capture and reflect the within-model uncertainty associated with fitting a dose-response curve. The method then goes on to consider the fundamental conceptual (e.g., mode of action) assumptions that lead to the selection of alternative dose-response functions and animal-to-human extrapolation models. This between-model uncertainty is used to derive a probability distribution function for each metric, which can then be analyzed to inform decisions that will be based on either or both of the metrics. From this perspective, it is fully legitimate to compute a probability distribution function for each metric, representing the uncertainty in an estimated MLE risk or 95th UCL risk, given that it can be computed in many different ways, depending on the particular combination of uncertain assumptions that is adopted. Similarly, moments of these computed probability distributions (means, standard deviations, etc.) can be determined, and these are especially useful for indicating how the distributions shift as particular assumptions are invoked, as part of a model sensitivity analysis, or in response to new knowledge regarding the scientific support for alternative assumptions.
The methodology relies on the assignment of probabilities to various assumptions and submodels in the cancer risk assessment. In general, these assignments are informed by the weight of evidence from scientific studies, arguments put forth in the scientific literature, National Toxicology Program (NTP) reports, IRIS Toxicological Reviews, and/or previous risk assessments where the relative scientific support for alternative assumptions has been evaluated. In addition, formal expert elicitation may be utilized to determine the probabilities for the component models and their dependencies. Expert elicitation has been used in a wide range of scientific studies (e.g., References 30–34), including environmental health risk assessment.(35–39) In the studies presented here, panels of experts were brought together to derive or formally elicit model probabilities. Experts often differ both in their assessments of current scientific knowledge and their beliefs regarding how proposed studies might change these assessments (e.g., with differing estimates of the sensitivity and selectivity of particular experiments with respect to particular hypotheses). In the context of the methods presented herein, we refer to assessments of current scientific knowledge as prior beliefs, and the new beliefs that result from new or proposed studies as posterior beliefs. The Bayesian belief networks presented herein consider both component assumptions for the model elements and scientific studies that can be used to test (and lend differential support to) these assumptions. Expert views regarding both can thus be included in the models.2
1.2. Applications Considered
Two of the initial applications of the distributional method were for detailed assessments of low-dose cancer risk for formaldehyde(2–4) and chloroform.(5, 6) These evaluations were based primarily on the use of animal bioassay studies to fit dose-response relationships. A distributional assessment of cancer risk due to occupational exposure to formaldehyde was also conducted by Fayerweather et al.(43) using available epidemiological data. These applications are briefly reviewed and the former(2,3) is used as the basis for demonstrating implementation and extension of the probability tree method for estimating cancer risk from exposure to formaldehyde. As noted above, the probabilities inputs to the distributional model are based primarily on expert judgment elicited using a combination of formal and informal methods.(3–6) However, the presentation is intended solely as a demonstration of methodology, not as a formal cancer risk assessment for formaldehyde, in part because not all of the processes believed to be important in determining the mode of action of formaldehyde are considered (e.g., References 44–47), and in part because the probability weights used in the tree are taken directly from Reference 2, reflecting available data and expert judgment circa 1990.
2. CRITICAL MODEL ELEMENTS AND ASSUMPTIONS
The probability tree models for formaldehyde(2–4) and chloroform(5,6) address uncertainty in the following elements of a dose-response characterization that is derived primarily from animal bioassay results.
- 1
Whether the agent is indeed a human carcinogen and, if so, for which target organ. As noted in Reference 1, estimates of the probability that a chemical is a human carcinogen can be based on screening tests for genotoxicity or mutagenicity, evidence for compounds with similar animal bioassay results, and confirmed (or at least better) information regarding human carcinogenicity, or estimates from SAR models. The assessment may also consider available epidemiological evidence and mechanistic biological information regarding compound delivery to, and behavior in, target tissues.
- 2
Mode of action. The determination of the mode of action is a critical step in selecting among alternative models for the dose-response relationship and interspecies extrapolation. Principal options generally include cytotoxicity to target cells, cell proliferation, and genotoxicity.
- 3
Dose scale for dose-response modeling. The way in which dose is characterized reflects our understanding of the mechanisms of agent absorption, distribution, metabolism, and excretion (ADME) in the test species and humans. In recent years, physiologically based pharmacokinetic (PBPK) models have been used to inform dosimetry assessments and dose scale selections (e.g., References 48–54).3 Furthermore, as we have learned more, these assessments have become more complex, considering multiple target tissues, metabolite formation, and dose-dependent mechanisms of toxicity.(60)
- 4
Dose-response model. The shape of the dose-response relationship is closely linked to the assumed carcinogenic mode of action in step 2, and is also affected by the dose scale in step 3. Four options are considered in both the formaldehyde and chloroform assessments: (a) a probit model representing highly nonlinear, threshold-like behavior at low dose; (b) a five-stage (multistage) model that results in sublinear relationships at low dose; (c) a five-stage model above 1 ppm formaldehyde, with linear interpolation to zero below 1 ppm; and (d) a one-stage (or one-hit) model that is essentially linear throughout the range of doses considered.
- 5
Experimental data set. In some cases more than one bioassay study is available for fitting the dose-response relationship. For example, the chloroform assessment of Reference 5 considered nine different bioassay studies conducted by different groups using rat and mouse, female and male, and liver and kidney endpoints.
- 6
Interspecies extrapolation. As noted in Reference 1, extrapolation across species is usually made assuming dosage rates scaled to the three-fourth power of bodyweight. Lacking detailed PBPK models to inform the estimate, other options typically considered include assuming a direct equivalence between the test species and human dosage rates, and the use of bodyweight scaled to the two-third power (corresponding to equivalence based on relative surface area).
3. IMPLEMENTATION OF THE DISTRIBUTIONAL APPROACH FOR LOW-DOSE FORMALDEHYDE CANCER RISK ASSESSMENT
The initial applications of the distributional approach for formaldehyde cancer risk assessment were based on animal bioassay studies and appeared in References 2 and 3. Fig. 1 presents the network model (described further below) developed here to consider the alternative assumptions in this assessment. The left portion of Fig. 1 presents the six components of the model and the alternatives available for each. Prior probabilities are assigned (for components 1, 2, 3, and 5) or derived (for components 4 and 6) for each of the component alternatives. The right side of Fig. 1 shows the two risk metrics that are computed conditional on the component assumptions: (1) the MLE risk and (2) the 95th UCL risk. The particular application shown here is from Reference 2, where the output metric is the added cancer risk resulting from lifetime inhalation of air containing 1 ppb (0.001 ppm) of formaldehyde. The lifetime exposure is assumed to begin at age 4, with exposure occurring 30 hours per week. The risk outputs are summarized by the computed probabilities (shown as percentages summing to 100) for each of 13 discretized, order-of-magnitude bins, with any risk value below 10−12 assumed to be zero and assigned to the first bin, denoted by e-25 to 1e-12.
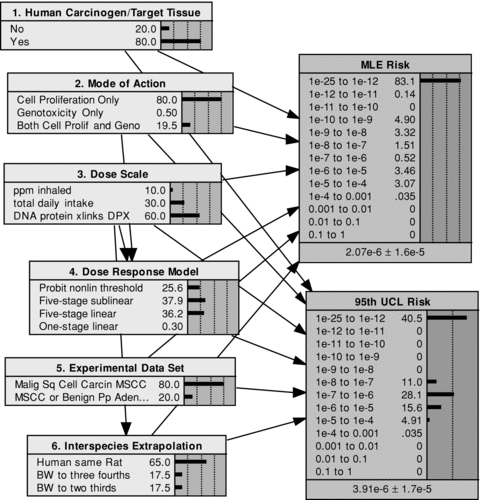
Compiled BBN model for formaldehyde low-dose cancer risk assessment with prior probabilities. (Probabilities shown as percentages summing to 100 in this and all subsequent network displays.)
The prior probabilities for the six components in Fig. 1 were assigned by Reference 2 as follows.
- 1
Human Carcinogen/Target Tissue. In the case of formaldehyde, human carcinogenicity was treated in a general manner, without specification of a target organ(s). The probability that formaldehyde is a human carcinogen was assigned a value of 0.8 by Holland and Sielken,(2) consistent with its EPA (B1) and IARC (2A) classifications as a probable human carcinogen.
- 2
Mode of Action. Three alternatives were considered for formaldehyde: (a) cell proliferation (inducing cell growth) only, (b) genotoxicity only, and (c) both cell proliferation and genotoxicity. Based on previous studies, Holland and Sielken(2) assigned the predominant probability (0.8) to cell proliferation only, with 0.195 probability assigned to both cell proliferation and genotoxicity, and only a probability of 0.005 assigned to genotoxicity only.
- 3
Dose Scale. Holland and Sielken(2) included the following dosimetry options for formaldehyde: (a) the concentration in the inhaled air, (b) total daily intake, and (c) a biomarker-based measurement of the covalent bonding of formaldehyde to DNA in respiratory tissues, as measured by the amount of formaldehyde-induced DNA protein cross-links (DPX). The different dose scales were assigned weights of 0.1 (ppm inhaled), 0.3 (total daily intake), and 0.6 (DPX), based on the then-current understanding of ADME mechanisms in rats and humans.(2)
- 4
Dose-Response Model. The dose-response model for formaldehyde is conditioned on the assumed mode of action and the dose scale. The probabilities for each dose-response model, conditioned on each combination of mode of action and dose scale, are shown in Table I, Panel A. These conditional probabilities imply that:
- •
The probit nonlinear-threshold model is used solely when cell proliferation is assumed as the only mode of action, indicating a more likely role for dosimetry based on the inhaled ppm and total daily intake measures;
- •
The five-stage sublinear model is applicable across all three modes of action and all three dose scales with relatively little differential preference between them;
- •
The five-stage model with linear interpolation to zero is relatively more likely when both cell proliferation and genotoxicity are assumed to be operative, and implies a somewhat greater weighting on the use of covalent bonding and DPX for the dose scale; and
- •
The one-stage linear model is associated solely with the genotoxic mode of action, and again implies a modest shift toward DPX as the preferred dose scale. The combination of a genotoxic mode of action and a linear dose-response relationship yields (together with the particular interspecies extrapolation methods described below) the highest estimates for low-dose cancer risk.
- •
- 5
Experimental Data Set. Estimates for the formaldehyde study were based on a CIIT (Chemical Industry Institute of Technology) rat inhalation study that identified malignant squamous cell carcinoma (MSCC) and benign polypoid adenoma in the exposed rat nasal cavities.(61) The two options for the data sets included are: (a) MSCC only (assigned by Holland and Sielken(2) an initial weight of 0.8), and (b) both MSCC and benign polypoid adenoma (assigned the remaining weight of 0.2). When the benign tumors are included, somewhat higher risk estimates result.
- 6
Interspecies Extrapolation. Holland and Sielken(2) link the interspecies extrapolation method for formaldehyde to the dose scale, with the use of the DPX dose scale allowing for preferential use of human-rat equivalence when making the interspecies extrapolation (that is, the critical cross-species differences in formaldehyde ADME are assumed to occur prior to the DPX-related covalent bonding of formaldehyde to DNA in respiratory tissues). The bodyweight-power extrapolations generally yield higher risk estimates than those obtained using the human-rate equivalence assumption. The probabilities for each interspecies extrapolation model, conditioned on the dose scale, are shown in Table I, Panel B.
| Mode of Action | Dose Scale | Dose-Response Model Prob[Dose-Response Model | Mode of Action ∩ Dose Scale] | |||
|---|---|---|---|---|---|
| Probit Nonlinear Threshold | 5-Stage Sublinear | 5-Stage Linear | 1-Stage Linear | ||
| A. Dose-Response Model Dependency on the Mode of Action and Dose Scale: | |||||
| Cell proliferation | ppm inhaled | 50 | 45 | 5 | 0 |
| Genotoxicity | ppm inhaled | 0 | 15 | 50 | 35 |
| Both | ppm inhaled | 0 | 50 | 50 | 0 |
| Cell proliferation | Total daily intake | 50 | 40 | 10 | 0 |
| Genotoxicity | Total daily intake | 0 | 10 | 50 | 40 |
| Both | Total daily intake | 0 | 40 | 60 | 0 |
| Cell proliferation | DNA protein ks | 20 | 40 | 40 | 0 |
| Genotoxicity | DNA protein ks | 0 | 2.5 | 22.5 | 75 |
| Both | DNA protein ks | 0 | 18.75 | 81.25 | 0 |
| Dose Scale | Interspecies Extrapolation Prob[Interspecies Extrapolation | Dose Scale] | |||
|---|---|---|---|---|
| Human Same as Rat | BW to 3/4ths | BW to 2/3rds | ||
| B. Interspecies Extrapolation Dependency on the Dose Scale: | ||||
| ppm inhaled | 20 | 40 | 40 | |
| Total daily intake | 50 | 25 | 25 | |
| DNA protein ks | 80 | 10 | 10 | |
3.1. Available Tools for Implementing Distributional Method
The distributional approach is based on the use of event (or probability) trees to elucidate all combinations of assumptions or values for each of the model components, with each final branch representing a unique combination of these assumptions. So, for example, for the formaldehyde model shown in Fig. 1, with six components involving 2, 3, 3, 4, 2, and 3 options for each, there are (2 × 3 × 3 × 4 × 2 × 3) = 432 branches on the tree. Each branch has associated with it a particular value of the risk metrics that are computed from the bioassay results using the set of assumptions associated with the branch.
Previous applications of the distributional method have used dedicated software to implement the probability tree calculations.(2–10)4 More recent advances in influence, decision, and event tree software (e.g., References 62–64) have provided additional options for implementing the method.5 A particular type of model for representing a set of events related by conditional probabilities is referred to as an influence diagram,(65–67) or BBN.(68, 69) BBNs can be used to structure a model for interrelated events, allowing probabilistic inference for elements of the model that are either data-rich or data-poor.(70) Software packages for BBNs are especially well suited for probability tree models, facilitating automated generation of the tree branches and calculation of the resulting probability for each, including incorporation of dependencies (in the form of conditional probabilities) between different model components and assumptions. The compiled BBN network allows computation of the effect of modifying any of the node probabilities by propagating updated probabilities throughout the network. This software does not reduce the burden of identifying the risk estimate at the end of each branch, as these must still be determined by fitting the appropriate dose-response model to the appropriate data set, with the appropriate low-dose calculation and animal-to-human extrapolation.
The distributional approach for formaldehyde is demonstrated here using the Netica BBN software package (http://www.norsys.com/). This platform was chosen because of its flexibility and effective user interface, providing for easy development of the network, straightforward input of prior and conditional probabilities, and visually appealing and informative options for displaying the results of compiled and updated networks. A number of similar software packages are available.6
For the prior network shown in Fig. 1, probabilities for each downstream node are computed by multiplying the probabilities along each branch of the network, then summing the probabilities of each branch associated with the corresponding value of the output node. This calculation is done automatically in Netica when the network is compiled. As indicated in Fig. 1, 83.1% of the prior probability of the compiled tree is associated with an MLE risk of zero, with the remaining 16.9% distributed among risk estimates ranging from 10−12 to 10−3 lifetime cancer risk. As expected, the 95th percentile UCL risk estimates are shifted upward, with now only 40.5% of the probability associated with zero risk and the remainder distributed among lifetime risks ranging from 10−8 to 10−3.
At the bottom of the output nodes for the MLE risk and the 95th UCL risk, summary numbers are provided indicating the mean ± standard deviation. The moments are dominated in this case by the probabilities computed for the few highest intervals of risk, over from 10−3 down to 10−7. As indicated, the mean of the 95th UCL risk is nearly double the mean of the MLE risk, while their standard deviations are nearly equal. While the mean values of the risk metrics are clearly at the upper tails of their respective distributions (as is common for highly skewed distributions that extend over logarithmic scales), changes in the mean provide a good first measure of how the uncertainty distribution for each of these risk metrics, each of regulatory interest, might shift in response to potential new information and associated reductions in uncertainty.
3.2. Model Sensitivity and the Potential Value of New Information
Continuing with the formaldehyde model presented in Fig. 1, the implications of resolving one or more of the uncertainties embodied in each of the model components are now explored. By way of illustration, Fig. 2 shows the results of fixing the values for two component nodes in the probability tree: for node 1, assuming that formaldehyde is a human carcinogen; and for node 6, a determination that interspecies extrapolation is properly made using BW to two-thirds.
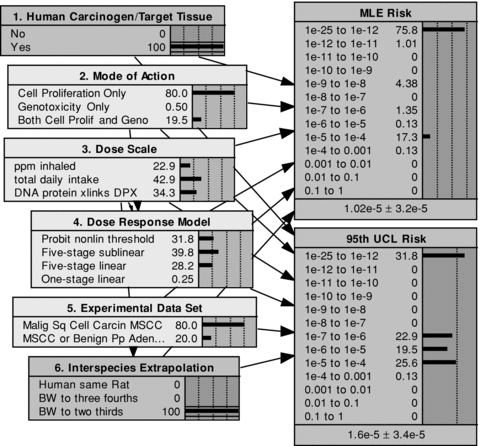
The effect of determining that formaldehyde is a human carcinogen and that BW to the two-thirds is the appropriate basis for interspecies extrapolation.
When comparing Fig. 2 to Fig. 1, eliminating the branches with no human carcinogenicity and confining the animal-to-human extrapolation to BW to two-thirds is shown to reduce the probability of zero risk from 83% to 76% for the MLE risk metric, and from 41% to 32% for the 95th UCL risk metric. The probabilities that the risk metrics exceed 10−6 increase from 6.6% to 18% for the MLE risk, and from 21% to 45% for the 95th UCL risk. The mean MLE risk and the mean 95th UCL risk both increase as well (by factors of between 4 and 5), from 2.1 × 10−6 to 1.0 × 10−5, and from 3.9 × 10−6 to 1.6 × 10−5, respectively.
Probabilistic inferences derived from resolving the uncertainty in node 6, interspecies extrapolation, also propagate backward through the network to upstream nodes. Since interspecies extrapolation is a child of the dose scale node, this (hypothetical) conclusion results in a back-propagating inference that shifts the dose-scale probability weight away from the DPX biomarker and toward the other two dose metrics. Since the dose scale node is also a parent of the dose-response model, small changes in the latter's probability weights also result.
The results in Fig. 2 illustrate the effects of a complete elimination of uncertainty in two of the model components (nodes 1 and 6), resulting from perfect information. In most cases, however, only partial resolution is possible, with studies acknowledged to provide only imperfect information. To illustrate the implications of imperfect information, consider studies aimed at resolving the mode of action in node 2. The modified BBN model that includes these studies is shown in Figs. 3A and 3B, with added node, mode of action study. Both of these figures show the prior state for the respective models. For the case shown in Fig. 3A, the study is assumed to achieve 100%“resolution,” yielding perfect information. For the case shown in Fig. 3B, the study is imperfect, with a resolution of 80%. The conditional probability table for the mode of action study given the true mode of action is shown in Table II for this case of 80% resolution.
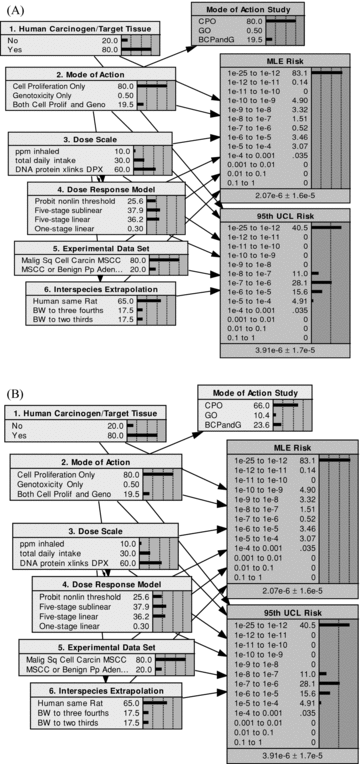
(A) Modified BBN model for formaldehyde low-dose cancer risk assessment with added node for mode of action study. Shown here with prior probabilities for case of perfect information (resolution = 100%). (B) Modified BBN model for formaldehyde low-dose cancer risk assessment with added node for mode of action study. Shown here with prior probabilities for a case of imperfect information (resolution = 80%).
| Mode of Action | Mode of Action Study Prob[Mode of Action Study Result |True Mode of Action] | ||
|---|---|---|---|
| CPO | GO | BCP and G | |
| Cell proliferation only | 80 | 10 | 10 |
| Genotoxicity only | 10 | 80 | 10 |
| Both cell prolif and geno | 10 | 10 | 80 |
As indicated, the study is assumed to yield the correct result 80% of the time, with the remaining 20% divided equally between the other two possible study outcomes.7
The effects of different results from the mode of action study are computed by clicking on the appropriate outcome in the mode of action study node (setting the particular outcome probability to 100%). This was done using networks with assumed values of the resolution for the mode of action study ranging from 50% to 100%. The resulting effects on the predicted mean of the 95th UCL risk and the probability that the 95th UCL risk is greater than 10−6 are presented in Figs. 4A and 4B, respectively.
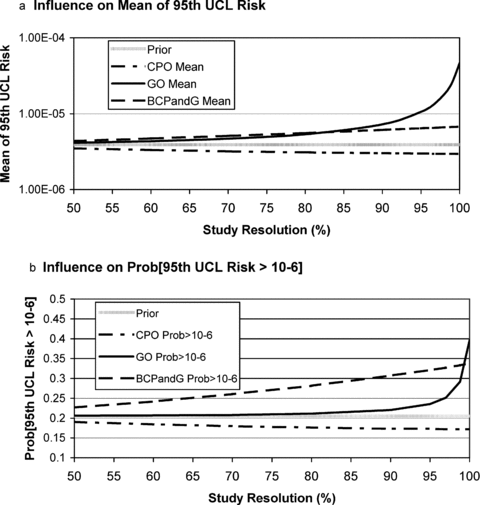
Effect of mode of action study outcomes on predicted risk model results for studies of varying resolution.
As shown in Fig. 4, when the study resolution is only 50%, the posterior output metrics for all study outcomes are very close to their prior values: 3.9 × 10−6 (prior mean, Fig. 4A), and 20.5% (prior probability of exceeding 10−6). As the study resolution increases, the study results are more effective in shifting the prior values: downward in the case of a CPO (cell proliferation only) finding, and upward in the case of a GO (genotoxicity only) or BCPandG (both cell proliferation and genotoxicity) finding. The CPO finding results in only modest decreases in the risk metrics, with little change over the range of study resolution. This is because the prior probability assigned to the CPO mode of action is already 0.8, so the CPO study result does not dramatically shift the prior probabilities in the network. The GP finding results in only small upward shifts in the risk metrics when the study resolution is low (between 50% and 80%—especially for the probability that the 95th UCL risk exceeds 10−6). However, as the study resolution approaches 100%, much larger increases in the risk metrics result. This is because the GO mode of action has a very low prior probability (0.005), so only a very highly resolved study can shift significant probability to this state. The BCP and G study result imparts a moderately high, and steadily increasing, upward effect on the risk metrics throughout the range of study resolution considered.
The results shown in Fig. 4 are suggestive of general patterns of information value associated with studies of differing quality. The assumed study outcomes and their probabilities are highly idealized. Furthermore, only the expected shifts in risk model outputs associated with each study outcome are shown. Information value has further dimensions that have been the subject of significant study in the decision analysis literature.(71–73) In particular, by partitioning the prior uncertainty into multiple (in this case, three) preposterior distributions, the variances associated with each, corresponding to the poststudy state of knowledge, are (in most, but not all cases74,75) reduced. This variance reduction may then enable decisions (e.g., whether to regulate a chemical as a carcinogen) with lower expected loss—when the losses are monetized, an expected monetary value for the information can then be computed. Information can also have value for conflict resolution,(76) increasing the probability that different stakeholders with different valuations for the outcomes and possibly different prior probabilities regarding the science will exhibit greater concordance in their posterior beliefs and subsequent decision preferences. In the following section, the analysis presented thus far is extended to consider mechanistic studies aimed at determining the cancer mode of action, and the demonstration of information value is limited to shifts in posterior beliefs regarding the mode of action. A more complete synthesis of cancer studies, risk assessment, cost-benefit analysis, and information value can build on this approach, but awaits further research and methods development.
4. PLANNING AND INTEGRATING RESULTS FROM MECHANISTIC STUDIES
In the previous section a generic study was posited to lend support for one of three possible modes action for formaldehyde carcinogenesis. Here, we consider multiple possible studies for addressing the genotoxicity of naphthalene, a similarly important chemical subject to numerous studies to assess its carcinogenicity. By enumerating possible studies and their outcomes, a framework is provided for consideration of the information value of specific projects in research planning and interpretation.
4.1. Genotoxicity Studies of Naphthalene
A symposium was held recently to address key scientific issues and uncertainties in cancer risk assessment for naphthalene, a compound undergoing current regulatory review. The naphthalene state-of-the-science symposium (NS3) was held to consider fundamental science issues related to carcinogenic mode of action and quantification of human cancer risk from exposure to naphthalene at environmentally relevant levels. Researchers conducting the most important primary scientific studies on metabolism, biochemistry, animal-to-human extrapolation, and mechanism of action presented their work. A set of reports was developed on the state-of-the-science for each issue, identifying significant scientific uncertainties and proposing specific scientific research that could resolve these uncertainties. Summary information on the symposium is available at: http://www.naphthalenesymposium.org/.
One of the key scientific issues addressed at the symposium concerned the question of whether naphthalene is genotoxic.(77) Like in the case of formaldehyde, answering this question is critical to the choice of dose-response functions, low-dose extrapolation, and resulting risk estimates at environmental concentrations. In the report of the symposium subgroup charged with addressing naphthalene genotoxicity,(78) scientific statements that can be made with a high degree of confidence are first presented.
- 1
Under conditions employed in the NTP bioassays.(79,80) naphthalene induces respiratory tumors in rodents—though only at sites showing signs of significant cytotoxicity.
- 2
Naphthalene metabolites are known to produce oxidative damage in cells, and have been shown to produce both stable and rapidly depurinating adducts under synthetic reaction conditions, but the adducts have not been identified in intact organisms.
Next, the workgroup identified critical questions that cannot now be answered with a high level of confidence, requiring further research and studies for their resolution:
- 1
Does naphthalene have characteristics of a genotoxic carcinogen?
- 2
Will biomarkers of naphthalene interactions with DNA be generated in animals or humans following environmental and/or occupational exposures?
- 3
Do specific molecular lesions in target cells determine the progression from preneoplastic tissue to tumors in rodents exposed to carcinogenic levels of naphthalene?
To address these questions the workgroup formulated a set of six scientific studies:
-
Study I. A short-term rat inhalation bioassay of molecular dosimetry of DNA adducts and cell proliferation studies in olfactory mucosa;
-
Study II. A mechanistic tumor initiation study in mouse skin measuring possible enzyme(s) for metabolic activation of naphthalene, stable and depurinating adducts, abasic sites, and analysis of H-ras mutations in preneoplastic skin and tumors (if they develop);
-
Study III. Measurement of DNA adducts of naphthalene in urine of exposed human populations for use as a possible biomarker;
-
Study IV. Examination of pathways of DNA damage response caused by naphthalene and its metabolites to identify the mode of action for naphthalene carcinogenicity;
-
Study V. An evaluation of the enzymology of naphthalene metabolism, with implications for the likelihood that specific metabolic pathways will occur in different species; and
-
Study VI. Bioassays with knockout and “humanized” mice to determine key enzymes in the initial metabolic activation of naphthalene in mice and study mediation processes for carcinogenicity in the liver or lung.
For each study a summary of the proposed experimental procedure was presented and a list of major inferences that could be drawn from different outcomes of the study was offered.
To illustrate the description and possible inferences that could result from a study, the following prospectus for Study IV is considered.
4.2. Study IV Pathways of DNA Repair
This study addresses the pathways of DNA damage response caused by naphthalene and its metabolites to identify whether naphthalene is a mutagenic or nonmutagenic carcinogen in mice. A series of isogenic cell lines deficient in various DNA metabolism pathways will be utilized to characterize the DNA damage responses caused by test compounds. Based on the results from the cultured cells, mice deficient in specific DNA damage responses (e.g., nucleotide excision repair, NER, responsible for stable bulky adducts) will be exposed to naphthalene.
Major inferences that could be drawn from different outcomes of the study:
- 1
DNA damage responses in a series of isogenic cells deficient in various DNA metabolism pathways: Identification of DNA damage responses caused by naphthalene metabolites would support the hypothesis that naphthalene has a genotoxic mechanism. Also, it would show which kind of DNA lesions (stable adducts, depurinating adducts, or abasic sites) significantly impact cells exposed to naphthalene or its metabolites. Failure to identify DNA damage responses caused by naphthalene metabolites would provide some evidence that naphthalene does not have a genotoxic mechanism.
- 2
Stable DNA adducts in target tissue: Identification of increased numbers of stable DNA adducts from naphthalene in the exposed DNA repair (NER)-deficient mouse lung versus wild-type mouse lung would support the hypothesis that naphthalene has a genotoxic mechanism and support the hypothesis that naphthalene could cause cancer through a genotoxic mechanism. Failure to identify increased numbers of DNA adducts from naphthalene in exposed DNA repair-deficient mouse lung, compared to its effect on wild-type mouse lung, would provide some evidence that naphthalene is not a genotoxic carcinogen.
- 3
Clara cell toxicity in mouse lung: Identification of more extensive Clara cell toxicity in the naphthalene-exposed DNA repair (NER)-deficient mouse lung versus wild-type mouse lung would support the hypothesis that Clara cell toxicity is associated with the existence of DNA damage. Failure to identify acceleration of Clara cell toxicity in the naphthalene-exposed DNA repair (NER)-deficient mouse lung compared to wild-type mouse lung would provide strong evidence that cell toxicity is independent of DNA damage.
- 4
Mouse lung tumor (long-term project): Identification of an increased incidence of lung tumors in the naphthalene-exposed DNA repair (NER)-deficient mouse compared to that in the wild-type mouse would support the hypothesis that naphthalene is a genotoxic mouse lung carcinogen. Failure to identify acceleration of Clara cell toxicity in the naphthalene-exposed DNA repair (NER)-deficient mouse lung compared to wild-type mouse lung would support the hypothesis that naphthalene is a nonmutagenic mouse lung carcinogen.
As indicated, the possible inferences from Study IV results consider both positive and negative study outcomes for the critical questions regarding mode of action for naphthalene using one of three terms: “supports the hypothesis,”“provides some evidence,” or “provides strong evidence.” Study results such as these can be considered in a probability tree/influence diagram model by translating the strength of evidence beliefs into study sensitivities and selectivities for the hypotheses in question.8
As in the case of prior probabilities and other conditional probabilities in the network model, different scientific experts may have different beliefs about the appropriate values for a study's sensitivity and selectivity (see, for example, References 31, 81, and 82). That is, the experts may differ in their beliefs regarding the importance of different findings for the questions at hand (a number of disagreements among experts were in fact apparent in the deliberations of the NS3 genotoxicity subgroup). The cancer risk assessment should thus include an examination of the implications of these differences as part of an overall sensitivity analysis of the probability model. In the example that follows, a representative set of study sensitivities and selectivities is used to illustrate the methodology. As with all examples in this article, this is in no way intended to represent an actual risk assessment for naphthalene, but rather to demonstrate a methodology for integrating mechanistic study results into a probability model.
Fig. 5 provides a simple network representation for two elements of the Study IV prospectus on pathways of DNA repair. The following study results are considered and the indicated conditional probabilities are assumed:
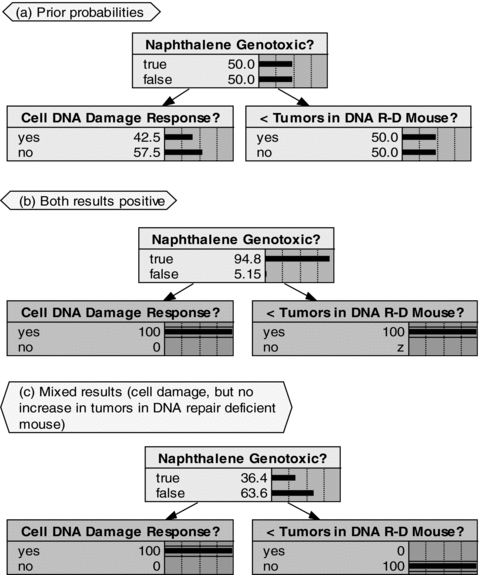
Illustrative consideration of selected experimental results for naphthalene Study IV (outcomes assumed independent, prior probability of genotoxicity set to 0.5, and sensitivities and selectivities chosen by author solely for illustration of methodology): (A) Prior probability before study; (B) Positive outcomes for both study results; and (C) Positive results for cell DNA damage, but negative results for increased tumors in DNA repair-deficient mouse.
- 1
DNA damage responses in a series of isogenic cells deficient in various DNA metabolism pathways:
- a
FNR = (1 – Sensitivity) = Prob[No DNA damage response | naphthalene genotoxic]= 0.35
- b
FPR = (1 – Selectivity) = Prob[DNA damage response | naphthalene not genotoxic]= 0.20;
- a
- 2
Increased incidence of lung tumors in naphthalene-exposed DNA repair-deficient mouse compared to wild-type mouse:
- a
FNR = (1 – Sensitivity) = Prob[No increase in lung tumors | naphthalene genotoxic]= 0.15
- b
FPR = (1 – Selectivity) = Prob[Increase in lung tumors | naphthalene not genotoxic]= 0.15.
- a
As indicated, the study results based on an increase in tumors in DNA repair-deficient mice are assumed to be both more sensitive and more selective for genotoxicity (with lower false negative and false positive rates) than the results from the study of DNA damage responses in isogenic cells deficient in DNA metabolism pathways. Fig. 5A shows the assumed prior conditions, with the prior probability that naphthalene is genotoxic assumed equal to 0.5. Fig. 5B shows the computed posterior probability that naphthalene is genotoxic given that both study elements yield positive results for genotoxicity. With the assumed prior and the assumed sensitivities and selectivities, the double positive result in Fig. 5B yields a nearly 95% posterior probability that naphthalene is genotoxic. In Fig. 5C mixed evidence (positive results for cell DNA damage, but no increase in tumors in DNA repair-deficient mice) results in a decrease in the probability that naphthalene is genotoxic from 50% to 36%. The net decrease is a consequence of the higher sensitivity and selectivity assumed for the mouse tumor results compared to the cell DNA damage results. The BBN thus provides a formal mechanism for synthesizing multiple sources of (sometimes contradictory) information in a transparent and replicable weight-of-evidence procedure.
5. DISCUSSION
The probability model/comprehensive approach provides a rational framework for enumerating the alternative assumptions in a cancer risk assessment, determining the implications of each for low-dose potency and cancer risk estimates, and considering the weight of evidence for the alternative assumptions to assign probabilities to each and compute the resulting probability distribution of risk. The method relies upon expert judgment for the selection of prior probabilities for top nodes in the model as well as for the selection of conditional probabilities that relate the states in downstream and upstream nodes. Given the diversity of scientific issues and disciplines embodied in the cancer risk model, it may be appropriate in many cases to elicit probabilities from different experts for different parts of the model. In addition, since experts often differ considerably in their scientific assessments, methods for exploring and demonstrating the implications of these differences are important, as is consideration of alternative methods for combining inferences from multiple experts.(82–85)
Having calculated a probability distribution for uncertain cancer risk and shown how this distribution can change through consideration of recent or proposed scientific studies, it is worthwhile to step back and consider just what these distributions (and their changes) represent.9 Is the key finding the change in support for different scientific models and assumptions that occur with different study outcomes, or the overall epistemic uncertainty of the resulting cancer risk estimate? While the probability tree method encourages a holistic consideration of the interaction among the risk assessment component models, experts are asked for their assessments regarding individual model probabilities. These are then combined and aggregated by the model to derive the uncertainty in the cancer risk. The strategy is thus one of “decomposition and recomposition.”(3) However, the set of component models and options considered is limited and does not recognize new formulations or component interactions that might be discovered with ongoing research. As such, the derived uncertainty distribution should be recognized as a conditional distribution. In particular, the distribution is conditional on: (1) the assumption that the suite of options and submodels considered for each component constitutes (or at least reasonably approximates) the full set of possibilities, (2) the assumption that all interactions and dependencies among the different components are captured by the conditional probabilities between linked nodes, and (3) the assumption that the combination of assigned probabilities for individual components (which may result from the elicitation of one or more experts) leads to a meaningful result that can itself be attributed to the individual assessments and their combination through the rules of probability. This surely argues for careful exploration of this method, recognizing that predicted risk results should be viewed as providing order-of-magnitude insights. Similarly, the shifts in support for alternative submodels and assumptions associated with different scientific studies and their findings should be considered primarily in terms of their direction (+ or −) and general magnitude (small, medium, or large).
The probability tree method has now been available for well over a decade in the scientific literature and in selected applications. It is thus fair to ask: Has the approach had an impact on the characterization of uncertainty in recent IRIS database entries for cancer risk assessment?
In a 2000 review conducted by the EPA and Versar, Inc., an evaluation of the treatment of variability and uncertainty in IRIS risk assessments was made.(86) Benzene, a very intensely studied carcinogen, was one of the compounds considered in the Versar-EPA report. The study reviewed the IRIS entry for benzene posted in 2000, with the result that two of the three expert reviewers reported that “EPA did not adequately characterize uncertainty,” failing especially to consider alternative models. The benzene entry has since been revised, with the latest update posted in April 2003 (http://www.epa.gov/iris/subst/0276.htm, accessed June 18, 2007). The Carcinogenicity Assessment for Lifetime Exposure section of the IRIS assessment provides an extensive review of the human, animal, and supporting data that lead to benzene's classification as a known human carcinogen. Rather than presenting single-point estimates for potencies and unit risk factors, a range of values is presented (albeit relatively narrow ranges considering the full set of uncertainties that typically affect even well-studied compounds such as benzene). These ranges are:
- 1
Oral Ingestion (extrapolation method—linear extrapolation of human occupational data): Oral Slope Factor — 1.5 × 10−2 to 5.5 × 10−2 per (mg/kg)/day Drinking Water Unit Risk — 4.4 × 10−7 to 1.6 × 10−6 per (μg/L).
- 2
Inhalation (extrapolation method—low-dose linearity utilizing maximum likelihood estimates of Crump, 1994, Reference 19 in this article): Unit Inhalation Risk—2.2 × 10−6 to 7.8 × 10−6 is the increase in the lifetime risk of an individual who is exposed for a lifetime to 1 μg/m3 benzene in air.
The ranges in each case extend over a factor of ∼3–4.
In Section II. C.3 of the IRIS assessment for benzene: Additional Comments (Carcinogenicity, Inhalation Exposure), the Agency makes note of an uncertainty analysis conducted by Crump(19) as part of the study used to derive the unit inhalation risk:
The two most important determinants of the magnitude of the unit risk number are the choice of extrapolation model to be used to estimate risk at environmental levels of exposure and the choice of the exposure estimates to which the Pliofilm workers (Rinsky et al., 1981, 1987) were subjected. Crump (1992, 1994) presented 96 unit risk calculation analyses by considering different combinations of the following factors: (1) different disease endpoints, (2) additive or multiplicative models, (3) linear/nonlinear exposure-response relationships, (4) two different sets of exposure measurements (Crump and Allen [1984]) versus exposure estimates by Paustenbach et al. [1993]), and (5) cumulative or weighted exposure measurements. The unit risk estimates range from 8.6 × 10−5 to 2.5 × 10−2 at 1 ppm (3,200 μg/m3) of benzene air concentration (Crump, 1992, 1994).
The method used by Crump(19) is clearly a variation of the probability tree approach presented in this article, with options available for five component models, yielding 96 unique combinations that define the branches of the model tree. The IRIS report does go on to justify its selection of a particular exposure study(86,87) and the use of a linear model for low-dose extrapolation, yielding the estimated range for the unit risk from lifetime inhalation of benzene as 2.2 × 10−6 to 7.8 × 10−6 at 1 μg/m3. The corresponding range from the Crump probability tree assessment is from 2.7 × 10−8 to 7.8 × 10−6 at 1 μg/m3. As such, the Crump probability tree model has the same upper bound as that determined by the Agency and reported in the IRIS assessment, but a lower bound that is a factor of 80 below that reported by the Agency. Neither study attempts to determine probabilities for the different values that occur within the ranges calculated.
The example provided for benzene indicates that the Agency is willing to present and discuss key uncertainties and resulting ranges for potency and unit risk values as part of an IRIS cancer risk assessment. While the need for bright lines in many regulatory applications is likely to continue to constrain the consideration of the full range of uncertainty in reported estimates, the door is open for broader explorations of the fundamental uncertainties that affect these estimates, both within the IRIS summaries and as part of the more detailed toxicological reviews.
In recent years, the emphasis in risk assessment has shifted (even) more strongly toward the need for improved fundamental understanding of the mechanistic physiological and cellular processes that affect animal and human dosimetry and ADME, as well as the modes of action for cancer, including cytotoxicity, cell proliferation, genotoxicity, and mutagenicity. Methods for uncertainty analysis that are able to interface with these studies can help to provide a stronger linkage between basic research and risk assessment activities that inform societal choices for chemical use, treatment, or cleanup. The distributional/probability tree method reviewed in this article is one approach that can begin to meet this need. By focusing attention on the fundamental assumptions in each of the components of a cancer risk assessment, and by determining how together they affect the resulting model predictions, the method provides the basis for a sounder determination of the full range of uncertainty in risk estimates. It also provides a tool for estimating the potential value of information of studies targeting different components of the risk model with differing sensitivity and selectivity. Readily available software packages for influence diagrams, decision trees, and Bayesian belief networks can help to facilitate the construction and evaluation of these models. Close interaction between risk assessors and health scientists who understand the current state of the art for key model components, and the potential insights and limitations of alternative study designs, can help to ensure that the models and uncertainty analyses that result are well informed and well informing.
Footnotes
ACKNOWLEDGMENTS
The initial plan for this article developed from discussions with John Evans, Joshua Cohen, and Lorenz Rhomberg. Special thanks to Robert Sielken who provided access to a comprehensive set of reports, papers, and software related to the distributional method for cancer risk assessment. Kan Shao and Royce Francis provided assistance in developing the Netica model. The author is indebted to the members of the genotoxicity workgroup of the Naphthalene State-of-the-Science Symposium (NS3) for their inputs and patience in identifying key factors and studies needed to better understand naphthalene genotoxicity: David Brusick, Ercole Cavalieri, Dhrubajyoti Chakravarti, Xinxin Ding, David Longfellow, Jun Nakamura, Eleanor Rogan, and James Swenberg. David Brusick also provided suggestions for this portion of the manuscript. Helpful suggestions at the NS3 were also provided by Kenneth Bogen and Richard Belzer. This article was greatly improved as a result of comments on an earlier draft by John Evans and three anonymous reviewers. Financial support for this article was provided by the U.S. Environmental Protection Agency (EPA), Contract #5-15238 through the Oak Ridge Associated Universities (ORAU), U.S. Department of Energy (DOE). This article has not been subject to formal peer review by the EPA, ORAU, or DOE, and no official endorsement should be inferred.




