Ranking Nuclear and Radiological Terrorism Scenarios: The Italian Case
Abstract
A quantitative criterion for ranking the different scenarios of nuclear and radiological terrorism has been developed. The aim of the model is not to predict terroristic events but only to indicate which scenario has the higher utility from the point of view of a terroristic organization in terms of balance between factors favoring and discouraging the attack, respectively. All these factors were quantified according to a scoring system that takes into account the logarithmic relationship between perceptions and stimuli. The criterion was applied to several scenarios, each of which was modeled in a simple but not trivial way in order to estimate the expected damage in terms of probable life losses from both radiative and nonradiative effects. The outcome from the ranking method indicates that the attractive scenario appears to be the detonation of a low yield improvised nuclear device in the metropolitan area of a major city.
1. INTRODUCTION
Due to the prevailing role of human intelligence and intent, terrorist attacks are intrinsically unpredictable events. However, despite this discouraging feature, several efforts have been made toward mathematical modeling of terrorism risk (Woo, 2002a; Major, 2002). The possibility of malevolent use of fissile material and radioactive sources was considered by the scientific community before (NCRP, 2001) and after (ICRP, 2006) the September 11, 2001 attacks. Repeated attempts of terrorist organizations to obtain certain radiological and nuclear agents have been reported (Salama & Hansell, 2005). Although so far there is no evidence about terrorists' capability to build and deploy radiological or nuclear weapons, such a possibility is considered a real threat. A mathematical model of nuclear terrorism risk indicates a 29% probability of a nuclear terrorist attack in the next decade (Bunn, 2006). Nevertheless, some authors are skeptical with respect to any predictive approach and suggest scenario benchmarking as a more realistic alternative (González, 2005), especially in view of emergency planning.
The approach presented in this article is placed halfway between a purely probabilistic investigation and a benchmark analysis. It retains the quantitative character but avoids any predictive attempt. Quantification is involved in the application of a mathematical criterion to summarize the outcomes from the simulation of relevant terrorism scenarios; the output from the model is a positive real number expressing the rank of each scenario in arbitrary units. By varying the input variables of scenario simulations into reasonable ranges, it is possible to give an estimate of rank spreading and to maximize the rank for each scenario. The results may be useful in resource optimization for both prevention and emergency management.
The interest of the authors was focused on their homeland, Italy; this context exhibits some peculiar characteristics such as the lack of operating nuclear power plants (there are only a few research reactors) and the presence of densely populated cities with high artistic and symbolic value. Nevertheless, the proposed criterion is entirely general and can be applied by the interested reader to any known scenario.
2. METHODS
Terrorist groups can prepare actions involving fissile or radioactive materials in different ways (NCRP, 2001; ICRP, 2006; González, 2005; Mettler & Voelz, 2002; Durante, 2003), ranging from employing radiological dispersal devices (RDD, also known as dirty bombs), sabotaging nuclear facilities, and detonating improvised nuclear devices (IND). It is commonly assumed that such attacks would most likely occur within an urban area in order to maximize their impact. A given scenario is characterized by 3 factors: (1) kind of weapon; (2) target type; and (3) target location. The spectrum of the effects depends on the particular scenario, but it is always possible to distinguish two broad categories: effects caused by ionizing radiations and effects caused by agents other than ionizing radiations. The former include acute radiation syndrome, radiation carcinogenesis, hereditary effects, and environmental contamination. The latter include, for instance, people injuries and damage to buildings and infrastructure. Psychosocial effects belong to both categories because they are caused by the combination of a toxic hazard (ionizing radiations) with a deliberate act of violence by human beings (terrorism) (NCRP, 2001).
A detailed analysis of finalities and capabilities of different terrorist groups is beyond the scope of the present work and has been made elsewhere (for an exhaustive review, see Ferguson & Potter, 2004). It is generally assumed that although most terrorist organizations are not likely to cause mass destruction through nuclear and radiological weapons, some may (Bunn et al., 2003b). Our interest is therefore focused on the limited number of terrorist groups whose motivational orientations and technical skills potentially cover all the range of nuclear and radiological weapons. The chain of causation through which a terrorist group pursues a nuclear or radiological attack is composed by the following steps: (1) choice of the target city (with the possibility to shift to another target in case of defense strengthening; see Woo, 2002b); (2) acquisition of the material required to perform the attack (perhaps bypassing or defeating safeguards); and (3) deployment and activation of the weapon (probably overcoming technical, logistical, and security barriers).
These steps indicate the elements to be considered as catalysts or disincentives for a given scenario (Ferguson & Potter, 2004; Putnam, 2002; Woo, 2002b): (1) value of the target city (including its symbolic and publicity value); (2) expected economic and human losses damage; and (3) technical, organizational, and economical efforts required for building, deploying, and activating the weapon.
In order to prioritize the different scenarios in a quantitative way, the above factors must be first converted into mathematical form. Because each of these factors can be considered as an inhibiting or activating stimulus S, its perception P by the terrorist group can be obtained by invoking the Weber-Fechner law (Weber, 1978; Fechner, 1907): 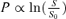 , where S0 is a threshold stimulus. The hypotheses underlying the criterion presented in this article are the following: (1) the preference of the terrorist group for a given scenario is directly proportional to the perception of positive (activating) stimuli and inversely proportional to the perception of negative (inhibiting) stimuli; (2) the perceptions of different kinds of stimuli can be treated as probabilities of independent events; (3) the preference of the terrorist group for a given scenario, given by the combination (2) of all perceptions, is a measure of the rank R of that scenario.
, where S0 is a threshold stimulus. The hypotheses underlying the criterion presented in this article are the following: (1) the preference of the terrorist group for a given scenario is directly proportional to the perception of positive (activating) stimuli and inversely proportional to the perception of negative (inhibiting) stimuli; (2) the perceptions of different kinds of stimuli can be treated as probabilities of independent events; (3) the preference of the terrorist group for a given scenario, given by the combination (2) of all perceptions, is a measure of the rank R of that scenario.
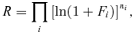 ((1a))
((1a))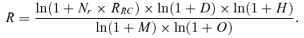 ((1b))
((1b))| Description | Symbol | Rationale | Units |
|---|---|---|---|
| Value of target city | V | Population of the city × RUR-CENSIS rating | Arbitrary |
| Human losses | H | Human losses due to ionizing radiation + human losses due to other effects | No. of people |
| Damage | D | Cost of property damage, lost economic activity, evacuation, etc. | $ |
| Material acquisition | M | Cost of material required to perform the attack | $ |
| Organizational effort | O | Man-years required to overcome logistical and technical difficulties, and to deploy and activate the weapon | $ |
The human losses H were separated into three components: (1) immediate and short-term deaths due to effects other than ionizing radiations, Hnr; (2) short-term deaths due to ionizing radiations (deterministic effects), Hrd; (3) long-term deaths due to ionizing radiations (stochastic effects), Hrs: H=Hnr+Hrd+Hrs. Psychosocial effects were indirectly taken into account by the assumption that stochastic effects, whose actualization is uncertain but largely contribute to the social stigma of exposed individuals, are weighted in the same manner as the remaining unambiguous effects.
The quantification of Hrd and H,rs was made by a simple and rough model. We assumed onset of deterministic effects above a threshold of 1 Gy-Eq of whole body absorbed dose AD weighted for relative biological effectiveness (RBE) with a sigmoid dose-response curve p(AD) corresponding to a median lethal dose LD50= 4.5 Gy-Eq (IAEA, 2005).
The stochastic effects were estimated by assuming a linear no-threshold relationship between total effective dose Etot (Sv) and excess lethal tumors probability, with a nominal probability coefficient pD= 6 × 10−2 Sv−1 (ICRP, 2007).
Thermal and mechanical effects of nuclear weapons were estimated through data reported in unclassified literature (McKinzie et al., 2001; Glasstone & Dolan, 1977; McNaught, 1983). Damage by conventional explosives sometimes coupled with radioactive substances was taken into account by considering the lethal air blast range RL as a function of the explosive yield in kilograms of TNT (ATF, 1999; DHS, 2005).
Whenever applicable, the HOTSPOT 2.06 Health Physics Codes, developed at the Los Alamos National Laboratories, were used to give further estimates of nuclear explosion effects and for evaluating the radiological consequences of radioactive releases following explosions or fires. It is well known that these codes rely on a simple Gaussian plume model; it has been suggested (González, 2005) that such a model usually fails to give accurate predictions in an urban environment: a three-dimensional model, based on the solution of the full Navier-Stokes equations, should be more adequate. However, such approach requires detailed knowledge of boundary conditions and is far beyond the aim of this work, where we are interested in the comparison of several, roughly simulated scenarios instead of the rigorous description of individual scenarios.
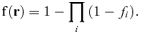 (2)
(2)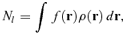 (3)
(3)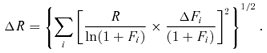 (4)
(4)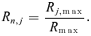 (5)
(5)The remainder of this section is devoted to the analysis of different scenarios.
2.1. Detonation of a Nuclear Weapon
The worst-case scenario involves a nuclear detonation in a densely populated area. The weapon may be either an improvised nuclear device (IND) assembled by using plutonium, or highly enriched uranium, or a ready-made device, such as a tactical nuclear warhead. It is generally assumed (NCRP, 2001; Mettler & Voelz, 2002; Putnam, 2002) that a terrorist organization would be limited to the construction of a nuclear weapon of less than about 10 kilotons (KT; one ton corresponds to the energy of 4.2 × 109 J liberated by the explosion of 103 kg of TNT). The possibility of a low-order nuclear detonation (also known as fizzle) due to warhead improper design or physical stress is also taken into account; this may lead to a yield as low as 10−2 KT.
The destructive effects of such a weapon are due to air blast, thermal flash, and ionizing radiation. The latter may be split into two categories: (1) initial radiation, released during the first minute from the detonation as an intense pulse of gamma rays and neutrons; and (2) residual radiation, emitted after the first minute from the detonation and due to radioactive debris, activation products, and early radioactive fallout. By weighting the neutron RBE energy dependence with a typical fission spectrum and by considering the dependence of doses on yield Y, distance r, and azimuth θ (McKinzie et al., 2001; Glasstone & Dolan, 1977; McNaught, 1983), we can compute the spatial distribution of the absorbed dose in tissue measured at the body surface due to initial radiation and the residual absorbed dose (which strongly depends also from the time te elapsed after the detonation and the permanence time Δt within the area interested by relevant radiation levels).
Assuming a ground-level explosion, the remaining effects may be characterized by the distance from the explosion where a given fatality rate is expected. Table II reports the approximate distances from the detonation point at which significant fatalities might occur. Notice that distances not associated with ionizing radiations are usually shorter than those reported in the literature (NCRP, 2001) because the reduction of weapon destructive power occurring with surface bursts with respect to air-bursts has been taken into account (Glasstone & Dolan, 1977). On the contrary, distances corresponding to prompt radiation are longer than usually reported because we have considered the whole body RBE-weighted absorbed dose instead of the sum of photon and neutron doses only.
| Yield (KT) | Total Destruction Range (100% Mortality) | Range for 50% Mortality from Thermal Burns (3.3 J m−2) | Range for 50% Mortality from Blast (O= overpressure; NM= outdoor nonpenetrating missiles; T= translational injuries; B= building destruction; PM= indoor penetrating missiles) | Range for 50% Mortality from Initial Radiation in the First Hour After Blast (4.5 Gy-Eq) | Range for 50% Mortality from Residual Radiation in the First Hour After Blast (4.5 Sv) | ||||
|---|---|---|---|---|---|---|---|---|---|
| O | NM | T | B | PM | |||||
| 0.01 | 5 | 40 | 30 | 30 | 30 | 40 | 60 | 490 | 1200 |
| 0.1 | 10 | 140 | 70 | 90 | 70 | 80 | 120 | 920 | 1800 |
| 1 | 20 | 430 | 150 | 220 | 190 | 170 | 260 | 1300 | 2300 |
| 10 | 40 | 1300 | 320 | 570 | 530 | 380 | 570 | 1700 | 3000 |
- Note: Blast effects like overpressure, outdoor nonpenetrating missiles, and translational injuries only affect people staying outdoors. Building destruction and penetrating glass missiles only affect people living indoors. The mortality ranges from thermal burns, and initial and residual radiation are obtained under the assumption of no shielding by buildings or other inner-city elements.
The parameters of interest for the model are: weapon yield and location, average population density, ratio of outdoor to indoor people, shielding by buildings, and local weather. It is convenient to separate the fatality rate into two components: fout(r, θ), corresponding to people staying outdoors when the explosion occurs, and fin(r, θ), corresponding to people inside buildings or underground. Each of these classes is characterized by different risk factors: for instance, people staying outdoors are subjected to both direct (overpressure) and indirect (nonpenetrating missiles and translational injuries) blast effects; people living indoors are subjected to indirect blast effects only (building damage and penetrating glass missiles).
The contributions to fin and fout were computed by using conventional methods reported in the literature (Glasstone & Dolan, 1977; McKinzie et al., 2001) and the HOTSPOT codes. Fig. 1 illustrates the fatality rates occurring for different weapon yields as a function of the distance from the explosion and for θ= 0°. It is easily seen that, for a given yield, a nuclear explosion is much more dangerous for people staying in open spaces than for people living inside buildings.
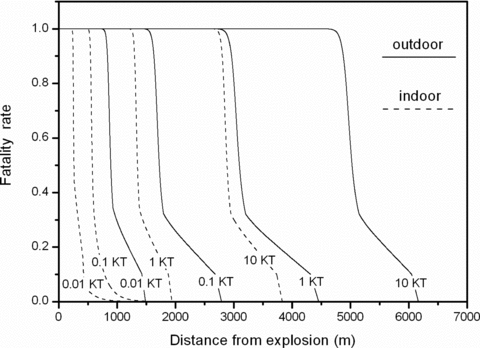
Fatality rates as a function of the distance from the explosion of an improvised nuclear device (IND) and for different weapon yields. The solid lines correspond to the fatalities occurring for people staying outdoors; the dashed lines correspond to the fatalities occurring for people living indoors.
2.2. Nuclear Sabotage
Due to the limited nuclear activities in Italy, the model will focus on the following scenarios only: (1) sabotage of a nuclear research reactor; and (2) sabotage of a nuclear fuel cycle plant in the decommissioning phase.
The core radionuclide inventories of research reactors are much poorer than those of nuclear power plants. In addition, the risk of core melt and fission product release in the event of a loss-of-coolant accident (LOCA) is lower with respect to power reactors. For instance, two among the four still-operating Italian research reactors are of the TRIGA (training, research, isotopes, general atomics) type, which have intrinsic shutdown capabilities as a consequence of their negative temperature coefficient of reactivity. Nevertheless, research reactors are less protected than power reactors and are usually located in or near a city, so a successful attack would result in significant radioactive release and contamination of a densely populated area (Bunn et al., 2003a).
Nuclear fuel cycle plants are located at some distance from population centers; usually, their radionuclide inventories are not of public domain. The defensive barriers of such plants in the decommissioning phase are probably of the same strength as those deployed by research reactors.
The parameters of interest for the model are: radionuclide inventory and released fractions, mode of sabotage attack, population density distribution around the target, ratio of outdoor to indoor people, shielding by buildings, and local weather. By assuming that the sabotage will involve conventional explosive, the effects of the blast will be taken into account by considering the fatality rate as a function of explosive yield and distance. The effects due to release of radioactivity following the attack will be simulated with the HOTSPOT computer codes.
2.3. Concealing a Radiation Exposure Device
A stolen or orphaned high-activity radioactive source may be used to build a radiation exposure device (RED) (ICRP, 2006). If the unshielded source is concealed in a place frequented by the public and not monitored for ionizing radiations, casualties and fatalities from the effects of ionizing radiations may occur before the source is detected. Source selection is guided by a tradeoff between effectiveness of the attack (which increases with activity) and capability to deploy the weapon (which decreases with activity). Radioactive sources of very low activity are unable to produce enough damage per unit time; on the other hand, sources of very high activity are difficult to shield or, if unshielded, will rapidly make terrorists unable to perform their attack. In practice, the terrorists' choice must fall within the following categories of gamma-emitting radioactive sources: industrial radiography, teletherapy, and research irradiators.
The parameters of interest for the model are: effective activity of the source (considering self-absorption and partial shielding), radiation quality and energy, population density distribution, and duration and reiteration of the attack.
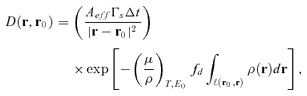 (6)
(6)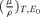 is the mass absorption coefficient of tissue at the energy E0 and where the factor:
is the mass absorption coefficient of tissue at the energy E0 and where the factor:
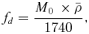 (7)
(7) equal to the average mass of an individual and the average population density, respectively, accounts for the partial shielding of the source by the people themselves. An average individual height of 1.74 m was assumed (this explains the numerical coefficient in Equation (7)); the symbol ℓ (r0, r) appearing in Equation (6) indicates the straight line connecting point Q to point P. Notice that Equation (6) takes into account primary radiation only; in this approximate model any contribution to the dose given by scattered radiation is considered negligible.
equal to the average mass of an individual and the average population density, respectively, accounts for the partial shielding of the source by the people themselves. An average individual height of 1.74 m was assumed (this explains the numerical coefficient in Equation (7)); the symbol ℓ (r0, r) appearing in Equation (6) indicates the straight line connecting point Q to point P. Notice that Equation (6) takes into account primary radiation only; in this approximate model any contribution to the dose given by scattered radiation is considered negligible.2.4. Activation of a Radioactive Dispersion Device
A radioactive dispersion device (RDD), obtained by coupling conventional explosive with an ordinary radioactive source or with fissile material, may be detonated to spread radioactive contamination over a large area (NCRP, 2001; DHS, 2005; ICRP, 2006). The effects of such a weapon are of two kinds: (1) mechanical, including air blast, fragmentation, and damage to buildings and infrastructures; (2) radiological, including external exposure from fragments and radioactive cloud, and internal exposure from inhalation of smoke, contamination of wounds, and inadvertent ingestion of contaminated material. The parameters of interest for the model are: conventional explosive yield, nature, activity, and respirable released fraction of the radioactive material, population density distribution, and local weather. The impact of each effect on the overall fatality rate was computed with the methods described in Section 2.2.
2.5. Contamination of Water and Foodstuff
The use of radioactive substances to contaminate drinkable water or foodstuff is usually considered a very ineffective terroristic attack method due to the enormous quantities of radioactive material needed to reach the required level of contamination. However, a recent poisoning episode with a lethal dose of 210Po has drawn the attention of authorities and public opinion to this attack modality.
The contamination of drinkable water was simulated by considering the following parameters:
- 1
W, the daily per capita needs of water;
- 2
Np, the number of people served by a given water reservoir;
- 3
Nd, the number of days the given water reservoir may supply without replacement;
- 4
wd, the daily per capita amount of water drunk;
- 5
A, the activity of radionuclide used to contaminate the water reservoir;
- 6
fs, the soluble fraction of the given radionuclide;
- 7
hing, the committed dose equivalent per unit intake by ingestion.
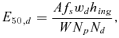 (8)
(8)3. RESULTS
The financial resources required to acquire an intact nuclear weapon are considerable. There are different ways to perform this task (theft with or without insider support, transfer from a state during political unrest, etc.), but all estimates indicate a budget of many million dollars (Ferguson & Potter, 2004); in our model we assumed M= 103× (Y/10) × 106$. In addition, many technical obstacles need to be overcome in order to detonate the weapon. Permissive action links (PALs)—designed to ensure that nuclear weapons cannot be exploded without the input of proper codes—and environmental sensing devices—designed to ensure that the weapons can be used only according to a specific mission profile—are implemented in most warheads. Disabling or bypassing these safeguards without expert assistance may be very difficult if not impossible. The terrorist task force should be composed of at least a dozen people, working for about one year; thus O≈ 106$ (we assumed a 105$ cost for a man-year).
The terrorists may also attempt to obtain fissile material from the weapon in order to build their own IND; another way to produce an IND is to acquire highly enriched uranium or plutonium (by purchase, diversion, etc.) or to fabricate the fissile material by reprocessing spent or fresh nuclear reactor fuel. The required amount of material depends on technical capability, weapon design, and yield (Cochran & Paine, 1995). Based on some estimates (Barnaby, 2004; Ferguson & Potter, 2004), we assumed a cost of fissile material of the order of 10 × (Y/10) × 106$; the cost of a small reprocessing plant should be of the order of 107$. A group composed by a dozen experts working for about one year is considered sufficient for this task; thus O≈ 106$.
In order to give an estimate of H we simulated the detonation of a nuclear weapon with a yield in the range 10−2–10 KT placed in the center of a city. By assuming a constant population density, we computed the number Nl/ρ of life losses per unit population density. The typical average population density of main Italian cities lies in the range 8 × 10−5 to 8 × 10−2 inhabitants per square meter (however, due to considerable tourist flows in most of them, these values are subjected to sudden although localized variations during the day). Nl/ρ depends on weapon yield and increases with outdoor to indoor people ratio Nout/Nin. Fig. 2 shows the case corresponding to Nout/Nin= 1 as a function of weapon yield. By varying Nout/Nin in the range ¼–4 the values of Fig. 2 may change up to approximately ± 20%. Taking into account the variability of the above parameters, we found that the human losses may range between a few hundred and 100,000 fatalities, approximately. However, these figures are subject to large variability due to their dependence on population distribution, local weather, fission fraction, and weapon design (McKinzie et al., 2001).
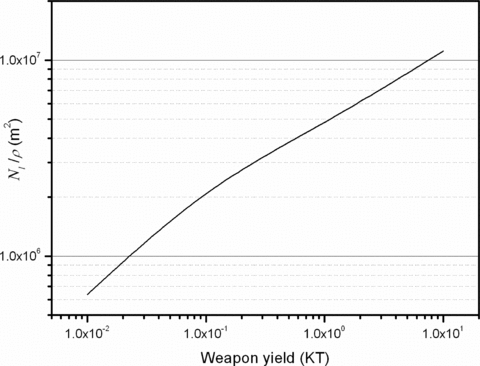
Expected number of life losses from IND detonation per unit population density as a function of weapon yield and for unit ratio Nout/Nin of outdoor to indoor people.
The economical damage produced by a nuclear explosion due to immediate property damage, radioactive contamination, people relocation, and long-term health effects has been estimated to be of the order of trillions of dollars. For instance, the detonation of a 10 KT weapon would result in about 1.2 trillion dollars of economic losses (Bunn et al., 2003b; Bunn, 2006). In our model, we assumed a scaling law for D with the weapon yield like D≈ 1012× (Y/10) $; thus, for the range of weapon yields considered in the present work, the economical damage lies between 109 and 1012$.
Sabotaging a nuclear facility, especially with a ground assault, is considered a less demanding task with respect to nuclear weapon detonation. The material cost can be estimated as M≈ 105$, while the assault commando would be composed of no more than 20 people with a training of approximately 6 months; thus O≈ 106$. The following scenarios were considered: (1) attack on a TRIGA class research reactor; (2) attack on a plutonium plant of a research center. The former is a pool-type reactor with a power of 250 kW and 250 MW in the stationary and pulsed regime, respectively. The intrinsically safe features of this kind of reactor makes core melting extremely difficult, if not impossible. However, pool draining followed by activation of conventional explosive may result in significant dispersion of core inventory. In our simulation, we assumed the release of (Bunn et al., 2003a): (1) 100% of noble gases and halogens; (2) 61% of caesium isotopes; (3) 7% of tellurides; and (4) 1% of low volatiles.
It was assumed that the plutonium plant contained approximately 4 kg of 239Pu. We simulated the dispersion of such fissile material following sabotage with conventional explosive. Fig. 3 illustrates the expected number of life losses (including the effects of the blast) as a function of population density. As expected, both curves increase with ρ, but for the research reactor there is a threshold density (1.7 × 10−3 m−2, approximately) under which no fatalities occur. By taking into account the effective location of these targets (downtown Pavia for the TRIGA reactor and about 40 km far from Rome for the plutonium plant), we found that H was approximately 40 people for plutonium plant sabotage and 10 people for nuclear reactor sabotage. The economical damage associated with reactor sabotage can be estimated by considering that the core inventory is roughly proportional to reactor power and that the damage associated with the Chernobyl disaster (where a RBMK-1000 reactor with a power of 1 GW was involved) amounted to more than $200 billion. Therefore, we assumed D≈ 3 × 1011× (P/1000) $, where P is the reactor power in MW; thus D≈ 108$ for the TRIGA reactor. The damage associated with the sabotage of plutonium plant was estimated by scaling the RDD damage discussed below with the different amount of plutonium involved.
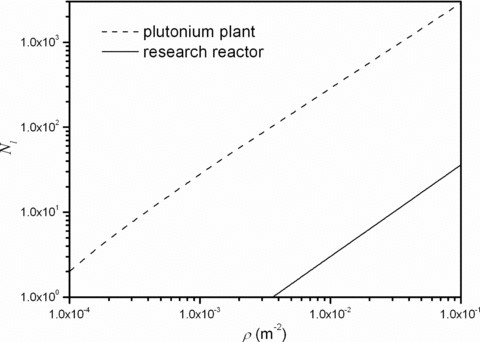
Expected number of life losses from nuclear sabotage as a function of population density. The solid line corresponds to sabotaging a TRIGA research reactor; the dashed line corresponds to sabotaging a plutonium plant.
The radioactive source required to build a RED can be obtained by theft or by purchase, with M≈ 5 × 104$. The terrorist group can be composed of 1–6 people operating for approximately 3 months, thus giving O≈ 0.3–2 × 105$. The effects of such a weapon were analyzed by considering a RED built with a 185 TBq 60Co teletherapy source placed within a big stadium. If the positioning of the source lasts less than 2 hours, a shield light enough to be transported by hands may be used without onset of determinist effects for the carriers. The geometry of a stadium was simplified with a simple rectangular frame. The population density was taken as constant within the stands and zero elsewhere. The expected number of life losses Nl depends on the position Q(r0) of the source. We found a number of positions where Nl was maximum; Fig. 4 illustrates the maximum expected number of life losses as a function of population density for two values of Δt. In this graph the components Nl,s and Nl,d of Nl, due to stochastic and deterministic effects, respectively, are also shown. For a duration Δt= 2 hours and a population density greater than 2.5 m−2, typical of a soccer match close to full stadium capacity, Nl,d becomes greater than Nl,s.
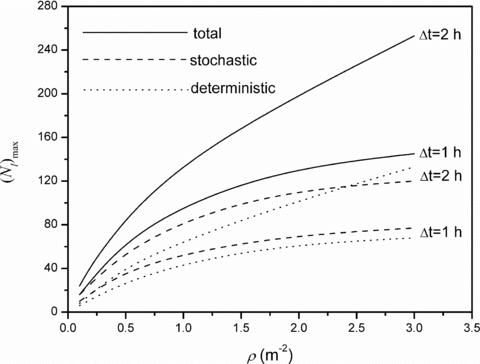
Maximum expected number of life losses following the concealing of a RED in a big stadium as a function of population density and for two different durations of the attack. The solid line represents the total number of life losses. The dashed and dotted lines represent the life losses attributable to stochastic and deterministic effects, respectively.
For typical densities of 0.3–3.0 m−2 and a duration of about 2 hours we found H≈ 60–250 fatalities. Notice that if the source is not detected, the attack may be repeated several times, thus multiplying the value of Nl by the corresponding factor. The economical damage associated with such scenario is mainly due to the cost of medical treatment and follow-up of the exposed people. By assuming approximately 130 people affected by radiation sickness (at a cost of approximately 2 × 104$ per person per year and a duration of 30 years) and 8 × 104 people requiring screening (at a cost of approximately 103$ per person), we estimated D≈ 2 × 108$.
Building a radioactive dispersion device has operational costs similar to those of a RED. If a conventional radioactive source is used, the material cost, too, is comparable to that of a RED; however, if fissile material is used, the cost grows up to M≈ 2 × 106$ per kilogram. We considered two kinds of RDD: the former built with 1 kg of weapon-grade plutonium and the latter built with a 185 TBq 60Co teletherapy source. We simulated the effects of the explosion with the HOTSPOT computer codes under two separate assumptions: (1) airborne released fraction of radioactivity fr= 1, regardless of explosive yield; and (2)fr proportional to the explosive yield (with a plateau at approximately 50 kg TNT). Fig. 5 reports the number Nl/ρ of expected life losses per unit population density as a function of explosive yield. Assumption (1) gives Nl/ρ as a decreasing function of explosive yield because the same amount of radioactivity is dispersed over a larger area with increasing the yield. The more realistic assumption (2) gives the increasing curves of Fig. 5; at low explosive yields these curves differ by almost two orders of magnitude with respect to the corresponding curves obtained under assumption (1). The incidence of blast effects was investigated by computing the ratio Nl,blast/Nl, where Nl,blast is the expected number of life losses due to the overpressure generated by the blast only; under assumption (1) this ratio never exceeds 20%, while under assumption (2) it may be as high as 50%. The total number of fatalities depends on population density and explosive yield; for a yield of 50 kg TNT we found H≈ 30 for both plutonium and cobalt RDD. Given the strong dependence of radioactive plume dispersion on weather conditions, this result is comparable to that of a previous analysis performed on a RDD made with 0.45 kg of explosive and 1 kg of 239Pu (Durante & Manti, 2002). Another simulation takes into account a RDD made with 23 kg of explosive and a 137Cs source whose activity lies in the range 370–3200 TBq (Dombroski & Fischbeck, 2006); in this case, the number of fatalities lies in the range ≈40–60, depending on evacuation speed. An analogous simulation has been made by considering up to 1,500 kg of high explosive (in a truck bomb) coupled with a 85-TBq 137Cs source (DHS, 2005). In this case, the blast is the main cause of fatalities (H= 180), so the radiological character of the weapon is overwhelmed by mechanical effects (we repeated this simulation with HOTSPOT and we found H≈ 60, probably due to different assumptions on population density). Therefore, the higher the explosive yield, the thinner the difference between a RDD and an improvised explosive device. There are large discrepancies in the current literature about the expected damage due to radioactive contamination of environment, buildings, and relocation of people living in contaminated areas. Current estimates range from 108 to 1011$ (Helfand et al., 2006; DHS, 2005; Ferguson & Potter, 2004). This large span is due to differences in the adopted intervention levels for cleanup, resettlement, and in the quotation of the lost properties.
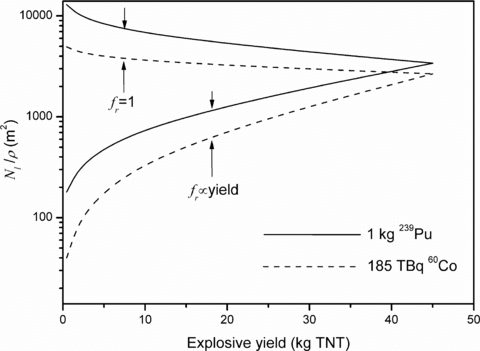
Expected number of life losses from activation of a radioactive dispersion device (RDD) per unit population density as a function of the explosive yield (expressed in kilogram of TNT) and under two different assumptions about the released fraction of radioactivity fr: full release, regardless of explosive yield and released fraction proportional to the explosive yield. The solid line corresponds to a RDD built with 1 kg of weapon-grade plutonium; the dashed line corresponds to a RDD built with a 185 TBq teletherapy source.
Finally, we considered the contamination of water reservoirs by means of 131I or 137Cs sources. These materials can be obtained at a cost comparable to that of a RED or by theft. The terrorist group can be composed of 1–6 people operating for approximately 3 months, thus giving O≈ 0.3–2 × 105$. A terrorist organization can easily steal or purchase the daily 131I supply from a nuclear medicine department. According to the Italian regulations about radioactive sources, the maximum daily iodine supply for diagnosis cannot exceed 1 TBq. The assumption was made that such amount was completely released in a water reservoir serving 1.5 × 105 people, with a daily water consumption of 400 liters per capita (including water distribution inefficiency) and a daily drinkable water intake of 1.5 liters per capita. From Equation (8), with fs= 100%, h(g)ing= 2.2 × 10−8 Sv Bq−1 and Nd= 1 (with Nd= 1 corresponding to the maximum radioactivity concentration) we obtained a committed collective dose S50≈ 80 man Sv. The expected number of life losses (from stochastic effects only) was therefore H≈ 5. The theft of a teletherapy source is technically more complex than a nuclear medicine supply, but the available activity is much higher. A 74-TBq 137Cs source made of highly soluble cesium chloride salts was considered; by assuming that such a source was powdered and released in a water reservoir with the same characteristics as above, under the assumption fs= 60% and with h(g)ing= 1.3 × 10−8 Sv Bq−1, we obtained a committed collective dose S50≈ 2200 man Sv. In this case, the expected number of life losses from stochastic effects was H≈ 130. Notice that the water concentrations 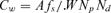 of both 131I and 137Cs are several orders of magnitude higher than guidance levels for these radionuclides in drinking water (WHO, 2004). The cost associated with screening for contamination a large number of people was estimated to be D≈Np× 102$.
of both 131I and 137Cs are several orders of magnitude higher than guidance levels for these radionuclides in drinking water (WHO, 2004). The cost associated with screening for contamination a large number of people was estimated to be D≈Np× 102$.
For each of the above scenarios we adjusted the Fi's to maximize R and then we ordered the ranks and proceeded to normalization according to Equation (5). The maximum rank was found for the detonation of a 0.1 KT IND in downtown Milan. Fig. 6 illustrates the normalized ranks of the above scenarios in decreasing order from left to right. The overall uncertainty for each scenario was computed by using Equation (1) together with estimates of ΔFi obtained either as standard deviation of a known set of values or (when only the range limits were known) as (maximum Fi– minimum Fi)/√12. For instance, the uncertainty on population density due to concentration variability within different districts of the same city (tourists flow included) was estimated ≈90% on the basis of published data. Another example is given by the component of ΔD due to the variability of the distance within which a building undergoes severe damage following a nuclear explosion; for a 10 KT weapon this distance may vary from approximately 400 m up to 1,300 m (depending on building type) and this accounts for an ≈80% uncertainty in the expected damage. Table III summarizes the relative uncertainties for each scenario class estimated with the above criterion.

Summary of the normalized maximum ranks of Equation (5) for the different scenarios analyzed in this work. The error bars correspond to one standard deviation.
| Scenario Class | ΔNr/Nr | ΔH/H | ΔD/D | ΔM/M | ΔO/O | ΔR/R |
|---|---|---|---|---|---|---|
| IND | 2% | 280% | 80% | 30% | 30% | 29–36% |
| Ready-made nuclear weapon | 2% | 280% | 80% | 30% | 30% | 27–35% |
| RED | 2% | 30% | 30% | 30% | 40% | 13% |
| RDD | 2% | 30% | 30% | 30% | 40% | 14–15% |
| Nuclear sabotage | 2% | 30% | 30% | 30% | 30% | 13–18% |
| Water contamination | 2% | 30% | 30% | 30% | 30% | 13–16% |
Despite the partial superposition due to the uncertainty, we can recognize three regions in the graph. (1) 80% <Rn≤ 100%, which includes all IND scenarios. Indeed, for this kind of weapon there is a tradeoff between effectiveness (given by its yield) and cost of fissile material. This gives a maximum at 0.1 KT, but this maximum is quite flat so that all IND scenarios appear to be equivalent. (2) 60 < Rn≤ 80%, which includes all ready-made nuclear weapons, the RED, water contamination with 137Cs, and the RDD made with high explosive yield and 137Cs. For the same reasons as above, all scenarios associated with ready-made nuclear weapons can be considered equivalent. (3) Rn≤ 60%, which includes all the remaining scenarios.
This result is particularly worrying from the point of view of prevention because a nuclear weapon, specially if made with highly enriched uranium, is extremely difficult do detect due to its low radiation signature and small dimensions. Apart from nuclear weapons (including the ready-made ones), the second scenario class in the ranking scale is the concealing of a RED in a stadium, followed by high explosive yield RDD and contamination of water reservoirs with cesium chloride. The activation of radioactive dispersion devices with lower explosive yield, which (according to some unverified media sources) is considered the most likely scenario by the Italian intelligence agency, has a relatively low rank; this is attributable to the rather small damage produced by such RDDs in terms of life losses. Indeed, according to some authors (Durante & Manti, 2002), chemical or biological weapons are much more efficient than dispersal of radioactivity. Nuclear sabotage and contamination of drinkable water with iodine are the less attractive scenarios for terrorists, the former due to the lack of valuable targets and the latter for the difficulty of reaching adequate radioactivity concentrations.
4. CONCLUSIONS
A quantitative criterion for ranking the different scenarios of nuclear and radiological terrorism has been developed. This model does not aim to predict terroristic events but only to indicate which scenario is the more convenient—from the point of view of a terroristic organization aiming to inflict as much damage as possible—in terms of a proper combination of the factors favoring and discouraging the attack.
These factors were quantified according to a logarithmic scale and the model was implemented to several scenarios typical of the Italian context. Each relevant scenario was modeled in a simple but not trivial way in order to estimate the expected damage in terms of probable life losses. The application of the ranking method indicates that the favorite scenario is a nuclear detonation with an improvised weapon in the historical center of an important town; other nonnuclear scenarios with relevant ranks are the concealing of a radiation exposure device and the activation of a radioactive dispersion device with high explosive yield.
The proposed criterion is completely general and can be applied to any given scenario, provided a proper modeling is given. Further improvements of this approach can be obtained by sharpening the knowledge of those parameters for which only a range of variability has been indicated in the present work, and by increasing the accuracy of scenario modeling, specially when considering the atmospheric release of radioactivity in metropolitan areas.




