Efficiency of Even Separation of Parallel Elements with Variable Contest Intensity
Abstract
The article considers strategic defense and attack of a system that can be separated into parallel elements. The defender distributes its resource between separation and protecting the elements from outside attacks. The vulnerability of each element is determined by an attacker-defender contest success function, which depends on a contest intensity that may increase or decrease through the separation process. The article determines criteria of separation efficiency for systems without performance redundancy and 1-out-of-N and Q-out-of-N systems with performance redundancy. For the systems with performance redundancy the cases of expected damage proportional to the probability that the demand is not met, and expected damage proportional to the unsupplied demand, are considered.
BASIC DEFINITIONS:
-
- Performance
-
- quantitative measure of task performing intensity of element or system (capacity, productivity, processing speed, task completion time, etc.).
-
- Demand
-
- required level of performance.
-
- Performance redundancy
-
- surplus performance that allows the system to meet a demand even if some of the elements are incapacitated (destroyed).
-
- Element
-
- lowest-level part of the system, which is characterized by its vulnerability and performance.
-
- Vulnerability
-
- probability of destruction.
-
- Protection
-
- technical or organizational measure aimed at reduction of destruction probability of system elements in the case of attack.
-
- Separation
-
- action aimed at preventing simultaneous destruction of several elements in the case of a single attack (can be performed by spatial dispersion, by encapsulating different elements into different protective casings, by using different power sources, etc.).
-
- Unsupplied demand
-
- difference between the demand and system performance in the case when the demand is not met.
-
- Loss of demand probability
-
- probability that the system cannot function at performance level that meets 100% of the demand.
NOTATIONS
-
- R, r
-
- attacker's and defender's resources
-
- T, t
-
- attacker's and defender's effort per single element
-
- m, μ
-
- contest intensities before and after separation
-
- s
-
- separation cost
-

-
- upper limit for the separation cost (when the separation is efficient)
-
- G
-
- cumulative system performance
-
- N
-
- number of identical separated system elements
-
- g
-
- performance of single element
-
- F
-
- system demand
-
- Q
-
- number of elements that should survive to prevent the unsupplied demand
1. INTRODUCTION
The September 11, 2001 attack illustrated that major threats today involve strategic attackers. Yet most risk analysis assumes strategic defenders facing a fixed and immutable threat.3 This article assumes that both the defender and attacker are fully strategic optimizing agents.4 We consider a system that delivers a service scaled by its performance. Examples of such systems are power generators, water supply systems, telecommunications systems, or, more generally, any system required to meet a demand of some kind. The defender has a resource that gets distributed between separating the system into multiple dispersed elements and protecting the elements from attacks by an attacker. The attacker has a resource that gets distributed evenly among all elements, or among a chosen subset of the elements.
The defender prefers the system to deliver its given performance without damage. The expected damage can be proportional to the probability of not meeting the demand, or proportional to the amount of unsupplied demand. The attacker prefers to inflict maximum damage by destroying as many system elements as possible. The phenomenon is modeled as a contest between a defender and an attacker over damage. Both agents allocate costly resources to win the contest. The vulnerability (probability of destruction in the case of attack) of each element depends on the attacker's and defender's resources allocated to this element, which is determined by an attacker-defender contest success function. Contests have variable intensity. Low intensity means that neither the defender nor the attacker can easily get the upper hand. This may be due to lack of decisiveness, fierceness, ability, resources, competence, or due to factors outside the defender's and attacker's control (weather, chance, etc.). High intensity gives significant advantage of slight force superiority over one's opponent, which is a characteristic of “winner-take-all” contests.
Let us illustrate the mechanisms through which the contest intensity gets changed. These mechanisms can in a multiplicity of ways be linked to distance between, positioning of, and size of elements. First, increasingly democratic attitudes and decision-making procedures by the defender and attacker reduce the ability of one side to gain an advantage. An example from democratic constitutions is separation of powers and bills of rights, which reduce the decisiveness of majority supremacy, which tends to moderate the intensity of factional struggles, and thus reduces the contest intensity.
Second, assume the presence of multiple systems with overlapping characteristics in kinds and degree of performance, multiple defenders, and multiple attackers. With stable market conditions, neither group (industrial imperium, company, business firm, enterprise) easily gets the upper hand in the fighting. This is possible when the groups have divided the market geographically or according to target consumer groups, or when heavy sunk costs in production technology, procedures, personnel training, marketing strategies, etc. hamper the way in which the groups can change their interference with each other, for example, through the entering of new markets and the employment of new strategies. Such stable market conditions can generate low contest intensity.
Third, an example from warfare, that increases the contest intensity is the combination of airplanes, tanks, and mechanized infantry in World War II, which allowed the offense to concentrate firepower more rapidly than the defense, which intensified the effect of force superiority (Hirshleifer, 1995 pp. 32–33). Clausewitz (1832) also acknowledged that the attacker has advantages such as surprise. Today, with the emergence of the cyber era, attacker advantages become even more common. An attacker can choose the time and how to attack, and sometimes even the place for where to attack. Within such a context Anderson (2001) argues that “defending a modern information system could … be likened to defending a large, thinly populated territory like the nineteenth century Wild West: the men in black hats can strike anywhere, while the men in white hats have to defend everywhere.”
Fourth, increasingly autocratic and dictatorial attitudes and decision-making procedures by the defender and attacker increase the ability of one side to gain an advantage. In political systems where winner takes all, contest intensity is very high, consensus building is difficult, and both sides may fight each other to death.
Fifth, high contest intensity can also arise in volatile industries where parameters frequently change, when massive financial resources can be compiled/concentrated (for example, by employing financial derivatives; options, futures) in time/place for hostile takeovers, when there are few legal constraints to dampen aggressive and disruptive behavior, when technological changes are rampant, when consumer preferences change quickly, when turnover is high, or when exchange rates, interest rates, and taxes fluctuate. In a market with one supplier intent on defending a system that delivers a product with a specified performance, and an attacker equally intent on preventing the product, contest intensity can be very high.
Besides protecting the system the defender has the additional option of separating the system into N independent identical parallel elements, which makes impossible destruction of more than one element by a single attack. This gives N contests between the defender and attacker. Separation is, and should also be, a rightfully acknowledged and standard practice for reducing system risk in the face of intentional attacks and nonintentional impacts (Westmark, 2004; Levitin & Lisnianski, 2001; Malakhoff et al., 1998). Separation is aimed at preventing the simultaneous destruction of several elements in the case of a single attack. It can be performed by spatial dispersion, by encapsulating different elements into different protective casings, by using different power sources, etc. The protection is a technical or organizational measure aimed at the reduction of the destruction probability of system elements in the case of attack.
The defender defends each element equally much, and the attacker attacks each element equally much. The defender distributes its resource between separation and protecting the elements from outside attacks. Both separation and protection are costly. The defender may decide not to separate, which means engaging in a single contest over the entire system with the attacker and spending all of the available resources into protecting the system. Another possible decision is to separate the system into many elements with weaker protection, and engage with the attacker in as many contests as there are elements.
The defender has to decide, first, whether or not to separate, second, how to allocate its resource between separation and protection, and third, how the allocation depends on the change in contest intensity through separation, depends on the relative amount of resources available to the defender and attacker, and depends on the system demand. This article analyzes the conditions of separation efficiency for different types of systems. We consider systems without performance redundancy, and 1-out-of-N systems and Q-out-of-N systems with performance redundancy. Depending on the attack success, each element is assumed to either work at a nominal performance or be destroyed (electronic devices, mechanical equipment, etc.). This is realistic since multistate systems that can work with different performance rates can usually be decomposed into two-state elements (for example, steam generator capacity can vary depending on availability of heating sections, which can be made dichotomous).
The contest intensity usually changes through the separation process, upward or downward, dependent on the multiplicity of ways in which separation can proceed. Let us exemplify how separation influences the contest intensity. First, the defender can regulate the distance between dispersed elements. Larger distance between elements makes it more difficult for the defender to deliver and deploy protective facilities, and more difficult for the attacker to arrange a concerted and focused attack since the attacker must extend its focus over a larger area. Hence larger distance between elements lowers the contest intensity. Second, the defender can position the dispersed elements in multiple locations (mountain, valley, forest, open terrain, underground, urban area, sea, air, etc.), and camouflage them in multiple manners, so that it gains an advantage. This makes it more challenging for the defender to arrange the protection, and hampers the attacker's ability to detect and engage. Such superiority of defense over attack, argued for by Clausewitz (1832) as relevant for classical warfare, can generate very low contest intensity. Clausewitz (1832, 6.1.2) states that “the defender enjoys optimum lines of communication and retreat, and can choose the place for battle.” Other examples of defender superiority generating low contest intensity are the use of trenches combined with the machine gun in World War I, castles and fortresses with cannon fire from higher elevations, and the use of checks, guards, and controls to minimize the attacker's ability to engage. The superiority of the defense over the attack appears to be even larger for production facilities and produced goods than for Clausewitz's mobile army (Hausken, 2004).
Third, the defender can alter the size of dispersed elements. Consider an industrial facility that can be attacked by missiles with limited precision. The attack resource is determined by the number of missiles and their warhead power. The defense resource is determined by the defender's strength of concrete anti-missile shields, and the defender's ability to make the dispersed elements sufficiently small. Size reduction can be very costly, may involve the use of alternative materials, and may reduce the protective shields of the elements. This leaves less resources for the defense of the elements, which means that the defender is more poorly equipped to defend, or may have to defend with less effective weapons. The concentrated facility covers a large area that can be easily reached by the missiles. The attack outcome strongly depends on the relation between the attacker's and defender's resources. When the system is separated, each separated element covers a much smaller area, which reduces the probability of missile hit. Chance plays a much greater role in the outcome of attacks against smaller targets, which reduces the contest intensity.
To illustrate mathematically how a system's vulnerability depends on separation and the contest intensity, assume that the attacker has twice as much resources as the defender. A contest can be modeled with the ratio 22/(22+ 12) = 4/5 (see Equation (1)) before separation where 2 is the attacker's resource, 1 is the defender's resource, and the exponent 2 is the contest intensity. This ratio expresses the system vulnerability, which increases if the attacker's resource increases above 2, or the defender's resource decreases below 1. If separation reduces the contest intensity from 2 to 1, the vulnerability decreases to 21/(21+ 11) = 2/3. The defender prefers the lower vulnerability if the separation cost needed for the lower vulnerability is acceptable. This result is different if the defender has more resources than the attacker, or if separation increases the contest intensity and the result depends on the number of elements and how damage compromises demand.
Section 2 presents the model. Section 3 analyzes the model without performance redundancy. Sections 4 and 5 consider 1-out-of-N systems and Q-out-of-N systems with performance redundancy. Sections 5.1 and 5.2 distinguish between whether the system totally fails or does not totally fail when the demand is not met. Section 6 concludes.
2. THE MODEL
We consider a system with total cumulative performance G. If no separation is imposed, a single successful attack destroys the entire system. The system can be separated into N independent identical elements with the same functionality. Each element has performance g=G/N. That is, each element can perform the same function as the system, but with N times smaller performance. A single successful attack on the separated system can destroy only one element, and cause system cumulative performance reduction from G to G(N− 1)/N. The damage caused by an attack is associated with reduction of the cumulative system performance in the case of destruction of some elements.
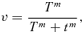 (1)
(1)The parameter m is a characteristic of the contest, which can be illustrated by the history of warfare. Low intensity occurs for components that are predictable, and where the individual ingredients of each component are dispersed, that is, physically distant or separated by barriers of various kinds. Neither the defender nor the attacker can get a significant upper hand. An example is the time prior to the emergence of cannons and modern fortifications in the 15th century. Another example is entrenchment combined with the machine gun, in multiple dispersed locations in World War I (Hirshleifer, 1995, pp. 32–33). High m occurs for components that are less predictable, and where the individual ingredients of each component are concentrated, that is, close to each other or not separated by particular barriers. This may cause “winner-take-all” battles and dictatorship by the strongest. Either the defender or the attacker may get the upper hand. The combination of airplanes, tanks, and mechanized infantry in World War II allowed both the offense and defense to concentrate firepower more rapidly, which intensified the effect of force superiority.
Separation means generating a more dispersed system, for example, physically distant elements or separation by barriers of various kinds. This may cause lower contest intensity m. But, the opposite can also occur. Separation may alter the visibility, accessibility, location, or other characteristics of the dispersed elements so that the net effect is higher contest intensity. See Hirshleifer (1995) for a discussion of factors that may alter the contest intensity.
3. NO PERFORMANCE REDUNDANCY
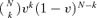 . The expected damage caused by destruction of k out of N elements is kg=kG/N. The expected damage is
. The expected damage caused by destruction of k out of N elements is kg=kG/N. The expected damage is
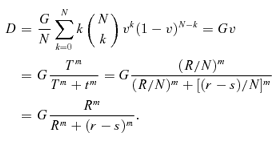 (2)
(2)This means that the expected damage is proportional to the cumulative system performance, proportional to the element vulnerability, and independent of the number N of elements. The expected system performance is G − D=G(1 −v). If the vulnerability is 0, the expected damage is 0, and the expected performance is G. If the vulnerability is 1, the expected damage is G, and the expected performance is 0.
 (3)
(3)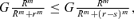 which compares the expected damage without and with separation, separation increases the expected damage. Even if separation costs nothing, it does not reduce the system expected damage. Hence separation with even allocation of the defender's effort is not beneficial. But, this presumes that the contest intensity m is preserved through the separation contest. Such preservation is not necessarily realistic. Quite the contrary. Separation alters the system so fundamentally that the contest intensity over system functionality can be expected to change, downward or upward. We thus assume that separation changes the contest intensity from m to μ. The expected damage after separation is
which compares the expected damage without and with separation, separation increases the expected damage. Even if separation costs nothing, it does not reduce the system expected damage. Hence separation with even allocation of the defender's effort is not beneficial. But, this presumes that the contest intensity m is preserved through the separation contest. Such preservation is not necessarily realistic. Quite the contrary. Separation alters the system so fundamentally that the contest intensity over system functionality can be expected to change, downward or upward. We thus assume that separation changes the contest intensity from m to μ. The expected damage after separation is
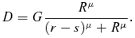 (4)
(4)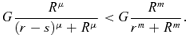 (5)
(5)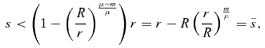 (6)
(6) for the separation cost s. The limit
for the separation cost s. The limit  is positive when R > r and μ < m, or when R < r and μ > m, and is otherwise negative (negative
is positive when R > r and μ < m, or when R < r and μ > m, and is otherwise negative (negative  means that the separation is always ineffective).
means that the separation is always ineffective).Proof: Follows from solving Equation (5) with respect to s, and assessing when  is positive.
is positive.
To interpret Proposition 1, assume first that R > r, which means that the attacker is advantaged with a larger resource than the defender. If separation increases the contest intensity, μ > m, then the attacker will get an even bigger advantage. (For example, R= 3, r= 2, m= 1, μ= 2 gives vulnerability v= 31/(31+ 21) = 3/5 before separation, and vulnerability v= 32/(32+ 22) = 9/13 after separation. The attacker prefers the latter higher vulnerability.) This gives 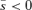 and the defender will not separate. However, if separation decreases the contest intensity, μ < m, then the defender disadvantaged with R > r has scope for improving its utility if the separation cost is not too large as determined by
and the defender will not separate. However, if separation decreases the contest intensity, μ < m, then the defender disadvantaged with R > r has scope for improving its utility if the separation cost is not too large as determined by 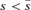 . (For example, R= 3, r= 2, m= 2, μ= 1 gives vulnerability v= 9/13 before separation, and vulnerability v= 3/5 after separation. The defender prefers the latter lower vulnerability if the separation cost needed for the lower vulnerability is acceptable.)
. (For example, R= 3, r= 2, m= 2, μ= 1 gives vulnerability v= 9/13 before separation, and vulnerability v= 3/5 after separation. The defender prefers the latter lower vulnerability if the separation cost needed for the lower vulnerability is acceptable.)
Conversely, assume secondly that R < r so that the defender is advantaged with a larger resource than the attacker. A lower contest intensity is not beneficial for an agent advantaged with a larger resource, so the defender is never willing to incur a separation cost if μ < m. (For example, R= 2, r= 3, m= 2, μ= 1 gives vulnerability v= 22/(22+ 32) = 4/13 before separation, and vulnerability v= 21/(21+ 31) = 2/5 after separation. The defender prefers the former lower vulnerability.) However, if μ > m, then the defender has scope for improving its utility if 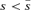 . (For example, R= 2, r= 3, m= 1, μ= 2 gives vulnerability v= 2/5 before separation, and vulnerability v= 4/13 after separation. The defender prefers the latter lower vulnerability if the separation cost needed for the lower vulnerability is acceptable.)
. (For example, R= 2, r= 3, m= 1, μ= 2 gives vulnerability v= 2/5 before separation, and vulnerability v= 4/13 after separation. The defender prefers the latter lower vulnerability if the separation cost needed for the lower vulnerability is acceptable.)
Summing up, if the attacker has the greater resource, then the defender separates if a sufficiently lower contest intensity is obtained through separation (m/μ > 1). If the defender has the greater resource, then the defender separates if sufficiently higher contest intensity is obtained (m/μ < 1).
Fig. 1 plots the limit  as a function of m/μ for various r when R= 1.
as a function of m/μ for various r when R= 1.
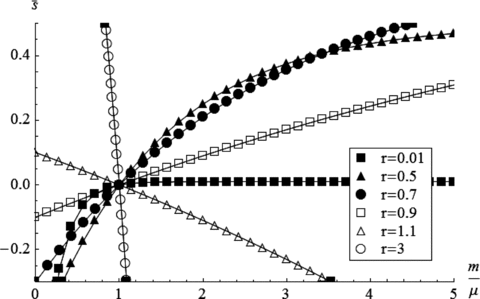
The limit  as a function of m/μ for various r when R= 1.
as a function of m/μ for various r when R= 1.
Compatibly with Proposition 1, observe the reversal as r increases from below to above R= 1. When r < 1, separation is never efficient when m/μ < 1, but is efficient for increasingly acceptable separation cost s as m/μ increases above 1. Conversely, when r > 1, separation is never efficient when m/μ > 1, but is efficient for increasingly acceptable separation cost s as m/μ decreases below 1.
The positive and negative ranges of  in Fig. 1 illustrate the mathematical logic of the four regions in Proposition 1, where
in Fig. 1 illustrate the mathematical logic of the four regions in Proposition 1, where  is positive or negative, and m/μ is less than or larger than 1. Negative separation cost is possible only when external actors outside the defender-attacker contest reimburse separation. For example, consider a profit-seeking company that also happens to defend a part of a critical infrastructure such as supply of electricity or water. Assume that the company rejects separation since its calculation gives negative
is positive or negative, and m/μ is less than or larger than 1. Negative separation cost is possible only when external actors outside the defender-attacker contest reimburse separation. For example, consider a profit-seeking company that also happens to defend a part of a critical infrastructure such as supply of electricity or water. Assume that the company rejects separation since its calculation gives negative  . If the government as an external actor, equipped with a different objective function, for example, linked to national interests, sees sufficient value in separation, it may be willing to reimburse the defender's separation cost.
. If the government as an external actor, equipped with a different objective function, for example, linked to national interests, sees sufficient value in separation, it may be willing to reimburse the defender's separation cost.
4. PERFORMANCE REDUNDANCY, 1-OUT-OF-N SYSTEM
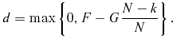 (7)
(7)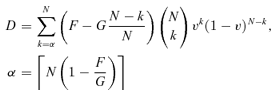 (8)
(8) is the smallest integer not less than x, and v is defined in Equation (1).
is the smallest integer not less than x, and v is defined in Equation (1).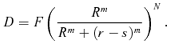 (9)
(9)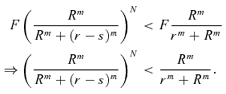 (10)
(10)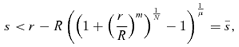 (11)
(11) for the separation cost s. The limit
for the separation cost s. The limit  increases in the number N of elements.
increases in the number N of elements.Proof: Follows from solving Equation (10) with respect to s.
Fig. 2 plots the limit  as a function of N for various r and μ when R=m= 1. It shows that the defender accepts higher separation cost as the number of elements increases.
as a function of N for various r and μ when R=m= 1. It shows that the defender accepts higher separation cost as the number of elements increases.
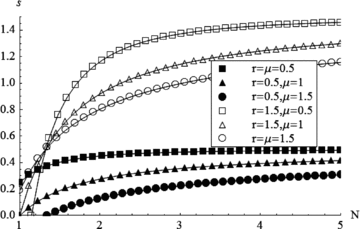
The limit  as a function of N for various r and μ when R=m= 1.
as a function of N for various r and μ when R=m= 1.
5. PERFORMANCE REDUNDANCY, Q-OUT-OF-N SYSTEM
Assume that the system is separated into N identical elements and (Q− 1)G/N < F≤QG/N for integer Q (1 ≤Q≤N). The system can meet the demand when at least Q out of N elements survive.
5.1. Damage Proportional to the Loss of Demand Probability
 (12)
(12)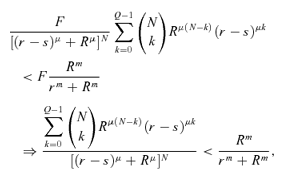 (13)
(13) for the separation cost s can be obtained for any Q and N by solving Equation (13) numerically with respect to s.
for the separation cost s can be obtained for any Q and N by solving Equation (13) numerically with respect to s.As F increases from 0 to G, Q increases as a stepwise function of F according to 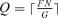 . For (Q– 1)G/N < F≤QG/N, Q does not depend on F and, therefore,
. For (Q– 1)G/N < F≤QG/N, Q does not depend on F and, therefore,  obtained from Equation (13) is a stepwise function of the demand F. Fig. 3 plots the limit
obtained from Equation (13) is a stepwise function of the demand F. Fig. 3 plots the limit  as a function of F for various r and μ when N= 10 and R=m= 1.
as a function of F for various r and μ when N= 10 and R=m= 1.
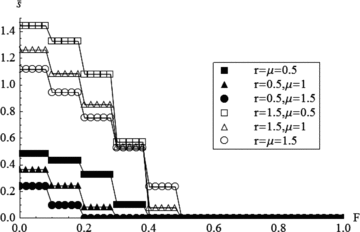
The limit  as a function of F for various r and μ when N= 10 and R=m= 1.
as a function of F for various r and μ when N= 10 and R=m= 1.
5.2. Damage Proportional to the Unsupplied Demand
 (14)
(14) (15)
(15)The upper limit  for the separation cost s can be obtained for any F and N by solving Equation (15) numerically with respect to s. The expected damage D always depends on F in Equation (14) and, therefore,
for the separation cost s can be obtained for any F and N by solving Equation (15) numerically with respect to s. The expected damage D always depends on F in Equation (14) and, therefore,  is a continuous function of the demand F.
is a continuous function of the demand F.
Proposition 3 The expected damage proportional to the loss of demand probability is always greater than the expected damage proportional to the unsupplied demand. When (Q− 1)G/N < F ≤ QG/N, the difference between the expected damage is proportional to the performance of a single separated element G/N and does not depend on F.
 (16)
(16)This difference is always positive. When (Q− 1)G/N < F≤QG/N, Q does not depend on F and, therefore, the difference in Equation (16) does not depend on F.
Proposition 3 implies that with the growth of the number of separated elements the difference between the expected damage proportional to the loss of demand probability and the expected damage proportional to the unsupplied demand decreases.
Fig. 4 plots the limit  as a function of F for various r and μ when N= 10 and R=m= 1.
as a function of F for various r and μ when N= 10 and R=m= 1.
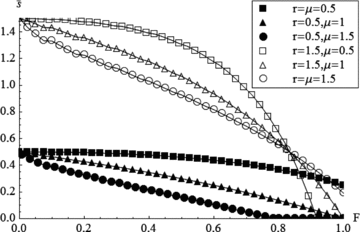
The limit  as a function of F for various r and μ when N= 10 and R=m= 1.
as a function of F for various r and μ when N= 10 and R=m= 1.
In Fig. 4, the upper limit  for the separation cost is higher than in Fig. 3 since the expected damage in Fig. 4 is always less than that in Fig. 3.
for the separation cost is higher than in Fig. 3 since the expected damage in Fig. 4 is always less than that in Fig. 3.
6. CONCLUSION
The article considers strategic defense and attack of a system that can be separated into independent identical parallel elements. Each element has the same performance. The defender distributes its resource between separation and protection of the elements from outside attacks. Separation leaves fewer resources for protecting each separated element, but prevents simultaneous destruction of all elements. The defender protects each element equally much. The attacker attacks each element equally much. The vulnerability of each element is determined by an attacker-defender contest success function, which depends on a contest intensity that may increase or decrease through the separation process.
For a system without performance redundancy the article determines an inequality for when the defender prefers to incur the cost of separating a system into parallel elements. The inequality is such that if the attacker has the greater resource, then the defender separates if sufficiently lower contest intensity is obtained through the separation process. If the defender has the greater resource, then the defender separates if sufficiently higher contest intensity is obtained through separation.
Introducing a 1-out-of-N system with performance redundancy, an analogous inequality is determined with an upper limit for the acceptable separation cost, which increases in the number N of groups. For the Q-out-of-N system with performance redundancy, separation efficiency conditions are determined for the cases of damage proportional to the probability that the demand is not met, and damage proportional to the unsupplied demand. For these systems the upper acceptable limit for the separation cost can be determined numerically as demonstrated in the examples. With the growth of the number of separated elements the difference between the expected damage proportional to the unsupplied demand, and the expected damage proportional to the probability that the demand is not met, decreases.
Further research can be devoted to system separation into nonidentical groups of elements and to the case when different separated groups have different contest intensities.
Footnotes
ACKNOWLEDGMENTS
We thank two anonymous referees of this journal for useful comments.




