A Median Model for Predicting United States Population-Based EQ-5D Health State Preferences
ABSTRACT
Objective: The D1 model that was developed to predict US societal preferences for EQ-5D health states addressed several important conceptual and statistical issues. However, it has been criticized for being too complex, failing to account for the nonnormal distribution of health state values, and the transformation of preferences for worse-than-death health states before estimation. This research was conducted to develop an improved model for predicting median preferences for EQ-5D health states for the US population.
Methods: Probability-weighted least absolute deviations regression was used to fit models to the time trade-off data collected in the US Valuation of the EQ-5D Health States study. No transformation was applied to the values for states considered worse than death. Several model specifications that differed with respect to explanatory variables were evaluated using two-sample cross-validation.
Results: The best-fitting model included only fixed effects for moderate or severe problems in each of the 5 EQ-5D dimensions and excluded a constant. This specification yielded rank correlations between observed and predicted values and median observed and predicted values of 0.635 and 0.991, respectively, as well as a median absolute error of 0.026. The predicted median preferences ranged from 1.00 for full health, to –0.81 for the worst possible health state.
Conclusions: Due to its simplicity and robustness, a median model is superior to other models for predicting US population preferences for EQ-5D health states. The predictions of this model are suggested for use in applications that require US societal health state values.
Introduction
The EQ-5D is a widely used generic measure of health status [1–3]. The instrument's descriptive system consists of the following five dimensions: Mobility, Self-Care, Usual Activities, Pain/Discomfort, and Anxiety/Depression. Each dimension has three levels reflecting “no health problems,”“moderate health problems,” and “extreme health problems.” A dimension for which there are no problems is said to be at level 1, while a dimension for which there are extreme problems is said to be at level 3. Thus, the vectors 11111 and 33333 represent the best health state and the worst health state, respectively, described by the EQ-5D. Altogether, the instrument describes 35 = 243 health states. Empirically derived weights can be applied to an individual's responses to the EQ-5D descriptive system to generate an index measuring the value to society of his or her current health.
The US Valuation of the EQ-5D Health States, more commonly referred to as the US EQ-5D valuation study, used a time trade-off (TTO) valuation task to enable the prediction of US societal preferences for the health states described by the EQ-5D [4]. The model used to generate these predictions, which is referred to as the D1 model, addressed a number of important statistical concerns. It excluded a constant, which would have implied a value <1 for full health (i.e., 11111), accounted for the correlation of observations within respondents using a random-effects specification, and incorporated sampling weights to provide estimates of model parameters that were generalizable to the US population. More importantly, it provided a conceptual framework for modeling health state values [4, p. 208]. However, the D1 model may be criticized for several shortcomings, including lack of parsimony, mean-based estimation, and the approach used to transform values for health states considered worse than death.
Dissimilar from the models developed in earlier TTO valuation studies conducted for the EQ-5D [5–8], the D1 model included several terms designed to capture the effects of interactions among dimensions on health state preferences [4, p. 208]. Consequently, the prediction algorithm based on the model's estimates is more complex than the algorithms developed in other investigations. The algorithm requires knowledge of the number of dimensions with moderate or severe health problems in addition to the level of health problems in each dimension. While it was important for the developers of the D1 model to account for possible interactions among EQ-5D dimensions, parsimony is often used as a model selection criterion in preference modeling and mapping studies [6–10]. The relative complexity of the D1 model prediction algorithm may render it difficult to use for some investigators.
A second concern with the D1 model relates to the distribution of health state preferences in the US EQ-5D valuation study, which was multimodal and negatively skewed. It is unlikely that the characteristics of the distribution had a great effect on the precision of the D1 model's estimates, though the additional assumption of normally distributed random effects was clearly violated. However, one may question the use of a linear model to predict mean health state values since the arithmetic mean is not the best estimate of central tendency for severely skewed data.
A third concern is the transformation that was applied to preferences for health states judged worse than death. To understand the impact of this transformation, one must first understand how preferences for worse-than-death health states are derived. Let i = 1, . . . , N index the respondent, and j = 1, . . . , Ji index the health state valued by the ith respondent. We allow that the number of valued health states could vary among respondents because of missing data. For the ijth health state valued worse than death, the TTO method elicits the number of years, sij < 10, where the ith respondent is indifferent between 1) life in the state being valued for sij years followed by life in full health for tij = 10 − sij years; and 2) immediate death. Thus, for each state considered worse than death, the TTO value, hij, is defined as −tij/(10 − tij) or simply −tij/sij. In the US EQ-5D valuation study, the smallest amount of time that a respondent could elect to spend in the state being valued was 0.25 years. Thus, the largest value that could be assigned to any state considered worse than death was hmax = −(10 − 0.25) = −39.
In most of the TTO modeling studies that have been conducted for the EQ-5D [5–8], the values for states worse than death have been transformed in order to reduce the effects of outliers on estimation results. Patrick and colleagues proposed a nonlinear method of transforming the values for worse-than-death health states by dividing each hij by 1 − hij[11]. The resulting transformed values are constrained to lie on the interval (−1, 0). Torrance proposed an alternative linear transformation to constrain the values for states worse than death to lie on the interval [−1, 0) by dividing each hij by the absolute value of hmax[12].
In developing the D1 model, Shaw and colleagues elected to apply the linear transformation to values for states judged worse than death. This decision was based on knowledge that the nonlinear transformation yields transpositions in the rankings of mean health state values and is, therefore, inconsistent with expected utility theory [13]. Unfortunately, the linear transformation is only rank-preserving when considering those health states valued worse than death. When health states considered worse than death are pooled with those considered better than death, the linear transformation fails to preserve the rank order of observed mean values. Thus, the linear transformation also yields predictions that are inconsistent with expected utility theory. Additionally, the application of the linear transformation in the development of the D1 model complicates the interpretation of the model's predictions. Because the dependent variable was a mixture of transformed and untransformed health state values, the predictions cannot be interpreted with respect to a single scale.
Objective
Using data collected in the US EQ-5D valuation study, the objective of this initiative was to develop an improved model for predicting median (as opposed to mean) US population-based preferences for the EQ-5D health states.
Methods
For the purpose of clarity, relevant elements of the original US EQ-5D valuation study methods are provided in the first four subsections below [4].
Sample Selection
The target population consisted of the 210,494,243 civilian noninstitutionalized adults, age 18 and older, who resided in the US (50 states plus Washington, DC) in 2002. This figure differs slightly from those previously published because it is derived from more recent population estimates. A multistage probability sample was selected from the target population with oversampling of Hispanics and non-Hispanic blacks. A total of 5237 persons were selected for interview.
Health State Assignment
To facilitate the evaluation of models for predicting health state preferences, the sample was divided into a modeling sample (i.e., sample in which all preliminary statistical modeling would be conducted) and a validation sample (i.e., holdout sample intended for use in validating models developed in the modeling sample). Persons who were selected for interview and who agreed to participate in the study were randomly assigned to one of five groups. Four of the groups comprised the modeling sample, while the fifth group comprised the validation sample. In addition to the states' Unconscious and Immediate Death, each participant was assigned 13 of a subset of 43 of the 243 health states described by the EQ-5D. Health state assignments were determined by group membership [4].
Interview Methodology
In a series of valuation exercises, the assigned health states were ranked from best to worst, rated on a visual analog scale, and valued using the TTO props methodology [14] (excluding the states 11111 and Immediate Death). Participants were also asked to complete a sociodemographic questionnaire, the Health Utilities Index 2/3 [12,15,16], the EQ-5D, and a single-item rating of overall health status. One hundred nine field interviewers administered the paper-and-pencil interview in English or Spanish. Of the 5237 individuals who were selected for participation, 4048 (77.3%) completed the interview.
Derivation of the Valuation Sample
The US EQ-5D valuation study was designed with the expectation that the modeling and validation samples would ultimately be combined to form a valuation sample in which the final predicted preferences would be generated. To maximize the quality of these predictions, a number of logical consistency criteria were applied to exclude participants with incomplete or inconsistent TTO data from the modeling of health state preferences. Individuals were excluded from the modeling and validation samples—and, consequently, the valuation sample—if they met any of the following conditions: 1) valued fewer than 12 health states; 2) gave the same value to all health states; 3) valued all health states worse than death; 4) valued 11111 or Immediate Death instead of Unconscious, and the value did not make sense; 5) were missing labels for health states other than Unconscious; 6) valued one or more incorrect health states for the assigned group; or 7), valued one or more health states more than once.
Similar criteria were applied to exclude respondents from the valuation sample used in the current study. However, we elected to include respondents who provided values for three or more health states (excluding Unconscious) in addition to those members of the modeling sample who valued incorrect health states for their assigned group. A total of 86 respondents were excluded from the valuation sample. The remaining 3962 respondents represented 97.9% of all interview participants (Table 1).
| Modeling sample (%) | Validation sample (%) | Valuation sample (%) | |
|---|---|---|---|
| Initial number of respondents included in sample | 3650 (100.0) | 398 (100.0) | 4048 (100.0) |
| Data problems | |||
| Valued 11111 or Immediate Death instead of Unconscious and value did not make sense* | 2 (0.1) | 1 (0.3) | 3 (0.1) |
| Missing valid TTO value and/or could not identify valued health state for ≥10 health states | 10 (0.3) | 1 (0.3) | 8 (0.2) |
| All health states valued the same | 59 (1.6) | 5 (1.3) | 64 (1.6) |
| All health states valued worse than Immediate Death | 6 (0.2) | 1 (0.3) | 7 (0.2) |
| Valued wrong set of health states for group | 0 (0.0) | 1 (0.3) | 1 (0.0) |
| Number of respondents with one or more data problems | 77 (2.1) | 9 (2.3) | 86 (2.1) |
| Number of respondents included in final sample | 3573 (97.9) | 389 (97.7) | 3962 (97.9) |
- Note: Twenty-one respondents appeared to value one or more health states more than once. If the health states in question were valued the same, then one of the duplicate valuations was excluded. If the health states in question were not valued the same, then all of the duplicate valuations were excluded.
- * Specifically, a value other than 1 for 11111 or 0 for Immediate Death.
Recalibration of the Sampling Weights
As part of this research, we developed an improved set of sampling weights for the valuation sample. Following the development of the D1 model, it became apparent that 26 participants in the US EQ-5D valuation study were misclassified as non-Hispanic. During the interview, these individuals had indicated that they were not Hispanic but then selected a Hispanic ethnicity in a follow-up question that was meant to be completed only by Hispanics/Latinos. Because of this misclassification, the sampling weights of the 26 participants were poststratified to the wrong control totals, which had an undue effect on the weights of the remaining respondents. Additionally, before it was known that population totals for the joint distribution of race/ethnicity and sex were available from the US Census Bureau, the original sampling weights had been raked using marginal totals for the two variables. Although the sampling weights were subsequently poststratified to more accurate joint totals, this raking added unnecessary variation to the weights.
We obtained the initial person-level weights that were developed for the US EQ-5D valuation study. Each weight represented the inverse of the conditional probability of selecting the ith person from a given address in a given 5-digit zip code in a given 3-digit zip code tabulation area (ZCTA). The sum of the initial weights for the 5237 individuals who were selected for interview was 175,604,067. This underestimated the total number of persons in the target population due to failure to account for non-Hispanic non-black addresses where no eligible person was selected. After recoding ethnicity for the 26 Hispanic respondents, the weights were poststratified to control totals for race/ethnicity (Hispanic, non-Hispanic black, other) and sex (male and female) for the US civilian noninstitutionalized population in September 2002 (data obtained from the US Census Bureau, May 3, 2007). This adjustment was also corrected for the exclusion of 1189 interview nonrespondents and 86 respondents who provided incomplete or logically inconsistent TTO data. The sum of the new sampling weights for the 3962 valuation sample members was 210,494,241.
Statistical Analyses
All statistical analyses took into account the clustered sampling design of the US EQ-5D valuation study, and the newly developed sampling weights were applied to adjust for respondents' unequal selection probabilities. Analyses were performed using Stata/MP[17] and with two-tailed α = 0.05.
Median and mean observed health state values. We estimated the median value, mean value, and difference between the median and mean values for 42 of the 45 health states included in the US EQ-5D valuation study (excluding Unconscious, Immediate Death, and 11111). Three sets of estimates were produced in which the values for states judged worse than death were left unaltered (i.e., not transformed), linearly transformed as per Torrance et al. [12], or nonlinearly transformed as per Patrick et al. [11]. The estimation of a variance–covariance matrix for the estimated medians, means, and median–mean differences was made difficult because of the complex sampling design of the study. We considered the application of bootstrapping because jackknifing yields severely biased variance estimates for quantiles and other nonsmooth statistics [18]. However, primary sampling units (i.e., 3-digit ZCTAs) were sampled without replacement using a systematic probability proportional to size algorithm in the US EQ-5D valuation study, and there is no bootstrap variant that results in a fully unbiased estimator of variance for this design [19]. Given that the first-stage sampling fraction was small (i.e., 60 out of 883 3-digit ZCTAs or 6.6%), the primary sampling units could reasonably be treated as though sampled with replacement. Therefore, we elected to estimate variances and covariances for the estimated parameters using a rescaled nonparametric block bootstrap procedure with 1000 replications [18]. In each replicate, 59 of the 60 primary sampling units were sampled with replacement. The sampling weights were then rescaled and poststratified to demographic control totals for race/ethnicity and sex. In large samples, such as ours, any bias in the variance estimates would be expected to be negligible unless extreme steps were taken to emphasize the selection of certain pairs of sampling units [20]. Ninety-five percent bias-corrected percentile bootstrap confidence intervals were derived for all estimated parameters [21].
Model fitting. Models were fit to the data using probability-weighted least absolute deviations (LAD) regression. Whereas ordinary least squares (OLS) regression estimates the conditional mean by minimizing the sum of squared residuals, LAD regression estimates the effects of regressors on the conditional median of the regressand. For this reason, it is often referred to as median regression. LAD regression is robust to extreme values of the response variable and is the maximum likelihood estimator (i.e., the most efficient among all unbiased estimators) when the disturbances follow a double exponential distribution.
We fit regression models using the following general specification:
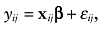(1)where i = 1, . . . , N indexed the respondent, j = 1, . . . , Ji, Ji ≤ 12, indexed the health state valued by the ith respondent (excluding Unconscious), and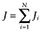 
; yij was the ijth element of y, an NJ × 1 vector of health state TTO values differenced from 1; xij was the ijth row of x, an NJ × (K + 1) matrix of observations on a set of k = 1, . . . , K explanatory variables plus a constant; β was a (K + 1) × 1 vector of parameters to be estimated; and εij was the ijth element of ε, an NJ × 1 vector of disturbances. The distribution of εij was not specified, though it was assumed that the conditional median of ε given x was zero. No transformation was applied to the TTO values for health states considered worse than death. The LAD estimate 
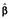of β was derived by using linear programming techniques to solve the minimization problem:
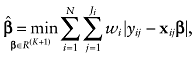(2)where wi was the sampling weight for the ith respondent. Due to having repeated observations on respondents, the sampling weights were poststratified by race/ethnicity and sex before model fitting so that the estimated population size would equal that of the target population. The rescaled nonparametric block bootstrap procedure (with 1000 replications) was used to estimate the variance–covariance matrix of parameter estimates. Detailed information pertaining to the estimation of weighted regression quantiles may be found in various sources [22–25].
The models included indicator variables for moderate (i.e., level 2) or severe (i.e., level 3) problems in each of the five EQ-5D dimensions. Two variables each were generated for the Mobility (M2, M3), Self-Care (S2, S3), Usual Activities (U2, U3), Pain/Discomfort (P2, P3), and Anxiety/Depression (A2, A3) dimensions. We refer to these 10 indicator variables as the main effects. In addition to a base model including only main effects terms, we considered alternative specifications that included one or more ancillary variables designed to measure interactions among the main effects or a location shift common to all main effects for a particular grade of health problems. For the purpose of this research, the constant was treated as an ancillary variable. Expected utility theory is founded on the principle that preferences for all individuals are measured on the same scale. To facilitate measurement in the TTO exercise, the values for 11111 and Immediate Death are set to 1 and 0, respectively. The inclusion of a constant in the model to predict health state preferences implies a value <1 for 11111, which is inconsistent with the theory that underlies the measurement of preferences. However, the constant can also be viewed as estimating a fixed effect common to all imperfect health states. Suppose that one were to include values for the health state 11111 in the estimation sample and constrained each of these to equal 1. The parameter estimate for a binary variable indicating any health state other than 11111 would be equivalent to the estimate for the constant when excluding 11111 from the sample. In this sense, there is little to distinguish the constant from the fixed effects for moderate or severe problems in any dimension that have been considered in previous research [4,6].
Numerous model specifications were considered. Results are presented for the following specifications, which were deemed to be of greatest interest to researchers and end-users of the predicted health state preferences:
- 1
MM-OC: Included indicator variables for moderate or severe problems in each of the five EQ-5D dimensions. These are also referred to as the main effects.
- 2
MM: Same as MM-OC plus a constant.
- 3
MM-N2: Same as MM-OC plus a fixed effect for moderate problems in any dimension (i.e., N2) and a constant.
- 4
MM-N3: Same as MM-OC plus a fixed effect for severe problems in any dimension (i.e., N3) and a constant.
- 5
MM-N2N3: Same as MM-OC plus N2, N3, and a constant.
- 6
MM-N3OC: Same as MM-N3 but without a constant.
- 7
MM-D1: Same as MM-OC plus variables indicating the number of dimensions with moderate or severe problems beyond the first (i.e., D1), the square of the number of dimensions with moderate problems beyond the first (i.e., I22), the number of dimensions with severe problems beyond the first (i.e., I3), and the square of the number of dimensions with severe problems beyond the first (i.e., I32).
- 8
MM-D1I2: Same as MM-D1 plus a variable indicating the number of dimensions with moderate problems beyond the first (i.e., I2).
Ninety-five percent bias-corrected percentile bootstrap confidence intervals were computed to evaluate the statistical significance of individual parameter estimates. Hypotheses involving multiple parameter estimates were evaluated using Wald F tests.
Model testing. As in the development of the D1 model, parameters were estimated in the modeling sample. Estimates were then applied to the validation sample data to generate fit indices for comparing the models. The same fit indices were computed to assess the apparent or native performance of each model in the valuation sample. These indices included the following: 1) sum of the absolute deviations between the observed and predicted values of the dependent variable in the modeling (valuation) sample; 2) model pseudo-R2 when fit to the modeling (valuation) sample data; 3) median absolute error (MAE) for predicting the 12 (42) health states valued by the validation (valuation) sample; 4) Spearman rank correlation between the observed and predicted TTO values for the validation (valuation) sample (i.e., r overall); 5) Spearman rank correlation between the median observed and predicted TTO values for the validation (valuation) sample (i.e., between-states r or r between); and 6) the number of prediction errors >0.05 or >0.10 in absolute magnitude. Pseudo-R2 was calculated as 1 minus the ratio of the sum of the absolute deviations between the observed and predicted values to the sum of the absolute deviations between the observed values and the unconditional median (i.e., the estimated intercept of the null regression model). All fit indices were probability weighted so as to be generalizable to the target population.
After selecting a model specification, parameters were reestimated in the valuation sample. Estimates of parameter estimate variances and covariances were derived using the rescaled nonparametric block bootstrap procedure with 1000 replications. The predictions of the selected model were compared with those of the D1 model.
Results
Median and Mean Observed Health State Values
Without applying any transformation to the values for states considered worse than death, health state values ranged from 1 to −39. The minimum value was −1 after applying the linear transformation to values for states worse than death and −0.975 after applying the nonlinear transformation to values for worse-than-death health states. After collapsing the data to health state-level medians (means), the values exhibited a minimum of −0.739 (−5.936) when no transformation was applied to the values for states worse than death. The minimum median (mean) value was −0.019 (−0.107) when the values for worse-than-death health states were linearly transformed as per Torrance et al. [12]. and −0.425 (−0.382) when the values for worse-than-death states were nonlinearly transformed as per Patrick et al. [11].
Table 2 presents observed median and mean values and differences between median and mean values for the 42 health states. Without applying any transformation to the values for states judged worse than death, the overall median (mean) of the mean values was −0.919 (−1.103). Following application of the linear transformation to values for states considered worse than death, the overall median (mean) was 0.397 (0.442). The overall median (mean) was 0.298 (0.346) after applying the nonlinear transformation to worse-than-death health state values. For all health states, the median value exceeded the mean value when no transformation was applied to the values for states worse than death. After transforming the values for worse-than-death health states, however, the mean value tended to exceed the median value for severe states of health. Without transforming the values for states worse than death, the distribution of health state values tended to be negatively skewed (i.e., skewed to the left). This skew was attenuated, and in some cases reversed, after transforming the values for worse-than-death health states.
| State | No. obs. | No transformation | Linear transformation | Nonlinear transformation | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Median | Mean | Difference | Median | Mean | Difference | Median | Mean | Difference | ||
| 21111 | 1754 | 0.975 (0.02) | 0.770 (0.07) | 0.205 (0.07) | 0.975 (0.02) | 0.869 (0.01) | 0.106 (0.02) | 0.975 (0.02) | 0.868 (0.01) | 0.107 (0.02) |
| [0.95, 1.00] | [0.62, 0.86] | [0.11, 0.36] | [0.95, 1.00] | [0.85, 0.89] | [0.08, 0.14] | [0.95, 1.00] | [0.84, 0.89] | [0.08, 0.14] | ||
| 11121 | 1278 | 0.950 (0.02) | 0.851 (0.02) | 0.099 (0.02) | 0.950 (0.02) | 0.881 (0.01) | 0.069 (0.02) | 0.950 (0.02) | 0.877 (0.01) | 0.073 (0.02) |
| [0.95, 1.00] | [0.80, 0.88] | [0.07, 0.15] | [0.95, 1.00] | [0.87, 0.89] | [0.05, 0.11] | [0.95, 1.00] | [0.86, 0.89] | [0.05, 0.12] | ||
| 11112 | 1752 | 0.925 (0.01) | 0.692 (0.08) | 0.233 (0.08) | 0.925 (0.01) | 0.830 (0.01) | 0.095 (0.01) | 0.925 (0.01) | 0.824 (0.01) | 0.101 (0.01) |
| [0.93, 0.98] | [0.50, 0.81] | [0.12, 0.42] | [0.93, 0.98] | [0.81, 0.85] | [0.07, 0.11] | [0.93, 0.98] | [0.80, 0.85] | [0.08, 0.11] | ||
| 11211 | 1785 | 0.925 (0.01) | 0.828 (0.03) | 0.097 (0.03) | 0.925 (0.01) | 0.865 (0.01) | 0.060 (0.01) | 0.925 (0.01) | 0.864 (0.01) | 0.061 (0.01) |
| [0.93, 0.99] | [0.75, 0.87] | [0.06, 0.16] | [0.93, 0.99] | [0.85, 0.88] | [0.04, 0.08] | [0.93, 0.99] | [0.85, 0.88] | [0.04, 0.08] | ||
| 12111 | 1284 | 0.925 (0.01) | 0.812 (0.02) | 0.113 (0.02) | 0.925 (0.01) | 0.839 (0.01) | 0.086 (0.01) | 0.925 (0.01) | 0.836 (0.01) | 0.089 (0.01) |
| [0.93, 1.00] | [0.77, 0.84] | [0.08, 0.15] | [0.93, 1.00] | [0.82, 0.86] | [0.06, 0.11] | [0.93, 1.00] | [0.81, 0.86] | [0.07, 0.11] | ||
| 12211 | 860 | 0.925 (0.01) | 0.508 (0.13) | 0.417 (0.13) | 0.925 (0.01) | 0.791 (0.02) | 0.134 (0.02) | 0.925 (0.01) | 0.782 (0.02) | 0.143 (0.02) |
| [0.90, 0.93]* | [0.19, 0.72] | [0.21, 0.75] | [0.90, 0.93]* | [0.75, 0.83] | [0.10, 0.17] | [0.90, 0.93]* | [0.74, 0.82] | [0.11, 0.18] | ||
| 11122 | 860 | 0.900 (0.03) | 0.613 (0.07) | 0.287 (0.07) | 0.900 (0.03) | 0.763 (0.02) | 0.137 (0.02) | 0.900 (0.03) | 0.753 (0.02) | 0.147 (0.02) |
| [0.88, 0.93] | [0.43, 0.71] | [0.18, 0.49] | [0.88, 0.93] | [0.73, 0.80] | [0.09, 0.17] | [0.88, 0.93] | [0.72, 0.79] | [0.11, 0.18] | ||
| 12121 | 897 | 0.900 (0.02) | 0.690 (0.06) | 0.210 (0.06) | 0.900 (0.02) | 0.789 (0.01) | 0.111 (0.02) | 0.900 (0.02) | 0.782 (0.01) | 0.118 (0.02) |
| [0.88, 0.93] | [0.52, 0.78] | [0.12, 0.40] | [0.88, 0.93] | [0.76, 0.81] | [0.09, 0.15] | [0.88, 0.93] | [0.76, 0.81] | [0.09, 0.16] | ||
| 22112 | 865 | 0.875 (0.04) | 0.064 (0.26) | 0.811 (0.25) | 0.875 (0.04) | 0.704 (0.03) | 0.171 (0.02) | 0.875 (0.04) | 0.691 (0.03) | 0.184 (0.02) |
| [0.88, 0.93] | [−0.52, 0.55] | [0.37, 1.40] | [0.88, 0.93] | [0.64, 0.76] | [0.15, 0.21] | [0.88, 0.93] | [0.63, 0.745] | [0.16, 0.23] | ||
| 22121 | 1284 | 0.850 (0.03) | 0.521 (0.08) | 0.329 (0.08) | 0.850 (0.03) | 0.738 (0.01) | 0.112 (0.02) | 0.850 (0.03) | 0.722 (0.02) | 0.128 (0.02) |
| [0.83, 0.93] | [0.32, 0.65] | [0.21, 0.55] | [0.83, 0.93] | [0.71, 0.76] | [0.08, 0.16] | [0.83, 0.93] | [0.69, 0.75] | [0.10, 0.17] | ||
| 21222 | 1287 | 0.800 (0.03) | 0.387 (0.07) | 0.413 (0.07) | 0.800 (0.03) | 0.681 (0.02) | 0.119 (0.02) | 0.800 (0.03) | 0.655 (0.02) | 0.145 (0.02) |
| [0.80, 0.85] | [0.25, 0.52] | [0.29, 0.578] | [0.80, 0.85] | [0.65, 0.71] | [0.07, 0.14] | [0.80, 0.85] | [0.61, 0.69] | [0.11, 0.17] | ||
| 22122 | 890 | 0.800 (0.03) | 0.413 (0.13) | 0.387 (0.13) | 0.800 (0.03) | 0.680 (0.02) | 0.120 (0.02) | 0.800 (0.03) | 0.657 (0.02) | 0.143 (0.02) |
| [0.78, 0.88] | [0.09, 0.60] | [0.20, 0.75] | [0.78, 0.88] | [0.65, 0.71] | [0.09, 0.17] | [0.78, 0.88] | [0.62, 0.69] | [0.11, 0.19] | ||
| 11312 | 889 | 0.775 (0.03) | 0.149 (0.16) | 0.626 (0.15) | 0.775 (0.03) | 0.642 (0.02) | 0.133 (0.02) | 0.775 (0.03) | 0.614 (0.02) | 0.161 (0.02) |
| [0.75, 0.83] | [−0.18, 0.45] | [0.36, 0.97] | [0.75, 0.83] | [0.61, 0.67] | [0.09, 0.17] | [0.75, 0.83] | [0.58, 0.65] | [0.12, 0.20] | ||
| 12222 | 1288 | 0.775 (0.03) | 0.174 (0.15) | 0.601 (0.14) | 0.775 (0.03) | 0.657 (0.02) | 0.118 (0.02) | 0.775 (0.03) | 0.632 (0.02) | 0.143 (0.02) |
| [0.73, 0.83] | [−0.14, 0.44] | [0.36, 0.90] | [0.73, 0.83] | [0.62, 0.70] | [0.08, 0.15] | [0.73, 0.83] | [0.59, 0.67] | [0.11, 0.18] | ||
| 21312 | 898 | 0.725 (0.02) | 0.115 (0.21) | 0.610 (0.21) | 0.725 (0.02) | 0.625 (0.02) | 0.100 (0.02) | 0.725 (0.02) | 0.602 (0.02) | 0.123 (0.02) |
| [0.73, 0.80] | [−0.41, 0.42] | [0.31, 1.11] | [0.73, 0.80] | [0.59, 0.66] | [0.07, 0.13] | [0.73, 0.80] | [0.56, 0.64] | [0.08, 0.15] | ||
| 22222 | 862 | 0.700 (0.03) | −0.447 (0.33) | 1.147 (0.32) | 0.700 (0.03) | 0.594 (0.03) | 0.106 (0.02) | 0.700 (0.03) | 0.570 (0.03) | 0.130 (0.02) |
| [0.63, 0.80] | [−1.22, 0.12] | [0.61, 1.87] | [0.63, 0.80] | [0.54, 0.64] | [0.04, 0.13] | [0.63, 0.80] | [0.51, 0.62] | [0.07, 0.16] | ||
| 11113 | 895 | 0.650 (0.04) | −0.215 (0.20) | 0.865 (0.18) | 0.650 (0.04) | 0.556 (0.02) | 0.094 (0.03) | 0.650 (0.04) | 0.497 (0.03) | 0.153 (0.03) |
| [0.60, 0.73] | [−0.69, 0.12] | [0.57, 1.28] | [0.60, 0.73] | [0.51, 0.59] | [0.05, 0.15] | [0.60, 0.73] | [0.44, 0.54] | [0.10, 0.21] | ||
| 13212 | 890 | 0.600 (0.04) | −0.639 (0.31) | 1.239 (0.31) | 0.600 (0.04) | 0.507 (0.02) | 0.093 (0.03) | 0.600 (0.04) | 0.455 (0.03) | 0.145 (0.03) |
| [0.58, 0.70] | [−1.35, −0.13] | [0.77, 2.00] | [0.58, 0.70] | [0.46, 0.55] | [0.05, 0.14] | [0.58, 0.70] | [0.40, 0.51] | [0.10, 0.20] | ||
| 13311 | 1284 | 0.525 (0.03) | −0.490 (0.21) | 1.015 (0.21) | 0.525 (0.03) | 0.473 (0.02) | 0.052 (0.02) | 0.525 (0.03) | 0.399 (0.02) | 0.126 (0.02) |
| [0.50, 0.63] | [−0.93, −0.09] | [0.62, 1.45] | [0.50, 0.63] | [0.44, 0.51] | [0.02, 0.09] | [0.50, 0.63] | [0.35, 0.45] | [0.08, 0.16] | ||
| 12223 | 892 | 0.500 (0.02) | −0.529 (0.19) | 1.029 (0.19) | 0.500 (0.02) | 0.455 (0.02) | 0.045 (0.01) | 0.500 (0.02) | 0.387 (0.02) | 0.113 (0.02) |
| [0.50, 0.60] | [−0.94, −0.18] | [0.67, 1.43] | [0.50, 0.60] | [0.42, 0.49] | [0.01, 0.06] | [0.50, 0.60] | [0.35, 0.43] | [0.07, 0.14] | ||
| 11131 | 895 | 0.475 (0.05) | −1.242 (0.34) | 1.717 (0.32) | 0.475 (0.05) | 0.390 (0.03) | 0.085 (0.03) | 0.475 (0.05) | 0.275 (0.03) | 0.200 (0.03) |
| [0.48, 0.58] | [−1.88, −0.59] | [1.11, 2.37] | [0.48, 0.58] | [0.34, 0.45] | [0.06, 0.13] | [0.48, 0.58] | [0.21, 0.35] | [0.17, 0.25] | ||
| 21232 | 890 | 0.475 (0.04) | −1.010 (0.31) | 1.485 (0.29) | 0.475 (0.04) | 0.405 (0.03) | 0.070 (0.03) | 0.475 (0.04) | 0.304 (0.04) | 0.171 (0.03) |
| [0.38, 0.50] | [−1.63, −0.47] | [0.97, 2.08] | [0.38, 0.50] | [0.35, 0.46] | [0.03, 0.11] | [0.38, 0.50] | [0.24, 0.37] | [0.14, 0.23] | ||
| 21323 | 889 | 0.425 (0.04) | −0.828 (0.25) | 1.253 (0.25) | 0.425 (0.04) | 0.385 (0.02) | 0.040 (0.02) | 0.425 (0.04) | 0.293 (0.02) | 0.132 (0.03) |
| [0.40, 0.50] | [−1.34, −0.42] | [0.84, 1.78] | [0.40, 0.50] | [0.35, 0.42] | [0.01, 0.10] | [0.40, 0.50] | [0.25, 0.34] | [0.09, 0.19] | ||
| 23321 | 1252 | 0.425 (0.04) | −1.173 (0.27) | 1.598 (0.26) | 0.425 (0.04) | 0.378 (0.02) | 0.047 (0.03) | 0.425 (0.04) | 0.290 (0.02) | 0.135 (0.02) |
| [0.38, 0.50] | [−1.74, −0.69] | [1.13, 2.13] | [0.38, 0.50] | [0.34, 0.42] | [−0.01, 0.10] | [0.38, 0.50] | [0.24, 0.34] | [0.09, 0.18] | ||
| 22323 | 897 | 0.400 (0.05) | −1.30 (0.28) | 1.697 (0.25) | 0.400 (0.05) | 0.361 (0.02) | 0.039 (0.04) | 0.400 (0.05) | 0.262 (0.03) | 0.138 (0.03) |
| [0.30, 0.50] | [−1.88, −0.78] | [1.22, 2.21] | [0.30, 0.50] | [0.31, 0.40] | [0.00, 0.11] | [0.30, 0.50] | [0.20, 0.32] | [0.10, 0.20] | ||
| 32211 | 893 | 0.300 (0.05) | −1.080 (0.23) | 1.380 (0.22) | 0.300 (0.05) | 0.324 (0.02) | −0.024 (0.03) | 0.300 (0.05) | 0.206 (0.03) | 0.094 (0.03) |
| [0.30, 0.40] | [−1.58, −0.66] | [0.98, 1.84] | [0.30, 0.40] | [0.29, 0.36] | [−0.07, 0.04] | [0.30, 0.40] | [0.16, 0.25] | [0.05, 0.16] | ||
| 22331 | 1290 | 0.200 (0.09) | −1.444 (0.21) | 1.644 (0.21) | 0.200 (0.09) | 0.293 (0.02) | −0.093 (0.07) | 0.200 (0.09) | 0.154 (0.03) | 0.046 (0.07) |
| [0.03, 0.38] | [−1.88, −1.06] | [1.28, 2.10] | [0.03, 0.38] | [0.26, 0.33] | [−0.25, 0.03] | [0.03, 0.38] | [0.10, 0.21] | [−0.09, 0.17] | ||
| 21133 | 891 | 0.175 (0.08) | −1.671 (0.37) | 1.846 (0.34) | 0.175 (0.08) | 0.278 (0.02) | −0.103 (0.06) | 0.175 (0.08) | 0.133 (0.03) | 0.042 (0.06) |
| [0.03, 0.30] | [−2.54, −1.06] | [1.27, 2.63] | [0.03, 0.30] | [0.22, 0.32] | [−0.24, −0.01] | [0.03, 0.30] | [0.07, 0.19] | [−0.08, 0.12] | ||
| 11133 | 1281 | 0.075 (0.10) | −1.857 (0.33) | 1.932 (0.31) | 0.075 (0.10) | 0.289 (0.03) | −0.214 (0.08) | 0.075 (0.10) | 0.147 (0.03) | −0.072 (0.07) |
| [0.00, 0.33] | [−2.55, −1.26] | [1.38, 2.51] | [0.00, 0.33] | [0.25, 0.35] | [−0.27, −0.04] | [0.00, 0.33] | [0.08, 0.22] | [−0.12, 0.09] | ||
| 23313 | 1255 | 0.025 (0.05) | −2.456 (0.38) | 2.481 (0.36) | 0.025 (0.05) | 0.222 (0.02) | −0.197 (0.04) | 0.025 (0.05) | 0.073 (0.03) | −0.048 (0.04) |
| [0.03, 0.30] | [−3.24, −1.71] | [1.81, 3.25] | [0.03, 0.30] | [0.18, 0.27] | [−0.23, −0.05] | [0.03, 0.30] | [0.02, 0.13] | [−0.08, 0.07] | ||
| 13332 | 896 | 0.000 (0.03) | −2.655 (0.40) | 2.655 (0.40) | 0.000 (0.00) | 0.132 (0.02) | −0.132 (0.02) | 0.000 (0.03) | −0.053 (0.03) | 0.053 (0.02) |
| [−0.08, 0.00]* | [−3.51, −1.93] | [1.95, 3.48] | [0.00, 0.00]* | [0.09, 0.18] | [−0.17, −0.09] | [−0.08, 0.00]* | [−0.11, 0.01] | [0.02, 0.09] | ||
| 22233 | 860 | 0.000 (0.04) | −2.705 (0.40) | 2.705 (0.39) | 0.000 (0.04) | 0.199 (0.02) | −0.199 (0.03) | 0.000 (0.04) | 0.047 (0.03) | −0.047 (0.03) |
| [0.00, 0.30] | [−3.49, −1.94] | [1.98, 3.49] | [0.00, 0.30] | [0.15, 0.25] | [−0.23, −0.16] | [0.00, 0.30] | [−0.01, 0.11] | [−0.09, 0.00] | ||
| 23232 | 887 | 0.000 (0.02) | −2.167 (0.41) | 2.167 (0.41) | 0.000 (0.02) | 0.207 (0.02) | −0.207 (0.02) | 0.000 (0.02) | 0.054 (0.03) | −0.054 (0.02) |
| [0.00, 0.25] | [−3.09, −1.48] | [1.51, 3.07] | [0.00, 0.25] | [0.17, 0.26] | [−0.24, −0.18] | [0.00, 0.25] | [0.00, 0.13] | [−0.10, −0.01] | ||
| 32223 | 886 | 0.000 (0.01) | −2.357 (0.42) | 2.357 (0.42) | 0.000 (0.00) | 0.188 (0.02) | −0.188 (0.02) | 0.000 (0.01) | 0.003 (0.03) | −0.003 (0.03) |
| [0.00, 0.00]* | [−3.30, −1.64] | [1.65, 3.25] | [0.00, 0.00]* | [0.15, 0.23] | [−0.23, −0.15] | [0.00, 0.00]* | [−0.06, 0.06] | [−0.06, 0.05] | ||
| 32232 | 888 | 0.000 (0.03) | −2.426 (0.38) | 2.426 (0.36) | 0.000 (0.00) | 0.138 (0.02) | −0.138 (0.02) | 0.000 (0.02) | −0.067 (0.03) | 0.067 (0.02) |
| [−0.08, 0.00]* | [−3.13, −1.71] | [1.72, 3.08] | [0.00, 0.00]* | [0.10, 0.18] | [−0.18, −0.10] | [−0.08, 0.00]* | [−0.11, −0.01] | [0.04, 0.12] | ||
| 32313 | 859 | 0.000 (0.01) | −2.842 (0.38) | 2.842 (0.38) | 0.000 (0.00) | 0.128 (0.02) | −0.128 (0.02) | 0.000 (0.01) | −0.052 (0.03) | 0.052 (0.02) |
| [−0.03, 0.00]* | [−3.59, −2.09] | [2.10, 3.59] | [0.00, 0.00]* | [0.09, 0.17] | [−0.17, −0.09] | [−0.03, 0.00]* | [−0.10, 0.00] | [0.01, 0.10] | ||
| 33212 | 895 | 0.000 (0.01) | −2.267 (0.50) | 2.267 (0.50) | 0.000 (0.01) | 0.190 (0.03) | −0.190 (0.02) | 0.000 (0.01) | 0.021 (0.03) | −0.021 (0.03) |
| [0.00, 0.08] | [−3.44, −1.50] | [1.50, 3.43] | [0.00, 0.08] | [0.13, 0.24] | [−0.23, −0.13] | [0.00, 0.08] | [−0.04, 0.08] | [−0.07, 0.04] | ||
| 33321 | 1281 | 0.000 (0.05) | −2.623 (0.31) | 2.623 (0.30) | 0.000 (0.00) | 0.136 (0.02) | −0.136 (0.02) | 0.000 (0.04) | −0.058 (0.02) | 0.058 (0.03) |
| [−0.18, 0.00]* | [−3.28, −2.05] | [2.10, 3.26] | [−0.01, 0.00]* | [0.11, 0.17] | [−0.17, −0.11] | [−0.15, 0.00]* | [−0.11, −0.01] | [0.04, 0.09] | ||
| 32331 | 858 | −0.176 (0.10) | −3.982 (0.54) | 3.806 (0.50) | −0.005 (0.00) | 0.052 (0.02) | −0.056 (0.02) | −0.150 (0.07) | −0.148 (0.03) | −0.002 (0.05) |
| [−0.33, −0.03] | [−5.07, −2.92] | [2.86, 4.83] | [−0.01, 0.00] | [0.01, 0.10] | [−0.10, −0.02] | [−0.28, −0.03] | [−0.21, −0.09] | [−0.08, 0.10] | ||
| 33232 | 895 | −0.290 (0.10) | −3.389 (0.41) | 3.099 (0.37) | −0.007 (0.00) | 0.049 (0.02) | −0.056 (0.02) | −0.225 (0.07) | −0.186 (0.03) | −0.039 (0.05) |
| [−0.48, −0.08] | [−4.33, −2.66] | [2.41, 3.85] | [−0.01, 0.00] | [0.01, 0.09] | [−0.09, −0.03] | [−0.30, −0.08] | [−0.23, −0.13] | [−0.12, 0.04] | ||
| 33323 | 886 | −0.429 (0.09) | −4.183 (0.62) | 3.755 (0.58) | −0.011 (0.00) | 0.005 (0.02) | −0.016 (0.02) | −0.300 (0.05) | −0.235 (0.03) | −0.065 (0.03) |
| [−0.60, -0.21] | [−5.44, −2.99] | [2.56, 4.87] | [−0.02, −0.01] | [−0.05, 0.05] | [−0.06, 0.03] | [−0.38, −0.18] | [−0.30, −0.18] | [−0.12, −0.02] | ||
| 33333 | 3911 | −0.739 (0.09) | −5.936 (0.36) | 5.197 (0.32) | −0.019 (0.00) | −0.107 (0.01) | 0.088 (0.01) | −0.425 (0.03) | −0.382 (0.02) | −0.043 (0.02) |
| [−0.91, −0.60] | [−6.69, −5.28] | [4.59, 5.80] | [−0.02, −0.02] | [−0.13, −0.09] | [0.07, 0.11] | [−0.48, −0.38] | [−0.42, −0.35] | [−0.08, −0.02] | ||
| Median (A) | 0.475 | −0.919 | 1.317 | 0.475 | 0.397 | 0.056 | 0.475 | 0.298 | 0.104 | |
| Mean (B) | 0.413 | −1.103 | 1.516 | 0.451 | 0.442 | 0.008 | 0.426 | 0.346 | 0.079 | |
| No. (%) A > B | 42 (100.0%) | 26 (61.9%) | 32 (76.2%) | |||||||
| No. (%) significant difference | 42 (100.0%) | 38 (90.5%) | 33 (78.6%) | |||||||
- Notes: The health states are sorted in descending order by estimated median value with no transformation applied for states worse than death. Bootstrap standard errors and bias-corrected percentile confidence intervals (based on 1000 replications) are presented. The bias correction could not be calculated for some median estimates. In these instances, denoted with (*), the bootstrap percentile confidence interval is presented instead.
- CI, confidence interval; SE, standard error.
When no transformation was applied to the values for states considered worse than death, the median (mean) of the differences between the median and mean values was 1.317 (1.516). After applying the linear transformation to values for worse-than-death health states, the median (mean) difference was 0.056 (0.008). The median (mean) difference was 0.104 (0.079) after applying the nonlinear transformation to values for states worse than death. Without transformation, the difference between the median and mean values was significant for all 42 health states. This difference was significant for 38/42 (90.5%) health states following application of the linear transformation and 33/42 (78.6%) health states following application of the nonlinear transformation.
Transformation of the values for worse-than-death health states had no influence on the rank order of the median values but yielded numerous transpositions in the rank order of the mean values. Dissimilar from the mean estimates, there were many duplicate median health state values. Irrespective of the transformation applied to the values for states considered worse than death, the median value was 0 (i.e., the same as that of Immediate Death) for 8/42 (19.1%) health states.
Model Fitting and Testing
Table 3 presents modeling sample parameter estimates, standard errors, and 95% bias-corrected percentile bootstrap confidence intervals for the eight model specifications. Each specification yielded main effects parameter estimates that were positive in sign and significant at the 5% level. Further, for each specification, the estimates for main effects representing severe health problems were greater in magnitude than the corresponding estimates for main effects representing moderate health problems. Excepting the MM-D1 and MM-D1I2 models, estimates for the main effects were fairly consistent in magnitude across the specifications. None of the models included a significant constant term.
| Variable | MM-N2 | MM-N3 | MM-N2N3 | MM-N3OC | MM-D1 | MM-D1I2 | MM | MM-OC |
|---|---|---|---|---|---|---|---|---|
| Main effects | ||||||||
| M2 | 0.047 (0.013) | 0.049 (0.012) | 0.049 (0.013) | 0.049 (0.013) | 0.050 (0.019) | 0.050 (0.018) | 0.038 (0.012) | 0.040 (0.013) |
| [0.014, 0.063] | [0.025, 0.066] | [0.023, 0.069] | [0.025, 0.068] | [0.019, 0.075] | [0.015, 0.075] | [0.000, 0.050] | [0.003, 0.055] | |
| M3 | 0.495 (0.019) | 0.477 (0.021) | 0.485 (0.023) | 0.477 (0.021) | 0.528 (0.022) | 0.527 (0.029) | 0.488 (0.018) | 0.488 (0.018) |
| [0.450, 0.526] | [0.447, 0.525] | [0.446, 0.529] | [0.447, 0.525] | [0.451, 0.556] | [0.466, 0.575] | [0.450, 0.524] | [0.450, 0.524] | |
| S2 | 0.050 (0.009) | 0.050 (0.009) | 0.050 (0.009) | 0.050 (0.009) | 0.060 (0.013) | 0.052 (0.012) | 0.050 (0.009) | 0.054 (0.009) |
| [0.026, 0.065] | [0.040, 0.075] | [0.038, 0.075] | [0.032, 0.066] | [0.033, 0.075] | [0.021, 0.075] | [0.038, 0.075] | [0.036, 0.074] | |
| S3 | 0.350 (0.016) | 0.347 (0.019) | 0.341 (0.018) | 0.347 (0.020) | 0.390 (0.020) | 0.395 (0.021) | 0.350 (0.016) | 0.352 (0.016) |
| [0.328, 0.394] | [0.314, 0.379] | [0.300, 0.375] | [0.313, 0.379] | [0.345, 0.425] | [0.373, 0.450] | [0.325, 0.384] | [0.319, 0.380] | |
| U2 | 0.052 (0.010) | 0.049 (0.009) | 0.049 (0.009) | 0.049 (0.008) | 0.051 (0.011) | 0.050 (0.011) | 0.050 (0.011) | 0.054 (0.010) |
| [0.038, 0.075] | [0.026, 0.063] | [0.025, 0.063] | [0.030, 0.063] | [0.050, 0.075] | [0.034, 0.075] | [0.025, 0.074] | [0.032, 0.071] | |
| U3 | 0.125 (0.017) | 0.102 (0.018) | 0.116 (0.018) | 0.102 (0.018) | 0.154 (0.021) | 0.152 (0.025) | 0.125 (0.018) | 0.129 (0.017) |
| [0.100, 0.150] | [0.076, 0.115] | [0.075, 0.142] | [0.080, 0.110] | [0.102, 0.178] | [0.095, 0.200] | [0.100, 0.151] | [0.100, 0.149] | |
| P2 | 0.047 (0.011) | 0.049 (0.011) | 0.049 (0.011) | 0.049 (0.010) | 0.048 (0.013) | 0.050 (0.012) | 0.038 (0.011) | 0.041 (0.011) |
| [0.025, 0.071] | [0.025, 0.069] | [0.025, 0.069] | [0.026, 0.067] | [0.015, 0.070] | [0.025, 0.075] | [0.013, 0.053] | [0.017, 0.056] | |
| P3 | 0.470 (0.021) | 0.451 (0.029) | 0.458 (0.026) | 0.451 (0.030) | 0.500 (0.029) | 0.500 (0.034) | 0.463 (0.024) | 0.465 (0.025) |
| [0.432, 0.509] | [0.377, 0.506] | [0.411, 0.508] | [0.365, 0.504] | [0.443, 0.573] | [0.446, 0.581] | [0.396, 0.500] | [0.396, 0.506] | |
| A2 | 0.053 (0.010) | 0.051 (0.009) | 0.051 (0.010) | 0.051 (0.009) | 0.068 (0.012) | 0.055 (0.012) | 0.063 (0.009) | 0.068 (0.008) |
| [0.027, 0.073] | [0.033, 0.069] | [0.029, 0.074] | [0.021, 0.066] | [0.044, 0.075] | [0.026, 0.075] | [0.050, 0.085] | [0.060, 0.085] | |
| A3 | 0.353 (0.015) | 0.326 (0.023) | 0.333 (0.023) | 0.326 (0.025) | 0.396 (0.022) | 0.395 (0.026) | 0.363 (0.017) | 0.366 (0.018) |
| [0.328, 0.378] | [0.282, 0.372] | [0.292, 0.375] | [0.274, 0.369] | [0.345, 0.428] | [0.350, 0.442] | [0.350, 0.388] | [0.347, 0.391] | |
| Ancillary terms | ||||||||
| N2 | −0.022 (0.030) | −0.009 (0.031) | ||||||
| [−0.075, 0.036] | [−0.074, 0.050] | |||||||
| N3 | 0.048 (0.026) | 0.033 (0.029) | 0.048 (0.024) | |||||
| [0.004, 0.098] | [−0.025, 0.086] | [0.011, 0.098] | ||||||
| I2 | −0.036 (0.031) | |||||||
| [−0.102, 0.022] | ||||||||
| I22 | 0.005 (0.002) | 0.011 (0.004) | ||||||
| [−0.001, 0.009] | [0.005, 0.020] | |||||||
| I3 | −0.011 (0.026) | −0.044 (0.023) | ||||||
| [−0.054, 0.059] | [−0.099, −0.007] | |||||||
| I32 | −0.006 (0.008) | −0.003 (0.007) | ||||||
| [−0.020, 0.010] | [−0.015, 0.011] | |||||||
| D1 | −0.022 (0.015) | 0.000 (0.025) | ||||||
| [−0.042, 0.020] | [−0.036, 0.075] | |||||||
| Constant | 0.025 (0.033) | 0.001 (0.013) | 0.009 (0.034) | 0.013 (0.013) | ||||
| [−0.054, 0.074] | [−0.031, 0.025] | [−0.075, 0.064] | [−0.014, 0.029] | |||||
| Wald test | ||||||||
| F (ν1, ν2) | 0.28 (2, 58) | 2.42 (2, 58) | 0.95 (3, 57) | 3.98 (1, 59) | 2.41 (4, 56) | 3.63 (5, 55) | 0.98 (1, 59) | |
| p-value | 0.755 | 0.098 | 0.421 | 0.051 | 0.060 | 0.007 | 0.326 |
- Notes: Bootstrap standard errors and bias-corrected percentile confidence intervals (based on 1000 replications) are presented. Wald tests were performed to evaluate the joint significance of ancillary variables included in the models. F test numerator and denominator degrees of freedom are represented by ν1 and ν2, respectively.
- CI, confidence interval; SE, standard error.
There was limited evidence supporting the inclusion of ancillary variables in the model to predict health state preferences. Estimates for the constant and the variable N2 were consistently insignificant. Based on its estimated confidence interval, the estimate for N3 was insignificant in the MM-N2N3 model but significant in the MM-N3 and MM-N3OC models. Estimates for the ancillary variables included in the MM-D1 model were neither individually nor jointly statistically significant. However, estimates for I22 and I3 were individually significant in the MM-D1I2 model, and the ancillary variables included in this model were jointly significant (F5, 55 = 3.63, p = 0.007).
Fit indices for the eight model specifications are presented in Table 4. The rank correlation and pseudo-R2 statistics varied trivially among the models. The MM-N3, MM-N3OC, and MM-D1 specifications yielded the smallest validation MAE. However, there were no important differences among the models when fit to the valuation sample data. The MM and MM-OC models fit as well or better than the other specifications. Based on these results, the MM and MM-OC models were selected for further evaluation.
| Index | MM-N2 | MM-N3 | MM-N2N3 | MM-N3OC | MM-D1 | MM-D1I2 | MM | MM-OC |
|---|---|---|---|---|---|---|---|---|
| Modeling sample | ||||||||
| Sum of deviations | 85,185 | 85,182 | 85,182 | 85,182 | 85,178 | 85,177 | 85,186 | 85,186 |
| Pseudo-R2 | 0.0764 | 0.0764 | 0.0764 | 0.0764 | 0.0764 | 0.0765 | 0.0764 | 0.0764 |
| Validation sample | ||||||||
| MAE | 0.072 | 0.039 | 0.047 | 0.039 | 0.043 | 0.062 | 0.061 | 0.057 |
| r (overall) | 0.605 | 0.605 | 0.605 | 0.605 | 0.605 | 0.605 | 0.605 | 0.605 |
| r (between) | 0.984 | 0.984 | 0.984 | 0.984 | 0.984 | 0.984 | 0.984 | 0.984 |
| No. errors > 0.05 | 7 | 6 | 6 | 5 | 5 | 7 | 7 | 7 |
| No. errors > 0.10 | 2 | 3 | 3 | 3 | 1 | 2 | 2 | 2 |
| Valuation sample | ||||||||
| Sum of deviations | 92,615 | 92,610 | 92,610 | 92,610 | 92,607 | 92,606 | 92,615 | 92,615 |
| Pseudo-R2 | 0.0767 | 0.0767 | 0.0767 | 0.0767 | 0.0768 | 0.0768 | 0.0767 | 0.0767 |
| MAE | 0.026 | 0.025 | 0.025 | 0.025 | 0.025 | 0.025 | 0.026 | 0.026 |
| r (overall) | 0.636 | 0.636 | 0.636 | 0.636 | 0.636 | 0.635 | 0.636 | 0.635 |
| r (between) | 0.992 | 0.992 | 0.992 | 0.992 | 0.991 | 0.991 | 0.992 | 0.991 |
| No. errors > 0.05 | 9 | 11 | 11 | 11 | 9 | 10 | 9 | 10 |
| No. errors > 0.10 | 3 | 5 | 5 | 5 | 4 | 5 | 3 | 3 |
- Notes: The optimization criterion for the median regression is the minimization of the sum of the absolute deviations between the observed and predicted values of the dependent variable. We present the sum of the absolute deviations for each model when fit in the modeling sample (N = 3573; 42,485 observations) and valuation sample (N = 3962; 47,129 observations). Pseudo-R2 was calculated as 1 minus this sum divided by the sum of the absolute deviations about the unconditional median (i.e., the estimated intercept of the null regression model).
- MAE, median absolute error.
Valuation Sample Estimates
Parameter estimates, standard errors, and 95% bias-corrected percentile bootstrap confidence intervals for the two specifications are presented in Table 5. As in the modeling sample, the two specifications yielded main effects parameter estimates that were positive in sign and significant at the 5% level. The parameter estimate for the constant in the MM model was statistically insignificant. The MM-OC model yielded somewhat larger estimates for main effects than did the MM model, though differences between the two specifications were small. For instance, the MM-OC and MM model estimates for M2 were 0.042 and 0.040, respectively, while the corresponding estimates for S2 were 0.057 and 0.053. The rescaled nonparametric block bootstrap procedure (with 1000 replications) was used to estimate a variance–covariance matrix for differences in parameter estimates between the two models. None of the coefficient differences was individually significant, and tests of parallelism (F10, 50 = 0.07, p = 1.000) and regression identity (F11, 49 = 0.06, p = 1.000) were insignificant. Variables indicating health state group assignment (i.e., groups 2–5 treating group 1 as the referent) were also jointly insignificant when included in the MM-OC model (F4, 56 = 0.81, p = 0.522). Because the exclusion of a constant did not yield any appreciable bias in the parameter estimates, the MM-OC model was chosen for comparison with the D1 model. The predicted US population preferences for the 243 EQ-5D health states and a description of the MM-OC model scoring algorithm are provided in Appendices 1 and 2, respectively. These appendices are available at: http://www.ispor.org/Publications/value/ViHsupplementary/ViH13i2_Shaw.asp.
| Variable | MM-OC | MM | Difference |
|---|---|---|---|
| M2 | 0.042 | 0.040 | 0.002 |
| (0.012) | (0.011) | (0.002) | |
| [0.008, 0.055] | [0.008, 0.053] | [−0.003, 0.005] | |
| M3 | 0.490 | 0.490 | 0.000 |
| (0.019) | (0.019) | (0.000) | |
| [0.458, 0.531] | [0.457, 0.531] | [−0.001, 0.000] | |
| S2 | 0.057 | 0.053 | 0.004 |
| (0.008) | (0.008) | (0.004) | |
| [0.042, 0.074] | [0.042, 0.075] | [−0.006, 0.009] | |
| S3 | 0.356 | 0.354 | 0.002 |
| (0.016) | (0.016) | (0.003) | |
| [0.341, 0.395] | [0.338, 0.395] | [−0.004, 0.006] | |
| U2 | 0.056 | 0.053 | 0.003 |
| (0.010) | (0.012) | (0.003) | |
| [0.033, 0.075] | [0.035, 0.080] | [−0.004, 0.007] | |
| U3 | 0.136 | 0.132 | 0.004 |
| (0.017) | (0.018) | (0.004) | |
| [0.107, 0.164] | [0.100, 0.163] | [−0.005, 0.009] | |
| P2 | 0.042 | 0.039 | 0.003 |
| (0.010) | (0.011) | (0.003) | |
| [0.019, 0.057] | [0.019, 0.050] | [−0.004, 0.007] | |
| P3 | 0.466 | 0.464 | 0.003 |
| (0.024) | (0.023) | (0.003) | |
| [0.400, 0.503] | [0.400, 0.500] | [−0.004, 0.006] | |
| A2 | 0.061 | 0.057 | 0.004 |
| (0.009) | (0.009) | (0.005) | |
| [0.047, 0.075] | [0.043, 0.075] | [−0.006, 0.010] | |
| A3 | 0.357 | 0.354 | 0.003 |
| (0.018) | (0.017) | (0.004) | |
| [0.324, 0.382] | [0.330, 0.382] | [−0.005, 0.008] | |
| Constant | 0.011 | −0.011 | |
| (0.012) | (0.012) | ||
| [−0.017, 0.025] | [−0.025, 0.017] | ||
| Parallelism | |||
| F (ν1, ν2) | 0.07 (10, 50) | ||
| p-value | 1.000 | ||
| Regression identity | |||
| F (ν1, ν2) | 0.06 (11, 49) | ||
| p-value | 1.000 |
- Notes: Bootstrap standard errors and bias-corrected percentile confidence intervals (based on 1000 replications) are presented. Wald tests of parallelism and regression identity were performed. F test numerator and denominator degrees of freedom are represented by ν1 and ν2, respectively.
- Abbreviations: SE, standard error; CI, confidence interval.
Comparison of MM-OC and D1 Model Predictions
Figure 1 presents values for the 243 EQ-5D health states predicted by the MM-OC and D1 models. The values for the D1 model are predicted means, whereas those for the MM-OC model are predicted medians. The MM-OC model predicted higher values for mild states of health and lower values for severe states of health than the D1 model. The decline from full health (i.e., 11111) to the next best health state was less precipitous for the MM-OC model (from 1.00 to 0.96 for health states 11121 and 21111) than the D1 model (from 1.00 to 0.86 for health state 11211). Predicted values for the MM-OC model ranged from 1.00 for full health to –0.81 for 33333, whereas the D1 model yielded predicted values of 1.00 and −0.11, respectively, for these same states. There were inconsistencies between the MM-OC and D1 models in the ranks of the predicted values for 237 (97.5%) of the 243 health states. Nevertheless, the two sets of predicted values were highly correlated (Spearman r = 0.99). As depicted in Figure 2, the relationship between the predicted values was adequately described by a second-order polynomial function.
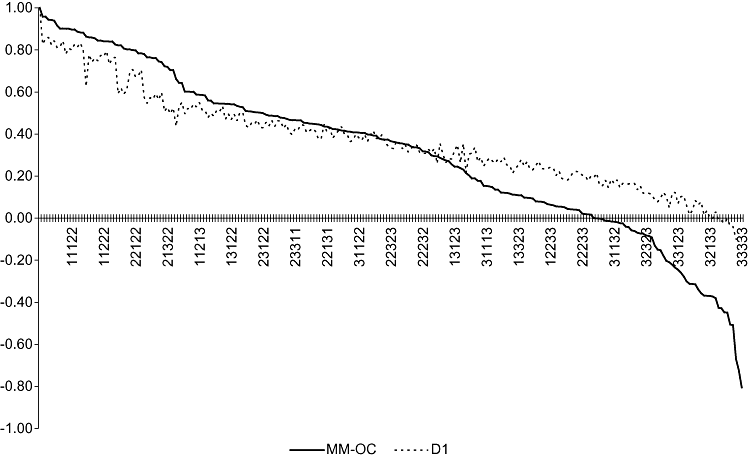
MM-OC and D1 model predicted values for the 243 EQ-5D health states.
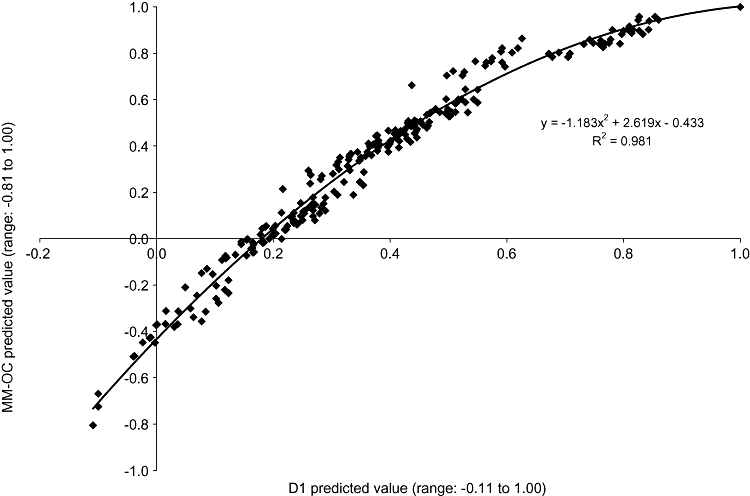
Correlation of MM-OC and D1 model predicted values.
As with the D1 model, the MM-OC model provided a better fit for mild health states than severe health states. The largest prediction errors occurred for moderate and severe states of health. These inaccuracies can be ascribed to the limited number of severe health states that were valued in the US EQ-5D valuation study. Even without the ancillary terms included in the D1 model, the MM-OC model provided a reasonable fit for the worst health states. With one exception, it also provided reasonably accurate predictions for the health states valued the same as Immediate Death (Figure 3).
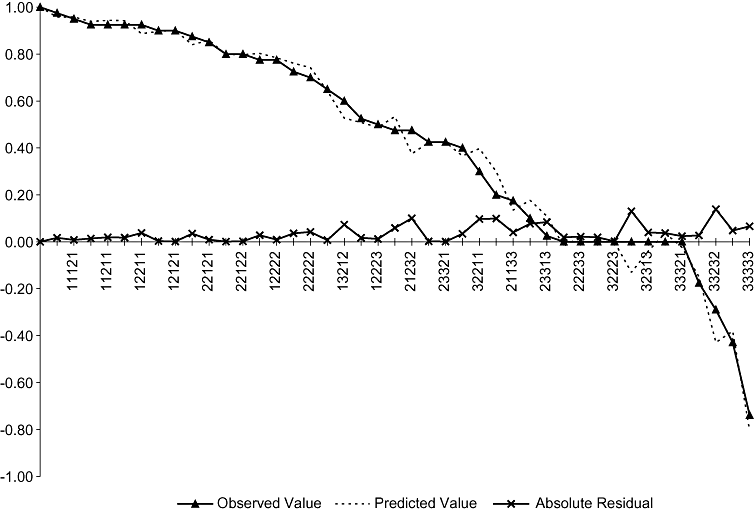
Observed, predicted, and absolute residual values for MM-OC model.
Discussion
This article describes the development of a median model for predicting US population-based preferences for EQ-5D health states. There are several reasons to believe that this modeling approach improves upon previous efforts to predict health state values using the US EQ-5D valuation study data. In addition, the approach described herein is likely to be useful to other researchers using statistical inference to model health state preferences [26].
Regardless of how one elects to treat the values for states considered worse than death, there are substantive differences between the mean and median values for EQ-5D health states. Given that EQ-5D health state preferences tend to be skewed in distribution, the median is a more appropriate measure of their central tendency than the mean. For the US valuation study data, a median model is more parsimonious than alternative mean-based models and, dissimilar from the latter, requires no transformation of the values for states worse than death. Our positive findings with regard to a median model are consistent with the recommendation by Lamers that median-based value sets be developed for the EQ-5D [27].
Application of the Median in Expected Utility Theory
One potential barrier to the adoption of a median model relates to the validity of using medians in the context of expected utility theory. According to expected utility theory, the utility of a lottery is a weighted average of the utilities of the possible outcomes, where the weights reflect the probability of each outcome's occurrence [13]. The role of the weighted average's counterpart, the weighted median, has been explored in decision making under risk. Let D = 〈(ai,bi)〉 be a collection of (weight, value) pairs for an object valued by i = 1, . . . , N individuals with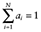 
and ai ∈ [0,1] ∀ i. It is assumed that the weights are either drawn from the unit interval and sum to 1 or are rescaled to have these properties. The weighted median is idempotent in that if all values equal some quantity, then the weighted median must also equal that quantity. It is commutative (or generally symmetric) in that the ordering of pairs within D has no bearing on the aggregation. Let 
be a second collection of (weight, value) pairs for the same valued object and i = 1, . . . , N individuals with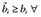 
i. The weighted median is monotonic in that the aggregation of 
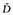is ensured to be greater than or equal to the aggregation of D. Because the weighted median is idempotent, commutative, and monotonic, it is a mean operator [28,29]. This quality allows it to be substituted for the weighted average when comparing lotteries. Like the weighted average, the weighted median is also bounded, and its aggregation is unaffected by the introduction of an element with zero weight. Because the expected value is a weighted averaging operator, the weighted median is a natural candidate for the expected value in environments in which payoffs are drawn from a linear scale [30].
Validity of the Median as an Aggregate Preference Measure
In some contexts, the median may not represent the best measure of aggregate preference. A notable example involves Black's median voter theorem [31], which states that the most preferred alternative of the median person will dominate all other alternatives in pairwise comparisons. Suppose that a group of individuals is asked to make pairwise comparisons among several health states. Assume that the health states can be ordered from low to high according to “healthiness” and that this ordering is independent of the individuals' valuations. Further, assume that the distribution of each individual's preferences along the healthiness continuum is unimodal (i.e., single-peaked). Given these assumptions, if one were to plot the most preferred health state of each individual along the healthiness continuum, then the median of these would be the alternative that would beat all others in pairwise majority votes (i.e., the Condorcet winner). While the median voter theorem is conceptually simple and often used in models of political preference, it fails to explain decision-making when individuals have multipeaked preferences[32]. Even when each individual behaves rationally and all of his or her preference orderings are transitive, multimodal preferences will result in a Condorcet cycle in which no single alternative is pairwise-preferred over all other alternatives.
The failings of the median voter theorem illustrate the difficulty had in aggregating ordinal preferences. In his Ph.D. dissertation, Kenneth Arrow considered the problem of using individuals' ordinal preferences to construct a societal utility function. His research culminated in the development of an impossibility theorem. According to Arrow's theory, there is no way to aggregate ordinal preferences for three or more alternatives and assure transitive societal rankings that fulfill the social choice criteria of universality, citizen sovereignty, nondictatorship, monotonicity, and the independence of irrelevant alternatives (IIA) [33]. The median voter theorem is a specific model for aggregating ordinal preferences that applies only when the universality condition is relaxed (i.e., some individuals' preference orderings are excluded from consideration).
Arrow's theory has no direct bearing on our research because models were fit to preferences measured on a cardinal scale. However, it does raise questions about the validity of recent efforts to generate tariffs of EQ-5D health state values through the aggregation of rankings across individuals [34,35]. In these investigations, preference weights were estimated using the rank-ordered logit model, which is founded on R. Duncan Luce's choice axiom [36]. Luce's research focused on the explanation of individual decision-making as opposed to the derivation of societal utility functions. Whereas Arrow placed an emphasis on the properties of the decision rule relating individuals' preferences to societal outcomes, Luce stressed the structure of admissible outcomes. The rank-ordered logit model entails a form of the IIA assumption that is even more restrictive than Arrow's binary IIA: namely, that each alternative possesses an intrinsic strength that is preserved over all possible subsets of alternatives [37,38]. To satisfy this assumption, restrictions must be placed on the preference orderings under consideration. Therefore, as with the median voter model, the rank-ordered logit model is not applicable to all possible preference orderings. While this may not be problematic when seeking to explain individuals' preferences in some contexts, it presents a serious threat to the validity of using rankings data to derive societal preference weights for the EQ-5D health states.
Impact of Median-Based Preferences in Cost-Utility Analyses
Given that there are differences between the median health state preferences generated in this study and the mean preferences predicted by the D1 model, it is likely that investigators will derive different estimates of cost-effectiveness depending on which set of predicted preferences is used. Relative to the health state preferences predicted by the D1 model, the predicted median health state preferences exhibit greater dispersion as health status decreases. This leads us to conclude that researchers will observe greater between-groups differences in quality-adjusted life years when using the median-based index as opposed to the mean-based index unless the members of all groups are very healthy. We anticipate that estimated incremental cost–utility ratios will be smaller when using the predicted median health state preferences as opposed to the predictions of the D1 model. A rigorous evaluation of the impact of using the predicted median health state preferences in cost–utility analyses and other applications is beyond the scope of our stated objective. However, this represents an important area for future study.
Conclusions
In summary, we have developed a novel model for predicting median US population preferences for EQ-5D health states. This model may be used as an alternative to the D1 model developed by Shaw et al. [4]. While we do not suggest that the D1 model is invalid, there are several reasons why the median model described herein may be preferred over the D1 model. These reasons include greater parsimony because of the exclusion of unnecessary interaction terms; a more appropriate (i.e., median-based) estimation method; and the prediction of values for worse-than-death health states on an untransformed scale. The prediction of medians (as opposed to means) may represent the optimal approach for generating societal tariffs of EQ-5D health state values, particularly when the TTO or standard gamble is used to elicit preferences.
Acknowledgments
The authors wish to thank Dr. Donald G. Saari and Dr. R. Duncan Luce for providing constructive feedback on issues relating to the aggregation of ordinal preferences.
Sources of financial support: Aspects of this article were reported at the 12th Annual International Meeting of the International Society for Pharmacoeconomics and Outcomes Research, Arlington, VA, May 19–23, 2007; at the 24th Plenary Meeting of the EuroQol Group, Kijkduin, The Netherlands, September 13–14, 2007; and at the 14th Annual Conference of the International Society for Quality of Life Research, Toronto, Canada, October 10–13, 2007. Financial support for the US Valuation of the EQ-5D Health States was provided by grant number 5 R01 HS10243 from the United States Agency for Healthcare Research and Quality (AHRQ).
