Performance Comparison of Likert and Binary Formats of SF-36 Version 1.6 Across ECRHS II Adults Populations
ABSTRACT
Objectives: To evaluate a binary response structure of SF-36 items assessing scaling assumptions, reliability, and validity of questionnaire.
Methods: An optimal scaling accounting for the nonmetric properties of the data was used to reduce SF-36 Likert item responses to give a binary coding. The binary recoding was compared with the original format regarding item analysis, underlying latent components and know-groups clinical validity using ordered correlation/regression methods. Data from the European Community Respiratory Health Survey Follow-up (ECRHS II) of 8854 subjects from 25 centers were analyzed to cross-validate the binary coding proposal.
Results: Overall, the testing comparison produces results indicating that the binary recoding of the SF-36 scales meets at least similar standards without jeopardizing the underling structure of the original format. Internal binary consistencyshows comparable values with the Likert ones and these are always higher than the minimum suggested. The Principal Component structure was well replicated and know-groups validity gives similar research findings for symptomatic, long-term illness and depression differences.
Conclusions: Although there is lost of information due to the reduction of response's chance, our results indicate that the SF-36 binary recoding gives the possibility to suggest a new version of smarter and easier methodology of administration, compilation, score calculation, and data processing. Consequently, it may be an alternative to the existing shorter versions, suitable in administering in clinical setting and clinical trials, in subjects with serious diseases, and by telephone.
Introduction
Among different questionnaires for assessing health status, the 36-item Short-Form Health Survey (SF-36) is probably the most widely used. It was developed more than a decade ago, and translated into about 50 languages successively [1–6]. SF-36 has proven useful in comparing general and specific population, measuring the health deficit of different diseases, or the health benefits of different treatments, and for screening individual patients. It is able to synthesize eight concepts with only 36 questions, and it is structured on three levels: items, multi-items scales, and scale clusters. Twenty-eight items are in ordinal form following the Likert format, seven items are in binary form, and a further item concerns reported health transition over the past year. Four multi-items scales regard the physical health concepts (physical functioning—PF, role limitations due to physical health problems—RP, bodily pain—BP, general health—GH); other four multi-items scales concern the mental health concepts (vitality—VT, social functioning—SF, role limitations due to personal or emotional problems—RE, and mental health perceptions—MH). Two summary measures of the SF-36 are referred to as physical component summary 36 (PCS-36) and as mental component summary 36 (MCS-36) scales. During years, SF-36 has been revised, rectified, and proposed in more specific and synthetic versions (SF-36v2TM, SF-12®, SF-12v2TM, SF-8TM, cf. http://www.sf-36.org), finding a better application in clinical trials.
The SF-36 scales (in all versions) are scored using Likert's method of summated ratings [7]. In this method, a number (weight) is assigned to each item response category, usually 1, 2, 3 for low, middle, high responses, respectively, or 1, 2, 3, 4, 5 for excellent, very good, good, fair, poor responses, respectively, and so on; weights for some items need to be recalibratedso that all items are weighted in the same direction. The scale score is then computed by summing the weights assigned to item responses and by linearly transforming scores to 0–100, where higher scores represent a better level of quality of life (QoL). Summated rating scales have the advantage of simplicity, and can achieve high levels of reliability and validity.
Nevertheless, the item weighting presupposes the equidistance (linearity) between numerical response labels assigned to Likert points. It is a well-known fact that the nonmetric proprieties of ordered categorical data imply that such arithmetic operations are not strictly appropriate for ordinal data [8]. The number of response categories also precludes the chance to administer the questionnaire in an easy and fast way (i.e., telephone research and very ill patients) [9,10], setting a burden on both patients and investigators. A solution may be to recode the 28 items of SF-36 questionnaire from Likert to binary, so to reduce all SF-36 items in binary format.
The European Community Respiratory Health Survey (ECRHS) [11,12] is an international longitudinal population-based study of more than 10,000 young adults, initially aged between 20 and 44 years from 1991 to 1993, randomly selected, and followed up 9 years later using the same standardized protocol, in all centers. The ECRHS was carried out in response to the rapid increase in asthma prevalence, which pointed to environmental factors being important in the development of the disease. At Follow-up, validated QoL questionnaires, including the SF-36, were administered. Although the primary aim of the Quality of Life Working Group is to appraise the burden of allergic conditions across Europe, in large populations with different asthma prevalence and risk factors, the settings of the study makes the ECRHS a unique opportunity for developing methodological work in the field of QoL assessment.
We therefore performed the present analysis based on the ECRHS data to investigate the following specific aims: 1) to aggregate ordinal responses in binary ones, using an approach that takes account of the nonmetric proprieties of the SF-36 data; 2) to evaluate the overall performance of the SF-36 binary recoding, regarding reliability and validity, scaling assumptions by ordered correlation/regression methods; and 3) to compare the equivalence of Likert and binary rescaled SF-36 questionnaire outcomes, and their implications for interpreting research findings.
Methods
Sample
Subjects were recruited from the ECRHS Follow-up (ECRHS II), a longitudinal study between 1998 and 2002 of the subjects who are previously considered in the second stage of the ECRHS I. This stage investigated two samples: a random sample selected from the responders to a mail short screening questionnaire, and a symptomatic sample, which comprised the responders to the screening questionnaire not included in the random sample who had reported nocturnal shortness of breath or asthma attacks in the last 12 months or asthma treatment.
The ECRHS II project used the SF-36 version 1.6 questionnaire. In all centers, the questionnaire was self-completed by the study subjects after the interviewer-administered main questionnaire and before lung function testing. Answers to the following long-standing illnesses binary (YES/NO) questions were preliminary recoded before administration of the SF-36 questionnaire: “Do you have any long-term limiting illness?” and “Do you have any of the following conditions?” using a checklist of 11 chronic illnesses.
Overall, 29 centers have participated in the ECRHS II, and 10,933 subjects have completed the main questionnaire, 1,961 subjects of four centers did not collect any QoL data, and 118 subjects of the other centers who did not answer any of the SF-36 questions were excluded from the analyses. Consequently, the SF-36 questionnaire was completed by 8854 subjects from 25 centers, of whom 6611 also completed the questionnaire of long-standing conditions. The centers were 23 European and two extra European, in total of 12 countries. Switzerland, Spain, and France account for about half of the subjects included (19.4%, 19%, and 12.1%, respectively). The remaining countries account for 5.5% in average of the observations. The symptomatic sample represented 16.8% of the total (cf. Table 1).
| ECRHS countries distribution | Random | Symptomatic | Total | |||
|---|---|---|---|---|---|---|
| Frequency | % | Frequency | % | Frequency | % | |
| Belgium | 533 | 7.2 | 64 | 4.3 | 597 | 6.7 |
| Spain | 1220 | 16.6 | 463 | 31.1 | 1683 | 19.0 |
| France | 1033 | 14.0 | 34 | 2.3 | 1067 | 12.1 |
| Italy | 491 | 6.7 | 55 | 3.7 | 546 | 6.2 |
| England | 530 | 7.2 | 129 | 8.7 | 659 | 7.4 |
| Iceland | 455 | 6.2 | 64 | 4.3 | 519 | 5.9 |
| Norway | 588 | 8.0 | 0 | 0.0 | 588 | 6.6 |
| Switzerland | 1346 | 18.3 | 369 | 24.8 | 1715 | 19.4 |
| Sweden | 368 | 5.0 | 79 | 5.3 | 447 | 5.0 |
| United States | 194 | 2.6 | 35 | 2.4 | 229 | 2.6 |
| Australia | 365 | 5.0 | 129 | 8.7 | 494 | 5.6 |
| Estonia | 243 | 3.3 | 67 | 4.5 | 310 | 3.5 |
| Total | 7366 | 100 | 1488 | 100 | 8854 | 100 |
- ECRHS, the European Community Respiratory Health Survey.
Binary Recoding
Multiple Correspondence Analysis (MCA) alias Homogeneity Analysis (HOMALS) [13] is performed to transform the answers from Likert format to the binary one. MCA can be introduced in many different ways (see the extensive review in [14]), and we have considered the Guttman's approach where MCA quantifies the raw (subjects) and column (categorical variables) of a table in such a way that an optimally “internal consistency criterion” is satisfied [14]. This method uses the Likert points as nominal categories responses, and enables optimal grading for each category response of the Likert questions (called “optimal weights”); consequently, an “optimal score” for each subject may be obtained. The optimal score of a subject is the sum of the optimal weights of the item options chosen.
From computational process in MCA the pairwise two-way frequencies tables of categorical variables are collected in a matrix (called “Burt matrix”), as in Principal Component Analysis (PCA) the pairwise correlations are collected in a “correlation matrix,” and the eigenvalues/eigenvectors of Burt matrix are computed by numerical methods. From the Guttman's optimal scaling point of view [15], only the first dimension is considered while the remaining dimensions are irrelevant. According to the criterion of internal consistency, the rescaled eigenvector values of the maximum eigenvalue (the first dimension) are the optimal “weight” quantifications of the variable (item) categories (options), the eigenvalue/n items are the squared correlation ratio (called “Guttman's eta”), while the reliability computed by Cronbach's alpha coefficient is a one-to-one transformation of Guttman's eta.
Optimal quantifications give weight and direction (positive or negative) independently of questionnaire format and successive items recalibration. Moreover, they allow checking the supposed equidistance of the ordinal Likert points plotting the optimal weights versus Likert points (called “transformation plots”). If the Likert equidistance assumption is rejected, it will be better to use optimal weights or a binary form to represent the questionnaire options. In fact, when the optimal weight is positive it will be recoded as 1, vice versa when negative as 0.
For Likert format the standard score (SS) is: 100 × (raw score − min)/(max − min), where the raw score is the sum of the subject option choices for all the items, after item recalibration, thus using the same system scoring, the raw score for binary format is given by the sum of the positive answers (= 1), and the SS is: 100 × (raw score/n items). Likert and binary forms scales have the same range of 0–100 expressed in percentage, with 100% indicating the most favorable level of QoL, 0% the least favorable, and scores in between the percent of the maximum possible score. Obviously in the 0–100 range, the binary form scale is an ordinal scale with limited number of levels =n items + 1, vice versa the Likert form scale is a continuous scale with a large number of levels =(n options − 1) × n items + 1.
Likert versus Binary
Likert scales and binary recordings of the original scales were compared to evaluate their equivalence regarding overall performance of the scoring system, scaling assumptions, reliability, and validity. Descriptive statistics were computed to characterize score distributions, and the percentage of responses on anchor points (extremes) was examined for each scale to detect floor or ceiling effects. Spearman–Brown formula of the Cronbach's alpha coefficient was used to determine the reliability/internal consistency of the scales [16]. High internal consistency has been suggested if alpha > 0.70 for group comparison, and alpha > 0.90 for individual comparison. To explore the heterogeneity/homogeneity among the Likert and binary forms of the SF-36 items across the 25 ECRHS centers (average cluster size was 354), the intraclass correlation coefficients (ICC) were also computed [17].
To check correlations across Likert, binary, and Likert-binary sets, the Pearson's correlation coefficients, polychoric correlations coefficients, and biserial correlations coefficients [18] were computed, respectively. Further, to identify the two health components (physical, mental) underlying the SF-36 questionnaire, both Pearson's correlation matrix (for Likert form scales) and polychoric correlations matrix (for binary form scales) were explored by means of PCA. The number of components was determined on the basis of eigenvalues of the correlation matrix greater than 1, and by looking for sharp breaks in the size of the eingenvalues using a scree plot [19]. Varimax rotation, and scale–component correlations, i.e., “factor loading,” greater than 0.40 in absolute value was chosen to identify a simple component structure, i.e., component with nonoverlapping clusters of SF-36 scales.
To get a single number describing the relationship between Likert and binary matrices output, we used the vector correlation coefficient (RV), a generalization of the Pearson determination coefficient, R2[20]. As the determination coefficient, also RV is bounded between 0 and 1, and Good, Strong, Excellent agreement between the two matrices has been suggested if RV > 0.50, RV > 0.70, RV > 0.90, respectively.
Finally, clinical (criterion-based) validity of the Likert scales and the binary recoding scales were assessed by means of know-groups comparison. Subjects were assigned to mutually exclusive groups differing in self-reported asthma-like symptoms, long-term limiting illness, and depression conditions. It was expected that physical component scales (PF, RP, BP) profiles would score worse in groups with asthma like symptoms or long-term limiting illness; that mental component scales (MH, SF, RE) profiles would score worse in groups with depression; and that GH and VT profiles score worse on groups with all negative conditions. Two-level random intercept regression models [21] with level 1 units (subjects) nested in level 2 units (ECRHS II centers) were fitted to rank the group differences on the SF-36 scales. Considering Likert scales and PF binary recoded scale as continuous responses, linear regression models were fitted. Vice versa, for other binary recoded scales linear or ordered logistic regression models were fitted, considering the binary forms scales as continuous or ordinal responses, respectively. The P-values of the regression parameter estimates were evaluated by t-test (= parameter/standard error) using robust standard errors; the significance level was set at P < 0.05, two-sided.
Descriptive data analyses and MCA were performed using SPSS software, version 11.5 (SPSS Inc., Chicago, IL, USA: http://www.spss.com), while polychoric/polyzerial correlations and two-level regression models were provided by Mplus software, version 3.13 (Muthén & Muthén, Los Angeles, CA, USA: http://www.statmodel.com).
Results
Binary Recoding
The internal criterion index (Guttman's eta) of the MCA scaling ranged from 0.56 (GH) to 0.88 (BP), while the Cronbach's alpha coefficient varied from 0.80 (GH; and SF) to 0.92 (PF), indicating an excellent optimal scaling.
The transformation plots of the optimal weights for each Likert scale are displayed in Figure 1. Generally, PF items seemed to describe a straight line, even if the optimal values of the second and the third answers of A and D items had a similar weight; the A and C items of the GH scale seemed to describe better a curve than a straight line having equal weights in the first and second answers, besides the fourth answer of the B item had an higher optimal weight than the fifth one; in VT scale the item points described better a double curve not respecting the linearity; in SF scale the first A item answer had a value lower than the second one; and finally, no one item described a straight line in MH scale. Therefore, only in BP scale the equidistance assumption was respected, while in the other scales this assumption was rejected.
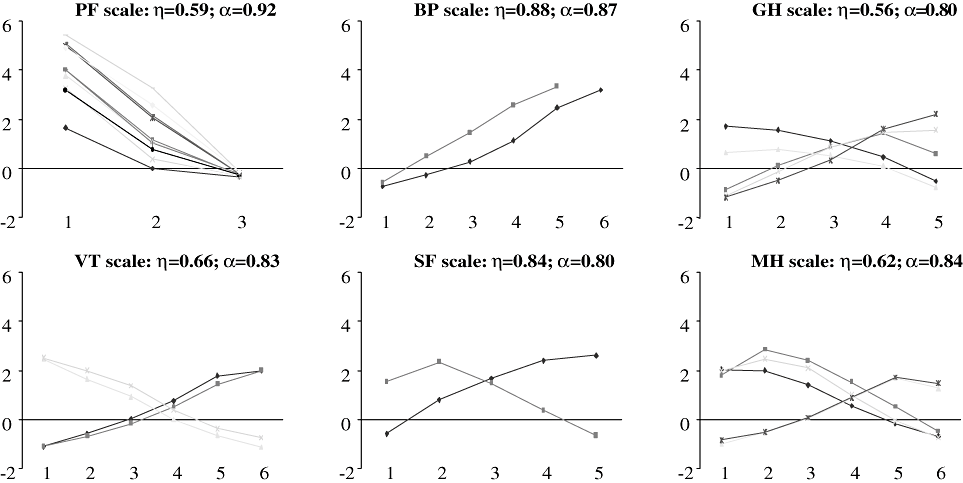
The transformation plots of Multiple Correspondence Analysis optimal weights for the Likert SF-36 scales: PF, physical functioning; BP, bodily pain; GH, general health; VT, vitality; SF, social functioning; MH, mental health.
The MCA optimal weights (normal type) and the binary recoding (bold type) of the SF-36 questionnaire are summarized in Table 2. Columns show the several Likert options, while rows show the different item number for each scale. Negative (positive) optimal weight values were recoded as 0 (1) for PF, BP, VT, and MH scales, while there was an opposite recoding for GH and SF scales. For example, the first answers of each PF scale item had always negative values, thus these were recoded with 0, while the third answers, being positive for the 10 items, were recoded as 1. The recode 0 represents the tendency toward a low QoL level, and vice versa 1 represents high QoL level.
| Binary recoding | Items | Options | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||||||||
| PF | a | 1.63 | 0 | −0.02 | 1 | −0.35 | 1 | ||||||
| b | 4.02 | 0 | 1.17 | 0 | −0.28 | 1 | |||||||
| c | 3.78 | 0 | 1.05 | 0 | −0.27 | 1 | |||||||
| d | 3.24 | 0 | 0.38 | 0 | −0.31 | 1 | |||||||
| e | 4.99 | 0 | 2.04 | 0 | −0.21 | 1 | |||||||
| f | 3.19 | 0 | 0.73 | 0 | −0.27 | 1 | |||||||
| g | 4.02 | 0 | 1.01 | 0 | −0.26 | 1 | |||||||
| h | 5.12 | 0 | 2.14 | 0 | −0.21 | 1 | |||||||
| i | 5.41 | 0 | 3.27 | 0 | −0.15 | 1 | |||||||
| j | 4.90 | 0 | 2.58 | 0 | −0.14 | 1 | |||||||
| BP | a | −0.74 | 1 | −0.29 | 1 | 0.28 | 0 | 1.12 | 0 | 2.46 | 0 | 3.20 | 0 |
| b | −0.59 | 1 | 0.48 | 0 | 1.45 | 0 | 2.55 | 0 | 3.33 | 0 | |||
| GH | a | 1.70 | 0 | 1.56 | 0 | 1.13 | 0 | 0.46 | 0 | −0.51 | 1 | ||
| b | −0.86 | 1 | 0.12 | 0 | 0.89 | 0 | 1.43 | 0 | 0.62 | 0 | |||
| c | 0.65 | 0 | 0.77 | 0 | 0.53 | 0 | 0.09 | 0 | −0.75 | 1 | |||
| d | −1.11 | 1 | −0.10 | 1 | 0.90 | 0 | 1.47 | 0 | 1.58 | 0 | |||
| x | −1.17 | 1 | −0.50 | 1 | 0.35 | 0 | 1.61 | 0 | 2.21 | 0 | |||
| VT | a | −1.10 | 1 | −0.60 | 1 | 0.02 | 0 | 0.74 | 0 | 1.78 | 0 | 1.98 | 0 |
| e | −1.12 | 1 | −0.71 | 1 | −0.17 | 1 | 0.52 | 0 | 1.42 | 0 | 1.99 | 0 | |
| g | 2.45 | 0 | 1.65 | 0 | 0.91 | 0 | −0.02 | 1 | −0.66 | 1 | −1.13 | 1 | |
| i | 2.51 | 0 | 1.99 | 0 | 1.38 | 0 | 0.36 | 0 | −0.37 | 1 | −0.76 | 1 | |
| SF | a | −0.59 | 1 | 0.78 | 0 | 1.67 | 0 | 2.41 | 0 | 2.59 | 0 | ||
| b | 1.54 | 0 | 2.34 | 0 | 1.47 | 0 | 0.36 | 0 | −0.67 | 1 | |||
| MH | b | 2.01 | 0 | 1.97 | 0 | 1.40 | 0 | 0.53 | 0 | −0.19 | 1 | −0.68 | 1 |
| c | 1.78 | 0 | 2.85 | 0 | 2.38 | 0 | 1.50 | 0 | 0.49 | 0 | −0.50 | 1 | |
| d | −1.01 | 1 | −0.57 | 1 | 0.02 | 0 | 0.85 | 0 | 1.66 | 0 | 1.26 | 0 | |
| f | 1.97 | 0 | 2.48 | 0 | 2.08 | 0 | 0.98 | 0 | −0.08 | 1 | −0.73 | 1 | |
| h | −0.88 | 1 | −0.52 | 1 | 0.05 | 0 | 0.89 | 0 | 1.72 | 0 | 1.48 | 0 | |
- BP, bodily pain; GH, general health; MCA, Multiple Correspondence Analysis; MH, mental health; PF, physical functioning; SF, social functioning; VT, vitality.
Item/Scale Analysis Comparison
Results of scaling assumptions (the item analysis) of Likert and binary forms are reported in Table 3. Considering the Likert format, the values of the intraclass correlation ranges were always below the ICC < 0.10 value, except GH and MH scales, indicating some specific clustering effects of the ECRHS centers.
| ICCscale(n items) | Original format items | Binary format items | ||||||
|---|---|---|---|---|---|---|---|---|
| CentersICC* | Iteminternal consistency† | rho‡ | alpha§ | CentersICC* | Item internal consistency† | rho‡ | alpha§ | |
| PF (10) | 0.002–0.022 | 0.55–0.76 | 0.45 | 0.89 | 0.000–0.024 | 0.52–0.72 | 0.42 | 0.88 |
| RP (4) | 0.004–0.009 | 0.72–0.82 | 0.67 | 0.89 | 0.004–0.009 | 0.72–0.82 | 0.67 | 0.89 |
| BP (2) | 0.014–0.022 | 0.75 | 0.70 | 0.82 | 0.023–0.025 | 0.65 | 0.65 | 0.79 |
| GH (5) | 0.028–0.100 | 0.40–0.71 | 0.41 | 0.77 | 0.036–0.106 | 0.42–0.53 | 0.35 | 0.73 |
| VT (4) | 0.024–0.068 | 0.61–0.67 | 0.54 | 0.82 | 0.017–0.062 | 0.51–0.57 | 0.39 | 0.72 |
| SF (2) | 0.016–0.051 | 0.65 | 0.65 | 0.79 | 0.031–0.071 | 0.60 | 0.60 | 0.75 |
| RE (3) | 0.008–0.016 | 0.65–0.74 | 0.62 | 0.83 | 0.008–0.016 | 0.65–0.74 | 0.62 | 0.83 |
| MH (5) | 0.023–0.170 | 0.58–0.70 | 0.49 | 0.83 | 0.024–0.144 | 0.51–0.58 | 0.40 | 0.77 |
- * Items intraclass correlation coefficients for ECRHS II centers (c = 25).
- † † Correlations between items and hypothesized scale corrected for overlap.
- ‡ ‡ Average interitem correlation (Homogeneity).
- § § Internal-consistency reliability (Cronbach's alpha).
- BP, bodily pain; ECRHS, the European Community Respiratory Health Survey; GH, general health; ICC, intraclass correlation coefficients; MH, mental health; PF, physical functioning; RE, role emotional; RP, role physical; SF, social functioning; VT, vitality.
Within each scale, the correlation between the items and their hypothetical latent variables (i.e., item internal consistency) corrected for overlap always exceeded the 0.40 success level. Higher range item–scale correlations were observed for both the PF (0.55–0.76) and GH (0.40–0.71) scales. The average item–scale correlation for each of the eight scales was high ranging from 0.41 (GH) to 0.70 (BP), while the reliability (the Cronbach's alpha) exceeded 0.70 for all scales and ranged from 0.77 (GH) to 0.89 (PF and RP). Comparable and substantial results were also observed with binary format.
Table 4 shows the number of items and levels, the frequency distributions of scale points for six ordinal scales from binary format and their matching values of continuous scale from original Likert format, and the corresponding descriptive statistics. The relationship between the two scoring systems could be considered as a nonlinear transformation from continuous to ordinal scale. For example, in BP scale the value of 0 represented the 28% of subject responses, and their Likert respective values ranged from 0 to 61, i.e., the first cutoff for original continuous BP was 61, and so on. Instead, PF scale, for its large item number, was considered as a continuous scale also from binary format, and the relationship between the two scoring system could be considered as a linear transformation of a continuous scale: the value 0 represented the 0.4% of subject responses, and their Likert respective values ranged from 0 to 9, and so on.
| Scale(n items) | Form(n levels) | Frequency relative (cumulative) distributions | Mean ± SD | % 0score | % 100score | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| PF (10) | L (21) | (0–10) | (10–20) | (20–30) | (30–40) | (40–50) | (50–60) | 91 ± 16 | 0.3 | 46 |
| B (11) | 0 | 10 | 20 | 30 | 40 | 50 | 88 ± 21 | 0.4 | 45 | |
| Freq (%) | 0.4 | 0.4 (0.8) | 0.7 (1.5) | 0.8 (2.3) | 1.2 (3.5) | 1.9 (5.4) | ||||
| L (21) | (60–70) | (70–80) | (80–90) | (90–99] | 100 | |||||
| B (11) | 60 | 70 | 80 | 90 | 100 | |||||
| Freq % | 2.6 (8.0) | 4 (12) | 11 (23) | 55 (32) | 45 (100) | |||||
| BP (2) | L (11) | (0–62) | (62–76) | (76–100) | 78 ± 24 | 0.6 | 42 | |||
| B (3) | 0 | 50 | 100 | 64 ± 44 | 28 | 55 | ||||
| Freq % | 28 (28) | 16 (44) | 55 (100) | |||||||
| RP (4) | L = B (5) | 0 | 25 | 50 | 75 | 100 | 87 ± 29 | 7 | 80 | |
| Freq % | 7 (7) | 3 (10) | 4 (14) | 6 (20) | 80 (100) | |||||
| GH (5) | L (21) | (0–51) | (51–67) | (67–76) | (76–82) | (82–92) | (92–100) | 73 ± 19 | 0.1 | 6 |
| B (6) | 0 | 20 | 40 | 60 | 80 | 100 | 52 ± 33 | 15 | 15 | |
| Freq % | 15 (15) | 15 (30) | 17 (47) | 19 (66) | 19 (85) | 15 (100) | ||||
| VT (4) | L (21) | (0–40) | (40–55) | (55–61) | (61–74) | (74–100) | 64 ± 19 | 0.2 | 2 | |
| B (5) | 0 | 25 | 50 | 75 | 100 | 61 ± 35 | 13 | 32 | ||
| Freq % | 13 (13) | 14 (27) | 20 (47) | 21 (68) | 32 (100) | |||||
| SF (2) | L (9) | (0–64) | (64–89) | (89–100) | 85 ± 21 | 0.4 | 54 | |||
| B (3) | 0 | 50 | 100 | 63 ± 43 | 27 | 53 | ||||
| Freq % | 27 (27) | 19 (46) | 53 (100) | |||||||
| RE (3) | L = B (4) | 0 | 33 | 50 | 67 | 100 | 85 ± 31 | 8 | 78 | |
| Freq % | 8 (8) | 7 (15) | 0 (15) | 8 (22) | 78 (100) | |||||
| MH (5) | L (26) | (0–51) | (51–61) | (61–71) | (71–77) | (77–88) | (88–100) | 75 ± 17 | 0 | 4 |
| B (6) | 0 | 20 | 40 | 60 | 80 | 100 | 62 ± 35 | 11 | 29 | |
| Freq % | 11 (11) | 11 (22) | 12 (34) | 17 (52) | 19 (71) | 29 (100) | ||||
- BP, bodily pain; GH, general health; MH, mental health; PF, physical functioning; RE, role emotional; RP, role physical; SF, social functioning; VT, vitality.
Mean scores were higher in Likert form, while standard deviation, floor and ceiling indices were higher in binary form. Obviously the most precise (least coarse) scales were the Likert scales with 20 or more levels (PF, GH, VT, and MH). They also defined the widest range of health states and therefore usually had lowest amount of ceiling and floor effects. The relatively coarse binary scales measure only three to six levels across a restricted range, and therefore had more frequent ceiling and floor effects. Nevertheless, substantial ceiling effects were observed for both formats, and these reflected the good health status of the surveyed ECRHS populations (30–54 years, randomly selected, from population-based registers).
Scale Summary Measures Comparison
Table 5 shows the scale and principal component correlations (“factor loadings”) and eingevalues computed by PCA after varimax rotation on Pearson's correlations matrix and polychoric correlations matrix, respectively. As hypothesized, eigenvalues for the first two components were generally greater than unity. The proportion of reliable variance explained in each SF-36 scales by two components ranged from 0.62 to 0.89 for a total of 73% for Likert format, and weakly higher values for binary format ranging from 0.59 to 0.93 for a total of 78%. The pattern of correlations observed between SF-36 scales and two rotated PC strongly supported their interpretation as physical and mental health summary measures, both for Likert and binary formats. We computed two RV coefficients between the Likert and binary recoding considering the physical and mental factor loading matrix (RV = 0.981), and the total and reliable variance explained matrix (RV = 0.712), showing an excellent and a strong agreement among factor loadings, and variance explained fitted with Likert or binary recoding, respectively.
| Rotated components | Original format scales | Binary format scales | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hypothesized associations | Correlations with components† | Varianceexplained | Correlationswithcomponents† | Varianceexplained | ||||||
| Physical | Mental | Physical | Mental | Total‡ | Reliable§ | Physical | Mental | Total‡ | Reliable§ | |
| PF | + | — | 0.80 | 0.12 | 0.66 | 0.71 | 0.81 | 0.06 | 0.66 | 0.73 |
| RP | + | — | 0.75 | 0.25 | 0.63 | 0.68 | 0.73 | 0.42 | 0.71 | 0.77 |
| BP | + | — | 0.76 | 0.21 | 0.62 | 0.67 | 0.77 | 0.27 | 0.67 | 0.74 |
| GH | * | * | 0.61 | 0.40 | 0.53 | 0.62 | 0.56 | 0.42 | 0.49 | 0.59 |
| VT | * | * | 0.37 | 0.73 | 0.66 | 0.76 | 0.36 | 0.75 | 0.69 | 0.78 |
| SF | * | + | 0.35 | 0.76 | 0.70 | 0.77 | 0.38 | 0.79 | 0.76 | 0.84 |
| RE | — | + | 0.16 | 0.78 | 0.64 | 0.71 | 0.25 | 0.85 | 0.77 | 0.86 |
| MH | — | + | 0.13 | 0.88 | 0.78 | 0.89 | 0.10 | 0.88 | 0.79 | 0.93 |
| Total variance explained | 0.308 | 0.346 | 0.653 | 0.726 | 0.305 | 0.386 | 0.692 | 0.779 | ||
- +, strong association (r ≥ 0.70); –, weak association (r ≤ 0.30).
- * Moderate association (0.30 < r < 0.70).
- † † Correlation between each SF-36 scale and varimax rotated principal component.
- ‡ Communality (h2), proportion of the total variance of each scale explained by the two components.
- § h 2 /α, proportion of the reliable variance of each scale explained by the two components.
- BP, bodily pain; GH, general health; MH, mental health; PF, physical functioning; RE, role emotional; RP, role physical; SF, social functioning; VT, vitality.
Know Group Validity Comparison
Table 6 reports the comparisons between groups with/without self-reported asthma-like symptoms, long-term limiting illness, and depression conditions, adjusting for the ECRHS centers by two-level regression models. There was a clear difference between groups both on Likert and binary scores in mean differences, after adjusting for the ECRHS centers, and the other groups in the model. Comparison of random/symptomatic samples revealed that symptomatic sample had lower average scores on all the SF-36 health scales, especially for the GH and RP scales. Subjects with long-term limiting illness had the lowest average profile on the physical scales (PF, RP, BP, GH), while those in the depressive group reported poorer average heath status on mental scales (VT, SF, RE, MH).
| Original format scales | ||||||||
| Mean differences† | PF | RP | BP | GH | VT | SF | RE | MH |
| Symptomatic | −5.2 | −7.6 | −5.7 | −7.0 | −5.4 | −4.9 | −6.5 | −4.2 |
| Long-term illness | −12.5 | −17.8 | −17.0 | −15.3 | −8.1 | −9.3 | −5.4 | −3.2 |
| Depression | −5.7 | −13.6 | −9.4 | −12.2 | −15.3 | −21.1 | −29.0 | −19.2 |
| Means‡ | 93.9 | 93.4 | 82.6 | 77.8 | 67.7 | 89.5 | 90.6 | 76.7 |
| SD (B)§ | 3.9 | 6.6 | 5.2 | 5.4 | 6.0 | 7.2 | 6.8 | 5.8 |
| SD (W)|| | 14.9 | 26.9 | 23.0 | 16.6 | 17.5 | 19.0 | 28.6 | 15.4 |
| Binary format scales | ||||||||
| Mean differences† | PF | RP | BP | GH | VT | SF | RE | MH |
| Symptomatic | −7.0 | −7.6 | −9.3 | −11.0 | −8.8 | −10.3 | −6.5 | −8.5 |
| Long-term illness | −17.6 | −17.8 | −24.6 | −21.3 | −13.7 | −15.6 | −5.4 | −7.0 |
| Depression | −7.1 | −13.6 | −15.4 | −17.3 | −24.0 | −32.2 | −29.0 | −30.0 |
| Means‡ | 93.2 | 93.4 | 71.8 | 58.0 | 67.3 | 70.2 | 90.6 | 63.3 |
| SD (B)§ | 5.1 | 6.6 | 8.3 | 9.0 | 9.8 | 13.7 | 6.8 | 11.9 |
| SD (W)|| | 19.7 | 26.9 | 41.6 | 29.9 | 33.2 | 40.0 | 28.6 | 31.6 |
| Binary format scales | ||||||||
| Odds ratios† | PF | RP | BP | GH | VT | SF | RE | MH |
| Symptomatic | — | 1.79 | 1.52 | 1.91 | 1.60 | 1.66 | 1.60 | 1.57 |
| Long-term illness | — | 3.59 | 2.97 | 3.64 | 2.06 | 2.15 | 1.60 | 1.49 |
| Depression | — | 2.68 | 2.08 | 3.01 | 3.87 | 4.76 | 5.78 | 5.84 |
| Means‡ | 93.2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SD (B)§ | 5.1 | 0.56 | 0.38 | 0.56 | 0.56 | 0.67 | 0.49 | 0.69 |
| SD (W)|| | 19.7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
- * n = 6359 subjects and c = 20 centers, excluding the missing values from N = 6611 subjects who completed the questionnaire of long-standing illnesses conditions.
- † All estimates were statistically significant (P < 0.05) testing t-test = estimate/standard error.
- ‡ ‡ Mean estimates of the random (between cluster) intercept effect.
- § § SD estimates of the random (between cluster) intercept effect.
- || || SD estimates of the residual (within cluster) effect.
- BP, bodily pain; ECRHS, the European Community Respiratory Health Survey; GH, general health; MH, mental health; PF, physical functioning; RE, role emotional; RP, role physical; SF, social functioning; VT, vitality.
Binary scores showed similar linear regression results, but with more distinctive differences in average profiles. In addiction, for binary form scales the results can be also expressed in cumulative odds ratios, finding the same ranking interpretations of the mean differences results.
For example, by adjusting for the ECRHS centers, and the other groups in the model, the estimated mean differences between the healthy subjects and depressed ones of MH and VT scales were equal to −19.2% versus −15.3% of the maximum possible score for Likert format; while a similar ranking, i.e., −30.0% versus −24.0%, but with more large values, was observed for binary format. Finally, the estimated cumulative odds of MH and VT scales, below any fixed level starting from 0 cut point to 5 cut point, were 5.84 versus 3.87 times greater in the healthy subjects than in the depressed ones.
Discussions
The scoring of a scale involves two arbitrary elements: the relative importance of each item in the weighing system, and the scoring system of options within each item. We have used a two-step approach for data analysis: 1) at the item-level, MCA method, that takes account of the nonmetric properties of the data considering ordinal responses as nominal responses; and 2) at the scale-level, ordered correlation/regression analysis, that takes account of the limited digits = n items + 1 (maximum 6 levels of GH and MH) in the scale since the polytomous representation of the binary items sum. These statistical methods were unaffected when changing the set of ordered labels.
The SF-36 questionnaire is a multi-item multidimensional questionnaire using well-accepted Likert standards, but little attention is paid to the specific properties of the ordered categorical data recorded. According to Likert models of parallel items, a construct is often regarded as being latent continuous, is operationalized to be measured by equally important items to increase the reliability and improve precision. The summative Likert scoring system is motivated by the scaling assumptions of highly correlated items and by use of arbitrary numbers, which indicate the ordered structure of the response alternative. It is also assumed that the precision increases with the number of digits in the scale [16].
For analytical convenience, there is a well-established tradition in regarding ordinal data as numeric (continuous) data. Nevertheless, there is negligible scientific evidence to support equidistance in any type of discrete ordinal scaling [22,23]. Ordinal data, irrespective of the type of labeling, thus contain information about ordering only and not about magnitude or distance. There is no reason to assume that response alternatives such as 1 = “definitely true,” 2 = “mostly true,” 3 = “don't know,” 4 = “mostly false,” and 5 = “definitely false” of items a–d of GH scale will yield equal interval scales for individual responses. It means that a set of numerical labels does not represent a mathematical value but serves as a convenient labeling device for ordinal data. These rank-invariant properties of ordinal data include a lack of equidistance between the categories, and that statistical treatment of the data should not be affected when changing the set of ordered labels [8].
One of the major conceptual limitations of Likert item is testing of equidistance (linearity) of option points response. Linearity assumption among response points is often not respected in SF-36 items, and it is necessary to recalibrate the individual answers even by arbitrary decimal values. From here our proposal is to recode Likert values with a method that must be easy to calculate and simple in its interpretation, as the binary format.
Considering SF-36 version 1.6, the constructs of role concerning the perceived limitations due to physical and emotional health problems (RE and RP) are already assessed by binary (yes/no) questions, and we extended the binary coding to the other SF-36 items. The coding 0/1, +/–, A/B is always linear, and the sums of the binary items representing the number of items answered by 1, +, A, which indicates a lack of problems, could be an appropriate rule of scoring.
The MCA processes ordinal data as nominal ones, and transforms them in continuous form by optimal quantifications. The MCA solution allows calculation of the optimal weights of the item options and their ranking, independently by an a priory recoding, enabling an optimal grading for each category response of the questionnaire. In this way, MCA allows to manage the nonlinear information contained in data. In addition, the direction (positive or negative) of optimal weights recodes the data in binary form making item answers linear, and with the same weight (0/1).
Despite the change of the score from summative Likert to cumulative binary, the SF-36 has the same characteristics in the score range of 0–100. Both scores are monotone approximations of underline latent variable constructs. The summative score using binary items is an ordinal scale with limited points, whereas the sum of Likert items is a continuous scale with a large number of points. Consequently, these bring to a low/high variability level, and floor and ceiling challenge.
Nevertheless, binary response format of the SF-36 items would bring various advantages. First, if the item number below the construct is low, i.e., less than 6 or 5, the relation is applicable between response probabilities for a polytomous item and response probabilities for a set of dependent binary item [24]. This perspective points to interesting route of considering the sum score of binary questions as the ordinal score on a polytomous variable, and if this way is taken, it may be possible to examine polychoric and biserial correlations across the binary form scales or to examine odds ratios of know-group comparison by processing ordinal logistic regression models.
Second, the ordinal scale would suggest easy cutoffs that should allow a smart interpretation of QoL differences coming from clinical studies. Considering regression coefficients (or mean differences), it is easier to understand unit change of ordinal score of a SF-36 scale obtained by binary format than unit change of continuous score of the same scale but in original format. For example, in GH scale the ordinal score has always an increasing step point of +20 in the range of 0–100, while using the continuous GH score has an increasing step point of +1 in the range of 0–100. Consequently, the GH group differences are more evident if measured in ordinal score than in continuous score. All this would permit a smart use of reliable change index to evaluate clinical significance in SF-36 outcomes [25].
Third, our study shows that the binary recoding of the original format provide similar results. The findings of this study, based on the ECRHS data, support that the psychometric questionnaire qualities would be fully respected by a binary model. The internal binary consistency shows comparable values with the Likert ones, and these are always higher than the minimum suggested (0.70). The hypothesized Principal Component structure of PCS and MCS of health underlying the SF-36 items was also observed in the binary recoding. Clinical validity produces results that support hypotheses suggested and are compatible with those of the Likert version.
A binary questionnaire would give a practical usefulness for physicians who administer and use it. Binary format would reduce the time to draw up, because it would not be necessary any more to recalibrate the opposite interpretation items, and the score scale would need only the simple sum of the positive (yes) answers. The binary score is better suited than summative Likert score for communicating survey results to practitioners, because it has an interpretation closely related to solving problems (positive or negative), whereas summative Likert has a more complicated interpretation in terms of number of points. Binary score is quick and simple, and allows immediate feedback to those testing.
From the patient point of view that fills in the SF-36, the binary format has an easier interpretation. It has only two possible choices for each question (yes and no, positive and negative, better and worst, etc.) avoiding errors due to misunderstanding and answer interpretation, because some patients may have difficulty interpreting Likert questions. In question 9 (MH scale), subjects appeared to recode the response choices as “bad” to “good” rather than “all of the time” to “none of the time.” More items b and c have an opposite interpretation of item h: subjects may respond “none of the time” to questions b and c regarding filling of anxiety and depression and they would respond “none of the time” again to question h “have you been an happy person” while saying “yes I am an happy person”[26].
Often clinical researches require short questionnaire of faster compilation, and SF-36 has showed to be long for administering; therefore, it is better to use a shorter version as SF-12 or SF-8. These ones, proposed until today, have not a regular application if there are missing data. In fact, a missing answer causes the not substitution possibility and so the score calculation could not be processed. In addition, the information lost reduces the statistical power causing selection bias [27]. Another negative feature of shorter versions is reduced possibility to define the summary measures, but it is not possible to define values regarding single scales causing a further loss of information. All of this is satisfied by the binary version that, with all the 36 original items, allows a good identification both of two health components and of the eight health concepts, pursued by the Likert. Besides, new version structure, if compared with the original format, should substantially reduce time spent to administer and fulfill the questionnaire, and its applying provides essentially the same prognostic information reducing the resources required.
The binary recoding and the scoring system are obtained on ECRHS data, a combination of random sample and symptomatic sample, nerveless if the optimal quantifications of SF-36 questionnaire performing HOMALS within samples were similar (data not shown), the binary scores were different across samples, indicating an homogeneous recoding, and a sensible scoring instrument. Although no computer data simulation was used to verify the findings of the present study, the results seem encouraging about the feasibility of downsizing Likert format offering a plausible alternative for purposes of monitoring the health status in general and in specific populations, even if binary version loses something of reliability and of general information.
Finally, the binary responses offer the chance to order unambiguously the items by frequency of positive (= 1) response for testing a Guttman's scalogram analysis, or for fitting of binary Item Response Theory [28] with parametric models (Rasch Model), or nonparametric models (Mokken model). These models are probabilistic versions of the deterministic Guttman scaling model, and many fit statistics in both the Rasch and Mokken models measure the closeness of the solution to the perfect Guttman scale. Rasch models known under names as the rating scale model, the graded scale response model, the partial credit model consider Likert data, but a reduction of computational burden and simple parameters interpretation provide practical and superior advantages of the dichotomous data with respect to polytomous data.
Conclusions
Despite the loss of information due to the reduction of response's possibility, our results indicate that the SF-36 binary recoding ensure the underlying structure of the original SF-36 is not jeopardized. In addition, it meets at least the same required standards giving the possibility to propose a new version of smarter and easier methodology of administration, compilation, score calculation, and data processing. Consequently, binary recoding may be a valid alternative to the already existing shorter versions, suitable in administering both in clinical setting and clinical trials, in subjects with serious diseases, and by telephone (reduction of times and costs).
The disadvantages of the new binary format are at present the lack of questionnaire testing, and comparability with other studies; and the lack of the interface with the well-established tradition of handling ordinal data as if they were interval too. Assuming quantitative properties simplifies the data analysis and such an approach will not be questioned, while the methods related to ordinal data analysis (polychoric and polyzerial correlations and ordered regression models) are not well-known in medical research.
Source of financial support: This study was partially supported by grants from Ministry of University and Research, University of Pavia.




