Larval growth and development in the caddisfly Cheumatopsyche brevilineata under natural thermal regimes
Abstract
Cheumatopsyche brevilineata (Iwata) is a filter-feeding caddisfly without distinct or distinguishable cohorts. In a semi-natural channel, we reared fourth and fifth instar larvae of C. brevilineata in individual cages with hourly recording of water temperature. We calculated the individual growth rate from the wet-weight gain of each larva, and the development rate from the ratio of larvae that progressed to the next instar or pupal stage during each rearing experiment. We analyzed the linear regressions of growth (increase in size) and development (physiological and morphological progression toward maturity) rates against the statistical parameters of water temperatures during each rearing period, i.e. mean and given percentiles of water temperatures. We presumed that the most appropriate parameter of water temperature to explain larval growth and development would show a peak value of the determination coefficients (r2) in the linear regressions. There were highly significant regressions in the growth rates for fourth and fifth instar larvae and in development rates for fourth instar larvae against every statistical parameter of water temperature, but not in the development rates for fifth instar larvae. For the growth of fourth and fifth instar larvae, we could not specify the most appropriate parameters of water temperatures, because we observed no clear peaks in the determination coefficients. For the development of fourth instar larvae, this parameter could be the 65th percentile value, where the development zero temperature and effective degree-days were 11.1°C and 56 degree-days, respectively.
INTRODUCTION
In studies on the growth (increase in size) and development (physiological and morphological progression toward maturity; Butler 1984) of aquatic insects, the importance of water temperature has received much attention (Lutz 1968; Ward & Stanford 1982; Sweeney & Vannote 1986; Sweeney et al. 1986). Low water temperature in general suppresses growth and development (Hynes 1970; Taylor 1982; Ward & Stanford 1982), and threshold water temperatures for growth and development have been referred to as growth zero temperature and development zero temperature, respectively (Campbell et al. 1974; Beck 1983).
Most laboratory studies on growth and/or development rates have been conducted under constant temperatures (Waters 1977; Humpesch & Elliott 1980; Marten & Zwick 1989; Zwick 1996; Stevens 1998) despite the fact that water temperature in natural streams and rivers fluctuates considerably diurnally and seasonally.
Most studies on growth and development under natural thermal regimes have used arithmetic means as statistical parameters of water temperatures (Taylor 1982; Tokeshi 1985; Takemon 1990; Benke 1998). However, as Beck (1983) and Sweeney (1984) suggested, use of the mean as the parameter of fluctuating water temperature should be reconsidered, because the responses of aquatic insects to water temperature fluctuations have rarely been studied. Another problem in understanding the nature of the growth and development of aquatic insects is that most studies in natural streams and rivers have been carried out on species or populations with distinct or distinguishable cohorts (Svensson 1977; Benke & Wallace 1980; Vannote & Sweeney 1980; Tokeshi 1985; Takemon 1990), despite the fact that cohorts are difficult to distinguish in many other species and populations.
We studied the nature of growth and development in a natural population of a filter-feeding caddisfly, Cheumatopsyche brevilineata (Iwata), in which cohorts cannot be clearly distinguished because of its multivoltinism and complicated life history patterns, with two long and partly overlapping emergence periods (S. Mochizuki, unpubl. data, 2002). We conducted a series of rearing experiments under natural thermal regimes to investigate growth and development in this species. We also tested some methods to obtain statistical parameters for water temperatures that would most appropriately explain growth and development under natural thermal regimes.
MATERIALS AND METHODS
Study site
We used an artificial channel constructed in the Aqua Restoration Research Center (ARRC) close to the Kiso River, Gifu Prefecture, central Japan (35°36′N, 136°46′E). The channel we used had a straight configuration, and was approximately 800 m long, 2.5–6.0 m wide. The bed of the channel had a slope between 1:200 and 1:800, and was covered by loose or embedded cobbles (diameter: 64.0–256.0 mm) with gravel (diameter: 2.0–16.0 mm) and sand (diameter: 0.063–2.0 mm). The water for the channels was supplied from nearby Shinsakai Creek. The mean water depth was approximately 0.15 m from April through to September 2002 and approximately 0.06 m from October 2002 through to March 2003. The current speed ranged from 0.03 to 0.16 m/s throughout the rearing period. The water temperature during a series of rearing experiments ranged from 0.4 to 30.5°C (Table 1).
| Period of experiment | Duration (days) | Water temperature range (°C) |
|---|---|---|
| 26 March−4 April 2002 | 9 | 9.5–22.0 |
| 4–18 April 2002 | 4 | 13.8–23.2 |
| 28 April−2 May 2002 | 4 | 15.6–19.8 |
| 28 May−1 June 2002 | 4 | 18.0–22.2 |
| 12–16 June 2002 | 4 | 21.6–28.8 |
| 12–16 July 2002 | 4 | 22.2–29.1 |
| 25–29 July 2002† | 4 | 25.1–30.5 |
| 10–14 August 2002† | 4 | 25.1–30.5 |
| 26–30 August 2002 | 4 | 23.5–29.1 |
| 15–19 September 2002 | 4 | 21.0–25.8 |
| 22–26 October 2002 | 4 | 15.9–21.3 |
| 10–19 November 2002 | 9 | 8.9–14.4 |
| 4–13 December 2002 | 9 | 5.2–14.4 |
| 29 December 2002–7 January 2003 | 9 | 0.7–9.8 |
| 23 January−2 February 2003 | 9 | 0.4–9.8 |
| 7–16 February 2003 | 9 | 5.2–14.1 |
| 7–16 March 2003 | 9 | 4.9–15.3 |
- † Experiment had a maximum water temperature exceeding 30.0°C.
Rearing experiments
The rearing cage was a tea strainer, which was spherical in shape (diameter 65 mm) and made of stainless steel wire mesh (of about 0.4 mm). Larvae of C. brevilineata were reared individually in the cage (Fig. 1).

Schematic diagram of a rearing cage.
We put soaked gravel (diameter: 2.0–8.0 mm) and sand (diameter: 0.4–2.0 mm; soaking time: 1–7 days) into the cages for substratum and material for larval retreats. The main food source for the larvae was fine particulate organic matter smaller than 0.4 mm, which is adequate for most hydropsychid larvae (Tanida 1982). The larvae were able to access sufficient food flowing through the mesh of the rearing cage.
We used fourth and fifth (=final) instar larvae collected using a Surber net in the same channel less than 0.5 h before the start of each experiment, because larvae younger than fourth instar could possibly escape through the mesh of the rearing cage. We placed the cages in slow riffles or runs in the middle reaches of the channel.
The live (wet) weight of each larva was measured to the nearest 0.01 mg with an electric balance (HR-120; AND, Tokyo, Japan) just before putting it into the rearing cage and just after completion of the rearing experiment. Excess surface water was wiped from each larva with a paper towel before the measurements were taken.
We recorded the water temperature at hourly intervals throughout the rearing period using a compact waterproof temperature logger (Tidbit; Onset, Cape Cod, MA, USA).
We carried out 17 series of rearing experiments from 26 March 2002 to 16 March 2003. We used 25–30 larvae at the beginning of each experiment, using a rearing duration of 96 h (4 days) when the minimum water temperature exceeded 10.0°C, and a rearing duration of 216 h (9 days) when it fell below 10.0°C (Table 1). In preliminary rearing experiments, there were no significant differences in growth rates between the rearing periods from 0 to 48 h and from 0 to 96 h (linear regression analysis; growth rate: −0.1–1.7 mg/day; slopes: 0–48 h, 0.219; 0–96 h, 0.246; P = 0.764). This shows that the initial cost of constructing retreats and capture nets is negligible, at least for the estimation of growth rates.
Data analysis
The growth rate in terms of wet weight (rg) was calculated by using the following formula (Ono 1972; Sweeney & Schnack 1977).
r g = {(wt − w0)/t}/{(w0 + wt)/2}
where w0 and wt are wet weight (mg) at the start and end of an experiment, respectively, and t is rearing duration in days.
To obtain the mean growth rate of fifth instar larvae, we excluded the larvae that progressed to prepupae and pupae in each rearing experiment period and also those that were liable to stop feeding before pupation. To identify the latter group, we calculated the maximum growth rates of the larvae that progressed to prepupal or pupal stages for each of the overwintering (rg = 0.025) and non-overwintering generations (rg = 0.056), and we presumed that the larvae that grew less than these values were liable to fast before pupation. To calculate the means of growth rates of fourth and fifth instar larvae in each experiment, we also excluded the maximum and minimum gains in wet weight and additional outliers specified by the Smirnov test (Ichihara 1990).
Assuming that age structure within each of the fourth and fifth instar groups is random at the start of each experiment, we can estimate the development rate (rd) by using the following formula:
r d = (ni/ns)/t
where ni is the number of larvae that progressed to the next stadium during the experiment, ns is the number that survived until the end of the experiment, and t is the rearing duration in days.
Tokeshi (1985) proposed the “maximum likelihood” method to estimate the most appropriate development zero temperature (i.e. threshold temperature for development) for the nymphal stages of Ephemera danica Müll. (Ephemeroptera: Ephemeridae), in which the development zero temperature with the highest determination coefficient (r2) in linear regressions of effective degree-days against body length was the most appropriate value. We modified Tokeshi's method to explain larval growth and development in C. brevilineata and used not only means but also other statistical parameters (percentiles from the 40th to the maximum [100th] at five-percentile intervals) of water temperatures under natural thermal fluctuations. We calculated the determination coefficients (r2) in the linear regressions of growth rates or development rates against given percentiles as well as the means of water temperatures in all experiments.
For the linear regressions of development rates, we excluded experiments in which less than ten larvae survived at the end of the experiment, the mortality rate exceeded 0.05 per day (Table 2), and the maximum water temperatures exceeded 30.0°C. As has been reported elsewhere (Heiman & Knight 1975; Sweeney 1984; Manly 1990; Stevens 1998), development rates decrease in high water temperatures (Fig. 2). We also excluded data with zero value and outliers specified by an analysis of leverage coefficients and standard deviations (Sokal & Rohlf 1973) in the linear regressions.
| Period of experiment | Fourth instar larvae | Fifth instar larvae | ||||||
|---|---|---|---|---|---|---|---|---|
| Initial number | Surviving number | Mortality rate (per day) | Number of larvae that progressed to fifth instar | Initial number | Surviving number | Mortality rate (per day) | Number of larvae that progressed to prepupal or pupal stage | |
| 26 March−4 April 2002 | 14 | 12 | 0.016 | 10 | 16 | 14 | 0.014 | 4 |
| 4–18 April 2002 | 10 | 9† | 0.025 | 1 | 20 | 20 | 0.000 | 0 |
| 28 April−2 May 2002 | 4 | 3† | 0.063‡ | 3 | 26 | 25 | 0.010 | 8 |
| 28 May−1 June 2002 | 13 | 11 | 0.039 | 7 | 17 | 14 | 0.044 | 0 |
| 12–16 June 2002 | 11 | 10 | 0.023 | 10 | 19 | 15 | 0.053‡ | 3 |
| 12–16 July 2002 | 12 | 10 | 0.042 | 10 | 18 | 16 | 0.028 | 5 |
| 25–29 July 2002 | 13 | 12 | 0.019 | 10 | 15 | 15 | 0.000 | 2 |
| 10–14 August 2002 | 11 | 6† | 0.114‡§ | 6 | 19 | 15 | 0.053‡§ | 4 |
| 26–30 August 2002 | 7 | 4† | 0.107‡§ | 3 | 23 | 20 | 0.033 | 3 |
| 15–19 September 2002 | 4 | 3† | 0.063‡ | 2 | 23 | 21 | 0.022 | 3 |
| 22–26 October 2002 | 15 | 14 | 0.017 | 6 | 15 | 14 | 0.017 | 0 |
| 10–19 November 2002 | 10 | 6† | 0.044 | 2 | 19 | 18 | 0.006 | 0 |
| 4–13 December 2002 | 8 | 5† | 0.042 | 0 | 17 | 17 | 0.000 | 0 |
| 29 December 2002–7 January 2003 | 8 | 6† | 0.028 | 0 | 21 | 19 | 0.011 | 0 |
| 23 January−2 February 2003 | 4 | 1† | 0.048 | 0 | 23 | 21 | 0.010 | 0 |
| 7–16 February 2003 | 7 | 5† | 0.032 | 0 | 19 | 19 | 0.000 | 0 |
| 7–16 March 2003 | 14 | 13 | 0.008 | 0 | 13 | 13 | 0.000 | 0 |
- † Fewer than ten larvae survived upon completion.
- ‡ ‡ Some cages were broken by anthropogenic disturbances.
- § § High mortality presumably due to high water temperature.
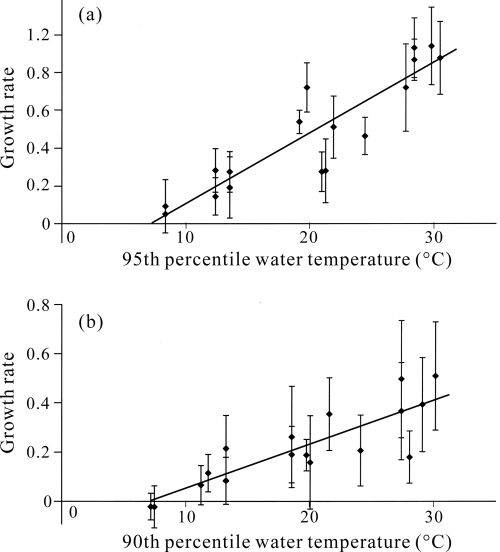
Regressions of growth rates against (a) 95th percentile water temperatures for fourth and (b) 90th percentile water temperatures for fifth instar larvae. Each ◆ indicates mean growth rate (rg) in each rearing experiment, with the vertical bar indicating standard error. Regression equations: (a) y = 0.037x − 0.267, r2 = 0.820; (b) y = 0.018x − 0.128, r2 = 0.735.
In the linear regressions of growth rates and development rates, we presumed that the most appropriate statistical parameter of water temperature to explain the growth and development had a peak value of determination coefficients. In the linear regressions, growth zero temperatures and development zero temperatures were estimated as the intercept on the x-axis (Campbell et al. 1974; Beck 1983).
The duration of each instar (ls) can be calculated by using the following formula:
l s = 1/rd.
We calculated the effective degree-hours as cumulative water temperature above the development zero temperature during the period of each instar.
RESULTS
Mortalities during experiments
The mortality rate ranged from 0 to 0.114 per day for fourth instar larvae and from 0 to 0.053 per day for fifth instar larvae (Table 2). Some high mortality rates exceeding 0.050 per day were thought to be caused by high temperatures (maximum temperature exceeding 29°C). Except for those cases, larval mortality rates were less than 0.048 per day and 0.044 per day for fourth and fifth instar larvae, respectively.
Growth
Growth rates for fourth instar larvae ranged from 0.051 to 0.939, and those for fifth instar from −0.021 to 0.508. The linear regressions of growth rates against every statistical parameter of water temperature were highly significant for both fourth and fifth instar larvae (P < 0.01, Table 3). The 95th and 90th percentile water temperatures showed the highest determination coefficients for fourth and fifth instar larvae, respectively. Regression analyses using these percentiles of water temperatures yield the growth zero temperatures as being 7.2°C and 7.1°C for fourth and fifth instar larvae, respectively (Fig. 3). However, we could not detect any clear peaks of determination coefficients either for fourth or fifth instar larvae.
| Means and given percentiles of water temperatures | Fourth instar larvae | Fifth instar larvae | Fourth instar larvae | |||
|---|---|---|---|---|---|---|
| r 2 | GZ | r 2 | GZ | r 2 | DZ | |
| Mean | 0.799 | 3.3 | 0.711 | 4.1 | 0.978 | 10.5 |
| 40th | 0.788 | 2.4 | 0.697 | 3.2 | 0.976 | 9.7 |
| 45th | 0.791 | 2.8 | 0.704 | 3.7 | 0.977 | 10.1 |
| 50th | 0.798 | 3.1 | 0.703 | 3.9 | 0.984 | 10.3 |
| 55th | 0.800 | 3.3 | 0.708 | 4.1 | 0.988 | 10.5 |
| 60th | 0.802 | 3.7 | 0.715 | 4.6 | 0.991 | 10.8 |
| 65th | 0.808 | 4.1 | 0.720 | 4.9 | 0.992† | 11.1 |
| 70th | 0.801 | 4.1 | 0.711 | 5.0 | 0.989 | 11.0 |
| 75th | 0.796 | 4.7 | 0.710 | 5.6 | 0.983 | 11.5 |
| 80th | 0.799 | 5.1 | 0.717 | 6.0 | 0.979 | 12.0 |
| 85th | 0.804 | 5.6 | 0.722 | 6.4 | 0.968 | 12.8 |
| 90th | 0.816 | 6.2 | 0.735† | 7.1 | 0.981 | 13.6 |
| 95th | 0.820† | 7.2 | 0.734 | 8.0 | 0.968 | 14.5 |
| Maximum (100th) | 0.819 | 8.9 | 0.717 | 9.6 | 0.918 | 15.4 |
- † Highest determination coefficient (r2).

Regressions of development rates (rd) for fourth instar larvae against (a) means and (b) 65th percentile water temperatures. ◆, included in regression analysis; ◊, not included in regression analysis due to high water temperature and/or low number of larvae at completion of rearing experiment. Regression equations: (a) y = 0.017x − 0.177, r2 = 0.978; (b) y = 0.018x − 0.198, r2 = 0.992.
The growth zero temperatures arrived at by using the mean water temperatures were 3.3°C and 4.1°C for fourth and fifth instar larvae, respectively. These values were lower than the growth zero temperatures arrived at by using the percentiles of water temperature with the highest determination coefficients.
Development
Development rates ranged from 0.092 to 0.250 and from 0.032 to 0.080 for fourth and fifth instar larvae, respectively. For fifth instar larvae, we could obtain no significant regressions of development rates against mean or any percentiles of water temperatures (P = 0.502–0.597). For fourth instar larvae, the linear regressions of development rates against every statistical parameter of water temperature were highly significant (P < 0.01; Table 3). There were two peaks in the determination coefficients at the 65th and 90th percentiles of water temperature, and the former was higher than the latter (Table 3).
The development zero temperature arrived at by using the 65th percentile water temperature was 11.1°C, which was higher than the one arrived at by using the mean water temperature (Fig. 2; Table 3). In rearing experiments, the longevity of fourth instar larvae (ls) ranged from 4 to 32 days. From the development zero temperature (11.1°C), we calculated the effective degree-hours for fourth instar larvae as being 1344 degree-hours (=56 degree-days).
DISCUSSION
Different enzymes involved in the physiological processes of growth and development have different optimum temperatures (Baldwin & Hochachka 1970; Shaklee et al. 1977; Shihab & Heath 1987). The use of arithmetic means alone as representative parameters of water temperature should be reconsidered, although it is not fully understood which statistical parameters are appropriate to explain growth and development under conditions of natural thermal fluctuations (Beck 1983; Sweeney 1984). We recorded water temperature hourly, thus enabling us to evaluate the actual, rather than the mean, water temperature that controls growth and development.
In the linear regressions of development rates against every statistical parameter of water temperature (i.e. means and percentiles from the 40th to the 100th), highly significant regressions were found only for fourth instar larvae, but not for fifth instar larvae. This was partly because our rearing durations of fifth instar larvae were too short to obtain a sufficient number of larvae that progressed to the pupal stage. Moreover, pupation involves much more complicated physiological processes than larval molts between instars (Sweeney 1984; Chapman 1998). Our individual rearing experiment was appropriate to estimate the development rates for fourth instar larvae, but we need to develop a better experimental design with a longer rearing duration for fifth instar larvae.
In the linear regressions of growth rates against every statistical parameter of water temperature, there were significant regressions for both fourth and fifth instar larvae. However, we could not detect any clear peaks of determination coefficients to specify the most appropriate parameter of water temperature. There were wide variations in individual growth rates for fourth and fifth instar larvae even within each experiment. Use of more individuals and a longer experimental period would be necessary to obtain more accurate mean growth rates.
Our results show that, at least for the development zero temperatures, the arithmetic means are not the best or only representative values of water temperature under conditions of natural thermal fluctuations. For fourth instar larvae, the growth zero temperature (7.2°C) and the development zero temperature (11.1°C), estimated based on the linear regressions with the highest determination coefficients, were distinctly different from each other, indicating that there was a range of water temperatures in which larvae grew without development. It is widely accepted that aquatic insects have some temperature ranges in which larva achieve growth without development (Wright et al. 1982; Butler 1984; Sweeney 1984).
ACKNOWLEDGMENTS
This research was carried out at the ARRC as a joint project of the Ecological Laboratory of Osaka Prefecture University and the ARRC, and was partly supported by the River and Watershed Environment Management Fund. We are grateful to the staff of the ARRC for assisting us in many ways. We wish to thank Mr H. Ichiyanagi for his valuable advice, and Dr M. Urabe for her significant contribution at the beginning of the study. Dr O. S. Flint Jr. and Dr P. Zwick kindly read an earlier version of the manuscript and provided indispensable comments.




