Opportunity and Educational Outcomes in Australia*
We are grateful to two anonymous referees for helpful comments. This work was supported by National Institutes of Health Grant MH66206 (to Wendy Slutske). Miller acknowledges financial assistance from the Australian Research Council.
Abstract
Despite the well-documented advantages of additional years of education, many Australians still leave school before completing Year 12, and less than one-half of high-school graduates complete tertiary studies. The reasons for this have been the subject of considerable research, with one of the primary aims being to investigate the role of inequality of opportunity as a determinant of educational attainment. Where inequality of opportunity adversely affects educational outcomes, appropriate policy intervention may be able to increase both efficiency and equity ( Behrman & Taubman, 1989 ). In this article, we use information on twins to assess the role of family background (or environment) in determining educational attainment in Australia, and to assess the changes in this role over recent decades. Our best estimate is that environmental diversity accounts for as little as 8 per cent of the variance in educational outcomes. Moreover, in the face of rather substantial changes in the arrangements for financing tertiary education in Australia, the influence of common family background on educational outcomes has not changed.
I Introduction
One of the main pathways to economic success in Australia, as in other countries, is the undertaking of additional years of education. The better educated are usually characterised by lower rates of unemployment, higher earnings and more prestigious occupational standing. Rates of return to additional years of schooling of over 8 per cent are typically reported in the literature. Yet despite these well-documented advantages of additional years of education, many Australians still leave school before completing Year 12, and less than one-half of high-school graduates complete tertiary studies. The reasons for this have been the subject of considerable research (see, e.g. Le & Miller, 2002, 2004, 2005; Cardak & Ryan, 2009). One of the aims of this research has been to investigate the role of inequality of opportunity as a determinant of educational attainment. As noted by Taubman (1978, p. 972), inequality of opportunity arises ‘…when decision makers face different sets of prices, interest rates, family income, and (when parents are the decision makers for the child’s investments) parental tastes’. Where inequality of opportunity adversely affects educational outcomes, appropriate policy intervention may be able to increase both efficiency and equity (Behrman & Taubman, 1989).
In Australia, there have been major attempts in recent decades to equalise educational opportunities. The values of allowances for students in secondary school have been increased,1 university education was made free in 1973, and when fees were introduced in 1989 they were accompanied by an income-contingent loans scheme. These initiatives have been argued by some authors to have equalised at least the Year 12 outcomes (see the discussion in Le & Miller, 2005), and to have reduced the impact of socioeconomic background on the chances of going to university (Marks et al., 2000). Most of this research has been based on the examination of the partial effects of measures of family socioeconomic background on participation rates at various levels of education. For example, Marks et al. (2000) examine the links between education participation and an index of family wealth for various youth cohorts. Le and Miller (2004) link education participation to father’s occupational status.
Behrman and Taubman (1989) used data on various kin groups to assess the role of family background in determining educational attainment in the USA. Their research was based on the seminal model developed by Becker (1975) in his Woytinsky lecture. This framework was also used by Miller et al. (2001), in a study of Australians born between 1924 and 1965. Miller et al. (2001) report that around 25 per cent of the variance in educational attainment in Australia was linked to family background (or common environmental) factors.2 A similar estimate is provided in Baker et al.’s (1996) analysis of the same dataset, separated into two birth cohorts using a 1950 threshold. The current research extends this work by using a much younger sample of twins, born between 1964 and 1971, and by using different year thresholds than Baker et al. (1996) to partition the sample they analysed. The main hypothesis under investigation is that the component of the variance in educational attainments that can be linked to family background has changed in recent decades, due to the policy initiatives that have altered the equality of opportunity in the education sector.
The structure of the article is as follows. Section II outlines the model used. Section III describes the dataset. The results of the statistical analyses are presented in Section IV, whereas discussion and concluding comments are given in Section V.
II Methodology3
(i) Becker’s Model
Becker (1975) set out a model of investment in human capital which provides the framework for the analyses that follow. This model was based on a supply curve and a demand curve for human capital investment, which were presented with investment amounts on the horizontal axis, and the interest rate (supply) and internal rate of return (demand) on the vertical axis. Under the influence of diminishing returns to human capital production and rising cost of the time input into the production process, the demand curve is downward sloping. The supply curve represents the marginal cost of financing human capital investments, and it will be upward sloping as individuals resort to progressively higher priced sources of funds to finance greater levels of human capital investments. Becker described the position of the demand curve as being dependent on an individual’s capacities, or genetic endowments, with the demand curve for individuals with greater genetic endowments being above and to the right of that of other groups. Due to capital market imperfections, the position of the supply curve depended on family background, with the supply curve for individuals from more affluent backgrounds being below and to the right of that of their less affluent counterparts. The model determines equilibrium values of the returns to investment and the level of human capital as functions of genetic endowments and family background (Taubman, 1981). We may write S = F(G, E), where S denotes the level of schooling, G genetic endowments and E is the family environment. A linear approximation to this is S = α1G + α2E.
(ii) Empirical Conceptualisation
Applied research has proposed various links between genetic endowments, family environment and educational attainment. Among the factors associated with family environment in the education research in Australia are the education levels of parents, the occupational attainments of parents, the number of siblings and household income (see Marks et al., 2000; Le & Miller, 2005; Cardak & Ryan, 2009). Educational attainment is expected to be positively related to parental income, greater among the more prestigious occupational groups, and negatively related to the number of siblings.
Early childhood achievements can be viewed as a measure of the genetic endowments that affect the position of the demand curve, and this forms an important variable in the research based on the Longitudinal Surveys of Australian Youth and related datasets (see Marks et al., 2000; Le & Miller, 2005). A positive link is expected between the decision to continue at school and early childhood achievement.
The inclusion of the variables noted before in regression models of the determinants of educational attainment permits explicit statistical control for these measurable aspects of genetic endowments and family environment. However, any unmeasurable aspects, such as motivation and the values placed on education within the family, cannot be held constant in this approach. This is an important aspect, as Williams et al. (1987, p. 11) conclude that it is ‘…differences in preferences for education that are associated with social status, rather than economic impediments, which underlie the always observed relationship between socioeconomic status and educational participation’.4 Some of these omitted variables issues can be addressed through study of data on twins.
(iii) The Twins Methodology
The study of educational attainments using data on twins exploits two features of twins reared together that can minimise the adverse consequences of the omitted variables problem noted above. First, identical (monozygotic or MZ) twins reared together will have, by definition, the same genetic endowments and have a shared family environment. Differences in the educational attainments of such twins must therefore be accounted for by individual-specific environmental factors (i.e. events specific to one twin only; see Loehlin & Nichols, 1976). Non-identical (dizygotic or DZ) twins who are reared together will share the same family background, but will differ in genetic endowments: non-identical twins share, on average, one-half of their genes and are thus no more alike than other siblings. Differences in the schooling attainments of non-identical twins can therefore be attributed to either individual-specific environmental factors or differences in genetic endowments. Quantification of the relative importance of these genetic and environmental factors can be based on the covariance matrices for MZ and DZ twins, or on twin correlations.
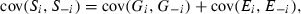 (1)
(1)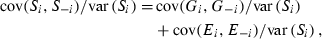 (2)
(2)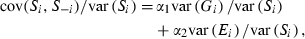 (3)
(3)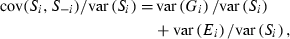 (4)
(4) (5)
(5)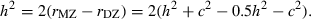 (6)
(6)Assuming no dominance, or non-additive genetic factors, c2 is obtained by subtracting the derived value of h2 from rMZ. As will be discussed in Section IV, this estimate of c2 will also include influences that stem from assortative mating, which appear to be substantially genetically based.8
(iv) The Twins Methodology and Equality of Opportunity
Estimates of the importance of heritability (h2) and common environmental factors (c2) in producing individual variations in educational attainments have been computed to assess how equal educational opportunity is, or to assess the impact of policies that purportedly have equalised educational opportunity. Thus, Behrman and Taubman (1989, p. 1246) use this approach in their analyses for the USA because ‘The share of the observed variation in schooling that is attributable to across-family variability in environment provides a measure of inequality in schooling opportunity’. Tambs et al. (1989) use an estimate of the common environmental factors to assess the success of the greater egalitarianism introduced into the Norwegian educational system. Similarly, Heath et al. (1985) use this nature-nurture decomposition as part of an assessment of the extent to which family background can predict educational success when education opportunity was altered in Norway. Finally, Baker et al. (1996) examine cohort differences in genetic and environmental influences on educational outcomes in Australia to assess the implications of the various attempts in earlier periods to promote equality of educational opportunities in this country.
The Baker et al. (1996) study covered twins born between 1893 and 1965. They disaggregated these into two cohorts, namely those born between 1893 and 1950, and those born between 1951 and 1965. The 1950 threshold was motivated by the major post-WWII changes in the primary and secondary schooling systems in Australia, such as the contribution of state funds to non-government schools.
There have been further changes in the educational system in Australia since those in the 1950s and 1960s that are the focus of the Baker et al. (1996) analyses. These include changes in the allowances for secondary school students (see footnote 1), and more major changes in post-secondary school education. The latter changes are listed in Table 1, along with the cohorts likely to be most affected in terms of university entrance decisions.
| Year | Event | Impact on: |
|---|---|---|
| 1974 | Free tertiary education | Twins born around 1956 onwards |
| 1986 | Higher Education Administration Charge (HEAC) | Twins born around 1968 onwards |
| 1989 | Higher Education Contribution Scheme (HECS) | Twins born around 1971 onwards |
The cohorts identified in the final column of Table 1 provide the basis for the disaggregation of the sample employed in the regression analyses below in this extension of the research of Baker et al. (1996). The way this is done is outlined in Section IV.
(v) Estimating h2 and c2
 (7)
(7)Given the definition of Rj, α3 will be twice the difference between the identical (MZ) and non-identical twins (DZ) in the regression coefficients on the outcome (S) measure for the co-twin described in footnote 10. In other words, 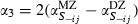 , which, given the model formulation, can also be expressed as α3 = 2(rMZ − rDZ), where rMZ and rDZ are the correlation coefficients discussed in relation to Equations (4) and (5), respectively. Thus, α3, under the standard assumptions of an additive model, random mating and non-common environment of a DZ twin is not correlated with his/her co-twin’s genes, provides a direct estimate of heritability (h2) of schooling levels.11
, which, given the model formulation, can also be expressed as α3 = 2(rMZ − rDZ), where rMZ and rDZ are the correlation coefficients discussed in relation to Equations (4) and (5), respectively. Thus, α3, under the standard assumptions of an additive model, random mating and non-common environment of a DZ twin is not correlated with his/her co-twin’s genes, provides a direct estimate of heritability (h2) of schooling levels.11
α 1 in Equation (7) is an estimate of the twin resemblance that is independent of the genetic resemblance captured in the model terms in Rj. α1 is therefore an estimate of common environmental, or family background, influence, c2.12
The additional covariates (Xij) in the model are limited to variables for gender and age. Direct measures of family background, such as family income and the number of children, could also be included. However, these are omitted here in favour of the indirect approach provided by the inclusion of the outcome for the person’s co-twin in the model outlined before.
All estimations presented in Section IV are based on the double-entry data method of Cherny et al. (1992b). This method accommodates the fact that there is no single way of categorising members of a twin pair as ‘twin’ and ‘co-twin’ by entering the data for each member of a twin pair in the estimating equation twice – once as twin (Sij) and once as co-twin (i.e. S−ij). Standard errors are computed to reflect the correlation within pairs of twins (see Kohler & Rodgers, 2001).
III Data
The primary data used in this study are from the Australian Twin Study of Gambling, and these are described in Slutske et al. (2009) and Le et al. (2010). The data were collected over 2004–2007 from members of the Australian Twin Registry Younger Twin Cohort. This comprises a volunteer panel of twins born between 1964 and 1971.13 The sample size for the Study of Gambling is 4764, covering 3750 twins from complete twin pairs and 1014 from incomplete pairs. Of the complete pairs, 867 are identical twins and 1008 are non-identical twins. In addition, the data analysed by Miller et al. (2001) are also used in some of the estimations.
The education data refer to the highest educational qualification obtained. These have been converted to a ‘years of schooling’ equivalent using assumed values for the post-secondary school qualification categories. These are listed in Appendix I. This continuous measure is used in preference to a dichotomous variable for the completion of tertiary studies to give comparability with prior studies. The main set of analyses that follow is based on the 3706 members of complete twin pairs (i.e. 1853 pairs of twins) where each member provided valid information on each of the variables used in the statistical analysis. An additional 2478 pairs of twins from the data on Australian twins born between 1924 and 1965 used by Miller et al. (2001) are also utilised in some estimations, to give a combined sample of 4331 twin pairs. The education variable from this earlier set of analyses has been recoded to give consistency with the Data Appendix definition. Variable definitions, along with means, are provided in Appendix I.
IV Statistical Analyses
The first set of findings, presented in Table 2, is for the sample restricted to the recently collected Australian Twin Study of Gambling. According to the column (i) results, heritability (h2) accounts for fully 41 per cent of the variation in the completed educational attainments of Australians born between 1964 and 1971. Common environmental factors (c2) have a smaller role to play, accounting for 21 per cent of the variance. Both estimates are highly significant, with ‘t’ values of 5.51 and 3.51, respectively.14,15
| Variable | (i) | (ii) |
|---|---|---|
| Constant | 10.381 (12.71) | 11.294 (11.50) |
| EDUC−ij | 0.214 (3.51) | 0.213 (3.49) |
| R j | −5.173 (5.28) | −5.187 (5.29) |
| R j × EDUC−ij | 0.406 (5.51) | 0.401 (5.51) |
| Agej | (a) | −0.025 (1.87) |
| Femaleij | (a) | 0.079 (1.08) |
| Adjusted R2 | 0.264 | 0.264 |
| Sample size | 3706 | 3706 |
- Notes: Absolute values of robust ‘t’ statistics in parentheses; (a) refers to variable not entered.
Column (ii) presents the results of the model following the inclusion of the variables for age and female. The age variable in these analyses is simply a control for birth cohort: Baker et al. (1996) and Le and Miller (2004) have both shown that there has been a secular increase in educational attainments in Australia. Previous research for Australia (e.g. Le & Miller, 2004) has shown that since the late 1970s females have had a higher school completion rate than males, and as the twins studied here would have completed their schooling during the 1980s, it is expected that the coefficient on the female variable will be positive.
The column (ii) results for the age and gender variables are consistent with the priors, although the estimated effects are small and the female variable is not statistically significant. The point estimates indicate that females have a higher educational attainment than males (coefficient of 0.079, with a ‘t’ value of 1.08), and that twins born in earlier years have lower educational attainments than twins born more recently (the coefficient on the age variable is −0.025, ‘t’ = 1.87). It is noted that the inclusion of the female and age variables has no material impact on the estimates of the contributions to the variations in educational attainments of heritability or common environmental factors.
As mentioned in footnote 11, the model of DeFries and Fulker (1985) can be generalised to allow for differential heritability and common environment effects on the basis of educational attainment (see Cherny et al., 1992a). This involves the addition to the model of interaction terms between the behavioural genetics model terms and the co-twin’s educational attainment. The results from this extension establish quite emphatically that there is no evidence that the heritability of educational attainment or the importance of common environment/family background varies by the level of education.16
Table 3 presents results from data pooled across the Australian Twin Study of Gambling (twins born between 1964 and 1971) and the older twin cohorts analysed in Miller et al. (2001) (born between 1893 and 1965, but the age restrictions they imposed removed twins born before 1924). The specification presented in column (i) includes a cohort dummy variable for membership of the Miller et al. (2001) dataset, and interaction terms between this dummy and the other variables in the model. These estimates show that the point estimate of heritability is higher in the earlier dataset, and the point estimate of the common environment component is marginally lower. Tests reveal that these findings are not sensitive to the recoding of the education data of Miller et al. (2001) undertaken here to give greater consistency with the Australian Twin Study of Gambling. The estimates for these interaction terms show that there are no statistically significant differences in the estimates of heritability and common environment between the twins in the Australian Twin Study of Gambling and those in the dataset used by Miller et al. (2001).
| Variable | (i) | (ii) | (iii) |
|---|---|---|---|
| Constant | 11.294 (11.50) | 10.479 (14.85) | 10.674 (13.48) |
| EDUC−ij | 0.213 (3.49) | 0.190 (3.75) | 0.176 (3.06) |
| R j | −5.187 (5.29) | −5.833 (7.22) | −5.908 (6.44) |
| R j × EDUC−ij | 0.401 (5.51) | 0.443 (7.31) | 0.450 (6.51) |
| Agej | −0.025 (1.87) | 0.009 (1.86) | 0.009 (1.75) |
| Femaleij | 0.079 (1.08) | −0.128 (2.07) | −0.199 (2.81) |
| Cohort (C) | 0.728 (0.62) | 1.586 (1.50) | −0.954 (0.41) |
| C × EDUC−ij | −0.049 (0.62) | −0.044 (0.55) | 0.072 (0.59) |
| C × Rj | −0.371 (0.30) | 0.440 (0.37) | 0.564 (0.30) |
| C × Rj × EDUC−ij | 0.064 (0.69) | 0.036 (0.38) | −0.048 (0.34) |
| C × Agej | −0.010 (0.75) | −0.044 (7.11) | −0.001 (0.01) |
| C × Femaleij | −0.917 (8.92) | −0.835 (7.64) | 0.349 (2.45) |
| Adjusted R2 | 0.342 | 0.341 | 0.342 |
| Sample size | 8662 | 8662 | 8662 |
- Notes: Absolute value of robust ‘t’ statistics in parentheses; the column (i) estimates have the cohort defined by membership of the dataset used by Miller et al. (2001); the column (ii) estimates have the cohort defined by birth year 1956, with older twins captured by the interaction terms; and the column (iii) estimates have the cohort defined by birth year 1968 with the younger twins captured by the interaction terms presented. This model also includes the interaction terms of column (ii), but these are not presented here for space reason.
The column (i) estimates show that females in the older cohort were associated with lower educational attainments than males. This result is consistent with the evidence in Miller et al. (2001), and carries across to the other disaggregations considered next.
The remaining columns of Table 3 examine alternative partitions of the sample. In Baker et al.’s (1996) study, the sample of twins born between 1893 and 1965 was separated into two birth cohorts using a 1950 threshold.17 These authors could not reject the hypothesis that their estimates of heritability and of the common environmental contribution to educational attainments were the same for those born between 1893 and 1950 and those born between 1951 and 1965. Models that allowed the estimates of heritability and common environment effects to differ for these cohorts generated values of h2 between 0.51 and 0.57 for the older cohort, and of between 0.48 and 0.57 for the younger cohort.18 The estimate of c2 for the older cohort varied between 0.20 and 0.23, and for the younger cohort between 0.16 and 0.26.
Column (ii) of Table 3 presents estimates where 1956 rather than 1950 is used as a cut-off period to partition the sample. The use of the 1956 cut-off is motivated by the changes described in Table 1. Thirty-eight per cent of the sample is in the older birth years with this disaggregation, and the differential regression effects for this part of the sample are captured by the interaction terms. These results mirror the findings in column (i), where the cohort variable was based on membership of the two datasets rather than by the year of birth. Specifically, they reveal the absence of statistically significant differences in the estimates of heritability and common environment effects between the two groups of twins considered here. This absence of statistically significant differences occurs despite the fact that the younger cohort would mostly have considered tertiary studies during a ‘free education’ regime, whereas the older group would have done so during a period when fees were charged.
In column (iii), a further cohort variable, for birth after 1968, together with a full set of interaction terms, is added to the model (the post-1968 birth cohorts were identified in Table 1 as the HEAC-liable groups). This cohort variable covers 12 per cent of the sample, and while the point estimates are consistent with an increase in the importance of common environmental influences and a decrease in heritability, these estimates cannot be distinguished statistically from the effects for the older cohorts of twins in the sample. Table 4 summarises this evidence, together with that from previous Australian studies.19
| Study | Cohort | h 2 | c 2 | e 2 |
|---|---|---|---|---|
| Miller et al. (2001) | 1924–1965 | 0.49 | 0.22 | 0.29 |
| Baker et al. (1996) | 1893–1965 | 0.57 | 0.24 | 0.19 |
| 1893–1950 | 0.51–0.57 | 0.20–0.23 | 0.20–0.29 | |
| 1951–1965 | 0.48–0.57 | 0.16–0.26 | 0.17–0.36 | |
| This study | 1964–1971 | 0.41 | 0.21 | 0.38 |
| 1924–1956 | 0.48 | 0.15 | 0.37 | |
| 1957–1968 | 0.45 | 0.18 | 0.37 | |
| 1969+ | 0.40 | 0.25 | 0.35 | |
| Perfect equality benchmark† | — | 1.0 | 0.0 | — |
- Note: †Based on Beyerstein et al. (2010, p. 161).
It is quite clear from Table 4 that the estimate of c2 has not varied appreciably over time. Within each set of analyses, the differences between the various estimates of c2 are not statistically significant. This is despite the expectation that where educational opportunities are equalised (e.g. through free tertiary education in 1974), there should be more uniform environmental factors, and so they should contribute less to the variations in educational attainment. Concomitantly, heritability should emerge in this situation as more influential.
Finally, there is one caveat that needs to be introduced. As noted by Baker et al. (1996) and Miller et al. (2001), the biometric model applied before assumes, among other things, that there is random mating with respect to the variable of interest, namely educational attainment. The available evidence, however, points to assortative mating on the basis of educational attainment among couple families with children. Birch et al. (2009), for example, report a correlation coefficient of 0.446 between the educational attainments of partners in this family type. This figure is remarkably similar to that reported in Baker et al. (1996), of 0.426, suggesting stability over time in this marital correlation. Martin (1978) discusses this in more detail, and develops an adjustment factor to accommodate this issue. The basic idea is that assortative mating will increase the genetic variance between families, so that what is estimated as shared environment (c2) before is cofounded with extra additive genetic variance arising from this assortative mating. Martin’s adjustment factor is based on the marital correlation for education attainment (μ). If the estimates of heritability and common environment obtained under the assumption of random mating above are denoted by 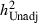 and
and 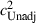 , respectively, then Martin (1978) shows that the adjusted common environment is given by
, respectively, then Martin (1978) shows that the adjusted common environment is given by 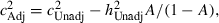 where
where 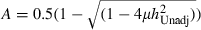 . Given
. Given 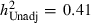 and
and 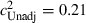 from Table 2,
from Table 2, 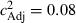 . However, as the same adjustment needs to be applied to the other estimates of Table 4, the conclusion in relation to the invariance over time of the common environment component of educational attainment remains.
. However, as the same adjustment needs to be applied to the other estimates of Table 4, the conclusion in relation to the invariance over time of the common environment component of educational attainment remains.
V Discussion and Conclusion
Chapman and Ryan (2002) examine the effects of HECS on access to higher education for the disadvantaged. They summarise the evidence in four points, which we repeat here in full (see Chapman & Ryan, 2002, p. 78).
- 1
The relatively disadvantaged in Australia were less likely to attend university even when there were no student fees. This provides further support for the view that a no-charge public university system (i.e. financed by all taxpayers) is regressive.
- 2
The introduction of HECS was associated with aggregate increases in higher education participation.
- 3
HECS did not result in decreases in the participation of prospective students from relatively poor families, although the absolute increases were higher for relatively disadvantaged students.
- 4
The significant changes to HECS introduced in 1997 were associated with increases in the participation of individuals irrespective of their family wealth.
These four points are simply saying that the introduction of free university education, and the subsequent change to a ‘fee and income-contingent loan’ regime, had little impact on the socioeconomic background of students at university. This is consistent with the evidence reported before, to the effect that the relative importance of a common family background to the understanding of the variance in educational attainments in Australia has not changed over time, even during a period when university education was made free.
In other words, in the face of rather substantial changes in the arrangements for financing tertiary education in Australia, the influence of common family background on educational outcomes has not changed. This suggests that other issues need to be addressed if the positive socioeconomic status gradient on university participation in Australia is to be altered. In this regard, the earlier debates in the behavioural genetics literature are instructive; see, for example, the letters in Science in 1976 (Jensen et al., 1976). These remind us that the estimates of heritability and common environment are obtained for a given environment, and low estimates of the effect of environmental diversity do not necessarily preclude new environmental modifications affecting individual differences in educational outcomes. These may require a focus on the early years of secondary schooling as well as on the Year 12-university transition. This prognosis is consistent with arguments advanced by Cardak and Ryan (2009). Thus, one could conclude as Havender does in the Jensen et al. (1976, p. 9) set of commentaries: ‘The potential thus exists for a considerable reduction in inequalities in IQ and realised school performance, and as a natural concomitant, in the social differences that correlate with the level of educational attainment’.
Footnotes
Appendix
Appendix I: Description of the Data
The variables used in the analysis are standard, and descriptions are provided only for the non-standard variables not already defined in the text.
Age: Age is determined from the age at the time of the interview. The year of birth is used to determine cohort membership (and can also be used to construct an age variable).
Education: The data on education are collected in categorical form: (i) 8–10 years of schooling; (ii) matriculation/Year 12; (iii) technical, teachers college, Technical and Further Education institute, business or secretarial college; (iv) university undergraduate training and (v) university post-graduate training. Full-time years equivalents of 9, 12, 13, 16 and 18 have been assigned to these categories to form a continuous education variable.
| Variable | Means |
|---|---|
| Female | 0.584 |
| Age | 37.604 |
| Education | 13.405 |
| Sample size | 3706 |




