Monopolistic Screening with Boundedly Rational Consumers*
This research was supported by ARC Discovery grant DP0881381, ‘Mechanism design under bounded rationality: The optimal contracts in the complex world’. The author is grateful to Svetlana Danilkina, Damien Eldridge and Ishaq Bhatti for helpful comments.
Abstract
In this paper, I revisit the monopolistic screening problem with two types assuming that consumers are boundedly rational. Bounded rationality implies that the revelation principle does not apply and the choice of the selling mechanism entails a loss of generality. I show that if the monopolist restricts attention to the mechanisms that offer menus of two choices, the profits are lower than in the case of fully rational consumers by the term of order ln λ/λ, where λ is the degree of rationality of the consumers. The monopolist, however, can approximate the profits earned when consumers are fully rational by using a more elaborate message game.
I Introduction
Theory of mechanism design is the main theoretical tool used to study designing rules of a game to achieve a specific social outcome. Non-linear tariffs charged by utility companies, auctions and taxes are all examples of mechanisms that can be analysed using the tools provided by mechanism design theory.
The main difficulty faced by a mechanism designer, who may be a seller of a good, a service provider or the government, is that the participants usually have private information that is referred to as their type. On a very general level, the mechanism design problem can be formalised in the following way. The designer asks the participants to choose a message from a set of allowable messages and send it to the designer. Based on the messages received, the designer selects a social outcome (the rule, which selects the outcome based on the set of messages received should be announced in advance). The designer can manipulate the set of allowable messages and the rule that translates the set of messages into the outcome to achieve the required goals.
Although the problem seems unmanageable at the first glance, the analysis is considerably simplified by the revelation principle.1 It states that, given any Bayes–Nash equilibrium in a message game, there exists another mechanism in which the participants are required to report their type and do so truthfully in the equilibrium, and everybody (the participants and the designer) get the same payoffs as in the equilibrium of the original message game.
The revelation principle allows a researcher to restrict her attention to direct mechanisms when searching for the optimal mechanism. Once the optimal direct mechanism is found, any other mechanism (not necessarily direct), which reproduces its payoffs is also optimal. An important assumption that underlies the revelation principle is that participants have a sufficiently high degree of rationality. This allows us to employ Bayes–Nash equilibrium as the solution concept. Recently, however, a growing body of empirical evidence has called into question the paradigm of rational behaviour.2 On the basis of this evidence, Conlisk (1996) convincingly argued for the incorporation of bounded rationality into economic models. A step in that direction was taken by McKelvey and Palfrey (1995), who developed a new equilibrium concept known as quantal response equilibrium (QRE). This equilibrium concept incorporates the idea of bounded rationality, modelled as probabilistic choice, into game theory. The revelation principle, however, does not extend to QRE.
There are two natural responses to the failure of the revelation principle in this context. The first is to search for some generalised version of the principle, which will allow us to restrict the set of mechanisms that need to be considered under the new solution concept. The second is to restrict attention to a particular class of mechanisms, for example, non-linear tariffs, and look for the optimal mechanism in this class. Although the second approach does not guarantee that one will arrive at the optimal mechanism, it is much more manageable than the first and is practically important, therefore I limit myself here to it, leaving the first approach to the future research.
In this paper I consider a particular problem, which serves as an important example of a general mechanism design problem: monopolistic screening. Assume a monopolist can produce a unit of a good at different quality levels. A consumer's marginal utility of quality is unknown to the monopolist, but she knows that it will take only one of two commonly known values with some commonly known probabilities. Assuming full rationality on the side of the monopolist and the consumers, one can prove that, without loss of generality, the monopolist can restrict her choice of mechanism to a choice of a non-linear tariff.3 As the set of types is finite, the equilibrium is characterised by a discrete set of qualities purchased and transfers made, with cardinality equal to the cardinality of the type space, that is, consumers of each type select a quality–transfer pair maximising their utility. Therefore, a non-linear tariff defined over all possible qualities will produce the same equilibrium outcome as a direct revelation mechanism.
This equivalence is, however, broken if the consumers are boundedly rational. I will model bounded rationality using the Luce (1959) model. Consumers behaving in accordance with this model will purchase any quality offered with positive probability as long as the set of the offered qualities is finite.4 Therefore, the three mechanisms that implement the same outcome with fully rational consumers, a non-linear tariff with connected product line, the direct revelation mechanism, and offering a menu of contracts and allowing the consumers to choose freely among them, will result in different outcomes if the consumers are boundedly rational. The outcome can be further altered by playing more elaborate message games.
Basov and Danilkina (2006) analyse a particular message game where each payoff-relevant outcome is presented in different multiplicities, called flavours. They show that if flavour proliferation is costless one can approach the optimal outcome under full rationality with exponential precision. In this paper I calculate the optimal pair of contracts, and compare the performance of this mechanism with the one presented in Basov and Danilkina (2006). This allows me to establish conditions on the value of proliferation costs, which can be alternatively interpreted as complexity costs, that support the use of elaborate message games and to demonstrate explicitly non-equivalence of different mechanisms.
Note that failure of the revelation principle identified in this paper is much more severe than the one identified by Martimort and Stole (2002) for common agency games. Indeed, in the latter case, the revelation principle can be replaced by the delegation principle, which is similar in spirit to the former and allows us to restrict attention to mechanisms, in which the principals offer menus of choices such that different choices on a menu differ only on payoff-relevant dimensions. Moreover, the taxation principle still holds, that is, the principals can be seen to be competing in offering non-linear tariffs. Under bounded rationality, in contrast, the principal may sometimes prefer to include payoff-irrelevant alternatives for the agent to choose from. The taxation principle also fails under these circumstances. This observation was first made in Basov and Danilkina (2006).
The paper is organised as follows. Section II starts with a reminder of the standard monopolistic screening model under perfect rationality, when the consumer can be one of two types and then moves on to define the model of boundedly rational behaviour and introduce the concept of nearly rational consumer. In Section III I find the optimal menu assuming it has only two items on it, and compare the profits generated by this menu with the ones generated by an elaborate message game. I also discuss under which conditions designing an elaborate message game is justified from the principal's point of view. Section IV concludes.
II The Model
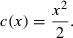 (1)
(1)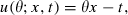 (2)
(2)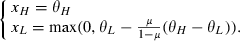 (3)
(3)Note that xH is at the efficient level (no distortions at the top) and xL is below the efficient level. I will assume that μ < θL/θH, so xL > 0 and both types of the consumers are sserved in the equilibrium under full rationality.
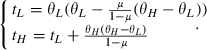 (4)
(4)For the detailed analysis of this case the reader could consult Mas-Collel et al. (1995, pp. 488–500).
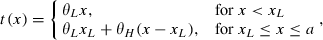 (5)
(5)(i) A Model of Boundedly Rational Behaviour
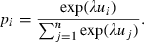 (6)
(6)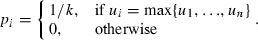 (7)
(7)Here, integer k is the cardinality of the set of the utility maximisers. At the other extreme, as λ = 0 the choice probabilities converge to 1/n, that is, the choice of an alternative becomes totally random and its probability does not depend on the utility level.
Luce's (1959) model allows one to define the concept of nearly rational consumer.
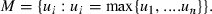 (8)
(8)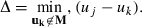 (9)
(9)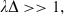 (10)
(10)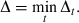 (11)
(11)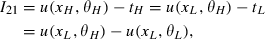
 (13)
(13)III The Optimal Menu of Contracts and a Comparison with Some Other Mechanisms
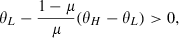 (14)
(14)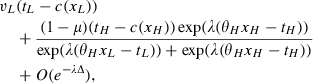 (15)
(15)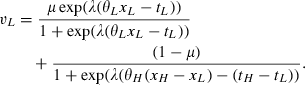 (16)
(16)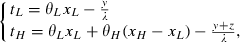 (17)
(17)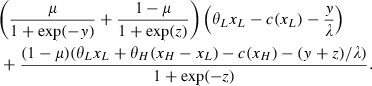 (18)
(18)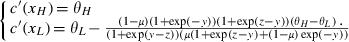 (19)
(19)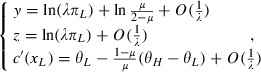 (20)
(20)Note that this outcome cannot be implemented by tariff of type (5) defined over a connected product line [0, a], as under bounded rationality, having given such a tariff will have a continuous rather than binary support on the distribution of choices. Therefore, two mechanisms equivalent under full rationality will no longer be equivalent under bounded rationality.
It can be shown that using continuous tariffs will decrease the profits of the monopolist comparatively to Equations (19) and (20). Now the question is whether the monopolist can improve her profits by using a more elaborate mechanism? I argue that the answer is yes, if there are no complexity costs. In particular, in this case it is possible to achieve profits, which are exponentially close to the profits under the assumption of full rationality.
 , where (x0, t0) is interpreted as the outside option and
, where (x0, t0) is interpreted as the outside option and  is the payment made by the fully rational consumers of type i ∈ {L, H}. The probability that the low-type consumer will buy option
is the payment made by the fully rational consumers of type i ∈ {L, H}. The probability that the low-type consumer will buy option 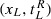 is equal to the probability that her message sL ∈ ML and is given by:
is equal to the probability that her message sL ∈ ML and is given by:
 (21)
(21)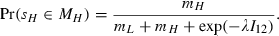 (22)
(22)It is clear that by choosing mL and mH sufficiently large both probabilities can be made exponentially close to one.
Note that although the message game described here allows the monopolist to achieve profits exponentially close to the profits she would have earned against fully rational consumers, it does so at the cost of expanding the cardinality of the strategy set of the consumer. Assuming that the consumer experiences complexity costs, which are increasing in cardinality of the strategy set, would restrict values of mL and mH. Alternatively, one may assume that the monopolist will experience menu costs. The last approach was taken in Basov and Danilkina (2006) to explain flavour proliferation with quality. Basov et al. (2008) apply this model to explain some empirical regularities of the Australian car market.
IV Conclusions
This paper discusses the problem of mechanism design with boundedly rational consumers. As the revelation principle does not hold under bounded rationality, the choice of a class of mechanisms entails a loss of generality. In this paper, I illustrated this explicitly by an example. An important feature of the example is that mapping of several messages in the same allocation allows the monopolist to manipulate probabilities without manipulating the payoffs. In particular, it enables the monopolist to push the probability of the ‘right’ choice arbitrary close to one. This feature allows one to hypothesise that a mechanism that reproduces the good of the given quality in different flavours can approximate arbitrary mechanism with arbitrary precision. The idea is to start with an arbitrary message game and find the equilibrium probabilities of different choices made by different types in a QRE. Then, consider a direct revelation mechanism. In general, the probabilities of different choices will not match those of the QRE, but now the principal can use flavour proliferation to adjust probabilities. Note that the hypothesis, if correct, does not rely on the degree of rationality of the consumers. Finding a rigorous proof of the result is a topic for future research.




