Environmental correlates for tropical tree diversity and distribution patterns in Borneo
ABSTRACT
Aim Identify environmental correlates for tropical tree diversity and composition.
Location Borneo, Southeast Asia.
Methods A GIS-environmental database with 5 arc minute (c. 10 × 10 km) resolution was combined with tree inventory data. Tree diversity, phylogenetic diversity (PD) and the two main compositional gradients were determined for 46 tree inventories. Akaike's information criterion and a data jackknifing procedure were used to select 50 explanatory models for diversity and composition gradients. The average of these models was used as our final diversity and compositional model. We applied Moran's I to detect spatial autocorrelation of residuals.
Results Tree diversity, PD and the two main compositional gradients in Borneo were all significantly correlated with the environment. Tree diversity correlated negatively with elevation, soil depth, soil coarseness (texture) and organic carbon content, whereas it correlated positively with soil C:N ratio, soil pH, moisture storage capacity and annual rainfall. Tree PD was correlated positively with elevation and temperature seasonality and was largely determined by gymnosperms. However, angiosperm PD also correlated positive with elevation. Compositional patterns were strongly correlated with elevation but soil texture, cation-exchange-capacity, C:N ratio, C and N content and drainage were also important next to rainfall seasonality and El Niño Southern Oscillation drought impact.
Main conclusions Although elevation is the most important correlate for diversity and compositional gradients in Borneo, significant additional variability is explained by soil characteristics (texture, carbon content, pH, depth, drainage and nutrient status) and climate (annual rainfall, rainfall seasonality and droughts). The identified environmental correlates for diversity and composition gradients correspond to those found in other tropical regions of the world. Differences between the regions are mainly formed by differences in the relative importance of the environmental variables in explaining diversity and compositional gradients.
INTRODUCTION
Explaining the diversity and distribution of tree species remains a challenging subject in tropical ecology. Only recently have people combined available local tree inventory data to address questions at regional and continental scales (Gentry, 1988; Oliveira-Filho & Fontes, 2000; Slik et al., 2003; ter Steege et al., 2003, 2006; Parmentier et al., 2007; Punyasena et al., 2008). However, these studies have mainly focused on the Neotropics posing the question whether observed correlations between tree diversity and composition gradients there are also valid in other parts of the tropics. Parmentier et al. (2007) found only limited similarity in environmental correlates of tree diversity and composition when they compared African and South American tropical forests in a single meta-analysis. This suggests that the world's tropical forests differ in the environmental structuring of their tree communities, and illustrates the importance of replicating such studies on different continents.
We studied tree diversity and compositional gradients in Borneo as an example of Southeast Asian tropical forest. Borneo has been identified as a biodiversity hotspot, and its lowland forests are among the world's most diverse (Kier et al., 2005). Most of Borneo's forests are dominated by the Dipterocarpaceae, which is atypical compared to other tropical forests around the world (Gentry, 1988; Slik et al., 2003). The structure of Borneo's forests also differs from other tropical regions because of the higher density and taller height of emergent trees, resulting in a relatively open upper canopy (Dail et al., 2004; Paoli et al., 2008). Borneo is also an island of large biophysical ranges having a rainfall gradient of almost 3 m (1585 to 4566 mm annually) and an altitudinal gradient of more than 4000 m. It contains a mosaic of forest types including: mangroves; peat and fresh water swamps; forest on ultramafic, poor white sand (kerangas/heath) and limestone soils; lowland mixed dipterocarp forest; montane and alpine forests (MacKinnon et al., 1996). Borneo's recent geological history is unusual because of the island's repeated connection to the Southeast Asian mainland, Sumatra and Java, during lowered sea levels of Pleistocene glacial periods (Morley, 2000).
There have been few studies addressing island-wide tree diversity and composition gradients on Borneo. Most were carried out at local and regional scales identifying elevation, annual rainfall and soils as environmental correlates for tree diversity and composition gradients (Newbery & Proctor, 1984; Potts et al., 2002; Miyamoto et al., 2003; Slik et al., 2003; Cannon & Leighton, 2004; Aiba et al., 2005). Despite this lack of Borneo-wide analyses, the island has been divided into seven bio-units (MacKinnon & MacKinnon, 1986; Ridder-Numan, 1998; Wong, 1998) based on a few plant and animal groups, unclear methods, spatially biased data and/or expert opinion. It therefore remains unclear to what extent island-wide floristic patterns are spatially structured in relation to the environment. Here we combine available Bornean tree inventory and environmental data into a single meta-analysis to identify environmental correlates for Borneo's tree diversity and compositional gradients.
METHODS
Our GIS-environmental database consisted of the five least correlated bio-climatic variables (Pearson's r < 0.75) of the WORLDCLIM dataset (http://www.worldclim.org) for Borneo (Hijmans et al., 2005): elevation, temperature seasonality, temperature annual range, annual rainfall and rainfall seasonality. To this we added El Niño Southern Oscillation (ENSO) drought impact defined as the relative difference between the normalized difference vegetation index (NDVI) of a severe ENSO year (July 1982–June 1983) and a non-ENSO year (July 1981–June 1982). We also selected 15 soil variables from the Food and Agriculture Organization (FAO) database for poverty and insecurity mapping (FAO, 2002). Principal component analysis (PCA) was used to summarize these data in five independent soil axes that together explained 83% of soil data variance (Table 1). Pearson's correlation was used to determine which of the original 15 FAO soil predictors were significantly correlated with each of the 5 PCA axes (Table 1). Soil axis 1 (31.6% data variance) was positively correlated with soil water availability and storage capacity, organic matter content, nitrogen content and base cation availability, but negatively with soil drainage; soil axis 2 (22.5% data variance) was positively correlated with topsoil organic carbon content, but negatively with soil pH, water storage capacity and topsoil base saturation; soil axis 3 (16.6% data variance) was negatively correlated with soil texture (coarseness) and topsoil clay-cation-exchange capacity; soil axis 4 (7.5% data variance) was negatively correlated with soil depth; whereas soil axis 5 (4.9% of data variance) was positively correlated with soil C:N ratio. All data layers were set at 5 arc minute resolution (~10 km at the equator) covering Borneo by 8577 grid cells. Our final data selection contained 11 environmental variables (Fig. 1). All data layer manipulations were performed with Manifold GIS (Manifold Net Ltd).
| Factor | Axis 1 (31.6%) | Axis 2 (22.5%) | Axis 3 (16.6%) | Axis 4 (7.5%) | Axis 5 (4.9%) |
|---|---|---|---|---|---|
| Base saturation topsoil | –0.047 | –0.462 | 0.042 | 0.135 | 0.350 |
| CEC clay topsoil | 0.262 | –0.189 | –0.336 | 0.313 | –0.082 |
| CEC soil topsoil | 0.342 | –0.106 | 0.148 | 0.035 | 0.137 |
| C:N ratio topsoil | 0.234 | 0.159 | –0.267 | –0.287 | 0.623 |
| Easy available water | 0.362 | –0.260 | –0.027 | 0.123 | –0.091 |
| Effective soil depth | 0.112 | –0.171 | –0.094 | –0.793 | –0.272 |
| Nitrogen topsoil | 0.338 | 0.133 | 0.232 | 0.145 | –0.234 |
| Organic carbon topsoil | 0.254 | 0.289 | 0.207 | 0.065 | –0.349 |
| Organic carbon pool | 0.350 | 0.216 | 0.157 | –0.089 | 0.078 |
| pH topsoil | –0.202 | –0.370 | 0.086 | 0.203 | –0.091 |
| Soil drainage | –0.382 | 0.121 | –0.096 | –0.062 | –0.292 |
| Soil moisture storage | 0.327 | –0.295 | 0.005 | –0.018 | –0.186 |
| Soil production index | –0.022 | –0.470 | 0.046 | –0.236 | –0.152 |
| Textural class subsoil | 0.133 | 0.017 | –0.555 | 0.030 | –0.158 |
| Textural class topsoil | 0.018 | 0.100 | –0.578 | 0.142 | –0.155 |
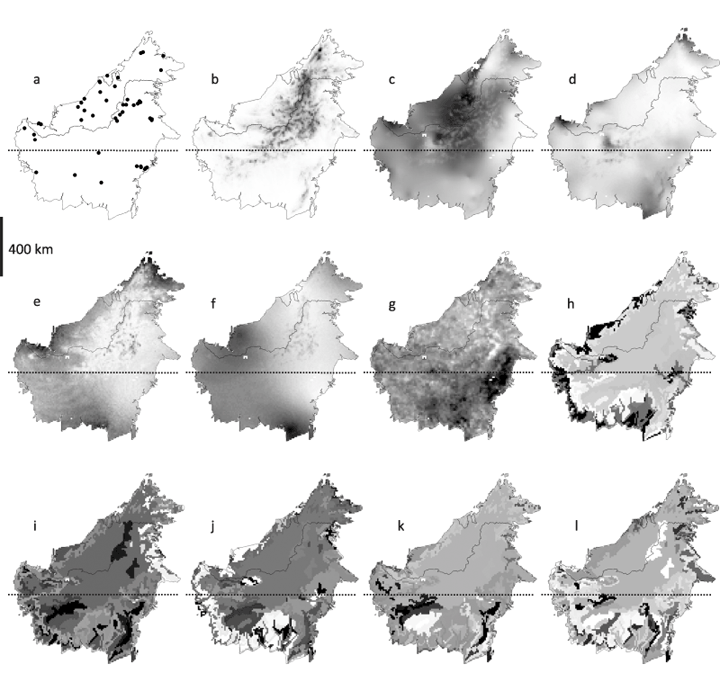
Data locations and environmental variables used in this study: (a) locations; (b) topography; (c) annual rainfall; (d) rainfall seasonality; (e) temperature seasonality; (f) temperature annual range; (g) ENSO drought impact; (h) soil axis 1, (i) soil axis 2, (j) soil axis 3, (k) soil axis 4, (l) soil axis 5. Values increase from white to black.
Plot tree inventory data with diameter at breast height (d.b.h.) ≥ 10 cm for 46 Bornean GIS-grid cells were available (Fig. 1a; Table 2). These locations covered a wide range of climatic, soil and altitudinal gradients (Fig. 2). Tree communities were assessed using generic data to avoid problems with incomplete species identifications (Slik et al., 2003). Patterns in generic diversity and composition match those of species well (Higgins & Ruokolainen, 2004). Inventories were standardized by pooling all plots and stems in each grid cell and randomly drawing 400 individuals. This was repeated five times for each grid cell to calculate reliable average tree species diversity and compositional values (Slik et al., 2003). The number of individuals per genus and the number of genera per 400 individuals were determined for each random draw.
| Location | Sample size (trees) | Sample area (ha) | Plot number | Longitude | Latitude | Elevation (m) | Diversity (n = 400) (±conf.) | Phylogenetic diversity (±conf.) | Source |
|---|---|---|---|---|---|---|---|---|---|
| Andalau | 12,648 | 20.2 | 10 | 114.5407E | 4.6240N | 61 | 81.2 ± 2.7 | 17.6 ± 0.4 | Ashton |
| Bako | 1892 | 2.4 | 4 | 110.4575E | 1.7075N | 58 | 85.0 ± 0.6 | 17.8 ± 0.6 | Ashton |
| Long Barang | 695 | 1.3 | 4 | 115.1240E | 1.8740N | 1026 | 105.6 ± 2.3 | 18.8 ± 1.0 | Valkenburg |
| Barito Ulu | 1562 | 2.5 | 3 | 114.0407E | 0.1258S | 287 | 88.8 ± 7.0 | 17.4 ± 0.9 | Brearley |
| Belalong | 9157 | 20.2 | 10 | 115.2073E | 4.5407N | 332 | 91.0 ± 3.3 | 16.6 ± 0.6 | Ashton, Poulsen |
| Berau 1 | 1137 | 1.5 | 5 | 117.2906E | 1.9575N | 74 | 78.0 ± 1.9 | 18.3 ± 1.2 | Slik |
| Berau 2 | 832 | 1.3 | 1 | 117.1239E | 2.0408N | 59 | 73.8 ± 3.2 | 17.5 ± 0.7 | Slik |
| Berau 3 | 7195 | 12.0 | 3 | 117.2072E | 1.8741N | 105 | 85.4 ± 4.2 | 17.3 ± 0.9 | STREK |
| Bukit Iju | 9267 | 9.1 | 15 | 112.7074E | 2.7074N | 111 | 89.2 ± 1.6 | 16.6 ± 0.6 | Ashton |
| Bukit Raya | 7522 | 9.1 | 15 | 112.9574E | 1.9575N | 141 | 91.6 ± 3.6 | 17.4 ± 0.5 | Ashton |
| Bukit Bangkirai | 827 | 1.6 | 3 | 116.8678E | 1.0300S | 72 | 79.4 ± 2.9 | 17.4 ± 0.2 | Slik |
| Bok Tisam | 3533 | 6.1 | 10 | 114.1240E | 3.6241N | 77 | 86.6 ± 3.9 | 16.9 ± 0.7 | Ashton |
| Danum Valley | 3454 | 8.0 | 2 | 117.7906E | 4.9573N | 300 | 73.2 ± 2.1 | 17.2 ± 0.5 | Newbery |
| Enggeng | 1900 | 4.0 | 4 | 115.7906E | 3.2074N | 819 | 57.6 ± 1.0 | 17.8 ± 0.3 | Wulffraat |
| Gunung Mulu | 652 | 1.4 | 3 | 114.9573E | 3.9574N | 551 | 97.4 ± 1.8 | 17.7 ± 0.4 | Martin, 1977 |
| Gunung Meratus | 575 | 1.4 | 62 | 116.2906E | 0.8758S | 103 | 96.8 ± 3.1 | 17.3 ± 0.7 | Slik |
| Gunung Mersing | 11,032 | 18.2 | 30 | 113.1241E | 2.5407N | 231 | 91.6 ± 4.0 | 17.3 ± 1.4 | Ashton |
| Gunung Palung | 2862 | 4.5 | 28 | 110.2075E | 1.2924S | 280 | 85.4 ± 3.2 | 17.1 ± 0.7 | Webb |
| Gunung Santubong | 907 | 1.2 | 2 | 110.3742E | 1.6241N | 9 | 71.4 ± 2.4 | 16.6 ± 0.9 | Ashton |
| ITCI 1 | 1132 | 2.4 | 3 | 116.6239E | 0.9591S | 141 | 81.0 ± 4.1 | 16.8 ± 1.2 | Eijk-Bos |
| ITCI 2 | 1813 | 4.8 | 4 | 116.5406E | 0.9591S | 322 | 99.8 ± 6.2 | 17.5 ± 1.3 | Eijk-Bos |
| Kinabalu 1 | 974 | 2.0 | 2 | 116.7073E | 6.0406N | 774 | 91.8 ± 2.9 | 17.2 ± 0.9 | Aiba |
| Kinabalu 2 | 2969 | 2.4 | 5 | 116.5406E | 6.0406N | 1958 | 55.4 ± 2.3 | 22.4 ± 1.0 | Aiba |
| Lahei | 1561 | 2.0 | 2 | 114.2074E | 1.8757S | 39 | 56.0 ± 3.1 | 17.9 ± 1.3 | PLOTNET |
| Lambir | 12,473 | 15.3 | 13 | 114.0407E | 4.2074N | 111 | 109.6 ± 6.0 | 17.3 ± 0.8 | Ashton, Nagamasu |
| Langap | 1421 | 1.0 | 35 | 116.4573E | 3.1242N | 118 | 100.6 ± 3.8 | 17.9 ± 0.4 | Sheil |
| Lio Mutai | 520 | 1.0 | 13 | 116.3739E | 2.9574N | 234 | 99.6 ± 0.5 | 17.9 ± 0.8 | Sheil |
| Long Jalan | 440 | 0.7 | 11 | 116.1240E | 2.8741N | 581 | 107.8 ± 1.0 | 18.4 ± 1.3 | Sheil |
| Lurah | 2711 | 5.0 | 5 | 115.4573E | 2.8741N | 991 | 44.8 ± 1.9 | 17.9 ± 0.7 | Wulffraat |
| Malinau | 480 | 0.8 | 12 | 116.5406E | 3.0407N | 257 | 95.2 ± 2.5 | 17.7 ± 0.6 | Sheil |
| Nyabau | 2848 | 3.0 | 5 | 113.1241E | 3.2074N | 44 | 76.4 ± 3.8 | 17.5 ± 0.5 | Ashton |
| Puak | 2267 | 4.5 | 5 | 115.7073E | 2.8741N | 1349 | 42.4 ± 2.1 | 20.2 ± 0.6 | Wulffraat |
| Saan | 416 | 0.5 | 1 | 115.4573E | 2.4574N | 855 | 35.0 ± 0.0 | 19.7 ± 0.0 | Wulffraat |
| Samboja | 6793 | 13.4 | 66 | 116.9573E | 0.9591S | 62 | 99.4 ± 3.7 | 17.8 ± 0.4 | Slik |
| Sangai | 7886 | 15.0 | 15 | 112.5408E | 1.4591S | 97 | 92.4 ± 2.0 | 17.1 ± 1.1 | Wilkie |
| Segan | 2467 | 3.0 | 5 | 112.9574E | 2.9574N | 160 | 95.0 ± 3.3 | 17.7 ± 1.4 | Ashton |
| Sempatung | 472 | 1.0 | 1 | 110.0409E | 1.0408N | 501 | 53.0 ± 1.1 | 17.9 ± 0.6 | Suzuki |
| Semule | 594 | 1.0 | 1 | 115.2907E | 2.2908N | 929 | 52.0 ± 1.4 | 18.9 ± 0.6 | Wulffraat |
| Sepilok | 18,745 | 48.0 | 12 | 117.9572E | 5.8740N | 32 | 87.0 ± 1.1 | 16.9 ± 0.5 | Nilus |
| Serimbu | 1082 | 2.0 | 2 | 110.1242E | 0.7075N | 129 | 93.4 ± 2.0 | 16.6 ± 0.5 | Suzuki |
| Sungai Iwan | 2306 | 5.6 | 6 | 115.0407E | 2.0408N | 737 | 53.6 ± 2.8 | 17.8 ± 0.6 | Wulffraat |
| Sungai Wain | 1976 | 2.8 | 200 | 116.7906E | 1.1257S | 35 | 87.6 ± 3.5 | 17.3 ± 0.9 | Slik |
| Sunujuh | 1254 | 2.0 | 2 | 109.4576E | 1.4575N | 27 | 77.6 ± 2.5 | 17.5 ± 1.0 | Suzuki |
| Ulu Bakong | 1705 | 3.0 | 5 | 114.0407E | 4.2907N | 41 | 81.0 ± 5.5 | 16.5 ± 0.5 | Ashton |
| Ulu Dapoi | 986 | 1.2 | 2 | 114.4574E | 3.1241N | 213 | 99.2 ± 1.1 | 17.1 ± 1.3 | Ashton |
| Ulu Temiai | 491 | 0.6 | 1 | 113.6241E | 2.2074N | 442 | 95.6 ± 2.0 | 18.0 ± 0.8 | Ashton |
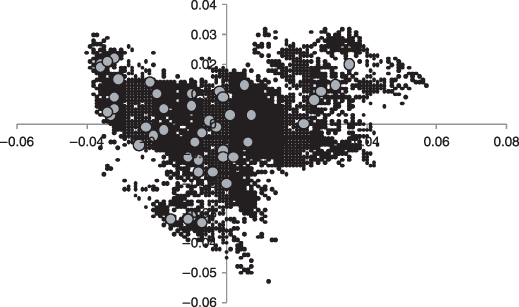
The first two axes, which together explain 39.9% of environmental data variance, of a principal components analysis of the 8577 Bornean grid cells used in our study (small black dots) based on the 11 environmental variables. The grid cells with tree inventory data are indicated with large grey dots to illustrate how much of environmental variability was encompassed by these locations.
We determined two diversity measures for each location; rarefied and phylogenetic diversity (PD). Rarefied diversity represents the average number of genera in five random samples of 400 stems per location. This procedure removed effects of different sample sizes on diversity estimates (Slik et al., 2003). To determine phylogenetic diversity we pruned down the angiosperm phylogeny group (APG (Stevens, 2001)) to the tree families present in our dataset using Phylomatic (Webb et al., 2007), choosing the maximally resolved seed plant tree option. Using published phylogenies we manually resolved this tree to genus level for most families (see Appendix S1 in supporting information). Genera that could not be resolved were placed as basal polytomies within their families. This phylogeny was used as input in PhyloCom's Bladj application (Webb et al., 2007). The Bladj application scales phylogenetic branch lengths to estimated time of evolutionary origin using known family ages (Wikstrom et al., 2001). The PD application in PhyloCom was used to calculate phylogenetic diversity (Faith, 1992), which represents proportion of total phylogenetic branch length captured by the species in the input sample. Phylogenetic diversity in each location was based on the average of 5 random selections of 38 genera (based on the lowest number of genera found in our random samples of 400 individuals). Because gymnosperms, as the most basal group in the phylogeny, can greatly influence the outcome of phylogenetic diversity calculations, we repeated the analysis with angiosperms only (based on 37 randomly selected genera, the lowest number found in our random samples of 400 individuals).
Tree compositional gradients were determined using Detrended Correspondence Analysis (DCA) in multi-variate statistical package (Kovach Computing Services, Anglesey, Wales, UK). DCA was performed using a log10 transformed matrix to reduce the effect of abundant genera. The DCA contained all random draws of 400 individuals. The scores of the locations on each of the DCA axes were determined by averaging the DCA axis scores of the five random draws per location.
Because our data came from different studies, the number of sampled trees, plots and sampled surface area differed for each grid cell introducing potentially confounding sampling effects. In combination with the fact that the exact locations of subplots within study areas were mostly unknown, this heterogeneous plot layout made it difficult to exclude the possibility that beta diversity was included in our diversity estimates. To minimize these sampling biases we applied multiple regression analysis with backward selection between the diversity and compositional values and the log-transformed number of plots, stems and sample area for each GIS-grid cell with inventory data (Statgraphics Plus for Windows 2.1, Rockville, MD, USA). This procedure identified significant correlations: (1) tree diversity with number of plots; (2) phylogenetic diversity with sample area; (3) CCA compositional axis 2 with number of plots, trees and sample area. The regression equations were used to calculate expected diversity and compositional values for each grid cell, which were subtracted from the observed values, to minimize confounding sample effects. All further analyses are based on these corrected diversity and composition values.
Relations between diversity and compositional gradients and the environmental variables were determined using Akaike's Information Criterion (AIC) using the model selection application Spatial Analysis in Macroecology (SAM, version 3.0, Rangel et al., 2006). This procedure always produces a single best model given a certain dataset. However, because data selection can greatly influence final model choice, especially in small datasets, we used AIC in combination with data jackknifing. Therefore, we produced 50 sub-datasets, each with 6 randomly excluded locations, selecting the best model (AIC) for each. Although this reduces the power of each separate analysis slightly (40 instead of all 46 locations used) it will produce 50 equally likely models, giving an estimate of data variability on model choice. For each of the 50 models we determined the multiple regression equations, which were used to calculate 50 diversity and composition estimates for each location. The average of these 50 values was used as our final diversity and compositional estimate for each location. The performance of our final model (correlation coefficients, R2-adjusted, F-ratio and P-values) was tested by regressing estimated against observed values. We tested for residual spatial autocorrelation (RSA) of our diversity and compositional models using Moran's I. Finally, the 50 regression equations were used to calculate average diversity and compositional values (± SD) for each grid cell in Borneo.
RESULTS
Tree diversity, phylogenetic diversity and CCA composition axes 1 and 2 were significantly correlated with environmental variables (Table 3). Only tree diversity showed significant spatial autocorrelation of residuals in the first distance class (69 km, Table 3). All models performed well with correlation coefficients between 0.52–0.92 and adjusted R2-values between 25.4–84.1%.
| Tree species diversity | Phylogenetic diversity all | Phylogenetic diversity angiosperms | Tree species composition axis 1 | Tree species composition axis 2 | |
|---|---|---|---|---|---|
| Correlation | 0.52 | 0.84 | 0.57 | 0.92 | 0.55 |
| R 2 (%) | 25.4 | 69.0 | 31.2 | 84.1 | 28.4 |
| F-ratio | 16.3 | 101.4 | 21.4 | 239.9 | 18.9 |
| d.f. | 45 | 45 | 45 | 45 | 45 |
| P | 0.0002 | < 0.0001 | < 0.0001 | < 0.0001 | 0.0001 |
| Multiple regression | |||||
| Variable 1 | (–) Elevation (84) | (+) Elevation (100) | (+) Elevation (100) | (+) Elevation (100) | (+) Rain seas. (88) |
| Variable 2 | (+) Soil 5 (64) | (+) Temp. seas. (82) | (–) Soil 2 (6) | (–) Soil 3 (94) | (+) Enso (34) |
| Variable 3 | (–) Soil 2 (14) | (–) Annual rain (48) | (+) Annual rain (4) | (–) Soil 5 (36) | (–) Soil 5 (22) |
| Variable 4 | (+) Soil 3 (12) | (–) Temp. range (34) | (–) Soil 5 (2) | (+) Soil 1 (18) | (–) Soil 3 (14) |
| Variable 5 | (+) Annual rain (12) | (–) Rain seas. (12) | (–) Enso (2) | (–) Annual rain (4) | (+) Soil 4 (12) |
| Variable 6 | (+) Soil 4 (10) | (–) Soil 2 (8) | (–) Enso (4) | (+) Temp. seas. (10) | |
| Variable 7 | (–) Soil 5 (4) | (+) Soil 2 (2) | (–) Temp. range (4) | ||
| Variable 8 | (–) Soil 3 (2) | (–) Temp. seas. (2) | (–) Soil 1 (2) | ||
| Variable 9 | (+) Soil 1 (2) | (–) Soil 2 (2) | |||
| Moran's I residuals distance classes (km) | |||||
| 68.9 | –0.200* | –0.045 | –0.107 | –0.101 | –0.138 |
| 186.5 | 0.017 | –0.016 | –0.012 | 0.012 | 0.092 |
| 272.2 | 0.097 | –0.023 | –0.069 | 0.063 | –0.138 |
| 345.7 | –0.060 | –0.094 | 0.066 | –0.032 | –0.104 |
| 412.9 | –0.029 | –0.018 | 0.112 | 0.006 | 0.039 |
| 488.7 | 0.062 | 0.086 | –0.079 | 0.043 | –0.023 |
| 577.7 | –0.009 | –0.011 | –0.103 | –0.071 | 0.075 |
| 683.7 | –0.040 | 0.001 | 0.011 | –0.135 | –0.005 |
| 957.1 | –0.036 | –0.081 | –0.018 | 0.015 | 0.004 |
Tree diversity had a correlation coefficient of 0.52 with the environment explaining 25.4% of data variability (Table 3). Tree diversity correlated negatively with elevation and positively with soil axis 5, indicating increasing diversity with increasing topsoil C:N ratio. Other, less important positive soil correlates for diversity were soil pH, moisture storage capacity and topsoil base saturation, whereas tree diversity decreased with increasing soil depth, soil coarseness (texture), organic carbon content and topsoil cation-exchange-capacity of the clay fraction. Increasing annual rainfall also correlated positive with tree diversity.
Tree phylogenetic diversity correlated strongly with environmental variables (0.84), and these explained 70.5% of data variability (Table 3). Elevation and temperature seasonality were the most important positive correlates for tree phylogenetic diversity, whereas annual rainfall, rainfall seasonality and temperature yearly range correlated negatively. Soil variables were of limited importance for tree phylogenetic diversity. Phylogenetic diversity was almost entirely determined by gymnosperms, which explained 74.2% of data variance between locations (correlation coefficient = 0.86, F-ratio = 126.3, d.f. = 45, P < 0.0001). Therefore, we repeated the analysis with angiosperms only, which lowered the correlation with the environment (0.52) and amount of explained data variability (31.2), but still resulted in a strong positive correlation between elevation and angiosperm phylogenetic diversity.
The main compositional gradient in Borneo (DCA axis one, explaining 9.5% data variability) was strongly associated with environmental variables (correlation coefficient 0.92, R2-adjusted 84.1%). Elevation was the major correlate in association with soil axis 3, indicating the importance of soil texture and topsoil cation-exchange-capacity of the clay fraction. Other variables affecting composition gradients were the soil C:N ratio, N content, C content and drainage.
The second compositional gradient in Borneo (DCA axis two, explaining 3.8% data variability) was significantly associated with environmental variables (correlation coefficient 0.55 and R2-adjusted 28.4%). This compositional gradient was mainly associated with rainfall seasonality and ENSO-drought impact. Other, less important correlates were temperature seasonality and soil texture, topsoil cation-exchange-capacity of the clay fraction, soil depth and topsoil C:N ratio.
Borneo-wide extrapolations of diversity and compositional gradients are shown in Fig. 3. Tree diversity is highest in lowland forests, decreasing steadily with elevation (3a). Variations in lowland tree diversity are mainly linked to soil axis 5, with highest diversity in areas with high topsoil C:N ratios. Tree phylogenetic diversity and angiosperm phylogenetic diversity both show an increase with altitude across Borneo (Fig. 3b,c). Phylogenetic diversity, contrary to angiosperm phylogenetic diversity, is also relatively high in lowland Sabah (northeastern Borneo). The most important compositional gradient across Borneo identifies montane, sub-montane, keranga, peat swamp and dipterocarp forests (Fig. 3d), whereas the second compositional gradient reflects rainfall seasonality in combination with ENSO-drought impact (Fig. 3e).
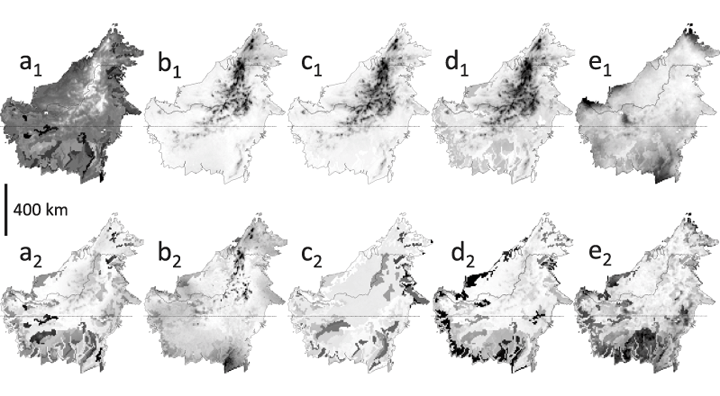
Borneo-wide modelling results for: tree diversity (a1) ± SD (a2); tree phylogenetic diversity (b1) ± SD (b2); tree phylogenetic diversity of angiosperms only (c1) ± SD (c2); tree species compositional axis 1 (d1) ± SD (d2); and tree species compositional axis 2 (e1) ± SD (e2). Values increase from white to black.
DISCUSSION
Diversity patterns
Tree diversity and phylogenetic diversity were strongly associated with elevation albeit in contrasting ways: tree diversity declined whereas phylogenetic diversity increased with elevation. Decline in tree diversity with elevation confirms findings elsewhere on Borneo (Kitayama, 1992; Pendry & Proctor, 1997; Aiba et al., 2005) and other tropical regions (Gentry, 1988; Romdal & Grytnes, 2007), although with exceptions (Lovett et al., 2006). These changes are possibly linked to declining temperatures and area size with increasing altitude (Bachman et al., 2004; Jimenez-Castillo et al., 2007). A comparable phylogenetic diversity study in eastern African tropical forest also reports increasing phylogenetic diversity with elevation (Tallents et al., 2005). In Borneo this increase in phylogenetic diversity is strongly determined by gymnosperms (Agathis Salsb., Dacrycarpus (Endl.) de Laub., Dacrydium Lamb., Falcatifolium de Laub., Nageia Gaertn. and Podocarpus L’Her. ex Pers.). However, when we repeated the analysis using only angiosperm genera, elevation was still the most important positive correlate for phylogenetic diversity. Apparently, basal plant lineages become more common at higher altitudes whereas lowland forests are characterized by communities of more closely related taxa. This suggests that lowland tropical forests serve as species sources (speciation centres) whereas high-elevation forests serve as species sinks. Such source–sink patterns are also observed along depth gradients in marine environments (Rex et al., 2005) and along latitudinal gradients (Roy & Goldberg, 2007). This would mean that over evolutionary timescales lowland forests are essential for the maintenance of tree diversity in tropical montane floras.
Tree diversity showed a consistent positive correlation with increasing soil C:N ratio, pH, moisture storage capacity and topsoil base saturation, whereas it declined with soil depth, coarseness, organic carbon content and cation-exchange capacity of the topsoil clay fraction. This combination of soil factors suggests increasing diversity in nitrogen limited, shallow soils with high water retention capacity, i.e. soils that are generally considered less fertile and productive. This seems to confirm findings from western Borneo, where diversity of Dipterocarpaceae increased with decreasing soil fertility (Paoli et al., 2006).
Despite a 3-m gradient in Borneo, annual rainfall was only selected in 12% of models as a correlate for tree diversity, contrasting with its importance for diversity in African and Neotropical studies (Gentry, 1988; ter Steege et al., 2003; Parmentier et al., 2007; Punyasena et al., 2008). This difference between Borneo and other tropical regions might be related to the fact that, measured over the long term, most areas in Borneo receive more than 100 mm of rain each month. This value is considered the minimum rainfall required to compensate for evaporation in the tropics, suggesting water stress plays a minor role in Borneo. This seems to be confirmed by the non-existent association between tree diversity and ENSO drought impact.
Composition patterns
Tree composition patterns were strongly associated with elevation, soil texture and, to a lesser extent, soil C:N ratio and fertility. Indeed, most studies in the tropics report shifts in tree species composition along altitudinal gradients (Gentry, 1988; Ashton, 2003) and soil types (Duivenvoorden, 1995; ter Steege et al., 2006). The most obvious changes with increasing elevation in Borneo are the lowered abundance of Dipterocarps commensurate with increases in Fagaceae, Lauraceae, Myrtaceae and gymnosperms. Many of the montane genera are characterized by large distribution ranges that often include temperate regions, whereas characteristic lowland genera are usually confined to the tropics (Qian et al., 2003). Low-temperature tolerance probably plays a role in floristic shifts along altitudinal gradients, with increasing cold tolerance offset by lower competitive ability under warmer conditions.
Our study confirms the importance of soils as correlates for compositional gradients in the tropics. Soil texture, drainage and nutrient availability have repeatedly been shown to be associated with floristic shifts (Newbery, 1991; Duivenvoorden, 1995; Aiba & Kitayama, 2002; Tuomisto et al., 2002; Phillips et al., 2003). Soil nutrients impact tree communities by influencing forest turnover rates and dynamics, with fertile soils generally favouring trees with high growth rates and short life spans, and poor soils favouring slow growing long-lived trees (Phillips et al., 1994). Soil texture and drainage are probably related to drought and flooding tolerance of trees, which can be potent selective forces (Slik, 2004; van Nieuwstadt & Sheil, 2005; McDowell et al., 2008). Many studies report annual rainfall, rainfall seasonality and droughts as variables associated with tree floristics (Slik et al., 2003; Chust et al., 2006; ter Steege et al., 2006; Parmentier et al., 2007). Our results do indeed indicate that rainfall seasonality and ENSO-drought impact are important correlates for floristic shifts in Borneo.
Impact of data quality and quantity
We were faced with considerable problems when trying to perform a meta-analysis using inventory data that were collected differently in each location. In fact, the scarcity of taxonomically reliable inventory data in Borneo resulting in only 46 inventoried grid cells formed a problem by itself. As a result not all forest types were equally represented with only few locations in kerangas and none in freshwater/peat swamp forests leading to high standard deviations for these forest types in our Borneo-wide analysis. Although our locations were spatially biased towards northern Borneo, and some locations were close together, we only found significant RSA for tree diversity over small distances (< 70 km). This violates the assumption that residuals should be independent and results in inflated Type I errors (Dormann et al., 2007). However, short-distance RSA, although causing inflated type I errors, does not seriously affect the interpretation of the regression coefficients estimated by ordinary least squares regressions (Diniz-Filho et al., 2007; Hawkins et al., 2007).
Different scales of environmental (c. 10 × 10 km grids) and inventory data form another complication as it is unlikely that plots covering a few hectares are representative of a 10 × 10 km area. Additionally, some grid cells contained more inventoried trees, plots or surveyed surface area than others, resulting in different levels of beta diversity captured per location. Although we have tried to correct our diversity and compositional values for these sampling biases, it is likely that they have at least partly influenced our results. Ideally, meta-analyses like ours should be performed on standardized plot layouts in combination with high-resolution environmental data. Unfortunately, such an approach is still difficult to realize in remote tropical areas like Borneo, where the availability of reliable inventory data itself already forms a problem, let alone reliable high-resolution data on soils and climate. Given the enormous diversity stored in tropical forests and the alarming rate in which these forests are disappearing, it is urgently needed to set up large-scale baseline studies that sample the remaining tropical forests in a standardized manner. Current deforestation completely erases the natural patterns of ecological communities that exist in these forests in taxonomic and genetic terms. Soon it might be too late to reconstruct these natural patterns, which are key for our understanding of how these systems have originated and maintained themselves over millions of years.
ACKNOWLEDGEMENTS
This work would be impossible without the help of Zainal Arifin, Arbainsyah, Ambriansyah, Andriansyah, Kade Sidiyasa, Johni, Ismayadi Samsoedin, Kuswata Kartawinata, Peter Ashton, Ismael Rachman, Afriastini, Edi Permana, David Newbery, Clara Eijk-Bos, Edo Goverse, Paul Kessler, Lanniari, and the following projects USAID, CIFOR, Tropenbos, PLOTNET, STREK, NWO-WOTRO, Indonesian Ministry of Forestry, LIPI. Three anonymous referees are thanked for their valuable comments on an earlier version of this manuscript.




