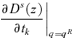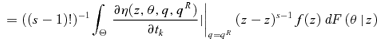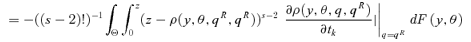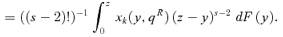Abstract
This article proposes graphical methods to determine whether commodity tax changes are “socially improving,” in the sense of improving social welfare or decreasing poverty for large classes of social welfare and poverty indices. It also shows how estimators of critical poverty lines and economic efficiency ratios can be used to characterize socially improving tax reforms. The methodology is illustrated using Mexican data.
1. introduction
Policies that affect consumer and producer prices have an impact on welfare, and there are many such policies. Some governments maintain high import tariffs or fail to implement regulations to foster competition. This may protect national producers by maintaining high domestic producer prices, but it also raises consumption prices, which hurts consumers. Most governments use sales and indirect taxes to raise tax revenues, thus affecting consumer and producer prices. This is particularly important for developing countries, which rely heavily on commodity taxation to generate tax revenues. Price subsidies on food, education, energy and transportation are also common in developing and developed countries alike.
Policy analysts must routinely evaluate the impact of such pricing policies on poverty and social welfare. Important information problems stand, however, in the way of anyone wishing to do this. The main objective of the article is to show how these problems can be (somewhat) circumscribed. We are particularly interested in demonstrating the empirical applicability of a “social improvement” approach. This approach makes it possible to identify marginal price changes that will be deemed socially desirable by wide spectra of social welfare and poverty analysts. The term “social improvement” thus encompasses both the classical welfare-dominance and the poverty-dominance approaches.
For expositional simplicity, we will focus in this article on the analysis of the social impact of indirect tax reforms. We will think of two goods, j and l, and will ask whether it is socially desirable (in a sense to be defined precisely below) to increase a tax rate on good j to decrease a tax rate on good l. Note that tax rates may be positive or negative, which also says that decreasing the tax on a good may mean increasing its rate of subsidy. In doing this, we keep producer prices constant for expositional simplicity, but this framework can be extended to the general equilibrium analysis of any government intervention that changes relative prices.
The first measurement difficulty is then to estimate the impact of price changes on consumer welfare. It is well known that this can be a complicated exercise and that its results can be sensitive to a number of important theoretical and econometric assumptions. The task is particularly problematic when the goal is to find globally optimal tax systems, since the tax analyst then needs reliable demand responses over extended price intervals for each household. Keeping in mind that actual changes in the tax system are “slow and piecemeal,”2 and that it would be unwise to ignore the role of the actual tax system as a departure (or anchor) point for the identification of desirable tax reforms, we focus here on the effect of marginal tax reforms. One immediate advantage is that evaluating the distributive impact of marginal tax reforms does not require estimates of individual demand and utility functions, but can instead be assessed directly from the observed data alone,3 as we review in Section 2.
The second difficulty resides in the choice of a social evaluation function with which the impact of the tax reform is to be measured.4 This choice poses a fundamental problem, since any particular selection of functional form and parameters for a social evaluation function necessarily embodies arbitrary value judgements. The strategy we follow in this article is instead to define classes of social evaluation indices that incorporate increasingly stronger judgements on the importance of distributive issues in designing tax policy. For this purpose, we consider social evaluation indices that take into account (though not necessarily with the same distributive weight) everyone's welfare—the traditional social welfare functions—as well as social evaluation indices that censor welfare at a poverty line and that are therefore not affected by changes in the welfare of the “rich”—in short, the much-used poverty indices. These classes of functions and indices are described in Section 3.
Verifying whether a tax reform is desirable then proceeds by checking whether it can command the unanimous approval of all those analysts who agree with some generally defined normative properties of the social evaluation indices. If so, the reform can be called “socially improving.” One well-known criterion to assess social improvement comes from the Pareto principle. Pareto improvement, however, is likely to provide a poor normative basis for the empirical analysis of tax reforms (for reasons that we discuss below in Section 6.3), and it is thus useful to consider “higher-order” ethical principles. We increase progressively the ethical content of our classes of social welfare and poverty indices by incorporating the anonymity—or symmetry—principle (for first-order improvement), the Pigou–Dalton principle of transfers (for second-order improvement), the principle of diminishing transfers (for third-order improvement), and subsequent “generalized” higher-order normative principles. These principles lead to the definition of what we term Pen-improving, Dalton-improving, Kolm-improving, and higher-order welfare-improving tax reforms. The definition of poverty-improving tax reforms proceeds in a similar way by censoring the social assessment at a poverty line. This is derived in Section 4.
The third difficulty lies in estimating the impact on tax revenues of changes in the structure of indirect taxation. It is well known that this impact is linked to the aggregate deadweight loss of taxation,5 and thus to the economic efficiency of a tax reform. Estimating the aggregate impact on tax revenues can be less difficult (in principle at least) than the estimation of household-specific changes in consumption, but the details of the estimation procedures can still lead to considerable disagreements among tax analysts. One solution is to carry out sensitivity analysis on the role of the unobserved economic efficiency parameter, in the manner of Ahmad and Stern (1984) for instance. We propose an alternative procedure that estimates the critical efficiency ratio up to which a tax reform can be said to be socially improving at a given ethical order. This leaves policy makers free to assess whether the actual efficiency ratio is likely (or can be safely estimated) to be below that critical value, and thus whether the tax reform can confidently be deemed socially improving. A similar device is constructed to handle, for poverty measurement, the role of poverty lines—whose estimation is also notoriously difficult and controversial. We show how to construct estimates of the critical poverty lines up to which a tax reform can be considered to be poverty improving. Policy makers and poverty analysts are then let free to assess or estimate whether those critical poverty lines are sufficiently high to encompass all plausible poverty line estimates. If that is so, the tax reform can be confidently described as poverty improving. These critical thresholds are derived in Section 5.
Social efficiency is checked in this article through the use of simple Consumption Dominance 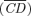 curves.
curves.  curves display cumulative consumption shares when these are weighted by powers of poverty gaps. First-order
curves display cumulative consumption shares when these are weighted by powers of poverty gaps. First-order  curves show the share in the total consumption of a good of those at a given income level. Second-order
curves show the share in the total consumption of a good of those at a given income level. Second-order  curves indicate the combined share in the total consumption of a good of those whose income lies below a given threshold. Higher-order
curves indicate the combined share in the total consumption of a good of those whose income lies below a given threshold. Higher-order  curves weight consumption shares by increasingly higher powers of poverty gaps. Increasing the tax on good j and decreasing the tax on good l is poverty improving at any given order of ethical dominance if the
curves weight consumption shares by increasingly higher powers of poverty gaps. Increasing the tax on good j and decreasing the tax on good l is poverty improving at any given order of ethical dominance if the  curve of that order for good l is higher than the
curve of that order for good l is higher than the  curve for good j at every threshold under a maximum poverty line. When that maximum poverty line extends to infinity, the tax reform can be called welfare improving. The second-order welfare improvement condition we obtain is equivalent to the Dalton improvement condition of Yitzhaki and Slemrod (1991) and Mayshar and Yitzhaki (1995). Our social improvement conditions become less stringent when we consider poverty instead of welfare improvement, since we can then focus exclusively on those below a maximum admissible poverty line and do not need to consider the impact of the reform on the entire population. Increasing the order of dominance also facilitates the search for socially improving tax reforms since more ethical structure is then imposed on the properties of the admissible social evaluation indices. These links are described in some detail in Section 6.
curve for good j at every threshold under a maximum poverty line. When that maximum poverty line extends to infinity, the tax reform can be called welfare improving. The second-order welfare improvement condition we obtain is equivalent to the Dalton improvement condition of Yitzhaki and Slemrod (1991) and Mayshar and Yitzhaki (1995). Our social improvement conditions become less stringent when we consider poverty instead of welfare improvement, since we can then focus exclusively on those below a maximum admissible poverty line and do not need to consider the impact of the reform on the entire population. Increasing the order of dominance also facilitates the search for socially improving tax reforms since more ethical structure is then imposed on the properties of the admissible social evaluation indices. These links are described in some detail in Section 6.
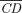 curves were first used by Makdissi and Wodon (2002) in the context of poverty reduction. This article uses them for the broader analysis of social improvement. The current paper also introduces the concept of first-order social improvement and shows how to test it, and also discusses how it differs from the traditional and important concept of Pareto improvement. The concept of social improvement further leads to an interpretation of the ratio of
curves were first used by Makdissi and Wodon (2002) in the context of poverty reduction. This article uses them for the broader analysis of social improvement. The current paper also introduces the concept of first-order social improvement and shows how to test it, and also discusses how it differs from the traditional and important concept of Pareto improvement. The concept of social improvement further leads to an interpretation of the ratio of  curves as a natural indicator of the distributive benefit of a tax reform, a benefit that can be compared to the average deadweight loss or economic efficiency cost of the reform. We also see how the concepts of critical economic efficiency ratios and critical poverty lines may help circumvent the difficulties faced by tax analysts.
curves as a natural indicator of the distributive benefit of a tax reform, a benefit that can be compared to the average deadweight loss or economic efficiency cost of the reform. We also see how the concepts of critical economic efficiency ratios and critical poverty lines may help circumvent the difficulties faced by tax analysts.
Tax policy analysis is clearly of practical and policy interest. It is thus essential to consider how the tools described above can be implemented empirically using survey data. A crucial part of this article is devoted to this through implementing estimators of  curves, critical poverty lines, and critical economic efficiency thresholds. These tools are applied in Section 7 to the analysis of Mexican consumption data. Section 8 concludes the article, and the proofs of the various lemmas and theorems can be found in the Appendix.
curves, critical poverty lines, and critical economic efficiency thresholds. These tools are applied in Section 7 to the analysis of Mexican consumption data. Section 8 concludes the article, and the proofs of the various lemmas and theorems can be found in the Appendix.
2. notation and definitions
Consider a vector q of K consumer prices. For expositional simplicity, and as is customary in the partial equilibrium literature, we set the vector of producer prices to 1 and assume them to be constant and invariant to changes in t, the vector of K tax rates. We then have q= 1 +t and dqk=dtk, where qk and tk denote respectively the price of and the tax rate on good k.
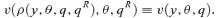 (1)
(1)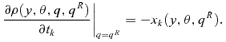 (2)
(2)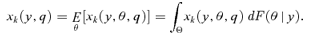 (3)
(3)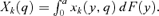 By (2), Xk(q) is also the average cost in well-being of an increase in the price of good k. We will often normalize by Xk(q) some of the various measures that will be associated to a good k, and we will distinguish these normalized measures with a
By (2), Xk(q) is also the average cost in well-being of an increase in the price of good k. We will often normalize by Xk(q) some of the various measures that will be associated to a good k, and we will distinguish these normalized measures with a  . Hence, as a proportion of per capita consumption, consumption of good k at income y is expressed as
. Hence, as a proportion of per capita consumption, consumption of good k at income y is expressed as 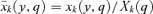 .
.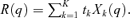 Assume that the government's tax reform increases the tax rate on the jth commodity and uses the proceeds to decrease the tax rate (or to increase the subsidy) on the lth commodity. As is conventional in the optimal taxation literature, total tax revenues are kept invariant to the tax reform. Revenue neutrality of the tax reform requires that
Assume that the government's tax reform increases the tax rate on the jth commodity and uses the proceeds to decrease the tax rate (or to increase the subsidy) on the lth commodity. As is conventional in the optimal taxation literature, total tax revenues are kept invariant to the tax reform. Revenue neutrality of the tax reform requires that
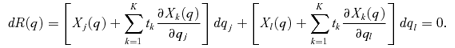 (4)
(4)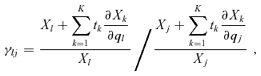 (5)
(5)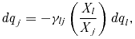 (6)
(6)3. measuring poverty and social welfare
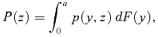 (7)
(7)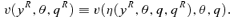 (8)
(8)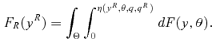 (9)
(9)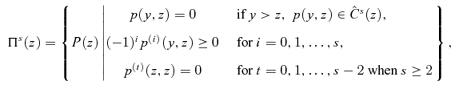 (10)
(10)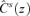 is the set of functions that are s-time piecewise differentiable10 over [0, z], and where the superscript (s) stands for an sth-order derivative with respect to y. We will return very shortly to the interpretation of the derivative assumptions.
is the set of functions that are s-time piecewise differentiable10 over [0, z], and where the superscript (s) stands for an sth-order derivative with respect to y. We will return very shortly to the interpretation of the derivative assumptions.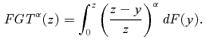 (11)
(11)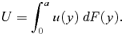 (12)
(12)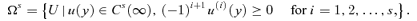 (13)
(13)It is useful at this point to provide a normative interpretation of the different classes of indices of poverty and social welfare. When s≥ 1, poverty indices weakly decrease (p(1)(y, z) ≤ 0) whereas welfare indices weakly increase (u(1)(y) ≥ 0) when an individual's income increases. These indices are thus Paretian but they also obey the well-known symmetry or anonymity axiom: Interchanging any two individuals' incomes leaves unchanged the poverty and social welfare indices. Ordering two distributions of living standards over the first-order classes of indices is equivalent to making the living standards “parade” simultaneously alongside each other, and verifying if one parade weakly dominates the other (this exercise was first suggested by Pen, 1971, chapter III). For poverty comparisons, the distributions of living standards are simply censored at z. For simplicity, we will refer to first-order welfare-improving tax reforms as “Pen-improving tax reforms.”
When s≥ 2, poverty indices are convex and welfare indices are concave. They must thus respect the Pigou–Dalton principle of transfers,12 which postulates that a mean-preserving transfer of income from a higher-income person to a lower-income person constitutes a social improvement, in the form of increasing social welfare or decreasing poverty. We follow the lead of Mayshar and Yitzhaki (1995) by denoting as “Dalton-improving tax reforms” those reforms that will be found to be second-order welfare improving.
By their third-order derivative, the poverty and social welfare indices that belong to Π3 and Ω3 must also be sensitive to favorable composite transfers. These transfers are such that a beneficial Pigou–Dalton transfer within the lower part of the distribution, accompanied by an adverse Pigou–Dalton transfer within the upper part of the distribution, will add to social welfare, provided that the variance of the distribution is not increased. Kolm (1976) was the first to introduce this condition into the inequality literature, and we therefore refer for simplicity to third-order welfare improving tax reforms as “Kolm-improving tax reforms.”Kakwani (1980) subsequently adapted this principle to poverty measurement.13
For the interpretation of higher orders of dominance, we can use the generalized transfer principles of Fishburn and Willig (1984). For s≥ 4, for instance, consider a combination of two exactly opposite and symmetric composite transfers, the first one being favorable and occurring within the lower part of the distribution, and the second one being unfavorable and occurring within the higher part of the distribution. Because the favorable composite transfer occurs lower down in the income distribution, indices that are members of the Π4 and Ω4 classes will respond favorably to this combination of composite transfers. Generalized higher-order transfer principles essentially postulate that, as s increases, the weight assigned to the effect of transfers occurring at the bottom of the distribution also increases. Blackorby and Donaldson (1978) describe these indices as becoming more Rawlsian. Thus, as shown in Davidson and Duclos (2000) for poverty indices, when s→∞ only the lowest income counts, although this result does not generalize to welfare dominance, as shown in Duclos and Makdissi (2004) and as will also appear later.
4. identifying socially improving tax reforms
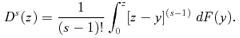 (14)
(14)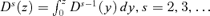 , and with D1(z) =F(z). More generally, in real income space we have
, and with D1(z) =F(z). More generally, in real income space we have
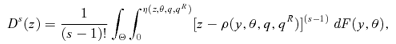 (15)
(15)Dominance curves are therefore just sums of powers of poverty gaps. They can thus be interpreted as ethically weighted sums of individual deprivation. For s= 1, we have what is often called the “poverty incidence curve”; D2(z) gives the “poverty deficit” or the “poverty intensity” curve. The larger the value of s, the larger the weights on the largest poverty gaps. Clearly, as can be seen by comparing (11) and (14), dominance curves have a convenient link with the FGT indices since FGTα(z) = (α)!z−α Dα+1(z).
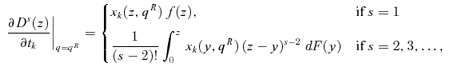 (16)
(16)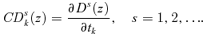 (17)
(17)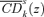 , are just the above CD curves for good k normalized by the average consumption of that good:
, are just the above CD curves for good k normalized by the average consumption of that good:
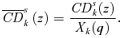 (18)
(18) curves are thus the ethically weighted (or social) cost of taxing k as a proportion of the average welfare cost. Note that the social cost depends on s and z. By (16),
curves are thus the ethically weighted (or social) cost of taxing k as a proportion of the average welfare cost. Note that the social cost depends on s and z. By (16), 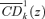 only takes account of the consumption pattern of those precisely at z. The
only takes account of the consumption pattern of those precisely at z. The 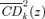 curve gives the share in the total consumption of k of those individuals with income less than z. For s= 3, 4, … , greater weight is given to the shares of those with higher poverty gaps. For z < a, the pattern of consumption and the welfare cost for some may be ignored in the computation of the social cost of taxing k. The social and average welfare cost coincide only when s= 2 and z≥a, since we have
curve gives the share in the total consumption of k of those individuals with income less than z. For s= 3, 4, … , greater weight is given to the shares of those with higher poverty gaps. For z < a, the pattern of consumption and the welfare cost for some may be ignored in the computation of the social cost of taxing k. The social and average welfare cost coincide only when s= 2 and z≥a, since we have 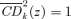 for all z≥a and all k.
for all z≥a and all k.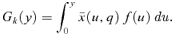 (19)
(19)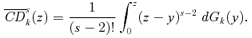 (20)
(20)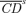 curves are FGTα indices (multiplied by a factor of zs−2/(s− 2)!), using α=s− 2 and a transformed income distribution Gk that weights individuals by their share in the total consumption of the good k. When multiplied by (s− 1)!/zs−1, the CD curves for s=α+ 1 have the convenient feature of providing the impact on the FGTα(z) indices of a marginal increase in the price of good k. This is important in its own right given the popularity of the FGT class of poverty indices.
curves are FGTα indices (multiplied by a factor of zs−2/(s− 2)!), using α=s− 2 and a transformed income distribution Gk that weights individuals by their share in the total consumption of the good k. When multiplied by (s− 1)!/zs−1, the CD curves for s=α+ 1 have the convenient feature of providing the impact on the FGTα(z) indices of a marginal increase in the price of good k. This is important in its own right given the popularity of the FGT class of poverty indices.Most importantly it would seem, CD curves can be used to test whether tax reforms are poverty or welfare improving. This is shown in Theorems 1 and 2, where γ is defined as in (5).
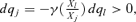 to be s-order poverty improving, that is, to decrease poverty weakly for all P(z) ∈Πs(z), for all z∈[0, z+] and for a given s∈{1, 2, 3, … }, is that
to be s-order poverty improving, that is, to decrease poverty weakly for all P(z) ∈Πs(z), for all z∈[0, z+] and for a given s∈{1, 2, 3, … }, is that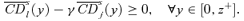 (21)
(21)Proof See the Appendix.
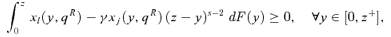 (22)
(22)Note that for s larger than 2, the  curves in (21) use poverty gaps (z−y) as weights on consumption patterns. But this procedure does not require more sampling information than for the construction of tests with lower values of s since the sample values of y are also needed for s= 1 and s= 2. Note also that for s larger than 2, one must use in (20) the value of z both in the upper bound of the integral and in the integrand itself. Further, and as is clear from (10), the ethical conditions imposed on Πs(z) are more demanding as s increases.
curves in (21) use poverty gaps (z−y) as weights on consumption patterns. But this procedure does not require more sampling information than for the construction of tests with lower values of s since the sample values of y are also needed for s= 1 and s= 2. Note also that for s larger than 2, one must use in (20) the value of z both in the upper bound of the integral and in the integrand itself. Further, and as is clear from (10), the ethical conditions imposed on Πs(z) are more demanding as s increases.
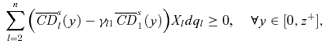 (23)
(23)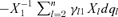 .
.Yitzhaki and Lewis (1996) also hint to an adaptation of their framework to poverty analysis, but it is less straightforward to do so than with CD curves. This is because poverty measurement censors well-being at poverty lines, whereas the tools used by Yitzhaki and Lewis (1996) censor the population at percentiles. One advantage of the CD curves over the concentration ones is indeed to focus on the consumption patterns of those under monetary thresholds, not on those who belong to certain percentiles of the population, as is more common in the inequality literature for instance. From a statistical perspective, censoring over percentiles has the additional disadvantage of introducing sampling variability over the value of the threshold—the value of p=F(z).
For welfare dominance, a theorem similar to Theorem 1 also applies.
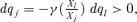 to be s-order welfare improving, that is, to increase social welfare weakly for all W∈Ωs and for a given s∈{1, 2, 3, … }, is that
to be s-order welfare improving, that is, to increase social welfare weakly for all W∈Ωs and for a given s∈{1, 2, 3, … }, is that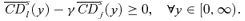 (24)
(24)Proof See the Appendix.
The only difference between the social improvement conditions of Theorems 1 and 2 is that the social-welfare test extends over the entire space [0, ∞), whereas the poverty test is limited to the range of potential poverty lines [0, z+]. For γ= 1, Theorem 1 says that the tax reform will reduce poverty in an ethically robust manner if the  curve of good l is higher than the
curve of good l is higher than the  curve of good j for every poverty line under z+. When the range of poverty lines is unbounded, Theorem 2 extends such poverty improvement to (global) welfare improvement. For γ≠ 1, one simply translates the
curve of good j for every poverty line under z+. When the range of poverty lines is unbounded, Theorem 2 extends such poverty improvement to (global) welfare improvement. For γ≠ 1, one simply translates the  curve of good j by the economic efficiency parameter γ before checking again the ordering of the
curve of good j by the economic efficiency parameter γ before checking again the ordering of the  curves up to the maximum poverty line. Ethical robustness of poverty reduction implies that poverty will be reduced by the tax reform for all choices of poverty indices within Πs(z) and for all choices of poverty lines within [0, z+]. Ethical robustness of welfare increase means that social welfare will be increased by the tax reform for all choices of social welfare functions in Ωs. A tax reform is Pen improving, Dalton improving, and Kolm improving if (24) holds for s= 1, 2, or 3, respectively.
curves up to the maximum poverty line. Ethical robustness of poverty reduction implies that poverty will be reduced by the tax reform for all choices of poverty indices within Πs(z) and for all choices of poverty lines within [0, z+]. Ethical robustness of welfare increase means that social welfare will be increased by the tax reform for all choices of social welfare functions in Ωs. A tax reform is Pen improving, Dalton improving, and Kolm improving if (24) holds for s= 1, 2, or 3, respectively.
5. critical poverty lines and efficiency ratios
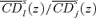 of normalized consumption dominance curves can be interpreted as the distributive benefit of taxing j instead of l. To see why, assume again an increase in the tax on good j and thus a fall in the price of good l. The socially weighted gain from this fall in ql, as a proportion of the average welfare gain, is given by
of normalized consumption dominance curves can be interpreted as the distributive benefit of taxing j instead of l. To see why, assume again an increase in the tax on good j and thus a fall in the price of good l. The socially weighted gain from this fall in ql, as a proportion of the average welfare gain, is given by 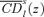 , which is therefore an indicator of the distributive benefit of taxing j. The same naturally holds for the distributive benefit of taxing l, which is given by
, which is therefore an indicator of the distributive benefit of taxing j. The same naturally holds for the distributive benefit of taxing l, which is given by 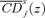 . Denote this distributive benefit ratio as
. Denote this distributive benefit ratio as 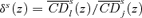 . If
. If 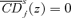 , the relative distributive benefit of taxing j is then effectively infinite, but for tractability we will then define it as γ++, which we may set to as large a finite value as we wish. δs(z) is thus given by
, the relative distributive benefit of taxing j is then effectively infinite, but for tractability we will then define it as γ++, which we may set to as large a finite value as we wish. δs(z) is thus given by
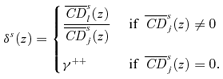 (25)
(25)Note that δ1(z) is a normalized ratio of Engel curves at income z. More precisely, it is the ratio, at z, of the share of good l over the share of good j, divided by the ratio of the average shares over the entire population.
Thus, δs(z) is the distributive benefit of taxing j relative to that of taxing l. Recall that γ is the economic cost of taxing j relative to that of taxing l. Comparing distributive benefit δs(z) to economic cost γ is crucial in determining whether a tax reform that increases tj and decreases tl is socially improving. We can indeed re-write the conditions of Theorems 1 and 2 by checking whether δs(z) ≥γ for all z∈[0, z+] and for all z∈[0, ∞) (Equations (21) and (24)), respectively. In words, a tax reform is s-order socially improving if its distributive benefit exceeds its economic cost over a range of alternative poverty lines. Note that when preferences are identical and homothetic, then by (19)Gj(y) =Gl(y) for all y, and therefore δs(z) = 1 whatever the values of z and s. There is then no distributive benefit to the tax reform whatever the social welfare or poverty objectives. The optimal tax system is then one in which the marginal deadweight loss of taxation is the same across the two goods.
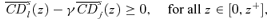 (26)
(26) and
and  are shown on Figure 1. Condition (26) is clearly also valid for all other values of γ < γ+. Hence, either (26) also holds for all superior values of γ > γ+, in which case we must have that δs(z) =γ++ for all z∈[0, z+], or there exists a critical value of γ beyond which (26) does not hold everywhere over [0, z+], and this is defined by
are shown on Figure 1. Condition (26) is clearly also valid for all other values of γ < γ+. Hence, either (26) also holds for all superior values of γ > γ+, in which case we must have that δs(z) =γ++ for all z∈[0, z+], or there exists a critical value of γ beyond which (26) does not hold everywhere over [0, z+], and this is defined by 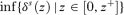 . Denoting this critical economic efficiency threshold as γs(z+), we have
. Denoting this critical economic efficiency threshold as γs(z+), we have
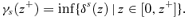 (27)
(27)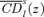 and
and 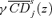 cross at z=z+.
cross at z=z+.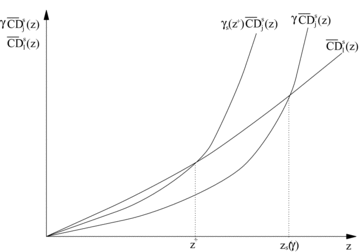
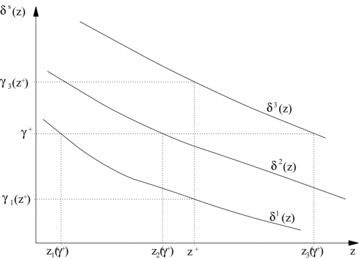
CD curves and critical social efficiency parameters
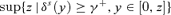 .14 We may then define zs(γ+) as
.14 We may then define zs(γ+) as
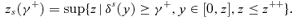 (28)
(28)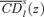 and
and 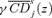 . Equations (27) and (28) say that increasing tj and decreasing tl is socially improving so long as γ and z are not allowed to exceed certain critical thresholds, which depend on the order of ethical dominance s. For a given γ+ and z+, zs(γ+) and γs(z+) give respectively the critical upper poverty line and the critical economic efficiency ratio up to which the tax reform is necessarily s-order poverty improving.
. Equations (27) and (28) say that increasing tj and decreasing tl is socially improving so long as γ and z are not allowed to exceed certain critical thresholds, which depend on the order of ethical dominance s. For a given γ+ and z+, zs(γ+) and γs(z+) give respectively the critical upper poverty line and the critical economic efficiency ratio up to which the tax reform is necessarily s-order poverty improving.z s (γ+) also gives the first poverty line (starting from z= 0) at which a poverty analyst using an FGTs−1(z) poverty index would be exactly indifferent to the tax reform when the MECF ratio is given by γ+. At all lower poverty lines, the FGT poverty analyst would choose increasing tj, and at poverty lines just higher than zs(γ+) he would prefer decreasing tj. Alternatively, γs(z+) gives the MECF ratio for which a FGTs−1 (z+) analyst would be exactly indifferent between reallocating or not the burden of indirect taxation across the goods j and l. At lower values of γ, the FGT analyst prefers taxing j further; at higher values, he prefers taxing l further.
6. discussion
Two points are worth mentioning at the outset. First, although notationally and expositionally more complicated, it would not be analytically much more difficult to allow for general equilibrium effects from changes in t. This would involve considering changes in producer prices, with effects on the welfare of producers, which would typically feed into changes in the consumer and the producer prices of goods other than those whose tax rates are changed by the government. The analysis would then take into account the sum of the welfare effects of the marginal changes in the various consumer and producer prices. We hope to consider such a generalization in future work.
Second, the tools developed above are in principle strictly limited to the analysis of infinitesimal price changes. For changes in tax rates that are not infinitely small, the impact of a change in tk on an exact measure of individual welfare is not precisely given by the pre-reform observed demand of good k times the change in tk. The proportional difference between the exact measure and the inexact measure that we use is approximately equal to one half the compensated price elasticity of good k times dtk/dqk. Hence, for a compensated price elasticity of 1, a 5% increase in the price of a good k leads approximately to a 2.5% error in the estimate of consumer welfare change when one uses the pre-reform consumption of k to compute that estimate. For many purposes, this error would seem relatively small.
6.1. Efficiency and Poverty and Welfare Improvements A tax reform cannot be Pen improving when γ≥ 1, as Lemma A.1 shows in the Appendix. Pen-improving tax reforms are, however, theoretically possible so long as γ < 1. Yitzhaki and Thirsk (1990) and Yitzhaki and Slemrod (1991) find that if γ is larger than one, a tax reform cannot be Dalton improving, a result that is also shown in Lemma A.2 in the Appendix. The proof of Proposition 2 also shows that γs(∞) ≤ 1 for any s= 3, 4, … Thus, for a reform to be welfare improving at any ethical order requires that it also be economically efficient, namely, that it weakly decreases the average deadweight loss.
A tax reform may, however, be poverty improving at any order—even at the first—even when γ > 1. For first- and second-order poverty improvement, the excess burden or economic efficiency cost of the reform then has to be paid by those households whose income is above the maximum poverty line z+, and to whose change in well-being poverty analysts are ethically indifferent. More surprisingly perhaps, for ethical orders s= 3, 4, … , a tax reform may be poverty improving when γ > 1 even when z+ > a (which says that all can then be considered poor, though not equally poor). We sum up these results in the following remark.
Remark 1 Welfare improvement of any order requires economic efficiency. Economic efficiency is not, however, needed for poverty improvement; for s > 2 this is true even in cases in which everyone may be considered poor.
If a tax reform is s-order poverty improving up to some z+, then it is also poverty improving up to z+ at the s+ 1 order (Lemma A.3). This is because a CD curve of order s can be obtained as the integral of the CD curve of order s− 1, as in the usual stochastic dominance setting (see Makdissi and Wodon, 2002, p. 230) and as is shown in Equation (A.5) in the proof of Lemma A.3. Lemma A.3 also says that if γs(z+) < γ++ and if there is strict dominance over a bottom range of z, then γs+1(z+) > γs(z+), meaning that, as the order of ethical dominance increases, economic efficiency becomes less constraining. Increasing the order of dominance also increases the range of poverty lines over which a reform is poverty improving. Indeed, if zs(γ+) < z++ and if there is strict dominance over a bottom range of z, then zs(γ+) < zs+1(γ+) (see Lemma A.4). Finally, if there is poverty improvement over a bottom range that extends to z+, with strict dominance over at least part of that range, then for any other finite threshold z+, there will also be poverty improvement for a sufficiently large order s (this is by lemma 1 of Davidson and Duclos, 2000).
These relationships are shown in Figure 2 using the distributive benefit ratios of Equation (25). When a reform's distributive benefit δs(z) over [0, z+] exceeds its economic cost γ, the reform is deemed poverty improving. At order s= 1, this is the case in Figure 2 for all γ up to γ1(z+). It is also necessarily true for all higher orders s= 2, 3, … . It can also be seen that the distributive benefit increases with s over [0, z+], which then graphically means that γs(z+) also rises with s ({e.g.}, γ3(z+) > γ1(z+) in Figure 2). Alternatively, for a given γ+, the critical poverty line zs(γ+) (up to which the distributive benefit is higher than the economic cost) increases with s; in Figure 2, this is shown by z3(γ+) > z2(γ+) > z1(γ+).
distributive benefit and economic efficiency
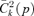 :
:
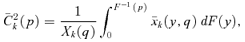 (29)
(29)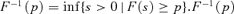 is often called the p-quantile, that is, roughly speaking, the income of the individual whose rank is p. Hence,
is often called the p-quantile, that is, roughly speaking, the income of the individual whose rank is p. Hence, 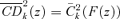 .
.There thus exists a parallel between the 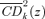 and the usual concentration curves. The
and the usual concentration curves. The 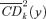 curve gives the share in good k of those below y, whereas
curve gives the share in good k of those below y, whereas 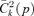 yields the share in k of those with rank p or below. This is illustrated in Figure 3. The northeast quadrant shows the distribution function p=F(z), the northwest quadrant shows the concentration curve, and the southeast quadrant shows the consumption dominance curve of order 2. The concentration and consumption curves are linked by the 45-degree line of the southwest quadrant. This is shown by the two rectangles that are also drawn, by which
yields the share in k of those with rank p or below. This is illustrated in Figure 3. The northeast quadrant shows the distribution function p=F(z), the northwest quadrant shows the concentration curve, and the southeast quadrant shows the consumption dominance curve of order 2. The concentration and consumption curves are linked by the 45-degree line of the southwest quadrant. This is shown by the two rectangles that are also drawn, by which 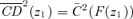 and
and 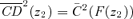 .
.
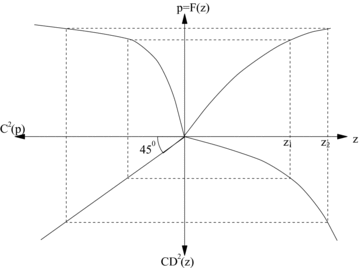
CD and concentration curves
Concentration curves thus act as dual  curves, just as it is well known that Generalized Lorenz curves15 act as dual D2(z) dominance curves. With the dual
curves, just as it is well known that Generalized Lorenz curves15 act as dual D2(z) dominance curves. With the dual 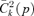 curves, Dalton improvement is tested by checking
curves, Dalton improvement is tested by checking 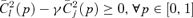 . If that condition is met, then condition (24) is also met for s= 2 and the reform then leads to a distribution that “generalized-Lorenz” dominates the status quo.
. If that condition is met, then condition (24) is also met for s= 2 and the reform then leads to a distribution that “generalized-Lorenz” dominates the status quo.
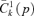 :
:
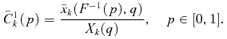 (30)
(30)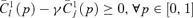 . As can be easily seen, this is equivalent to checking
. As can be easily seen, this is equivalent to checking 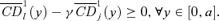 Similarly, first-order poverty improvement can be tested by checking whether
Similarly, first-order poverty improvement can be tested by checking whether 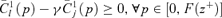 . Using primal as opposed to dual curves has, however, the advantage of simplifying testing procedures for dominance orders higher than 2.16 Apart from this, the empirical application of these two approaches makes similar demands on the data, although their comparative statistical efficiency is a topic better left for future investigation.
. Using primal as opposed to dual curves has, however, the advantage of simplifying testing procedures for dominance orders higher than 2.16 Apart from this, the empirical application of these two approaches makes similar demands on the data, although their comparative statistical efficiency is a topic better left for future investigation.6.3. Pareto Improving Tax Reforms We mentioned above that Pen improvement implies robustness of social welfare increase over all social welfare functions that are increasing and anonymous (or symmetric) in real incomes. Pareto improvement does not, however, impose anonymity as a property of the social evaluation exercise. This difference between these two improvement concepts may be subtle, but it is fundamental to the usefulness of practical searches for socially improving tax reforms.
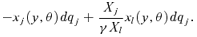 (31)
(31)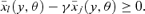 Thus:
Thus: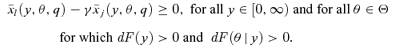 (32)
(32)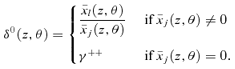 (33)
(33)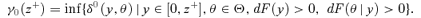 (34)
(34)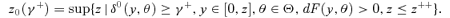 (35)
(35)An arguably more important issue is whether in practice γ0(z) is significantly lower than γ1(z+), or whether z0(γ+) is substantially lower than z1(γ+). We can expect condition (32) to be very restrictive empirically (as has been argued before17). In fact, it would not be misleading to suggest that a search for Pareto-improving tax reforms will normally be doomed to failure. This is due to the considerable heterogeneity of preferences typically found in the observed consumption patterns of a real population of individuals. With Pareto improvement as a social welfare constraint, it will be very difficult to identify any socially improving movement away from the current tax system, thus giving a sort of “vetoing status” to existing tax systems, whatever the defects of these systems may be. Furthermore, the identification of Pareto-improving tax reforms requires the observation of consumption patterns that are free of measurement errors.18 This is less of a problem for Pen improvement since it is the expected value of consumption patterns that matters, and in computing those expected values the measurement errors are (at least partially) averaged out. Whether the concept of Pen improvement eases the search for socially improving reforms is ultimately, of course, an empirical issue, to which we will revert later.
7. empirical illustration
This section briefly illustrates the above normative and statistical tools to household-level data from Mexico's 1996 ENIGH, a nationally representative survey with detailed income and consumption modules. In 1996, there was a VAT exemption on food expenditures in Mexico. The rationale for the exemption is apparent in Figure 4, which provides (normalized) expected food and nonfood expenditures  and
and  at different incomes z. Per capita incomes (on the horizontal axis) have been normalized by cost of living indices (the regional poverty lines used in the latest poverty assessment for Mexico completed at the World Bank), so that cost-of-living differences between urban and rural areas are taken into account. A value of one indicates that a household is at the level of the urban/rural poverty line. With these poverty lines, 60.9% of the population is poor (those with per capita income below z= 1). The estimators and associated sampling distributions are those developed in Duclos et al. (2004). Note that the illustration does not address issues related to administrative distortions; the policy recommendations may thus not be immediately implementable.
at different incomes z. Per capita incomes (on the horizontal axis) have been normalized by cost of living indices (the regional poverty lines used in the latest poverty assessment for Mexico completed at the World Bank), so that cost-of-living differences between urban and rural areas are taken into account. A value of one indicates that a household is at the level of the urban/rural poverty line. With these poverty lines, 60.9% of the population is poor (those with per capita income below z= 1). The estimators and associated sampling distributions are those developed in Duclos et al. (2004). Note that the illustration does not address issues related to administrative distortions; the policy recommendations may thus not be immediately implementable.
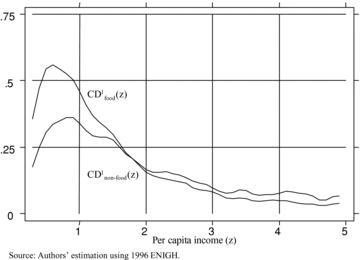
normalized CDcurves for food and nonfood expenditures, s= 1
The two 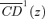 curves cross at
curves cross at 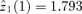 , which is also the critical first-order poverty line z1(γ) shown in the bottom panel of Table 1 for γ= 1. Note that the standard error of the sampling distribution of
, which is also the critical first-order poverty line z1(γ) shown in the bottom panel of Table 1 for γ= 1. Note that the standard error of the sampling distribution of 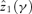 is estimated to be 0.099, which implies that a 95% confidence interval for the true value z1(γ) would be [1.60, 1.98]. Simply stated, this means that if γ= 1, we can be 95% certain that for any poverty line below 1.60 it is first-order poverty improving to implement a balanced-budget indirect tax reform by reducing at the margin taxes (or providing a subsidy for) on food expenditures and increasing taxes on nonfood expenditures.
is estimated to be 0.099, which implies that a 95% confidence interval for the true value z1(γ) would be [1.60, 1.98]. Simply stated, this means that if γ= 1, we can be 95% certain that for any poverty line below 1.60 it is first-order poverty improving to implement a balanced-budget indirect tax reform by reducing at the margin taxes (or providing a subsidy for) on food expenditures and increasing taxes on nonfood expenditures.
| Value of second-order CD curves at various poverty lines z | |||
|---|---|---|---|
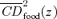 |
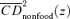 |
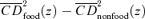 |
|
| z= 0.5 | 0.141 | 0.070 | 0.071 |
| (0.004) | (0.002) | (0.002) | |
| z= 1.0 | 0.410 | 0.247 | 0.163 |
| (0.007) | (0.006) | (0.004) | |
| z= 2.0 | 0.700 | 0.504 | 0.196 |
| (0.007) | (0.010) | (0.006) | |
| Critical efficiency ratios γs(z+) for different maximum poverty lines z+and for different orders of dominance s | |||
| z += 0.5 (28.5% of population covered) | z += 1 (60.9% of population covered) | z += 2 (85.0% of population covered) | |
| γ1(z+) | 1.782 | 1.354 | 0.947 |
| (0.032) | (0.027) | (0.029) | |
| γ2(z+) | 2.021 | 1.657 | 1.390 |
| (0.041) | (0.025) | (0.018) | |
| γ3(z+) | 2.140 | 1.822 | 1.551 |
| (0.049) | (0.028) | (0.020) | |
| Critical poverty lines zs(γ) for different ratios of economic efficiency costs γ and for different orders of dominance s(*) | |||
| γ= 0.5 | γ= 1.0 | γ= 1.5 | |
| z 1(γ) | 4.272 | 1.793 | 0.752 |
| (0.127) | (0.099) | (0.030) | |
| z 2(γ) | – | – | 1.483 |
| – | – | (0.156) | |
| z 3(γ) | – | – | 2.347 |
| – | – | (0.145) | |
- Source: Authors' estimation using 1996 ENIGH. Sample size is 14,022 observations.
- Standard errors in parentheses. (*) Only poverty lines higher than 0.25 are considered.
However, and as expected, this reform is not Pen improving for γ+= 1 since we do find a critical poverty line at which the two curves intersect. Furthermore, although a first-order poverty improving (including headcount-reducing) food/nonfood tax reform is feasible for poverty lines below z1(1), a substantial share of the poor would lose from such a reform. Given the average food and nonfood expenditure shares, with γ= 1 a one percentage point tax reduction for food must be compensated by a 0.340 percentage point tax increase on nonfood expenditures for budget neutrality. Hence, any poor household whose food expenditure share is below one fourth will lose from such a reform. The relative importance of these losers appears in Figure 5, which gives the cumulative population share and the cumulative share of losers as functions of the poverty line. The ratio of the two cumulative shares represents the share of the population below a given poverty line that loses from the reform. It turns out that 19.0% of the population below z= 1 and 14.3% of the population below z= 0.5 would lose from this hypothetical tax reform. Hence, this reform is clearly not Pareto improving, and would not be so even if we were to censor the assessment of its impact at a poverty line. In fact—and as anticipated in Section 6.3—Pareto-improving food and nonfood tax reforms are virtually impossible, whatever the MECF economic efficiency parameter. This is due to the fact that for both food and nonfood expenditures, there are households with either zero or very low expenditure levels across the income distribution, so that  is zero for virtually any z+.
is zero for virtually any z+.
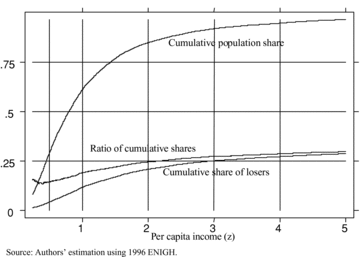
share of losers from food/nonfood tax reform
Taxing nonfood expenditures and reducing taxes (or providing subsidies) for food expenditures is Dalton improving for a wide range of values of γ. This is demonstrated in Figures 6 and 7—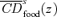 is everywhere above
is everywhere above  for s= 2 and 3. The top panel of Table 1 gives the values of the
for s= 2 and 3. The top panel of Table 1 gives the values of the 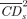 curves for z= 0.5, 1, and 2, as well as the difference between the curves (all differences are statistically greater than zero). For s= 2, these curves represent the cumulative shares of food and nonfood expenditures accounted for by those with per capita income below a certain level. For example, the population below z= 1 accounts for 41.0% of total food expenditures and 24.7% of total nonfood expenditures. Figures 6 and 7 also provide the distributive benefit ratio δ2(z) and δ3(z). As long as the economic cost γ of taxing food items relative to nonfood items is below δ2(z), taxing nonfood items to give relief to food items is beneficial.
curves for z= 0.5, 1, and 2, as well as the difference between the curves (all differences are statistically greater than zero). For s= 2, these curves represent the cumulative shares of food and nonfood expenditures accounted for by those with per capita income below a certain level. For example, the population below z= 1 accounts for 41.0% of total food expenditures and 24.7% of total nonfood expenditures. Figures 6 and 7 also provide the distributive benefit ratio δ2(z) and δ3(z). As long as the economic cost γ of taxing food items relative to nonfood items is below δ2(z), taxing nonfood items to give relief to food items is beneficial.
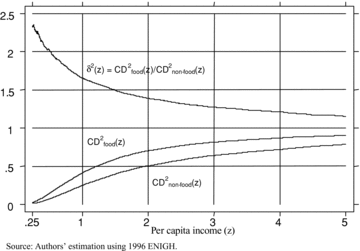
normalized CDcurves for food and nonfood expenditures, s= 2
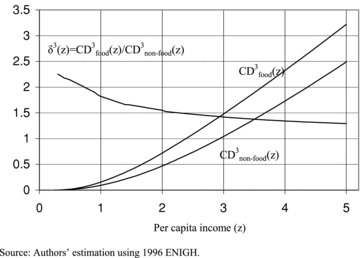
normalized CDcurves for food and nonfood expenditures, s= 3
The critical efficiency ratios γs(z+) under which the tax reform is Dalton improving are provided in the middle panel of Table 1. For s= 2, γ2(z+) is equal to, respectively, 2.021 for z+= 0.5, 1.657 for z+= 1, and 1.390 for z+= 2. If, following standard practice in Latin America, we consider those with per capita income below half the poverty line as extreme poor, the tax reform would reduce all distributive-sensitive poverty indices for the extreme poor even if the economic cost of nonfood taxation were 100% higher than that of food taxation.
The bottom panel of Table 1 also gives the critical poverty lines 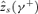 under which the tax reform would remain poverty improving with various MECF ratios. For example, with γ+= 1.5, the tax reform is second-order poverty reducing up to a poverty line of 0.752 (with a standard error of 0.03). For γ+= 1, there is no critical poverty line for s= 2 or higher. This is due to the fact that
under which the tax reform would remain poverty improving with various MECF ratios. For example, with γ+= 1.5, the tax reform is second-order poverty reducing up to a poverty line of 0.752 (with a standard error of 0.03). For γ+= 1, there is no critical poverty line for s= 2 or higher. This is due to the fact that 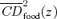 and
and 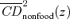 do not intersect. Remember also that when multiplied by
do not intersect. Remember also that when multiplied by 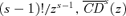 gives the impact on the FGTs−1(z) poverty indices of a marginal change in the price of a good or a marginal increase in the tax on that good. Since the differences between the
gives the impact on the FGTs−1(z) poverty indices of a marginal change in the price of a good or a marginal increase in the tax on that good. Since the differences between the 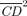 curves are statistically significant for the values of z considered in Table 1, a tax reform would lead to a statistically significant reduction in the poverty gap whatever these values of z. This does not necessarily mean that universal food subsidies are the best policy option for poverty reduction. In Mexico, universal subsidies for tortillas have recently been terminated, with the savings used for better-targeted social programs, including school stipends targeted to poor children living in poor rural areas. Still, within the options provided by indirect tax reforms, it may be Dalton improving to increase the tax on nonfood expenditures while providing subsidies for food expenditures.
curves are statistically significant for the values of z considered in Table 1, a tax reform would lead to a statistically significant reduction in the poverty gap whatever these values of z. This does not necessarily mean that universal food subsidies are the best policy option for poverty reduction. In Mexico, universal subsidies for tortillas have recently been terminated, with the savings used for better-targeted social programs, including school stipends targeted to poor children living in poor rural areas. Still, within the options provided by indirect tax reforms, it may be Dalton improving to increase the tax on nonfood expenditures while providing subsidies for food expenditures.
4-7 are provided for broad food and nonfood expenditure aggregates, but the tools can equally well be applied to more specific items. In Figure 8, we compare the 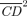 curves for a mixed bundle of food (including baby food, packaged food, deserts, drinks, and food consumed away from the home) and pasteurized milk. The estimated curves cross for a value of z slightly larger than the reference poverty line z= 1, but Table 2 (which is analogous to Table 1) indicates that the difference between the two curves is not statistically significant at z= 1 (and, similarly, that γ2(z+= 1) is not statistically larger than one). Still, since the
curves for a mixed bundle of food (including baby food, packaged food, deserts, drinks, and food consumed away from the home) and pasteurized milk. The estimated curves cross for a value of z slightly larger than the reference poverty line z= 1, but Table 2 (which is analogous to Table 1) indicates that the difference between the two curves is not statistically significant at z= 1 (and, similarly, that γ2(z+= 1) is not statistically larger than one). Still, since the 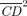 curve for milk is below that for the mixed bundle up to
curve for milk is below that for the mixed bundle up to 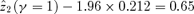 (allowing for a 95% confidence interval), it is certainly feasible with γ= 1 to reduce extreme poverty for all distributive-sensitive poverty indices by taxing milk and providing a subsidy for the items in the mixed-food bundle. Yet, since the second-order CD curves cross, this is not a Dalton-improving tax reform for γ= 1. It can be shown that this is also not a Kolm-improving tax reform for γ= 1 either, since the
(allowing for a 95% confidence interval), it is certainly feasible with γ= 1 to reduce extreme poverty for all distributive-sensitive poverty indices by taxing milk and providing a subsidy for the items in the mixed-food bundle. Yet, since the second-order CD curves cross, this is not a Dalton-improving tax reform for γ= 1. It can be shown that this is also not a Kolm-improving tax reform for γ= 1 either, since the 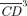 curves intersect as well, albeit at a higher value of z (as predicted by Lemma A.4).
curves intersect as well, albeit at a higher value of z (as predicted by Lemma A.4).
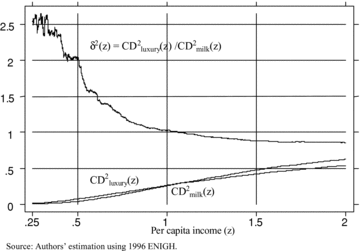
normalized CDcurves for mixed bundle and pasteurized milk, s= 2
| Value of second-order CD curves at various poverty lines z | |||
|---|---|---|---|
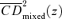 |
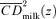 |
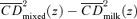 |
|
| z= 0.5 | 0.075 | 0.037 | 0.038 |
| (0.005) | (0.003) | (0.005) | |
| z= 1.0 | 0.263 | 0.256 | 0.007 |
| (0.009) | (0.008) | (0.010) | |
| z= 2.0 | 0.537 | 0.627 | −0.09 |
| (0.012) | (0.011) | (0.012) | |
| Critical efficiency ratios γs(z+) for different maximum poverty lines z+and for different orders of dominance s | |||
| z += 0.5 (28.5% of population covered) | z += 1 (60.9% of population covered) | z += 2 (85.0% of population covered) | |
| γ1(z+) | 1.222 | 0.8 | 0.705 |
| (0.080) | (0.043) | (0.072) | |
| γ2(z+) | 1.997 | 1.028 | 0.856 |
| (0.181) | (0.039) | (0.019) | |
| γ3(z+) | 2.214 | 1.256 | 0.946 |
| (0.250) | (0.059) | (0.025) | |
| Critical poverty lines zs(γ) for different ratios of economic efficiency costs γ and for different orders of dominance s (*) | |||
| γ= 0.5 | γ= 1.0 | γ= 1.5 | |
| z 1(γ) | 11.39 | 0.6 | 0.421 |
| (0.065) | (0.033) | (0.028) | |
| z 2(γ) | – | 1.062 | 0.613 |
| (0.212) | (0.083) | ||
| z 3(γ) | – | 1.623 | 0.795 |
| (0.140) | (0.052) | ||
- Source: Authors' estimation using 1996 ENIGH. Sample size is 14,022 observations.
- Standard errors in parentheses. (*) Only poverty lines higher than 0.25 are considered.
As in Table 1, Table 2 provides the critical efficiency ratios γ2(z+) and the critical poverty lines 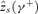 under which taxation of pasteurized milk and subsidies for the items in the mixed bundle is socially improving. As s increases, economic efficiency is clearly less of a constraint. This is apparent in the fact that γs(z+) increases with s (as anticipated by Lemma A.3). Again, building up the ethical content of the classes of poverty indices considered ({i.e.}, increasing s) increases the range of poverty lines and/or economic efficiency ratios over which the reform can confidently be deemed good for poverty reduction.
under which taxation of pasteurized milk and subsidies for the items in the mixed bundle is socially improving. As s increases, economic efficiency is clearly less of a constraint. This is apparent in the fact that γs(z+) increases with s (as anticipated by Lemma A.3). Again, building up the ethical content of the classes of poverty indices considered ({i.e.}, increasing s) increases the range of poverty lines and/or economic efficiency ratios over which the reform can confidently be deemed good for poverty reduction.
8. conclusion
This article shows how one can use simple Consumption Dominance curves to assess the social improvement of indirect marginal tax reforms. The methods are similar in spirit to checking for nonintersecting (second-order) concentration curves, but they are more general in that they enable the analyst to choose the order of ethical dominance in which he is interested and to censor individual welfare at some upper bound of poverty lines if so desired.
The proposed graphical tools have considerable normative appeal, in that they may be used to determine whether commodity-tax changes can be deemed to improve social welfare or decreasing poverty for large classes of social welfare and poverty indices and for broad ranges of poverty lines. They also provide detailed and useful descriptive information on the distribution of expenditures across the entire income distribution. The article further implements recently developed estimators of critical poverty lines and economic efficiency ratios that can be used to characterize socially improving tax reforms—as well as their sampling distribution. The methodology is illustrated using Mexican data.
Footnotes
 continuity assumption is made for analytical simplicity since it could be relaxed to include indices whose (s− 1)th derivative is discontinuous (and that are therefore not s-time piecewise differentiable).
continuity assumption is made for analytical simplicity since it could be relaxed to include indices whose (s− 1)th derivative is discontinuous (and that are therefore not s-time piecewise differentiable).
Appendix
A.1. Lemmas
Lemma A.1 γ1(a) < 1.
Lemma A.2 γ2(a) ≤ 1.
Proof Note that, by definition, δ2(a) = 1 since 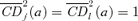 . Since
. Since 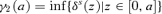 , it must be that γ2(a) ≤ 1. ▪
, it must be that γ2(a) ≤ 1. ▪
Lemma A.3 If a tax reform is s-order socially improving up to some z+, then it is also socially improving up to z+ at the s+ 1 order. Furthermore, if a tax reform is s-order socially improving up to some z+, and if there is strict s-order dominance over at least part of a bottom range of z∈[0, w], then γs+1(z+) ≥γs(z+), with strict inequality if γs(z+) < z++.
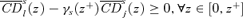 . For (s+ 1)-order social improvement, we consider the sign of
. For (s+ 1)-order social improvement, we consider the sign of 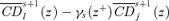 . Again, this equals
. Again, this equals
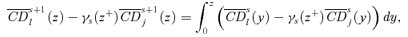 ((A.5))
((A.5))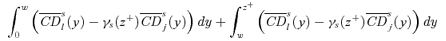 ((A.6))
((A.6))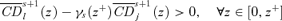 . Hence, it must be that γs+1(z+) ≥γs(z+), with strict inequality if γs(z+) < z++. ▪
. Hence, it must be that γs+1(z+) ≥γs(z+), with strict inequality if γs(z+) < z++. ▪Lemma A.4 Let a tax reform be s-order socially improving up to some zs(γ+), for some givenγ+, with strict dominance over at least part of [0, zs(γ+)]. Then, zs+1(γ+) ≥zs(γ+), with strict inequality if zs(γ+) < z++.
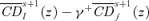 . This equals
. This equals
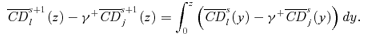 ((A.7))
((A.7))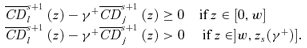 ((A.8))
((A.8))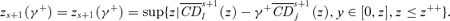 From (A.8), note that
From (A.8), note that 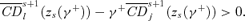 Hence, it must be that zs+1(γ+) > zs(γ+) if zs(γ+) is not constrained by the upper bound z++. ▪
Hence, it must be that zs+1(γ+) > zs(γ+) if zs(γ+) is not constrained by the upper bound z++. ▪Lemma A.5 γ0(z+) ≤γ1(z+) , with strict inequality if there is heterogeneity in the ratio of Engel curves for goods xl and xj at each y∈[0, z+] and if γ1(z+) < γ++.
Proof First, let γ1(z+) =γ++. This implies that δ1(y) =γ++, that 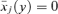 , and thus that
, and thus that 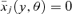 and δ0(y, θ) =γ++ for all θ for which dF(θ | y) > 0, and for all y∈[0, z+]. Hence, γ0(z+) =γ++≤γ1(z+).
and δ0(y, θ) =γ++ for all θ for which dF(θ | y) > 0, and for all y∈[0, z+]. Hence, γ0(z+) =γ++≤γ1(z+).
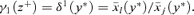 Let Θ1 and Θ2 be two exclusive and exhaustive subsets of preferences at y* with values of Engel curve ratios
Let Θ1 and Θ2 be two exclusive and exhaustive subsets of preferences at y* with values of Engel curve ratios 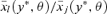 set respectively to ρ1(y*) and ρ2(y*) (a proof with an arbitrarily greater number of subsets follows along the same lines). Then, by definition,
set respectively to ρ1(y*) and ρ2(y*) (a proof with an arbitrarily greater number of subsets follows along the same lines). Then, by definition,
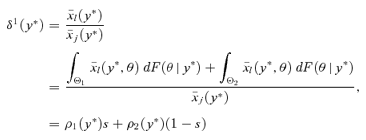
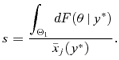 ((A.9))
((A.9))Lemma A.6 z 0(γ+) ≤z1(γ+) , with strict inequality if there is heterogeneity in the ratio of Engel curves for goods xl and xj at y=z1(γ+) and if z1(γ+) < z++.
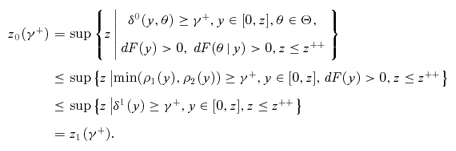
A.2. Proofs of Theorems
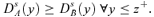 ((A.10))
((A.10))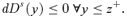 ((A.11))
((A.11))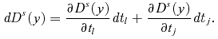 ((A.12))
((A.12))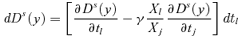 ((A.13))
((A.13))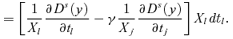 ((A.14))
((A.14))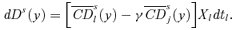 ((A.15))
((A.15))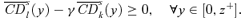 ((A.16))
((A.16))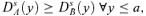 ((A.23))
((A.23))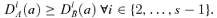 ((A.24))
((A.24))This test simplifies if you use a result of Duclos and Makdissi (2004). To see how, first define a binary relation >*s.
Definition A.1 D A (y) > *s DB(y) if and only if DiA(y) −DiB(y) > 0 for the smallest i≤s such that DiA(y) ≠DiB(y).
We then obtain the following lemma.
Lemma A.7 (Duclos and Makdissi, 2004) 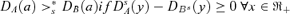 .
.
This establishes a link between the s-order dominance conditions over ℜ+ and the dominance conditions at the limit a of the distribution at some lower order. Note, moreover, that when DA(a) >*s DB(a), it must be that lim y→∞[DiA(y) −DiB(y)]≥ 0 for all i= 1, 2, … (see Duclos and Makdissi, 2003). We thus have:
Corollary A.1 If DsA(y) −DsB(y) ≥ 0 ∀y∈ℜ+, then lim y→∞[DiA(y) −DiB(y)]≥ 0 for all i≤s.
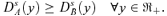 ((A.25))
((A.25))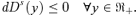 ((A.26))
((A.26))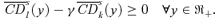 ((A.27))
((A.27))Note from Lemma A.2 that we cannot have Dalton improvement if γ > 1. Hence, by Corollary A.1, we cannot have higher-order social improvement either. ▪



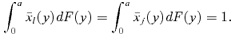
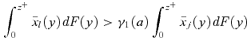
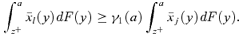
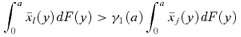
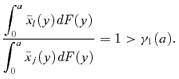
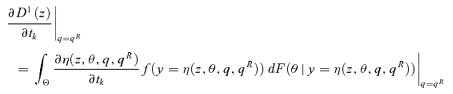
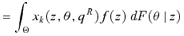
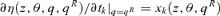 .
.