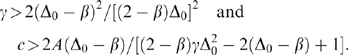Mergers in Multidimensional Competition
Abstract
Horizontal mergers are often driven by the desire to exploit R&D complementarities. We investigate the positive features of such a merger when oligopolists compete both in process R&D and on the product market. For a non-trivial degree of R&D complementarity, we show that the merger has the following intuitively appealing features independently of the strategic variable in market competition: insiders benefit; outsiders are harmed; and insiders end up larger than outsiders. These results contrast with those of traditional models of merger to achieve market power alone, which are known to be counterintuitive and sensitive to the mode of product market competition.
INTRODUCTION
A key feature of R&D investment is its public good aspect both within and across firms: use of a new technology in one plant does nothing to preclude its application to production elsewhere. Indeed, the total return to an R&D investment is greater, the more widely its results are disseminated across plants.1 The corporate structure of British Petroleum Amoco (BP), the world's second-largest integrated oil company, reveals the profitability gains from information pooling and the role played by integration in facilitating it: BP comprises around 100 semi-autonomous business units, which are encouraged to share information extensively through ‘peer assists’ (whereby units can call on personnel from other units to help solve operating problems).2 More specifically, it appears that horizontal mergers are often driven by the opportunities they create (via knowledge transfers between plants) for the exploitation of R&D complementarities. The experience of BP illustrates this: a central justification for the BP–Atlantic Richmond (ARCO) mega-merger, approved by the Federal Trade Commission in 2000, was that, by committing the firms to sharing their accumulated technical expertise, it would significantly reduce extraction costs at the enormous Prudhoe Bay oil field in Alaska.3
Using a framework of ‘multidimensional’ (two-stage) competition, where firms compete both in process R&D and on the product market, this paper analyses the use of horizontal mergers to exploit R&D complementarities between firms. A key contribution is that the size of the synergy benefit of merger, caused by the existence of R&D complementarities, is determined endogenously.4 We are concerned primarily with the conditions under which such arrangements are profitable for the participating (‘inside’) firms and with the implications of such mergers for the relative position of non-participating (‘outside’) firms.
Despite the apparently widespread use of horizontal merger to exploit complementarities in firms' R&D stocks, the formal literature on R&D pooling has focused almost exclusively on research joint ventures (RJVs), whereby firms share technological knowledge while, in principle, continuing to compete against each other in the product market.5 In addition to their empirical relevance, we justify our focus on horizontal mergers because in many cases RJVs may prove impossible to form, forcing firms to search for other methods of exploiting R&D complementarities. For example, firms participating in an RJV clearly have a strong incentive not to reveal all their R&D results to their partners. If an RJV is to achieve different results from thoroughgoing non-cooperative behaviour, this problem must be overcome. In principle, a solution is for the participants to contract out all R&D activities to a third party; however, in practice contracts are likely to be prohibitively costly to establish and enforce. In such cases horizontal merger, which precommits participating firms to sharing all their R&D outputs with other insiders (joint profit maximization), will be an attractive alternative to forming an RJV.1, 1
We model horizontal mergers motivated by the exploitation of R&D complementarities in a two-stage game played by oligopolistic firms, each producing a substitute brand of a differentiated good. In the first stage the firms choose how much to invest in process R&D, and in the second stage they compete on the product market. We solve the game backwards to isolate its subgame-perfect Nash equilibrium. Aside from our modelling of R&D complementarities, our setup is standard to allow for comparisons with the existing formal literature.8 The marginal cost of a firm that is not merged with another depends only on its own R&D investment. (There are no interfirm spillovers.) However, a merged firm's marginal cost is decreasing both in its own R&D level and (at a slower rate) in the combined R&D spending of other insiders. We restrict attention to a single bilateral merger, where two firms cooperate in both the R&D and production stages.9 Therefore, R&D complementarities are reflected in the fact that a merged firm's effective R&D stock is a weighted sum of its own spending and that of the other insider; this is the synergy effect of merger. The weight on the merger partner's R&D spending (the degree of R&D complementarity) depends on the technical closeness between brands. If production processes are quite similar (e.g. because brands are distinguished only by some non-technical attribute such as colour), we would expect a merged firm's effective R&D stock to be approximately the unweighted sum of both insiders' spending on R&D. On the other hand, if production processes are quite heterogeneous (e.g. because quite different machinery is used to produce different brands), we would expect an insider's effective R&D stock approximately to equal its own R&D spending.10
Our results stem from a comparison between the game's equilibria with and without a bilateral merger. They can be interpreted in relation to the findings of the canonical analyses of horizontal mergers under Cournot competition (Salant et al. 1983) and Bertrand competition (Deneckere and Davidson 1985), both of which took firms' marginal costs as identical and exogenously given. Moreover, a key contribution of our approach, the novelty of which is that mergers affect competition in two dimensions (R&D and the product market), is that it permits a solution to the well-known ‘merger paradox’. The merger paradox refers to the difficulty of constructing a model of partial horizontal mergers where (a) insiders generally gain, (b) outsiders generally lose and (c) insiders are larger (in sales terms) than outsiders in the post-merger equilibrium. We regard (a), (b) and (c) as intuitively appealing properties that any reasonable model of horizontal mergers should be capable of satisfying. Properties (a) and (b) seem desirable because mergers are both frequently proposed by firms and invariably fiercely opposed by outsiders.11 We advocate (c) because, as Perry and Porter (1985, p. 219) argue, it seems right that a merger, by pooling the insiders' assets, should make the integrated firm larger than its rivals. Unfortunately, when firms compete in only one dimension (on the product market), models of horizontal mergers under both Cournot and Bertrand competition have been unable simultaneously to satisfy criteria (a), (b) and (c).12 In particular, while insiders generally lose from merger under Cournot competition, under Bertrand they generally gain. These converse profitability effects for insiders are particularly troubling because they hinge on an unobservable characteristic of the market, the strategic variable in competition.
To gain an intuitive feeling for our results on the profitability effects of merger, consider how a merger affects the market equilibrium in stage 2. For a given distribution of R&D spending across brands, a merger exerts two opposing influences on insiders' behaviour in market competition. First, the traditional ‘market power’ (or ‘strategic’) effect reflects the insiders' attempts to move towards the monopoly solution. As is well known, under both Cournot and Bertrand competition the market power effect makes the insiders less aggressive. The second effect of merger on market competition, which works in the opposite direction, is the ‘R&D pooling’ effect. Under both Cournot and Bertrand behaviour, this makes the insiders more aggressive as they exploit R&D complementarities (between given R&D stocks) and their marginal costs fall. Which of the two effects dominates is determined by the degree of technical closeness between brands (i.e. R&D complementarity), which governs the strength of the R&D pooling effect relative to the market power effect.
In our linear model, quantities are strategic substitutes under Cournot competition but prices are strategic complements under Bertrand. Therefore, under Bertrand competition the R&D pooling effect benefits insiders but harms outsiders, whereas the market power effect benefits both types. Because both effects benefit insiders under Bertrand competition, the only question is whether outsiders gain or lose from merger. For low levels of technical closeness (R&D complementarity), the market power effect dominates, so all firms gain from merger; we label this the ‘Pareto gain’ case. As brands become technically closer (i.e. as the degree of R&D complementarity rises), the R&D pooling effect strengthens relative to the market power effect. Eventually, for sufficiently technically close brands, the R&D pooling effect dominates, so insiders gain from merger but outsiders lose; we label this the ‘intuitive outcome’.13
The profitability effects of merger are more complex under Cournot competition because the insiders do not always gain. As with Bertrand, the R&D pooling effect benefits insiders but harms outsiders under Cournot competition. However, the market power effect now works in precisely the opposite direction, harming insiders but benefiting outsiders. The polar cases, where one of the two effects of merger on market equilibrium obviously dominates, are clear. For low levels of technical closeness the market power effect dominates; insiders lose from merger but outsiders gain, á laSalant et al. (1983). For sufficiently technically close brands the R&D pooling effect dominates; insiders gain from merger but outsiders lose—the ‘intuitive outcome’. In between, for intermediate levels of technical closeness (R&D complementarity), the market power and R&D pooling effects are of ‘roughly equal’ strength, and all firms gain from merger—the ‘Pareto gain’ outcome.14
Our central result on the profitability effects of merger is that, for sufficiently technically close brands, bilateral mergers in multidimensional competition benefit the insiders but harm outsiders independently of the strategic variable in market competition. We refer to a post-merger equilibrium with these features as the ‘intuitive outcome’ because it fulfils ‘reasonable criteria’ (a) and (b) introduced above. The largeness of the areas in both strategy and parameter space over which our model generates the ‘intuitive outcome’ becomes a particularly valuable feature when contrasted with the profitability effects generated by ‘traditional’ models of merger to achieve market power alone, which are well known to be both counterintuitive and highly sensitive to the (unobservable) mode of product market competition.
Our results on the implications of merger for firm size can be understood by considering the determination of process R&D levels in stage 1. The profitability of extra R&D investment depends on the size of the resulting process innovation and on the level of output to which that innovation will be applied in production. A merger does not alter the relationship between R&D investment and cost reduction for outsiders, but it enhances the efficiency of R&D investment for insiders, because both own-brand and merger-partner marginal costs are reduced. The effect of merger on firm outputs follows from the discussion above of profitability effects. In sales volume terms, the greater the degree of technical closeness between brands, the larger insiders will be relative to outsiders in product market equilibrium (because the stronger the R&D pooling effect will be relative to the market power effect).15 This feature is independent of the choice between Cournot and Bertrand competition.16 These output effects of merger mean that an insider's R&D incentive (marginal return) is increasing in the degree of technical closeness between brands, while that for outsiders is decreasing.17 Therefore, for inside brands the volumes of both process R&D and output are increasing in technical closeness, whereas for outside brands both are decreasing in technical closeness.18 This gives our final key result, the conditions under which ‘reasonable criterion’ (c) are satisfied: independently of the strategic variable in market competition, insiders are larger than outsiders in post-merger equilibrium for sufficiently technically close brands. Furthermore, combining this result with our findings on the profitability effects of merger, our modelling structure is capable of simultaneously fulfilling all our ‘reasonable criteria’ (i.e. profitable mergers; harmed outsiders; and insiders larger than outsiders) under both Cournot and Bertrand competition when brands are sufficiently technically close.
The remainder of the paper is organized as follows. In the next two sections we solve for the equilibrium outcomes of multidimensional competition under Cournot and Bertrand competition in the market stage. We pay particular attention to the profitability effects of merger by comparing the no-merger and post-merger equilibria. Section IV concludes.
I. QUANTITY COMPETITION
We consider a market populated by N initially identical firms that compete in two stages of competition. In the first stage they invest in R&D, which lowers their marginal cost of production. In the second stage, once marginal costs have been determined and revealed, they compete in quantities. We first calculate the equilibrium outcome under the assumption that the firms remain independent and then compare this with the outcome generated when firms 1 and 2 merge before stage 1 competition begins.
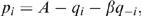 (1)
(1)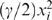 .
.If a merger between firms 1 and 2 takes place, then there are two implications. First, the merged firms choose R&D and output levels to maximize their joint profits. Second, the merged firms share the results of their research and this generates within-firm spillover effects. In particular, we assume that the firms' marginal costs become c1=c−x1−θx2 and c2=c−x2−θx1, where θ measures the degree of technical closeness between brands, which determines the magnitude of within-firm spillovers following merger. The basic idea that we are trying to capture is that the bilateral merger enables the integrated firm to exploit the technical closeness between brands by applying R&D conducted on one brand to the production process of the other brand it owns. The magnitude of θ therefore depends upon the technical closeness of the brands offered by the two firms. For example, if the production processes are quite heterogeneous (e.g. if different machinery is used to produce the different brands), we would expect θ to be quite small. On the other hand, if the production processes are quite similar (so that the brands are distinguished by some non-technical attribute such as colour), we would expect R&D activity to generate considerable (within-firm) spillovers.
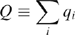
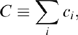
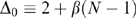
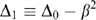
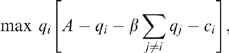 (2)
(2)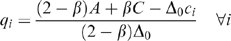 (3)
(3)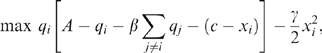 (4)
(4)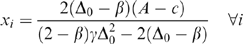 (5)
(5)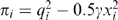 .19
.19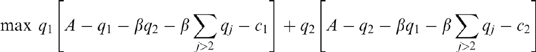 (6)
(6)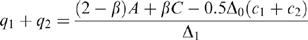 (7)
(7)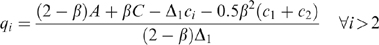 (8)
(8)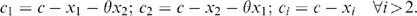 (9)
(9)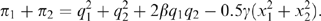
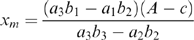 (10)
(10)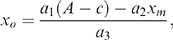 (11)
(11)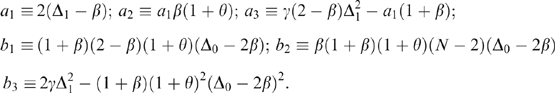
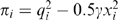 . Similarly, equilibrium profits for the merged firm can be obtained from (7) and (9)–(11).
. Similarly, equilibrium profits for the merged firm can be obtained from (7) and (9)–(11).Our results are summarized in Figure 1, where the parameter space is divided into three regions. The degree of product differentiation (β) is measured on the horizontal axis, with a value of zero representing independent goods and a value of one representing perfect substitutability across brands. The level of merger-induced R&D spillovers is measured on the vertical axis, with higher values indicating stronger complementarities in R&D across the merged firm's brands. The θM(β) curve shows combinations of β and θ for which the insiders earn the same profits with and without the merger. Thus, below this curve the R&D spillovers are not strong enough to generate gains for the insiders. The θo(β) curve shows combinations of β and θ for which the outsiders earn the same profits with and without the merger. Above this curve, the R&D spillovers for the merged firm are strong enough that the outsiders are harmed by the merger. It follows that in the region labelled SRR we get the standard Salant, Switzer and Reynolds (Salant et al. 1983) result: insiders are harmed by the merger while outsiders gain. In the region labelled PG (for Pareto gain), both insiders and outsiders benefit from the merger.20 Finally, in the region labelled IO (for intuitive outcome) we find that insiders gain from the merger while outsiders are harmed.
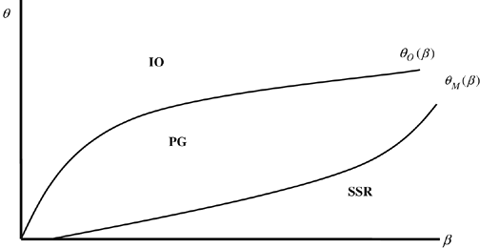
Outcomes with quantity competition
For θ=θo the outsiders earn the same profits with and without the merger. For θ=θM the insiders earn the same profits with and without the merger. In the SSR region we have the Salant et al. (1983) outcome; in the PG region all firms gain from the merger (so there is a Pareto gain); and in the IO outcome we have the ‘intuitive outcome’ (the insiders gain from the merger while the outsiders lose). The curves in Figure 1 correspond to the case in which N=10, γ=2, A=3, and c=2.
The forces that generate our results can be explained with the aid of Figure 2, which shows the aggregate output produced by the insiders ( ) and outsiders (
) and outsiders ( ) in the second stage of the game. Of course, since quantities are strategic substitutes, these values vary inversely with each other. The solid lines represent best-response outputs in the absence of the merger, so that the no-merger Nash equilibrium is represented by their intersection.
) in the second stage of the game. Of course, since quantities are strategic substitutes, these values vary inversely with each other. The solid lines represent best-response outputs in the absence of the merger, so that the no-merger Nash equilibrium is represented by their intersection.
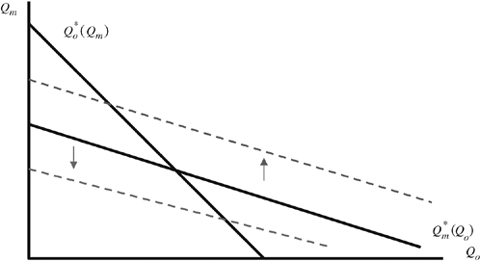
The impact of the merger with quantity competition
The solid lines show how aggregate output by the insiders and the outsiders vary with each other in the no-merger case. Their intersection determines the no-merger Nash outcome. The shift down to the dashed line is due to the ‘market power’ effect of the merger. The shift up to the dashed line is due to the ‘R&D pooling’ effect of the merger.
We begin by focusing on the insiders' output choice in the second stage of competition, holding brand R&D levels fixed at the equilibrium no-merger level. When the insiders merge, it is in their collective interest to produce less output than they would in the absence of the merger in order to push price up towards its collusive level; thus, their total output would be lower than it would be without merger. This change in behaviour is reflected by the downward shift of the 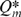 curve to the dashed line in Figure 2. Since best-reply functions are downward-sloping under quantity competition, this shift results in higher aggregate output by the outsiders. As a result, the merger leaves the insiders with a lower market share and a (slightly) higher price; but, because the increase in price is dampened by the expansion of the outsiders, the insiders typically lose. On the other hand, the outsiders wind up selling more output at a higher price, so they always gain. This is the traditional market power effect of a horizontal merger that drives the results in Salant et al. (1983)—the merger causes the insiders to produce less. This usually harms the insiders while benefiting the outsiders.
curve to the dashed line in Figure 2. Since best-reply functions are downward-sloping under quantity competition, this shift results in higher aggregate output by the outsiders. As a result, the merger leaves the insiders with a lower market share and a (slightly) higher price; but, because the increase in price is dampened by the expansion of the outsiders, the insiders typically lose. On the other hand, the outsiders wind up selling more output at a higher price, so they always gain. This is the traditional market power effect of a horizontal merger that drives the results in Salant et al. (1983)—the merger causes the insiders to produce less. This usually harms the insiders while benefiting the outsiders.
In addition to the market power effect, there is another force at work that alters the outcome in the second stage. Since the merger generates R&D spillovers for the insiders, if we hold the firms' R&D investments at their no-merger levels, the merger lowers the marginal costs of the insiders (as the insiders' R&D stocks are pooled within the merged firm). This shifts up their best-reply function towards the dashed line in Figure 2, tending to increase insider output while cutting that by outsiders. We refer to this change in behaviour resulting from R&D pooling by the insiders as the R&D pooling effect. Which of the market power and R&D pooling effects dominates, and the consequent net direction of shift in the insiders' best reply function, is determined by the degree of technical closeness between brands θ, which governs the relative strength of the R&D pooling effect.
Now we turn to the first stage. The impact of the merger on R&D spending by the insiders is not obvious. The profitability of extra R&D investment depends both on the size of the resulting process innovation and on the level of output to which that innovation will be applied. On the one hand, since the merger creates spillovers in R&D for the insiders (a larger process innovation), there is an incentive for the insiders to spend more on R&D following the merger than they would spend in its absence. This is the synergy effect of merger on R&D investment, which results from the pooling of the insiders' R&D stocks following merger. On the other hand, for a given level of brand R&D spending, the impact of merger on insiders' output is ambiguous and depends upon which of the market power and R&D pooling effects dominates in stage 2.
When merger-induced R&D spillovers are very weak, a merger works to reduce the output of inside brands (i.e. the market power effect dominates the R&D pooling effect in stage 2), and this effect itself outweighs the (weak) synergy effect so that the marginal return to R&D for insiders falls and the merger leads to a reduction in R&D spending by the insiders. As the level of merger-induced R&D spillovers rises, the market power effect in stage 2 weakens relative to the R&D pooling effect so that insiders' output (for given R&D investments) tends to rise following merger. By itself, expanding output makes extra R&D investment profitable, and this tendency is reinforced by a strengthening of the synergy effect as θ rises. Therefore, only modest spillovers are required for a merger to raise the marginal return to insiders of R&D investment, implying that, for most values of θ, the merger leads insiders to spend more on R&D than they would do otherwise. Increased R&D investment leads to lower marginal costs for all insiders and reinforces the R&D pooling effect in stage 2, shifting the insiders' best-reply function in Figure 2 up to the dashed line.21 We refer to changes in behaviour arising from changes in the first stage of competition as the R&D investment effect. Note that, as long as merger permits a non-trivial degree of R&D spillovers, the R&D pooling and R&D investment effects work in the same direction—both make the insiders more aggressive and shift up their combined best-reply function. For future reference, we refer to the combination of these two as the total R&D effect of the merger. If the R&D effect were the only impact of the merger, the insiders would end up producing more and the outsiders would end up producing less; the insiders would gain and the outsiders would lose. It follows that the R&D effect works in the opposite direction to the traditional market power effect—it causes the insiders' aggregate output to increase. This benefits insiders while harming the outsiders.
When the goods are almost independent (i.e. when β is low) the market power effect of merger is weak, and it takes only a low level of R&D spillovers for the R&D effect to dominate. When this occurs, we have the ‘intuitive outcome’. As β increases (i.e. as the goods become more similar), the market power effect becomes more important and a higher value of θ is required to generate the intuitive outcome.
When R&D spillovers are weak (θ is low), the market power effect dominates for even low values of β and we have the SSR outcome. However, as θ increases the R&D effect becomes more important, and a higher value of β is then needed for the market power effect to dominate. For intermediate values of θ and β, the two effects roughly balance out, and all firms benefit from the merger. In this case the outsiders benefit because the market power effect makes the insiders collectively less aggressive when choosing output; and the insiders benefit because the R&D effect results in greater R&D spending and lower marginal costs.
The curves in Figure 1 correspond to the case in which there are ten firms in the industry. If there are fewer firms, then, holding all else equal, a bilateral merger generates larger positive benefits for the outsiders, implying that strong R&D spillovers for the insiders are required to make the outsiders indifferent towards the merger. Thus, as N falls the θo(β) curve shifts up. As for the insiders, as N falls a bilateral merger is more likely to be profitable solely for market power reasons (there are fewer outsiders to increase output in response to the merger). Thus, as N falls the θM (β) curve shifts to the right. As a result, for low values of N the PG region is quite large. This region shrinks as N increases, with the SSR and IO regions becoming larger.
In multidimensional competition where product market interaction is Cournot, we have shown that some firms in an industry must benefit from a bilateral merger. The identity of the winners—outsiders only (SSR), all firms (PG) or insiders only (IO)—depends on the degree of complementarity between the insiders' R&D stocks, θ. The greater the degree of R&D complementarity that merger allows the insiders to exploit, the more likely it is that a merger will toughen competition on the product market (despite its ‘market power’ effects), and consequently will benefit insiders but harm outsiders. This is our intuitive outcome, because in reality we observe that mergers are both frequently proposed by firms and invariably fiercely opposed by outsiders. Moreover, when the degree of R&D complementarity is sufficiently high, the insiders end up larger (in production volume terms) than the outsiders after a merger. This intuitively appealing size advantage, which contrasts with the size disadvantage traditionally predicted (e.g. by SSR), occurs because a merger enhances the efficiency of insiders' R&D stocks in delivering marginal cost reductions, and consequently encourages insiders to invest more in R&D. In the next section we examine the robustness of these findings by assuming instead that firms compete in prices on the product market.
II. PRICE COMPETITION
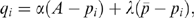 (12)
(12)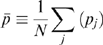
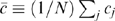 , so that
, so that  is the average marginal cost in the industry.
is the average marginal cost in the industry.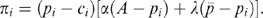 (13)
(13)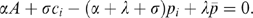 (14)
(14)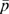 in the Bertrand equilibrium. We obtain
in the Bertrand equilibrium. We obtain
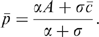 (15)
(15)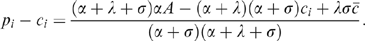 (16)
(16)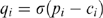 . It follows that we can write firm i's total profits as
. It follows that we can write firm i's total profits as
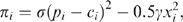 (17)
(17)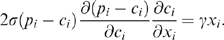 (18)
(18)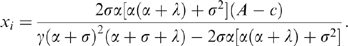 (19)
(19)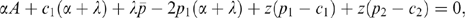 (20)
(20)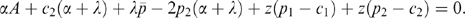 (21)
(21)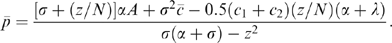 (22)
(22)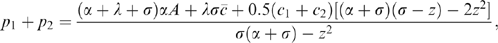 (23)
(23)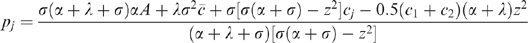 (24)
(24) (25)
(25) (26)
(26)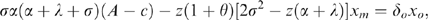 (27)
(27)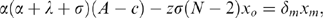 (28)
(28)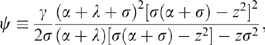
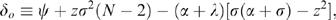
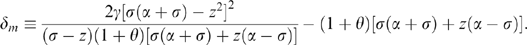
Our results for the price game are summarized in Figure 3, which is divided into two regions. Figure 3 has one less region than Figure 1 because, with price competition, insiders always benefit from the merger (i.e. there is no θM(β) curve in Figure 3). As with Figure 1, the θO(β) curve shows combinations of β and θ for which outsiders earn the same profits with and without the merger. For higher values of θ, outsiders are harmed by the merger. It follows that, as with quantity competition, in the PG region all firms gain from the merger while in the IO region insiders gain while outsiders are harmed. As is clear from Figure 3, the PG region is quite small, so that for almost all parameter values we get the intuitive outcome. Thus, with weak R&D spillovers a model in which firms compete in process-oriented R&D followed by Bertrand competition yields predictions about horizontal mergers that accord well with intuition.22
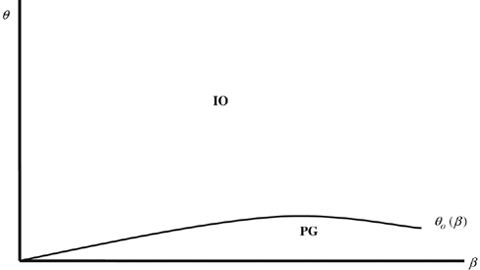
Outcomes with price competition
For θ=θo the outsiders earn the same profits with and without the merger. In the PG region all firms gain from the merger (so there is a Pareto gain); and in the IO outcome we have the ‘intuitive outcome’ (the insiders gain from the merger while the outsiders lose). The curves in Figure 3 correspond to the case in which N=10, γ=2, A=3, and c=2.
The forces that generate our results can be explained with the aid of Figure 4, which shows the price charged by a typical insider (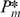 ) and a typical outsider (
) and a typical outsider (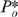 ) in the second stage of the game. Of course, since prices are strategic complements, these values vary directly with each other. The solid lines represent these profit-maximizing values in the absence of the merger, so that the no-merger Nash equilibrium is represented by their intersection.
) in the second stage of the game. Of course, since prices are strategic complements, these values vary directly with each other. The solid lines represent these profit-maximizing values in the absence of the merger, so that the no-merger Nash equilibrium is represented by their intersection.
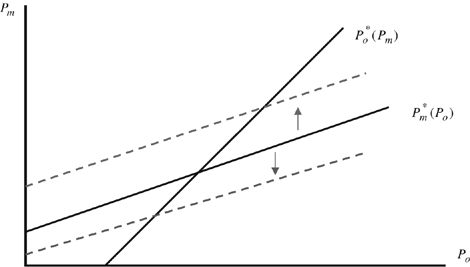
The impact of the merger with price competition
The solid lines show how the price of a typical insider and a typical outsider varies with each other in the no-merger case. Their intersection determines the no-merger Nash outcome. The shift up to the dashed line is due to the ‘market power’ effect of the merger. The shift down to the dashed line is due to the ‘R&D pooling’ effect of the merger.
We begin by focusing on the insiders' price decision in the second stage of competition, holding brand R&D levels fixed at the no-merger equilibrium level. When the insiders merge, it is in their collective interest to increase their prices towards the collusive level. Thus, the merger leads insiders to charge higher prices than they would otherwise. This change in behaviour is reflected by the upward shift of the 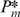 curve to the dashed line in Figure 4. Since best-reply functions are upward sloping under price competition, this shift results in higher prices for outsiders as well. As a result, the merger causes all firms to increase their prices, with insiders' prices increasing by a greater amount than outsiders' (for stability). All firms benefit from the merger, but outsiders benefit by a greater amount. This is the market power effect of a horizontal merger that drives the results in Deneckere and Davidson (1985)—the merger causes insiders to charge higher prices, and this benefits both insiders and outsiders.
curve to the dashed line in Figure 4. Since best-reply functions are upward sloping under price competition, this shift results in higher prices for outsiders as well. As a result, the merger causes all firms to increase their prices, with insiders' prices increasing by a greater amount than outsiders' (for stability). All firms benefit from the merger, but outsiders benefit by a greater amount. This is the market power effect of a horizontal merger that drives the results in Deneckere and Davidson (1985)—the merger causes insiders to charge higher prices, and this benefits both insiders and outsiders.
In addition to the market power effect, there is another force at work that alters the outcome in the second stage. Since the merger generates R&D spillovers for insiders, if we hold the firms' R&D investments at their no-merger levels, the merger lowers the marginal costs for insiders. This shifts their best-reply functions down towards the dashed line in Figure 4. As with Cournot competition, we refer to this change in behaviour as the ‘R&D pooling effect’.
We now turn to the first stage of competition. The qualitative impact of the merger on R&D spending is the same as it is under quantity competition. On the one hand, there is a synergy effect: because the merger creates spillovers in R&D for insiders, there is an incentive for insiders to spend more on R&D following the merger than they would in its absence. On the other hand, the impact of merger on the size of the output base over which insiders' process innovations will be spread is, as with quantity competition, ambiguous. As with quantity competition, when merger-induced spillovers are very weak, the synergy effect is dominated by the contraction in insiders' outputs, and the merger leads to a reduction in R&D spending by the insiders. However, only modest merger-induced spillovers are required for merger to raise the marginal return to R&D for insiders, implying that, for most values of θ, the merger leads the insiders to spend more on R&D than they would do otherwise.23 This leads to lower marginal costs for all insiders and shifts down their best-reply functions for the second stage of competition.24 As a result their prices fall, as is reflected by the shift down to the dashed line in Figure 4. This is the same R&D investment effect that we encountered under quantity competition. As before, the R&D investment effect simply reinforces the shift in the best-reply function caused by the R&D pooling effect. As a result, we have an overall R&D effect that causes insiders to become more aggressive in the second stage of competition. If the overall R&D effect were the only impact of the merger, all firms would end up charging lower prices; insiders would gain (from the reduction in costs) and outsiders would lose. It follows that the overall R&D effect works in the opposite direction to the market power effect—it causes the insiders' prices to fall. This benefits the insiders while harming the outsiders. As Figure 3 indicates, it takes only weak merger-induced spillovers for the overall R&D effect to dominate the market power effect, so that for almost all parameter values we obtain the intuitive outcome.
In multidimensional competition where product market interaction is Bertrand, we have shown that inside firms always benefit from a bilateral merger. Whether outsiders gain (PG) or lose (IO) depends on the degree of complementarity between the insiders' R&D stocks, θ. For a non-trivial degree of R&D complementarity, we generate intuitively appealing results under Bertrand competition: (a) insiders gain from merger, (b) outsiders lose and (c) insiders end up larger than outsiders in production terms. The toughening of product market competition caused by the merger-induced exploitation of R&D complementarities accounts for (a) and (b), and it contributes—together with the ‘synergy’ effect of merger—to (c). Moreover, a comparison of our Cournot and Bertrand results shows that, for a sufficiently large degree of R&D complementarity, we obtain this intuitive outcome independently of the strategic variable in market competition.25 This contrasts sharply with the findings of existing models of merger to achieve market power alone, which are known to be highly sensitive to the mode of product market competition. In contrast, the strategic variable in market competition, an unobservable characteristic of real-world product markets, plays no role in this important qualitative result.
III. CONCLUSION
The motivation for our analysis was the empirical proposition that horizontal mergers often appear to be motivated by a desire to exploit complementarities between the insiders' R&D stocks. The merger in 2000 between BP and ARCO, which was justified on the grounds that the resulting pooling of technical knowledge would significantly reduce oil extraction costs, provides a solid example of this mechanism. We studied the equilibrium outcomes of multidimensional competition, where firms compete in process R&D and then on the product market, and the positive effects of a prior bilateral merger. Our modelling structure incorporated two distinct motives for merger:
- 1
A traditional market power motive;
- 2
A novel R&D pooling motive to reflect the empirical driver of mergers noted above: a merged firm can apply the process R&D conducted on one inside brand to the production of the merger-partner's brand, thereby exploiting the public good nature of R&D output to generate extra process innovations from given R&D stocks.
The game was solved backwards, generating predictions for the effects of merger on both process R&D investments and product market actions. In particular, because R&D investments are determined endogenously and merger allows R&D complementarities to be exploited, our model can be interpreted as providing an account of the size of the synergy benefits of merger.
Our most significant results occur whenever the degree of R&D complementarity (or ‘technical closeness’) between brands is non-trivial. In this case, relative to the (symmetric) no-merger equilibrium, a bilateral merger has the following positive properties: (a) insiders (i.e. merger participants) benefit; (b) outsiders (i.e. non-participants) are harmed; (c) insiders end up larger than outsiders. We describe the conjunction of these three features as the ‘intuitive outcome’, because it accords with our basic intuition on the effects of merger. The mechanism behind these results is that a non-trivial degree of R&D complementarity simultaneously encourages extra process R&D investment by the insiders and, by toughening competition on the product market, discourages R&D spending by the outsiders. Importantly, we obtain these intuitively appealing results independently of the strategic variable in market competition (price v. quantity). This represents a significant advance on the findings of existing models of merger to achieve market power alone, which are well known to be both extremely counterintuitive and highly sensitive to the assumed mode of product market competition. In contrast, the strategic variable in market competition, an unobservable characteristic of real-world product markets, plays no role in our central qualitative results.
An assumption of our analysis is that merger represents the only means of exploiting R&D complementarities. In particular, we ruled out (inter-firm) contractual methods, such as RJVs. In many cases this is an appropriate assumption: contracts are often extremely costly both to write and to enforce, and cataloguing desired actions in all appropriate states of the world is a formidably complex task. In this connection it is interesting to note that BP and ARCO had tried, before finally merging in 2000, to exploit the complementarities between their stocks of technical expertise via contractual means for over twenty years without success (Farrell and Shapiro 2001, p. 705). However, an interesting extension of our analysis (especially in the case of Bertrand competition on the product market) would be to allow for RJVs alongside merger and to compare the profitabilities of those two alternative vehicles for exploiting R&D complementarities.
ACKNOWLEDGMENTS
For helpful comments, we are grateful to seminar participants at Loughborough University, Nottingham University and the Spring 2005 Midwest Economic Theory Meeting at Vanderbilt University, and to two anonymous referees. Financial assistance from the Leverhulme Trust under programme grant F114/BF is also gratefully acknowledged.
NOTES