Are the Welfare Losses from Imperfect Targeting Important?
Abstract
We quantify and compare the size of the welfare losses arising from the use of alternative ‘imperfect’ welfare indicators as substitutes for the conventionally preferred consumption indicator. We find that the size of the welfare losses associated with different indicators varies considerably. An asset-based index and the share of food as targeting indicators were found to have the highest welfare losses relative to all other targeting indicators examined. Our preferred welfare index implies that the losses from the two best targeting indicators (i.e. reported expenditures and reported income) are statistically significant but very low (less than 5%).
INTRODUCTION
Over the last decade or more, developing countries have placed much more emphasis on targeted programmes as part of their overall poverty alleviation strategy (Grosh 1994; Coady et al. 2004). This reflects an increased bias against ‘universal’ programmes (e.g. food subsidies), which are viewed as being very badly targeted, and result in substantial ‘leakage’ of the poverty budget to non-poor households (Cornia and Stewart 1995). Poor targeting may then result in a much smaller impact on the welfare of low-income (or ‘poor’) households. In countries where poverty alleviation budgets, and social expenditures in general, are being cut back in response to budgetary crises, these concerns tend to be magnified.
In order to target transfers to households efficiently, one needs an observable indicator that is highly correlated with programme objectives, in this case household welfare (Besley and Kanbur 1993). The purpose of this paper is to evaluate the range of indicators that has been used in practice or suggested in the literature. As a starting point, and consistent with the literature, we take household consumption as our ‘ideal’ indicator of household welfare, or ‘gold standard’ (Ravallion 1994a; Deaton 1997; Deaton and Zaidi 2002). This is perceived in the economics literature as a better indicator of lifetime welfare (i.e. ‘permanent income’) or persistent poverty. However, it is also perceived as being time consuming and expensive to collect. Hence it is not always available in household surveys, and one is often forced to rely on alternative indicators that can be constructed with data that already exist or can be more easily or cheaply collected. When evaluating these alternative indicators as targeting variables, one needs to address the trade-off between the inevitable targeting errors that will result and the cost savings. In this paper we are concerned with the former.
The structure of the paper is as follows. In the next section we discuss briefly the theoretical considerations for choosing consumption as the reference indicator, as well as some other indicators that we here consider as alternatives to consumption for targeting programme benefits. These are motivated by their greater availability, by their ease and lower cost of collection, or simply by the fact that they are commonly used or suggested for use in the literature or by policy-makers. In Section II we set out the methodology used to evaluate the welfare losses resulting from having to use these alternative, and ‘imperfect’, welfare indicators. Our preferred approach is based firmly within standard welfare theory, but we also incorporate other welfare indices that are commonly used in the literature, namely various poverty indices and indices of ‘undercoverage’ and ‘leakage’. The data used to simulate programme interventions are based on rural and urban households in Mexico surveyed as part of the 1996 National Survey of Household Income and Consumption (ENIGH). Our results are presented in Section III, while Section IV summarizes and concludes.
I. HOUSEHOLD WELFARE AND ITS MEASURES: SOME THEORETICAL CONSIDERATIONS
In general, the ideal indicator to be used for targeting the benefits of a programme depends intimately on the objectives of the programme. To relate the analysis to existing programmes, we will focus attention to the new poverty alleviation programmes that are popular with governments in Latin America. These programmes target their benefits directly to the population in extreme poverty in rural areas, and aim to alleviate poverty through cash and in-kind benefits provided on the condition that beneficiary families send their children to school and visit health centres on a regular basis.1 Examples of such programmes include the PROGRESA programme (now renamed Oportunidades) in Mexico, the Bolsa Familia programme in Brazil, the Family Allowance programme (PRAF) in Honduras, Bono de Desarrollo Humano in Ecuador, Red de Proteccion Social in Nicaragua, the Familias en Accion in Colombia and the PATH programme in Jamaica.
While the receipt of transfers in these programmes is conditional on enrolment and attendance of the child at school, for the purposes of this paper we ignore those human capital objectives that are related to poverty in the long run and focus solely on the programmes' objective of alleviating poverty in the short to medium run. The presence of multiple objectives often lies behind the use of transfer rules that are not optimal from a more narrowly defined income perspective of welfare. But such transfer schemes may also reflect the recognition of the measurement error present in all indicators as well as of social, political and administrative constraints. In any case, the approach outlined below could be very easily extended to include comparisons with other types of transfer schemes.
In the case of the programmes mentioned above, the target population is the set of poor households, with a ‘poor household’ defined as having a ‘low level of resources over its lifetime’. This arguably captures only one of a number of important dimensions of welfare, namely the ability of households to purchase goods through markets.2 But it is an important dimension which is commonly focused on in both policy analysis and the relevant literature.
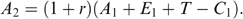 (1)
(1)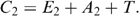 (2)
(2)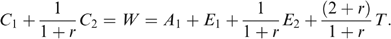 (3)
(3)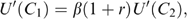 (4)
(4)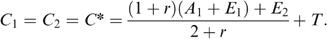
In addition, more elaborate models, involving more than two periods and assumptions about the functional form of the utility function and the formation of household expectations, can be used to show that the level of household consumption in each period is determined by permanent income or the lifetime wealth of the household (Deaton 1992).6 In combination, these theoretical results suggest that consumption is less susceptible to seasonal (or intertemporal) variation, and provide a strong basis for the use of cross-sectional measures of household consumption at any point in time to target programme resources towards households with lower lifetime wealth.
Aside from the theoretical considerations for the use of consumption as the best available indicator of household welfare, there is a variety of practical considerations (e.g. Deaton 1997). From the household's perspective, information about consumption may be a less sensitive topic than information about income, though it should be acknowledged that all the targeting indicators considered herein are likely to be under-reported, perhaps by different degrees, to the extent that households believe that the purpose of data collection is for the targeting of certain programme benefits.7 However, how such under-reporting varies systematically across the true welfare distribution is less clear.
Among the main difficulties associated with collecting data on consumption for the purposes of programme targeting is the fact that consumption data are more time-consuming and thus more expensive to collect.8 These features may explain the prevalence and use of alternative indicators of household welfare. Among the indicators used to measure households most frequently are household income and assets.9
One welfare indicator commonly used is the current income of the household. Many surveys collect data on household income only, rather than on household consumption. It is apparent from the simple model above that current income (E1) is only one component of a household's lifetime wealth. This in turn implies that income-based measures of household welfare within a cross-section of households are likely to provide misleading information about the lifetime economic opportunities of a household. Moreover, current income is usually more variable over time than consumption, especially since the latter can be smoothed through formal as well as informal arrangements. Another serious impediment to relying on current income as a measure of lifetime wealth is the fact that in poor rural economies there is a prevalence of agricultural activities and multiple income earning activities performed mostly at home. The relative infrequency of transactions through formal markets implies that imputation procedures may be required to estimate the value of family labour used in agricultural production and the net profits of the household from agricultural and other home production (Skoufias 1994).
Another indicator used in place of consumption is an asset index, which summarizes the accumulated wealth stock or savings and dissavings of the household.10 As is the case for current income, the value of household assets (A1) is only one component of a household's lifetime wealth. The problems of using assets as an indicator of the household's long-run welfare stem from the dual role that assets play in the case of borrowing constraints. In the absence of formal credit and insurance markets, assets (savings) not only provide a means of transferring wealth from period to period, but also serve the role of buffering consumption from bad income shocks. If the absence of formal credit and insurance markets leads households to accumulate assets for eventual use as a buffer to smooth consumption, targeting based on an asset index may wrongly exclude households that have a higher level of assets simply because these households face higher risks and keep more assets as a buffer for consumption (Deaton 1997).
On the basis of these preceding arguments, we use household total consumption per capita as the ‘gold standard’ household welfare indicator, against which all other indicators are compared.11 Before moving to the discussion of the simulations and the results, it is necessary to elaborate further on two additional points about the use of consumption as the ‘gold standard’. The comparison of alternative indicators relative to consumption is made in the context of a situation where both consumption and income are collected with very detailed modules. In reality, consumption and income are not uniformly collected across surveys ranging from consumption and income modules that collect information for hundreds of food and non-food items and income from many explicit and very detailed sources, to those asking very few questions about total household consumption and total income. As Lanjouw and Lanjouw (2001), demonstrate, variations in the way total consumption or total income are collected in surveys can result in substantially different estimates of poverty.12 The analysis conducted here cannot shed much light on the welfare losses that would be incurred by collecting information on household consumption or income poorly.
Lastly, it is important to acknowledge up front that the degree to which consumption is in fact the ‘ideal’ indicator for lifetime household wealth depends on the extent to which the assumptions used by the theoretical model reflect the situation faced in reality.13 Examples of such assumptions relate to the nature of the utility function (convexity of marginal utility of consumption or non-additivity over time), the presence of credit market and liquidity constraints, the risk faced by households and the presence of formal and informal insurance mechanisms. Specifically, if one were to replace the quadratic utility function in favour of the more realistic assumption of a utility function with a convex marginal utility of consumption, then households facing higher uncertainty—as measured by the household's intertemporal variance of consumption growth—are likely to consume less in the present owing to their increased precautionary savings (e.g. Deaton 1992; Browning and Lusardi 1996). In this situation targeting based on current consumption does not necessarily select the households with lower levels of lifetime wealth, but rather the households facing greater variance in their (future) consumption. The precautionary saving motive may lead to slightly wealthier households having a lower level of current consumption than less wealthy households simply because the former face a higher risk than the latter.14 Thus, non-poor households facing higher risks may be incorrectly included in a poverty alleviation programme using consumption-based targeting.
It is in light of these circumstances that some authors, such as Filmer and Pritchett (2001), take the view that the lifetime economic status of the household is an unobservable, and that both household consumption and asset indices serve as imperfect proxies for this unobservable. We choose to use consumption as the point of reference for the performance of the other targeting indicators, on the grounds that it is widely accepted as the best available indicator, especially for targeting currently poor households.
II. METHODOLOGY AND DATA
In this section we set out the methodology employed in the paper to evaluate the alternative indicators of household welfare. We start by assuming a given poverty alleviation budget B, which is to be disbursed as a uniform transfer to Np‘poor’ households so that each household receives 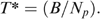 Ideally, we would like to use household consumption information to choose which households are to be classified as ‘poor’ and thus are to receive the transfer. However, in practice such information is often not available or is deemed too costly to collect, so we need to use another indicator that is only imperfectly correlated with household consumption. We can therefore view the use of these alternative indicators as different (competing) programmes and evaluate these alternative programmes accordingly.
Ideally, we would like to use household consumption information to choose which households are to be classified as ‘poor’ and thus are to receive the transfer. However, in practice such information is often not available or is deemed too costly to collect, so we need to use another indicator that is only imperfectly correlated with household consumption. We can therefore view the use of these alternative indicators as different (competing) programmes and evaluate these alternative programmes accordingly.
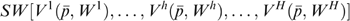 (5)
(5)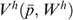 is the indirect ‘lifetime’ utility function for household h, corresponding to an intertemporal model of consumption outlined in the previous section;
is the indirect ‘lifetime’ utility function for household h, corresponding to an intertemporal model of consumption outlined in the previous section; 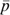 is the vector of current and future discounted commodity prices faced by the household (see e.g. Deaton and Muellbauer 1980; Blundell and Walker 1986); and Wh is the lifetime wealth of the household, defined through the household budget constraint as
is the vector of current and future discounted commodity prices faced by the household (see e.g. Deaton and Muellbauer 1980; Blundell and Walker 1986); and Wh is the lifetime wealth of the household, defined through the household budget constraint as
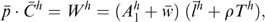
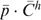 is total household consumption expenditure on commodities,
is total household consumption expenditure on commodities, 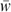 is a vector of present and future discounted wages,
is a vector of present and future discounted wages, 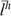 is the vector of lifetime household labour supply and Th is the lump-sum transfer from the government to the household, assumed to be the same per period and discounted at the rate ρ.16
is the vector of lifetime household labour supply and Th is the lump-sum transfer from the government to the household, assumed to be the same per period and discounted at the rate ρ.16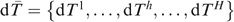 where
where 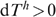 for beneficiary households and dTh=0 for non-beneficiary households. The social welfare impact of any transfer programme is then
for beneficiary households and dTh=0 for non-beneficiary households. The social welfare impact of any transfer programme is then
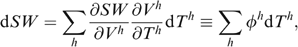 (6)
(6)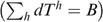 gives
gives
 (7)
(7)In our empirical analysis below we treat budget as fixed across alternative programmes and thus focus on λ alone.
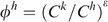
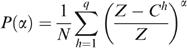
The poverty approach can be interpreted within the above framework as attaching a welfare weight of zero to everybody above the poverty line (i.e. regardless of distance above the poverty line) and also, essentially, transferring amounts in excess of the minimum required to take a poor household up to the poverty line. The extent to which the implicit welfare weights increase as income falls further below the poverty line is determined by the parameter α. The headcount index has a number of shortcomings as a welfare index, not least the fact that it suggests that resources should be concentrated on those just below the poverty line. The poverty gap index, P(1), attaches equal weight to all transfers to poor households, regardless of the depth of their poverty, although the portion of the transfer exceeding the poverty gap is valued at zero (i.e. does not contribute to a decrease in the extent of poverty as measured by this index). Values of α > 1 try to address this issue by attaching a greater weight to extra income to households the further they fall below the poverty line. However, as with P(1), it does not differentiate between ‘leakage’ of programme resources to households that are just above the poverty line and households that are far above the poverty line. Most would subscribe to the view that the social value of income to someone just above the poverty line is very close to that for someone just below it. Our above specification of welfare weights takes this issue into consideration. Higher values of the parameter ɛ can adequately capture our greater concerns for the poorest of low-income households. Using the welfare-theoretic approach, we essentially use the concept of a poverty line solely as the basis of a targeting rule. But, for the sake of completeness, we also evaluate the alternative programmes (or targeting indicators) from the perspective of poverty reduction.
Yet another approach commonly found in the literature is that of the extent of ‘undercoverage’ associated with a transfer programme (Cornia and Stewart 1995). ‘Undercoverage’ is defined as the percentage of the poor population (as identified by consumption levels) wrongly classified as non-poor by the imperfect targeting indicator (i.e. ‘errors of exclusion’). Let 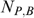 and
and 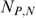 be, respectively, the number of actually poor households (i.e. defined by consumption levels) that are included in and excluded from the programme (subscripts B and N denote being a ‘beneficiary’ and ‘non-beneficiary’). Then ‘undercoverage’ is defined as
be, respectively, the number of actually poor households (i.e. defined by consumption levels) that are included in and excluded from the programme (subscripts B and N denote being a ‘beneficiary’ and ‘non-beneficiary’). Then ‘undercoverage’ is defined as 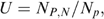 where
where 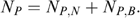 Note that, if we assume restrictive welfare weights such that φ=1 for poor households and φ=0 for non-poor households, then λ=(1−U), a measure of coverage: since the number of households in the programme (NB) is by construction set equal to the number of poor households Np, undercoverage (coverage) is zero (unity) for a perfectly targeted programme (Coady and Skoufias 2004). Therefore undercoverage can be interpreted as a welfare indicator for a restrictive set of welfare weights when transfers are uniform across households. Note also that, since
Note that, if we assume restrictive welfare weights such that φ=1 for poor households and φ=0 for non-poor households, then λ=(1−U), a measure of coverage: since the number of households in the programme (NB) is by construction set equal to the number of poor households Np, undercoverage (coverage) is zero (unity) for a perfectly targeted programme (Coady and Skoufias 2004). Therefore undercoverage can be interpreted as a welfare indicator for a restrictive set of welfare weights when transfers are uniform across households. Note also that, since 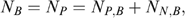 where
where 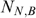 is the number of non-poor households (defined by consumption) that are wrongly identified as programme beneficiaries, then leakage
is the number of non-poor households (defined by consumption) that are wrongly identified as programme beneficiaries, then leakage 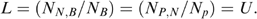
In our empirical analysis we address the following questions: (i) How much do the welfare impacts of the various programmes (i.e. based on alternative welfare indicators) vary? (ii) How sensitive is this variation to the degree, or nature, of our aversion to inequality (i.e. different values of ɛ or α)? (iii) How different are the results across the various welfare indices (i.e. welfare, poverty and undercoverage indices)? (iv) Are the welfare losses identified statistically significantly different from zero? (v) What are the features of the various indicators that make them more or less attractive as targeting devices? (vi) How sensitive are our results to a change in the size of the programme budget or to an urban–rural focus?
Data and the construction of the key indicators
The data used to simulate programme interventions are based on 4378 rural and 9001 urban households in Mexico surveyed as part of the 1996 National Survey of Household Income and Consumption (ENIGH). In calculating monthly total consumption, we include both food/non-food expenditures and the value of food items consumed out of own production.17 Loans, and purchases of durable assets by the household, were not included in the consumption aggregate.18 Also, all values were adjusted for inflation over the six-month frame of reference for the survey.
The indicators evaluated against consumption are: (i) reported consumption expenditures (purchases), (ii) reported income; (iii) an asset index; (iv) the share of food in household expenditures and (v) the probability of being poor. The details of constructing each of these indicators are discussed next.
Reported consumption expenditures A reliable measure of total household consumption is usually built up from several components (e.g. Deaton and Grosh 2000). The most critical components are (i) reported expenditures on (or purchases of) individual (or groups of) goods and services, (ii) consumption out of own production or in-kind consumption received from employers and (iii) the use value or service flow derived from the use of durable goods owned by the household (e.g. Deaton and Zaidi 2002). Very often data on consumption out of own production (auto-consumption) or on the ownership of and use-value from consumer durables are not available. The extent to which the targeting of households based on purchases alone, excluding the consumption out of own production or the use-value of assets, leads to imperfect targeting is likely to vary, even within a country, depending on the extent to which markets and consumption out of own-production are more or less prevalent across urban and rural areas.
Reported income Monthly household income is constructed by aggregating reported income received from the following sources: working, business, cooperatives, rents, pensions, transfers (from within and outside the country), the PROCAMPO programme, loan repayments, asset sales, and other sources.
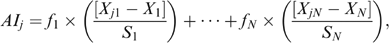
The asset index is constructed solely on the basis of indicator variables about the ownership of consumer durables and characteristics of the household dwelling, very much in line with the asset index of Filmer and Pritchett (2001). The list of consumer durables includes ownership of a car, bicycle, small truck, radio, stereo, television, VCR, food blender, air-fan, heater, gas stove, refrigerator and washing machine. The indicator variables summarizing dwelling characteristics identify whether the floor of the dwelling is earthen; the quality of materials used in the walls and roof; access to running water; drainage of water to a septic tank; and access to rubbish collection, electricity and telephone services. Including variables such as access to public services in the construction of the asset index gives the index a multi-dimensional flavour. All in all, the first principal component explained only 14% of the total variance in the data. Although we included a very wide range of assets, the absence of information on land-holdings means that our assessment of this indicator can be viewed as incomplete.19
The last two indicators are motivated more by practical than theoretical considerations. The food share occupies a prominent place in the economic literature as an indicator of household welfare. Engel's Law, for example, implies that for a household of given size and composition there is a negative relationship between the food share and income or total outlay (see e.g. Deaton 1997). Thus, ceteris paribus, households with a higher food share are more likely to be those with a lower level of welfare. As discussed in Deaton (1997), the use of the share of the budget on food as an indicator of welfare is based on the empirical regularities first observed by Engel. However, as Nicholson (1976) argues, the link between the share of food and the level of household welfare is based more on an assumption than on solid analytical reasoning.
The last indicator, the probability of being poor, is a variant of the reported income indicator, with the difference that it attempts to approximate the ‘permanent income’ of the household. One alternative to using directly the reported income of the household, which is subject to seasonal fluctuations, is to combine its reported income information with other household data in order to estimate the probability that a household is poor. Poor households may then be targeted on the basis of their estimated probability of being poor using some predetermined probability cutoff. For example, policy-makers responsible for Mexico's PROGRESA programme used the following alternative to reported income. First, a binary variable was constructed that took the value 1 if reported household income fell below the income poverty line, and 0 otherwise. Then discriminant analysis was carried out with this binary variable as the dependent variable and variables summarizing the age and gender composition of household members, the level of schooling and occupation of the household head, the durable assets of the household and the characteristics of its dwelling. The discriminant score was then used as the basis for categorizing households as poor and non-poor, with the poor receiving the transfers.
We construct a similar poverty indicator using the same general steps as above but using a logit model in place of the discriminant analysis and the discriminant score.20 In constructing the probability of being poor index, we use the following set of explanatory or predicting variables: the dependency ratio (the number of non-working members divided by household size); the household size divided by the number of rooms in the dwelling; the age of the household head; number children in the household less than 12 years of age; the proportion of children less than 15 years old not attending school; and binary variables identifying whether the household head is female; the highest level of schooling completed by the head of the household (e.g. primary, junior high school); whether the household head is self-employed/employed in agricultural occupations; whether there is running water in the household dwelling; whether the floor of the dwelling is made of earth (as opposed to other materials such as concrete); and variables about the ownership of some important consumer durable goods, such as a car, a stereo, a television, a VCR, a gas stove, a refrigerator or a washing machine. It is quite possible that the performance of the ‘probability of being poor’ indicator could be improved by expanding the list of predicting variables to include additional household head and dwelling characteristics, and/or by combining this method with community level targeting (see e.g. Coady et al. 2004). We chose the above variable list because these variables are actually used by at least one programme, the PROGRESA programme in Mexico, to select beneficiary households.21
In order to evaluate the performance of the alternative indicators, we classified households as being (actually) poor using our ‘gold standard’ of household consumption and a (relative) poverty line drawn at the median of the rural sample (i.e. 50% of the rural population is assumed to be poor). The welfare weights were also calculated on the basis of household per capita consumption. For each of the other indicators, we then determined which are the beneficiary households receiving the cash transfer by taking those falling into the bottom 50th percentile according to this indicator. Using the various welfare indices, we then compared the welfare impact of the various programmes (i.e. alternative indicators) with that which would result from ‘perfect targeting’, i.e. using consumption. The calculation of the poverty rates is based on using the same poverty line for all the targeting indicators, i.e. the median of the consumption per capita.
In all of our simulations, the number of beneficiary households is the same and each beneficiary household receives the same transfer.22 The transfer was 201 pesos per household in June 1994 prices, which is slightly higher than the poverty line of 179 pesos per capita, while the total budget amounts to 48.6% of the poverty gap. The poverty gap is defined as the sum (across all poor households) of the difference between the poverty line and the per capita consumption expenditure of the household both multiplied by the number of persons in the household.
III. SIMULATION RESULTS
In order to get some feel for the imperfect nature of these alternative welfare indicators, we start by constructing a graph that captures both the magnitude of the targeting errors associated with each indicator and the distribution of this error, i.e. where in the distribution of consumption these errors manifest themselves. For each indicator, we classify a household as ‘poor’ if it is classified as a poor household by that indicator and thus included in the programme, and as ‘non-poor’ if it is left out of the programme. This classification is compared with that suggested by our reference indicator, i.e. consumption. We construct a new variable that takes the value 1 when households that are classified as ‘poor’ and ‘non-poor’ according to consumption are classified incorrectly as ‘non-poor’ and ‘poor’ respectively according to the alternative indicator (i.e. identifying errors of exclusion and inclusion, respectively); otherwise the variable takes the value 0. In 1, 2 we plot the mean of this variable against the log of reported consumption per capita using non-parametric methods.
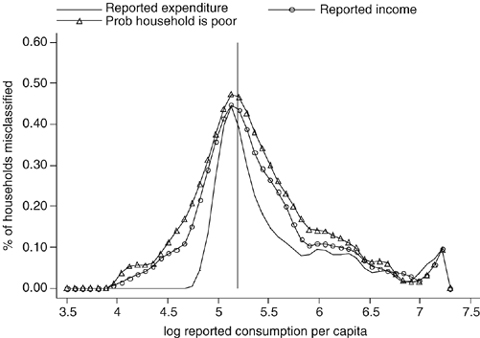
Misclassification of households using alternative welfare indicators.
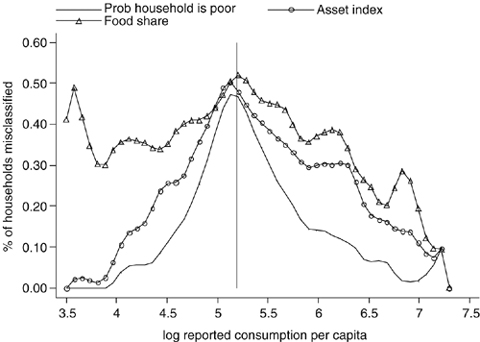
Misclassification of households using alternative welfare indicators.
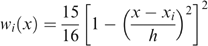
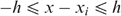 and 0 otherwise. The quantity h is a bandwidth that is set so as to trade off bias and variance, and it tends to zero with the sample size. We set the bandwidth to the value of 0.5.
and 0 otherwise. The quantity h is a bandwidth that is set so as to trade off bias and variance, and it tends to zero with the sample size. We set the bandwidth to the value of 0.5.The value on the y-axis can be seen as the ‘predicted error probability’ (PEP). The height of the curve captures the extent of the targeting errors being made at various points in the distribution. The shape captures where in the distribution these errors are being made. For example, a curve that is ‘bell-shaped’ and concentrated around the poverty line indicates that most of the error involves a misclassification of households that lie just above and below the poverty line.
Figure 1 plots the PEP curve associated with reported expenditure, excluding consumption out of own production, reported income and the probability of being poor. From this figure we can see that the most efficient targeting indicator relative to consumption is ‘reported expenditure’. The fact that the curves for reported income and the indicator of the probability of being poor lie everywhere above that for reported expenditure tells us that not only is the proportion of targeting errors greater using the former, but they are also more costly from a welfare perspective, since a larger proportion of the poorest households are excluded, and a larger proportion of the richest are included. Figure 2 plots the PEP curve associated with the ‘probability of being poor’ indicator, which had the highest PEP curve in Figure 1, against the PEP curve for the asset index and the food share. We can see from this figure that the most inefficient targeting indicator is food share.23
The preceding insights are reinforced by our undercoverage measure (U: see Table 1). Using both measures, the worst performers are food share and the asset index. For these two targeting indicators undercoverage lies in the range 32.4%–40.9%. Even the best indicator—reported purchases—has an undercoverage rate of 14.0%. These levels of mistargeting are suggestive of large welfare losses arising from our inability to use reported total consumption to identify which households receive transfers.24
| λ(5) | λ(2) | λ(1) | P(0) Headcountindex | P(1)Poverty gap | P(2) Severity index | U (%) | |
|---|---|---|---|---|---|---|---|
| No transfer (no anti-poverty programme) | 0.5000 | 0.1768 | 0.0836 | ||||
| Targeting based on reported consumption | 62.4705 | 3.5419 | 1.7512 | 0.3346 | 0.0923 | 0.0351 | 0.00 |
| Targeting based on reported purchases | 62.2456 | 3.4430 | 1.6953 | 0.3947 | 0.0993 | 0.0362 | 13.98 |
| −(0.36) | −(2.79) | −(3.19) | (17.95) | (7.63) | (3.13) | ||
| Targeting based on reported income | 60.8355 | 3.2832 | 1.6315 | 0.3970 | 0.1068 | 0.0399 | 20.88 |
| −(2.62) | −(7.30) | −(6.84) | (18.63) | (15.70) | (13.58) | ||
| Targeting based on the probability of being poor | 59.6845 | 3.2085 | 1.6022 | 0.4080 | 0.1105 | 0.0416 | 23.98 |
| −(4.46) | −(9.41) | −(8.51) | (21.91) | (19.73) | (18.54) | ||
| Targeting based on asset index | 54.7229 | 2.8867 | 1.4759 | 0.4082 | 0.1163 | 0.0458 | 32.39 |
| −(12.40) | −(18.50) | −(15.72) | (21.98) | (26.00) | (30.35) | ||
| Targeting based on food share | 40.5614 | 2.4025 | 1.3316 | 0.4114 | 0.1257 | 0.0534 | 40.89 |
| −(35.07) | −(32.17) | −(23.96) | (22.94) | (36.19) | (52.05) |
- a Sample: all households in rural areas; poverty line: 50th percentile of consumption in rural areas.
To examine the welfare losses resulting from inefficient targeting, in Figure 3 we graph for selected indices (i.e. λ(5), λ(2), P(2) and the undercoverage rate U) the percentage difference from the value of the corresponding index with ‘perfect’ targeting. Upon inspection of this figure, one can draw the following inferences.
Welfare losses for alternative welfare indicators.
The preferred welfare indices λ(ɛ) suggest very small welfare losses, less than 7.3% for the two best targeting indicators, i.e. reported purchases/expenditures and reported income. In particular, using λ(5), it appears that the welfare losses from the best performer among the alternative indicators are quite low, of the order of less than 0.5%. Considering the implications of this finding for data collection needs for targeting purposes, we conducted further sensitivity tests and discuss our findings below.
The undercoverage index consistently suggests substantially higher welfare losses from imperfect targeting than from our preferred welfare index λ(ɛ). For example, when reported purchases are used as a targeting indicator, the undercoverage welfare index (U) suggests that the welfare losses are 13.98%; in contrast, the size of the welfare losses associated with λ(2) and λ(5) are 2.79% and less than 0.5%, respectively. This reflects the pattern observed earlier in Figure 1, which showed that, for this targeting indicator, the targeting errors were highly concentrated around the poverty line. In other words, the mistargeting involves transferring income between households with very similar welfare weights even for a very high degree of inequality aversion. Given that the undercoverage index does not distinguish whether the incorrectly excluded households were close or far away from the cut-off point, it is no surprise that the welfare losses associated with these welfare indices appear to be much higher than the welfare losses associated with our preferred welfare indices.
The severity of poverty index P(2) suggests lower welfare losses arising from imperfect targeting than from undercoverage, and higher welfare losses than under the preferred welfare index λ(ɛ). Interestingly, the welfare losses suggested by P(2) are especially high for the worst performing indicator (i.e. food share) and especially low (or practically the same as the low welfare losses suggested by the λ(2) welfare index) for the best performing indicator (i.e. reported expenditures). Of course, the welfare losses suggested by any P(α) will be even higher, ceteris paribus, the larger the transfer to households, since transfers higher than the poverty gap do not contribute to lowering P(α).25
Irrespective of the welfare index used, the ranking of the welfare losses is insensitive to the targeting indicator used; i.e. all of the lines in Figure 3 are monotonically increasing. For example, the use of P(2) as an index of welfare also implies that the lowest welfare losses are associated with the use of reported expenditures. Using reported income yields a higher level of welfare losses than using reported expenditures, while the probability of being poor yields even higher welfare losses, followed by the asset index and the food share.26 The use of undercoverage (U) as a welfare indicator yields a similar ranking, except for the way in which it ranks the welfare losses associated with the asset index relative to the probability of being poor. As already hinted at, the relatively weak performance of probability-of-being-poor and asset indices should not be extrapolated to make inferences about the performance of proxy means tests in general, since the latter are often combined with other targeting methods (e.g. geographic targeting). It is also possible that proxy means based on predicting consumption (i.e. with consumption as a left hand-side variable) may perform better than the two proxy mean-like indicators examined here.
In order to examine the extent to which these patterns hold when we use an urban sample of households, we also estimated the welfare indicators of Table 1 using the sample of urban households and as a poverty line the 25th percentile of reported consumption of urban households (see Table A1 in the Appendix. As can be easily seen, the same patterns observed for the rural sample hold here. The two best performing indicators are reported purchases and expenditures and reported income, and for these indicators the welfare losses in the urban sample are as low as those observed for the same targeting indicators in the rural sample. For example, using λ(5), the welfare losses are less than 5%, as for the rural sample. Additional sensitivity tests were conducted by focusing on the sample of rural households and decreasing the budget used for our simulations to 75% and 50% of that used in the earlier simulations in rural areas. Since the patterns observed resembled those in Table 1, we chose not to present them.
Given our findings that the welfare losses across alternative indicators tend to cluster within small ranges for the best (or worst) performers, and since for our preferred welfare indices the losses for the best performers appear quite low, we investigated a number of related issues in further detail. Specifically, we examined whether the welfare loss associated with each imperfect targeting indicator is statistically different from zero, and whether the answers are sensitive to our aversion to inequality. To address these questions, we used 1000 bootstrap samples (each sample randomly selected with replacement). For each sample, we calculated the index value for each targeting indicator and, based on the 1000 different values of the indices, we estimated the mean welfare loss and its associated standard error.
The mean values of the λ(5) and λ(2) indices along with their associated standard errors are reported in columns (1) and (2) of Table 2. In column (3) of the table we report the mean welfare loss, defined as the percentage difference from the index value using reported consumption and the standard error of the estimated welfare loss. Focusing on λ(5), we can easily infer that the welfare losses are significantly different from zero. Within the 1000 bootstrap samples, there was no single instance where the welfare index with the imperfect targeting indicator was equal to or greater than the welfare index using reported consumption. This finding suggests that using indicators based on income or food share or assets is likely to result in significantly higher welfare losses. Nevertheless, the better performing indicators, such as reported income and the probability of being poor, exhibited welfare losses that were significantly lower than the rest of the indicators.27
| Targeting indicator | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| λ(5) | St. error | Mean welfare loss | St. error of welfare loss | |
| Reported consumption | 62.4705 | 2.98748 | ||
| Reported expenditure | 62.2456 | 2.98321 | 0.360045 | 0.05414 |
| Reported income | 60.8355 | 2.94291 | 2.617196 | 0.47636 |
| Probability of being poor | 59.0360 | 2.89769 | 5.497713 | 0.86349 |
| Asset index | 54.7229 | 2.81711 | 12.40194 | 1.49619 |
| Food share | 40.5614 | 2.36865 | 35.07108 | 2.26257 |
| Targeting indicator | λ(2) | St. error | ||
| Reported consumption | 3.54192 | 0.075648 | ||
| Reported expenditure | 3.44296 | 0.07496 | 2.793848 | 0.16514 |
| Reported income | 3.28319 | 0.07302 | 7.30486 | 0.41421 |
| Probability of being poor | 3.16793 | 0.07570 | 10.55903 | 0.67556 |
| Asset index | 2.88667 | 0.07253 | 18.49974 | 0.86851 |
| Food share | 2.40246 | 0.06268 | 32.17081 | 1.09449 |
- a Over 1000 bootstrap samples.
- Simulations were based using the 50th percentile of reported consumption per capita as a relative poverty line and a budget equal to 48% of the poverty gap.
Generally similar results hold when focusing on λ(2). One notable difference is that using λ(2) as a measure of welfare yields welfare losses that are typically higher than those obtained using λ(5). For example, for reported expenditure the mean welfare loss (expressed as the percentage difference from the value of the index using reported consumption), is 0.36% with λ(5) and 2.8% with λ(2). The only exception is the food share indicator, for which the value of λ(2) is lower than it is for λ(5). Given that this indicator yields a high proportion of targeting errors at the lower part of the distribution of consumption (see Figure 2), a higher aversion to inequality (i.e. ɛ=5) results in a higher welfare loss than when ɛ=2. On the basis of this evidence, we conclude that the degree of aversion to inequality has an impact on the welfare loss associated with specific targeting indicators.
IV. SUMMARY AND CONCLUSIONS
In this paper we quantify and compare the size of the welfare losses from using alternative ‘imperfect’ welfare indicators as substitutes for the conventionally preferred consumption indicator. We find that the size of the welfare losses associated with different indicators varies considerably. Our preferred welfare index implies that the losses from the two best targeting indicators (i.e. reported expenditure and reported income) are very low if not trivial (less than 5%). One plausible explanation for the good performance of the reported expenditure indicator may be the fact that the preferred consumption indicator itself was rather incomplete. It is quite possible that a more comprehensive indicator of consumption that included the value of services a household receives from all the durable goods in its possession, including housing, might have resulted in a weaker performance of the reported expenditure indicator.
Our analysis also shows that the welfare losses suggested by our preferred welfare index are always lower than those suggested by the poverty and undercoverage welfare indices. This reflects the fact that most of the targeting errors (i.e. exclusion and/or inclusion errors) are highly concentrated around the poverty line, so that the differences in welfare weights between those receiving and not receiving the transfers are insufficient to make much of a difference to the overall welfare impact.
An asset-based index and the share of food as targeting indicators were found to have the highest welfare losses relative to all other targeting indicators examined in this paper. We also find, based on our preferred welfare indicator, that the size of the estimated welfare losses associated with using the better performing alternative indicators (e.g. reported expenditures or reported income) depends on the extent of aversion to inequality. Recognizing that welfare indices are subject to sampling error leads us to conclude also that there are significant welfare losses associated with different targeting indicators.
It is quite possible that the profile of consumption and other household characteristics are so different across countries that these results are country-specific. We hope that future work on this issue will test the robustness of our conclusions across countries.
ACKNOWLEDGMENTS
We are grateful to Gaurav Datt, Benjamin Davis, Rafael Flores, Saul Morris and three anonymous referees for helpful comments and suggestions. Most of the work on this paper was undertaken when both authors were Research Fellows at the International Food Policy Research Institute, Washington, DC. The findings, interpretations and conclusions expressed here are entirely our own. They do not necessarily represent the views of the World Bank or the IMF, their executive directors, or the countries they represent.
NOTES
Appendix
Table A1 presents the welfare and poverty indices under various targeting/transfer schemes.
| λ(5) | λ(2) | λ(1) | P(0) Headcountindex | P(1) Povertygap | P(2) Severity index | U (%) | |
|---|---|---|---|---|---|---|---|
| No transfer (no anti-poverty programme) | 0.2500 | 0.0731 | 0.0295 | ||||
| Targeting based on reported consumption | 16.2451 | 2.4798 | 1.5161 | 0.1652 | 0.0381 | 0.0124 | 0.00 |
| Targeting based on reported expenditures | 15.9067 | 2.3314 | 1.4325 | 0.2076 | 0.0429 | 0.0131 | 21.06 |
| −(2.08) | −(5.98) | −(5.51) | (25.69) | (12.41) | (5.98) | ||
| Targeting based on reported income | 14.8589 | 2.1814 | 1.3709 | 0.2085 | 0.0465 | 0.0149 | 28.70 |
| −(8.53) | −(12.03) | −(9.57) | (26.23) | (21.90) | (20.13) | ||
| Targeting based on the probability of being poor | 13.7242 | 2.0384 | 1.3102 | 0.2096 | 0.0497 | 0.0165 | 33.94 |
| −(15.52) | −(17.80) | −(13.58) | (26.90) | (30.27) | (33.47) | ||
| Targeting based on asset index | 11.7753 | 1.7566 | 1.1763 | 0.2138 | 0.0524 | 0.0180 | 46.65 |
| −(27.51) | −(29.16) | −(22.41) | (29.39) | (37.38) | (45.84) | ||
| Targeting based on food sharein total consumption | 8.6519 | 1.4064 | 1.0295 | 0.2181 | 0.0576 | 0.0211 | 58.20 |
| −(46.74) | −(43.29) | −(32.09) | (32.02) | (51.05) | (70.65) |
- a Sample: all households in urban areas; poverty line: 25th percentile of consumption in urban areas.




