Is it Fair to ‘Make Work Pay’?
Abstract
We present a new fair allocation, coined a ‘Pareto-efficient and Shared Resources Equivalent’ allocation, which compensates for different productive skills, but not for different tastes for working. We illustrate the optimal second-best allocation in a discrete Stiglitz economy. The question of whether we should have regressive or progressive taxes for low earners crucially depends on whether the low-skilled have a strictly positive skill or zero skill. Our simulation results suggest that ‘making work pay’ policies can be optimal, according to our fairness criterion, but only in the unreasonable case in which all the unemployed are never willing to work.
INTRODUCTION
Focusing on the tax benefit system as a whole, many European countries combine a sizeable basic income with high (empirical) marginal taxes for the low income earners. These programmes are praised for their redistributional appeal, directing large transfers towards the low incomes in society. But at the same time, critics have held these schemes responsible for large unemployment traps, because they do not provide incentives to (start) work(ing). Therefore, some continental European countries—such as Belgium, Finland, France, Germany, Italy and the Netherlands—have recently proposed and/or introduced tax credit schemes (see Bernardi and Profeta 2004 for an overview). At the same time, the United States and the United Kingdom, with a much longer tradition in tax credit schemes, have reinforced the role of their tax credits. The increased policy interest for such ‘making work pay’ schemes, i.e. policies aiming at subsidizing the low income earners, lies in their ability to tackle two problems at the same time. They have a positive effect on employment (the number of people working and, to a lesser extent, the aggregate labour hours), while they increase the income of poor household (see Pearson and Scarpetta 2000 for an overview).
While ‘making work pay’ schemes may attain desirable objectives, it is not clear whether it is also optimal to make work pay given the government's budget constraint. The ‘welfarist’ optimal income tax literature consists of three canonical models, depending on whether labour supply responses are modelled intensively and/or extensively (Heckman 1993). First, in a Mirrlees (1971) economy, individuals respond via the intensive margin, i.e. by varying their labour hours or effort. Marginal taxes should be non-negative everywhere (Mirrlees 1971), excluding the possibility of subsidizing work. At the bottom, the marginal tax has to be zero, but only on condition that everybody works (Seade 1977). Once there exists a nucleus of non-workers, the marginal tax rate has to be positive (Ebert 1992) and, according to some numerical simulations (Tuomala 1990), rather high. Using the empirical earnings distribution, (i) a U-shaped pattern of positive marginal tax rates and (ii) high marginal tax rates at the bottom turn out to be optimal in many cases (for (i) see Diamond 1998; Saez 2001; Salanié 1998; for (ii), see Piketty 1997; Bourguignon and Spadaro 2000; Choné and Laroque 2005).
Second, in Diamond's (1980) approach individuals respond via the extensive margin; i.e. they choose to work or not work. Marginal tax rates can be negative, suggesting at least the possibility of subsidizing the work of low earners. Third, Saez (2002) presents a unifying framework where individuals can respond via both margins. Support for one of the two income transfer schemes depends on the relative importance of both response margins and on the redistributive tastes of government. Saez proposes a sizeable basic income (around $7300 per year), but combined with a tax exemption at the bottom (for incomes up to $5000 per year).
In the same year of Mirrlees' seminal contribution, Rawls (1971) criticized the welfarist approach, in which only utilities are allowed to judge the desirability of different social states (see also Kolm 1968 for an early statement of this critique). Rawls (1982) presents the following example of expensive preferences. Otherwise identical individuals differ in their preferences towards food—some are happy with a simple meal, some only with an expensive one. Rawls asks whether we really want to distribute resources in such a way that those with expensive tastes get more resources than others. If we do not like such a distribution, we have to use an argument to decide which tastes are too expensive. Such an argument has to be based on non-utility factors; hence it implies a rejection of the welfarist approach.
In the aftermath of Rawls' influential work, many alternative theories of distributive justice were proposed. Although very diverse in equalizandum, they almost all had Dworkin's (1981)‘cut’ in common. Dworkin claims that not all individual characteristics can (should) be considered morally arbitrary; therefore one has to make a clear cut between endowments (e.g. skills, talents, handicaps) and ambitions (e.g. preferences, effort, tastes). Dworkin introduces personal responsibility: individuals are responsible for their ambitions—as long as they identify with them—but not for their endowments. As a consequence, a fair distribution scheme should be ambition-sensitive, but endowment-insensitive.
In an optimal income tax setting, fairness could require that differences in productive skill (endowment) be compensated for, but not differences in taste for working (ambition).1Schokkaert et al. (2004) introduce such fairness considerations in different ways and calculate the corresponding optimal linear income tax, which turns out to be positive. Allowing for nonlinear tax schemes, results change drastically. Boadway et al. (2002) analyse the optimal nonlinear income tax according to a weighted utilitarian or maximin social planner where different weights are chosen for different tastes. Negative marginal taxes (for the low income earners) are optimal where sufficient weight is given to the hard-working individuals. Fleurbaey and Maniquet (2006, 2007) characterize fair social orderings to analyse nonlinear income taxes. In both theoretical studies, it is optimal to direct the largest subsidies to the hard-working poor (the agents having the lowest skill and choosing the largest labour time), so long as the lowest skill is strictly positive.
In the next section we present a new fair allocation, coined a ‘Pareto-efficient and Shared Resources Equivalent’ (PESE) allocation. As the name suggests, the optimal allocation is Pareto-efficient and all individuals are indifferent between their bundle and what they would get if it were physically possible to divide or share all resources, including the productive skills. Section II characterizes a fair social ordering, which rationalizes the PESE allocation. In Section III we introduce a ‘discrete’Stiglitz (1982, 1987) economy with (i) four types of individuals (defined by a low or high productive skill and a low or high taste for working), and (ii) a government that wants to install fair taxes, but cannot observe individuals' type. We show that fairness recommends subsidizing the low earners, so long as the low-skilled individuals have a strictly positive skill. Where the low-skilled have a zero skill, subsidies can never be optimal. These theoretical results are in line with those found in Fleurbaey and Maniquet (2006, 2007). In Section IV we enhance realism by simulating fair taxes for Belgian singles, while carefully paying attention to the calibration of the compensation (hourly wages) and responsibility (taste for working) variable. Similar to the welfarist simulation results often found in Mirrlees economies, our non-welfarist fairness criterion also suggests a U-shaped pattern of positive marginal tax rates in almost all cases. Negative marginal tax rates, and hence ‘making work pay’ policies, can be optimal only in the unreasonable case in which all the unemployed are never willing to work.
I. EQUALITY OF RESOURCES REVISITED
When all resources in society are alienable and divisible, Dworkin (1981) proposes to divide resources equally (endowment insensitivity), followed by an auction to reallocate resources according to taste (ambition sensitivity). This leads to a Pareto-efficient and envy-free allocation. To study fair income taxation, however, we have to introduce productive resources (skills); these are not alienable, and therefore a problem arises. In labour economies Pareto-efficient and envy-free allocations do not, in general, exist.
A first class of solutions tries to extend the above Dworkinian auction by assigning property rights over leisure. Varian (1974) analyses two rather extreme solutions. One may divide consumption goods equally and either (i) assign each individual his own leisure, or (ii) give each individual an equal share in each of the agents' (including his own) leisure time. After trade, the resulting competitive (and hence Pareto-efficient) equilibria are called, respectively, (i) wealth-fair and (ii) income-fair. In the wealth-fair allocation, productive talents are a private good and the resulting allocation does not compensate at all for inabilities. In the income-fair allocation, productive talents are a collective good. The high-skilled worker has to buy back his expensive leisure and is therefore punished for being a high-skill type, resulting in a slavery of the talented. Intermediate solutions exist where skills are neither purely private nor purely collective (Fleurbaey and Maniquet 1996; Kolm 1996; Maniquet 1998).
A second class of solutions starts from the concept of fair equivalence (see e.g. Kolm 2004 for an overview and a critique). Pazner and Schmeidler (1978) define an allocation as fair-equivalent if everyone is indifferent between his bundle in this allocation and the bundle he would receive in a ‘hypothetical’ fair, i.e. envy-free, allocation. It then suffices to define an interesting ‘hypothetical’ fair allocation and to see whether there exist any Pareto-efficient ones, among all fair-equivalent allocations. The resulting allocation is called a ‘Pareto-efficient and fair-equivalent’ (PEFE) allocation. Pazner and Schmeidler (1978) propose an egalitarian allocation—where everybody consumes the same consumption–leisure bundle—as the fair one. We propose a different fair allocation, which we coin a ‘shared resources’ allocation. This is the one that would result if it were (physically) possible to divide or share all resources, including the productive ones. To make this idea more precise, we introduce some notation.
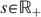 defines production (called gross income in the sequel) in a linear way, or y=sℓ, with ℓ∈[0,1] the amount of labour. We denote a skill profile by
defines production (called gross income in the sequel) in a linear way, or y=sℓ, with ℓ∈[0,1] the amount of labour. We denote a skill profile by  . Preferences—containing the trade-off between consumption and labour—are represented by continuously differentiable utility functions:
. Preferences—containing the trade-off between consumption and labour—are represented by continuously differentiable utility functions:
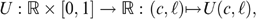
 .
.Individuals are (held) responsible for their tastes, but not for their skills. Therefore, we want to compensate individuals for different outcomes that are due only to different skills, but not for different outcomes that are caused only by different tastes for working. Where skills are alienable—think, e.g. of individuals as farmers who receive, as a matter of brute bad luck, either a blunt or a whetted scythe (the skill s) to harvest crops (the consumption c)—there is a particularly simple and attractive way to obtain a fair allocation:
- (a)
each individual pays (or receives) the same lump-sum amount of money
 ,
, - (b)
each individual can use each skill (including his own) for a time equal to 1/n at most.
Individuals are assumed to be rational: given (b), the budget set that maximizes net incomes (for all possible labour choices) starts using the highest skill for the first 1/n time units, followed by the second highest skill for an additional 1/n time units, and so on. Given a, we call such a budget set, the ‘shared resources’ budget set, and the resulting allocation (which ultimately depends on the tastes in society) is called the ‘shared resources’ allocation in the sequel.
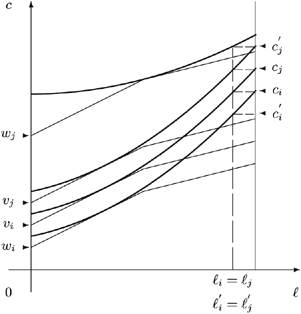
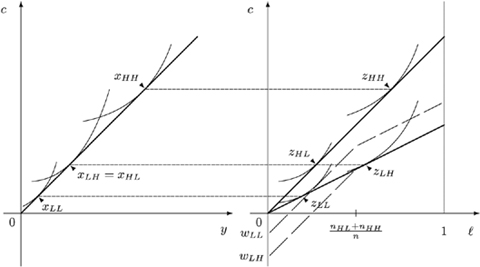
To illustrate these concepts, suppose (i) there are only two skill types possible in society, say low (L) and high (H), which are equally represented in the skill pool s, and (ii) there are only two possible tastes for working, also called low (L) and high (H). An allocation z=(zLL, zLH, zHL, zHH) contains one bundle 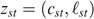 for each of the four types st, with s referring to the skill (low or high) and t referring to the taste (low or high). Figure 1 illustrates the budget sets and (resulting) allocations where (a) each individual receives the same lump-sum amount of money a but productive resources are not shared, and (a)+(b) each individual receives the same lump-sum amount a and in addition the productive resources are shared (each individual can work with each of the skills half-time at most).
for each of the four types st, with s referring to the skill (low or high) and t referring to the taste (low or high). Figure 1 illustrates the budget sets and (resulting) allocations where (a) each individual receives the same lump-sum amount of money a but productive resources are not shared, and (a)+(b) each individual receives the same lump-sum amount a and in addition the productive resources are shared (each individual can work with each of the skills half-time at most).
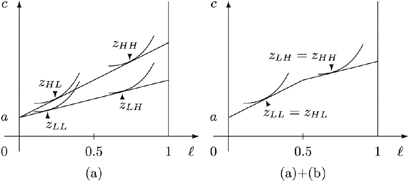
Allocation change when sharing productive resources.
Sharing productive resources is not technically feasible in many cases. Typically, owing to inborn characteristics such as intelligence, talents, handicaps and so on, labour market productivities are always inalienable. Still, we could consider as an interesting ‘hypothetical’ case the allocation that would arise if it were possible to divide and share all resources equally. But, the resulting hypothetical ‘shared resources’ allocation is not necessarily Pareto-efficient in the actual economy.2 Therefore, we propose to focus on the Pareto-efficient and Shared Resources Equivalent (PESE) allocation.
More precisely, given the skill and preference technology, it is possible to construct a unique allocation z such that, for each individual, the marginal rate of substitution equals his skill level (Pareto-efficient) and each individual is indifferent between his actual bundle and his bundle in a ‘shared resources’ allocation (shared resources equivalent, for a given lump-sum amount of money a in the hypothetical economy). Figure 2 illustrates this PESE allocation for the same economy as in Figure 1.3
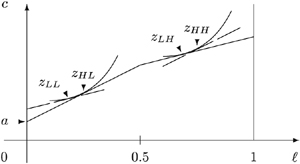
A Pareto-efficient and shared resources equivalent allocation.
We are now ready to define a PESE allocation in general. Let  be the set of allocations
be the set of allocations  , containing one bundle zi=(ci, ℓi) for each individual i in N. We define a well-being concept closely linked to the PESE allocation.
, containing one bundle zi=(ci, ℓi) for each individual i in N. We define a well-being concept closely linked to the PESE allocation.
-
Well-being: For each allocation
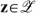 , the vector of well-being levels
, the vector of well-being levels 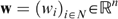 is defined by the amounts of money wi that would make individual i indifferent between (i) receiving (or paying) this amount of money wi and sharing all productive resources equally, and (ii) his actual bundle zi. Because the well-being vector w depends on the allocation z and the economy e=(s, U), we write w=W(z, e), with wi=Wi(z, e).
is defined by the amounts of money wi that would make individual i indifferent between (i) receiving (or paying) this amount of money wi and sharing all productive resources equally, and (ii) his actual bundle zi. Because the well-being vector w depends on the allocation z and the economy e=(s, U), we write w=W(z, e), with wi=Wi(z, e).
Notice that in the PESE allocation presented in Figure 2 the well-being levels are the same for all individuals and are equal to a. This leads to the following general definition of PESE allocations, which belong to Pazner and Schmeidler's (1978) class of PEFE allocations.
-
PESE allocation: An allocation
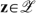 is a PESE allocation if and only if z is Pareto-efficient and all individuals have the same well-being.
is a PESE allocation if and only if z is Pareto-efficient and all individuals have the same well-being.
II. A ‘SHARED RESOURCES’ SOCIAL ORDERING
In cases where it is not possible to recognize the less from the more productive and the lazy from the hard-working individuals, it is more convenient to characterize a ‘shared resources’ social ordering for such a second-best setting.
We start with two observations. First, a bundle that puts an individual on a higher indifference curve leads to a higher well-being level (and vice versa). As such, our definition of well-being corresponds with one specific but, according to us, interesting cardinalization of preferences. Second, well-being has to be interpreted as a ‘relative’ measure of fair treatment, in the spirit of the PESE allocation. If two individuals had the same well-being, they would be treated equally fairly, because both individuals would be indifferent between their actual bundle and the bundle they would choose if (a) they received the same lump-sum amount of money and (b) all productive resources were shared equally. If one individual had a strictly lower well-being than another, he would be treated unfairly with respect to the other, because both individuals would be indifferent between their actual bundle and the bundle they would choose if (b) all productive resources were shared equally, but (a) the former individual received a strictly lower lump-sum amount of money.
Because for each individual well-being is ordinally equivalent to utility (point one in the previous discussion), we want social welfare to increase when all well-beings increase: this guarantees that the weak Pareto principle—strictly higher utilities should lead to strictly higher social welfare—is satisfied. At the same time, well-being differences are due to unfair treatment (point two in the previous discussion), which we want to eliminate as much as possible. Therefore, a fair social ordering should combine Pareto efficiency with a maximal priority for the worst-off in terms of well-being. More precisely, the ordering should satisfy the following property.
-
Fairness: For each economy
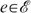 and for all allocations
and for all allocations  implies that z should be strictly socially preferred to z′.
implies that z should be strictly socially preferred to z′.
First, possible candidates are the maximin and the leximin rule applied to well-beings, but in the sequel we do not bother about ranking allocations with equal minimal well-being levels, basically because the above definition is sufficient for optimization purposes. Second, the ‘shared resources’ social ordering has some formal similarity with Fleurbaey and Maniquet's (2005)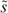 -implicit budget leximin function, where
-implicit budget leximin function, where 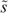 is a reference skill level. In the present case, the reference skill
is a reference skill level. In the present case, the reference skill 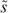 is piece-wise linear and endogenously defined by the skill pool in society. As such, laissez-faire allocations are selected where all individuals have the same skill. Third, some readers might find the chosen priority too extreme; this extreme viewpoint can be easily derived from weaker assumptions, our next topic.
is piece-wise linear and endogenously defined by the skill pool in society. As such, laissez-faire allocations are selected where all individuals have the same skill. Third, some readers might find the chosen priority too extreme; this extreme viewpoint can be easily derived from weaker assumptions, our next topic.
We discuss the issue here in an informal way, while providing a characterization result in Appendix A. First, we restrict ourself to a ‘consequentialist’ social ordering, which here means that only individual well-being levels matter for social evaluation. We can interpret consequentialism here as a responsibility axiom: individual utility levels are irrelevant to rank allocations. Furthermore, we add Fleurbaey and Maniquet's (2006) principle to compensate for differences in outcomes that are due only to differences in skills. More precisely, their compensation principle is a weak one: it requires only that a Pigou–Dalton transfer (in terms of net income) from a rich to a poor individual—with both the same preferences and the same labour—should be welfare-improving. Combining consequentialism with this weak compensation principle leads to a much stronger principle, called Hammond's (1976) equity: if one individual is worse off than another (in terms of well-being), then any increase in the former's well-being at the cost of any decrease in the latter's well-being should be approved of. A similar result occurs in Fleurbaey and Maniquet (2006). Once Hammond equity is obtained, it is only a small step to the above fairness definition. More precisely, it suffices to add the Pareto principle: higher utilities and thus higher well-beings improve social welfare.
III. FAIR TAXES: THEORY
In the previous section we characterized a fair social ordering, inspired by the PESE allocation. In this section we analyse what happens when the government uses this fair social ordering to calculate optimal taxes in a discrete Stiglitz economy (1982, 1987) with four types, which are not observable to the government.
All individuals in N={1, …, n} can have four types, denoted (s, t)∈S×T, where s is the skill level and t the taste for working; we abbreviate types as st∈ST. Each type st is represented by nst>0 individuals, with 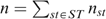 . Skills can be low or high, or s∈S={L,H}, with 0<L<H; later on, we come back to the issue of zero skills. Tastes for working can also be low or high, or t∈{L,H}, which correspond with a utility function Ut.4
. Skills can be low or high, or s∈S={L,H}, with 0<L<H; later on, we come back to the issue of zero skills. Tastes for working can also be low or high, or t∈{L,H}, which correspond with a utility function Ut.4
As before, utility functions belong to 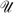 , but we impose some additional properties. Let Vst represent the preferences in the consumption–income space for type st; more precisely,
, but we impose some additional properties. Let Vst represent the preferences in the consumption–income space for type st; more precisely, 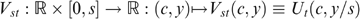 .5 We impose two additional properties on the utility functions Ut (see Stiglitz 1982, 1987 for the first and Boadway et al. 2002 for the second property):
.5 We impose two additional properties on the utility functions Ut (see Stiglitz 1982, 1987 for the first and Boadway et al. 2002 for the second property):
-
Single-crossingness: A higher taste for working t corresponds with a lower marginal rate of substitution (denoted
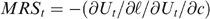 ), expressing the view that individuals with a higher taste for working require less compensation (in terms of net income c) for working a little longer. Formally: MRSL>MRSH in
), expressing the view that individuals with a higher taste for working require less compensation (in terms of net income c) for working a little longer. Formally: MRSL>MRSH in  .
. -
Indistinguishable middle type: The types LH and HL have the same preferences in the consumption–income space. Formally, there exists a continuous and strictly increasing function
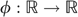 , such that
, such that 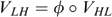 in
in 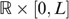 .
.
 ) are also single-crossing; more precisely,
) are also single-crossing; more precisely,
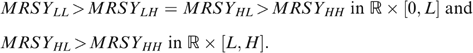
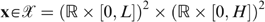 , containing one bundle xst=(cst, yst) for each type st∈ST. The programme of the government is to find the best allocation(s) x—‘best’ according to the fair social ordering defined in Section II— subject to (i) incentive compatibility constraints (no type envies another type's bundle) and (ii) a feasibility constraint (the sum of all taxes is larger than the government requirement
, containing one bundle xst=(cst, yst) for each type st∈ST. The programme of the government is to find the best allocation(s) x—‘best’ according to the fair social ordering defined in Section II— subject to (i) incentive compatibility constraints (no type envies another type's bundle) and (ii) a feasibility constraint (the sum of all taxes is larger than the government requirement  ). Recall our definition of well-being in Section I; with a slight abuse of notation, we write the well-being of type st in allocation x as wst=Wst(x, e). We get
). Recall our definition of well-being in Section I; with a slight abuse of notation, we write the well-being of type st in allocation x as wst=Wst(x, e). We get
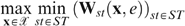 ((*))
((*))-
Incentive compatibility constraints IC st,(st)′:
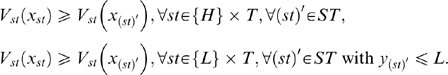
-
Feasibility constraint:
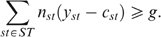
Since the programme defined by (*) focuses on minimal well-being, the equity–efficiency trade-off is extreme: priority is given to the worst off (in terms of well-being), irrespective of the change in the average well-being level. The traditional welfarist optimal tax literature captures the equity–efficiency trade-off by the social marginal value of consumption as a function of income, expressed in terms of the value of public funds; see e.g. Saez (2001). In the present non-welfarist approach this trade-off is more complex: it is captured by a function of all well-beings—putting all weight on the worst-off—where each well-being is in turn a function of the received consumption–income bundle as well as the individual's taste for working and the skill profile in society. As a result, the social marginal value of consumption can differ for taxpayers with the same income. For example, when the LH type has the lowest well-being, the LH and HL types might have the same income (owing to the ‘indistinguishable middle type’-property), but different social marginal values of consumption.
Consider now an economy with four types {LL, LH, HL, HH}, with strictly positive skills and tastes represented by utility functions satisfying single-crossingness and indistinguishable middle type. Figure 3 presents the laissez-faire outcome for such a particular economy (with g=0). Notice that the dashed lines—with the kink at 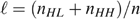 , the proportion of high skilled—in the right hand panel allow us to measure individual well-being. In Lemma 1 of Appendix B, we show that in any implementable allocation type LL cannot have a higher well-being than type HL, and type LH cannot have a higher well-being than type HH. Hence, programme (*) can focus on the low-skilled types LL and LH. In the laissez-faire equilibrium of Figure 3, type LH has a lower well-being than type LL. Therefore programme (*) departs from this laissez-faire situation by increasing type LH's (and type HL's) well-being at the cost of decreasing some other types' well-being.
, the proportion of high skilled—in the right hand panel allow us to measure individual well-being. In Lemma 1 of Appendix B, we show that in any implementable allocation type LL cannot have a higher well-being than type HL, and type LH cannot have a higher well-being than type HH. Hence, programme (*) can focus on the low-skilled types LL and LH. In the laissez-faire equilibrium of Figure 3, type LH has a lower well-being than type LL. Therefore programme (*) departs from this laissez-faire situation by increasing type LH's (and type HL's) well-being at the cost of decreasing some other types' well-being.
Laissez-faire equilibrium for a particular economy.
The resulting allocation ‘makes work pay’: contrary to the low-income type LL, the middle-income types LH and HL receive a subsidy. Such a ‘making work pay’ feature still holds at the optimum. Proposition 1 tells us that the lowest income type, the ‘undeserving poor’ with type LL, must always receive lower subsidies (or pay higher taxes) than the second lowest income type, the ‘hard-working poor’ with type LH; this result is in line with Fleurbaey and Maniquet (2006, 2007).6
Proposition 1. Consider a four type economy with skills 0<L<H and tastes represented by utility functions 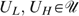 , which satisfy single-crossingness and indistinguishable middle type. Consider a government who optimizes the programme defined by (*). In an optimal allocation
, which satisfy single-crossingness and indistinguishable middle type. Consider a government who optimizes the programme defined by (*). In an optimal allocation  we must have
we must have 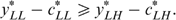
We have to put this result in perspective, however. Although it is reasonable to assume that all individuals (with a capacity for work) have strictly positive productive skills, some might be constrained in their choice owing to labour market frictions. Minimum wage laws, rationing and so on may prevent individuals, in particular the low-skilled, from working. Suppose, in our four-type economy, that the low-skilled individuals are willing, but cannot work because of such constraints, which are beyond their responsibility. In such a case their skills are nullified and, as shown in Appendix B, the LH-type individuals always have the lowest level of well-being. Because these individuals will never work, maximizing the minimal well-being boils down to maximizing the basic income in society; see Fleurbaey and Maniquet (2006, 2007) for a similar result. This turns Proposition 1 round, or, the LL- and LH-type individuals (with 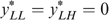 ) must always receive higher subsidies (or pay lower taxes) than the second lowest income type (here the HL-type individuals). Notice that the ‘indistinguishable middle type’-property is not needed for this result.
) must always receive higher subsidies (or pay lower taxes) than the second lowest income type (here the HL-type individuals). Notice that the ‘indistinguishable middle type’-property is not needed for this result.
Proposition 2. Consider a four-type economy with skills L=0<H and tastes represented by utility functions 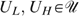 which satisfy single-crossingness. Consider a government that optimizes the programme defined by (*). In an optimal allocation
which satisfy single-crossingness. Consider a government that optimizes the programme defined by (*). In an optimal allocation  , we must have
, we must have 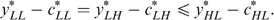
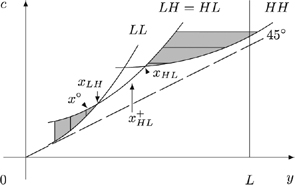
Propositions 1 and 2 are both based on simple fictitious economies. In Proposition 1 everyone is able to work, whereas in Proposition 2 the low-skilled types LL and LH cannot work, even if they want to. In a more realistic setting, unemployment is the result of a low ability and/or a low willingness to work. Consider now the following economy {0K, L0, LK′, HK′}, where the first two types never work but for different reasons: type 0K is never able to work because his skill equals zero, and type L0 is not willing to work, where t=0 denotes an infinite work aversion. Figure 4 presents the laissez-faire allocation for such an economy.
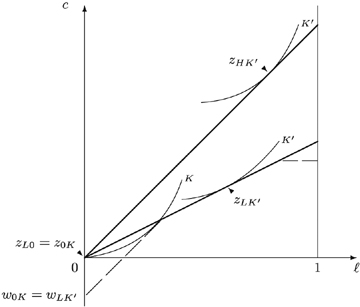
A more realistic scenario.
As before, type LK′ can never have a greater well-being than type HK′. Also, type 0K can never have a greater well-being than type L0. So programme (*) can focus on types 0K and LK′. In this economy it is not clear whether 0K or LK′ has the lowest well-being. We have constructed Figure 4 in such a way that both types have the same well-being.
However, choosing a lower (resp. higher) taste for working for type 0K would lead to a higher (resp. lower) well-being for type 0K. This indeterminacy leaves open whether it is optimal to ‘make work pay’ in a more realistic setting. At least one could expect that the higher the taste for working for type 0K, the higher the optimal basic income would be. This intuition will be confirmed in the next section, where we simulate fair taxes for a sample of Belgian singles. Simulation allows us to focus (i) more realistic economies with many different types and, more importantly, (ii) different and more realistic scenarios concerning the willingness of the unemployed to work. The different scenarios in (ii) have a crucial impact on the tax benefit scheme for the low earners.
IV. FAIR TAXES: SIMULATION RESULTS
Calibration
We use a sample of singles from the 1997 wave of the Panel Study for Belgian Households.7 We include only singles with a capacity for work (students, pensioners, sick or handicapped singles are excluded). We observe (i) the pre-tax yearly labour income y; (ii) the amount of labour ℓ, normalized such that 0ℓ1, where ℓ=1 corresponds to 2925 hours, i.e. 45 weeks times 65 hours; (iii) the gross hourly wage rate σ (observed only for those who worked, i.e. both y,ℓ≠0), which leads to a gross yearly wage rate s=2925σ; and (iv) the total net unemployment benefit β (observed only for those who were partly or completely unemployed in 1997), from which we derive the net yearly unemployment benefit b=β/(1−ℓ), i.e. the net unemployment benefit one would obtain if full-time unemployed (ℓ=0).
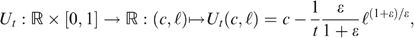
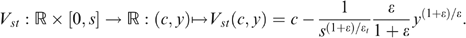
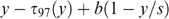 , with τ97(·) the actual tax system for singles in Belgium in 1997 (reported in Appendix C) and b(1−y/s) the benefit when working ℓ=y/s units of time. Both the separate tax and benefit parts and the resulting budget set (the solid line), are illustrated in Figure 5.
, with τ97(·) the actual tax system for singles in Belgium in 1997 (reported in Appendix C) and b(1−y/s) the benefit when working ℓ=y/s units of time. Both the separate tax and benefit parts and the resulting budget set (the solid line), are illustrated in Figure 5.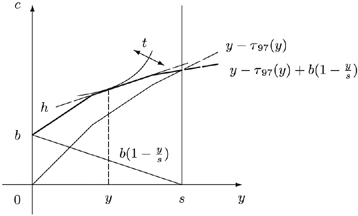
Calibration of the taste parameter t.
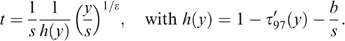
Second, since we could observe only gross yearly wages s (resp. net yearly unemployment benefits b) for individuals who worked in 1997 (resp. individuals who received unemployment benefits in 1997), we complete our data-set by imputing values for s and b, whenever unobserved, via a Heckman selection model (see Greene 2003 for a definition). Thus, in estimating s and b, we correct for a possible sample selection bias resulting from the fact that we observe only wages s for those who worked and benefits b for those who were (permanently or temporarily) unemployed. The variables used for the imputation as well as the estimation results are described in Appendix D.10
We end up with a heterogeneous sample of 621 singles who differ in the skills s and tastes t that drive their labour market behaviour; Appendix E contains some descriptive statistics for our data-set. Two points are worth mentioning here. The non-responsibility parameter s and the responsibility parameter t in our data-set are barely correlated: using a low labour supply elasticity ɛ=0.1 for singles, the correlation between s and t equals −0.071, suggesting independently distributed skills and tastes. With a strong correlation, compensating for skills only (and not for tastes) would be a dubious exercise. In addition, given the nature of our quasi-linear preferences, all unemployed receive a taste for working t=0. Put differently, all unemployed are considered unwilling to work. We relax this crucial assumption later on.
Results
Rather than using allocations as in the government programme (*), we use a piecewise linear tax benefit scheme as our instrument to approximate a nonlinear tax scheme. As we are concerned mainly with the lowest incomes, we consider a piecewise linear tax benefit scheme up to yearly gross earnings of €20,000 in steps of €500 and we use a constant marginal tax rate afterwards. Using either a wider range of piecewise linear taxes (up to €80,000 in steps of €500) or a finer grid (up to €20,000 in steps of €250) does not change our results for the lowest incomes drastically. Remarkably, using a wider range leads to approximately constant marginal tax rates for incomes above €20,000 which, except for the very high incomes, approximate 1/(1+s), the optimal linear tax rate when maximizing basic income (see Atkinson 1995). Given such a tax benefit scheme, individuals choose their best bundle (according to their tastes and skills), and therefore incentive constraints are automatically satisfied. For the feasibility constraint, we use the total government requirement (g) in the actual system, which (in per capita terms) is equal to 3851. Finally, to obtain realistic proposals, we add participation constraints to the government programme (*), such that no one prefers the bundle (0,0) to the allocated bundle in the optimum.
Three simulations
In this subsection we report and discuss simulation results for three cases: a sensitivity analysis with respect to the main parameters is postponed to the next subsection. No income effects and a low labour supply elasticity do not seem unrealistic for singles; see e.g. Blundell and MaCurdy (1999) for an empirical assessment. Using a labour supply elasticity ɛ=0.1, Figure 6 depicts the chosen bundles in the consumption–gross income space for the following cases.11
Optimal allocation for the Rawlsian case, the 100% and<100% case.
First, we present the Rawlsian optimal allocation (denoted RAWLS in Figure 6), i.e. the one that maximizes the basic income, as a benchmark case. This installs a high basic income equal to €9363 and high (and almost constant) positive marginal tax rates for the bottom incomes.
Second, we show the optimal allocation according to our fair social ordering in the extreme case that all unemployed are never willing to work (denoted 100% in Figure 6). This gives a low (yearly) basic income equal to €518, moderate subsidies fading in around €3000 and fading out around €10,500, followed by progressive taxes. Thus, it seems fair to ‘make work pay’, even if it brings about a very low basic income.
Third, the 100% case is clearly an extreme viewpoint. For example, minimum wage laws in Belgium could keep some individuals (especially those with low skills s) from working, and therefore our calibration might underestimate their true taste parameter t, thereby overestimating their well-being level w. More reasonably, at least some of the observed unemployment must be involuntary, especially in the case of singles. Suppose unemployment is voluntary for p% of the unemployed: their taste levels remain equal to zero. The other (1−p)% are constrained; i.e. although they would like to work, they are and will always remain constrained at y=0, but we want to use their ‘true’ taste parameter to calculate well-being levels. Taste levels are unfortunately unknown (and difficult to infer from our data), therefore we assume that all the constrained unemployed can be assigned the same taste level in a way to be explained later on. Although it simplifies matters, giving them the same taste level allows us to disregard the exact value of p, so long as it differs from 100%. The reason is that all the constrained unemployed end up with the same well-being and our maximin-type criterion is not sensitive to population size. Thus, for example, only one (or all but one) constrained unemployed individuals would lead to the same result. For the moment, we suppose that the tastes of the unemployed equal the average taste of those currently working. Although one might be inclined to choose a lower taste level for the constrained unemployed, we refer to the fact that skills and tastes in our data-set are approximately uncorrelated.
The optimal allocation for this case is denoted<100% in Figure 6.12 We get a sizeable basic income of €6318. In addition, it displays a U-shaped pattern of positive marginal tax rates: high marginal taxes for the bottom incomes, followed by an almost neutral region (for incomes between €4000 and €10,500) and again high marginal taxes afterwards. Although not all individuals with zero skill are able to work (as in Proposition 2 of Section III), the<100% case does not maximize the basic income. Recall from the discussion at the end of Section III that individuals with zero skill do not necessarily have the lowest well-being in more realistic economies.
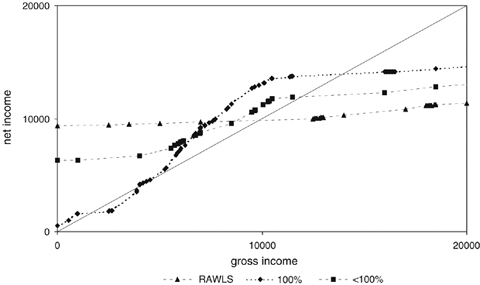
Table 1 summarizes for all three cases (in columns) and for different gross income groups G (in rows) (i) the proportion of individuals |G|/n and (ii) the average tax rate (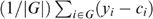 ). Average tax rates are monotonically increasing in gross income, except in the 100% case, which is in line with our previous observation that ‘making work pay’ can be optimal only in the unreasonable case where none of the unemployed is ever willing to work.
). Average tax rates are monotonically increasing in gross income, except in the 100% case, which is in line with our previous observation that ‘making work pay’ can be optimal only in the unreasonable case where none of the unemployed is ever willing to work.
| Income group | Rawls | 100% | <100% | |||
|---|---|---|---|---|---|---|
| Prop. | Avg. tax | Prop. | Avg. tax | Prop. | Avg. tax | |
| 0 | 0.21 | −€9363 | 0.19 | −€518 | 0.19 | −€6318 |
| 0<y5000 | 0.07 | −€5595 | 0.05 | −€98 | 0.05 | −€4294 |
| 5000<y10,000 | 0.06 | −€2679 | 0.06 | −€2222 | 0.05 | −€1610 |
| 10,000<y15,000 | 0.14 | €3370 | 0.17 | −€2424 | 0.18 | −€615 |
| 15,000<y20,000 | 0.26 | €7205 | 0.23 | €2785 | 0.24 | €4972 |
| 20,000<y | 0.26 | €15,856 | 0.30 | €13,104 | 0.29 | €14,714 |
Sensitivity analysis
As we believe that no one would be willing to defend the 100% case, we focus on the <100% case for our sensitivity analysis. We investigate the impact of changing (i) the labour supply elasticity and (ii) the taste level assigned to the constrained unemployed. Although we arbitrarily choose to halve and double the original parameter values, other choices lead to the same qualitative results.
First, the labour supply elasticity ɛ equalled 0.1 in our previous simulations. Figure 7 shows the impact of halving and doubling ɛ on our optimal allocation. For comparison, we still present the three cases depicted in Figure 6, here denoting the <100% case by ‘eps=0.1’ for obvious reasons.
Measuring the impact of varying ɛ.
Changing ɛ has a large impact on both marginal tax rates and installed basic income, but the U-shaped pattern of marginal tax rates remains intact; see Saez (2001) for similar results in welfarist Mirrlees economies. As expected, choosing a higher labour supply elasticity leads to lower marginal tax rates everywhere, and for a given budget constraint it installs a (substantially) lower basic income. Furthermore, it introduces subsidies for gross income earners between €6000 and €10,000, but even so the largest subsidies are directed towards the unemployed. For lower values of ɛ, marginal tax rates are everywhere positive, excluding ‘making work pay’-type policies.
Second, the taste level assigned to the constrained unemployed equalled the average taste of the working class in the previous section. Here we consider two additional cases: half the average taste of those currently working (denoted HALF in Figure 8) and double of the average taste (denoted DOUBLE in Figure 8). These variants have a clear interpretation. The HALF case (resp. DOUBLE case) corresponds with the assumption that each constrained unemployed needs twice as much (resp. half as much) as the additional consumption for a unit of additional labour for the ‘average’ worker. Figure 8 presents the HALF and DOUBLE cases, as well as all cases displayed in Figure 6, denoting the <100% case by ONE.
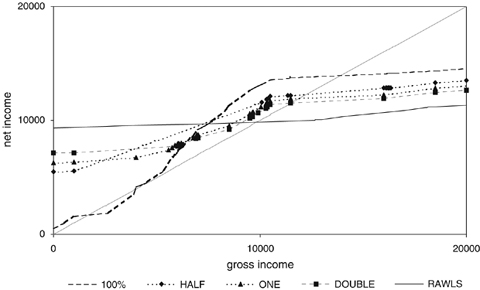
Measuring the impact of varying tastes.
Choosing less or more conservative estimates for the tastes of the constrained unemployed plays a moderate role. As expected from our discussion of Figure 4 in the previous section, the greater their taste for working, the lower their well-being, which puts upward pressure on the optimal basic income. Furthermore, halving or doubling the assigned taste level does not alter the U-shaped pattern of positive marginal tax rates.
To conclude, our sensitivity analysis suggests that a U-shaped pattern of marginal tax rates is optimal according to our fairness criterion. Furthermore, negative marginal tax rates and hence ‘making work pay’ policies never occur except for higher labour supply elasticities.
V. CONCLUSION
Given the increased importance that many governments attach to ‘making work pay’ policies, we examine whether subsidizing low earners is optimal according to a specific ‘fair’ social ordering. Fairness considerations are kept simple in this paper: we want to compensate individuals for differences in productive skills, but we keep them responsible for their tastes for working.
We consider a discrete Stiglitz (1982, 1987) economy with four types—defined by a low or high productive skill and a low or high taste for working—and a government that wants to install fair taxes, but cannot observe individuals' type. We show that fairness recommends subsidizing the low earners, as long as the low-skilled individuals have a strictly positive skill. Where the low-skilled have a zero skill, subsidies can never be optimal.
As these theoretical results hold only for simple fictitious economies, we simulate fair taxes for a sample of Belgian singles. Our fairness criterion suggests a U-shaped pattern of positive marginal tax rates in almost all cases. This strongly suggests that negative marginal tax rates, and hence ‘making work pay’ policies, cannot be optimal in the reasonable case in which at least some unemployed are willing to work but cannot, owing to exogenous labour market constraints.
ACKNOWLEDGMENTS
We would like to thank Geert Dhaene, Marc Fleurbaey, Serge-Christophe Kolm, François Maniquet, Kristian Orsini, Glenn Rayp, Erik Schokkaert and Dirk Van de gaer; also seminar participants at Namur and Tilburg and conference participants at PET (Marseille, 2005) and EEA (Amsterdam, 2005) for useful comments. Roland Iwan Luttens gratefully acknowledges financial support from the Federal Public Planning Service Science Policy (Interuniversity Attraction Poles Program—Belgian Science Policy, contract no. P5/21) Roland Iwan Luttens and Erwin Ooghe are postdoctoral fellows of the Fund for Scientific Research—Flanders.
NOTES
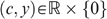 .
.
Appendices
APPENDIX A: A CHARACTERIZATION
We provide a characterization for the rule presented in Section II. A rule f maps economies into orderings, or 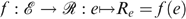 , with
, with 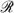 the set of all orderings (complete and transitive binary relations) defined over allocations z in
the set of all orderings (complete and transitive binary relations) defined over allocations z in 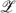 ; call Pe and Ie the corresponding asymmetric and symmetric relation. We define some properties for f.
; call Pe and Ie the corresponding asymmetric and symmetric relation. We define some properties for f.
Our Pareto principle is equal to the Pareto Indifference and the Weak Pareto Principles together; i.e. if everyone is indifferent between allocations z and z′, then z should also be socially indifferent to z′, and if everyone strictly prefers allocation z to z′, then z should also be socially strictly preferred to z′. Formally:
-
Pareto: For each economy
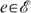 and for all allocations
and for all allocations 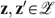 : If
: If 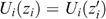 for all i∈N, then zIez′. If,
for all i∈N, then zIez′. If, 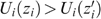 for all i∈N, then zPez′.
for all i∈N, then zPez′.
In line with the idea of compensating for differences in outcomes which are due only to differences in skills, compensation (Fleurbaey and Maniquet 2006) suggest that a Pigou–Dalton transfer (in terms of net income) from a rich to a poor individual with the same preferences and the same labour should be welfare-improving:
-
Compensation: For each economy
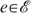 , for all allocations
, for all allocations 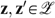 and for all individuals i, j∈N: if (i)
and for all individuals i, j∈N: if (i) 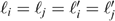 and Ui=Uj, (ii) ∃δ>0 such that
and Ui=Uj, (ii) ∃δ>0 such that 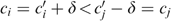 and (iii)
and (iii) 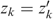 for all k≠i, j, then zRz′.
for all k≠i, j, then zRz′.
Finally, in line with (i) our well-being definition and (ii) the idea that individuals are responsible for their tastes, Utility Independence requires the ranking of two allocations to be the same (i) whenever they give rise to the same well-being vector, (ii) irrespective of the utility profile:
-
Utility independence: For all economies
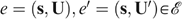 , and for all allocations
, and for all allocations 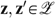 : If W(z, e)=W(z, e′) and W(z′, e)=W(z′, e′), then
: If W(z, e)=W(z, e′) and W(z′, e)=W(z′, e′), then  .
.
Given these axioms, we should focus on the minimal well-being in society:
Proposition A1. If a rule 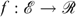 satisfies Pareto, Compensation and Utility Independence, then, for each economy
satisfies Pareto, Compensation and Utility Independence, then, for each economy 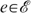 and for all allocations
and for all allocations 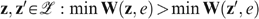 implies zPez′.
implies zPez′.
Proof. First, we show in three steps that Pareto Indifference (the first part of the Pareto axiom) and Utility Independence for f are equivalent with Neutrality for f:
-
Neutrality: For all economies
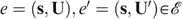 and for all allocations
and for all allocations 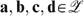 : If W(a, e)=W(b, e′) and W(c, e)=W(d, e′), then
: If W(a, e)=W(b, e′) and W(c, e)=W(d, e′), then 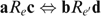 .
.
- 1
If f satisfies Neutrality then it also satisfies Pareto Indifference. Suppose the antecedent of Pareto Indifference is true for a certain economy
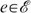 and two allocations
and two allocations 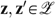 ; i.e.
; i.e. 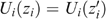 for all i∈N. As such, zi lies on the same indifference curve as
for all i∈N. As such, zi lies on the same indifference curve as 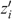 for all individuals and, by definition of our well-being concept, W(z, e)=W(z′, e). Let e′=e, and define allocations a=d=z and b=c=z′. As a consequence, W(a, e)=W(b, e′) and W(c, e)=W(d, e′) are true by construction. Using Neutrality, we get
for all individuals and, by definition of our well-being concept, W(z, e)=W(z′, e). Let e′=e, and define allocations a=d=z and b=c=z′. As a consequence, W(a, e)=W(b, e′) and W(c, e)=W(d, e′) are true by construction. Using Neutrality, we get 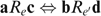 , or, equivalently,
, or, equivalently,  (·). Because of completeness of Re, we must have either zRez′(and also z′Rez via (·)) or z′Rez (and also zRez′ via (·)). Both cases lead to zIez′, establishing Pareto Indifference.
(·). Because of completeness of Re, we must have either zRez′(and also z′Rez via (·)) or z′Rez (and also zRez′ via (·)). Both cases lead to zIez′, establishing Pareto Indifference. - 2
If f satisfies Neutrality, then it also satisfies Utility Independence. Suppose the antecedent of Utility Independence is true, i.e. that there exist two economies,
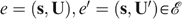 , and two allocations,
, and two allocations, 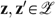 , such that
, such that 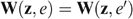 and
and 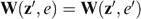 . Simply choose a=b=z and c=d=z′ such that W(a, e)=W(b, e′) and W(c, e)=W(d, e′) holds. Using Neutrality, we get
. Simply choose a=b=z and c=d=z′ such that W(a, e)=W(b, e′) and W(c, e)=W(d, e′) holds. Using Neutrality, we get 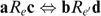 , or, equivalently,
, or, equivalently,  , establishing Utility Independence.
, establishing Utility Independence. - 3
If f satisfies Pareto Indifference and Utility Independence, then it also satisfies Neutrality. Suppose the antecedent of Neutrality holds, i.e. that there exist two economies, e=(s, U) and
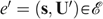 , and four allocations,
, and four allocations, 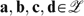 , such that
, such that 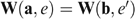 and
and 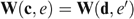 . Let us focus on an arbitrary individual i∈N. Because
. Let us focus on an arbitrary individual i∈N. Because 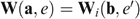 , the indifference curves of Ui through ai and of
, the indifference curves of Ui through ai and of 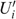 through bi are tangent to the same ‘shared resources’ opportunity set defined by s. Given
through bi are tangent to the same ‘shared resources’ opportunity set defined by s. Given  , both indifference curves must cross at least once in
, both indifference curves must cross at least once in  . Choose a bundle αi where both cross. Repeating this construction of αi for all individuals, we get an allocation
. Choose a bundle αi where both cross. Repeating this construction of αi for all individuals, we get an allocation  such that
such that 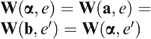 . In the same way, define an allocation
. In the same way, define an allocation 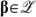 such that
such that 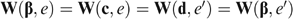 . Using Pareto Indifference and transitivity of Re and Re′, we get
Using Utility Independence, we get
. Using Pareto Indifference and transitivity of Re and Re′, we get
Using Utility Independence, we get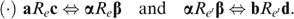
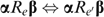 . Using (·), we get
. Using (·), we get 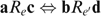 , establishing Neutrality.
, establishing Neutrality.
Second, a rule f satisfies Neutrality if and only if there exists a unique ordering R* defined over  , such that, for each economy
, such that, for each economy  and for all allocations
and for all allocations 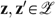 we have zRez′ if and only if
we have zRez′ if and only if 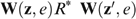 . It suffices to notice that our setup is sufficiently rich to obtain consequentialism: for any two well-being vectors
. It suffices to notice that our setup is sufficiently rich to obtain consequentialism: for any two well-being vectors 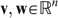 , there exist two allocations
, there exist two allocations 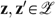 and an economy
and an economy 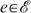 such that
such that 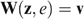 and
and 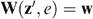 ; we refer to Bossert and Weymark (2004, theorem 2) for a proof. Consequentialism has to be interpreted as follows: only well-being levels matter to rank two allocations (given a fixed size n of the population and a fixed skill vector s).
; we refer to Bossert and Weymark (2004, theorem 2) for a proof. Consequentialism has to be interpreted as follows: only well-being levels matter to rank two allocations (given a fixed size n of the population and a fixed skill vector s).
Third, the unique ordering R* inherits certain properties from f: R* must satisfy weak Pareto* (if vi>wi for all i∈N, then 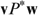 ). This follows from Pareto and Anonymity for f straightforwardly. We show that, given Compensation for f, R* must also satisfy the following.
). This follows from Pareto and Anonymity for f straightforwardly. We show that, given Compensation for f, R* must also satisfy the following.
-
Hammond equity * : For all well-being vectors
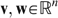 and for all individuals i, j∈N, if (i) wi<vi<vj<wj and (ii) vk=wk for all k≠i, j, then
and for all individuals i, j∈N, if (i) wi<vi<vj<wj and (ii) vk=wk for all k≠i, j, then 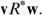
Suppose the antecedent of Hammond Equity* holds, or there exist two well-being vectors 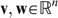 and two individuals i, j∈N such that wi<vi<vj<wj and vk=wk for all k≠i, j hold.
and two individuals i, j∈N such that wi<vi<vj<wj and vk=wk for all k≠i, j hold.
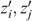 and a utility function
and a utility function 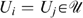 such that
such that 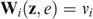 ,
, 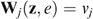 and
and 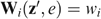 ,
, 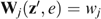 and the antecedents of the Compensation principle are satisfied for i, j; i.e. (i)
and the antecedents of the Compensation principle are satisfied for i, j; i.e. (i) 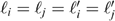 and Ui=Uj; and (ii) ∃δ>0 such that
and Ui=Uj; and (ii) ∃δ>0 such that 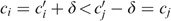 . The bundles zi, zj and
. The bundles zi, zj and 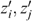 can be extended with bundles
can be extended with bundles 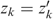 for the other individuals k≠i, j to obtain allocations z and z′, such that
for the other individuals k≠i, j to obtain allocations z and z′, such that  holds for all k≠i, j. Using Compensation, we must have zRez′, and thus, via neutrality, also
holds for all k≠i, j. Using Compensation, we must have zRez′, and thus, via neutrality, also 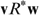 must hold.
[ Compensation and Neutrality imply Hammond Equity*.]
must hold.
[ Compensation and Neutrality imply Hammond Equity*.] Finally, under weak Pareto* and Hammond Equity* for R*, it can be easily verified that vP*w holds whenever min v>min w for any vectors  , which, given neutrality, completes our proof.
, which, given neutrality, completes our proof.
APPENDIX B: PROOFS OF PROPOSITIONS 1 AND 2
To prove Propositions 1 and 2, we need two ‘tricks’ and two lemmas. We start with the tricks.
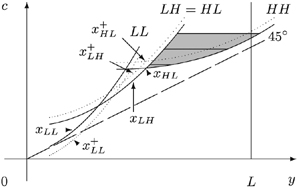
 as in Figure A2. The bundles xLL and xHH lie somewhere in the left and right shaded zones, respectively, to satisfy the incentive constraints. The bundle x° is constructed to satisfy
as in Figure A2. The bundles xLL and xHH lie somewhere in the left and right shaded zones, respectively, to satisfy the incentive constraints. The bundle x° is constructed to satisfy 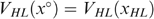 and MRSYHL(x°)=1. Now, consider the allocation
and MRSYHL(x°)=1. Now, consider the allocation 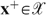 , with
, with 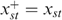 for all types st≠HL and
for all types st≠HL and 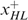 constructed by moving xHL on his indifference curve towards the bundle x°. It is clear that the allocation x+ is implementable. Furthermore, given the preference technology defined by
constructed by moving xHL on his indifference curve towards the bundle x°. It is clear that the allocation x+ is implementable. Furthermore, given the preference technology defined by 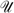 we have
we have 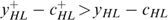 . Thus, the allocation x+ is also feasible, with
. Thus, the allocation x+ is also feasible, with 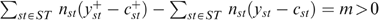 .
[ The allocations x and
.
[ The allocations x and  illustrating trick 1.]
illustrating trick 1.]The amount of money m can now be freely redistributed to the net income of all types (while still satisfying all incentive constraints), resulting in a weak Pareto improvement and hence also an improvement according to the government's programme (*). More generally, we obtain the first trick:
-
Trick 1: Consider an implementable and feasible allocation
 and a type st whose bundle xst can be moved along his indifference curve (i) without violating incentive constraints and (ii) making an amount of money m free for redistribution. The allocation x cannot be optimal according to programme (*), because everyone can be made strictly better off (by redistributing the amount of money m to the net incomes of all types), without violating incentive constraints.
and a type st whose bundle xst can be moved along his indifference curve (i) without violating incentive constraints and (ii) making an amount of money m free for redistribution. The allocation x cannot be optimal according to programme (*), because everyone can be made strictly better off (by redistributing the amount of money m to the net incomes of all types), without violating incentive constraints.
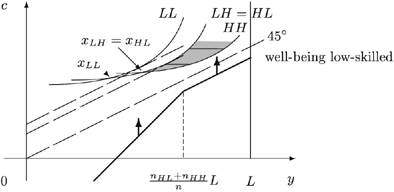
To illustrate the second trick, consider an implementable and feasible allocation  as in Figure A3. Again, the bundle xHH lies somewhere in the right shaded zone to satisfy the incentive constraints. Now it is possible to construct a feasible and implementable allocation
as in Figure A3. Again, the bundle xHH lies somewhere in the right shaded zone to satisfy the incentive constraints. Now it is possible to construct a feasible and implementable allocation  , transferring in x some net income from type LL to the other types LH, HL and HH. Whether or not the resulting allocation is better according to programme (*), ultimately depends on the well-being levels in society: if LL is strictly better off than one of the other types, it is always possible to find an allocation x+ that is better according to programme (*). We summarize the second trick as follows.
, transferring in x some net income from type LL to the other types LH, HL and HH. Whether or not the resulting allocation is better according to programme (*), ultimately depends on the well-being levels in society: if LL is strictly better off than one of the other types, it is always possible to find an allocation x+ that is better according to programme (*). We summarize the second trick as follows.
-
Trick 2: Consider an implementable and feasible allocation
 and one or more types st whose bundle(s) xst can be moved downwards (i) without violating incentive constraints and (ii) making an amount of money m>0 free for redistribution to the other types. The allocation x cannot be optimal according to programme (*) if all donor type(s) st are strictly better off in x than in (one of) the other types.
and one or more types st whose bundle(s) xst can be moved downwards (i) without violating incentive constraints and (ii) making an amount of money m>0 free for redistribution to the other types. The allocation x cannot be optimal according to programme (*) if all donor type(s) st are strictly better off in x than in (one of) the other types.
In addition to the two tricks, we need two lemmas. The first lemma tells us that the programme (*) can, loosely speaking, focus on the lower-skilled, because they are always worse off in terms of well-being:
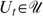 ), but different skills 0L<H. In an implementable allocation
), but different skills 0L<H. In an implementable allocation  , with VHt(xHt)VHt(xLt) (resp. VHt(xHt)>VHt(xLt)) the lower-skilled type Lt is always worse off (resp. strictly worse off) than the higher-skilled type Ht, i.e.
, with VHt(xHt)VHt(xLt) (resp. VHt(xHt)>VHt(xLt)) the lower-skilled type Lt is always worse off (resp. strictly worse off) than the higher-skilled type Ht, i.e. 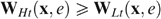 (resp.
(resp. 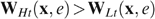 ).
[ The allocation x and
).
[ The allocation x and 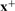 illustrating trick 2.]
illustrating trick 2.] Proof. Consider two types with the same taste for working, t∈T. We prove the case where skills satisfy 0<L<T and VHt(xHt)VHt(xLt); the other cases are analogous. Call (cLt, yLt) and (cHt, yHt) their bundles. Individuals with the same taste t have the same utility functions Ut and thus also the same indifference curves and therefore the same well-being level for bundles on the same indifference curve. Because our well-being measure is ordinally equivalent with utility, measured by Ut, it suffices to show that 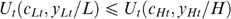 . Suppose not; i.e. (i)
. Suppose not; i.e. (i) 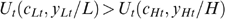 . Because VHt(xHt)VHt(xLt) we get, by definition of VHt, that (ii)
. Because VHt(xHt)VHt(xLt) we get, by definition of VHt, that (ii) 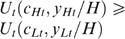 . Combining (i) and (ii), we obtain
. Combining (i) and (ii), we obtain 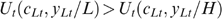 , a contradiction, given
, a contradiction, given 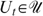 and 0<L<H. □
and 0<L<H. □
Lemma 2 tells us that it cannot be optimal—according to the government's programme (*)—to treat the indistinguishable middle types LH and HL differently in case 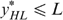 . Otherwise (if
. Otherwise (if 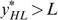 ) it might be optimal to treat them differently, but only under certain conditions.
) it might be optimal to treat them differently, but only under certain conditions.
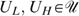 , which satisfy single-crossingness and indistinguishable middle type. Consider a government that optimizes the programme defined by (*). In an optimal allocation
, which satisfy single-crossingness and indistinguishable middle type. Consider a government that optimizes the programme defined by (*). In an optimal allocation  , we must have
, we must have
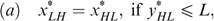
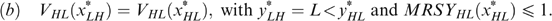
 and
and 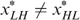 . We show that it is always possible to construct another allocation
. We show that it is always possible to construct another allocation  , which is feasible, implementable and strictly better than x* according to the government's programme (*). Because
, which is feasible, implementable and strictly better than x* according to the government's programme (*). Because 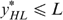 , the incentive compatibility constraints ICLH,HL and ICHL,LH require
, the incentive compatibility constraints ICLH,HL and ICHL,LH require
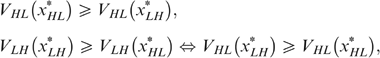
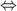 is due to indistinguishable middle types. We must have
is due to indistinguishable middle types. We must have 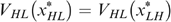 , or
, or 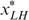 and
and 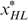 must lie on the same indifference curve.
must lie on the same indifference curve.Given our preference technology 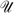 , there are only two cases for
, there are only two cases for 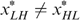 . Assume
. Assume 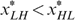 , i.e.
, i.e. 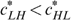 and
and  ; for the other case
; for the other case 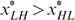 , simply switch subscripts HL and LH in the sequel. Define a bundle
, simply switch subscripts HL and LH in the sequel. Define a bundle 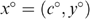 in
in  such that xo also lies on the same indifference curve through
such that xo also lies on the same indifference curve through 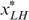 and
and 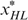 , i.e.
, i.e. 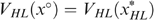 , and choose (i)
, and choose (i) 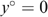 , if
, if 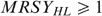 everywhere in
everywhere in  , (ii)
, (ii)  , if
, if  everywhere in
everywhere in 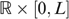 , or (iii)
, or (iii) 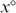 such that
such that 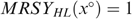 . Each case leads to any of the following three cases: (α)
. Each case leads to any of the following three cases: (α) 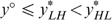 ; (β)
; (β) 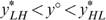 or (γ)
or (γ) 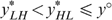 . In each of these cases (α), (β) and (γ) it is possible to use trick 1, by moving either
. In each of these cases (α), (β) and (γ) it is possible to use trick 1, by moving either 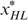 to the left on his indifference curve (in cases (α) and (β)) or
to the left on his indifference curve (in cases (α) and (β)) or 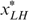 to the right on his indifference curve (in case (γ)), contradicting that
to the right on his indifference curve (in case (γ)), contradicting that 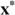 was optimal.
was optimal.
Proof of part (b). Suppose 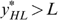 . We show that
. We show that 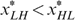 , with
, with 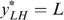 and
and 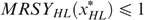 , must hold. Recall that, in case
, must hold. Recall that, in case 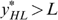 , the incentive constraint
, the incentive constraint 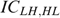 does not exist, because type HL's bundle is not attainable for LH.
does not exist, because type HL's bundle is not attainable for LH.
We first show that the incentive constraint 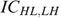 must bind; i.e.
must bind; i.e. 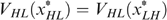 . Suppose not; i.e. suppose
. Suppose not; i.e. suppose 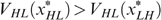 . Single-crossingness ensures that
. Single-crossingness ensures that 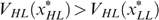 and thus LL is strictly worse off than HL (Lemma 1); for the same reason, LH is strictly worse off than HH. Now, it is possible to use trick 2, transferring from type HL (and possibly HH as well, if
and thus LL is strictly worse off than HL (Lemma 1); for the same reason, LH is strictly worse off than HH. Now, it is possible to use trick 2, transferring from type HL (and possibly HH as well, if 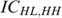 binds) to types LL and LH, which must improve the lowest well-being, contradicting that
binds) to types LL and LH, which must improve the lowest well-being, contradicting that 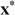 was optimal according to programme (*).
was optimal according to programme (*).
Now we are back in the same situation as in part (a), because both 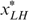 and
and 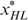 , with
, with  , lie on the same indifference curve (of type HL); i.e.,
, lie on the same indifference curve (of type HL); i.e., 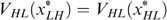 , but here
, but here 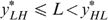 . Now proceed as in part (a). Define the bundle
. Now proceed as in part (a). Define the bundle 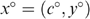 in
in  such that
such that  also lies on the same indifference curve through
also lies on the same indifference curve through 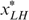 and
and 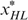 , i.e.
, i.e. 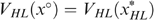 , and choose (i)
, and choose (i) 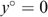 , if
, if 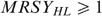 everywhere in
everywhere in 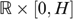 , (ii)
, (ii) 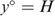 , if
, if 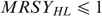 everywhere in
everywhere in 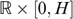 , or (iii)
, or (iii) 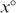 such that
such that 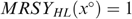 . Now,
. Now, 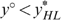 is not possible (otherwise we can use trick 1, moving
is not possible (otherwise we can use trick 1, moving 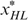 to the left on his indifference curve); thus,
to the left on his indifference curve); thus, 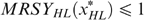 . As a consequence,
. As a consequence, 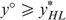 must hold. Now,
must hold. Now, 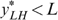 is not possible (because then
is not possible (because then 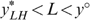 and using trick 1 again we could move
and using trick 1 again we could move 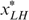 to the right on his indifference curve). Thus
to the right on his indifference curve). Thus 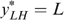 , which completes the proof. □
, which completes the proof. □
We are now ready to prove Propositions 1 and 2, on the basis of Lemmas 1 and 2 and tricks 1 and 2.
Proof of Proposition 1
Consider a four-type economy with skills 0<L<H and tastes represented by utility functions 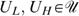 , which satisfy single-crossingness and indistinguishable middle type. Consider a government that optimizes the programme defined by (*). In an optimal allocation
, which satisfy single-crossingness and indistinguishable middle type. Consider a government that optimizes the programme defined by (*). In an optimal allocation  , we must have
, we must have 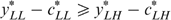 .
.
Our proof consists of two parts, depending on whether (a) 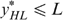 in the optimum
in the optimum  , or (b)
, or (b) 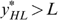 . Given the definition of
. Given the definition of 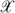 , one of these cases must hold. We show, for both cases, that
, one of these cases must hold. We show, for both cases, that 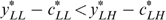 is not possible.
is not possible.
Proof of part (a). Suppose 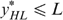 (thus
(thus 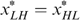 via Lemma 2) and
via Lemma 2) and 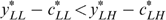 . We consider four possible cases, depending on whether or not
. We consider four possible cases, depending on whether or not 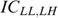 and/or
and/or 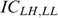 bind. In an optimum
bind. In an optimum  of the programme (*), one of these four cases must hold. For all cases, we show that it is possible to construct a strictly better allocation according to programme (*), which also satisfies the feasibility and incentive compatibility constraints.
of the programme (*), one of these four cases must hold. For all cases, we show that it is possible to construct a strictly better allocation according to programme (*), which also satisfies the feasibility and incentive compatibility constraints.
- 1
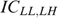 and
and  bind. This requires
bind. This requires 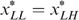 , which contradicts
, which contradicts 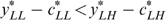 .
. - 2
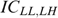 binds but
binds but 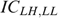 does not bind. (2a) If
does not bind. (2a) If 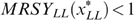 , we could use trick 1 moving
, we could use trick 1 moving 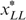 somewhat to the right on his indifference curve. (2b) We must have
somewhat to the right on his indifference curve. (2b) We must have 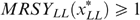 , from (2a). But, given the preference technology defined by
, from (2a). But, given the preference technology defined by  ,
, 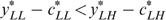 is not possible, a contradiction.
is not possible, a contradiction. - 3
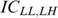 does not bind but
does not bind but 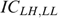 binds. (3a) Let us first focus on type LH. If
binds. (3a) Let us first focus on type LH. If 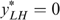 , then incentive constraints and single-crossingness require
, then incentive constraints and single-crossingness require 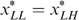 , which violates
, which violates 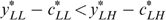 . So
. So  . If
. If 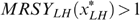 , we can use trick 1 again, by moving both
, we can use trick 1 again, by moving both 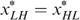 to the left on their (common) indifference curve. So
to the left on their (common) indifference curve. So 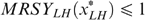 must hold. (3b) We focus now on type LL. We must have either (i)
must hold. (3b) We focus now on type LL. We must have either (i)  or (ii)
or (ii)  . In case (ii) we have
. In case (ii) we have 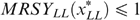 (otherwise we can use trick 1, by moving
(otherwise we can use trick 1, by moving 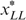 somewhat to the left on his indifference curve). (3c) From Lemma 1, either type LH or LL has the minimal well-being. Figure A4 illustrates (3a), (3b(ii)) and
somewhat to the left on his indifference curve). (3c) From Lemma 1, either type LH or LL has the minimal well-being. Figure A4 illustrates (3a), (3b(ii)) and 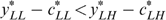 ; type HH's bundle is somewhere in the shaded zone. We measure well-being in (c, y) rather than in
; type HH's bundle is somewhere in the shaded zone. We measure well-being in (c, y) rather than in 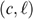 -space. Therefore, one has to divide the slopes of the shared resources budget line by the skill level of the individual under consideration, here a low-skilled individual, and to multiply the proportion of high-skilled
-space. Therefore, one has to divide the slopes of the shared resources budget line by the skill level of the individual under consideration, here a low-skilled individual, and to multiply the proportion of high-skilled 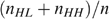 (which defines the kink in the budget set where the slope changes from H/L>1 to 1) by the skill level of the individual under consideration. As a consequence, it is easy to verify that type LH is always strictly worse off than type LL, irrespective of the proportion of high-skilled
(which defines the kink in the budget set where the slope changes from H/L>1 to 1) by the skill level of the individual under consideration. As a consequence, it is easy to verify that type LH is always strictly worse off than type LL, irrespective of the proportion of high-skilled  and irrespective of whether (3b(i)) or (3b(ii)) applies.
and irrespective of whether (3b(i)) or (3b(ii)) applies.
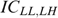 does not bind, it is always possible to use trick 2 by transferring a small amount of money from LL to the other types LH, HL and HH, improving the minimal well-being in society: a contradiction.
[ Type LL is strictly better off compared to type LH.]
does not bind, it is always possible to use trick 2 by transferring a small amount of money from LL to the other types LH, HL and HH, improving the minimal well-being in society: a contradiction.
[ Type LL is strictly better off compared to type LH.]- 4
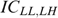 and
and 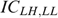 do not bind. Using trick 1, it can be verified that only the following cases are possible: (i)
do not bind. Using trick 1, it can be verified that only the following cases are possible: (i) 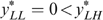 ,
, 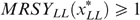 and
and 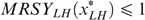 , or (ii)
, or (ii) 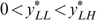 ,
, 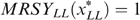 and
and 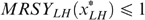 . We are back in the same situation as in step 3. In both cases (i) and (ii) and, given
. We are back in the same situation as in step 3. In both cases (i) and (ii) and, given 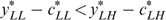 , type LH is strictly worse-off than LL, irrespective of the proportion of high-skilled. Here again, trick 2 can be used to obtain a contradiction.
, type LH is strictly worse-off than LL, irrespective of the proportion of high-skilled. Here again, trick 2 can be used to obtain a contradiction.
Proof of part (b). Suppose 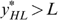 (thus
(thus 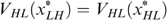 , with
, with 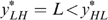 and
and 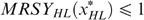 via Lemma 2) and
via Lemma 2) and 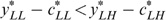 . It is again possible to consider four cases, depending on whether or not
. It is again possible to consider four cases, depending on whether or not 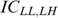 and/or
and/or 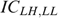 bind, and to show, for each case, a contradiction. Actually, the proof is completely analogous as in steps 1–4 of part (a) and is therefore omitted.
bind, and to show, for each case, a contradiction. Actually, the proof is completely analogous as in steps 1–4 of part (a) and is therefore omitted.
Proof of Proposition 2
Consider a four-type economy with skills 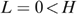 and tastes represented by utility functions
and tastes represented by utility functions 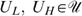 , which satisfy single-crossingness. Consider a government that optimizes the programme defined by (*). In an optimal allocation
, which satisfy single-crossingness. Consider a government that optimizes the programme defined by (*). In an optimal allocation  , we must have
, we must have 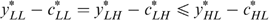
Proof. Suppose 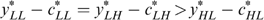 holds.
holds.
- 1
Because L=0 and
 , we must have
, we must have 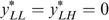 ; also, given the incentive constraints,
; also, given the incentive constraints, 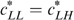 must hold.
must hold. - 2
Owing to Lemma 1, the lowest well-being is either LH or LL; thus, given step 1, we must maximize the basic income, i.e. maximize
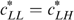 .
. - 3
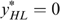 is excluded, otherwise we must have
is excluded, otherwise we must have 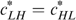 (owing to incentive constraints) and
(owing to incentive constraints) and 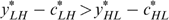 would be violated.
would be violated. - 4
So
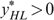 holds from step 3. Now,
holds from step 3. Now, 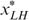 and
and 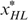 must lie on the same indifference curve, or
must lie on the same indifference curve, or 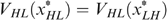 . Otherwise (see the proof of Lemma 2, part (b)) it would be possible to improve the situation of the worst-off types LL and LH, at the cost of the better-off types HL and HH (on the basis of trick 2).
. Otherwise (see the proof of Lemma 2, part (b)) it would be possible to improve the situation of the worst-off types LL and LH, at the cost of the better-off types HL and HH (on the basis of trick 2). - 5
If
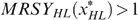 at
at 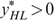 , we can use trick 1, by moving
, we can use trick 1, by moving 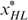 to the left on his indifference curve.
to the left on his indifference curve. - 6
To summarize, we must have
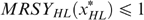 and
and 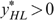 while
while 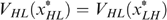 and
and 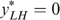 . But this contradicts
. But this contradicts 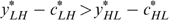 , given our preference technology defined by
, given our preference technology defined by 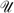 .
.
APPENDIX C: THE BELGIAN TAX SYSTEM FOR SINGLES
| Pre-tax income y | Marginal tax rate (%) |
|---|---|
| <€5032 | 0 |
| €5033–€6272 | 25 |
| €6273–€8304 | 30 |
| €8305–€11,849 | 40 |
| €11,850–€27,268 | 45 |
| €27,269–€40,902 | 50 |
| €40,903–€59,990 | 52.5 |
| >€59,990 | 55 |
.
APPENDIX D: IMPUTATION VIA A SAMPLE SELECTION MODEL
We present the variables used for imputing gross hourly wages σ and net hourly benefits bh; and we show the estimates for both sample selection models (Tables A2 and A3)
| Coeff. | St. error | Pr>|z| | |
|---|---|---|---|
| Wage equation | |||
| age | 0.497 | 0.123 | 0.000 |
| agesq | −0.003 | 0.002 | 0.075 |
| dumeduc2 | 1.364 | 1.141 | 0.232 |
| dumeduc3 | 2.834 | 1.103 | 0.010 |
| dumeduc4 | 4.508 | 1.160 | 0.000 |
| dumeduc5 | 5.617 | 1.149 | 0.000 |
| sex | −0.917 | 0.383 | 0.017 |
| cons | −2.680 | 2.568 | 0.297 |
| Selection equation | |||
| dumhealth2 | −0.576 | 0.176 | 0.001 |
| dumhealth3 | −0.686 | 0.227 | 0.002 |
| dumhealth4 | −1.221 | 0.476 | 0.010 |
| dumdepri2 | 0.014 | 0.186 | 0.938 |
| dumdepri3 | −0.243 | 0.185 | 0.188 |
| dumdepri4 | −0.486 | 0.249 | 0.051 |
| dumdepri5 | −0.799 | 0.342 | 0.019 |
| dumhealth2 | 0.374 | 0.173 | 0.031 |
| dumhealth3 | 0.113 | 0.196 | 0.563 |
| dumhealth4 | 0.160 | 0.297 | 0.591 |
| dumhealth5 | −0.657 | 0.352 | 0.062 |
| dumsmoke2 | −0.041 | 0.245 | 0.868 |
| dumsmoke3 | −0.219 | 0.138 | 0.114 |
| child | −0.355 | 0.153 | 0.020 |
| depperson | −0.232 | 0.210 | 0.269 |
| age | 0.179 | 0.040 | 0.000 |
| agesq | −0.002 | 0.001 | 0.000 |
| dumeduc2 | 0.587 | 0.254 | 0.021 |
| dumeduc3 | 0.784 | 0.243 | 0.001 |
| dumeduc4 | 1.584 | 0.305 | 0.000 |
| dumeduc5 | 1.685 | 0.291 | 0.000 |
| sex | −0.507 | 0.139 | 0.000 |
| cons | −2.016 | 0.728 | 0.006 |
- Notes
-
No. of observations = 644, from which 136 censored and 508 uncensored. Wald's
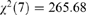 with
with 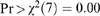 and likelihood ratio test of independent wage and selection equations results in
and likelihood ratio test of independent wage and selection equations results in 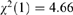 with
with 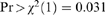 .
.
| Coeff. | St. error | Pr>|z| | |
|---|---|---|---|
| Wage equation | |||
| age | 0.115 | 0.051 | 0.025 |
| agesq | −0.001 | 0.001 | 0.120 |
| dumeduc2 | 0.361 | 0.259 | 0.163 |
| dumeduc3 | 0.470 | 0.271 | 0.083 |
| dumeduc4 | 0.181 | 0.358 | 0.613 |
| dumeduc5 | 0.575 | 0.410 | 0.161 |
| sex | −0.317 | 0.187 | 0.091 |
| divorce | 0.376 | 0.197 | 0.057 |
| widow | −0.504 | 0.582 | 0.386 |
| cohabit | −0.035 | 0.196 | 0.858 |
| cons | −0.226 | 0.921 | 0.806 |
| Selection equation | |||
| dumhealth2 | 0.304 | 0.154 | 0.048 |
| dumhealth3 | 0.416 | 0.203 | 0.040 |
| dumhealth4 | 0.384 | 0.415 | 0.355 |
| dumdepri2 | 0.137 | 0.163 | 0.400 |
| dumdepri3 | 0.244 | 0.166 | 0.142 |
| dumdepri4 | 0.470 | 0.237 | 0.048 |
| dumdepri5 | 0.334 | 0.329 | 0.311 |
| dumhealth2 | −0.464 | 0.154 | 0.003 |
| dumhealth3 | 0.020 | 0.173 | 0.909 |
| dumhealth4 | 0.369 | 0.254 | 0.145 |
| dumhealth5 | 0.889 | 0.339 | 0.009 |
| dumsmoke2 | 0.114 | 0.214 | 0.596 |
| dumsmoke3 | 0.228 | 0.124 | 0.065 |
| child | 0.304 | 0.143 | 0.033 |
| depperson | 0.158 | 0.192 | 0.410 |
| age | −0.108 | 0.040 | 0.007 |
| agesq | 0.001 | 0.001 | 0.006 |
| dumeduc2 | −0.376 | 0.242 | 0.120 |
| dumeduc3 | −0.707 | 0.232 | 0.002 |
| dumeduc4 | −1.049 | 0.265 | 0.000 |
| dumeduc5 | −1.428 | 0.270 | 0.000 |
| sex | 0.373 | 0.128 | 0.004 |
| divorce | 0.027 | 0.162 | 0.868 |
| widow | 0.036 | 0.490 | 0.941 |
| cohabit | −0.329 | 0.144 | 0.022 |
| cons | 1.247 | 0.717 | 0.082 |
- Notes
-
No. of observations = 638, from which 480 censored and 158 uncensored. Wald's
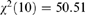 with
with 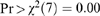 and likelihood ratio test of independent wage and selection equations results in
and likelihood ratio test of independent wage and selection equations results in 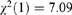 with
with 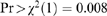 .
.
.
Imputing gross hourly wages σ
In the wage equation, the independent variables are:
- •
age and its square (age, agesq)
- •
educational dummies indicating the highest achieved education level of the individual, starting from primary education (base case), lower secondary education (dumeduc2), higher secondary education (dumeduc3), higher education short type (dumeduc4), higher education long type (dumeduc5)
- •
a gender dummy (sex) taking the value of 1 for females
In the selection equation, the independent variables are:
- •
physical health dummies, indicating the general health situation of the individual, ranging from very good (base case), good (dumhealth2) and reasonable (dumhealth3) to bad (dumhealth4)
- •
mental health dummies, indicating how often the individual feels depressed, ranging from never (base case), seldom (dumdepri2), at times (dumdepri3) and regularly (dumdepri4) to frequently (dumdepri5); and how often the individual longs for death, ranging from never (base case), seldom (dumdeath2), at times (dumdeath3) and regularly (dumdeath4) to frequently (dumdeath5)
- •
smoking dummies, indicating smoking behaviour, ranging from never (base case) and occasionally (dumsmoke2) to daily (dumsmoke3)
- •
care dummies, indicating whether the individual has to take care of his children (child), taking the value of 1 if affirmative; and/or has to take care of others (depperson) taking the value of 1 if affirmative
- •
the independent variables of the wage equation
Imputing net hourly benefits bh
The dependent variable is the marginal benefit per hour 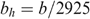 , with b the net yearly benefit. The independent variables are identical to those in the Heckman selection model, imputing σ. In addition, we add in both the benefit and the selection equation civil status dummies, indicating whether the individual is divorced (divorce), taking the value of 1 if affirmative; widowed (widow), taking the value of 1 if affirmative; living together (cohabit), taking the value of 1 if affirmative.
, with b the net yearly benefit. The independent variables are identical to those in the Heckman selection model, imputing σ. In addition, we add in both the benefit and the selection equation civil status dummies, indicating whether the individual is divorced (divorce), taking the value of 1 if affirmative; widowed (widow), taking the value of 1 if affirmative; living together (cohabit), taking the value of 1 if affirmative.
APPENDIX E: SOME DESCRIPTIVE STATISTICS
Table A4 reports the number of observations (n), the minimum (min), the 25th percentile (p25), the median (p50), the 75th percentile (p75) and the maximum (max) for the following variables: age, normalized labour  , observed gross hourly wages σ, imputed gross hourly wages
, observed gross hourly wages σ, imputed gross hourly wages  , observed and imputed gross hourly wages
, observed and imputed gross hourly wages 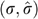 , observed net hourly benefits bh, imputed net hourly benefits
, observed net hourly benefits bh, imputed net hourly benefits 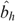 and observed and imputed net hourly benefits
and observed and imputed net hourly benefits 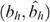
| n | min | p25 | p50 | p75 | max | |
|---|---|---|---|---|---|---|
| Age | 621 | 16 | 25 | 33 | 42 | 70 |
| ℓ | 621 | 0.000 | 0.231 | 0.554 | 0.615 | 1.000 |
| σ | 502 | 1.495 | 9.585 | 11.864 | 15.700 | 38.271 |
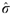 |
119 | 1.262 | 4.796 | 6.665 | 9.421 | 19.214 |
σ, 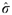 |
621 | 1.262 | 8.594 | 11.065 | 14.404 | 38.271 |
| bh | 143 | 0.166 | 0.915 | 1.849 | 3.051 | 3.661 |
 |
478 | 0.002 | 0.072 | 0.214 | 0.510 | 2.089 |
bh, 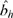 |
621 | 0.002 | 0.115 | 0.345 | 0.928 | 3.661 |
.