A Test of Diminishing Marginal Value
Abstract
The notion of diminishing marginal value had a profound impact on the development of neoclassical theory. Early neoclassical scholars had difficulty convincing contemporaries of the new paradigm's value until political economists used the critical assumption of diminishing marginal value to link utility and demand. While diminishing marginal value remains a key component of modern economic intuition, there is little direct verification of this behavioural property. This paper reports experiments on a myriad of subject pools to examine behaviour in both price and exchange settings. We report results from nearly 900 subjects across 19 treatments and find strong evidence of diminishing marginal value.
INTRODUCTION
The assumption that having more of a good will lead an individual to place a lower value on an additional unit of that good, which we call diminishing marginal value, is a pervasive component of economists' beliefs about human behaviour. Robert Frank (2000), summarizing this intuition, writes that ‘the more one consumes of something, the less one is willing to pay to obtain more of it. Even a hungry person would be willing to pay less for a second sandwich than for the first.’1
This concept was highly influential in the development of economic thought. Initiated in the 1870s, the ‘Marginalist Revolution’ represented such a severe break from the prevailing approaches that many contemporaries reasoned that the new paradigm was ‘quackery’ because it lacked a direct connection between utility and demand. Combining the critical assumption of diminishing marginal value with equivalent marginal utilities (per dollar spent) across goods, H. H. Gossen (1854) initially made this connection.2 In 1871 Jevons independently developed his own results linking demand and utility, making use of diminishing marginal utility (see Jevons 1965). Other figures in the Marginalist School also appealed frequently to diminishing utility. Walras wrote: ‘The want which we have for things, or utility which things have for us, diminishes gradually as consumption increases’ (see Walras, 1954); and Jevons wrote: ‘Each increment of food is less necessary, or possesses less utility, than the previous one.’
This presumption of diminishing marginal value was based on its plausibility and intuition, not on specific empirical evidence. Our goal is to fill this gap. A great many other aspects of neoclassical behaviour have been shown to fail when examined ‘under the microscope’ of experimental economics. Our goal is to subject diminishing marginal value to this same scrutiny.
The task requires us to be more precise about what is being measured. Early writers wrote in terms of diminishing utility. In this paper we look at diminishing marginal value (DMV) where value is measured in terms of either money or another good that must be exchanged for the good in question. Diminishing marginal value must be measured in one of these units. Note that the link between preferences and demand has been considerably refined since the nineteenth century; we focus here directly on the idea expressed by Jevons and Walras, which formed the germ of early economic progress.
To test for DMV, we conducted three types of experimental treatments. The first set of treatments uses a standard willingness-to-accept format and examines whether the compensation an individual requires to give up a unit of some good decreases when the individual has more of that good. This is a money-based measure of diminishing marginal value and it has the most general applicability. For example, public finance economists would frequently be interested in knowing whether additional units of a publicly provided good become less valuable as more of the good is provided. Since public provision of such goods typically require a ‘general sacrifice’ that might best be measured in money terms, a money-based measure of diminishing marginal value (for the good in question) is most informative for making the necessary inference.
In a second set of treatments we examined subjects' willingness to trade one unit of an endowed good for one unit of another good. We gave our experimental subjects different amounts of the endowed good. Diminishing marginal value means that more individuals are willing to make a trade when they have more of the endowed good. This is a goods-based measure of DMV. This formulation comes closer, we feel, to the kind of exchange situation that the early writers envisioned. Furthermore, it enables us, with some additional experiments, to trace out a demand curve, thereby roughly following the early linkage.
The properties of the utility function are most interesting for public goods since these are goods for which demand curves are usually missing. Although a true policy-relevant experiment is essentially impossible to conduct, we designed a third set of treatments to test whether DMV is exhibited in collective choice. In these treatments, subjects were endowed with one good and asked whether they were willing to trade it for one unit of another good; however, the trade would take place only if a majority of subjects agreed to it, and all subjects would be required to trade their good in that case. We tested for DMV by changing the endowment of the initial good for all subjects and examining whether more individuals were willing to vote to make the trade when they had more of the initial good.
The evidence we found for DMV is strong. In the money-based treatments, which elicited a continuous measure of value, all possible comparisons show a decrease in the value of the items as the endowment of the good in question increased. We found consonant results in the exchange treatments: increases in the endowment significantly increased subjects' willingness to trade part of it away (i.e. the trading rate) in all of our treatments, in both individual choice and collective choice situations.
Previous research has largely been content to test whether estimated demand curves are consistent with utility maximization. These studies, which are legion, frequently imply an underlying utility function that would indeed exhibit DMV.3 What is at stake in our research is an explicit test of the ‘utility-based’ behaviour, which may then be connected with the more common ‘demand-based’ picture of behaviour.
In Section II below we report a set of demand curve experiments which we then link to the DMV results using a specific utility function. If we allow for a reference-point effect, these experiments show demand curves that are highly consistent with the DMV behaviour we previously uncovered.
Although DMV is highly intuitive, it may be worthwhile to consider the basis of this intuition. A sufficient condition for DMV is that utility be concave in the good in question and that an increase in the endowment of the good not reduce the marginal utility of money ‘too much.’4 The first of these properties is the historical neoclassical idea. The second property means that having more of the good in question does not so greatly reduce utility from other goods that money itself becomes less valuable.
DMV may also be understood by framing the issue in terms of the quasi-concavity of preferences, hence without explicitly invoking concavity. If preferences are quasi-concave, then either {good A valued in terms of good B} or {good B valued in terms of good A} must exhibit DMV. It is difficult to see why one of these values should exhibit DMV and not the other. Therefore, DMV might better be thought of as following from quasi-concavity when the goods in question are such that preferences for them can be expected to exhibit similar properties.
I. EXPERIMENTAL DESIGN AND RESULTS
Our treatments fall into three categories, depending on whether value is measured in terms of money or another good and, for the goods-based experiments, on whether there is individual or collective choice. Within each category, we statistically test for diminishing marginal value, using subjects who are randomly allocated into one treatment cell.
Treatments are summarized in Appendix A. Except for treatment A, our subject pool consists of non-student subjects operating in non-classroom settings. The subject pool consists of ‘middle America’, although we cannot claim to have a representative sample of the US population.
Treatments involving goods–money tradeoffs
Our first set of treatments was carried out with subjects in suburban Washington DC in the mid-1990s. We conducted seven similar treatments with 13 different subject groups, all but one of which were local civic groups. Each group began with one of seven different endowments of goods consisting of mugs and flashlights. Each subject's compensation demanded (CD), also known as willingness-to-accept, was elicited for different parts of that endowment using an open-ended format—the Becker–deGroot–Marschak (BDM) mechanism.
Experimental procedure To illustrate the general approach, we describe the procedure for treatment C in detail.5 Each subject was given one mug and three flashlights. We first asked subjects to consider selling back the mug. Each participant was asked to write down the minimum payment he would accept for selling the mug back to us; this is his ‘compensation demanded’. We then repeated the following BDM procedure three times for practice and then for a real transaction. The administrator drew an offer price randomly out of an envelope. If the subject's compensation demanded was higher than the offer price, the subject kept his mug. If his CD was less than or equal to the offer price, he returned his mug to us and received a cheque for the randomly drawn price. All subjects were offered the same price.
Next, we asked subjects to consider selling back their flashlights. Each subject wrote down the minimum payments he required to be willing to sell us back one, two, and three flashlights. We then randomly drew a piece of paper that stated the number of flashlights (per person) we would be buying back. Subjects were told each option had equal probability.
We then randomly drew the offer price. For example, we might first randomly draw the instruction to buy back two of each subject's three flashlights and then draw an offer price of $19. (This is a price for the two flashlights, not a per-flashlight price.) Subjects who had offered to sell two flashlights for $19 or less then turned in two of their flashlights and received a cheque for $19. They kept their remaining flashlight. Subjects who had offered to sell two flashlights for more than $19 kept all three flashlights and received no money.
In our experiments, subjects were not told the distribution of offer prices, a design feature that makes our mechanism different from the BDM mechanism as it is most frequently administered. In particular, we did not tell subjects what the upper limit of the distribution was, i.e. the highest potential offer price. Concealing this information was useful to us for two reasons. First, it emphasized to subjects that distribution information should be irrelevant in their responses; that is, it helped reinforce our instruction that their best strategy would be to determine and report their compensation demanded regardless of what they believed about possible offer prices. Second, it gave the subjects no information about what anyone else (i.e. the experimenters) believed might be likely values for CD. The latter feature is obviously important in studying ‘true’ preferences.
Although the BDM mechanism is theoretically incentive-compatible, questions have been raised about its performance. Harrison (1992) pointed out that the costs to subjects of not reporting their true values are small. Rutström (1998) found that values elicited by a slightly different version of the BDM were different from English and Vickrey auctions, both also incentive-compatible. Such issues, however, should not be significant in examining differences in behaviour across the same type of experiment, as was done here.
Summary statistics are presented in Table 1. The table presents, for each treatment, the mean compensation demanded, the standard error and the sample size. We dropped responses that were implausibly high (more than double the item's purchase price6). See Appendix A for the number of observations analysed in each treatment.
| Treatment | |||||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | |
| CD for 1 mug | $4.40 | $3.60 | $5.02 | — | — | — | $5.06 |
| (0.53) | (0.44) | (0.30) | (0.80) | ||||
| 61 | 67 | 125 | 51 | ||||
| CD for 2 mugs | $8.67 | $6.77 | — | — | $9.18 | $9.12 | — |
| (1.25) | (0.73) | (0.76) | (1.10) | ||||
| 61 | 67 | 41 | 25 | ||||
| CD for 3 mugs | $13.70 | $10.09 | — | — | $13.32 | $13.56 | — |
| (2.31) | (1.07) | (1.01) | (1.79) | ||||
| 61 | 67 | 41 | 25 | ||||
| CD for 1 flashlight | — | — | $5.50 | $6.06 | — | $6.44 | — |
| (0.47) | (1.19) | (0.76) | |||||
| 59 | 15 | 25 | |||||
- Note: The numbers are the mean, standard error and number of observations.
Several treatments used endowments of two different goods as a way of helping subjects become familiar with the BDM mechanism. In these treatments we first test whether the compensation demanded to give up a good depends on the endowment of the other good, rather than just on the endowment of the same good, which is the essence of our DMV test.
In performing this test, we adopted the null hypothesis that the compensation demanded for a particular item is independent of the endowment of the other item. There are six tests: C versus G (CD for 1 mug); E versus F (CD for 2 mugs; CD for 3 mugs); E and F combined versus A (CD for 2 mugs; CD for 3 mugs); and D versus F (CD for 1 flashlight). Results strongly suggest we should not reject the null hypothesis; the t-values are 0.05, 0.04, 0.12, 0.35, 0.20 and 0.27, respectively. These results allow us to pool experiments based only on the endowment of the good being valued.
Results Testing for diminishing marginal value relies on an examination of data between treatments. In each comparison we tested whether the mean compensation demanded for a good is lower in the treatment where the subjects have more of that good. We tested this hypothesis for the mean compensation demanded for one mug; for two and three mugs; and for one flashlight. Endowments were, respectively, one, three or four mugs; three or four mugs; and one or three flashlights. Results are presented in Tables 2, 3 and 4.
| Mug endowment | |||
|---|---|---|---|
| 1 (treatments C, G) | 3 (treatment A) | 4 (treatment B) | |
| Compensation demanded to give up 1 mug | $5.03** | $4.40 | $3.60 |
| (0.31) | (0.53) | (0.44) | |
| 176 | 61 | 67 | |
- Note: Entries are the mean, standard error, and number of observations.
- ** Significantly different from column 4 at the 99% level. The t-statistics for 1 v. 3 and 3 v. 4 are 1.10 and 1.16, respectively.
| Mug endowment | ||
|---|---|---|
| 3 (treatments A, E, F) | 4 (treatment B) | |
| Compensation demanded to give up 2 mugs | $8.92** | $6.77 |
| (0.68) | (0.73) | |
| 127 | 67 | |
| Compensation demanded to give up 3 mugs | $13.55** | $10.09 |
| (1.20) | (1.07) | |
| 127 | 67 | |
- Note: Entries are the mean, standard error, and number of observations.
- ** Significantly different from column to the right at the 99% level.
| Flashlight endowment | ||
|---|---|---|
| 1 (treatments D, F) | 3 (treatment C) | |
| Compensation demanded to give up 1 flashlight | $6.30 | $5.50 |
| (0.64) | (0.47) | |
| 40 | 59 | |
- Note: Entries are the mean, standard error, and number of observations. The t-statistic for 1 v. 3 is 1.00.
The pattern of responses is clear. All five adjacent pairs of values show CD declining as the endowment increases, a clear demonstration of diminishing marginal value. The null hypothesis of no difference is rejected in three of six tests.
Results are even more striking in the individual treatments. There are eleven possible treatment comparisons: C v. A, G v. A, and A v. B (one mug); A v. B, E v. B, and F v. B (two and three mugs); and D v. C and F v. C (one flashlight). All 11 of these reveal compensation demanded decreasing in the endowment.
To examine the joint null hypothesis of no diminishing marginal value, we constructed the following test. Suppose that in a comparison of any two treatments there is a 50–50 chance that one of the values (mean compensation demanded) will be higher than the other. In other words, consider a null hypothesis that when A is compared with B the probability that {mean CD in treatment A} > {mean CD in treatment B} is 1/2; similarly, the probability that {mean CD in treatment B} > {mean CD in treatment A} is 1/2. Under the null, the probability that n independent comparisons will show {mean CD in lower-endowment treatment} > {mean CD in higher-endowment treatment} in all n cases is thus (1/2)n.
To ensure that probabilities are independent, we compare any two treatments only once. This leaves seven possible pairs.7 Under the null, the probability that we will observe diminishing marginal value in all seven is (1/2)7=0.0078. Thus, the hypothesis of no diminishing marginal value is rejected at the 99% level.
Individual choice treatments involving goods–goods trades
In an effort to provide a test of diminishing marginal value in a different setting, we recruited subjects from a real-world marketplace—the floor of a sports card show in a large southern US city in April 2001—and observed their willingness to trade unique commodities. This set of treatments is similar in spirit to the field experiments reported in List (2003, 2004). In the treatments reported in this section, we observe trading patterns of sports memorabilia and examine whether varying the initial endowment level influenced subjects' willingness to execute a trade.
The design is uncomplicated. A subject is initially given an endowment of good a (or b) and has the option to trade with the experimenter a fixed amount of that endowment for a specified amount of good b (or a). The trading rate is the proportion of participants who decide to execute the trade. A separate group of subjects is endowed with a higher amount of a and given the same opportunity to trade (1 unit of a for 1 unit of b; only one trade per subject). Subjects exhibit DMV for good a if the trading rate is higher for subjects with a higher endowment of a. Note that this closed-ended format (‘yes/no’) is simpler than the open-ended format used by the BDM mechanism. Knetsch (1989) and Kahneman et al. (1990) have used similar mechanisms to test for reference-point effects.
Our test uses two unique goods. Good a was a 14 June 1996 Kansas City Royals game ticket stub, which was issued for admission to the baseball game in which Cal Ripken Jr broke the major league record for consecutive games played. Good b was an 12 October 1997 Tampa Bay Buccaneers game ticket stub, which was issued for admission to the football game in which Barry Sanders surpassed Jim Brown to become the fourth all-time rushing leader in the history of the National Football League. We were fortunate to obtain these unique pieces of sports memorabilia in quantity because one of the authors attended the sporting events and collected the ticket stubs from in and around the stadiums. Although we have rarely seen the goods sold in markets, in certain regions (e.g. Ripken in Baltimore and Sanders in Detroit) the stubs have sold for $40 each.
The procedure follows List (2003, 2004). The administrator asked subjects entering the trading card show if they would fill out a demographic survey that would take about five minutes. If the candidate subject agreed, she was given an initial endowment as ‘payment’ for completing the survey. Upon completion of the survey, the administrator retrieved the other good from under the table and informed the subject that she had the opportunity to trade. The subject was allowed to inspect both goods, after which she either made the trade or kept the original bundle. The endowment was changed at the top of each hour, so subjects' treatment was based on the time they visited the table at the card show. No subjects participated in more than one treatment. We summarize our experimental treatments in Appendix A.
Results Trading rates are reported in Tables 5 and 6. Table 5 contains the results for subjects who started with the Ripken stub and had the option to trade for a Sanders stub. Table 6 contains results for subjects who started with the Sanders ticket stub.
| Good a endowment | ||
|---|---|---|
| 1 (treatment H) | 3 (treatment J) | |
| % traded (1 unit of a for 1 unit of b) | 22.5 | 77.5 |
| (n=40) | (n=40) | |
| Good b endowment | ||
|---|---|---|
| 1 (treatment I) | 3 (treatment L) | |
| % traded (1 unit of b for 1 unit of a) | 27.5 | 87.5 |
| (n=40) | (n=40) | |
Both sets of treatments show strong evidence of diminishing marginal value, as there is a substantial and significant increase in trading rates when endowment levels are increased. When subjects had 1 unit of endowed good a, 9 out of 40 subjects (22.5%) were willing to trade for a unit of b. When subjects had 3 units of a, 31 out of 40 subjects (77.5%) were willing to trade one unit for one unit of b, a more than tripling of the trading rate. Similar results occurred when b was the endowed good.8
Collective choice treatments
An understanding of DMV may have its most important implications for goods that are exogenously supplied, such as public goods. Therefore we replicated the private good trading treatments with a collective choice analogue. These treatments are identical in terms of endowments and feasible trades, as illustrated in Appendix A, but now the decision was cast in terms of a public-choice decision over a collective good. If more than 50% of the subjects voted in favour of providing the collective good, then all subjects had to turn in the requisite payment (their ticket stubs) and the collective good (the alternative ticket stubs) was provided. If fewer than 50% voted in favour of the public good, then all subjects kept their initial endowment and the collective good was not provided. Since it was necessary to have group decision-making, instead of running these treatments on the floor of the sports card trading show, we used an adjacent room in the same building. Appendix B contains a summary of the experimental instructions.
Results Results are presented in Tables 7 and 8. Again, there is strong evidence of diminishing marginal value. In Table 7, 14 out of 40 subjects (35%) voted to trade their one Ripken stub for one Sanders stub when their endowment was one Ripken stub. More than double that proportion (28 out of 35 subjects, or 80%) voted to make that trade when their initial endowment was three Ripken stubs. Similar behaviour occurred when subjects started out with one or three Sanders stubs, as shown in Table 8.
| Good a endowment | ||
|---|---|---|
| 1 (treatment N) | 3 (treatment P) | |
| % voting to trade (1 unit of a for 1 unit of b) | 35.0 | 80.0 |
| (n=40) | (n=35) | |
| Good b endowment | ||
|---|---|---|
| 1 (treatment O) | 3 (treatment R) | |
| % voting to trade (1 unit of b for 1 unit of a) | 29.7 | 85.7 |
| (n=37) | (n=42) | |
We again calculated Irwin–Fisher statistics to test whether these differences are significant. We find that there is a significant difference in trading rates for both types of good. Subjects traded significantly more often when they were endowed with three units than when they were endowed with one (z=−3.92 for Ripken and z=−5.06 for Sanders).
The reference-point effect and cross-sectional inconsistency of preferences
Our experiments have presented clear evidence in favour of DMV. But in addition, a comparison across tables (Table 5v. Table 6; Table 7v. Table 8) provides evidence about the ‘cross-sectional inconsistency’ of preferences, which has potentially much greater implications.
Consider a comparison between treatments H and I. For preferences to be consistent, the proportion of people who choose b over a should be equal to one minus the proportion who choose a over b; similarly for the comparison between treatments N and O. In words, subjects should exhibit the same preference for a over b regardless of which good they have in hand. This prediction clearly fails in our trading exercises. Subjects showed (in aggregate) a preference for the ‘in hand’ good over the good that was merely sitting on the table. This behaviour is a form of status quo bias (Samuelson and Zeckhauser, 1988), now more commonly referred to as a reference-point effect.
Note that preferences can fail in this way and still exhibit DMV, and vice versa; therefore we leave the implications of this phenomenon for a separate paper. However, it will be necessary to deal with this reference-point effect in the following section.
II. UTILITY AND DEMAND
Diminishing marginal value played a key historical role in connecting demand and utility. In this section we use our experimental sports card results to show the empirical link. This exercise requires (i) a specific utility function, (ii) the DMV treatments reported above and (iii) a further set of treatments with different trading prices, which allows us to observe demand. We first describe the demand treatments.
Demand curve treatments
A further set of treatments with different trading prices provides data that can be used to construct demand curves. These are demand curves denominated in goods, relevant for a simple two-good economy. Subjects were endowed with three units of either a or b. In treatment J, already described, the subject could trade one unit of a for one unit of b, so the price of the non-endowed good, b, is 1 (only one trade allowed per subject). In treatment K the subject must trade two units of a for one unit of b, so the price of b is now 2. In treatments L and M the subjects were endowed with three units of b; the price of a was 1 in treatment L and 2 in treatment M.
We expect a lower trading rate as the price rises. Results are shown in Tables 9 and 10. Results show demand curves that are clearly downward-sloping. In both cases the treatment with a higher price for the good being ‘bought’ had a significantly lower proportion traded.
| Price of good b | ||
|---|---|---|
| 1 (treatment J) | 2 (treatment K) | |
| % traded (demand for b) | 77.5 | 47.5 |
| (n=40) | (n=40) | |
| Price of good a | ||
|---|---|---|
| 1 (treatment L) | 2 (treatments M) | |
| % traded (demand for a) | 87.5 | 42.5 |
| (n=40) | (n=40) | |
Linking utility and demand
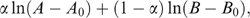 (1)
(1)To convert trading decisions to ‘consumption’, we calculated items per 100 subjects. This is easiest to understand in terms of the budget constraints for each particular treatment, which are shown in Table 11. In treatment J, 100 subjects begin the treatment with 3a each; thus, the endowment is A=300. One unit of a can be traded for one unit of b. Thus, the budget constraint is A+B300. If the trading rate were 75% (75% of subjects opt to trade an a for a b) then those 100 subjects would end up with 75b, leaving them with 225a. The final consumption levels would be A=225 and B=75.
| Treatment | Budget constraint | A0 | B0 |
|---|---|---|---|
| H | a+b=100 | 100β | 100γ |
| I | a+b=100 | 100γ | 100β |
| J | a+b=300, a200 | 300β | 300γ |
| K | a+2b=300, a100 | 300β | 300γ |
| L | a+b=300, b200 | 300γ | 300β |
| M | 2a+b=300, b100 | 300γ | 300β |
An appropriate scale is also needed for A0 and B0. The reference-point effect described above requires us to recognize that this scale may be specific to each treatment, dependent on both the endowment and the framing of the decision problem. We set the baseline for the endowed good at βY, where Y is income (Table 11), and the baseline for the non-endowed good at γY. A reference-point effect implies β>γ; a finding of β=γ implies no reference-point effect. This format is arbitrary but useful. Our main goal here is to construct a model that provides a transparent role for reference-point effects yet is also well behaved as a model of choice and demand in all other regards. Values for A0 and B0 based on this approach are shown in Table 11.
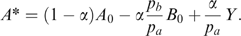 (2)
(2)Results We used data from experiments H–M to estimate (2) using maximum likelihood methods. Estimated parameters and approximate standard errors are α=0.56 (0.04), β=0.60 (0.05) and γ=0.12 (0.04). Actual and predicted values for choice variables are shown in Table 12. These results show a high degree conformity with observed choices, although we recognize that such an assessment is necessarily qualitative.
| Treatment | Predictions | Actuala |
|---|---|---|
| A* (from (2)) | A (Tables 5, 6, 9, 10) | |
| H | 76 | 77.5 |
| I | 28 | 27.5 |
| J | 227 | 222.5 |
| K | 207 | 205 |
| L | 84 | 87.5 |
| M | 50 | 42.5 |
- a All numbers normalize the number of subjects to 100.
The hypothesis β=γ is rejected at above the 99% level. Since 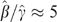 in our experiments, being endowed with a good makes the good roughly five times more valuable than not being so endowed.
in our experiments, being endowed with a good makes the good roughly five times more valuable than not being so endowed.
Previous research has largely been content to find well behaved demand curves, while the underlying behaviours such as DMV have been largely unexplored. Our calculations yield a joint model of DMV and demand, provided we make allowance for the reference-point effect.9
III. CONCLUDING COMMENTS
DMV is an historically important idea that helped lead the early neoclassicists to adopt a utility-based model of behaviour, although it is not the link between utility and demand in a theoretical sense, and early writers sometimes conflated it with other relevant concepts. For modern economists, this property remains a widely assumed behavioural feature, often the core of our intuition—indeed, it is often difficult to imagine behaviour without DMV. Yet, the empirical evidence for it has remained unexplored and untested. This gap has clearly needed redressing. Given the rising evidence of anomalies in neoclassical preferences, it is desirable to look for empirical support for even the most basic postulates of demand theory.
In our tests, the range of endowments being valued is small. Such small ranges provide powerful tests of our hypothesis. They do not, however, allow us to predict behaviour under larger endowments. We also have looked at only three types of good, while we expect the effect of the endowment on marginal value to be different for different goods. Economists will be most interested next, we feel, in knowing which kinds of goods are likely to have strong DMV and which are likely to have constant marginal value or even increasing marginal value. We leave these questions for a subsequent paper.
ACKNOWLEDGMENTS
We thank Ted Gayer, Glenn Harrison, John Worth and two anonymous referees for helpful comments.
NOTES
Appendices
APPENDIX A: SUMMARY OF EXPERIMENTAL TREATMENTS
Table A1 presents a summary of the experimental treatments.
| Treatment | Subjects | No.subjects | No.analysed | Endowment |
|---|---|---|---|---|
| Private good with price elicitation | ||||
| A | Undergraduate students | 37 | 36 | 3 mugs |
| Parent–Teachers' Assn (PTA) | 10 | 6 | 3 mugs | |
| PTA | 26 | 19 | 3 mugs | |
| B | Parents of Swim Club | 52 | 48 | 4 mugs |
| PTA | 20 | 19 | 4 mugs | |
| C | Parents of Cub Scouts | 30 | 26 | 1 mug, 3 flashlights |
| Lions' Club | 42 | 34 | 1 mug, 3 flashlights | |
| PTA | 27 | 24 | 1 mug, 3 flashlights* | |
| PTA | 50 | 48 | 1 mug, 3 flashlights* | |
| D | ‘Mothers of Multiples’ | 18 | 15 | 1 flashlight, 3 different mugs |
| E | PTA | 41 | 41 | 1 mug, 3 mugs (different style)* |
| F | PTA | 27 | 27; 25 | 1 flashlight, 3 mugs* |
| G | PTA | 50 | 50 | 1 mug, 3 binoculars |
| Private good with exchange mechanism | ||||
| H | Sportscard consumers | 40 | 40 | 1 Ripken stub |
| I | Sportscard consumers | 40 | 40 | 1 Sanders stub |
| J | Sportscard consumers | 40 | 40 | 3 Ripken stubs |
| K | Sportscard consumers | 40 | 40 | 3 Ripken stubs |
| L | Sportscard consumers | 40 | 40 | 3 Sanders stubs |
| M | Sportscard consumers | 40 | 40 | 3 Sanders stubs |
| Public good with exchange mechanism | ||||
| N | Sportscard consumers | 40 | 40 | 1 Ripken stub |
| O | Sportscard consumers | 37 | 37 | 1 Sanders stub |
| P | Sportscard consumers | 35 | 35 | 3 Ripken stubs |
| Q | Sportscard consumers | 33 | 33 | 3 Ripken stubs |
| R | Sportscard consumers | 42 | 42 | 3 Sanders stubs |
| S | Sportscard consumers | 35 | 35 | 3 Sanders stubs |
- * In these treatments, compensation demanded was elicited only for returning 2 or 3 items out of the 3-item endowment. Subjects were not asked their CD to return 1 item of the 3-item group.
APPENDIX B: FURTHER EXPERIMENTAL PROCEDURES FOR VOTING EXPERIMENT
The instructions for the (proposed trade of Sanders ticket stub for Ripken ticket stub) benchmark public goods treatment read as follows:
Welcome to Lister's Referendum. Today you have the opportunity to vote on whether ‘Mr Twister’, this small metal box, will be ‘funded’. If ‘Mr Twister’ is funded, I will turn the handle and N [the amount of people in the room] Kansas City Royals game ticket stubs dated June 14, 1996, which were issued for admission to the baseball game in which Cal Ripken Jr broke the world record for consecutive games played, will be distributed—one to each participant. [illustrate] To fund Mr Twister, all of you will have to give me your Barry Sanders ticket stub, which was issued for admission to the football game in which Barry Sanders surpassed Jim Brown to become the fourth all-time rushing leader in the history of the National Football League. Below please find the proposition and referendum rules.
Proposition
Everyone in the room will contribute their Barry Sanders ticket stub to the fund. The contribution will be used for the purpose of funding Mr Twister, a mechanism that if funded will distribute one Kansas City Royals game ticket stub dated June 14, 1996, to each participant. [illustrate]
Referendum rules
• If more than 50% of you vote YES on this proposition, all of you will give me your Barry Sanders ticket stub. In return, ‘Mr Twister’ will be funded and I will crank the handle, providing one Kansas City Royals game ticket stub dated June 14, 1996, to each participant. [illustrate]
• If 50% or fewer of you vote YES on this proposition, no one will give me their Barry Sanders ticket stub and ‘Mr Twister’ will not be funded. Hence no one will receive a Kansas City Royals game ticket stub dated June 14, 1996.
After the instructions were read aloud, the vote to fund Mr Twister was taken. Each subject filled out his or her decision sheet.
We note several key aspects of our experimental treatments. First, no subjects participated in more than one treatment. Second, similar to the private-good treatments, before voting on the proposition every subject had a chance to inspect both goods. Third, again following the private-good treatments, we randomized subjects into treatments to assure an equal representation across treatments.




