Distinguishing the Source of Market Power
This manuscript reports research conducted in part by the Michigan Agricultural Experiment Station, the Texas Agricultural Experiment Station, and the Washington State University Agricultural Research Center.
The authors express appreciation to two anonymous AJAE reviewers for their constructive comments on earlier drafts of this manuscript.
Abstract
Structural models used to measure market power, though widely employed, continue to be criticized. We compare alternative market power tests, including nonparametric and Solow residual-based (SRB) tests. We develop SRB methods that permit nested testing for both monopolistic and monopsonistic market power by the same firm. These tests and a set of nonparametric tests are implemented to examine market power exertion by U.S. cigarette manufacturers from 1977 to 1993. All tests indicate that cigarette manufacturers exerted monopsonistic power in the upstream tobacco market. They are mixed on whether monopolistic power exertion was exerted in the downstream market.
New empirical industrial organization (NEIO) analysis often employs an econometric structural model in which market power exertion is measured via a conduct parameter (Bresnahan 1982, 1989; Lau 1982). Although the NEIO approach is widely accepted and regularly implemented in empirical studies, there is considerable debate about the accuracy of the approach (Corts 1999; Genesove and Mullin 1988; Boyer 1996). For example, Corts (1999) presents an analytical argument that the conduct parameter fails to accurately measure market power. Using dynamic oligopoly simulations, he shows that mismeasurement can be quite large.
As debate continues regarding the usefulness of structural market power tests, alternative market power measurement methods are being developed. Alternatives such as nonparametric and Solow residual-based (SRB) market power tests rely on different assumptions and circumvent the issue of functional form choice for behavioral equations (Ashenfelter and Sullivan 1987; Varian 1984; Hall 1988; Domowitz, Hubbard, and Petersen 1988; Roeger 1995). Neither of these approaches assumes a particular technology specification. Additionally, each requires less data than structural market power tests because demand or supply relationships in the opposing markets need not be specified.
These alternative test procedures have addressed some of the criticisms raised about traditional NEIO methods. However, according to Geroski (1988, p. 108), “none of the different weapons which have been brought to bear on the problem of collusion are as sharp as one might wish.” For example, separate SRB tests developed to measure monopolistic and monopsonistic market power have used identical models (Hall 1988; Hyde and Perloff 1994). Thus, the question remains whether this approach is useful in distinguishing between monopolistic and monopsonistic power as the underlying source of market power exertion. Importantly, alternative methods have not been compared to determine whether they produce similar estimates of market power exertion for the same industry.
We extend existing SRB and nonparametric methods to test for monopolistic market power in the downstream market and monopsonistic market power in the upstream market power (i.e., pure middleman monopoly). Importantly, the SRB methods are extended to permit nested testing for market power in both output and input markets. Conveniently, each test requires the same data whether unidirectional or bidirectional market power is admitted. We conduct tests using two SRB methods and two revealed preference-based (Varian 1984) nonparametric methods. The SRB parametric tests are adapted from earlier procedures developed by Hall (1988), Domowitz, Hubbard, and Petersen (DHP) (1988), and Roeger (1995). The nonparametric tests are adapted from Ashenfelter and Sullivan's (1987) procedures.
We implement these tests to examine market power in the U.S. cigarette manufacturing industry for the period 1977 to 1993. We truncate the data at 1993, in part, because of significant tobacco industry events that occurred after that point, which may have altered the structure of the market.1 This industry provides an appealing market for analysis since Ashenfelter and Sullivan (1987), Hall (1988), Domowitz, Hubbard, and Petersen (1988), and Roeger (1995) all include results from the tobacco industry. Additionally, although it has long been the target of monopolistic market power studies (Ashenfelter and Sullivan 1987; Hall 1988; Roeger 1995; Sullivan 1985; Sumner 1981), the industry's potential monopsonistic market power in procuring tobacco from domestic growers has received little attention.2
Given the high level of concentration that exists in U.S. cigarette manufacturing, monopolistic power exertion in output markets is certainly plausible. In 1996, the four-firm concentration ratio was 97, with market shares of 42.3%, 28.8%, 18.7%, and 7.2% for the four largest firms. However, these concentration measures, coupled with farm program-induced inelastic supply over the sample period, also support the possibility of cigarette manufacturers exerting monopsonistic market power in procuring domestic tobacco. U.S. tobacco growers produced 1,268 million pounds of tobacco in 1995 and 844 million pounds in 2003. Approximately 72% of U.S. production has been sold domestically for cigarette production over the last decade (USDA, Tobacco Yearbook 2003, Table 29). While there are thousands of tobacco growers, each has access to a limited number of buyers for the product. Tobacco is also a highly specialized crop, both in production and in use. Rogers and Sexton (1994) suggested that raw agricultural products, such as tobacco, will typically face narrower relevant markets with respect to both product class and geography than the markets for their finished products. Although the U.S. tobacco farm program essentially ended with the 2005 marketing season, the program over the sample period was structured in such a way that cigarette manufacturers' “buying intentions” directly impacted quota levels and price determination (Capehart 2000). These unique industry characteristics increased the potential for monopsonistic market power exertion in domestic tobacco procurement.
We examine the relationship between cigarette manufacturers and wholesalers as well as the behavior of cigarette manufacturers in procuring domestic tobacco. While manufacturing data at the two-digit SIC level is often used to examine monopolistic market power in the industry (e.g., Roeger 1995; Hall 1988), we conduct our analysis using more specific four-digit SIC code data. We use wholesale cigarette price and quantity data rather than the retail data used by some previous studies (Sumner 1981; Sullivan 1985; Ashenfelter and Sullivan 1987).3 We also incorporate costs of domestic and imported tobacco, labor, advertising, capital, and materials.
Measuring Imperfect Competition
Market power is defined as deviation from marginal-cost or value-of-marginal-product pricing. Such deviations may be in the form of monopolistic market power, where output price is greater than marginal cost (MC), or in the form of monopsonistic market power, where input price is less than the value of marginal product (VMP). SRB market power tests measure this price-cost relationship by comparing actual growth in the output/capital ratio with the expected growth given the rate of technical progress and growth in the labor/capital ratio (Hall 1988). Differences between actual and expected growth are attributed to market power. Nonparametric market power tests employ a revealed preference approach founded on the weak axiom of profit maximization (WAPM). For consistency with competitive behavior, WAPM states that the observed input and output quantity choices at output price, p, and input prices, r, must yield profit at least as great as any other possible quantity choice set (Varian 1984). If a firm is exerting market power, it will be evidenced by the quantity choices made in each period.
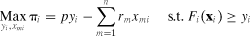 (1)
(1)All of the tests used in this article maintain the joint hypothesis of regularity, monotonicity, and concavity of a single-output production function with n inputs. In addition, the SRB tests maintain a differentiable production function that exhibits constant returns to scale and Hicks-neutral technical change. All tests assume competitive behavior in all markets except the one(s) for which market power is tested (cigarette supply, y, for monopoly and domestic tobacco demand, xn, for monopsony).
SRB Tests
Because SRB tests rely on statistical parameter estimation, they have the advantage over nonparametric tests of facilitating computation of confidence intervals associated with hypothesis tests of market power exertion. However, as noted, they require the additional assumptions of differentiability, constant-returns-to-scale (CRS) technology, and Hicks-neutral technical change. Hall's (1988) and DHP's (1988) monopolistic market power tests use a primal approach based on the Solow residual. Roeger (1995) extends their work by incorporating a primal-dual measure of the Solow residual. We add tests for monopsonistic market power and nest monopoly and monopsony tests within a more general specification.
Primal Approach
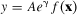 (2)
(2)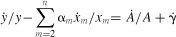 (3)
(3) and is approximated discretely by zt − zt-1. The left side of (3) is the Solow residual and will be denoted SR.
and is approximated discretely by zt − zt-1. The left side of (3) is the Solow residual and will be denoted SR.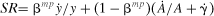 (4)
(4)Equation (4) gives our version of DHP's estimating equation for monopolistic market power exertion and is similar to Hall's. Both of their tests yield a testable hypothesis for market power where positive values of βmp indicate monopolistic market power exertion.5 In equation (4), 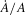 the productivity shock, represents an unobservable error term. Since the firm simultaneously determines input use and output level,
the productivity shock, represents an unobservable error term. Since the firm simultaneously determines input use and output level, 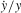 is likely correlated with
is likely correlated with  and requires an instrumental variable procedure to obtain a consistent estimate of βmp. However, estimation results can be sensitive to instrument choice (Roeger 1995).
and requires an instrumental variable procedure to obtain a consistent estimate of βmp. However, estimation results can be sensitive to instrument choice (Roeger 1995).
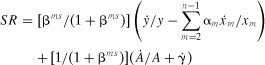 (5)
(5)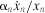 is likely correlated with the productivity shock,
is likely correlated with the productivity shock, 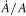 .
.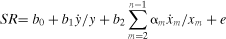 (6)
(6)Perfect competition in all input and output markets is revealed by b1 = b2 = 0. Monopolistic market power in y with perfect competition in all input markets is revealed by b2 = 0 and b1 = βmp > 0. Monopsonistic market power in xn with perfect competition in output and all other input markets is revealed by b1 = −b2 = βms/(1 + βms) > 0. Joint monopolistic-monopsonistic market power is revealed by b1 > 0, b2 < 0, and b1 ≠ −b2. In each case, b0 includes (1 − b1)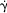 and e includes (1 − b1)
and e includes (1 − b1)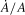 .
.
Primal-Dual Approach
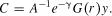 (7)
(7)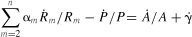 (8)
(8)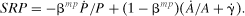 (9)
(9)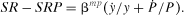 (10)
(10)Following Roeger (1995), under the maintained assumptions that factors can be instantaneously adjusted and no measurement errors exist in the data, the difference between the primal and dual Solow residuals should be equal to zero in all periods if there is no monopolistic market power exertion. In reality, there are measurement errors associated with data collection and all inputs are not adjusted instantaneously. As a result, an error term must be appended to equation (10) to form the estimating equation.
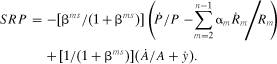 (11)
(11)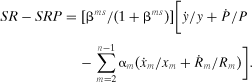 (12)
(12)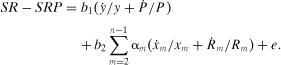 (13)
(13)Monopolistic market power in y with perfect competition in all input markets is revealed by b2 = 0 and b1 = βmp > 0. Monopsonistic market power in xn with perfect competition in output and all other input markets is revealed by b1 = −b2 = βms/(1 + βms) > 0. Joint monopolistic-monopsonistic market power is revealed by b1 > 0, b2 < 0, and b1 ≠ −b2.
An additive error term is included for estimation, but this equation includes no intercept. Unlike the primal approach, the error term should not generally be correlated with the explanatory variable since it represents errors in measurement rather than systematic errors in productivity growth, 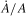 , associated with input use. Consequently, ordinary least squares estimation is expected to yield an unbiased and efficient estimate of βms under the maintained hypothesis. However, under certain conditions, the error term associated with equation (13) may exhibit correlation with the regressors, serial correlation, and/or heteroskedasticity, requiring appropriate econometric corrections.8
, associated with input use. Consequently, ordinary least squares estimation is expected to yield an unbiased and efficient estimate of βms under the maintained hypothesis. However, under certain conditions, the error term associated with equation (13) may exhibit correlation with the regressors, serial correlation, and/or heteroskedasticity, requiring appropriate econometric corrections.8
Nonparametric Tests
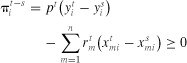 (14)
(14)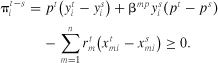 (15)
(15)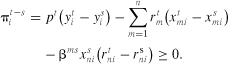 (16)
(16)Ashenfelter and Sullivan Test
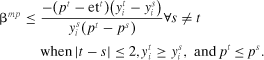 (17)
(17)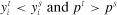 . Market power exertion, βmp > 0, can only be rejected in favor of more competitive structures.11 This measure could then be used to obtain an approximate measure of nt, the distribution of “numbers equivalent of Cournot firms” for all comparisons, where nt ≥ 1/βmp and represents the smallest number of Cournot firms that the industry can support (Sullivan 1985).
. Market power exertion, βmp > 0, can only be rejected in favor of more competitive structures.11 This measure could then be used to obtain an approximate measure of nt, the distribution of “numbers equivalent of Cournot firms” for all comparisons, where nt ≥ 1/βmp and represents the smallest number of Cournot firms that the industry can support (Sullivan 1985).Revised Nonparametric Tests
In our nonparametric market power tests, two of the admitted weaknesses of Ashenfelter and Sullivan's (1987) test are surmounted and the test is extended to monopsonistic behavior. The assumptions of a stable cost function and a stable demand curve in the opposing market are relaxed for these revised tests by incorporating all input costs, including those for advertising. While Ashenfelter and Sullivan (1987) attempted to limit these problems by considering only pairs of points from the same region and close in time, a more precise remedy can be implemented.
It is reasonable to assume that the cost structure of a firm or industry may change over time. These changes can be accounted for by including measures of cost for each period. It is also reasonable to assume that substitute prices, income or consumer preferences, and thus market demand may shift over time. When comparisons are only made between “near” data points, valuable information from comparisons where shifts did not occur may be lost. Since a demand shift unmatched by a shift in supply will cause output price and quantity to move in the same direction between observations, deleting comparisons where Δyi has the same sign as Δp can also reduce the likelihood of false rejections (Love and Shumway 1994). Such movements are clearly not attributable to market power exertion. Similarly, in the monopsony case, input prices and quantities may move in opposite directions between observations due to shifts in input supply unmatched by shifts in input demand. In developing the analogous test for monopsonistic market power, we delete comparisons between time periods when Δrn does not have the same sign as Δxni.
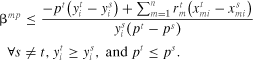 (18)
(18) (19)
(19)Data and Implementation
Data used in this study consist of annual observations from the U.S. cigarette manufacturing industry for the period 1977 to 1993. Domestic cigarette production is taken from USDA Tobacco Situation and Outlook Yearbook (TSO) (various issues) as the sum of four types of cigarettes: standard cigarettes (70 mm nonfilter), filter tip cigarettes (80 mm), king (85 mm nonfiltered and filtered), and extra long (100 mm filter tip). Annual prices used to generate the Divisia price index are reported in TSO and are calculated by weighting corresponding wholesale cigarette price revisions by the fraction of the year that the price was in effect. Excise tax data are also taken from TSO. The Divisia price index for domestic production is constructed net of excise taxes.
Domestic tobacco price and quantity data are taken from TSO and consist of estimated leaf used for unstemmed flue-cured, unstemmed burley, and unstemmed Maryland tobacco. Prices used to calculate a Divisia price index for domestic tobacco are annual average prices received by growers for each tobacco type.
The source for imported tobacco data is the U.S. Department of Commerce's U.S. Imports for Consumption and General Imports: FT246 and FT247 (annual 1977–1993). The category of tobacco used in cigarette production is called cigarette leaf tobacco. It includes five types of tobacco: unstemmed Oriental, unstemmed flue-cured, unstemmed burley, stemmed tobacco except cigar leaf, and scrap tobacco except cigar leaf. Again, a Divisia price index is created using prices for each category computed from quantity and import value information.
Residual materials cost is calculated by subtracting the cost of domestic and imported tobacco from cost of materials as reported in the U.S. Bureau of the Census' Annual Survey of Manufacturers (1977–1994, various issues). The price index of residual materials is proxied by the producer price index for materials as reported in the Economic Report of the President (1993). A quantity index for residual materials is constructed by dividing the residual materials cost by the producer price index for materials.
Data on advertising expenditures are taken from TSO (1977–1994, various issues). A quantity index for advertising is obtained by dividing the cigarette industry's reported annual expenditures on advertising by the cost per thousand advertising price index for magazines. The price index for magazines is chosen as a proxy for the cost per unit of advertising since magazine advertisements represent a major portion of advertising expenditures for cigarette manufacturers. This index is constructed from indices reported in USDA's Food Marketing Review, 1992–1993 (1994) and from Advertising Age (1977–1994, various issues).
Cost of labor and the number of employees in cigarette manufacturing data are taken from USBC's Annual Survey of Manufacturers, various issues. Total compensation is divided by the number of employees to calculate average annual compensation per employee. A Divisia price index is then constructed to represent the price of labor.
Capital price is calculated as the annual cost per unit of capacity. Total capacity is the proxy for quantity of capital. Total capacity is recovered by dividing actual cigarette production by the capacity utilization rate as reported in USBC's Annual Survey of Manufacturers Current Industrial Reports, Tobacco and Tobacco Products (various years). Annual total cost of capital is calculated assuming a 10-year depreciation rate of new capital expenditures (also from USBC's Annual Survey of Manufacturers) with no salvage value. A 5-year moving average of Moody's AAA corporate bond rate from the Economic Report of the President (1993) is used to estimate annual interest costs. Total annual capital service cost is the sum of depreciation charges and interest charges. Dividing total capital services cost by total capacity gives capital price per unit of capacity. We then construct indices for the price and quantity of capital.
Prices of imported tobacco, residual materials, advertising, and labor inputs are then aggregated into a single Divisia price index for the SRB tests of market power. A quantity index for this aggregate “other” input category is constructed by dividing the total cost of these four categories by the aggregate “other” input price index. For these tests, capital is treated as the numeraire input, x1.
Instruments used in the estimation include excise tax and advertising expenditure for the potentially endogenous cigarette output price and farm labor wage rate and flue-cured tobacco basic marketing quota for the potentially endogenous tobacco input price. The farm labor wage rate is taken from state-level data for Kentucky and North Carolina (Ball 1996). The marketing quota data are from USDA's Tobacco Situation and Outlook Yearbook (1977–1994, various issues).
We estimate primal and primal-dual SRB market power tests nesting monopolistic and monopsonistic counterparts. The monopoly tests are compared to Hall's (1988), Roeger's (1995), and DHP's (1988) original results. We implement Ashenfelter and Sullivan's (1987) original method for comparison to their original results. Our revised version of Ashenfelter and Sullivan's (1987) method is employed to more accurately assess nonparametric evidence for monopolistic and/or monopsonistic market power in this industry over our data period. SHAZAM and GAMS programs are used to conduct the tests.
Results
Test statistics for nested SRB monopolistic and monopsonistic market power are reported in table 1. Although OLS is generally regarded as an acceptable estimation method for the primal-dual model, both the primal and primal-dual models were estimated by 2SLS. Equation performance and tests statistics for the primal-dual model were qualitatively the same for OLS, AR1, and 2SLS estimation. Both estimated models had very high-adjusted R2 and insignificant autocorrelation. Both slope parameters were significant in each model. In both models, the hypothesis of perfect competition in output and all input markets was soundly rejected at the 5% level of significance in favor of the alternate hypothesis of imperfect competition in one or more markets. The hypothesis that monopoly was the only source of market power was also rejected by both models, while the hypothesis that monopsony was the only source of market power was rejected only by the primal-dual model. Thus, both the primal and the primal-dual SRB models render the same conclusion that cigarette manufacturers exercised significant monopsonistic market power in tobacco purchases. Only the primal-dual model found evidence that significant monopolistic market power was exerted in cigarette sales over the data period. In each case, the evidence of monopsonistic market power was stronger than the evidence for monopolistic market power.
| Statistic | Primal (Equation 6) | Primal-Dual (Equation 13) |
|---|---|---|
| Parameter estimate:b | ||
| b 0 | 0.0014 | - |
| (0.67) | ||
| b 1 | 0.7883 | 1.0663 |
| (3.86) | (22.20) | |
| b 2 | −0.8577 | −1.4822 |
| (−3.78) | (−14.10) | |
| Adjusted R2 | 0.97 | 0.99 |
| Durbin-watson statistic | 2.61 | 1.49 |
| H0: perfect competition, b1 = b2 = 0: | ||
| F-statistic | 7.83 | 274.59 |
| p-value | 0.0059 | 0.00000 |
| H0: monopoly only source of market power, b2 = 0: | ||
| T-statistic | −3.78 | −14.10 |
| p-value | 0.0023 | 0.00000 |
| H0: monopsony only source of market power, b1 = −b2: | ||
| T-statistic | −0.60 | −5.87 |
| p-value | 0.56 | 0.00004 |
- a Both equations were estimated by 2SLS. Equation performance and test statistics for the primal-dual equation were similar to OLS and AR(1) estimates.
- b t-statistics are in parentheses.
Table 2 compares regression results from our SRB market power tests constrained to permit monopolistic or monopsonistic market power, but not both, with Hall's (1988), Roeger's (1995), and DHP's (1988) original results. Our data differ from that of Hall (1988) and of Roeger (1995) in that we use four-digit industry-level data rather than the more aggregated two-digit industry-level data. We include three rather than two input categories. We also account for cigarette manufacturers' advertising, tobacco, other materials, labor, and capital input costs in the specification. Hall's (1988) and Roeger's (1995) estimates yielded identical Lerner indexes, βmp, of 0.64. However, Hall's (1988) estimate was derived from his estimate of λH, the monopoly markup's reciprocal, which was not statistically significant. Both DHP's and our primal approaches, using the four-digit data set, resulted in more conservative estimates of βmp. DHP obtained a significant 0.37 Lerner index estimate of monopolistic market power. In contrast, our estimate was only 0.12 and, like Hall's (1988), was not statistically significant. Using the primal-dual approach, our estimate of the monopoly Lerner index when monopoly was the only source of market power considered was a significant 0.51, a little lower than Roeger's (1995) 0.64 but large enough to imply that the industry set cigarette price at more than twice marginal cost. Except for Hall's (1988) and our primal estimates, the other SRB estimates revealed significant monopolistic power when that was treated as the only possible source of market power.
| Primal | Primal-Dual | ||||
|---|---|---|---|---|---|
| Study | λH | βmp | Adjusted R2 | βmp | Adjusted R2 |
| Monopoly only source of market power: | |||||
| Hallb | 0.36 | 0.64 | na | — | — |
| (1.88) | |||||
| DHPc | 0.37 | 0.97 | — | — | |
| (8.09) | |||||
| Roegerd | — | — | 0.64 | 0.95 | |
| (23.05) | |||||
| This studye | 0.12 | 0.24 | 0.51 | 0.73 | |
| (0.25) | (4.17) | ||||
| Monopsony only source of market power: | βms | βms | |||
| This studyf | 3.95 | 0.97 | 10.36 | 0.95 | |
| (4.16) | (12.14) | ||||
- a t-statistics are in parentheses.
- b Results for two-digit industry-level annual data (1953 to 1984) as reported by Hall using military spending, oil price, and party of the president as instruments.
- c Results for four-digit industry-level annual data (1958 to 1981) as reported by Domowitz, Hubbard, and Petersen using military spending and import price as instruments.
- d Results for two-digit industry-level annual data (1953 to 1984) as reported by Roeger.
- e Results for four-digit industry-level data, including input and advertising costs. No significant evidence of autocorrelated errors was found.
- f Results for four-digit industry-level data, including input and advertising costs, estimated by 2SLS. No significant evidence of autocorrelated errors was found.
When monopsony was considered to be the only source of market power, both our primal and primal-dual estimates revealed significant market power. Unlike the monopoly Lerner index, the monopsony Lerner index is not bounded by 1.0. Both estimates were statistically significant: 3.95 for the primal estimate and 10.36 for the primal-dual estimate. The high magnitude of these estimates of the monopsony Lerner index imply that cigarette manufacturers paid tobacco producers only between 9% and 20% of tobacco's value of marginal product in cigarette manufacturing. These estimates imply a more substantial markdown of tobacco price due to monopsonistic behavior than the 28% previously estimated by Raper, Love, and Shumway (2000).
Table 3 reports the percentage of observation pairs consistent with alternative “numbers equivalent of Cournot firms” (CNE) hypotheses based on the nonparametric tests.12 The CNE represents the least number of firms with Cournot behavior that the industry could support. Although there were only eight cigarette manufacturers in 1992, we also report results for n = 9 and n = ∞. It is possible that firms exhibit behavior more competitive than Cournot behavior, which would result in a CNE greater than n = 8. The percentages based on Ashenfelter and Sullivan's (1987) nonparametric monopolistic market power estimates and reported in their paper are listed as Test A1. Table 3 also includes the monopoly-power CNE for the slightly modified Ashenfelter and Sullivan (1987) method (equation 17) following their implementation procedure with our data (Test A2), as well as both monopoly-power and monopsony-power CNE using our revised versions of Ashenfelter and Sullivan's (1987) test (18, 19).
| Percentage Consistent with Numbers Equivalenta | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Monopolistic Market Power | Monopsonistic Market Power | ||||||||||
| Numbers Equivalent Hypothesesb | Test A2 | Test B1 | Test B2 | Test B3 | Test B4 | ||||||
| Test A1 op = 702 | Neg pΔ op = 14 | Pos pΔ op = 14 | Neg pΔ op = 65 | Pos pΔ op = 63 | Neg pΔ op = 65 | Pos pΔ op = 63 | Pos rΔ op = 90 | Neg rΔ op = 90 | Pos rΔ op = 90 | Neg rΔ op = 90 | |
| n = 1 | 24.4 | 7.1 | 7.1 | 23.1 | 12.7 | 6.2 | 6.3 | 44.4 | 24.4 | 94.4 | 93.3 |
| n = 2 | 45.2 | 7.1 | 7.1 | 23.1 | 12.7 | 6.2 | 7.9 | 74.4 | 55.6 | 96.7 | 96.7 |
| n = 3 | 60.4 | 14.3 | 7.1 | 26.2 | 17.5 | 12.3 | 22.2 | 83.3 | 76.7 | 96.7 | 97.8 |
| n = 4 | 69.7 | 21.4 | 21.4 | 29.2 | 27.0 | 27.7 | 42.9 | 92.2 | 85.6 | 96.7 | 98.9 |
| n = 5 | 75.1 | 35.7 | 21.4 | 35.4 | 30.2 | 46.2 | 52.4 | 93.3 | 92.2 | 97.8 | 98.9 |
| n = 6 | 79.3 | 35.7 | 35.7 | 40.0 | 36.5 | 47.7 | 61.9 | 93.3 | 93.3 | 98.9 | 98.9 |
| n = 7 | 82.9 | 42.9 | 35.7 | 43.1 | 42.9 | 52.3 | 68.3 | 93.3 | 93.3 | 98.9 | 98.9 |
| n = 8 | 85.2 | 57.1 | 50.0 | 43.1 | 47.6 | 58.5 | 76.2 | 96.7 | 93.3 | 98.9 | 98.9 |
| n = 9 | 86.5 | 57.1 | 57.1 | 46.2 | 50.8 | 63.1 | 85.7 | 97.8 | 93.3 | 98.9 | 98.9 |
| n = ∞ | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
- a Codes: op denotes number of observation pairs, Neg pΔ denotes a negative cigarette price change, Pos is positive, and r is tobacco price. Tests A1–A2 follow A&S in assuming a stable cost function (i.e., ignoring all costs) and comparing observations not more than two years apart. Test A1 denotes original A&S results using state-level annual data from 45 states for the period 1955 to 1982, as reported in the first column of their table III. Test A2 denotes our application using U.S. four-digit SIC data for the period 1977 to 1993. Tests B1–B4 follow a revised A&S method using U.S. four-digit SIC data for the period 1977 to 1993. Tests B1 and B3 incorporate domestic tobacco costs only, while Tests B2 and B4 incorporate all input costs (including advertising). Tests B1 and B2 compare all observations except those where cigarette demand shifts occur in the same direction as its price. Tests B3 and B4 compare all observations except those where domestic tobacco supply shifts occur in the opposite direction as its price.
- b n represents the number of firms with Cournot behavior that would be supported by the industry as evidenced by the data. Thus, a lower n represents less competitive behavior.
Our revised versions of Ashenfelter and Sullivan's (1987) test compare all observations except those where cigarette demand shifts occur in the same direction as its price for the monopoly tests (or domestic tobacco supply shifts occur in the opposite direction as its price for the monopsony tests). In the revised tests, we consider two cost alternatives: (a) the only nonconstant cost is presumed to be domestic tobacco (Tests B1 and B3), and (b) all costs are incorporated in the analysis (Tests B2 and B4). The results for each of our tests are reported in two columns—one for positive changes in cigarette or tobacco price and the other for negative changes.
The CNE's from Ashenfelter and Sullivan's (1987) original study suggest that the cigarette industry has some monopolistic market power but is not a perfect cartel. For example, 70% of the observations supported a CNE of four Cournot firms (CNE-4 for Test A1). The interpretation is that these observations supported behavior consistent with an industry having no less than four Cournot firms. We found considerably less evidence of monopolistic market power when we applied Ashenfelter and Sullivan's (1987) original method to our data (Test A2)—21% of the observations supported a CNE of four Cournot firms. The support for small CNE's was similar we applied our revised Ashenfelter-Sullivan (1987) method to our data. When domestic tobacco costs were incorporated and all observations were compared (except when cigarette demand shifted in the same direction as its price), 28% of the observations supported CNE-4–29% for negative cigarette price changes and 27% for positive cigarette price changes (Test B1). When all costs were incorporated and all relevant observations were compared, CNE-4 was supported by more, but still only 35%, of the observations (Test B2)-28% for negative cigarette price changes and 43% for positive cigarette price changes.
In the monopsonistic market power tests, 89% of the observations supported a CNE-4 when domestic tobacco costs were incorporated in the analysis (Test B3)—92% for positive tobacco price changes and 86% for negative tobacco price changes. When all input costs were incorporated (Test B4), CNE-4 increased to 98%–97% for positive tobacco price changes and 99% for negative tobacco price changes. In other words, 98% of the observations, omitting only domestic tobacco supply shifts where quantity moves in the opposite direction of its price, support an industry of no less than four Cournot firms. We can also consider full monopolistic or monopsonistic market behavior, as defined by a CNE-1. The revised tests, including all input costs, indicate that only 6% of the observations support a CNE-1 for monopoly (Test B2) while 94% of the observations support a CNE-1 for monopsony (Test B4).
As with the monopolistic market power test (for CNE-4 and above), failure to account for all costs in the revised test understated monopsonistic market power exertion. Results from the revised Ashenfelter and Sullivan (1987) method imply that it was primarily monopsonistic market power, rather than monopolistic market power, that was being exerted by cigarette manufacturers over the observed time period. Both tests of monopsonistic market power imply a much smaller number of CNE's in the industry than do the corresponding tests of monopolistic market power.
Because of the nature of the inequalities, it is not possible to precisely convert the CNE's to Lerner monopoly and monopsony indexes. However, as approximate measures, the CNE's do provide relevant information. For example, based on the nonparametric tests that make use of all cost information and compare the largest number of observations (Tests B2 and B4), half the observations supported a βmp in the neighborhood of 0.2 and a βms > 1 while 75% of the observations supported a βmp in the neighborhood of 0.1 and a βms > 1. Like the SRB test results, the nonparametric test results imply (a) that cigarette manufacturers' clearly exercised market power in purchasing domestic tobacco, and (b) that evidence of market power exertion in the sale of cigarettes was less than what was evidenced in the purchase of domestic tobacco.
Summary and Conclusions
Parametric SRB and nonparametric market power tests offer alternatives to the structural method commonly used in empirical studies of market power. In this study we employ primal and primal-dual SRB monopsonistic market power tests analogous to SRB monopolistic market power tests developed by Hall (1988); Domowitz, Hubbard, and Petersen (1988); and Roeger (1995). The resulting monopsony tests are distinct from the monopoly tests, unlike previously developed monopsony tests using the Solow residual approach. Both forms of market power are nested within more general specifications, which are implemented to test for monopolistic and monopsonistic power exertion. Ashenfelter and Sullivan's (1987) nonparametric market power test was modified to permit a nonstable cost function and to compare a much wider range of observations.
All test results consistently indicate that the cigarette manufacturing industry has exercised market power. They are also consistent in revealing that the industry exerted substantial monopsonistic market power in the purchase of domestic tobacco. While the evidence that it exerted monopolistic market power in the sale of cigarettes is mixed, the tests consistently reveal evidence of greater monopsonistic than monopolistic market power exertion.
Both classes of tests maintain few auxiliary hypotheses and are relatively easy to implement. They bear consideration as alternatives to the more structured NEIO models for empirically testing for market power in other industries.
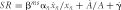 . Equation (5) was derived from this equation by multiplying both sides by rn/VMPn and rearranging to leave only SR on the left side of the equation. Recall that SR is the left side of equation (3).
. Equation (5) was derived from this equation by multiplying both sides by rn/VMPn and rearranging to leave only SR on the left side of the equation. Recall that SR is the left side of equation (3).



