Estimating unobservable valuation parameters for illiquid assets
For valuable research assistance, we are very grateful to Kevin Counsell. We have also benefited from discussions on this topic with Robert Cameron, Lew Evans, Jack Hodder and Martin Lally, and from helpful comments provided by session participants at the 2008 New Zealand Finance Colloquium, but any remaining errors and ambiguities are solely our responsibility.
Abstract
A problem that often arises in applied finance is one where decision-makers need to choose a value for some parameter that will affect the cash flows between two parties involved in the operation of an illiquid asset. Because the values of the cash flows also depend on various unobservable parameters, identifying the value of the policy parameter that achieves the desired allocation between the parties is no simple task, often resulting in disputes and the invocation of ad hoc approaches. We show how this problem can be solved using an extension of the well-known ‘implied volatility’ technique from option pricing, and apply it to the determination of equilibrium rental rates on ground leases of commercial land.
1. Introduction
The general class of problems that we consider in this paper arise when decision-makers need to choose a value for some parameter that will affect the cash flows between two parties involved in the operation of an illiquid asset. For example, this parameter could be the annual rental on a piece of leased equipment or land, or it might be the choice of exercise price for stock options to be issued to company executives.
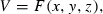 (1)
(1)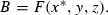
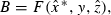
where ẑ is the collection of estimates of the unobservable exogenous parameters.
Apart from the construction of F, the key step in this process is estimation of the unobservable exogenous parameters z. To achieve the desired split of cash flows between the parties, the components of z must be estimated as accurately as possible, a particularly difficult task when the underlying asset generating the cash flows is illiquid and market data are scarce.
One possible approach is to use additional theoretical models that describe the determination of the unknown parameters, and then to estimate the inputs to these models using historical data. That is, ẑ is estimated outside the model given by equation (1). However, doing so introduces several new problems. First, the restrictions imposed by these additional models might be inconsistent with those of the original model; hence, this leads to policy choices that inadvertently combine ‘apples and oranges’ in an ad hoc manner. Second, when there are several unobserved parameters, using different models to estimate each ignores the dynamics of their joint determination. Third, even where these problems do not arise, the models or the data used to estimate the unobserved parameters may simply be ill-suited to illiquid assets. For example, suppose the unobservable parameter is a risk-adjusted discount rate. Then an obvious approach is to use some theoretical model of risk adjustment, such as the Capital Asset Pricing Model (CAPM). But the latter is strictly applicable only to the highly liquid assets traded in financial markets and, therefore, may provide highly biased estimates of discount rates for less liquid non-financial assets.
An alternative, and more consistent, approach is to estimate z within the model described by equation (1). That is, given data on actual market values for assets similar to the one of interest, we back out the value of z implied by (1). This method is, of course, akin to that commonly used in the field of option pricing to estimate stock price volatility.1 Valuing a stock option using standard pricing methods requires knowledge of the underlying stock volatility, which is unobservable. But reliable estimates can be obtained by inferring the volatility level that is consistent with (i.e. implied by) the observed market price of a similar option written on the same stock. This volatility estimate is then plugged back into the pricing formula in order to calculate the original option's value. Somewhat surprisingly, this approach has not previously been applied to the more general class of problems described above, perhaps because it is not immediately clear how, or whether, it can be easily extended to the situation where z is a vector (i.e. when there are multiple unobserved parameters). In addition, once one moves outside financial markets, illiquidity problems mean that it would be unusual to observe multiple claims and market prices for the same underlying asset.2
In this paper, we show how the within-model approach can be generalized to accommodate these issues. Suppose first that there exist market data on sales of n assets that are similar to the one that is the central object of study. For each such sale we observe the sales price (Vn), the policy parameter associated with that particular asset (xn), and the observable exogenous parameters (yn). We can then use these data to estimate the unobservable exogenous parameters (z) using the regression equation
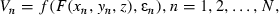 (2)
(2)for some function f of the theoretical market value F and a noise term ɛn. This form offers a variety of possibilities. For example, as we shall see below, one possibility is f(V, ɛ) = Veɛ, or equivalently
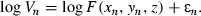
Of course, as the function F will typically be non-linear, equation (2) is likely to be somewhat complex. But so long as the exact form of F is known and the necessary data are available, this is easily accommodated by standard non-linear regression methods. In this way, we can obtain internally consistent estimates of z implied by a single valuation framework and, therefore, avoid the need to use a variety of ad hoc methods and estimates.
In the remainder of the present paper, we illustrate this approach using the concrete example of the rent-setting problem. In particular, we focus on the determination of equilibrium rental rates for ground leases of commercial land, as such transactions are economically significant and have received considerable recent attention in the literature (e.g. Dale-Johnson, 2001; Lally and Randal, 2004; Grenadier, 2005). The next section sets out a ground lease valuation model corresponding to equation (1), identifies the unobservable parameters, and shows how equation (2) can be used to estimate these. Section 3 applies this last step to some real-world data, and Section 4 offers some concluding remarks.
2. Application: ground lease rentals
Ownership and use of long-lived assets, such as land and infrastructure investments, are often separated. Historically, land was provided as an endowment to institutions such as churches and universities, or to fund the development of railways, and the beneficiaries of such endowments obtained use of the land in perpetuity (Jackson, 1999). More recently, investors have used long-term renewable leases to allow specialization in the ownership and management of commercial real estate and infrastructure assets.
Long-term leases of unimproved land (commonly known as ground leases) normally provide for periodic reviews of the lease payments. In such reviews, the first step typically involves seeking agreement between the lessor and lessee, and where there is no agreement, through an arbitration process. Such leases have the following general characteristics:
1 Rental payments are due every m years in advance and are fixed in nominal terms for T years at which time they are reviewed.
2 There are n rent revisions scheduled during the life of the lease (i.e. the lease has a total length of nT years).
3 The rent set at each review is based on the current market value of the land leased in an unimproved state, with no account taken of the value of the improvements affected by the lessee.
4 All expenses associated with the use of the property are payable by the lessee.
5 If the lease is forfeited or not renewed, all buildings and other improvements on the land revert to the lessor free from any payment or compensation.
6 The lessee may assign, sublease or sell his or her interest in the land with the consent of the lessor.
7 The lessor may assign or sell his or her interest in the land.
A crucial aspect of these leases, at both the date of inception and at subsequent review dates, is the setting of the rental payments to be made by the lessee. For the lease to be acceptable to both parties, the present value of these payments over the life of the lease must be equal to the market value of otherwise-equivalent unimproved freehold land. At a higher rental rate, the present value of rental payments is greater than the land value and the lessee would prefer to buy the land. At a lower rental rate, the present value of rental payments is less than the land value and the lessor would prefer to sell the land. From the financial economist's perspective, the interesting question is: what is the equilibrium rental rate? As a practical matter, this issue arises whenever the lessor and lessee are unable to agree. We now show how the approach described in the previous section can be used to shed light on this question.
2.1. The valuation model
The first step is to build a valuation model corresponding to the function F in equation (1). Because estimation of (2) requires that the model be applicable to sales of leases occurring at any date during the rental cycle, we need to allow for the possibility that an arbitrary number of years, S, has elapsed since the most recent review date. Suppose that similar unimproved land was determined to have value L0 at the most recent review date, and that an annual rental payment of C was set, and that the current value of such land is LS.
When viewed from time S, the change in rent payments at the next review can be broken into two parts. First, unimproved land values have already grown by a factor of LS/L0 in the current cycle. Second, they are expected to grow by a factor of eg(T–S) over the remainder of the cycle, where g is the continuously compounded expected annual growth rate in unimproved land value (which we assume to be constant). Therefore, the expected annual rent payment during the next rent period equals
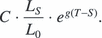
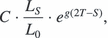
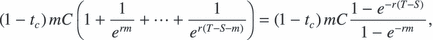

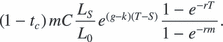
Putting the pieces together shows that the market value of the lessor's interest in this lease is currently equal to
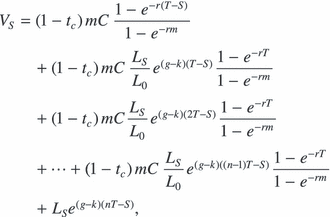
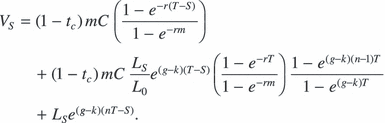 (3)
(3)2.2. Setting the policy parameter
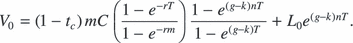
The rental payment C that makes this equal to the land value is the level of C such that
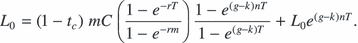
Solving this equation for C yields
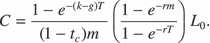 (4)
(4)Clearly, implementation of equation (4) requires us to estimate the unobservable exogenous parameters g and k. However, note that C does not depend on the individual values of g and k, but only on their relative value, as indicated by the term φ = k – g. If φ is high, then the proportion of total return offered by expected capital gain is low and, hence, the required rental rate is high; if φ is low, then the proportion of total return offered by expected capital gain is high and, hence, the required rental rate is low. As a result, alternative combinations of g and k that yield the same value of φ have no effect on C.
One way of implementing equation (4) is to estimate g and k using additional external models. For example, the CAPM could be used to calculate k while g could be estimated as the average annual growth rate in historical land price data. However, as discussed in Section 1, this approach has significant disadvantages.4 Instead, as we now show, a simpler method that requires only the original valuation model is possible.
2.3. Estimating the unobservable parameters
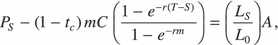 (5)
(5)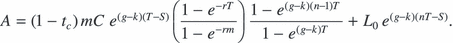
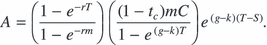
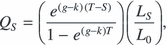 (6)
(6)
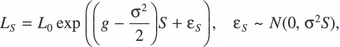
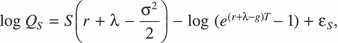 (7)
(7)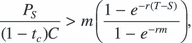
3. Example
To illustrate the approach described in Section 2.3, we consider a lease that requires rent to be paid annually (m = 1), set the tax rate equal to 0.33, the current risk-free interest rate r′ to 0.045 (i.e. the rate prevailing on the rent-setting day for the lease whose equilibrium rental rate we wish to determine), use the 5 year government bond rate prevailing on the date that the sale occurred as a proxy for r, and use data from 30 ground lease sales that occurred in the Wellington region of New Zealand between April 1993 and March 2007.9 The details of these transactions are listed in Table 1. Such a limited dataset is often encountered in practice and is therefore ideal for our purposes: if our method is able to obtain precise estimates even when confronted with such poor data, it should be useful in most practical situations.
| Sale | T | S | C | P | r |
|---|---|---|---|---|---|
| 1 | 21.083 | 0.764 | 35 438 | 390 000 | 0.042 |
| 2 | 14.075 | 0.833 | 149 688 | 1 855 000 | 0.049 |
| 3 | 5.000 | 0.833 | 60 000 | 640 000 | 0.039 |
| 4 | 13.997 | 0.842 | 87 857 | 850 000 | 0.047 |
| 5 | 5.000 | 0.917 | 6 977 | 110 000 | 0.049 |
| 6 | 7.000 | 1.303 | 100 000 | 920 000 | 0.057 |
| 7 | 14.000 | 1.314 | 59 500 | 740 000 | 0.039 |
| 8 | 5.000 | 1.750 | 24 464 | 330 000 | 0.048 |
| 9 | 2.964 | 1.881 | 90 000 | 800 000 | 0.048 |
| 10 | 5.000 | 2.167 | 39 000 | 420 000 | 0.058 |
| 11 | 5.000 | 2.250 | 5 450 | 62 500 | 0.052 |
| 12 | 12.000 | 2.333 | 315 000 | 3 302 500 | 0.057 |
| 13 | 21.000 | 2.400 | 24 625 | 352 000 | 0.044 |
| 14 | 21.000 | 2.917 | 172 500 | 2 350 000 | 0.038 |
| 15 | 7.000 | 3.333 | 28 125 | 354 000 | 0.057 |
| 16 | 21.000 | 3.583 | 12 378 | 165 000 | 0.048 |
| 17 | 5.000 | 4.167 | 516 250 | 9 831 375 | 0.043 |
| 18 | 5.000 | 4.167 | 225 060 | 4 083 750 | 0.043 |
| 19 | 5.083 | 4.917 | 13 500 | 235 000 | 0.056 |
| 20 | 7.000 | 4.919 | 15 148 | 168 000 | 0.040 |
| 21 | 7.000 | 5.667 | 47 303 | 525 583 | 0.046 |
| 22 | 21.000 | 8.658 | 41 915 | 450 000 | 0.057 |
| 23 | 12.000 | 8.917 | 122 000 | 2 000 000 | 0.039 |
| 24 | 21.000 | 9.333 | 550 400 | 5 181 500 | 0.047 |
| 25 | 21.000 | 9.917 | 76 000 | 875 000 | 0.039 |
| 26 | 20.000 | 10.333 | 6 175 | 65 000 | 0.039 |
| 27 | 21.000 | 12.000 | 514 528 | 4 100 000 | 0.039 |
| 28 | 13.997 | 12.342 | 87 857 | 6 700 000 | 0.040 |
| 29 | 21.000 | 15.083 | 51 800 | 550 000 | 0.044 |
| 30 | 21.083 | 18.667 | 30 987 | 750 000 | 0.040 |
- This table summarizes data from 30 ground lease sales that occurred in the Wellington region between April 1993 and March 2007. T is the term of the lease in years, S is the number of years between the date on which the sale occurred and the previous rent review date, C is the annual rent payment on the lease as set at the last review date, P is the price at which the lease was sold, and r is the after-tax 5 year government bond rate prevailing on the date that the sale occurred.
Estimating equation (7) using the Table 1 data yields the results appearing in Table 2.10 The first three columns show the maximum likelihood estimates of the long-run expected growth rate in the value of unimproved land (ĝ), the risk premium component of the expected return on such land (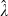 ), and the volatility in the growth of land value (
), and the volatility in the growth of land value (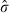 ); asymptotic standard errors for these estimates are given in parentheses. The fourth column shows the resulting estimate of φ = r′ + λ – g. The final three columns then use equation (4) to estimate the rental rate R̂ = C/L0 for this lease, assuming lease terms of 5, 10 and 21 years, respectively. We use the delta method (see Greene, 2003; Xu and Long, 2005) to obtain standard errors for
); asymptotic standard errors for these estimates are given in parentheses. The fourth column shows the resulting estimate of φ = r′ + λ – g. The final three columns then use equation (4) to estimate the rental rate R̂ = C/L0 for this lease, assuming lease terms of 5, 10 and 21 years, respectively. We use the delta method (see Greene, 2003; Xu and Long, 2005) to obtain standard errors for 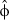 and R̂.
and R̂.
| R | |||||||
|---|---|---|---|---|---|---|---|
| Sample | ĝ | 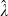 |
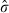 |
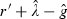 |
T = 5 | T = 10 | T = 21 |
| Full (n = 30) | 0.078 | 0.106 | 0.266 | 0.073 | 0.100 | 0.094 | 0.084 |
| (0.027) | (0.030) | (0.034) | (0.005) | (0.006) | (0.004) | (0.002) | |
| Sales to outside investors (n = 12) | 0.075 | 0.104 | 0.234 | 0.074 | 0.101 | 0.095 | 0.085 |
| (0.039) | (0.043) | (0.048) | (0.006) | (0.007) | (0.005) | (0.003) | |
| Sales to the lessee (n = 18) | 0.080 | 0.107 | 0.285 | 0.072 | 0.099 | 0.093 | 0.084 |
| (0.037) | (0.042) | (0.047) | (0.007) | (0.008) | (0.006) | (0.004) | |
-
Assuming a lease with annual rent payments (m = 1.0) and a current risk-free interest rate of 4.5 per cent (r′ = 0.045), this table uses the data in Table 1 to obtain maximum likelihood estimates of g, λ and σ from equation (7). These are in turn used to obtain estimates of, first, φ = r′ + λ − g, and then, from equation (4), the rental rate R for varying length of lease. Asymptotic standard errors are in parentheses; for
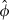 and r̂, these are calculated using the delta method. The second and third panels repeat this exercise for ground lease sales where the purchaser is an outside investor and the lessee, respectively.
and r̂, these are calculated using the delta method. The second and third panels repeat this exercise for ground lease sales where the purchaser is an outside investor and the lessee, respectively.
We first check the model specification: if correctly specified, then the standardized residuals (i.e. the residual for each sale divided by 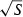 ) should be normally distributed. The Bera–Jarque test statistic for normality of the adjusted residuals equals 0.170. Since the test statistic is asymptotically distributed according to
) should be normally distributed. The Bera–Jarque test statistic for normality of the adjusted residuals equals 0.170. Since the test statistic is asymptotically distributed according to 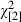 , implying a p-value of 0.919, we cannot reject the null hypothesis that the residuals are normally distributed at conventional levels of significance.
, implying a p-value of 0.919, we cannot reject the null hypothesis that the residuals are normally distributed at conventional levels of significance.
Turning to the Table 2 parameter estimates, we see that ĝ = 0.078, 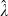 = 0.106, and
= 0.106, and 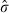 = 0.266. Together, these estimates imply
= 0.266. Together, these estimates imply 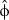 = 0.073 and, for a 10 year lease, R̂ = 9.4 per cent. The corresponding rental rates for 5 and 21 year leases are 10.0 and 8.4 per cent, respectively. Overall, the equilibrium rental rate lies approximately halfway between the implied expected return on unimproved land (4.5 per cent + 10.6 per cent = 15.1 per cent) and the risk-free interest rate of 4.5 per cent, reflecting the fact that the lease payments are certain between rent reviews but are subject to the risk of changes in land value at the review dates.
= 0.073 and, for a 10 year lease, R̂ = 9.4 per cent. The corresponding rental rates for 5 and 21 year leases are 10.0 and 8.4 per cent, respectively. Overall, the equilibrium rental rate lies approximately halfway between the implied expected return on unimproved land (4.5 per cent + 10.6 per cent = 15.1 per cent) and the risk-free interest rate of 4.5 per cent, reflecting the fact that the lease payments are certain between rent reviews but are subject to the risk of changes in land value at the review dates.
These results have two features of particular interest. First, the implied 10.6 per cent risk premium for unimproved land is consistent with other risk premium estimates for illiquid assets (see e.g. Kerins et al., 2004; Acharya and Pedersen, 2005). Hence, our within-model approach appears to adequately capture liquidity risks. Second, φ is very precisely estimated even though g and λ are not. This can be seen more clearly in Figure 1, which plots the ‘confidence ellipse’ for the latter two parameter estimates. For any combination of g and λ inside the region bounded by the solid curve, we cannot reject the null hypothesis (at a 5 per cent level) that the parameters take these values. However, we can reject this hypothesis for any combination outside the region bounded by the solid curve. The narrow shape of the ellipse indicates that the estimates of g and λ are highly positively correlated, the source of which is apparent from equation (6). Other than via the LS term, PS depends only on φ and not on the individual values of g and λ, so the regression model –equation (7)– is close to being under-identified. As a result of this property, any estimation error in ĝ will tend to be substantially offset by an estimation error in 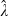 . Consequently, although the components of φ have relatively substantial estimation errors, φ itself does not. And since the rental rate is a function of φ only (and not g and λ separately), the precision in estimating φ feeds through into the estimated rental rates. For example, the lease with 10 yearly rent reviews (T = 10) has an estimated rental rate of 9.4 per cent with a 95 per cent confidence interval of (0.086, 0.102).
. Consequently, although the components of φ have relatively substantial estimation errors, φ itself does not. And since the rental rate is a function of φ only (and not g and λ separately), the precision in estimating φ feeds through into the estimated rental rates. For example, the lease with 10 yearly rent reviews (T = 10) has an estimated rental rate of 9.4 per cent with a 95 per cent confidence interval of (0.086, 0.102).
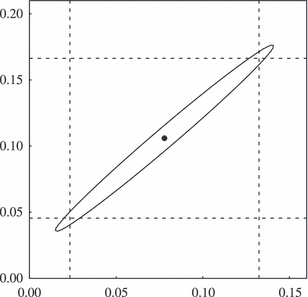
Confidence ellipse for average growth rate and risk premium.The point in the middle of the graph shows the point estimate of g and λ, whereas the two sets of dashed lines show the 95 per cent confidence intervals for each parameter separately. For any combination of g and λ inside the region bounded by the solid curve, we cannot reject the null hypothesis (at a 5 per cent level) that the parameters take these values. However, we can reject this hypothesis for any combination outside the region bounded by the solid curve.
Our sales data sample contains two types of transactions: those where the lease is sold to an outside investor and those where it is sold to the lessee. In case the dynamics underlying these two cases differ, we repeat our estimation exercise for each group separately. Although this results in slightly higher standard errors due to the smaller number of observations (as can be seen in the second and third panels of Table 2), it has no meaningful effect on the rental rate point estimates: regardless of the type of transaction, the estimated rental rate is essentially identical to that obtained for the full sample.
4. Concluding remarks
Disputes over inter-party payments relating to asset ownership or assignment frequently arise. Financial economists can often provide apparent solutions to such debates via analytical models that offer a simple formula for the variable in dispute. However, such formulae invariably contain unobservable parameters that themselves become the focus of dispute.
A common approach to estimating these parameters consists of applying historical data to additional analytical models that describe the determination of the relevant parameters. However, the problems associated with this approach can lead to significant errors. In this paper, we have described an alternative within-model approach that involves only the application of the original analytical framework to actual market transactions in the asset that is the subject of dispute. This approach has the singularly attractive feature that all unknown parameters (including the policy, or disputed, parameter) are calculated within a single valuation framework, thus avoiding the need to appeal to additional models that may or may not be consistent with the original model, or to use data that may or may not be relevant to the asset of interest.
Applying the within-model approach to the determination of ground lease rental rates, we have, first, developed a simple model of rent determination, and then, in conjunction with data on ground lease sales, used this model to estimate both the unobservable parameters on which the rental rate depends and the rental rate itself. All estimates obtained in this way appear to be economically plausible and are statistically precise, despite our data sample having considerable limitations. In general, our approach can be used wherever an appropriate asset valuation model is available and there are sufficient secondary market transactions to provide a viable dataset.




