Influence of cultural factors on price clustering and price resistance in China's stock markets
doi: 10.1111/j.1467-629x.2007.00221.x
Abstract
This paper builds on prior research by analysing the impact of cultural factors on both price clustering and price resistance in China's stock markets. The results support the presence of cultural factors impacting on price clustering with the digit 8 showing a higher propensity for clustering and the digits 4 and 7 showing a lower propensity in the A-share market, where stock is denominated in renminbi and traded by mainland Chinese. These results are further supported by an analysis of the B-share market, where cultural factors have no (or less) impact on the price of Chinese stocks traded by foreign investors in US dollars (or in Hong Kong dollars). A range of measures for price resistance show the digits 0 and 5 to be significant resistance points in the A-share market. Although digit 8 cannot be considered as a resistance point, its resistance level is highest among the remaining numbers. In conclusion, cultural factors help to explain not only price clustering in the Chinese stock markets but price resistance levels as well, albeit at a weak level.
1. Introduction
The issue of price clustering and resistance has been studied extensively across a range of financial markets with a particular emphasis on the issue in stock markets. For the Asian stock markets where there is a significant Chinese community, Brown et al. (2002) and He and Wu (2006) find an additional set of results for clustering and resistance for specific numbers (4 and 8) that are of particular significance in Chinese culture. The focus of the present paper is to extend the previous analysis via further consideration of the two mainland Chinese stock markets. The results of the present paper offer support for Chinese cultural factors affecting price clustering and, although it is not as strong a finding, cultural factors are also found to have a weak influence on price resistance levels.
This paper is structured as follows. Section 1 reviews the evidence and theory on price clustering and resistance. Section 2 discusses the data used to analyse price clustering and resistance in China's stock markets. Sections 3 and 4 present methodologies and results for price clustering and price resistance, respectively; Section 5 offers conclusions.
2. Price clustering and resistance: evidence and theory
2.1. Price clustering
Osborne (1962) and Niederhoffer (1965, 1966) seem to have been the first to test whether some prices are more frequently observed than others, and they find that stock prices in US markets are clustered on whole numbers, less on halves or quarters and least commonly on the odd eighths. Osborne (1962) samples closing prices and finds that 60.8 per cent were at even eighths; hence, the tendency for even eighths to appear more frequently than odd eighths being termed the ‘Osborne effect’. Niederhoffer (1965) documents clustering of limit orders on the books of specialists on the New York Stock Exchange and finds that 84 per cent of them are at the even eighths. The ratio of limit order closing prices at the even eighths (0, 2, 4, 6) to those at the odd eighths (1, 3, 5, 7) was 8.8:1. He finds clustering in the closing prices of actively and inactively traded shares, in high-priced and low-priced shares, and in noon closing prices. Higher-priced shares traded mostly at the integers and lower-priced shares settled at even numbers of eighths. Moreover, Niederhoffer (1966) suggests that there is also a tendency for limit orders to be placed at familiar whole numbers, such as 10, 25 and 50.
Harris (1991) confirms that stock price clustering is pervasive and the clustering distributions from the mid-nineteenth century appear to be no different from those observed in the late twentieth century. He finds that clustering increased with price level and volatility. Moreover, price clustering is also found in international markets, such as in the Australian Stock Exchange by Aitken et al. (1996) and on the Stock Exchange of Singapore (SES) by Hameed and Terry (1998). Aitken et al. (1996) find that clustering increases with the price of the stock, market volatility, own stock volatility, trade size and the size of the bid-ask spread. It decreased with trading frequency and was also lower for stocks with options traded on them. Hameed and Terry (1998) investigate the distribution of daily closing prices for 234 stocks that were traded on the SES Main Board between January 1980 and July 1994. The SES is an order-driven market with no market makers. Prices ending in multiples of 10 cents were more common than prices ending in odd multiples of 5 cents; prices were more likely to end in even cents than odd cents, and least likely to end in fractional cents; and whole dollars occurred more frequently than half dollars, which were more frequent than price multiples of 10 cents. They also find that price clustering increased with a stock's price level and decreased with trading volume.
Brown et al. (2002) analyse price clustering for large and small stocks for six Asia–Pacific stock markets and find evidence that clustering occurs at 0, 5 and even integers. Furthermore, they find that clustering at 0 and even numbers increases with the level of the stock price and declines with the precision with which a price is known. They also find that in the case of the Hong Kong market there is some support for cultural factors explaining a preference for 8 and the avoidance of 4.
In terms of the impact of cultural factors on price clustering, Heeler and Nguyen's (2001) work on the patterns of price endings for samples of online shopping retail prices in US and five Asian markets (Malaysia, Hong Kong, Singapore, Japan and China) is of interest. Similar to the USA, they find for the Asian markets that 0 and 5 are overrepresented as compared to 1, 2, 3, 4, 6 and 7. They also find significant overrepresentation of 8 as compared to 9 for the Asian markets. The percentage of 8-endings for online prices in these markets is as follows: Malaysia, 19.8 per cent; Hong Kong, 14.8 per cent; Singapore, 13.1 per cent; Japan, 24.4 per cent; and China, 19.3 per cent; compared with 17.3, 3.0, 26.6, 1.8 and 9.9 per cent for the 9-ending, respectively. Using daily data from 1998 to 2000 inclusive, He and Wu (2006) add to the literature on the impact of cultural factors on price clustering by examining the topic for both the Shanghai Stock Exchange (SHSE) and the Shenzhen Stock Exchange (SZSE) in China. They find support for clustering on 10s and 5s for economic reasons (see Section 1.3 of their paper for a discussion of these reasons) and the last decimal point of prices cluster on 8 for cultural reasons.
2.2. Price resistance
In addition to prices showing clustering effects, there is also evidence that price resistance/barriers can occur.1 Most research concerning price barriers has been carried out on stock indices. Donaldson and Kim (1993) examine the Dow Jones Industrial Average (DJIA) for the period 1974–1990 and find round numbers (such as 100 levels) functioned as support or resistance levels. When such a level was passed through, the DJIA moved more up or down more than usual. Ley and Varian (1994) analyse the DJIA over the period 1952–1993 and find fewer observations around the 100 levels. Koedijk and Stork (1994) study indices in the US, Belgium, Germany, Japan and UK stock markets over the period 1980–1992 and find relatively few observations near 100 levels and, furthermore, these levels were less often passed through. The present paper links the studies of price clustering and price resistance together for the first time.
2.3. Cultural explanations of price clustering and resistance
There are many arguments regarding why prices might cluster, ranging from the process of number development to cultural explanations, and because these have been explored by a number of authors (e.g. Mitchell, 2001; Brown et al., 2002; Sonnemans, 2006), only a brief review is offered here. The basic arguments underpinning clustering can be categorized into five groupings: process of number development, behavioural explanations, rational economic reasons, market collusion reasons and cultural reasons. Of course, these different theories are unlikely to be mutually exclusive and might comingle in a variety of ways. The process of number development argues that clustering occurs because existing decimal systems encourage people to think in groups of 10 or multiples of such. We are conditioned from an early age to do mental arithmetic on the basis of 10 and this means people find it easier to make calculations based on this root; hence, the tendency to cluster on 10s and 5s. When this learning process is coupled with cultural conventions, which might themselves derive from the ease of using this root, then a number preference develops that eventually leads to clustering.
The second set of arguments relate to behavioural theories. There are two broad arguments within this grouping. First, individuals are seen as using simple heuristics, such as anchoring, to provide approximations to help them make decisions. These approximations involve rounding numbers and have a tendency to work from the root of 10 and this eventually leads to price clustering. Second, given the inability of individuals to carry out complex information retrieval and calculations (i.e. they are boundedly rational), they simplify information processing and mental calculations by rounding numbers from a base of 10. Essentially, the rounding leads to more cost-effective decision-making but it is derived from the limitations of humans to store and use data.
The third group of explanations have a more rational economic base. The focal point literature (see Sugden, 1995) argues that people select numbers they believe others will easily recognize because this facilitates negotiation and decision-making. Ball et al. (1985) argue that clustering can be viewed as a means to lower negotiation costs and they introduce the notion of ‘degree of price resolution’ with the implication that rounded prices involve a ‘lesser’ degree of price resolution than finer prices. This argument was taken further by Harris (1991) who argues that clustering exists because traders use a discrete grid of prices to simplify and lower negotiation costs. A second set of ‘rational economic’ arguments involves the notion that individuals work in a sphere of haziness in trying to value items (see Loomes, 1988) and clustering is the result of individuals trying to overcome this sphere of haziness. A related argument was forwarded by Ball et al. (1985) who hypothesize that clustering is positively related to the degree of uncertainty concerning the true price. Harris (1991) and Godek (1996) show that clustering increases with price levels and price volatility.
The fourth set of arguments (see Christie and Schultz, 1994; Christie et al., 1994) involves the notion that clustering might be a result of implicit collusion among institutions within the market (e.g. interest rates have a ‘habit’ of moving in similar quanta to external shocks). Nonetheless, other studies (e.g. Godek, 1996) have challenged the collusion argument and argue that clustering occurs because of contractual arrangements (e.g. best prices) and normal business activities (pre-arranged order flows).
The final set of arguments to be considered here, and the focus of the present paper, is concerned with cultural factors. In Chinese culture, numbers are not just figures but they also carry special significance and symbolism. Even the pronunciations or sounds of the numbers can suggest good or bad luck. The number 8 represents good luck to the Chinese because it sounds like multiply in Chinese, which indicates becoming wealthy. This explanation is consistent with the results of Heeler and Nguyen (2001) where the 8-ending is found to be popular in Hong Kong and Malaysia, which both have large Chinese communities (90 and 30 per cent, respectively). In Japan, the number 8 also has great symbolic significance. The Japanese writing of the number 8 looks like the shape of a mountain (sue-hirogari in Japanese) and, therefore, the number 8 signifies ‘fan out’, ‘grow’ and ‘be prosperous’. In contrast, the number 4 in China suggests bad luck, as it sounds like die in Chinese and the number 7 sounds like anger, which is also not fancied by the Chinese. From this perspective, there should be more price clustering on the number 8 and less on the numbers 4 and 7.
The existence of number preference might affect investors’ financial decision-making in two ways. On the one hand, it forms a clustering point where the price of investors’ choice will more often end with that number. On the other hand, it forms a psychological barrier (a resistance point) when investors make their investment decisions. Prior work (e.g. Aitken et al., 1996; Hameed and Terry, 1998) has established that individual stock prices cluster on round numbers, and Sonnemans (2006) also finds that for individual stocks round numbers also act as price barriers. Therefore, there is a suggestion of a relationship between price clustering and price barriers.
There are a number of possible explanations of the relationship between clustering and resistance. First, if stock price clustering is caused by a relatively large number of limit orders at round numbers, this might also cause barriers or resistance points at these numbers. Second, Niederhoffer (1965, 1966) concludes that trading rules based on reversals after hitting specific round numbers is profitable. Third, Mitchell (2001) argues that although clustering and psychological barriers (resistance) might have similar behavioural interpretations and explanations for their existence, they do not necessarily occur synonymously, nor must they be related. Clustering in financial markets is a concentration of the distribution associated with particular digits. In contrast, resistances suggest that investors are reluctant to approach or break through certain price levels. Therefore, a key difference between clustering and resistance is that the direction of the price movement is relevant to resistance but not clustering. This is reflected in our empirical design, where resistance is studied by examining price reversals and crosses around digits, whereas clustering is studied by examining the prices of all transactions. Details on the empirical designs are given in the clustering and resistance sections.
3. Data
There are two stock markets in China (the SHSE and SZSE) and two types of share are traded on both markets: A-shares are denominated in renminbi (RMB) and can only be traded by domestic Chinese investors, and B-shares are denominated either in US dollars in the SHSE or in Hong Kong dollars in the SZSE and are traded mainly by foreign investors.
The trading systems in the SHSE and the SZSE are purely order-driven with an electronic consolidated open limit order book. Orders are matched with a price and time priority scheme. Limit orders are submitted by buyers and sellers, and auctioned off continuously. Matched orders are executed and then dispatched from the system, whereas unmatched orders remain in the system until they are executed or deleted. The transaction prices of a particular trade are generated contingent on the best bid or ask prices and the time of order submissions.
Trading hours of the SHSE and the SZSE are from 09.30 to 11.30 hours in the morning and from 13.00 to 15.00 hours in the afternoon. The market opening is based on a batch auction that operates from 09.15 to 09.25 hours, being followed by continuous auction after 09.30 hours. After a lunch break, the market reopens in the afternoon directly with a continuous auction without the batch auction.
The minimum tick sizes are 1 cent (RMB 0.01) for A-shares in both exchanges, $US0.001 for B-shares in the SHSE and $HK0.01 for B-shares in the SZSE. The present study examines the clustering and resistance of the multiples of these price ticks. Each regular trade's price and volume, and the best bid and ask price and volume are extracted, and additional variables are derived from the existing database. The last significant digit of each price (from digit 0–9) is extracted to test whether it is a clustering/resistance point.
A total of 1050 A-shares (566 on the SHSE and 484 on the SZSE) and 100 B-shares (52 on the SHSE and 48 on the SZSE) are used in the present study. The analysis was conducted for both sets of stocks for June 2002. As a means of providing a comprehensive and detailed analysis of price clustering and price resistance, a range of measures is considered and these are discussed in the following two sections.
4. Price clustering
4.1. Measures of price clustering
Prior studies (e.g. Sonnemans, 2006) have used the occurrence of prices (frequency) to measure price clustering. However, because price clustering means that some prices are more frequently ‘observed’, a single measurement of the appearance frequency might not to be sufficient; more specifically, price clustering might have volume and duration characteristics. If the reason for price clustering is because specific numbers are preferred by investors, then it seems reasonable to expect not only the frequency of trades but also the volume of trades at preferred digits to be higher than those of non-preferred ones. Furthermore, the duration of a price ending with preferred digits will be on display longer to the market than those of non-preferred ones.
Therefore, it would seem reasonable for price clustering to be associated with greater volumes of transactions at certain prices and for prices to stay longer at the clustering points. To capture these different aspects, price clustering is examined from the 3-D perspective of Frequency (F), Percentage Trading Volume (PcntV) and Percentage Time Duration (PcntTD). The measures of these dimensions are constructed as follows.
F, the frequency Fi of each digit is calculated as follows.
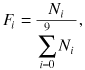 ()
()where i = 0, 1, 2, . . . , 8, 9, and Ni is the number of transactions of digit i.
PcntV: the trading volume (vi,t) of each transaction t of digit i is summed to obtain the total trading volume of digit i (Vi). To create a measure that is comparable across different stocks, percentage volume (PcntVi) is used.
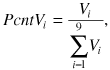 ()
()where i = 0, 1, 2, . . . , 8, 9; 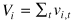 ; and vi,
t is the trading volume of transaction t of digit i.
; and vi,
t is the trading volume of transaction t of digit i.
PcntTD: the time duration (τi, t) of each trade t of digit i is calculated by using the next trade's timestamp minus the current trade's timestamp.2 All the time durations are summed to obtain the total displayed time duration of digit i (Ti). The time duration is then standardized to obtain PcntTDi as follows:
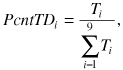 ()
()where i = 0, 1, . . . , 8, 9; Ti=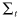 τi,
t; and τi,
t is the displayed time duration of trade t of digit i, which is calculated by using the next trade's timestamp minus the current trade's timestamp.
τi,
t; and τi,
t is the displayed time duration of trade t of digit i, which is calculated by using the next trade's timestamp minus the current trade's timestamp.
The last significant digit of prices should be uniformly distributed if there is no clustering point. A sign test is performed to examine whether the measures of frequency, volume and duration for each digit deviate from 1/10, which is the theoretical distribution value for a digit.3 After performing a sign test on each individual digit, a pool test is used to test the departures from uniform distribution for all digits.4
4.2. Empirical results: price clustering
Table 1 reports the results for F, PcntV and PcntTD for digits 0–9 for A-shares for the Shanghai and Shenzhen markets. For the sake of brevity the results for B-shares are not tabulated but are discussed when they are directly relevant to the main arguments of the present paper (fully tabulated results are available from the authors on request). The statistics for digits 0, 5 and 8 for all three measurements of frequency, volume and duration are higher than those for the other digits. For example, for the Shanghai market (Panel A), there are more than 21 per cent of transactions trading on digit 0, 14 per cent of transactions on digit 5 and 11 per cent on digit 8. They are all significantly higher than 10 per cent. In contrast, transactions on all the other digits are significantly less than 10 per cent, which is the theoretical probability of each digit's frequency given no clustering is presented. Those statistics for digits 4 and 7 are exceptionally lower with only approximately 6 per cent of trades occurring for digits 4 and 7. Although the percentage volume and duration measures show similar results to those reported for frequency, they provide some interesting additional insights. Specifically, when volume is used as a clustering measure, 0 is a much stronger clustering point. This suggests that not only more trades occur at a round number, but that the size of this trade is also relatively larger. In contrast, the effect of volume clustering on number 8 is smaller than the effect of frequency clustering. Finally, the pooled sign tests in Table 1 confirm the statistical significance of the differences across the digits.
|
Panel A: Shanghai Stock Exchange A-share (RMB) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Digit | F | PcntV | PcntTD | ||||||
| Median (%) | SD (%) | s-Stat | Median (%) | SD (%) | s-Stat | Median (%) | SD (%) | s-Stat | |
| 0 | 21.14 | 5.86 | 279*** | 26.57 | 7.53 | 282*** | 20.51 | 5.90 | 278*** |
| 1 | 7.79 | 1.43 | –251*** | 7.25 | 1.69 | –254*** | 7.66 | 1.51 | –250*** |
| 2 | 8.73 | 1.53 | –189*** | 7.89 | 1.86 | –232*** | 8.79 | 1.65 | –176*** |
| 3 | 7.78 | 1.65 | –247*** | 6.74 | 1.75 | –267*** | 7.89 | 1.79 | –235*** |
| 4 | 6.33 | 1.73 | –268*** | 5.25 | 1.78 | –275*** | 6.34 | 1.79 | –272*** |
| 5 | 14.03 | 2.48 | 267*** | 14.68 | 2.58 | 267*** | 14.07 | 2.54 | 263*** |
| 6 | 8.50 | 1.49 | –212*** | 7.55 | 1.74 | –248*** | 8.71 | 1.63 | –189*** |
| 7 | 6.35 | 1.66 | –273*** | 5.38 | 1.73 | –275*** | 6.46 | 1.75 | –269*** |
| 8 | 11.25 | 1.31 | 193*** | 10.53 | 1.76 | 76*** | 11.46 | 1.55 | 187*** |
| 9 | 7.47 | 1.61 | –243*** | 6.46 | 1.95 | –258*** | 7.21 | 1.69 | –242*** |
| S | 5213 | 5621 | 4965 | ||||||
| P_Chi_Sqr | 0*** | 0*** | 0*** | ||||||
|
Panel B: Shenzhen Stock Exchange A-share (RMB) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Digit | F | PcntV | PcntTD | ||||||
| Median (%) | SD (%) | s-Stat | Median (%) | SD (%) | s-Stat | Median (%) | SD (%) | s-Stat | |
| 0 | 19.95 | 6.06 | 240*** | 25.49 | 6.82 | 240*** | 19.44 | 6.09 | 237*** |
| 1 | 7.71 | 1.41 | –219*** | 7.24 | 1.72 | –217*** | 7.62 | 1.49 | –222*** |
| 2 | 8.76 | 1.53 | –151*** | 7.95 | 1.76 | –193*** | 8.82 | 1.62 | –138*** |
| 3 | 8.11 | 1.67 | –191*** | 7.07 | 1.84 | –220*** | 8.08 | 1.82 | –175*** |
| 4 | 6.80 | 1.74 | –227*** | 5.73 | 1.77 | –235*** | 6.79 | 1.83 | –225*** |
| 5 | 13.74 | 2.15 | 225*** | 14.62 | 2.39 | 235*** | 14.06 | 2.39 | 219*** |
| 6 | 8.50 | 1.50 | –175*** | 7.68 | 1.71 | –207*** | 8.74 | 1.64 | –149*** |
| 7 | 6.59 | 1.70 | –230*** | 5.62 | 1.83 | –232*** | 6.68 | 1.79 | –229*** |
| 8 | 11.13 | 1.53 | 151*** | 10.57 | 1.93 | 66*** | 11.25 | 1.73 | 148*** |
| 9 | 7.77 | 1.50 | –213*** | 6.74 | 1.72 | –228*** | 7.52 | 1.60 | –215*** |
| S | 4267 | 4764 | 4019 | ||||||
| P_Chi_Sqr | 0*** | 0*** | 0*** | ||||||
-
This table reports results of price clustering for A-shares in the Shanghai and Shenzhen Stock Exchanges. It reports medians and standard deviations (SD) of the three clustering measures: Frequency (F), Percentage Trading Volume (PcntV) and Percentage Time Duration (PcntTD) for digits 0–9. s-Stat is the sign test statistics (H0: the population median of the clustering measure is equal to 0.1). S is the pool statistic where the calculation is based on the p-value of s-Stat in order to test the joint significance of the s-Stats.
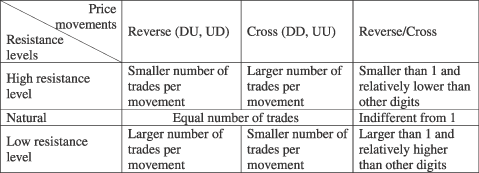
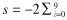 ln Pi. Under the null hypothesis, S has a χ2 distribution with 2*10 degrees of freedom. P_Chi Sqr is the p-value of the S-statistics. *** denotes significance at the 1 per cent level.
ln Pi. Under the null hypothesis, S has a χ2 distribution with 2*10 degrees of freedom. P_Chi Sqr is the p-value of the S-statistics. *** denotes significance at the 1 per cent level.
The finding of price clustering at 0 and 5 is consistent with previous research (e.g. Osborne, 1962; Niederhoffer, 1965, 1966; Harris, 1991; Brown et al., 2002). The results also support the marketing research by Heeler and Nguyen (2001), who find that not only digits 0 and 5 are overrepresented in Asia but also digit 8 is significantly over-represented in pricing commodities. Furthermore, the preference for digit 8 and the aversion to digits 4 and 7 support the cultural preference hypothesis in the context of the Chinese markets.
The results for B-share markets further confirm that Chinese culture is one of the factors affecting price clustering in the China A-share market. In the Shanghai B-share market, where stock is traded in $US0.001, prices only cluster on the digit 0 (i.e. in multiples of 1 cent). In the HK$0.01-dominated Shenzhen B-share market, clustering can be found on digits 0, 5 and 8 in the frequency analysis. For the volume and duration analyses, the digit 8 is not found to be significant. The weaker results for the B-share markets are expected given the presence of international investors. The weak presence of a culture effect in the Hong Kong dollar-dominated Shenzhen B-share market is expected because of the participation of Hong Kong Chinese.
To summarize, the analysis of price clustering in the A- and B-share markets in China suggests that cultural preference is one of the factors explaining price clustering. The analysis now moves on to examine whether cultural preference can help explain price resistance in the Chinese markets.
5. Price resistance
5.1. Measures of price resistance
Prior studies have examined the price resistance within the context of stock indices. Donaldson and Kim (1993) find that the DJIA closed on average fewer times on index values in the neighbourhood of 100 levels. Ley and Varian (1994) also find fewer observations around the 100 levels for the DJIA. In contrast to these prior studies, the purpose here is to analyse price resistance in the context of individual stocks. In addition, some new measures of price resistance are developed.
As discussed earlier, the key difference between the analysis of price clustering and resistance is that the direction of price movement only matters when analysing resistance. It is more difficult for prices and it takes more volume and time to cross a price resistance level. Before moving on to the detail of each measure, there is a discussion of how price movements are classified into a ‘reverse’ or a ‘cross’ pattern.
Paths of price movements are classified into down–down (DD), down–up (DU), up–up (UU) and up–down (UD). The movements of DU and UD are classified as a reverse whereas DD and UU are classified as a cross. After the price movement patterns around each price are defined, measurements of resistance level can then be constructed. The resistance analysis is focused on the relative statistics of the four different movements for each digit. Two measures are developed: the Frequency (F) and Average Number of Trades (AvgNT). Details of the measures are given in the following discussion.
The Frequency (F) of the four price movement patterns around each digit is examined. It is calculated in a similar manner as the frequency of trades discussed in the last subsection.
The aggregation process of the frequency of price movements is as follows. For each digit in each company the number of each of the four type of movements is counted (e.g. NMi,
DU is the number of trades for DU movement of digit i). The frequency of each type of movement for this digit is calculated by dividing the number of a specific price movement by the total number of price movements of this digit (e.g. Fi,
DU = NMi,
DU/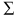 NMi). Furthermore, the ratio between the reverses and the crosses, the RC ratio, is calculated as RC = (Fi,
DU + Fi,
UD)/(Fi,
DD + Fi,
UU).
NMi). Furthermore, the ratio between the reverses and the crosses, the RC ratio, is calculated as RC = (Fi,
DU + Fi,
UD)/(Fi,
DD + Fi,
UU).
To summarize the result for all companies, the medians of the frequency and the RC ratio are reported. Two statistical tests are performed to formally examine the level of resistance for each digit. First, a sign test is used to examine whether the RC ratio is statistically different from 1 for each digit. Second, a pairwise test on the statistical difference of the RC ratio between digits is used. The higher the RC ratio, the higher the resistance level of a digit. In fact, for those having an RC ratio significantly less than 1, prices are much less likely to bounce back once they reach this digit. They serve as ‘passing points’ as opposed to ‘resistance points’.
As well as analysing the frequencies of different movements around digits, the components of each movement are also examined. At least two trades are needed to form one of the four price movement patterns. For example, a sequence of prices of 101, 100 and 102 form a pattern of DU for digit 0. The two trades that form this pattern are the trade at 100 and the trade at 102. In this case, the price movement pattern belongs to digit 0. The price arriving at digit 0 is down from 101 and the price leaving digit 0 is up to 102. A complete price movement pattern can take more than two trades. For example, a sequence of price 101, 100, 100, 100 and 99 forms a pattern of DD for digit 0. Because once it arrived at 100 it stayed at this level for another two trades, the movement is not complete until the price leaves 100 and moves down to 99. The total number of trades for this price movement is 4. This extra information is used in this study to examine the resistance level. We suggest that the higher a digit's resistance level, the more trades it takes to cross this digit and the fewer trades it takes to reverse after approaching the digit.
The Average Number of Trades (AvgNT) of each type of price movement of digit i is calculated for each company (e.g. AvgNTi,
DD = 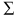 NTi,
DD/Count(NMi,
DD)). This measure is further standardized by the average number of trades of the same price movement (e.g. StdAvgNTi,
DD = AvgNTi,
DD/AvgNTDD, where AvgNTDD=
NTi,
DD/Count(NMi,
DD)). This measure is further standardized by the average number of trades of the same price movement (e.g. StdAvgNTi,
DD = AvgNTi,
DD/AvgNTDD, where AvgNTDD= 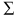 NTDD/Count(MDD)). The purpose of this standardization for each price movement pattern is to remove the effect of market condition on the measure. To see why this is needed, consider a stock in a bull market, where price is more likely to increase trade by trade. Therefore, the average number of trades it takes to move price up will be smaller than the average number of trades to bring price down during the period, regardless of the last digit of the price. This standardized measure is similar across the four different price movement patterns within a digit. It is also similar across digits for the same price movement pattern. For a neutral digit (neither high nor low resistance level), StdAvgNTi is expected to be equal to 1. For example, if digit i is a neutral digit, then StdAvgNTi,
DD = StdAvgNTi,
DU= StdAvgNTi,
UD = StdAvgNTi,
UU = 1. In other words, for digit i, the average number of trades it takes to form four different price movement patterns is the same.
NTDD/Count(MDD)). The purpose of this standardization for each price movement pattern is to remove the effect of market condition on the measure. To see why this is needed, consider a stock in a bull market, where price is more likely to increase trade by trade. Therefore, the average number of trades it takes to move price up will be smaller than the average number of trades to bring price down during the period, regardless of the last digit of the price. This standardized measure is similar across the four different price movement patterns within a digit. It is also similar across digits for the same price movement pattern. For a neutral digit (neither high nor low resistance level), StdAvgNTi is expected to be equal to 1. For example, if digit i is a neutral digit, then StdAvgNTi,
DD = StdAvgNTi,
DU= StdAvgNTi,
UD = StdAvgNTi,
UU = 1. In other words, for digit i, the average number of trades it takes to form four different price movement patterns is the same.
The RC ratio is calculated based on the standardized number of trade measure: RC_NT = (StdAvgNTi, DU+StdAvgNTi, UD)/(StdAvgNTi, DD+StdAvgNTi, UU).
The relationship between the components of price movement and resistance level is summarized in Figure 1. It suggests that the RC ratio of the number of trades should be less than 1 for digits with high resistance level. In other words, the higher a digit's resistance level, the fewer number of trades it takes to reverse and the more number of trades it takes to cross when approaching the digit. Furthermore, when comparing the resistance level across digits, the lower the RC ratio, the higher the resistance level of the digit.5
The relationship between component of price movements and resistance level. DU, down–down; UD, up–down; DD, down–down; UU, up–up.
5.2. Empirical results: price resistance
The analysis of price resistance is based on comparisons of the measures for the four different price movements for each digit and across digits. The two measures discussed here are the frequency of the price movement patterns and the standardized number of trades per movement. Tables 2 and 3 report results for the frequency measure and Tables 4 and 5 for the number of trades measure.
|
Panel A: Shanghai Stock Exchange A-share (RMB) |
||||||
|---|---|---|---|---|---|---|
| Digit | Reverse | Cross | RC | s-Stat | ||
| F_DU (%) | F_UD (%) | F_DD (%) | F_UU (%) | |||
| 0 | 17.58 | 18.04 | 15.78 | 15.44 | 1.15 | 235*** |
| 1 | 9.16 | 7.69 | 9.20 | 8.53 | 0.95 | –75*** |
| 2 | 9.02 | 8.99 | 9.40 | 9.41 | 0.96 | –67*** |
| 3 | 8.08 | 8.06 | 8.52 | 8.62 | 0.94 | –105*** |
| 4 | 6.32 | 7.49 | 7.06 | 7.60 | 0.94 | –76*** |
| 5 | 13.27 | 13.65 | 13.11 | 13.09 | 1.03 | 47*** |
| 6 | 9.18 | 8.29 | 9.36 | 9.19 | 0.95 | –84*** |
| 7 | 6.54 | 7.05 | 7.30 | 7.40 | 0.93 | –89*** |
| 8 | 11.75 | 11.16 | 11.65 | 11.08 | 1.00 | 10 |
| 9 | 7.85 | 8.49 | 8.21 | 8.88 | 0.98 | –34*** |
| S | 814 | |||||
| P_Chi_Sqr | 0.000 | |||||
|
Panel B: Shenzhen Stock Exchange A-share (RMB) |
||||||
|---|---|---|---|---|---|---|
| Digit | Reverse | Cross | RC | s-Stat | ||
| F_DU (%) | F_UD (%) | F_DD (%) | F_UU (%) | |||
| 0 | 17.14 | 17.35 | 14.64 | 14.52 | 1.16 | 206*** |
| 1 | 9.03 | 7.74 | 8.96 | 8.39 | 0.96 | –50*** |
| 2 | 9.11 | 9.13 | 9.46 | 9.58 | 0.95 | –56*** |
| 3 | 8.51 | 8.27 | 8.97 | 8.90 | 0.95 | –70*** |
| 4 | 6.62 | 7.88 | 7.48 | 7.82 | 0.93 | –70*** |
| 5 | 12.90 | 13.40 | 12.72 | 12.65 | 1.04 | 67*** |
| 6 | 9.09 | 8.38 | 9.30 | 9.13 | 0.96 | –66*** |
| 7 | 6.95 | 7.29 | 7.65 | 7.89 | 0.93 | –88*** |
| 8 | 11.39 | 10.86 | 11.50 | 11.02 | 0.99 | –6 |
| 9 | 8.03 | 8.73 | 8.44 | 8.98 | 0.97 | –34*** |
| S | 725 | |||||
| P_Chi_Sqr | 0.000 | |||||
-
This table reports the analyses of the frequency of the four price movement patterns for A-shares. The frequency measures are calculated for four different price movement patterns for each digit (i.e. F_DD (down–down), F_DU (down–up), F_UD (up–down), and F_UU (up–up)). The ratio between reverses and the crosses (RC) is calculated as the frequency reverse movements (i.e. F_DU + F_UD) over the frequency of cross movements (i.e. F_DD and F_UU) for each digit. It reports medians of these measures. s-Stat is the sign test statistics (H0: the population median of the RC ratio is equal to 1). S is the pool statistic where the calculation is based on the p-value of s-Stat in order to test the joint significance of the s-Stats.
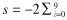 ln Pi, under the null hypothesis, S has a χ2 distribution with 2*10 degrees of freedom. P_Chi Sqr reports the p-value of the S statistics. ***, ** and * denote significance at the 1, 5 and 10 per cent levels, respectively.
ln Pi, under the null hypothesis, S has a χ2 distribution with 2*10 degrees of freedom. P_Chi Sqr reports the p-value of the S statistics. ***, ** and * denote significance at the 1, 5 and 10 per cent levels, respectively.
|
Panel A: Shanghai Stock Exchange A-share (RMB) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 191*** | 194*** | 203*** | 182*** | 137*** | 197*** | 201*** | 164*** | 169*** |
| 1 | –1 | 18 | 1 | –82*** | 6 | 6 | –60*** | –24** | |
| 2 | 12 | 16 | –84*** | 4.5 | 24** | –59*** | –20 | ||
| 3 | –7 | –104*** | –15 | 6 | –78*** | –36*** | |||
| 4 | –91*** | –16 | 14 | –75*** | –30** | ||||
| 5 | 94*** | 96*** | 22* | 47*** | |||||
| 6 | 9 | –50*** | –26** | ||||||
| 7 | –78*** | –41*** | |||||||
| 8 | 36*** | ||||||||
|
Panel B: Shenzhen Stock Exchange A-Share (RMB) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 169*** | 169*** | 176*** | 170*** | 130*** | 177*** | 177*** | 164*** | 157*** |
| 1 | 20* | 8 | 30*** | –81*** | –2 | 20* | –30*** | –5 | |
| 2 | 4 | 15 | –73*** | 13 | 14 | –54*** | –8 | ||
| 3 | 3 | –87*** | 0 | 21* | –63*** | –24** | |||
| 4 | –91*** | –12 | –1 | –72*** | –15 | ||||
| 5 | 90*** | 112*** | 56*** | 43*** | |||||
| 6 | 29*** | –54*** | –22* | ||||||
| 7 | –70*** | –36*** | |||||||
| 8 | 28** | ||||||||
- This table reports analysis of the reverse : cross (RC) ratio of the frequency measures for A-shares. The frequency measures are calculated for four different price movement patterns for each digit (i.e. F_DD (down–down), F_DU (down–up), F_UD (up–down) and F_UU (up–up)). The RC ratio is calculated as the frequencies of the reverse movements (i.e. F_DU + F_UD) over the frequencies of the cross movements (i.e. F_DD and F_UU) for each digit. Sign tests are performed to examine the statistical difference of RC ratio between digits. Sign test statistics (s-Stat) are reported. A positive s-Stat in a cell suggests that the RC ratio of the corresponding row digit is larger than that of the column digit, and vice versa. ***, ** and * denote significance at the 1, 5 and 10 per cent levels, respectively.
|
Panel A: Shanghai Stock Exchange A-share (RMB) |
||||||
|---|---|---|---|---|---|---|
| Digit | Reverse | Cross | RC | s-Stat | ||
| NT_DU (%) | NT_UD (%) | NT_DD (%) | NT_UU (%) | |||
| 0 | 111.14 | 109.87 | 122.98 | 121.17 | 0.90 | –240*** |
| 1 | 94.66 | 95.47 | 90.40 | 91.39 | 1.04 | 113*** |
| 2 | 96.36 | 97.04 | 94.09 | 94.47 | 1.02 | 85*** |
| 3 | 95.80 | 95.89 | 93.10 | 93.61 | 1.02 | 88*** |
| 4 | 94.55 | 94.08 | 90.76 | 91.15 | 1.04 | 104*** |
| 5 | 102.52 | 101.94 | 104.89 | 105.18 | 0.97 | –86*** |
| 6 | 96.34 | 96.63 | 94.44 | 94.39 | 1.02 | 66*** |
| 7 | 94.29 | 94.73 | 89.33 | 91.49 | 1.04 | 102*** |
| 8 | 99.47 | 98.53 | 99.42 | 98.76 | 1.00 | –18 |
| 9 | 94.26 | 95.04 | 89.69 | 92.09 | 1.04 | 122*** |
| S | 1065 | |||||
| P_Chi_Sqr | 0.000 | |||||
|
Panel B: Shenzhen Stock Exchange A-Share (RMB) |
||||||
|---|---|---|---|---|---|---|
| Digit | Reverse | Cross | RC | s-Stat | ||
| NT_DU (%) | NT_UD (%) | NT_DD (%) | NT_UU (%) | |||
| 0 | 110.99 | 109.52 | 123.12 | 122.78 | 0.90 | –211*** |
| 1 | 94.13 | 95.62 | 91.23 | 90.50 | 1.04 | 110*** |
| 2 | 96.12 | 97.64 | 94.39 | 94.95 | 1.02 | 50*** |
| 3 | 96.13 | 96.57 | 93.35 | 93.36 | 1.03 | 81*** |
| 4 | 95.05 | 94.95 | 90.23 | 91.91 | 1.05 | 105*** |
| 5 | 102.42 | 101.91 | 105.21 | 105.76 | 0.96 | –102*** |
| 6 | 97.13 | 97.11 | 94.77 | 94.64 | 1.02 | 65*** |
| 7 | 94.96 | 95.11 | 89.72 | 91.24 | 1.04 | 103*** |
| 8 | 99.16 | 98.57 | 100.14 | 98.38 | 0.99 | –24 |
| 9 | 94.55 | 95.35 | 90.76 | 92.14 | 1.04 | 85*** |
| S | 1029 | |||||
| P_Chi_Sqr | 0.000 | |||||
-
This table reports the analyses of number of trades (NT) of the four price movement patterns for A-shares. The standardized NT measures for four price movement patterns are calculated for each digit (i.e. NT_DD (down–down), NT_DU (down–up), NT_UD (up–down) and NT_UU (up–up)). The reverse : cross (RC) ratio is calculated as the frequencies reverse movements (i.e. NT_DU + NT_UD) over the frequencies of cross movements (i.e. NT_DD and NT_UU) for each digit. It reports medians of these measures. s-Stat is the sign test statistics (H0: the population median of the RC ratio is equal to 1). S is the pool statistics calculated based on the p-value of s-Stat in order to test the joint significance of the s-Stats.
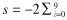 ln Pi, under the null hypothesis, S has a χ2 distribution with 2*10 degrees of freedom. P_Chi Sqr report the p-value of the S statistics. ***, ** and * denote significance at the 1, 5 and 10 per cent levels, respectively.
ln Pi, under the null hypothesis, S has a χ2 distribution with 2*10 degrees of freedom. P_Chi Sqr report the p-value of the S statistics. ***, ** and * denote significance at the 1, 5 and 10 per cent levels, respectively.
|
Panel A: Shanghai Stock Exchange A-share (RMB) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | –212.5*** | –200*** | –206.5*** | –202*** | –149*** | –188*** | –212*** | –180*** | –213*** |
| 1 | 21.5* | 34.5*** | 17.5 | 127.5*** | 52.5*** | –2.5 | 100.5*** | –7.5 | |
| 2 | –7.5 | –38*** | 104*** | 21* | –32*** | 48*** | –46*** | ||
| 3 | –20.5* | 114.5*** | 20.5* | –23.5* | 61.5*** | –34.5*** | |||
| 4 | 116*** | 26** | –4 | 84*** | –16 | ||||
| 5 | –89*** | –116*** | –60*** | –138*** | |||||
| 6 | –56*** | 47*** | –48*** | ||||||
| 7 | 93*** | 1 | |||||||
| 8 | –103*** | ||||||||
|
Panel B: Shenzhen Stock Exchange A-share (RMB) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | –198*** | –181.5*** | –188*** | –184.5*** | –143*** | –185*** | –178.5*** | –161*** | –184*** |
| 1 | 37.5*** | 24** | 0.5 | 121*** | 37*** | –4.5 | 92*** | 10 | |
| 2 | –16.5 | –43.5*** | 106.5*** | –8.5 | –37.5*** | 57.5*** | –17.5 | ||
| 3 | –12.5 | 108*** | 27** | –18.5 | 70*** | –2 | |||
| 4 | 136.5*** | 36.5*** | 4.5 | 93.5*** | 25.5** | ||||
| 5 | –121*** | –127.5*** | –59*** | –115*** | |||||
| 6 | –34.5*** | 54*** | –18 | ||||||
| 7 | 96.5*** | 16.5 | |||||||
| 8 | –69*** | ||||||||
- This table reports the analysis of the reverse : cross (RC) ratio of the standardized averaged NT measures for A-shares. The standardized NT measures are calculated for four different price movement patterns for each digit (i.e. NT_DD (down–down), NT_DU (down–up), NT_UD (up–down) and NT_UU (up–up)). The RC ratio is calculated as the standardized average number of trades of the reverse movements (i.e. NT_DU + NT_UD) over that of the cross movements (i.e. NT_DD and NT_UU) for each digit. Sign tests are performed to examine the statistical difference of the RC ratio between digits. Sign test statistics (s-Stat) are reported. A positive s-Stat in a cell suggests the RC ratio of the correspondent row digit is larger than that of the column digit, and vice versa. ***, ** and * denote significance at the 1, 5 and 10 per cent levels, respectively.
Table 2 presents the results for the analysis of the frequency of the four price movement patterns. The RC ratio is the key statistic for measuring resistance levels for each digit. Panels A and B show identical results for the two A-share markets. Digits 0 and 5 have RC ratios that are statistically larger than 1. This indicates that price endings with digits 0 and 5 are resistance points in A-share markets. The RC ratio of digit 8 is statistically indifferent from 1. This suggests when approaching digit 8, price is equally likely to reverse as to cross this price level. Therefore, digit 8 is a neutral point. Finally, the RC ratios for the rest of the digits are all significantly lower than 1. Prices ending with these digits serve as passing points, as crosses are more common than reverses.
All the RC ratios for the B-share markets suggests that no resistance point is found for any particular digit, with digits 7 and 6 having the lowest resistance levels.
In summary, there is evidence from Table 2 that suggests that cultural factors have some influence on price resistance. First, digit 8 is the only neutral point found in shares traded in renminbi. Its resistance level is only lower than those of digits 0 and 5 and is higher than other digits. Second, examining the magnitudes of the RC ratio shows that digits 4 and 7 have the lowest resistance levels. In other words, price is most likely to cross (pass) when price approaching digits 4 or 7. Digits 4 and 7 are the easiest passing points in shares traded in renminbi. Third, the culture effect found in the A-share markets is not found in the B-share markets. This further supports that cultural factors have an influence on price resistance.
Table 3 presents the pairwise comparisons of the RC ratios and shows similar results for the two A-share markets. The RC ratios for digits 0, 5 and 8 are significantly larger than those of other digits. The RC ratios for the rest of the digits have no clear order and are indifferent from each other in most cases. The RC ratio of digit 7 is lower than most digits and indifferent from that of digit 4 in both panels. For the B-share market, most RC ratios are indifferent from each other. In general, the results of Table 3 support the results of Table 2 where cultural factors were found to have a weak influence on price resistance in the A-share markets.
Table 4 presents the results for analysis of the number of trades for four price movement patterns. In contrast to the analysis shown in Table 2, the RC ratio is expected to be lower than one for a resistance point. Panels A and B show that the RC ratios of the number of trades for digits 0 and 5 are the lowest. In other words, it takes more trades to cross a price end with these digits and less trades to bounce back. The RC ratios of digit 8 are indifferent from (significantly lower than) 1 in Panel A (Panel B). This suggests that digit 8 is a weak resistance point. The RC ratios for the rest of the digits are all significantly larger than 1, which suggests that they are all passing points.
There are no resistance or passing points found in shares trading in the US dollar-denominated B-share market. The Hong Kong dollar B-share market shows a slightly different result. Digit 0 is found to be a resistance point and digits 3 and 7 are passing points. However, digits 0 and 7 are only significant at the 10 per cent level.
In summary, these results show that the price resistance of specific digits is much more profound in A-share markets than in B-share markets and, furthermore, cultural factors have some influence, albeit weak, on price resistance levels. Besides the resistance points formed by rounding bias (i.e. digits 0 and 5), digit 8 is found to have the highest resistance level among the rest of the digits.
Table 5 reports the pairwise analysis of the RC ratio for the number of trades. Panels A and B show that the RC ratios for 0, 5 and 8 are significantly lower that those of the rest of the digits. The RC ratios are indifferent from each other for most of the rest of the digits.
The results for the B-share markets show no significant results.
In overall summary, the analyses of frequency and the average number of trades of four price movement patterns confirm that the digits 0 and 5 act as resistance points and the digit 8 as a weak resistance point in the A-share markets. There is little evidence to support resistance points in the B-share markets.
6. Conclusions
The purpose of the present paper has been to examine the impact of cultural factors on both price clustering and resistance in China's stock markets. The results clearly show the impact of cultural factors with there being a higher propensity to cluster on digit 8 (along with the digits 0 and 5, which has been a common finding in most prior work on price clustering in stock markets) and a lower propensity to cluster on digits 4 and 7. The finding is further supported in an analysis of the B-share market where there are fewer Chinese investors. No cultural influence on price clustering is found in the Shanghai B-share market ($US), while only a weak cultural influence on price clustering is found in the Shenzhen B-share market ($HK) where there are more Hong Kong investors.
A range of measures show that cultural factors have a lot less influence on price resistance than price clustering. The resistance points found are the digits 0 and 5 for the A-share markets. A weak resistance point, digit 0, is found for the Shenzhen B-share market ($HK). No resistance point is found in the Shanghai B-share market ($US), although digit 0 does have the highest level of resistance compared to others. Although digit 8 cannot be considered as a resistance point in both A-share and B-share markets, its resistance level is the highest among the rest of the digits in the A-share markets. These findings suggest that cultural factors do have an, albeit weak, influence on price resistance.
In conclusion, cultural factors help to explain price clustering in Chinese financial markets and although not as strong a finding, they also have some influence on price resistance levels.
Footnotes
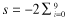 ln Pi. Under the null hypothesis, S has a χ2 distribution with 2*10 degrees of freedom. Large values of S are evidence against the null hypothesis (Cox and Hinkley, 1974).
ln Pi. Under the null hypothesis, S has a χ2 distribution with 2*10 degrees of freedom. Large values of S are evidence against the null hypothesis (Cox and Hinkley, 1974).




